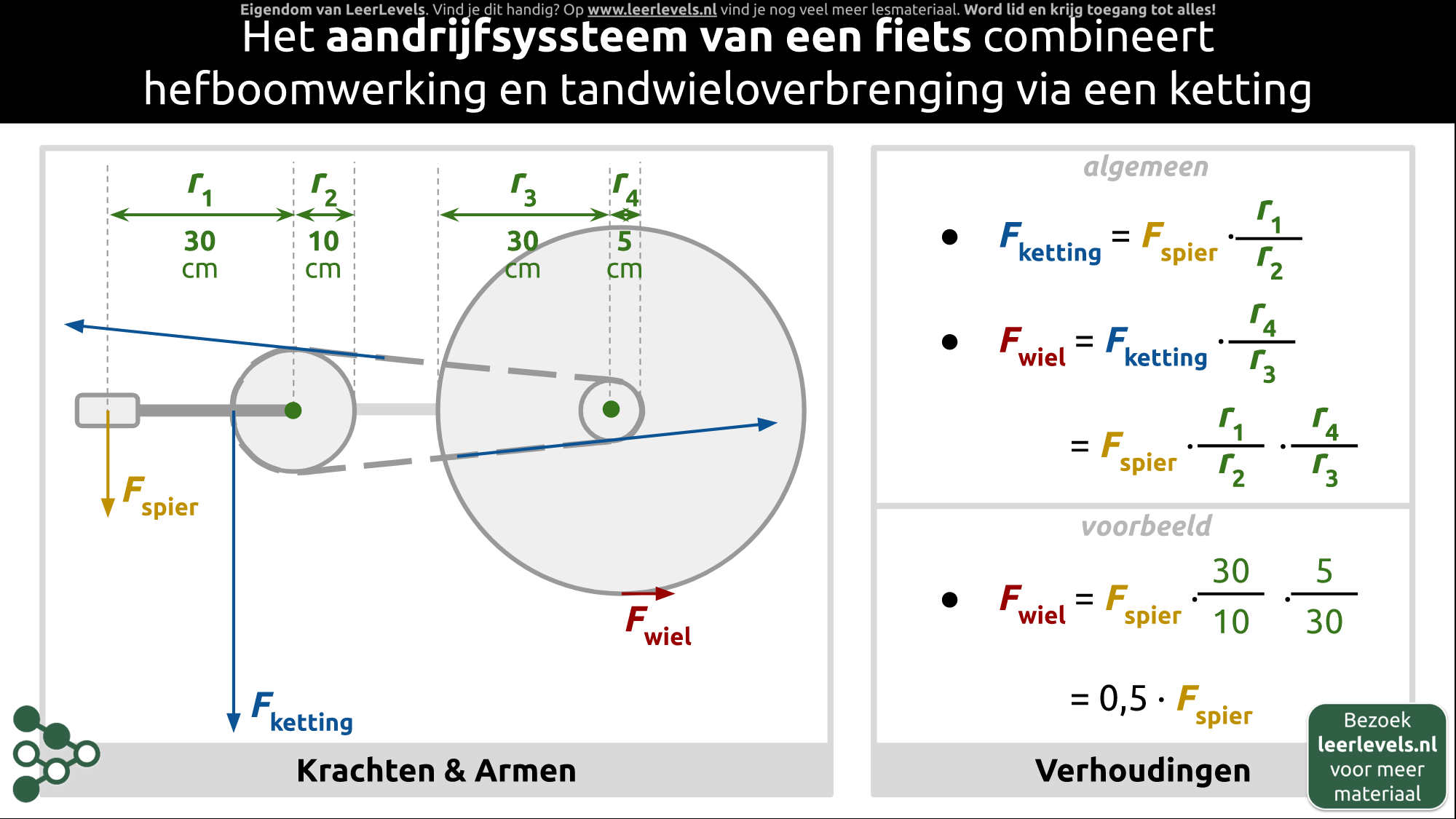
Een fiets heeft een systeem waardoor je vooruit kunt komen. Het begint allemaal bij de trappers die zijn verbonden met het achterwiel door middel van een ketting. Als je op de trappers trapt, komt er kracht vrij die er voor zorgt dat het wiel gaat draaien. Door de grootte van de tandwielen kun je met weinig kracht veel snelheid maken, maar andersom werkt het ook. Als je hard moet trappen, kun je minder snelheid maken. Als je bijvoorbeeld 50 Newton kracht uitoefent met je spieren, levert dit 25 Newton kracht op het wiel op. Dat is ongeveer de helft van wat je hebt gegeven. Dit komt doordat de kracht wordt vergroot door het gebruik van de verschillende tandwielen.

(Afbeelding: Animatie voor Aandrijfsysteem fiets)

Terug naar overzicht Meld je aan

Aantekeningen

Expert aantekeningen

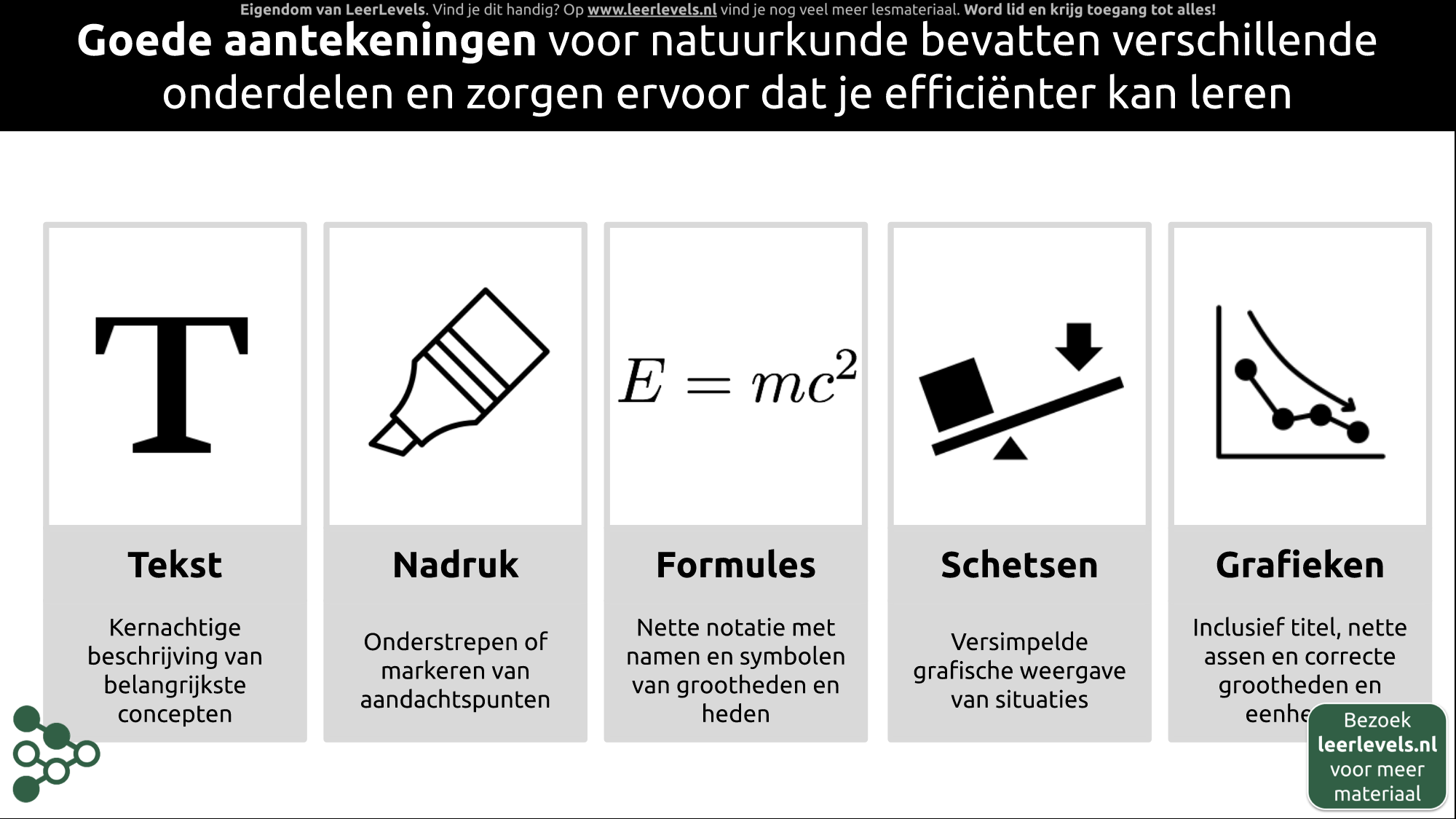
Goede aantekeningen voor natuurkunde zijn essentieel om het onderwerp effectief te leren. Ze bevatten de volgende onderdelen:

- Een tekst met een beknopte beschrijving van de belangrijkste concepten.
- Belangrijke punten, zoals formules, worden onderstreept of gemarkeerd om ze te benadrukken.
- Formules moeten netjes genoteerd worden, waarbij de symbolen en grootheden in eenheden correct worden weergegeven.
- Schetsen en afbeeldingen zeggen meer dan duizend woorden; een grafische weergave van situaties kan helpen om het begrip te vereenvoudigen.
- Grafieken dienen een duidelijke titel te hebben en moeten de grootheden en eenheden correct gebruiken.

(Afbeelding: Animatie voor Expert aantekeningen)

Terug naar overzicht Meld je aan

Aarde

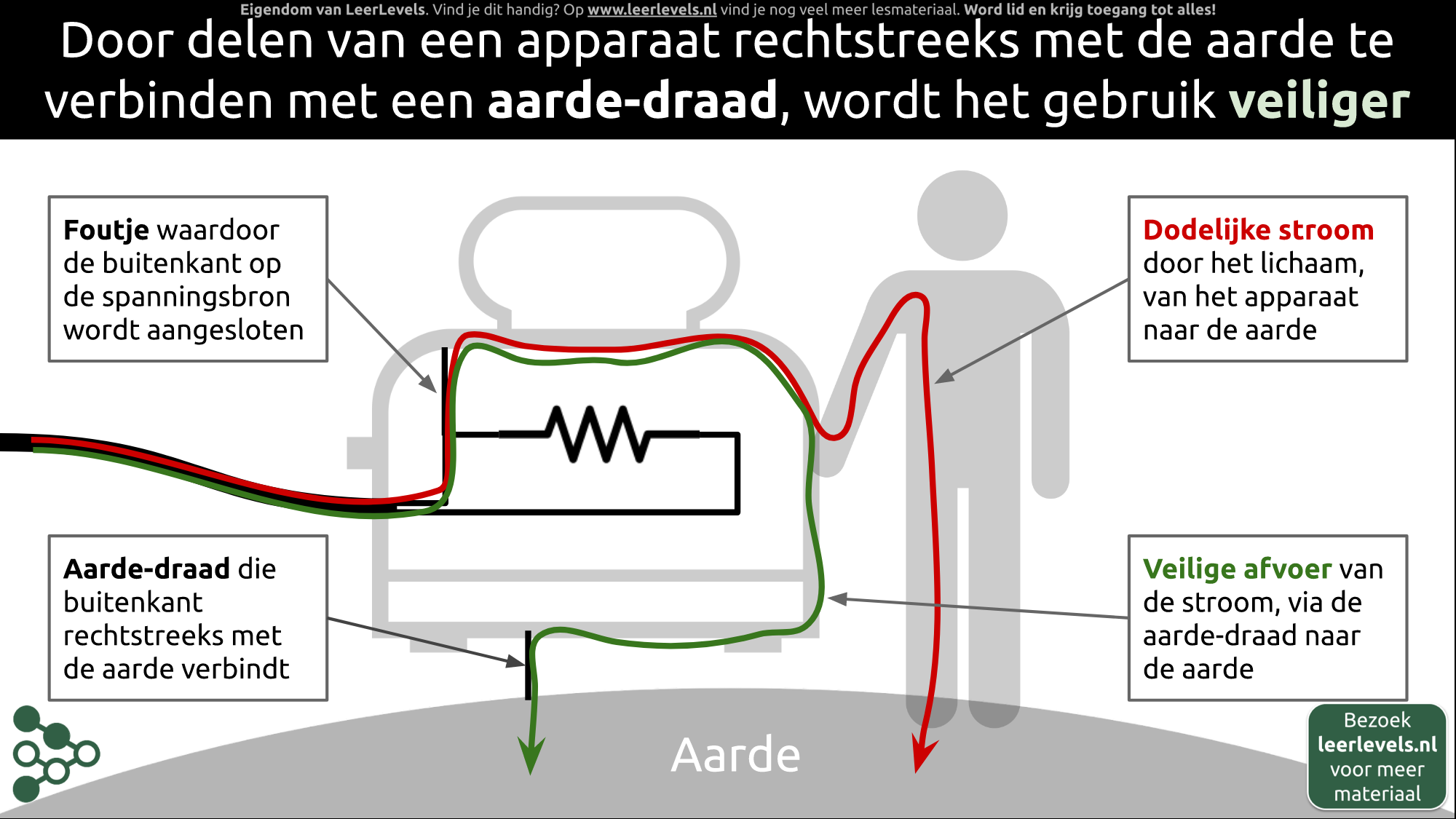
Het is belangrijk om apparaten die elektriciteit gebruiken te aarden. Dit betekent dat we een aardedraad gebruiken om de buitenkant van het apparaat direct te verbinden met de aarde. Als we dit niet doen en er ontstaat schade aan het apparaat, kan elektriciteit via de buitenkant van het apparaat ons lichaam binnenkomen en zo een levensgevaarlijke elektrische stroom veroorzaken. Door de buitenkant van het apparaat te verbinden met de aarde via de aardedraad, kan de stroom veilig via de aardedraad naar de aarde worden afgevoerd en voorkomen we dat deze door ons lichaam gaat en ons verwondt of zelfs doodt. Dit maakt het gebruik van het apparaat veiliger. We moeten altijd zorgen dat alle elektrische apparaten die we gebruiken goed zijn geaard.

(Afbeelding: Animatie voor Aarde)

Terug naar overzicht Meld je aan

Aarding

Geaard snoer

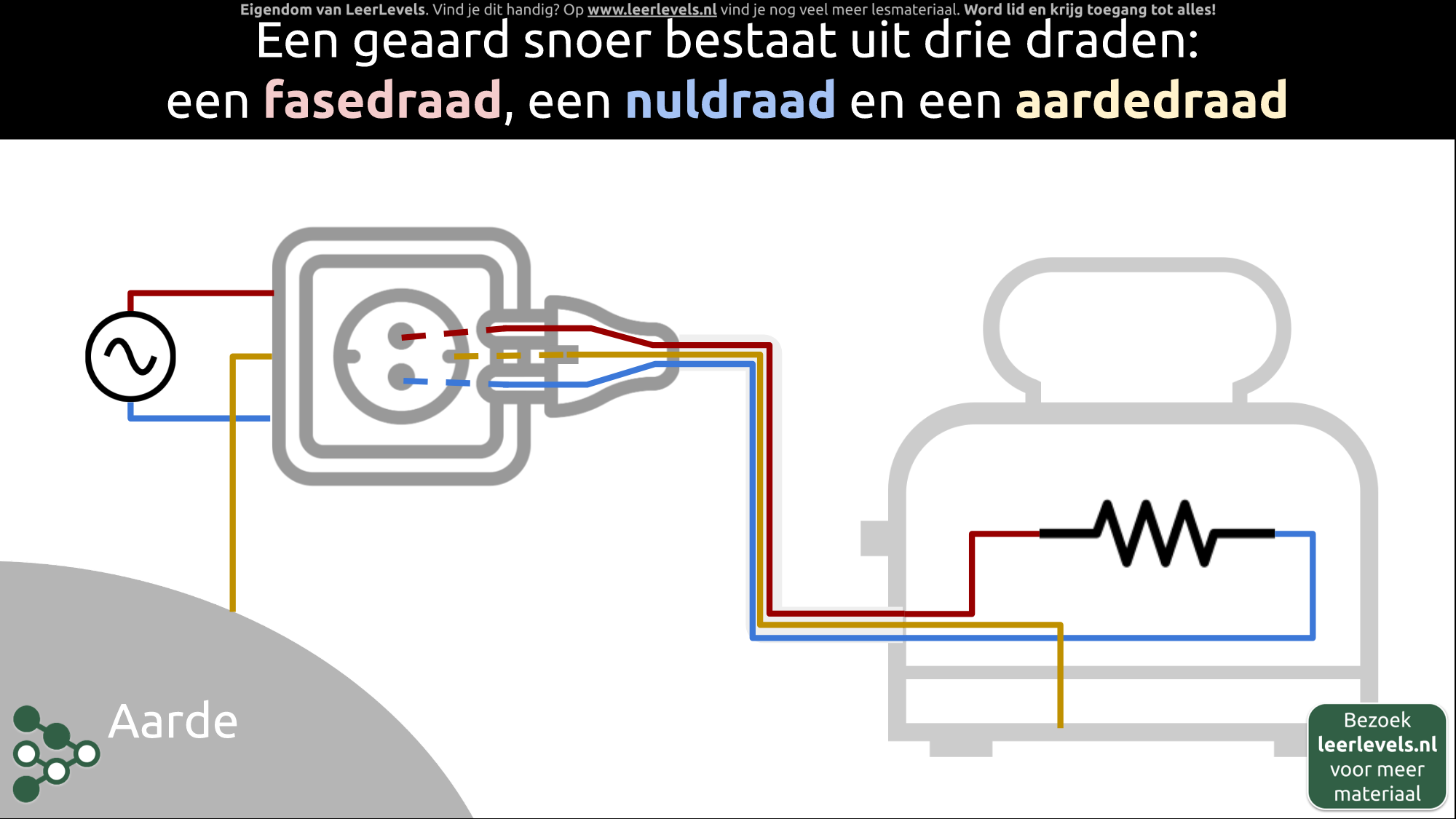
Een geaard snoer heeft drie draden: een fasedraad, een nuldraad en een aardedraad. Als je bijvoorbeeld een broodrooster aansluit op het stopcontact, verbind je de fasedraad en de nuldraad met de rood en blauwe snoeren. De aardedraad wordt gebruikt om te zorgen dat als er iets misgaat met de broodrooster, de stroom via de aarde gaat in plaats van door jou heen. Je verbindt de aardedraad met de pinnetjes aan de zijkant van het stopcontact. Het is belangrijk om nooit je handen in het stopcontact te steken, maar de pinnetjes aan de zijkant zijn veilig om aan te raken omdat ze verbonden zijn met de aarde.

(Afbeelding: Animatie voor Geaard snoer)

Terug naar overzicht Meld je aan

Aardlekschakelaar

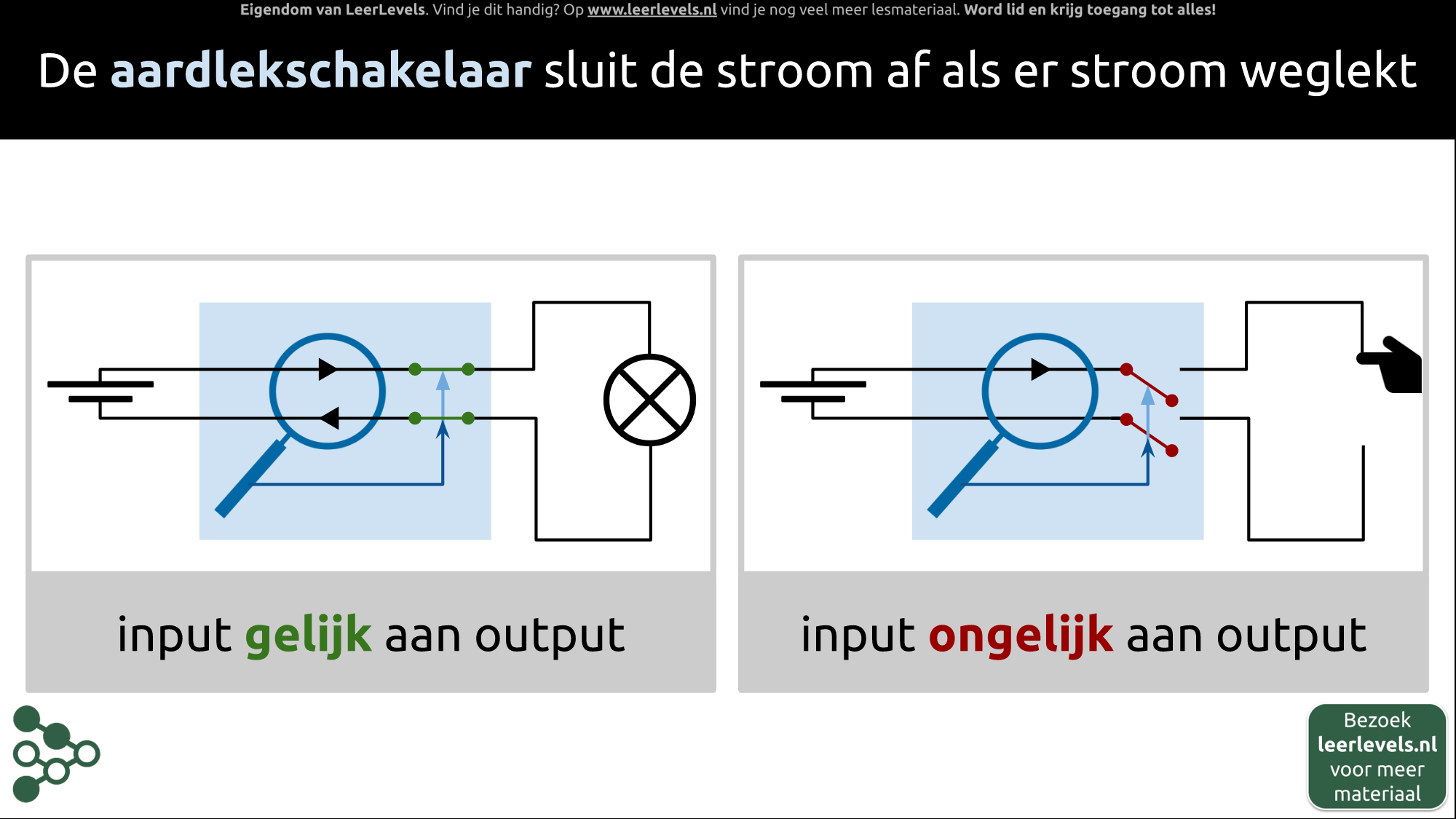
De aardlekschakelaar schakelt de stroom uit wanneer er een lek naar de aarde is. Dit gebeurt door te controleren of de input even groot is als de output; de stroom moet dus onbelemmerd kunnen doorstromen. Als er meer stroom terugkomt dan eruit gaat, zal de aardlekschakelaar de stroom uitschakelen. De functie van de aardlekschakelaar is om te controleren of de input en output gelijk zijn.

Als er niets mis is en de stroomdruk op de input en output gelijk is, zal de stroom zonder belemmering doorgaan. Wanneer de stroom naar rechts gaat maar niet terugkeert, grijpt de aardlekschakelaar in en onderbreekt de stroom, zodat er geen stroom meer kan weglekken. Dit verkleint de kans op gevaarlijke situaties.

De aardlekschakelaar werkt zeer snel en fungeert als een extra beveiligingssysteem, maar het garandeert geen volledig veilige situatie.

(Afbeelding: Animatie voor Aardlekschakelaar)

Terug naar overzicht Meld je aan

Absorptie en emissie

Absorptie en emissie concept

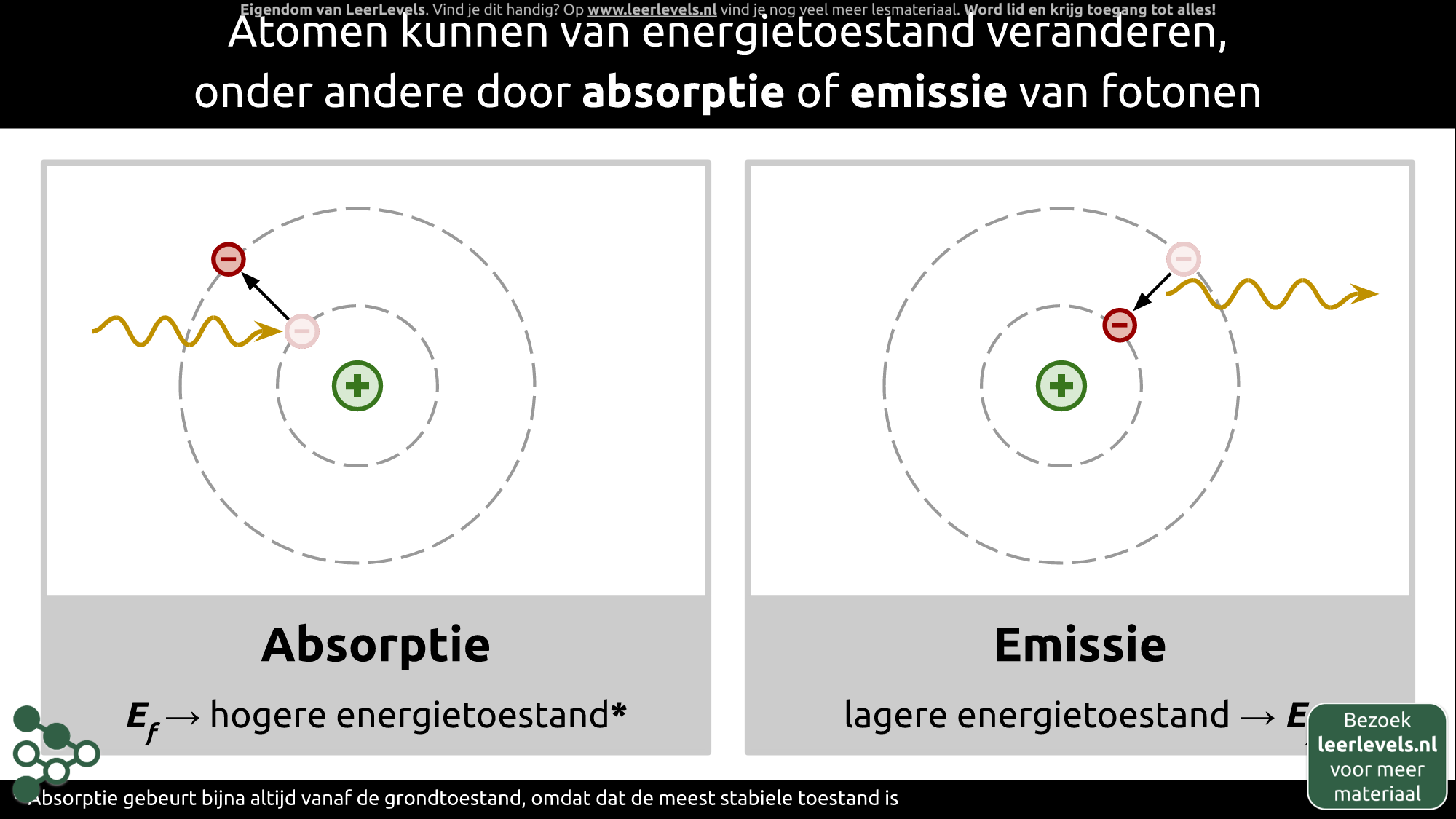
Atomen kunnen hun energietoestand veranderen door het absorberen of uitzenden van fotonen. Stel dat een atoom zich in de grondtoestand bevindt, waarbij het elektron zich in de laagste schil bevindt. Door de absorptie van een foton kan het elektron naar een hogere energietoestand worden verplaatst. Dit gebeurt vaak vanuit de grondtoestand, omdat dit de meest stabiele toestand is.

Het omgekeerde proces, namelijk emissie, is ook mogelijk. Wanneer een atoom in een aangeslagen, hoge energietoestand verkeert, kan het elektron terugvallen naar een lagere schil. Hierbij komt een foton vrij. De energie van dat foton komt overeen met het energieverschil tussen de energietoestanden.

(Afbeelding: Animatie voor Absorptie en emissie concept)

Absorptie en emissie fotonenergie

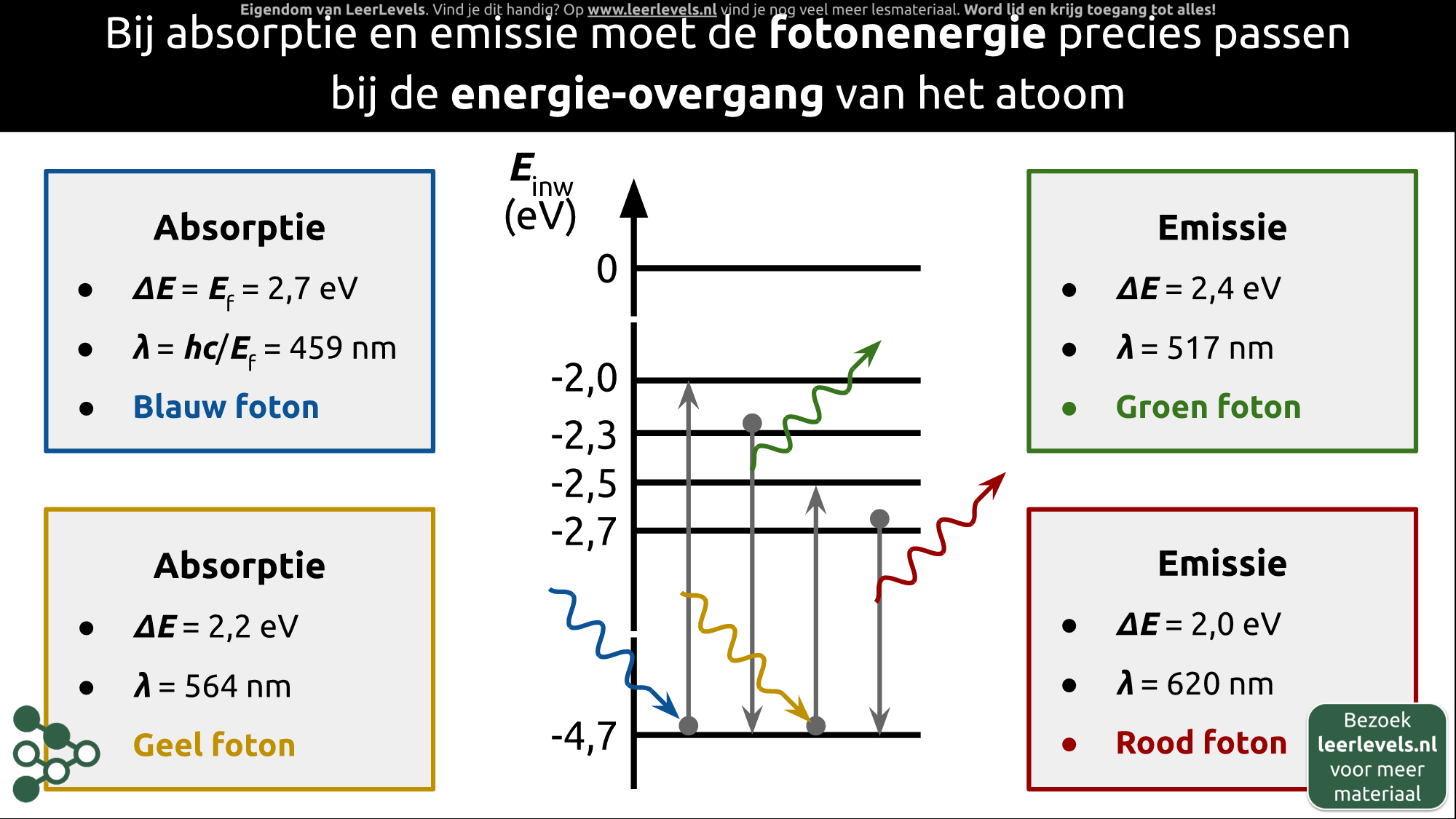
Bij absorptie en emissie moet de energie van een foton precies overeenkomen met de energie-overgang van een atoom. In dit voorbeeld gebruiken we een denkbeeldig atoom met bepaalde energieën om het uit te leggen. Als het elektron van -4,7 eV naar -2,0 eV gaat, moet er energie worden toegevoegd (door absorptie van een foton). De golflengte van dat foton kan worden berekend door te kijken naar het energieverschil, hier 2,7 eV. Met de formule λ = (h · c)/(Ef) kunnen we de golflengte berekenen. In dit geval is de golflengte 459 nm, van een blauw foton. Voor de emissie van een groen foton (golflengte van 517 nm) moet het elektron terugvallen van -2,3 eV naar -4,7 eV. Het belangrijkste is dat de energie van het foton precies past bij de energie-overgang.

(Afbeelding: Animatie voor Absorptie en emissie fotonenergie)

Absorptie- en emissiespectrum

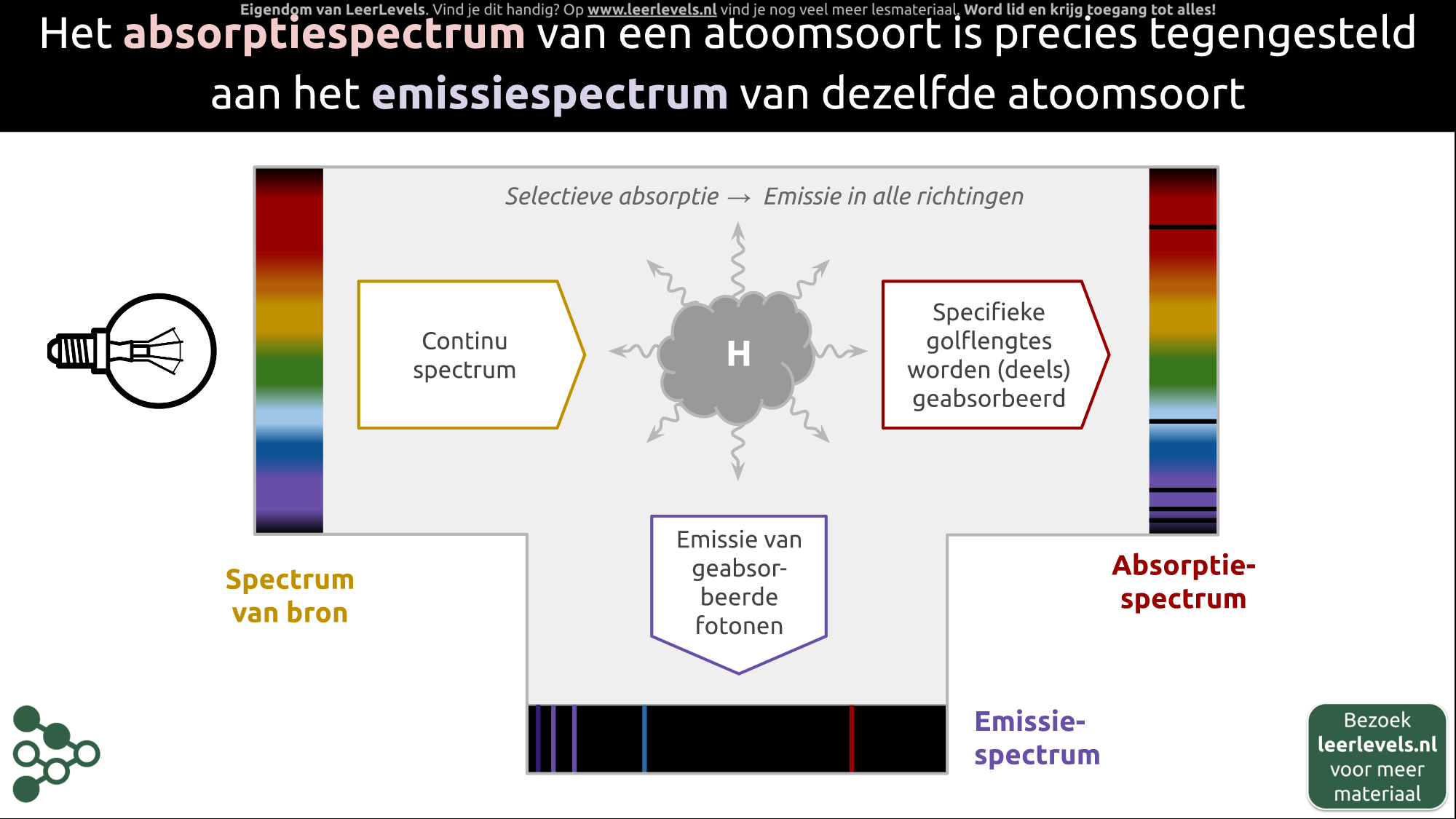
Het absorptiespectrum van een bepaalde atoomsoort is het tegenovergestelde van het emissiespectrum van diezelfde atoomsoort. Stel dat we een lichtbron observeren die een continu spectrum uitzendt, en we laten dit licht door een specifieke atoomsoort gaan, zoals waterstof. Voordat het licht het waterstof heeft gepasseerd, vertoont het een continu spectrum waarin alle kleuren aanwezig zijn. Zodra het licht echter door het waterstof beweegt, worden specifieke golflengtes geabsorbeerd, waardoor er sommige kleuren in het spectrum ontbreken. Dit komt doordat deze kleuren licht overeenkomen met energiesprongen (naar een aangeslagen toestand) in een waterstofatoom. Na de absorptie volgt er een emissie waarbij de aangeslagen toestanden terugvallen naar hun oorspronkelijke staat. Het licht dat deze emissie vrijkomt verspreidt zich niet alleen rechtdoor, maar in alle richtingen. Het resultaat is dat slechts een klein deel van het opnieuw uitgezonden licht rechtdoor gaat, met nagenoeg zwarte lijnen in het spectrum als gevolg. Onder een hoek van 90 graden zie je alleen het licht dat eerst is geabsorbeerd en daarna weer is uitgezonden. Dit wordt het emissiespectrum genoemd. Vanwege de verspreiding in alle richtingen is de intensiteit van het gedetecteerde emissiespectrum veel lager dan de intensiteit van het gedetecteerde absorptiespectrum.

(Afbeelding: Animatie voor Absorptie- en emissiespectrum)

Terug naar overzicht Meld je aan

Activiteit

Activiteit concept

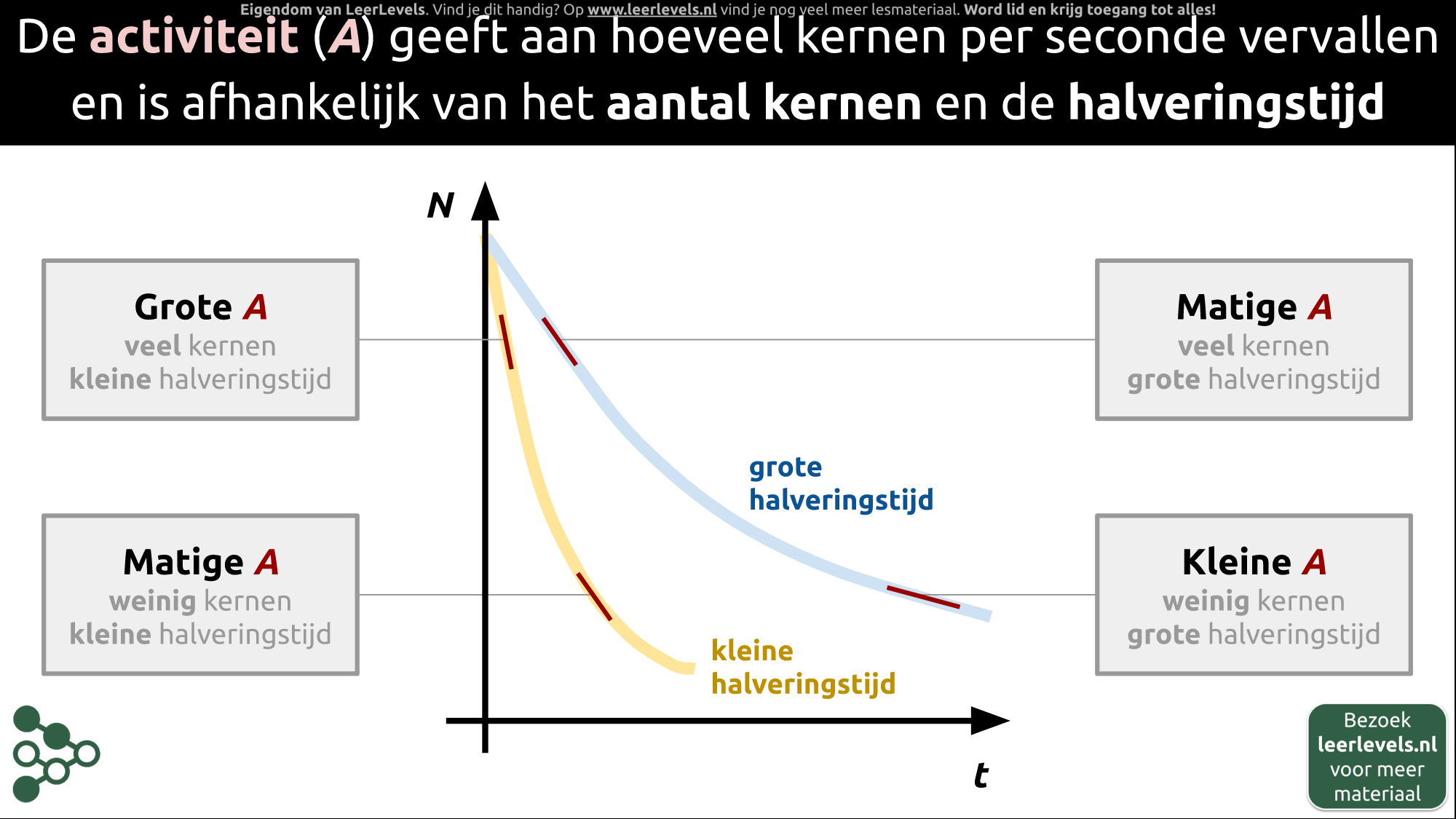
De activiteit van een atoom geeft aan hoeveel kernen per seconde vervallen en hangt af van het aantal kernen en de halveringstijd. Als we een atoom met een kleine halveringstijd bekijken, zal de activiteit aan het begin hoog zijn en snel afnemen. Dit is te zien aan de steile helling van de grafiek van het aantal kernen (N) in functie van de tijd (t). Als er minder kernen over zijn, neemt de activiteit af en wordt de helling minder steil. Bij een atoom met een grotere halveringstijd zal de activiteit aan het begin lager zijn en geleidelijk afnemen. Dit is te zien aan de geleidelijke helling van de grafiek van N in functie van t. Als er minder kernen over zijn, neemt de activiteit nog verder af en wordt de helling bijna vlak. Activiteit wordt uitgedrukt in becquerel (Bq), wat het aantal vervallende kernen per seconde aangeeft.

(Afbeelding: Animatie voor Activiteit concept)

Activiteit formules

Voor instabiele kernen zijn er drie formules om hun activiteit te berekenen:
- A0 is de beginactiviteit op tijdstip 0
- A = aantal vervallen kernen per seconde, uitgedrukt in Bequerel (Bq)
- t is de verstreken tijd in seconden
- t½ is de halveringstijd in seconden
- dN/dT is de helling van de raaklijn in een Nt-diagram
Het min-teken is nodig omdat een afnemend aantal kernen juist een positieve activiteit betekent. In de formules wordt verder gebruik gemaakt van:
- t voor de tijd in seconden
- N voor het huidige aantal kernen
- ln(2), oftewel het natuurlijk logaritme van 2, wat ongeveer 0,6931 is.

(Afbeelding: Animatie voor Activiteit formules)

Terug naar overzicht Meld je aan

Adhesie

Adhesie en cohesie

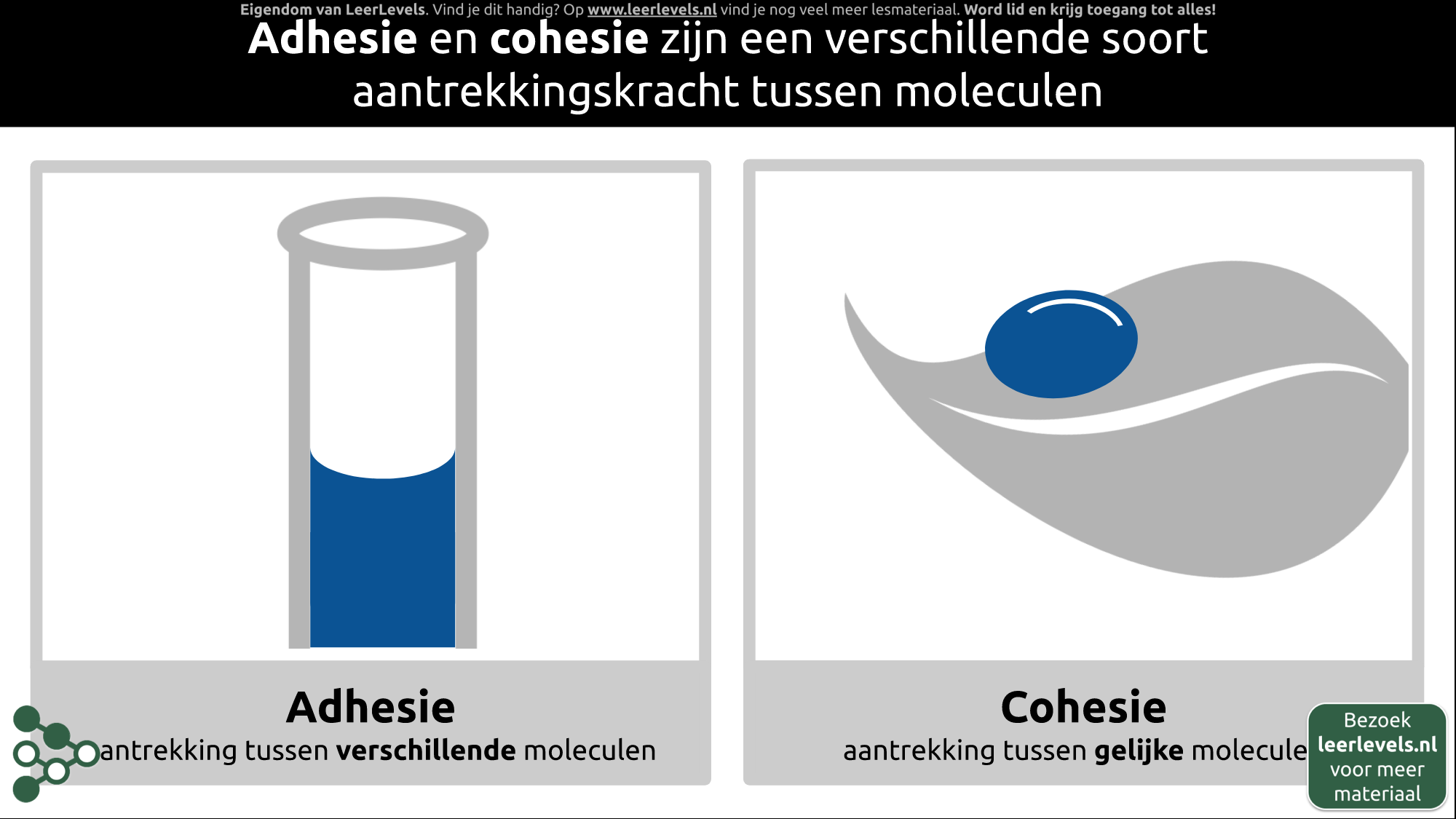
Adhesie en cohesie zijn verschillende soorten aantrekkingskrachten tussen moleculen. Adhesie verwijst naar de aantrekkingskracht tussen uiteenlopende soorten moleculen. Een voorbeeld hiervan is te zien wanneer je naar een reageerbuis met water kijkt en merkt dat het water naar het glas toe trekt. Hierdoor ontstaat er een bolle meniscus, wat het resultaat is van de aantrekkingskracht tussen het glas en het water.

Cohesie daarentegen betreft de aantrekkingskracht tussen gelijke moleculen. Dit is zichtbaar bij waterdruppels die aan elkaar blijven kleven en elkaar aantrekken, waardoor ze als mooie bolletjes op een blad liggen. Kortom, bij adhesie treedt de aantrekkingskracht op tussen verschillende moleculen, terwijl bij cohesie deze kracht zich voordoet tussen gelijke moleculen.

(Afbeelding: Animatie voor Adhesie en cohesie)

Terug naar overzicht Meld je aan

Afmetingen

Afmetingen uit figuren halen

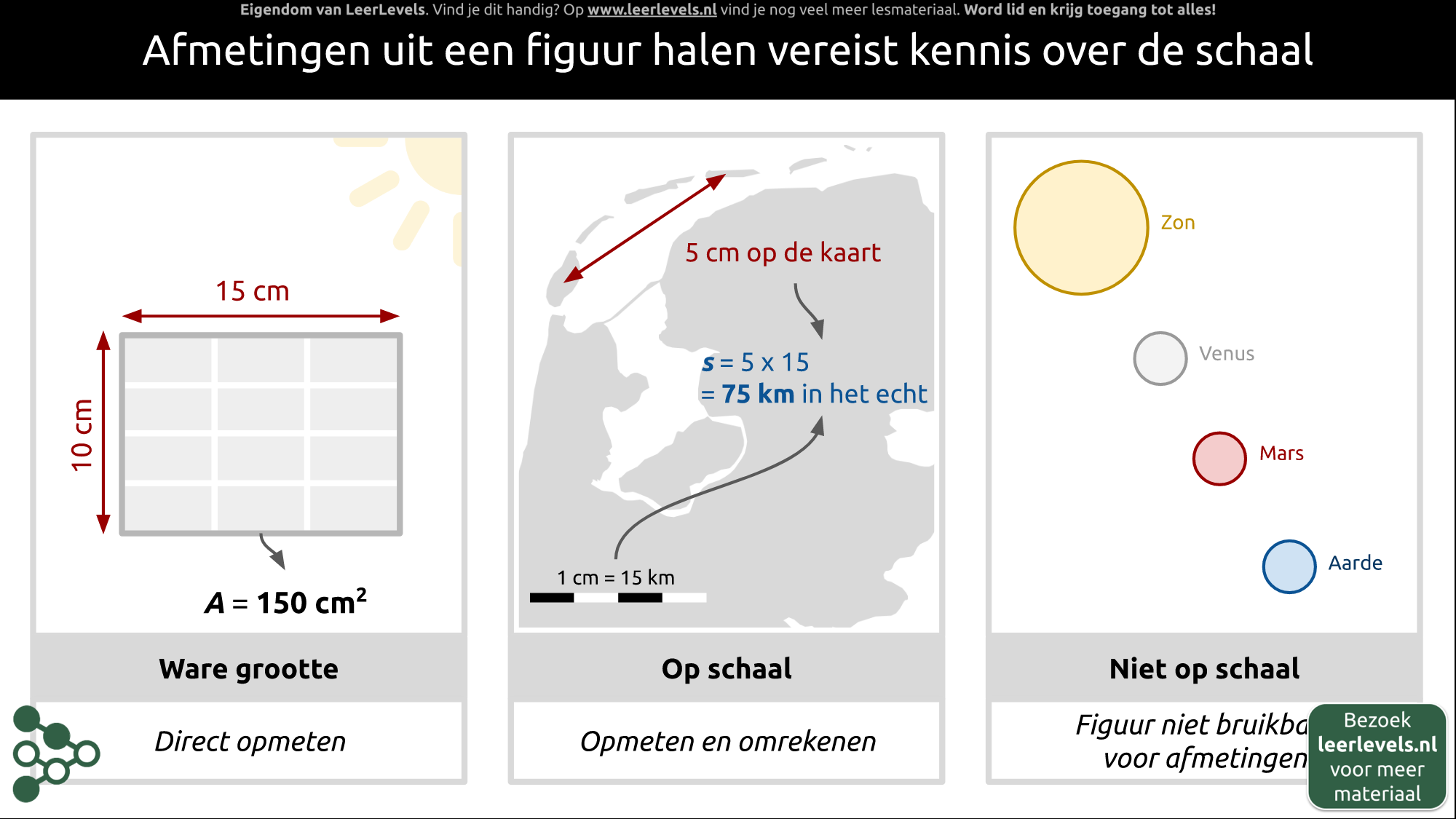
Als je afmetingen wilt halen uit een figuur, moet je weten welke schaal er gebruikt is. Als het figuur op ware grootte is, kun je direct de afmetingen meten en berekenen. Bij tekeningen op schaal, zoals een kaart, moet je eerst de schaalverdeling bekijken. Voor afstanden moet je de afstand op de kaart meten en omrekenen naar de werkelijke afstand. Bij afbeeldingen van planeten is de schaal niet bruikbaar en moet je informatie zoeken in tabellen met de juiste gegevens.

Voorbeeld: Als op een kaart de afstand tussen Texel en Ameland 5 cm is en de schaal is 15 km per cm, dan is de werkelijke afstand 5 cm x 15 km/cm = 75 km.

(Afbeelding: Animatie voor Afmetingen uit figuren halen)

Terug naar overzicht Meld je aan

Afstand

Afstand concept

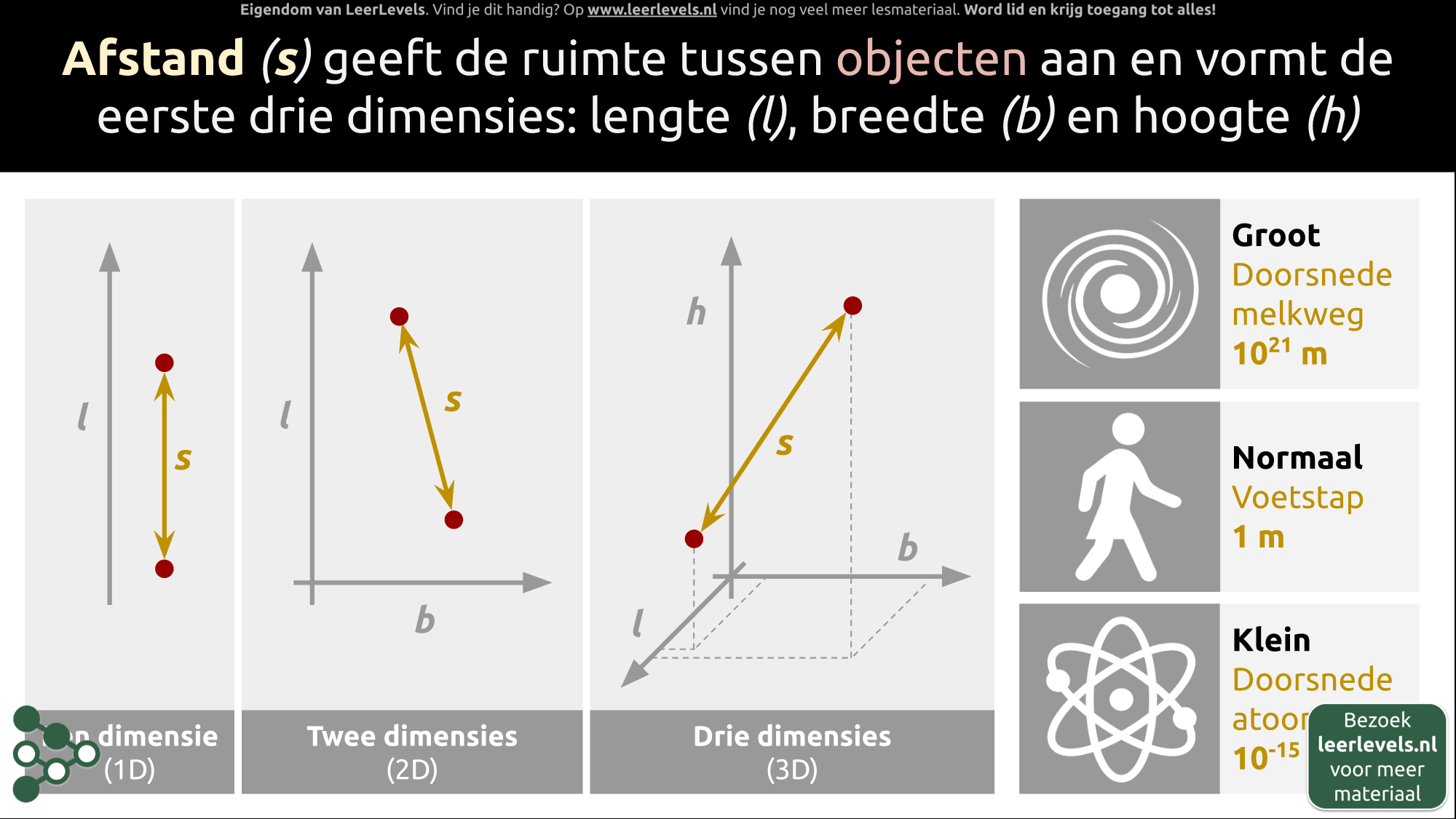
Afstand betekent de ruimte tussen objecten en heeft drie dimensies: lengte, breedte en hoogte. In één dimensie is afstand de afstand tussen twee punten in lengte. In twee dimensies, dus in lengte en breedte, is er ook afstand tussen twee punten. In drie dimensies is er een extra dimensie van hoogte. Afstand tussen objecten kan worden aangegeven met een pijl, maar hoe het precies gemeten wordt hangt af van de situatie. De afstand is altijd de ruimte tussen die objecten. Afstanden kunnen in de natuur heel groot of heel klein zijn. Bijvoorbeeld, de doorsnede van een atoomkern is ongeveer 10⁻¹⁵ meter, een flinke voetstap is ongeveer één meter en de doorsnee van onze melkweg is 10²¹ meter. Deze afstanden zijn altijd meetbaar als ruimtes tussen objecten.

(Afbeelding: Animatie voor Afstand concept)

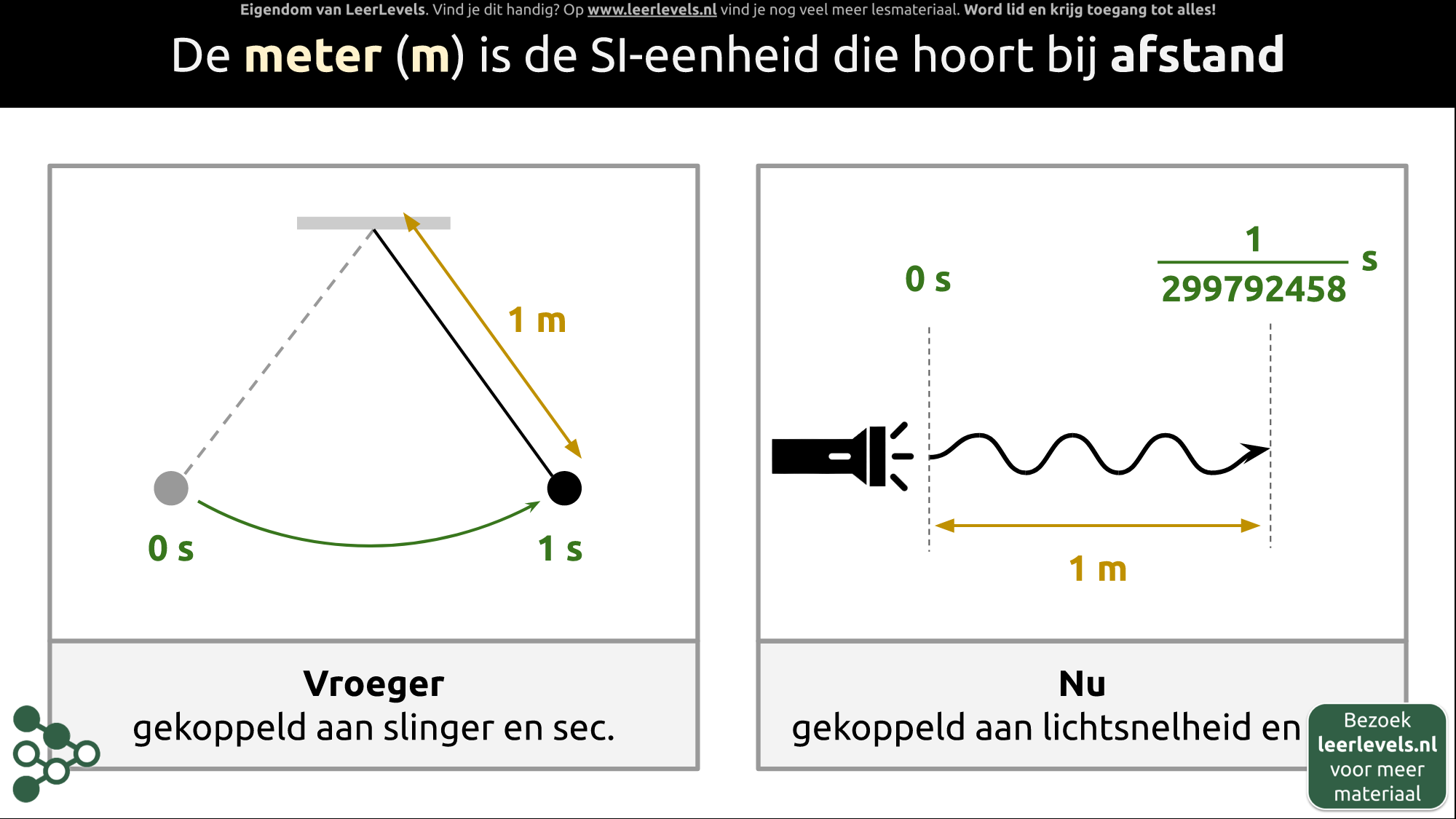
Eenheid meter

Een meter is de maat voor afstand en deze lengte is afgesproken tussen mensen. Vroeger werd de meter bepaald met een slinger die heen en weer bewoog tussen twee uitersten en precies één meter lang was. Maar deze methode bleek niet altijd betrouwbaar omdat de slinger zich anders gedroeg op een berg dan beneden in een dal. Nu wordt de meter gekoppeld aan de snelheid van licht en een seconde is erg kort. Als het licht vertrekt op tijdstip nul, is het precies 1 meter verder na 1/299792458 seconde. Dit is nu de definitie van een meter en het is altijd precies even lang, overal ter wereld.

(Afbeelding: Animatie voor Eenheid meter)

Terug naar overzicht Meld je aan

Algemene gaswet

Algemene gaswet formule

De algemene gaswet gaat over hoe druk, volume en temperatuur van gas zich verhouden. Als je een gas bij een hogere temperatuur hebt, zal de druk hoger zijn en/of zal het gas meer ruimte innemen. De algemene gaswet kan worden afgeleid uit de wet van Boyle of de ideale gaswet.

De wet van Boyle zegt dat p1 x v1 = p2 x v2. De uitbreiding daarvan is dat p x v / t altijd hetzelfde is. Dus als je de druk vermenigvuldigt met het volume en dat dan deelt door de temperatuur, krijg je steeds dezelfde waarde. Let op: temperatuur moet in Kelvin worden gebruikt.

De ideale gaswet zegt dat p x V = n x R x T. Als je dat opschrijft als p x V / T = n x R, dan is dat ook een constante waarde. Dit geldt als de gasconstante en het aantal mol constant blijven. Dit leidt weer tot dezelfde formule: p1 x V1 / T1 = p2 x V2 / T2. Dat is dus de algemene gaswet.

(Afbeelding: Animatie voor Algemene gaswet formule)

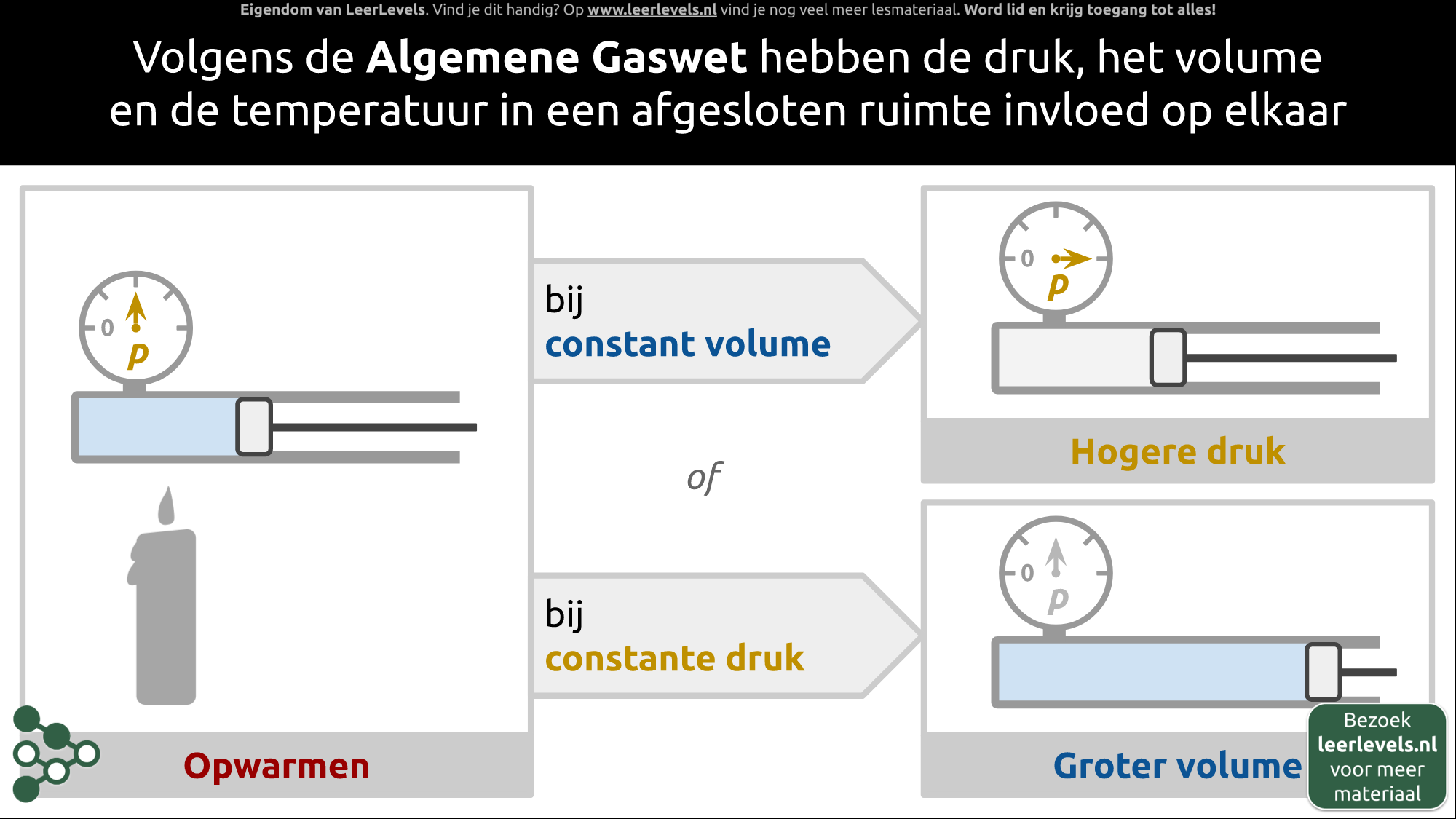
Algemene gaswet concept

De algemene gaswet zegt dat de druk, het volume en de temperatuur van een afgesloten ruimte elkaar beïnvloeden. Als we een zuiger gebruiken als voorbeeld en deze opwarmen met een kaarsje, zijn er twee mogelijkheden. Als we het volume constant houden, zal de druk toenemen omdat de deeltjes in de zuiger sneller gaan bewegen. Als we de zuiger de vrijheid geven om te bewegen, blijft de druk constant, maar zal het volume toenemen door de warmere deeltjes die meer ruimte nodig hebben om te bewegen. Veranderingen in temperatuur beïnvloeden dus de druk en het volume, afhankelijk van wat we constant houden. De algemene gaswet benadrukt dat deze grootheden onlosmakelijk met elkaar verbonden zijn.

(Afbeelding: Animatie voor Algemene gaswet concept)

Rekenen met de algemene gaswet

Om de algemene gaswet toe te passen voor een ballon die opwarmt in de zon, kan je de volgende vijf stappen volgen:

1. Stel de vraag: "Wat wordt het nieuwe volume van de ballon?"
2. Noteer de gegeven waarden: V1 = 10 L, T1 = 283 K en T2 = 313 K. De druk p blijft gelijk.
3. Gebruik de formule V2 = V1 · (T2/T1) om het nieuwe volume V2 te berekenen. Dit komt neer op V2 = 10 L · (313 K/283 K), wat gelijk is aan 11 L.
4. Vul de waarden in de formule in: V1, T1 en T2.
5. Geef het antwoord: het nieuwe volume van de ballon is 11 L.

Bij deze berekening is de formule V2 = V1 · (T2/T1) gebruikt en zijn de gegeven grootheden ingevuld. Het antwoord van 11 L lijkt logisch, gezien de ballon opwarmt en dus zal uitzetten. De significantie en eenheid van het antwoord zijn respectievelijk één decimal en liter.

(Afbeelding: Animatie voor Rekenen met de algemene gaswet)

Terug naar overzicht Meld je aan

Amplitude

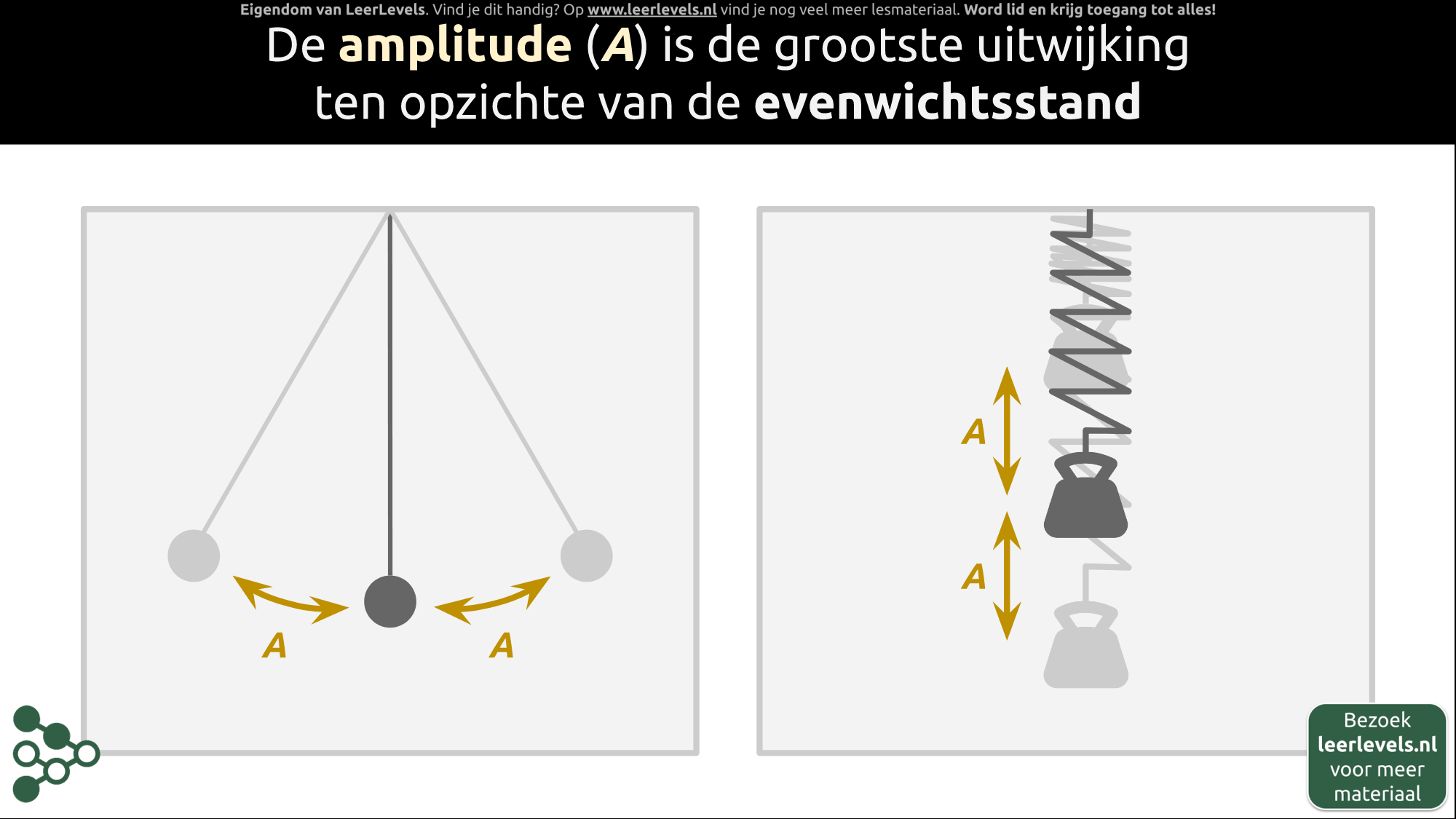
De amplitude (A) is de maximale uitwijking ten opzichte van de evenwichtsstand. Bij een slinger bevindt de evenwichtsstand zich in het midden. De amplitude is de afstand van de evenwichtsstand tot een van de uiterste standen, en dit geldt voor beide kanten.

In een massa-veer-systeem is er ook een evenwichtsstand. De amplitude is de afstand van de evenwichtsstand tot de onderste uiterste stand. Hetzelfde geldt voor de afstand van de evenwichtsstand tot de bovenste uiterste stand.

(Afbeelding: Animatie voor Amplitude)

Terug naar overzicht Meld je aan

Ampère

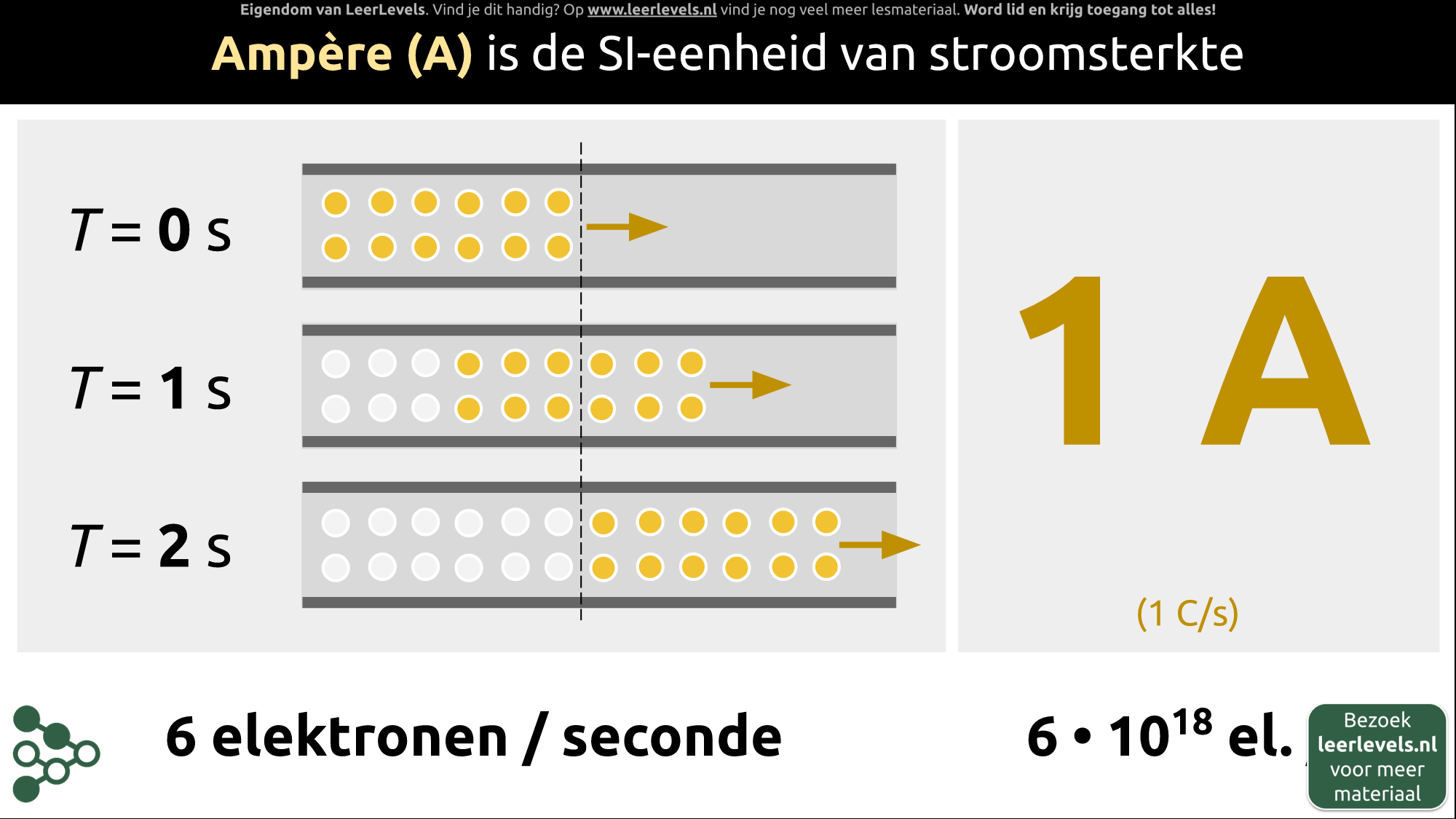
Ampère is de officiële eenheid van stroomsterkte. Stel je voor dat je naar verschillende toestanden van een draad kijkt. Op tijdstip t = 0 bevinden zich twaalf ladingen in de draad. Een seconde later zijn zes van die ladingen verschoven. Nog een seconde later bevinden alle twaalf ladingen zich op dezelfde lijn. Elke seconde stromen er zes elektronen voorbij.

Wanneer we het hebben over een stroom van één ampère, oftewel één coulomb per seconde, gaat het niet om zes elektronen per seconde, maar bewegen er 6 × 10¹⁸ elektronen per seconde. Dat zijn ontzettend veel ladingen.

(Afbeelding: Animatie voor Ampère)

Terug naar overzicht Meld je aan

Annihilatie

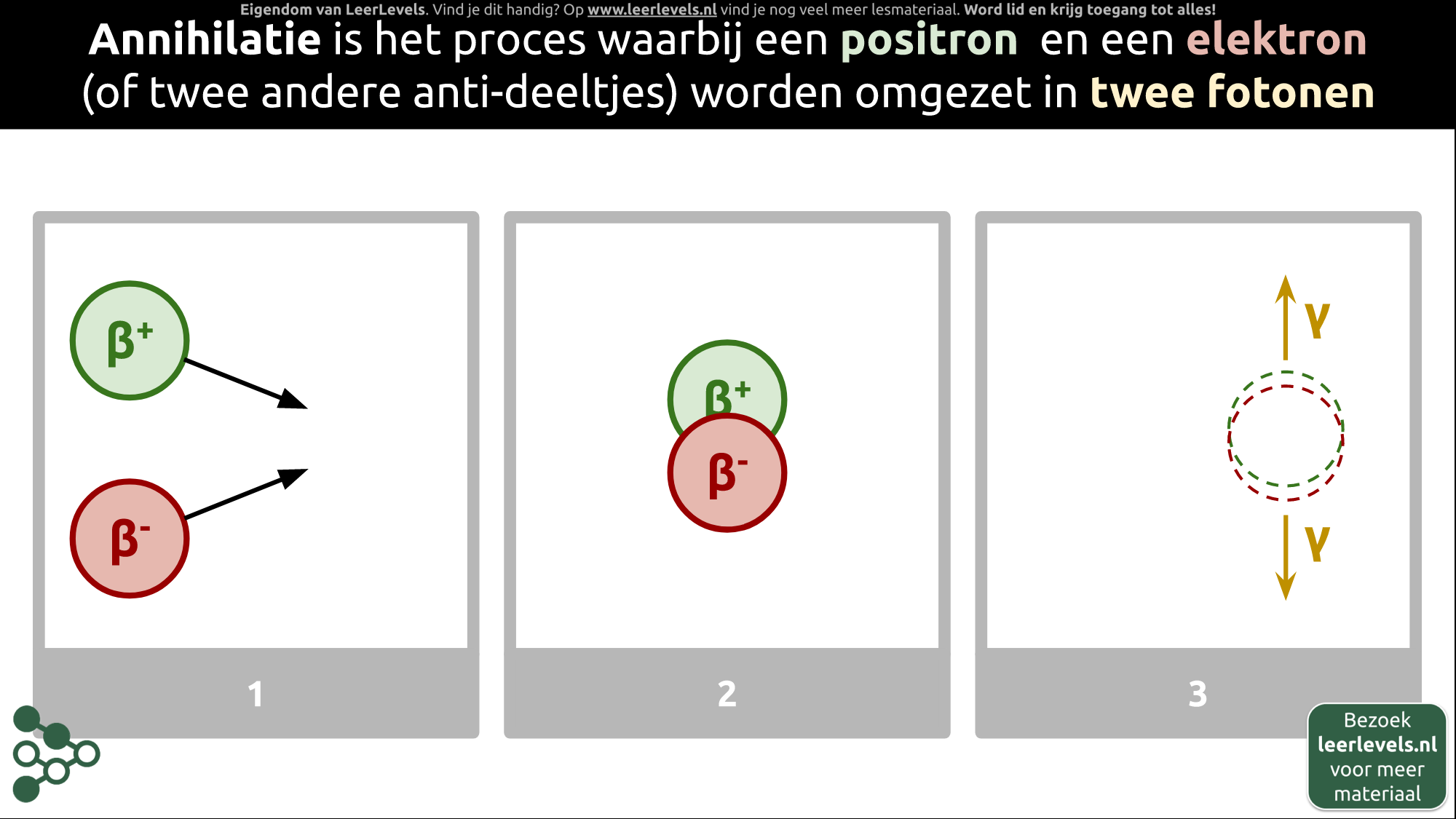
Annihilatie is het proces waarbij een positron en een elektron (of twee andere anti-deeltjes) omgezet worden in twee fotonen. Dit betekent dat als een positron en een elektron elkaar tegenkomen, ze verdwijnen en er twee fotonen ontstaan die in tegengestelde richting bewegen. Dit komt doordat de energie van de deeltjes, die ze hadden in de vorm van massa, behouden blijft en wordt omgezet in energie in de vorm van fotonen. Positronen en elektronen zijn elkaars antideeltjes, wat betekent dat ze samen kunnen annihileren.

(Afbeelding: Animatie voor Annihilatie)

Terug naar overzicht Meld je aan

Arbeid

Arbeid concept

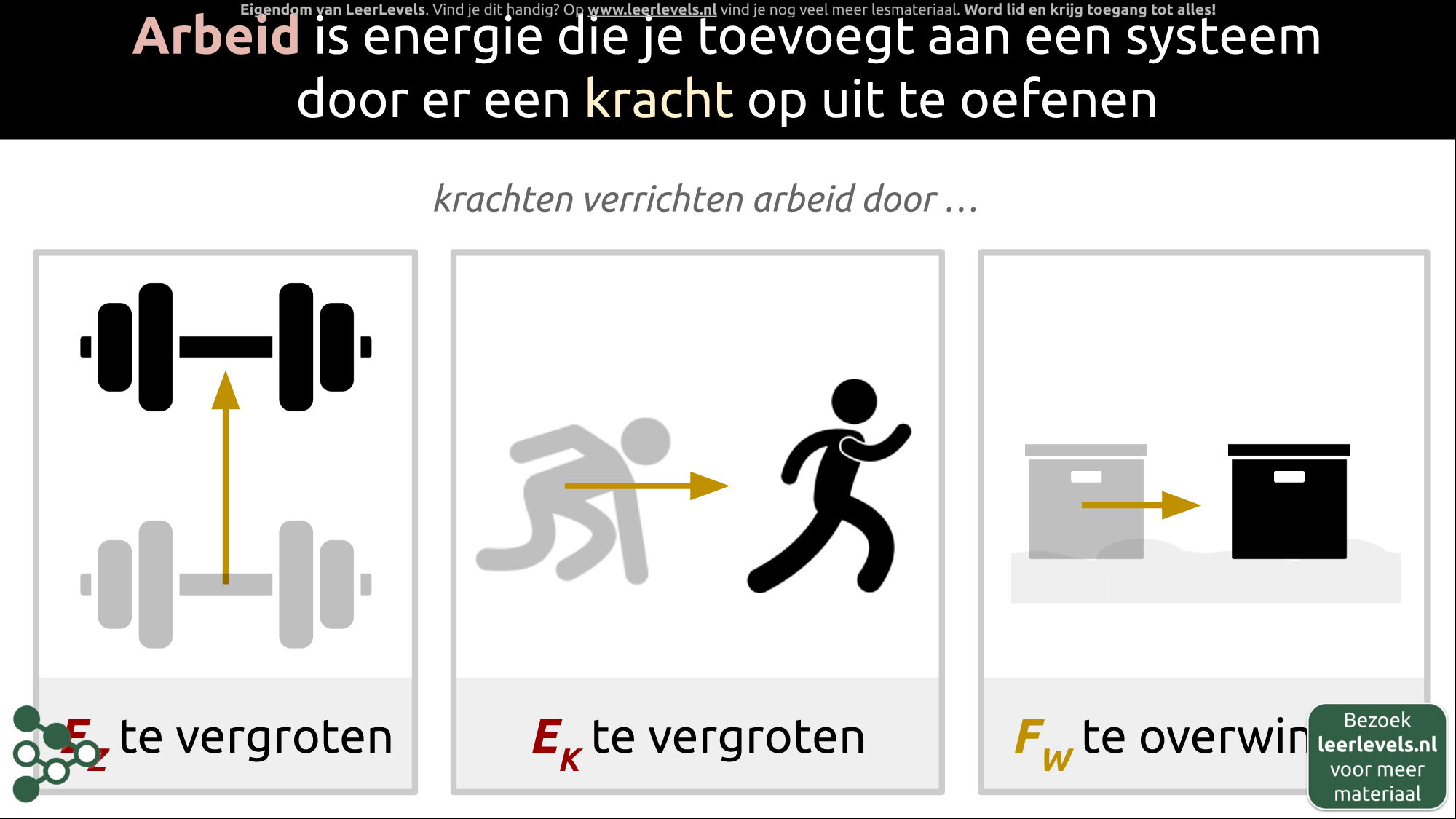
Arbeid is de energie die je toevoegt aan een systeem door er kracht op uit te oefenen. Krachten kunnen op verschillende manieren arbeid verrichten:

1. Verhogen van zwaarte-energie: Wanneer je energie toevoegt aan een systeem in de vorm van zwaarte-energie, moet je bijvoorbeeld je spieren gebruiken om iets op te tillen. Hierbij verricht je arbeid door moeite te doen om het gewicht omhoog te krijgen. Deze inspanning wordt omgezet in zwaarte-energie.

2. Verhogen van kinetische energie: Stel dat je een sprinter bent en kracht zet om jezelf te versnellen en een bepaalde snelheid te bereiken. Hierbij verrichten je spieren arbeid. De energie die je gebruikt, wordt omgezet in de kinetische energie van je lichaam. Omdat energie niet verloren kan gaan, wordt deze efficiënt overgedragen.

3. Overwinnen van wrijvingskracht: Als je een doos wilt verschuiven over een ruw oppervlak zoals zand, kost het kracht om de doos voort te duwen. Hierbij moet je de wrijvingskracht overwinnen. Meestal wordt de arbeid die je verricht omgezet in warmte door de wrijving.

(Afbeelding: Animatie voor Arbeid concept)

Arbeid formule

De arbeid die door een kracht wordt verricht, is recht evenredig met zowel de grootte van de kracht als de afstand waarover de kracht wordt uitgeoefend. Dit kan in formulevorm worden weergegeven als

W = F · s

waarbij W staat voor arbeid in joule (J), F voor kracht in newton (N), en s voor de afstand in meters (m). Het symbool W voor arbeid komt van het Engelse woord "work".

(Afbeelding: Animatie voor Arbeid formule)

Arbeid en zwaarte-energie

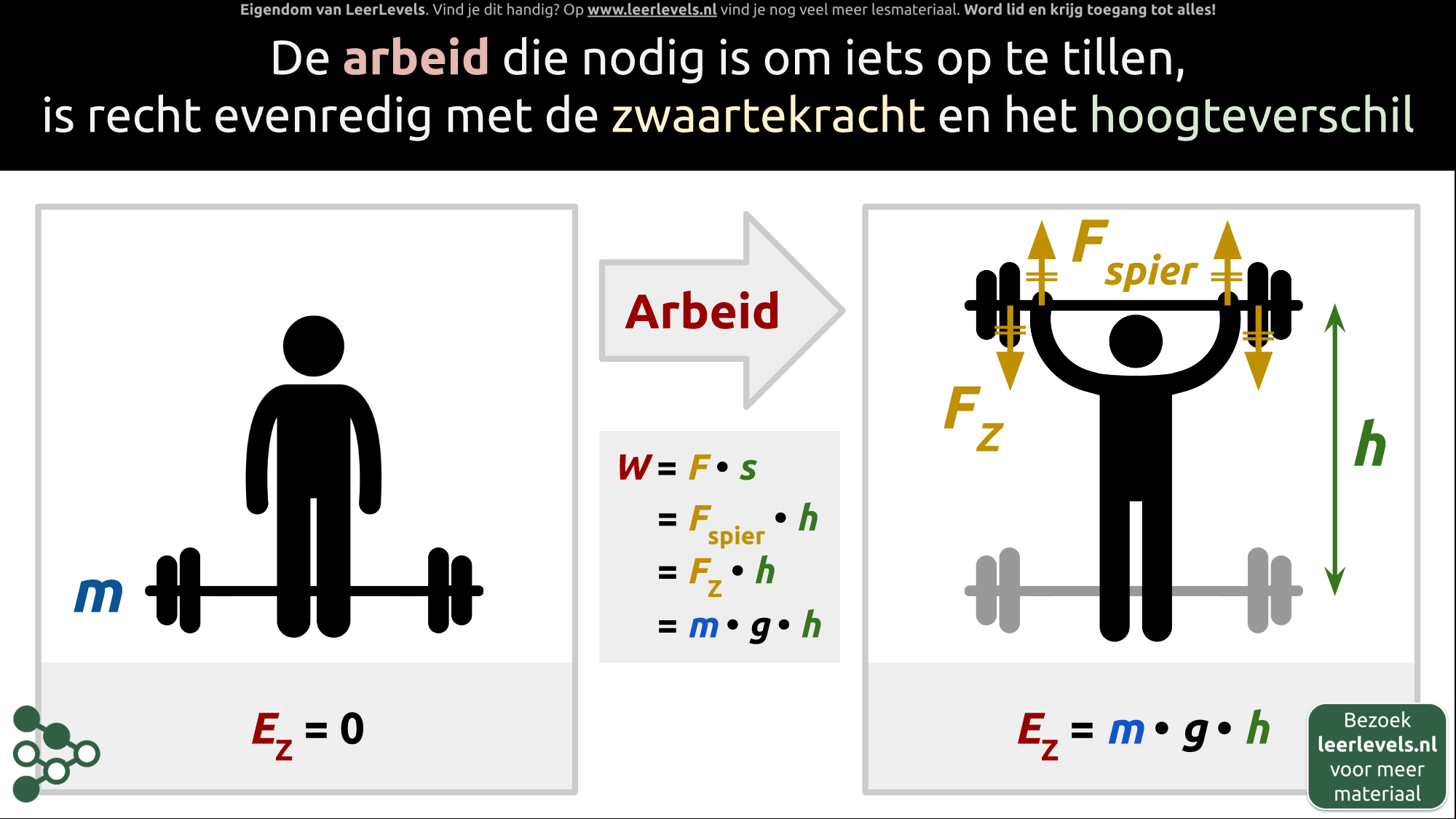
De arbeid die nodig is om iets op te tillen, is recht evenredig met de zwaartekracht en het hoogteverschil. Laten we eens kijken naar een persoon met een halter met massa m. Zolang deze halter op de grond ligt, is er geen sprake van zwaarte-energie, omdat het niet kan vallen. Zodra de halter wordt opgetild tot een bepaalde hoogte, ontstaat er zwaarte-energie. Door het tillen met spierkracht is arbeid verricht.

De grootte van deze arbeid kan berekend worden. Voor elke arbeid geldt: arbeid is kracht maal afstand, oftewel W = F · s. In dit geval is de kracht de spierkracht die de halter omhoog tilt, en de afstand is de hoogte h waarop de halter zich bevindt. Dit kan dus worden opgeschreven als W = Fspier · h.

De spierkracht moet gelijk zijn aan de zwaartekracht, omdat de spierkracht nodig is om de zwaartekracht te overwinnen. Dus, we kunnen ook noteren: W = Fz · h. Voor de zwaartekracht op een voorwerp geldt dat deze gelijk is aan de massa maal de valversnelling: Fz = m · g, waarbij g ongeveer 10 N/kg of 10 m/s² is. De zwaarte-energie is dus gelijk aan m · g · h.

(Afbeelding: Animatie voor Arbeid en zwaarte-energie)

Arbeid en kinetische energie

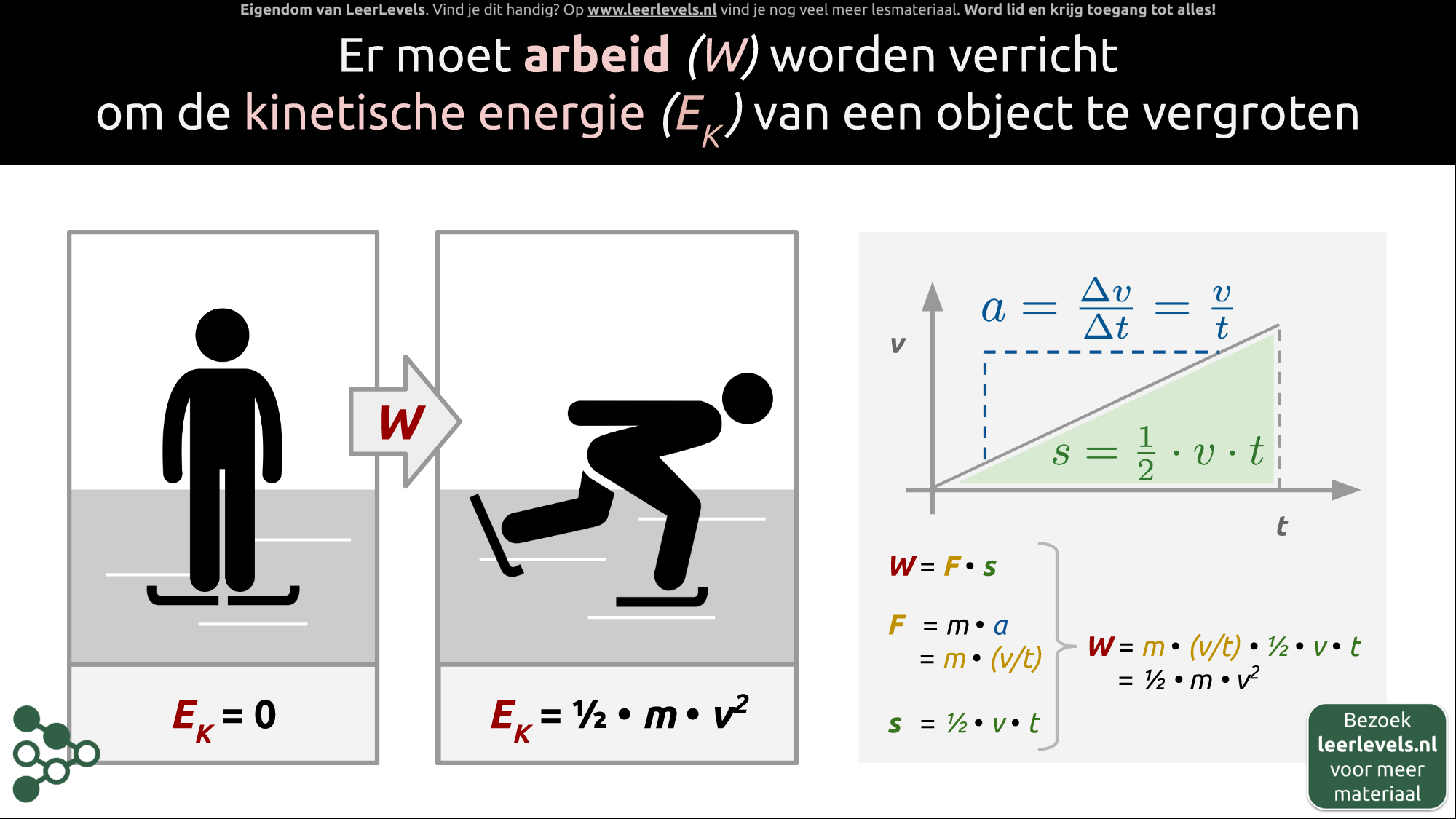
Om de kinetische energie (EK) van een object te vergroten, moet er arbeid (W) worden verricht. Stel dat een schaatser stilstaat; in dat geval heeft de schaatser geen snelheid en dus geen kinetische energie. Wanneer de schaatser arbeid verricht, komt hij in beweging. Om de toename van de kinetische energie van de schaatser te bepalen, beginnen we met de formule voor arbeid:

W = F · s

Om de afgelegde afstand te bepalen, kijken we naar de oppervlakte onder het (v,t)-diagram. We nemen aan dat de snelheid van de schaatser lineair toeneemt. De afgelegde afstand is dan gegeven door:

s = ½ · v · t

Voor de kracht geldt:

F = m · a = m · v/t

Als we nu alle formules combineren, krijgen we:

W = m · v/t · ½ · v · t

Dit vereenvoudigt tot:

W = ½ · m · v²

De verrichte arbeid is dus gelijk aan de verandering in de kinetische energie van de schaatser.

(Afbeelding: Animatie voor Arbeid en kinetische energie)

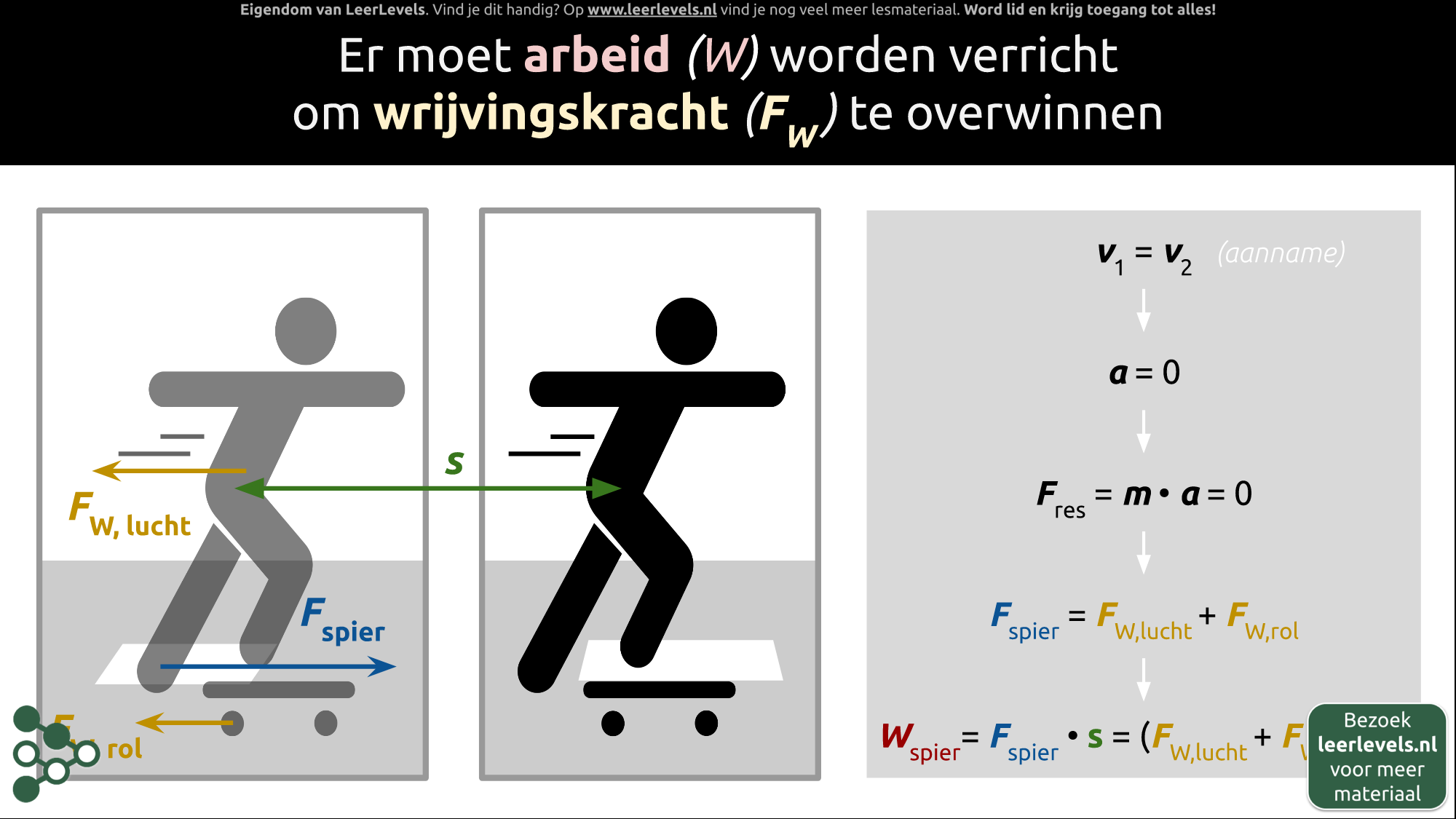
Arbeid en wrijving

Om vooruit te komen op een skateboard moet je arbeid verrichten door wrijvingskracht te overwinnen. Als je skatet met een bepaalde snelheid en even later dezelfde snelheid houdt een stukje verderop, hangt de totale arbeid die je moet verrichten om van A naar B te komen af van de wrijvingskracht. Er spelen twee krachten een rol: luchtwrijving en rolwrijving. Om de totale arbeid te berekenen, kan je de spierkracht naar voren gelijkstellen aan de krachten naar achteren en de afstand die je aflegt vermenigvuldigen met de som van de lucht- en rolwrijving: W = (Flucht + Frol) × s. Hierbij staat Flucht voor de kracht van de luchtwrijving, Frol voor de kracht van de rolwrijving en s voor de afgelegde weg.

(Afbeelding: Animatie voor Arbeid en wrijving)

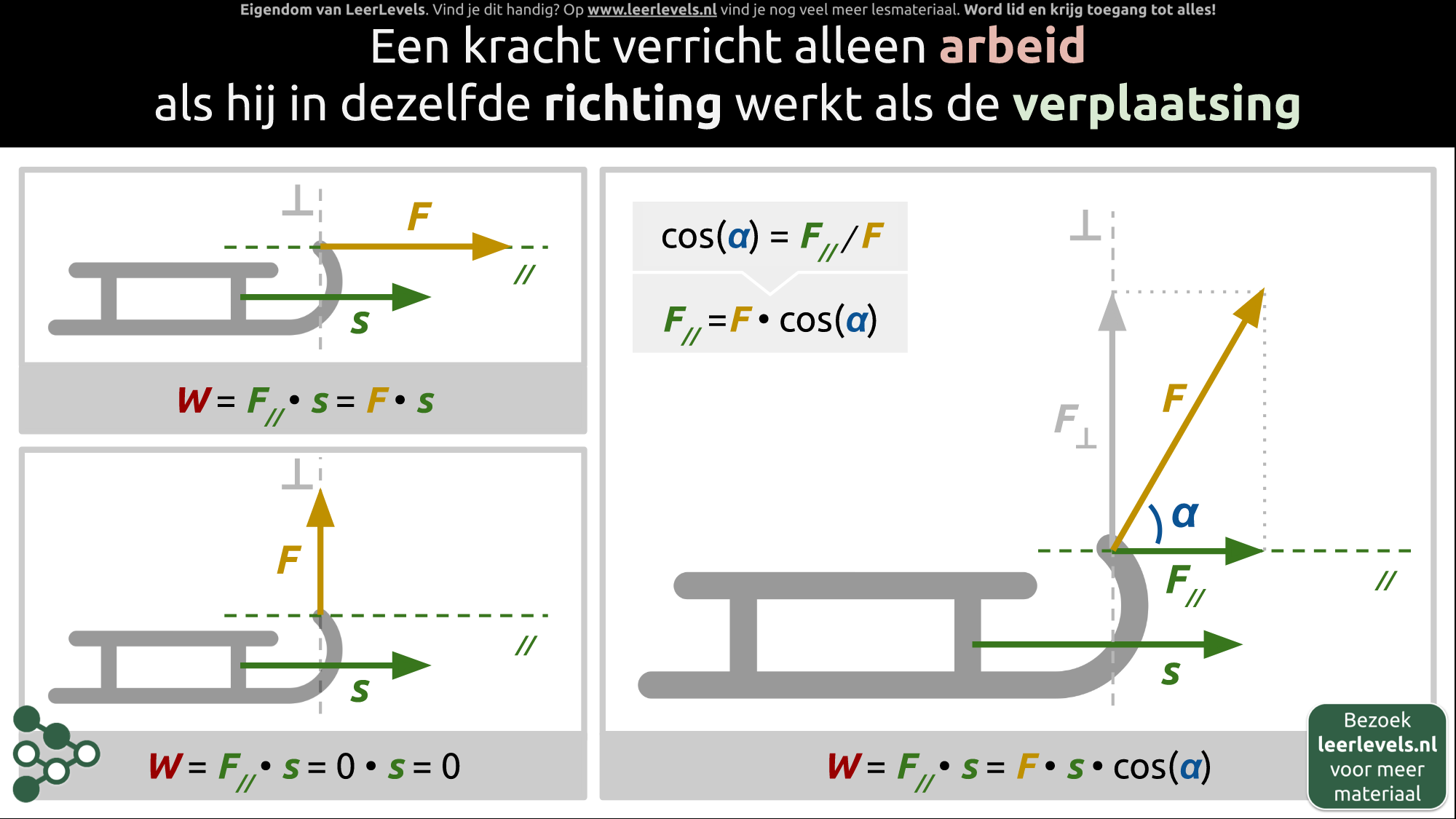
Arbeid onder een hoek

Een kracht verricht alleen arbeid als deze in dezelfde richting werkt als de verplaatsing. Wanneer de kracht parallel is aan de bewegingsrichting, is de verrichte arbeid gelijk aan

W = F · s

waarbij W de arbeid is in J, F de kracht in N en s de afstand in m.

Bij een schuine kracht beschouwen we alleen de component van de kracht die parallel is aan de bewegingsrichting. Als je een object verplaatst door een schuine kracht uit te oefenen, is de verrichte arbeid gelijk aan

W = F · cos(α) · s

waarin α de hoek is die de kracht maakt met de bewegingsrichting.

Als de kracht loodrecht staat op de bewegingsrichting, verricht deze kracht geen arbeid.

(Afbeelding: Animatie voor Arbeid onder een hoek)

Arbeid bij veranderlijke kracht

Bij een veranderlijke kracht kun je de arbeid bepalen met de oppervlaktemethode en het kracht-afstand diagram. Stel je voor dat je een route fietst waarbij je op verschillende stukken verschillende krachten uitoefent:

- Deel 1: Gedurende 4 meter een kracht van 0,25 kJ
- Deel 2: Gedurende 2 meter een kracht van 0,5 kJ
- Deel 3: Gedurende 4 meter een kracht van 0,25 kJ
- Deel 4: Gedurende 5 meter een kracht van 0,20 kJ
- Deel 5: Gedurende 4 meter een kracht van 0,25 kJ

De totale arbeid die je verricht is gelijk aan de oppervlakte onder het (F, s)-diagram, wat overeenkomt met de som van de arbeid verricht in alle delen. Dit houdt in dat:

W = W1 + W2 + W3 + W4 + W5

Als we de waarden invullen, krijgen we:

W = 4 · 0,25 + 2 · 0,5 + 4 · 0,25 + 5 · 0,20 + 4 · 0,25 = 4,9 kJ

(Afbeelding: Animatie voor Arbeid bij veranderlijke kracht)

Werk concept

Werk, ook wel arbeid genoemd, is de inspanning die nodig is om een proces te laten plaatsvinden. Deze inspanning kan van verschillende aard zijn en is van toepassing op diverse processen. Bijvoorbeeld, als je iets wilt versnellen, is er arbeid nodig om die versnelling te bereiken. Hetzelfde geldt voor het optillen of vervormen van objecten. Al deze inspanningen vallen onder de termen 'werk verrichten' of 'arbeid verrichten'.

(Afbeelding: Animatie voor Werk concept)

Terug naar overzicht Meld je aan

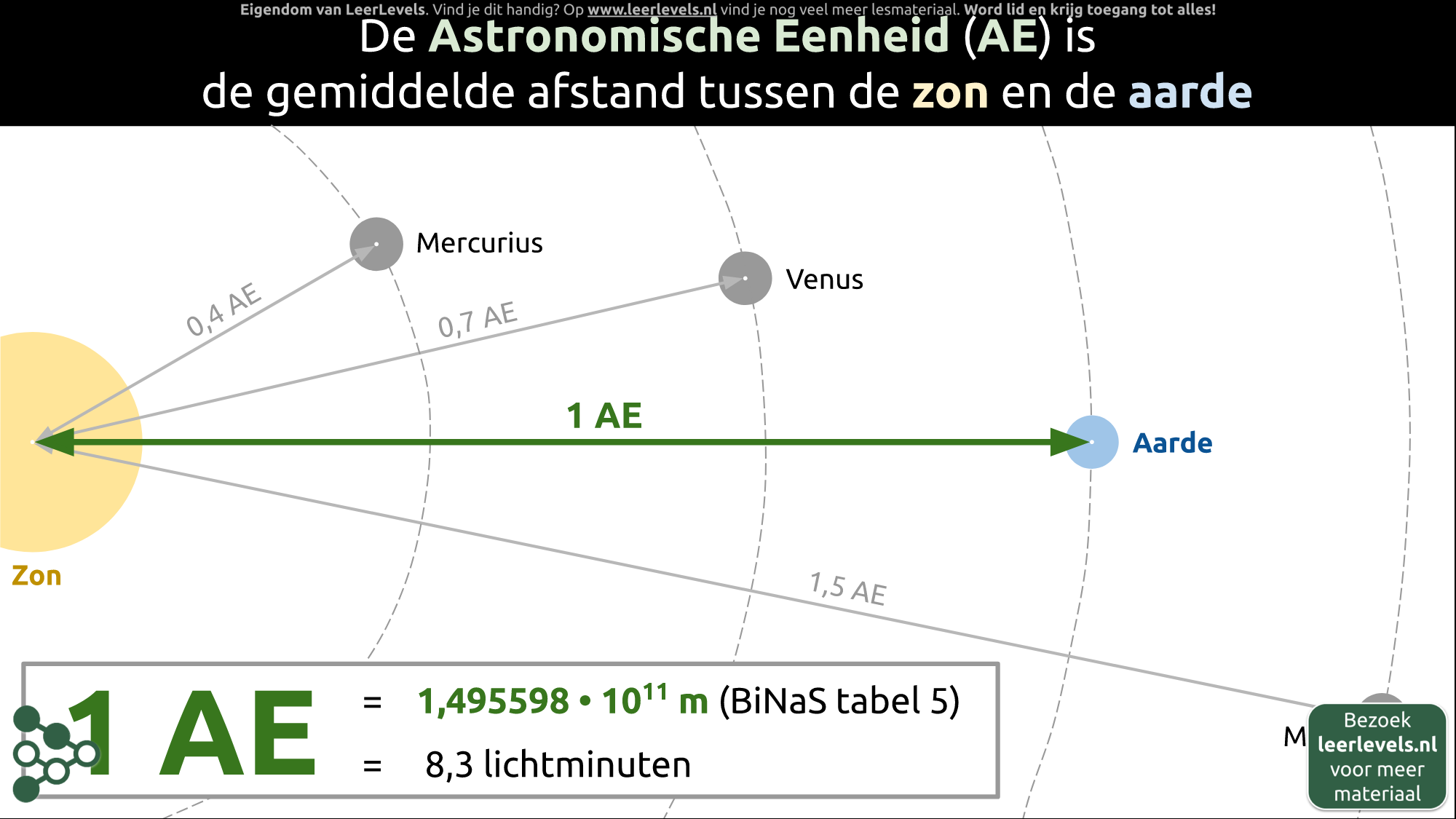
Astronomische eenheid

De astronomische eenheid (AE) is de afstand tussen de zon en de aarde. Het is ongeveer 150 miljoen kilometer (1,5 × 10¹¹ meter), wat gelijkstaat aan de afstand die licht in 8,3 minuten aflegt. Door de AE te gebruiken als afstand in het heelal, hoeven we geen hele grote getallen te gebruiken. Zo staat Mercurius ongeveer 0,4 AE van de zon, Venus op 0,7 AE en Mars op 1,5 AE. Dit maakt het vergelijken van afstanden tussen planeten veel makkelijker.

(Afbeelding: Animatie voor Astronomische eenheid)

Terug naar overzicht Meld je aan

Atomaire massa-eenheid

De atomaire massa-eenheid (u) is ongeveer gelijk aan de massa van één kerndeeltje. Als je de massa van een koolstof-12 atoom kent, is één u gelijk aan 1/12 daarvan, dit is 1,66 × 10⁻²⁷ kg. Deze waarde kun je vinden in tabel 7 van de Binas. In dezelfde tabel staat ook de waarde van 931,5 MeV of 1,492 × 10⁻¹⁰ joule, wat dezelfde energie-eenheid is met een andere notatie. Als massa wordt omgezet in energie via een reactie, komt er energie vrij. Als je een massadefect van één u hebt, kun je de bijbehorende energie berekenen met de formule E = mc². Dit geeft 931,5 MeV of 1,492 × 10⁻¹⁰ joule.

(Afbeelding: Animatie voor Atomaire massa-eenheid)

Terug naar overzicht Meld je aan

Atoom

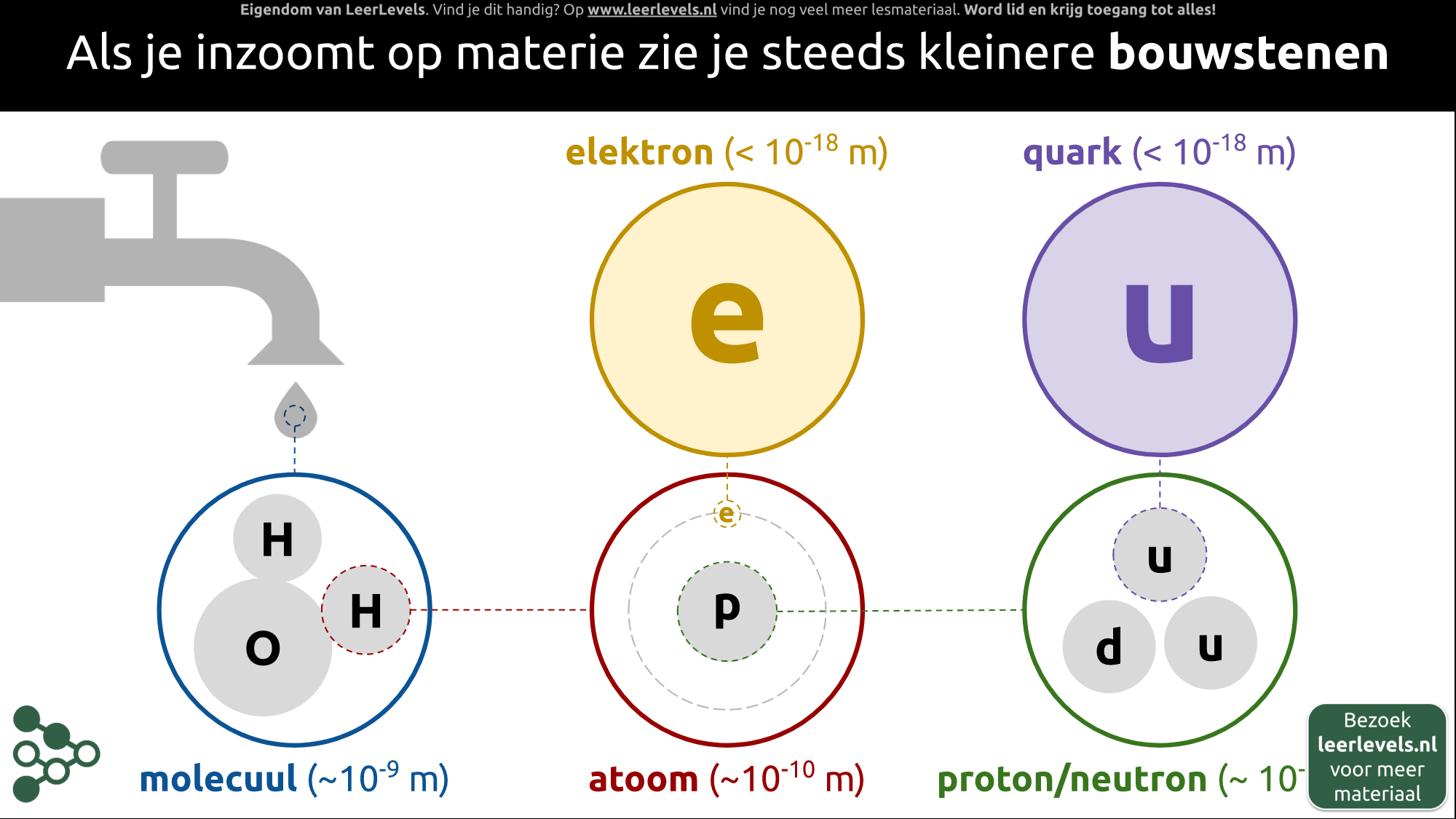
Atoombouw

Als we naar hele kleine dingen kijken, zien we dat alles uit nog kleinere onderdelen bestaat. Een druppel water bestaat bijvoorbeeld uit heel veel piepkleine watermoleculen. Zo'n molecuul is ongeveer 0,000000001 meter groot. In elk watermolecuul zitten twee waterstofatomen en een zuurstofatoom. Als we naar het waterstofatoom gaan kijken, dan zien we dat dit heel klein is, namelijk ongeveer 0,0000000001 meter. Het waterstofatoom heeft een proton in het midden en daar draait een elektron omheen. Het elektron zelf is ook weer heel klein, ongeveer zo'n 0,000000000000000001 meter groot. Als we nog verder inzoomen op het proton, dan zien we quarks. Quarks zijn net zo groot als elektronen, namelijk ongeveer 0,000000000000000001 meter.

(Afbeelding: Animatie voor Atoombouw)

Notatie atoom

De notitie van een atoom geeft aan hoeveel protonen, neutronen en elektronen het heeft. Het typische atoom kan worden genoteerd als A/X, waarbij A het massagetal is (aantal neutronen en protonen in de kern) en X het symbool van het element is. Het atoomnummer (aantal protonen) wordt aangeduid met Z. Neutronen hebben een grote massa maar geen lading. Helium vier, He-4, heeft bijvoorbeeld twee protonen en twee neutronen. Een atoom is neutraal als er evenveel negatief geladen elektronen zijn als positief geladen protonen in de kern.

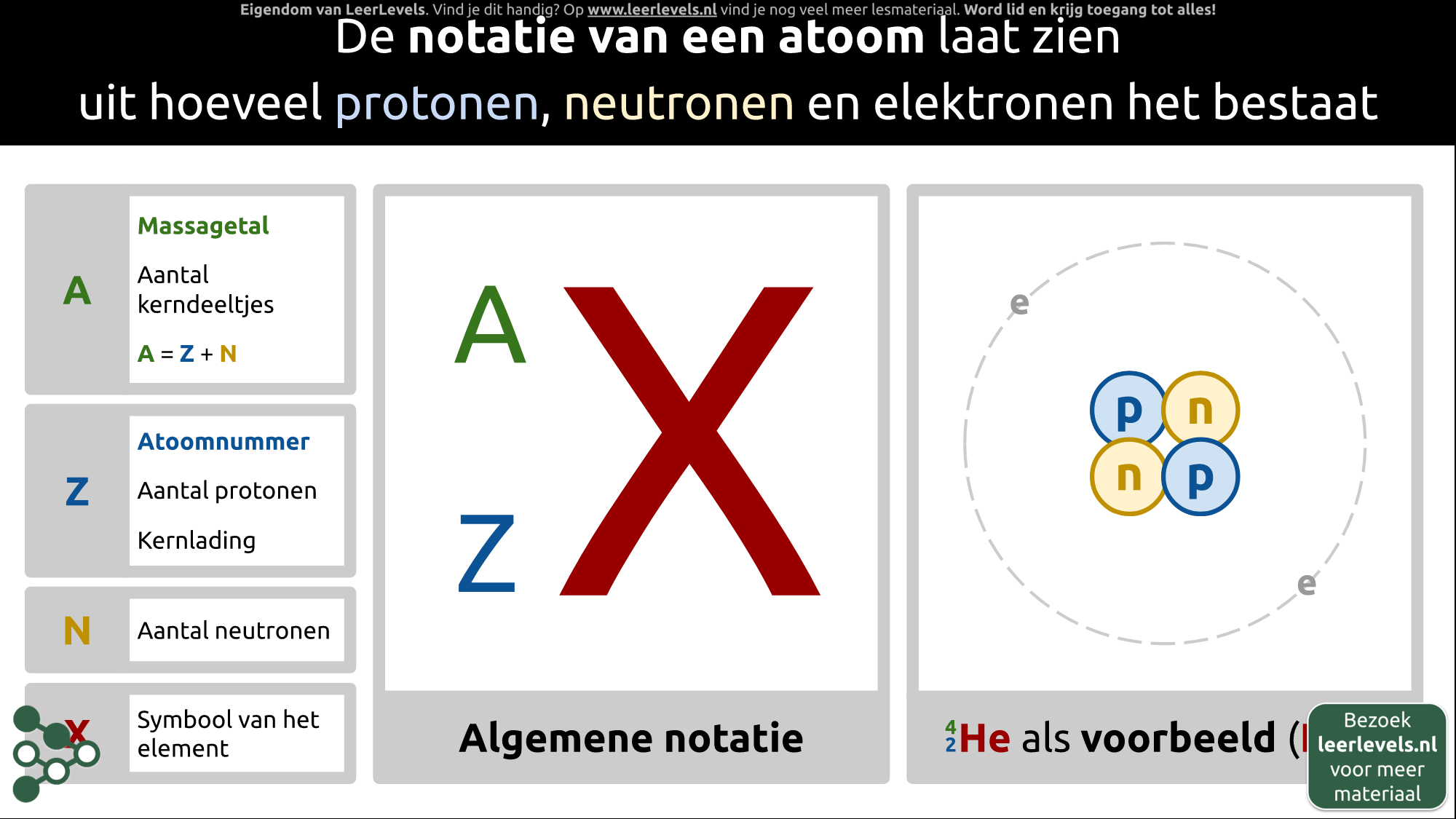
(Afbeelding: Animatie voor Notatie atoom)

Terug naar overzicht Meld je aan

Atoommodel

Quantummechanisch atoommodel waterstof

In een waterstofatoom wordt het elektron gevangen door het proton, en de energie bepaalt in welke orbitaal het elektron zich bevindt. Laten we beginnen met de grondtoestand. De bijbehorende golffunctie is als volgt weergegeven: er is een scherpe piek bij r = 0, in het midden van het waterstofatoom. Op de plek waar het proton zich bevindt, is de kans het grootst. Je zou daarom kunnen verwachten dat de kans het grootst is in de kern. Dit blijkt echter niet het geval te zijn.

Als je veel metingen uitvoert, tref je de elektronen vooral aan in een wolk rondom de oorsprong, maar niet precies op r = 0. Dit heeft te maken met de precieze betekenis van de kansverdeling. De kans is afhankelijk van het oppervlak van een bol met straal r, en bij r = 0 is het oppervlak van die bol nul. Ondanks de grote waarde van de golffunctie daar, is de kans om een elektron te vinden bij r = 0 dus nul. Het kwadraat van de golffunctie geeft een kans weer, maar dit is een kans per klein stukje oppervlak.

In de eerste aangeslagen toestand ziet de golffunctie er anders uit. Je kunt dan deeltjes niet alleen in een schil rondom de oorsprong vinden, maar er is ook een tweede bolvormige schil. Voor waterstof zijn deze verdelingen goed bekend en ze zijn onder andere te vinden in BiNaS tabel 23. Het belangrijkste is dat je de golffunctie kunt vertalen naar de kans om het deeltje ergens te vinden.

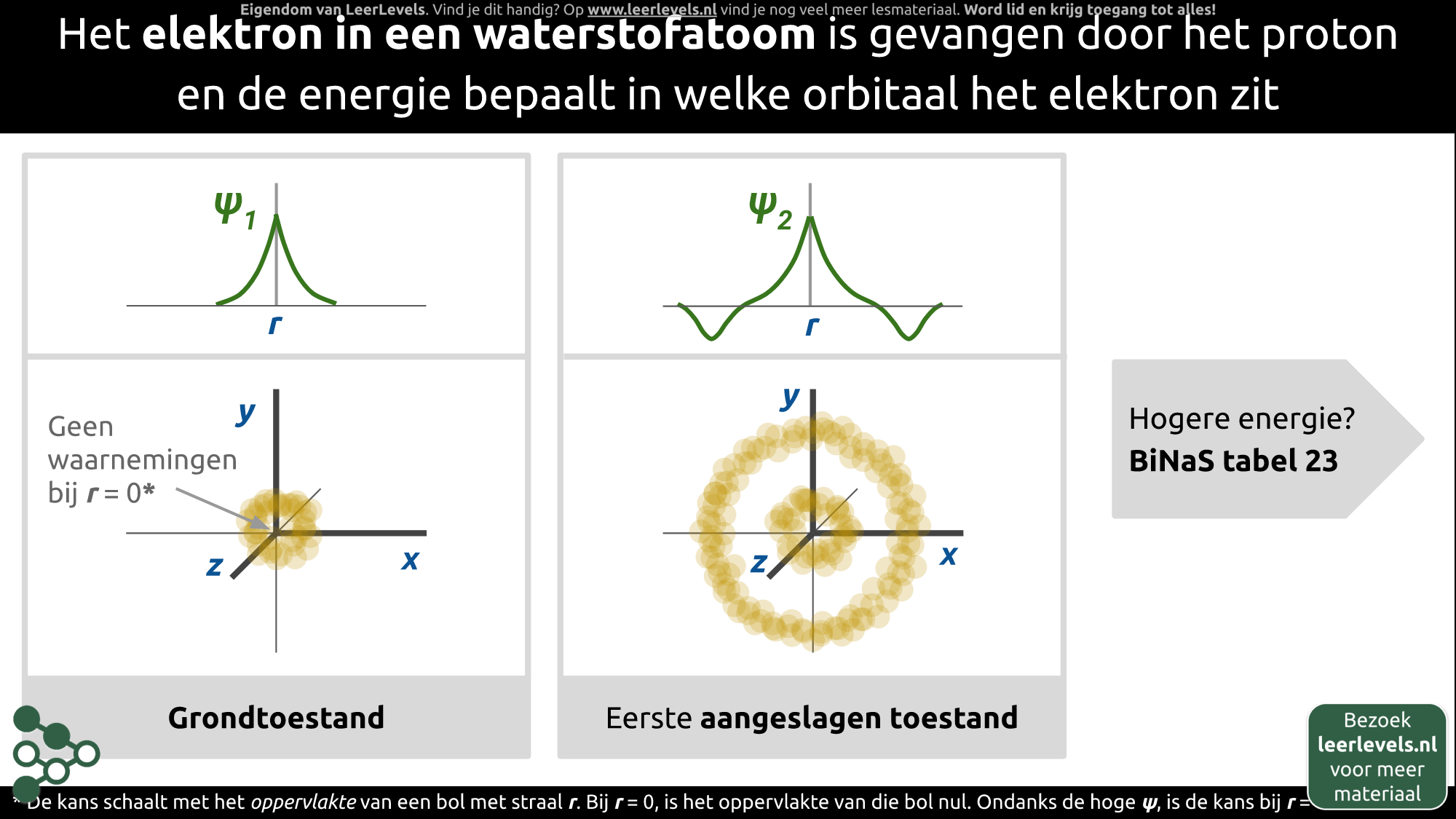
(Afbeelding: Animatie voor Quantummechanisch atoommodel waterstof)

Terug naar overzicht Meld je aan

Atoommodellen

Het natuurkundige model van een atoom wordt steeds verfijnder dankzij wetenschappelijke ontdekkingen. Vroeger dachten we dat een atoom leek op een krentenbol met een grote positieve lading en enkele kleine negatieve ladingen erin. Vervolgens kwam Rutherford met zijn experiment waarbij hij deeltjes op goud schoot. Uit dit experiment concludeerde hij dat atomen bestaan uit afzonderlijke positieve kernen met een soort wolk van elektronen eromheen. Daarna introduceerde Bohr een verdere verfijning van dit idee. Hij stelde voor dat de elektronenwolk bestond uit schillen rondom de kern, waarbij elektronen zich op vaste afstanden van de kern bevinden.

Tegenwoordig gebruiken we het quantummechanische model. In dit model wordt de locatie van elektronen beschreven met een bepaalde waarschijnlijkheidsfunctie. Dit komt niet omdat wij als mensen nog niet goed genoeg kunnen meten waar de elektronen zijn, maar omdat deze onzekerheid een fundamentele eigenschap is van deeltjes zoals elektronen.

Voor veel verschijnselen biedt het Bohrmodel goede voorspellingen, maar het quantummechanische model is het model dat op dat voor alsnog het beste past bij alle experimenten.

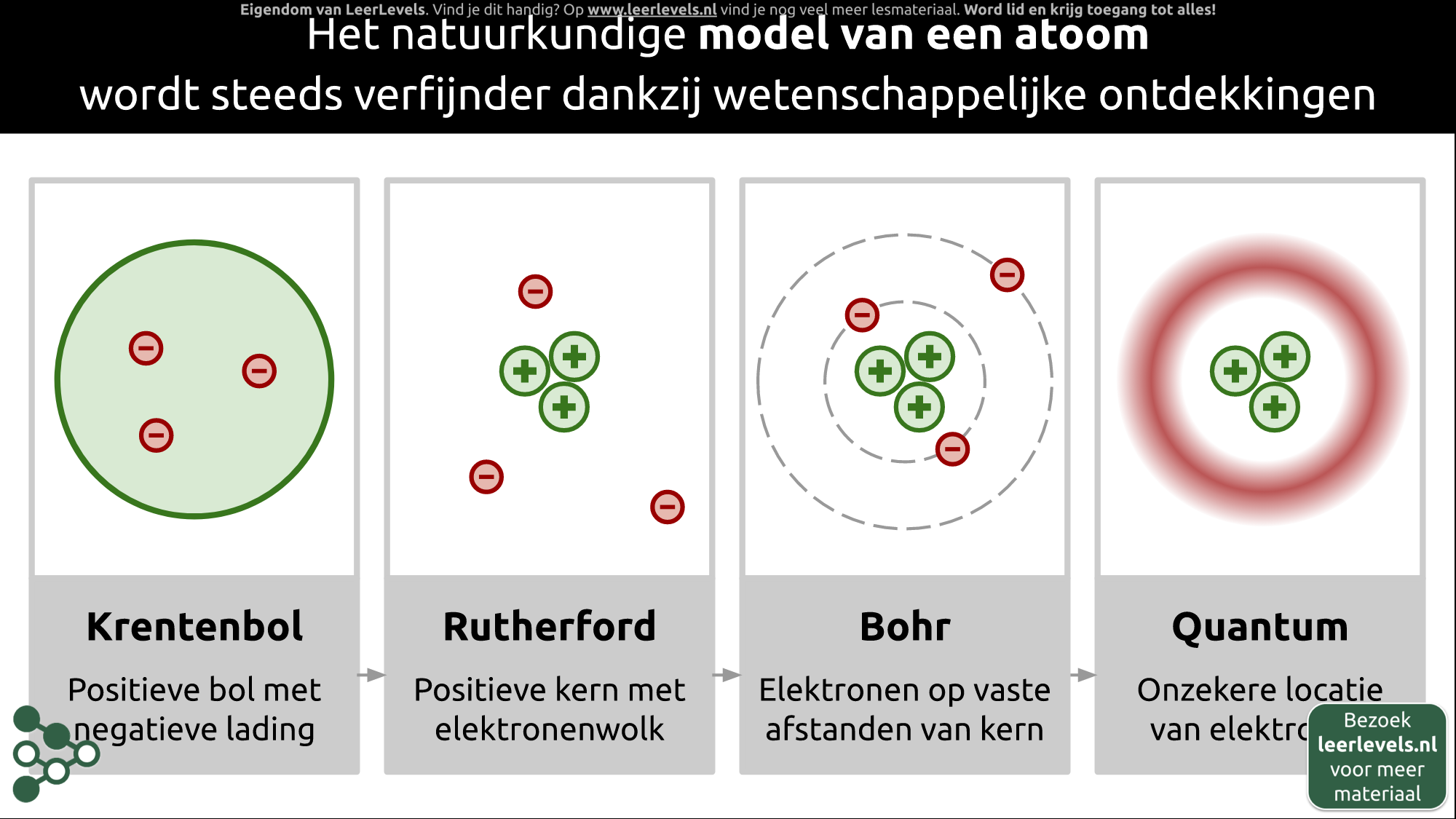
(Afbeelding: Animatie voor Atoommodellen)

Terug naar overzicht Meld je aan

Baansnelheid

Baansnelheid planeet afleiding

Als een planeet om een ster draait, wordt het op zijn plek gehouden door zwaartekracht. Deze kracht zorgt ervoor dat de beweging cirkelvormig is. Door de middelpuntzoekende kracht en gravitatiekracht te berekenen, kunnen we de baansnelheid van de planeet berekenen. De formule hiervoor is v = wortel(GM/r), waarbij v staat voor de baansnelheid in m/s, G voor de gravitatieconstante, M voor de massa van de ster en r voor de afstand tussen de planeet en de ster in meters.

(Afbeelding: Animatie voor Baansnelheid planeet afleiding)

Baansnelheid planeet formule

De snelheid waarmee een planeet zich voortbeweegt in zijn baan is afhankelijk van de massa van het centrale object en de straal van die baan. Dit wordt weergegeven in de formule:

v = √((GM)/(r))

waarin v de baansnelheid is in m/s, G de gravitatieconstante, M de massa van het centrale object in kg, en r de baanstraal in m.

(Afbeelding: Animatie voor Baansnelheid planeet formule)

Terug naar overzicht Meld je aan

Beeldafstand

Beeldafstand formule

Door de lenzenformule om te schrijven, kan je een formule afleiden waarmee je in één keer de beeldafstand kunt berekenen.

We beginnen met de lenzenformule die we omschrijven naar

1/b = 1/f - 1/v

De breuken rechts van het " = " teken tel je vervolgens bij elkaar op. Je krijgt dan

1/b = (v-f)/(v · f)

Als we de breuken links en rechts van het " = " teken omkeren, dan krijgen we de uitdrukking

b = (v · f)/(v - f)

Hierin is b de beeldafstand, v de voorwerpsafstand en f de brandpuntsafstand in meter. Met deze formule kan je dus in één keer de beeldafstand berekenen als de voorwerpsafstand en brandpuntsafstand gegeven zijn.

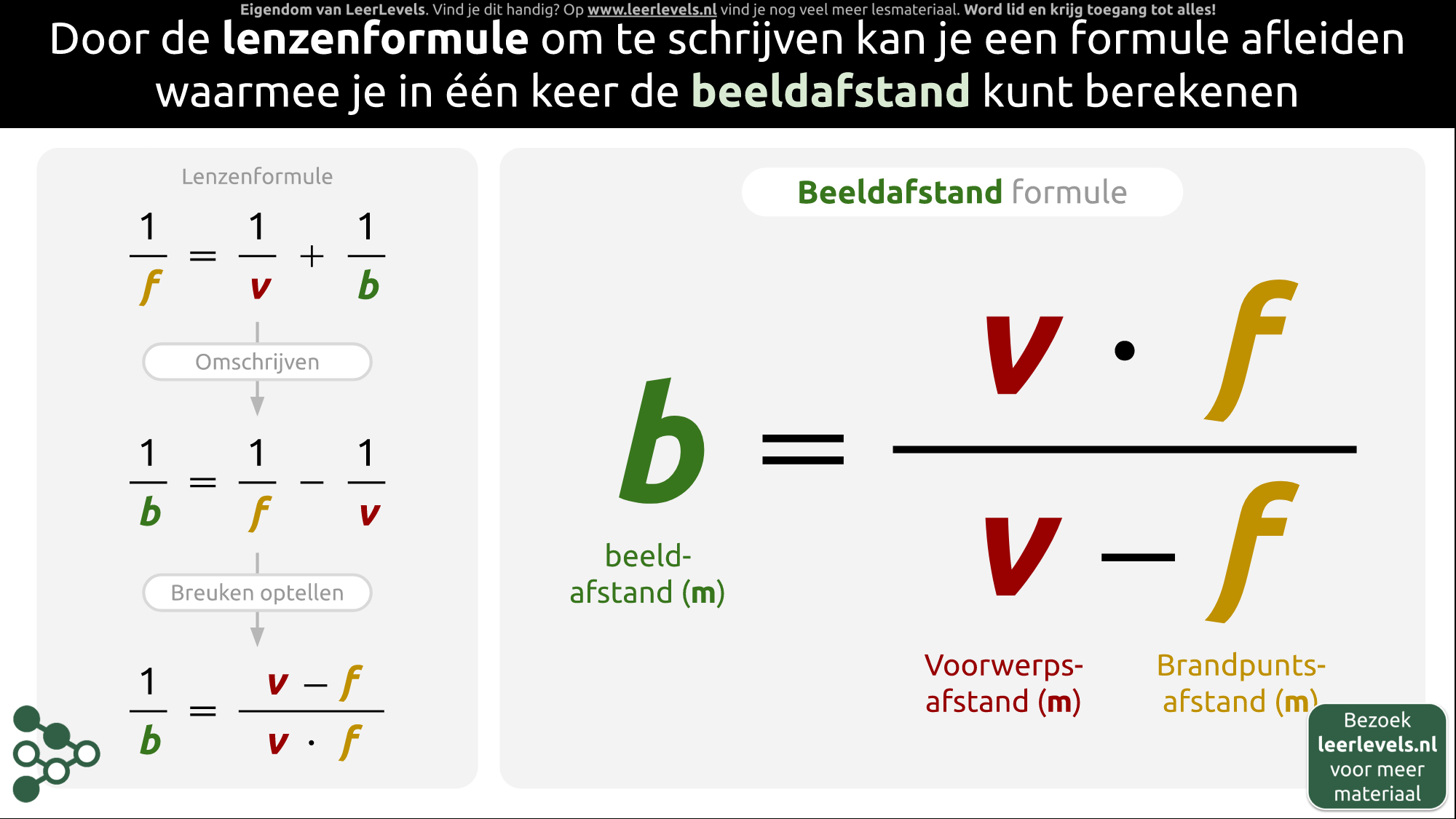
(Afbeelding: Animatie voor Beeldafstand formule)

Beeldafstand en voorwerpsafstand

Als je naar iets kijkt met een lens, is er een afstand tussen het object en de lens, dit noemen we de voorwerpsafstand. Als het beeld aan de andere kant van de lens wordt geprojecteerd, noemen we de afstand tussen het beeld en de lens de beeldafstand. Bij het gebruik van een positieve lens met een optische as en een object links daarvan, noemen we de afstand tussen het object en de lens v. Als het beeld aan de andere kant komt te staan, noemen we de afstand tussen het beeld en de lens b.

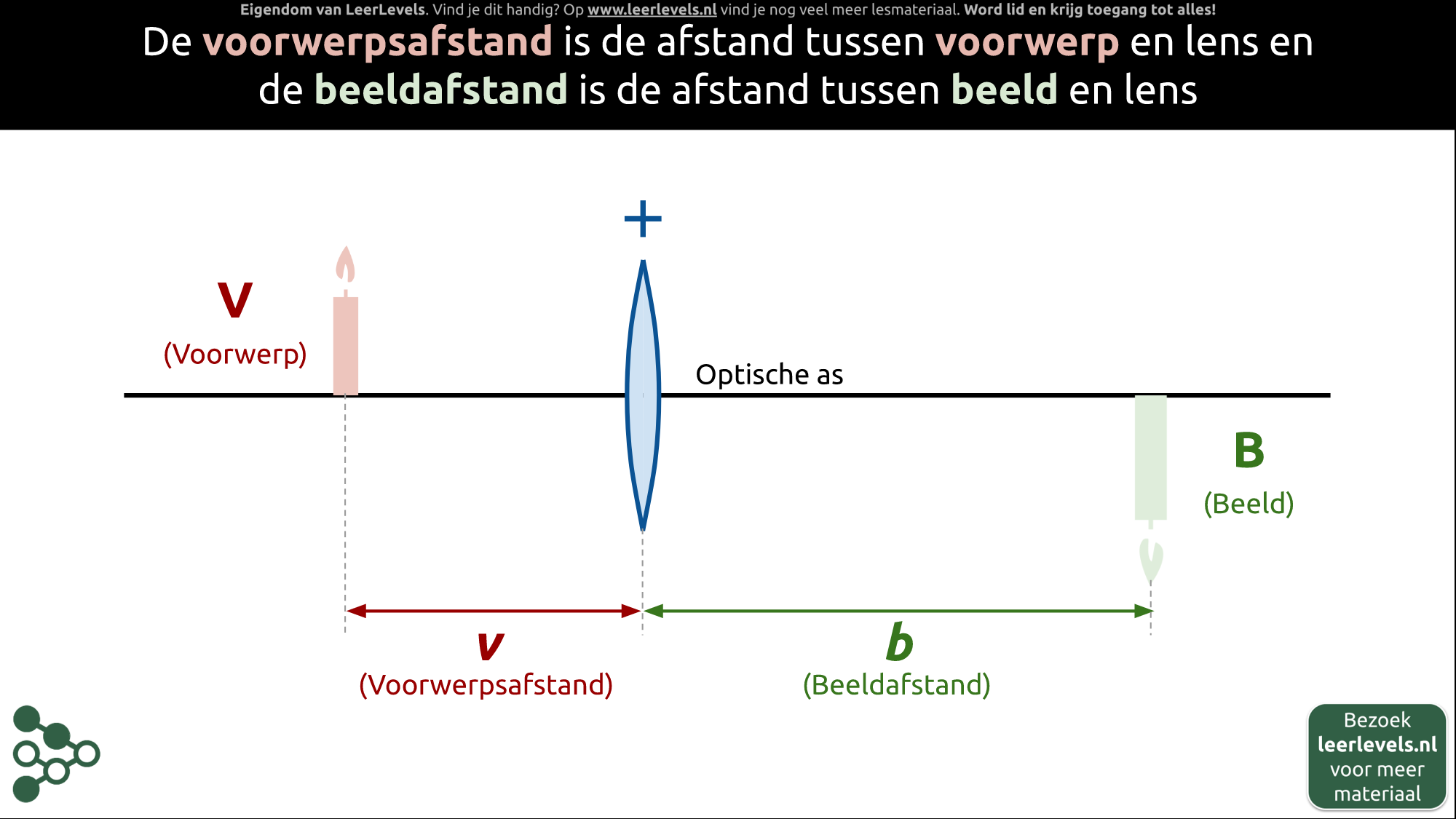
(Afbeelding: Animatie voor Beeldafstand en voorwerpsafstand)

Terug naar overzicht Meld je aan

Beeldvorming

Beeldvormende technieken

Er zijn verschillende manieren om in het lichaam te kijken, bijvoorbeeld met echo, röntgen, CT-scan, nucleaire diagnostiek en MRI. Elke techniek heeft zijn eigen voordelen en nadelen. Echo maakt gebruik van ultrasoon geluid om weefsels en organen in kaart te brengen, zoals bij een zwangerschap. Het is snel en goedkoop, maar werkt niet goed voor botten en kan problemen veroorzaken in de longen. Röntgen gebruikt gammastraling en werkt goed voor botten en bloedvaten, maar niet voor zachte weefsels. CT-scan is vergelijkbaar met röntgen, maar werkt vanuit verschillende hoeken en is daarom geschikt voor organen en weefsels. Het nadeel is dat het een hogere dosis straling gebruikt dan röntgen. Nucleaire diagnostiek maakt gebruik van een tracer om processen in het lichaam te volgen, maar levert ook een hoge stralingsdosis op. MRI maakt gebruik van radiogolven en magnetische velden en werkt goed bij gewrichten en organen, maar is duur en kan niet worden gebruikt als er ijzer in het lichaam aanwezig is. Elke techniek heeft dus zijn eigen voor- en nadelen.

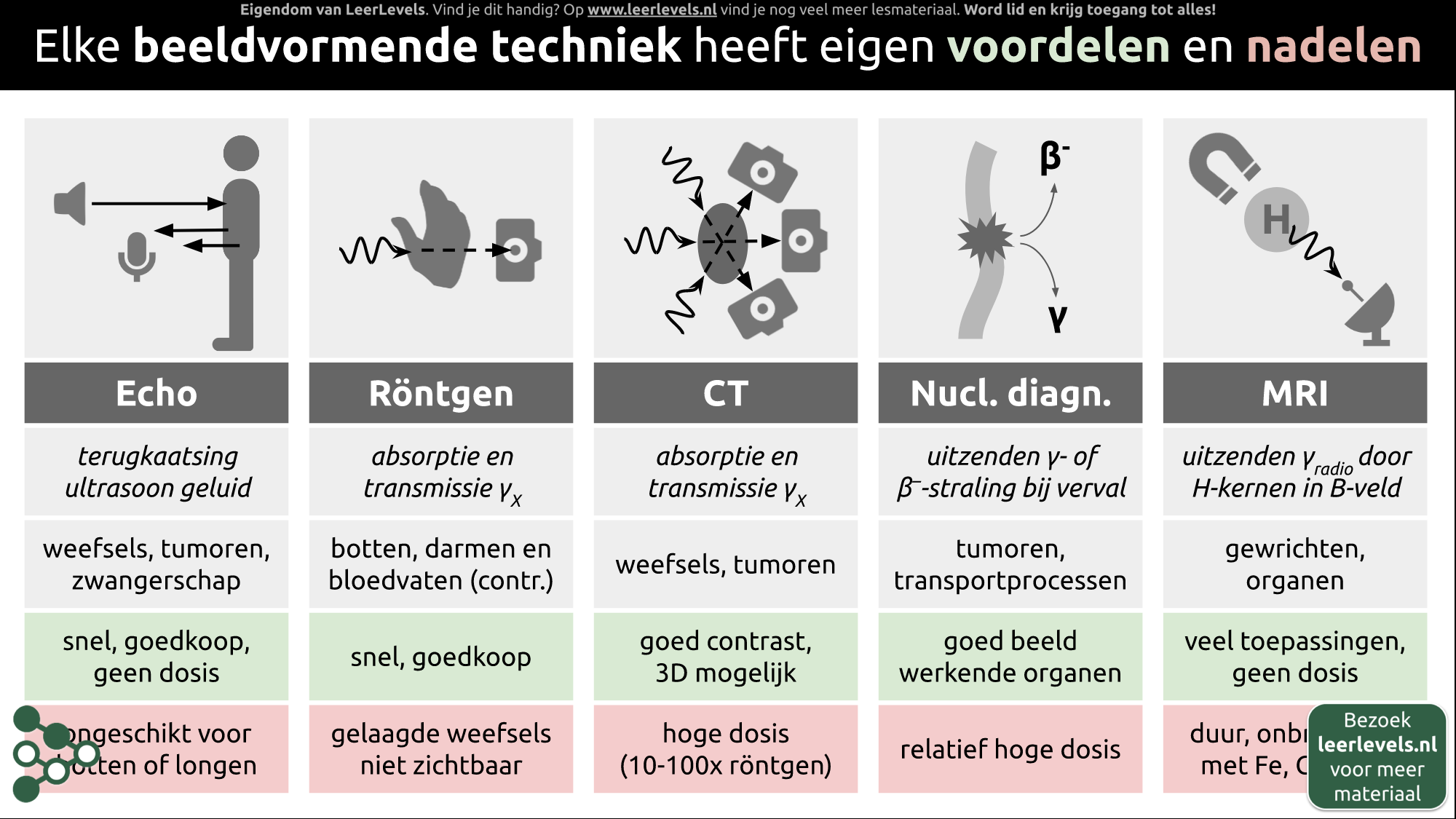
(Afbeelding: Animatie voor Beeldvormende technieken)

Terug naar overzicht Meld je aan

Bestraling

Bestraling en besmetting

Bij besmetting kom je in direct contact met een radioactieve bron. Dit gebeurt bijvoorbeeld wanneer je een drankje drinkt dat een radioactieve stof bevat, je huid insmeert met iets radioactiefs, of als je geïnjecteerd wordt met radioactieve materialen. In al deze gevallen komt de radioactieve bron op of in je lichaam terecht. Dit is zeer schadelijk, omdat niet alleen jij, maar ook alles en iedereen in je omgeving aan straling wordt blootgesteld. Dit noemen we besmetting.

Bestraling betekent daarentegen dat je je op een afstand van de radioactieve bron bevindt en alleen invloed ondervindt van de uitgezonden straling. In dit geval word je zelf geen bron van straling. Daarom is besmetting aanzienlijk gevaarlijker dan bestraling.

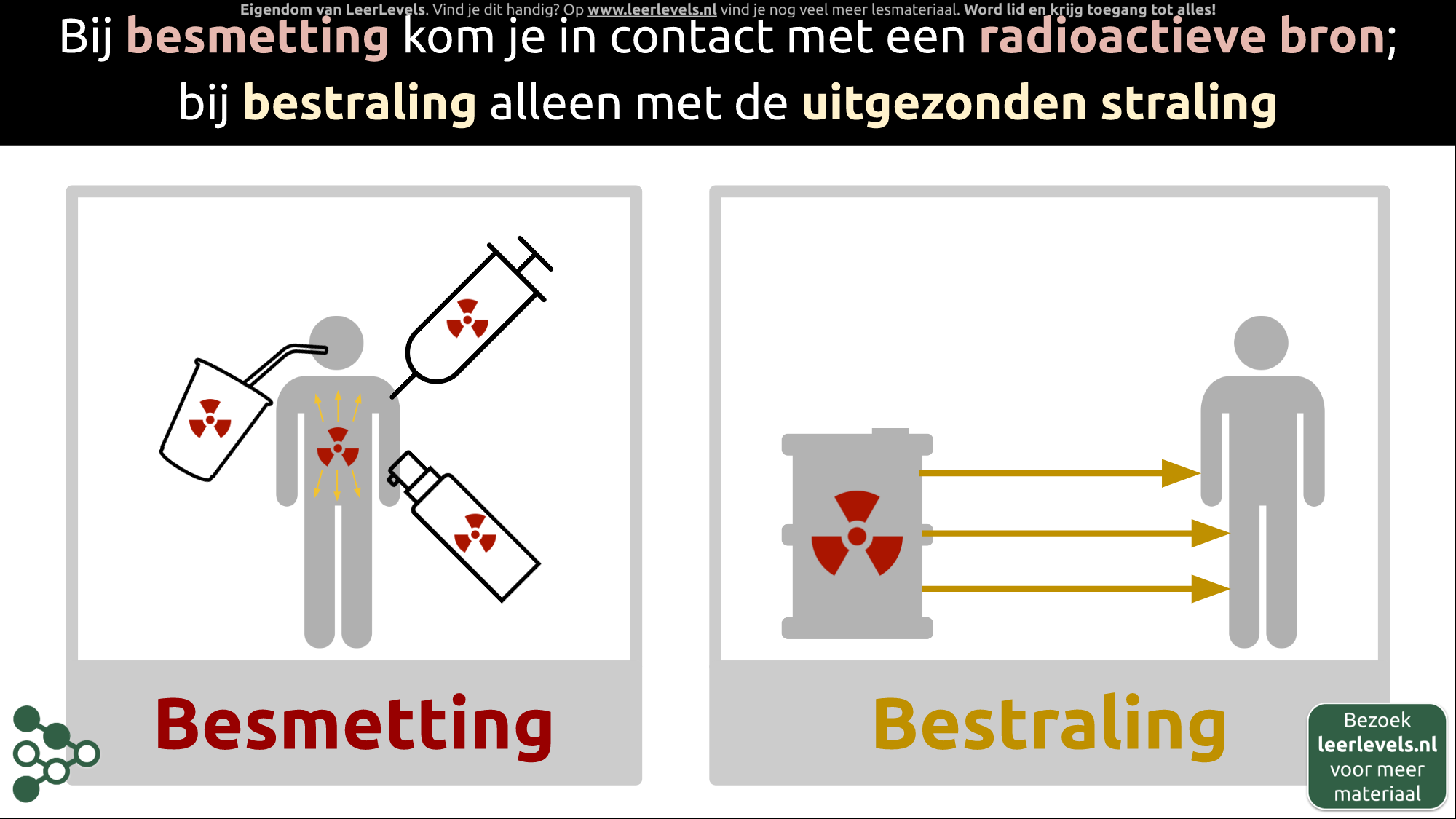
(Afbeelding: Animatie voor Bestraling en besmetting)

Terug naar overzicht Meld je aan

Beweging

Soorten beweging

In de natuurkunde zijn er vier soorten bewegingen die vaak voorkomen: stilstaande beweging, eenparige beweging, eenparig versnelde beweging en trilling. Bij stilstaande beweging verandert de plaats niet en is de snelheid en versnelling altijd 0. Een eenparige beweging heeft een constante snelheid en dus ook 0 versnelling en resultante kracht. Bij een eenparig versnelde beweging is de versnelling constant en kan de snelheid verschillen. Bij trilling beweegt iets steeds op en neer. Het is belangrijk om deze namen te kennen omdat het aangeeft welke beweging je vaker zult gaan toepassen. Formules en grootheden (s(t), v(t), a(t)) kunnen helpen bij het inzichtelijk maken van de bewegingen, maar de grafieken kunnen verschillen afhankelijk van de situatie. Bij trillingen ontstaat het door een terugwerkende kracht die recht evenredig is met de uitwijking, maar met een minteken.

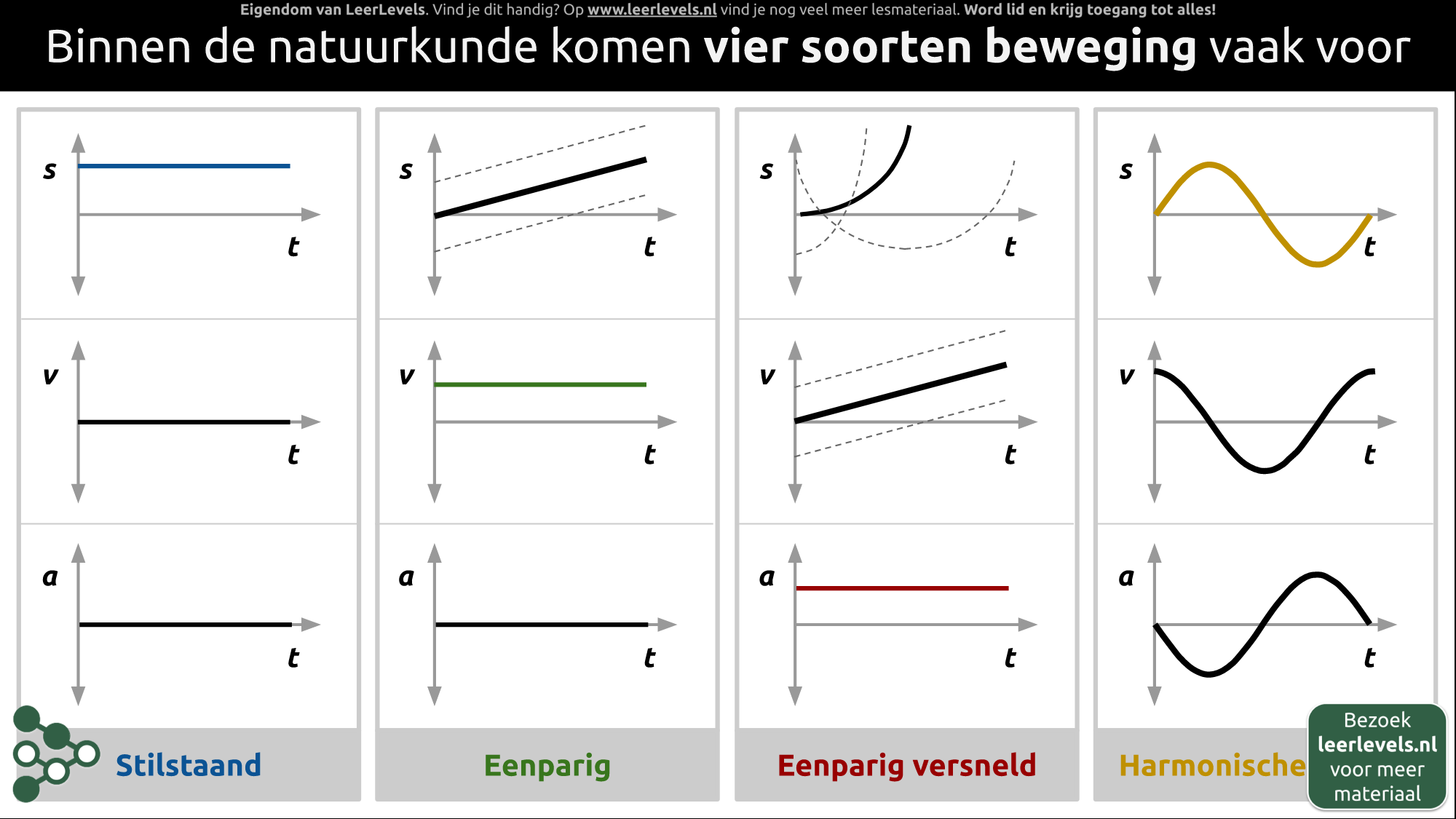
(Afbeelding: Animatie voor Soorten beweging)

Terug naar overzicht Meld je aan

Bewegingsdiagram

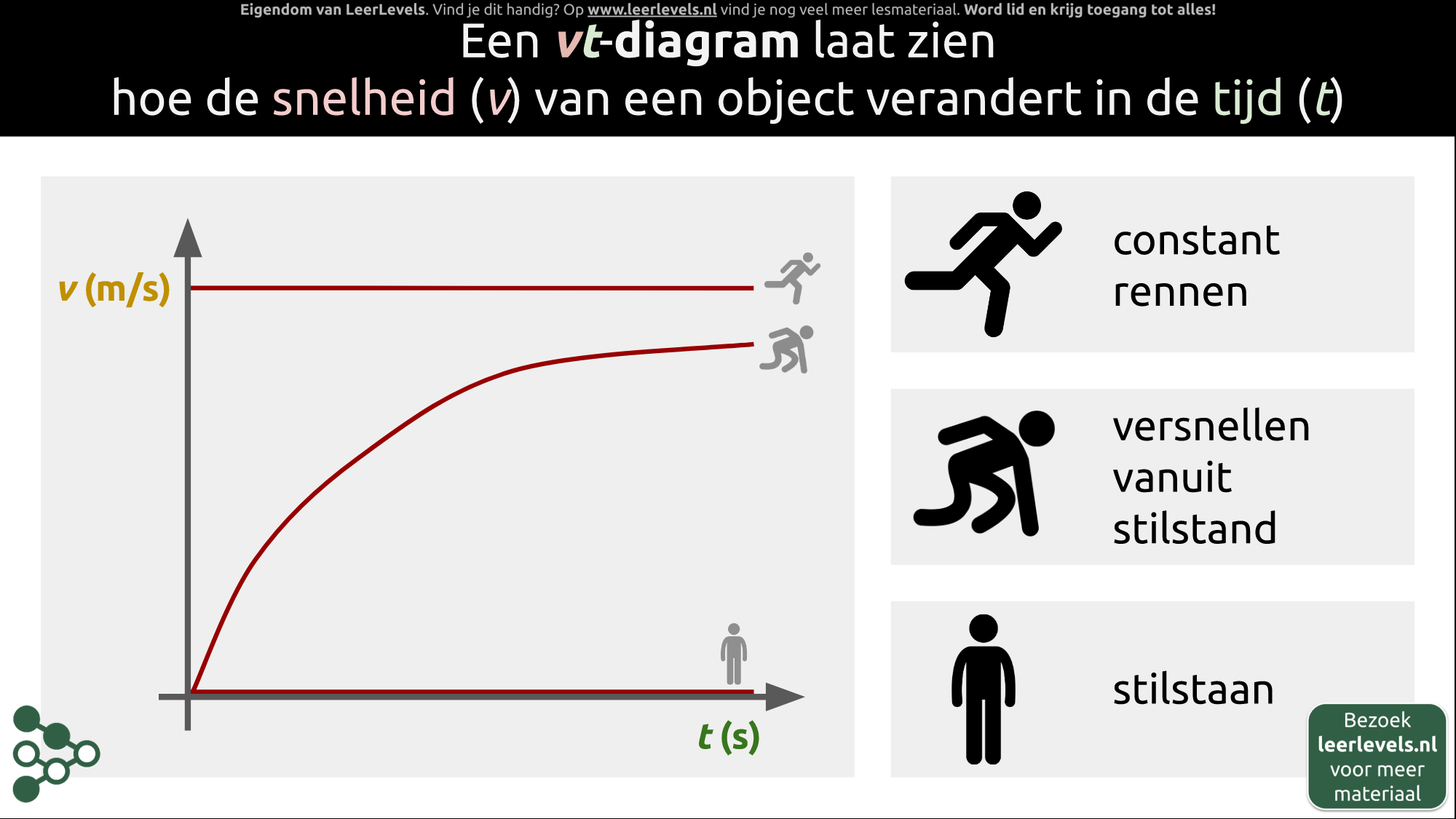
vt-diagram

Het diagram laat zien hoe snel een object beweegt over tijd. De x-as is de tijd en de y-as is de snelheid in meter per seconde. Als de lijn vlak is, betekent dit dat het object constant beweegt met dezelfde snelheid. Als de lijn de x-as snijdt, betekent dit dat het object stilstaat. Als de lijn stijgt, betekent dit dat het object versnelt totdat het zijn maximale snelheid bereikt en deze behoudt. De vt-grafiek laat dus zien hoe de snelheid verandert in de tijd.

(Afbeelding: Animatie voor vt-diagram)

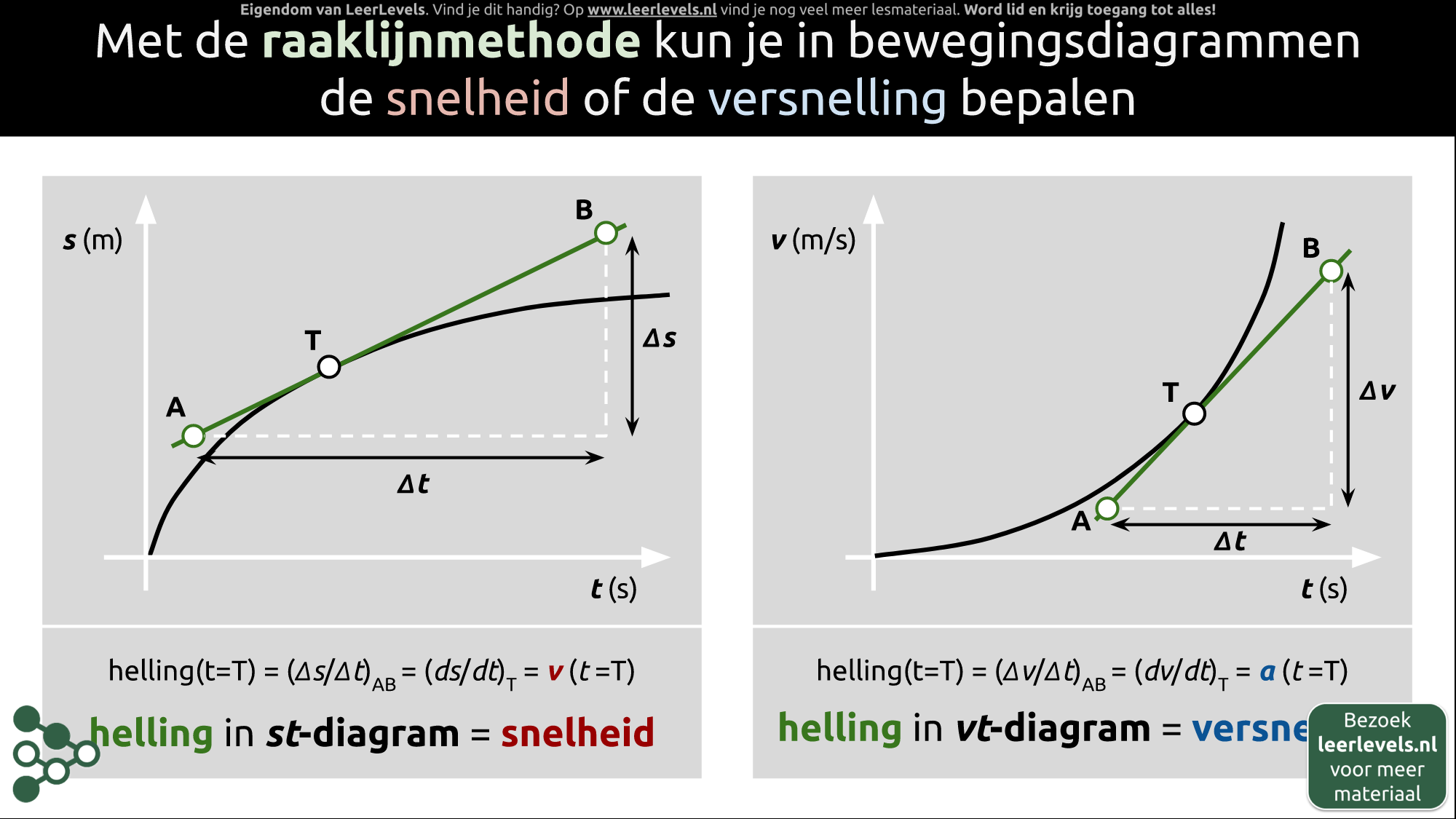
Raaklijnmethode en bewegingsdiagrammen

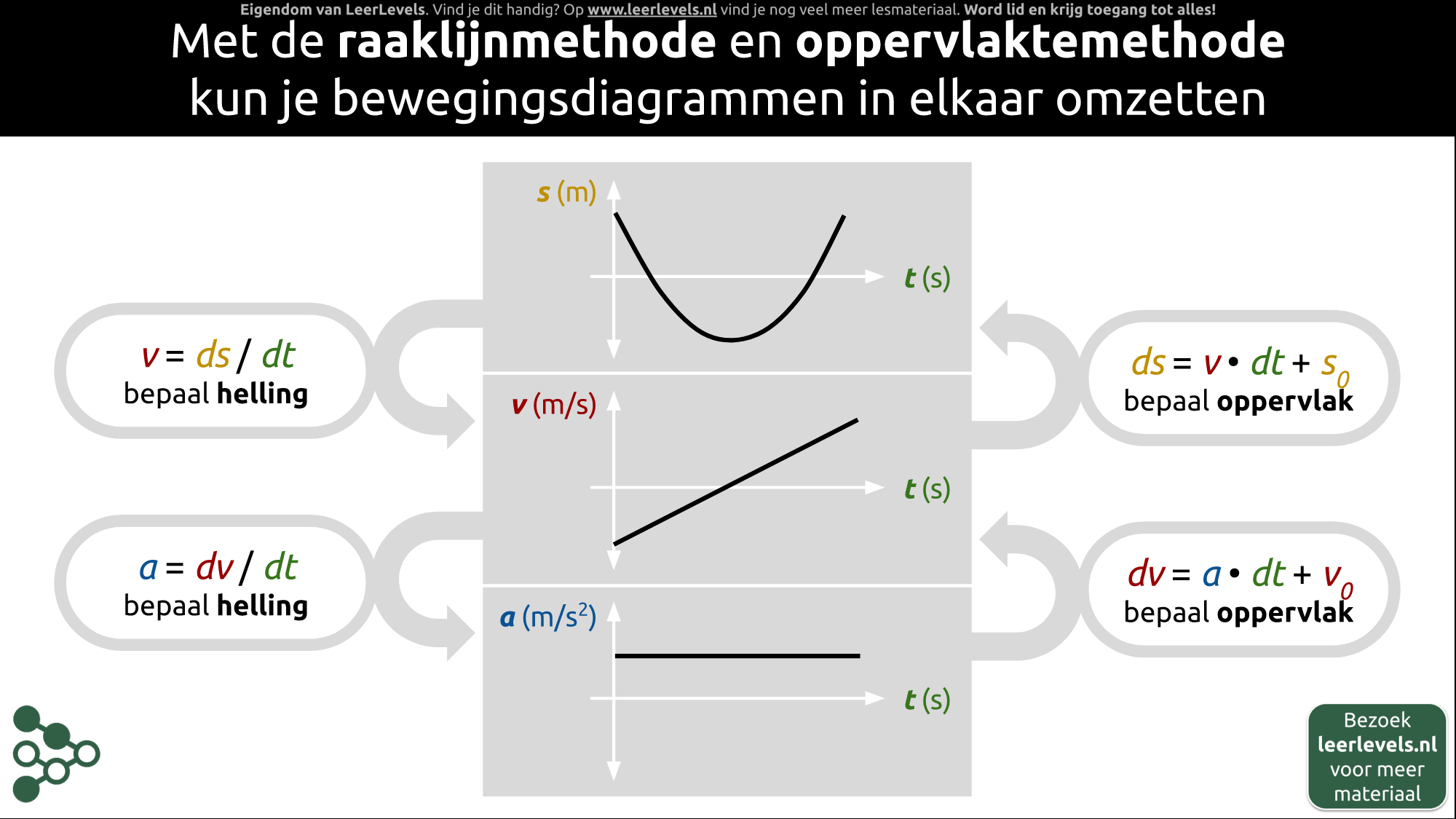
Met de raaklijnmethode kun je de snelheid en versnelling van een bewegend object bepalen. Dit doe je met een st-diagram voor de snelheid en een vt-diagram voor de versnelling. Om de snelheid te bepalen kies je een tijdstip en trek je een raaklijn door dat punt. De helling van deze raaklijn (Δ s / Δ t) is de snelheid op dat tijdstip. De helling in het st-diagram is dus de snelheid. Voor de versnelling gebruik je dezelfde methode, maar dan met het vt-diagram. Trek een raaklijn door punt T en bepaal de helling (Δ v / Δ t), die gelijk is aan de versnelling op dat moment. De helling in het vt-diagram is dus de versnelling. Kortom, de raaklijnmethode is een handige manier om snelheid uit een st-diagram en versnelling uit een vt-diagram te bepalen.

(Afbeelding: Animatie voor Raaklijnmethode en bewegingsdiagrammen)

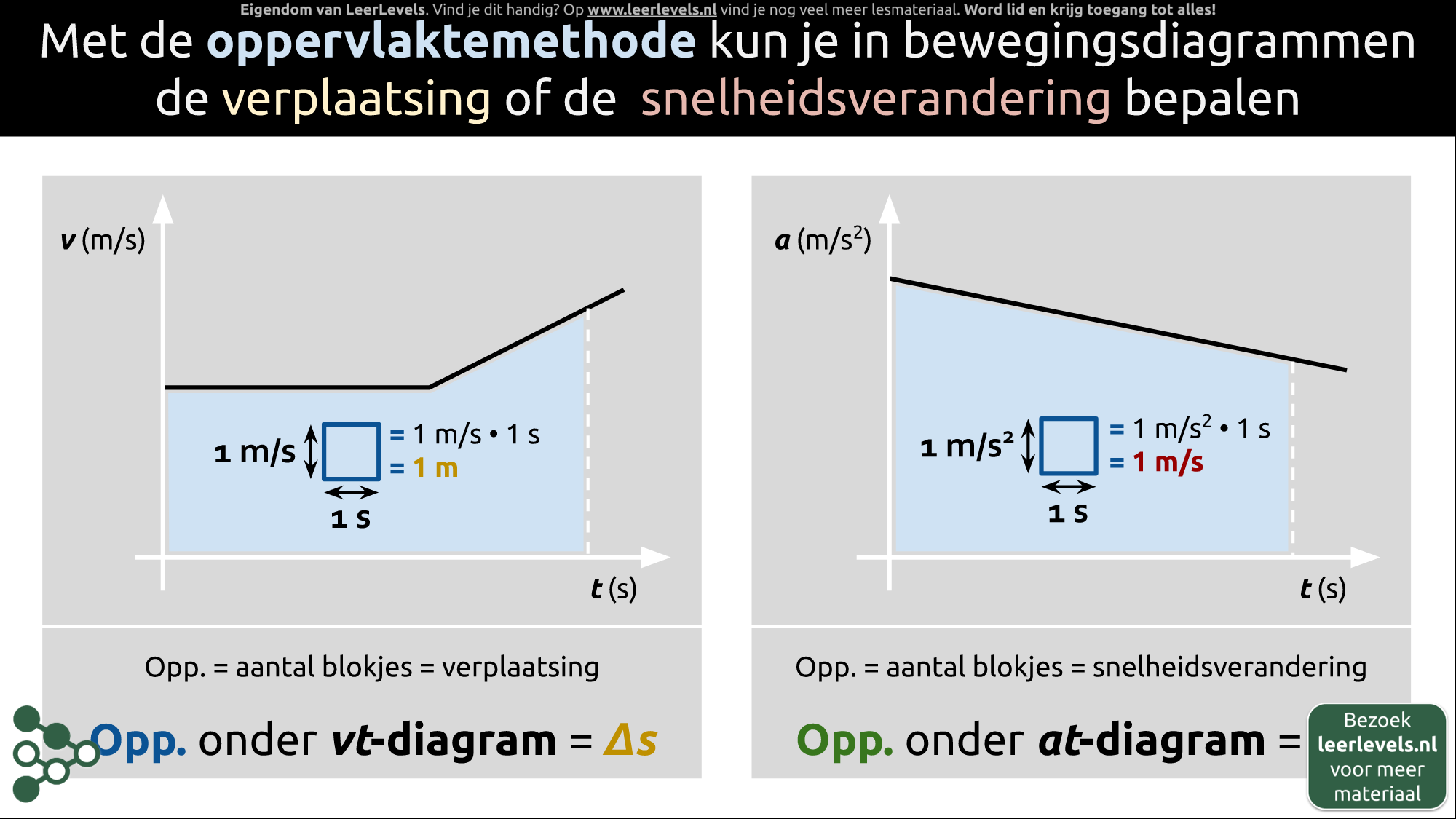
Oppervlaktemethode en bewegingsdiagrammen

Met de oppervlaktemethode kun je uit bewegingsdiagrammen de verplaatsing of snelheidsverandering bepalen. Het oppervlak onder een vt-diagram komt overeen met de verplaatsing delta x. Elk vierkantje onder deze grafiek komt overeen met een afstand van 1 meter. Het oppervlak van een klein vierkant oppervlak van 1 s bij 1 m/s is precies 1 meter. Voor een at-diagram geldt iets vergelijkbaars: het oppervlak onder de grafiek komt overeen met het verschil in snelheid tussen het begin- en eindpunt van het oppervlak. Het oppervlak van een klein vierkantje is gelijk aan 1 m/s² · 1 s = 1 m/s. Elk vierkantje is dus gelijk aan 1 meter per seconde.

(Afbeelding: Animatie voor Oppervlaktemethode en bewegingsdiagrammen)

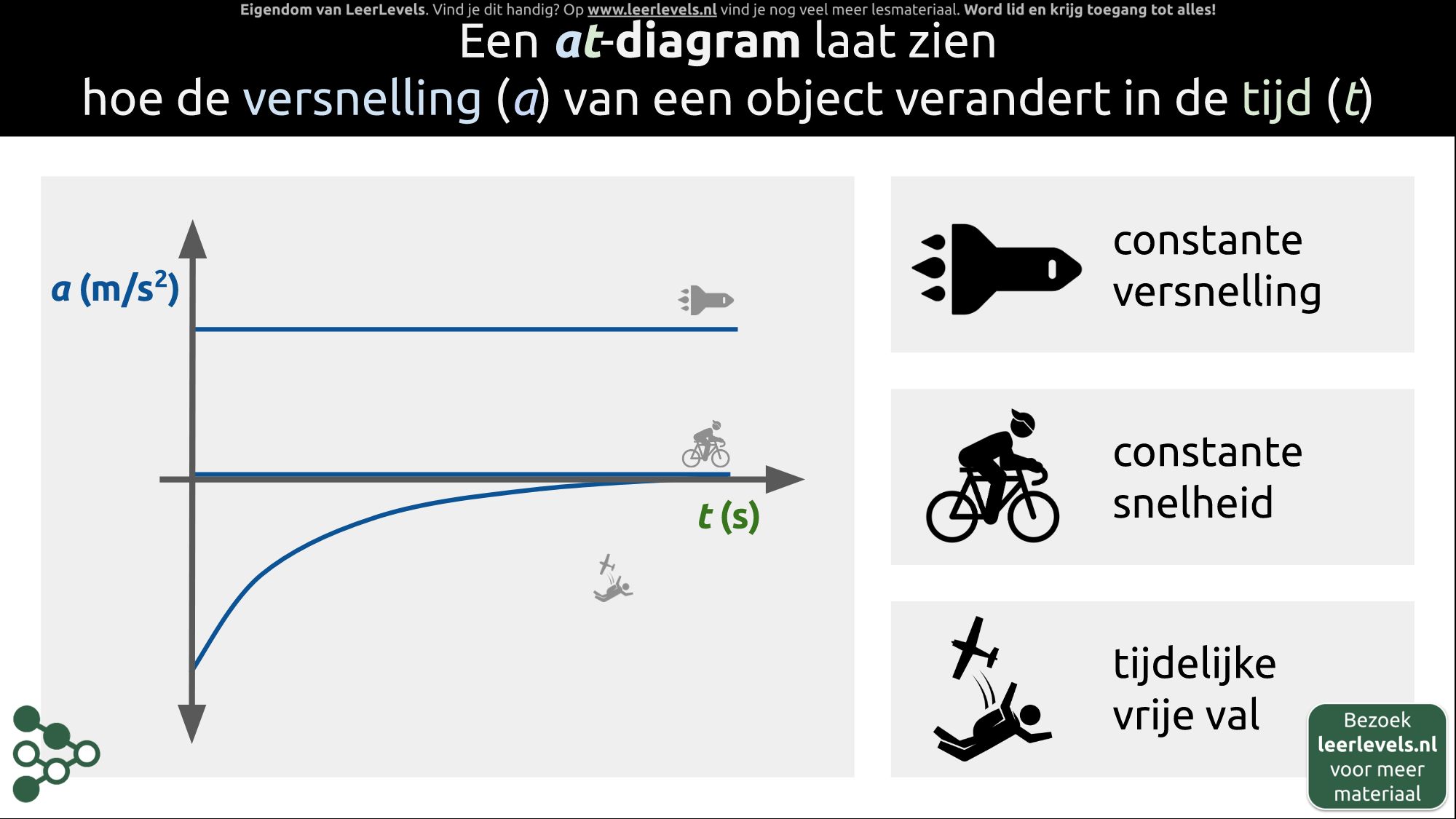
at-diagram

Een at-diagram laat zien hoe de versnelling van een object verandert in de tijd. Dit wordt weergegeven door een grafiek met tijd in seconden op de x-as en versnelling in meter per seconde kwadraat op de y-as. Er zijn verschillende soorten bewegingen die kunnen voorkomen in een at-diagram. Bijvoorbeeld een beweging met constante versnelling, zoals een raket die omhoog gaat, of een beweging waarbij de snelheid constant blijft, zoals fietsen naar school.

Een andere beweging begint met een grote negatieve versnelling en deze versnelling wordt steeds kleiner. Dit kan bijvoorbeeld de beweging zijn van iemand die uit een vliegtuig springt. Deze persoon versnelt in het begin erg snel door de zwaartekracht, maar naarmate hij/zij sneller naar beneden gaat, krijgt hij meer luchtwrijving. Op een gegeven moment is de luchtwrijving even groot als de zwaartekracht, waardoor deze krachten elkaar opheffen en je een versnelling van nul hebt. In het begin is dus sprake van een grote versnelling, maar uiteindelijk compenseert de zwaartekracht de luchtwrijving.

Een at-diagram kan verschillende vormen hebben, maar ze laten allemaal zien hoe de versnelling van een object verandert in de tijd. Versnelling wordt uitgedrukt in meter per seconde kwadraat en tijd in seconden.

(Afbeelding: Animatie voor at-diagram)

Bewegingsdiagrammen omzetten

Bij bewegingsdiagrammen kun je met de raaklijnmethode en oppervlaktemethode andere diagrammen maken. Het st-diagram laat de afstand zien die is afgelegd in de tijd. Als je een vt-diagram wilt maken, kijk je naar de helling van het st-diagram op elk punt. Dat vertelt je de snelheid op dat punt. Als het st-diagram naar beneden gaat, is de snelheid negatief. Als het st-diagram op zijn laagste punt is, is de snelheid nul. Als het st-diagram omhoog gaat, wordt de snelheid positief. Je kunt ook een at-diagram maken. Daarvoor kijk je naar de helling van het vt-diagram op elk punt. Die helling geeft de versnelling weer. Een vt-diagram is een rechte lijn omdat de snelheid constant is. Het at-diagram is dan een horizontale lijn boven nul omdat de versnelling positief is. Als je van een at-diagram naar een vt-diagram wilt, neem je het oppervlak onder het at-diagram en dat vertelt je hoe de snelheid verandert. Maar het vertelt je niet wat de snelheid vóór dat moment was. Als je van vt naar st wilt, kun je ook de oppervlaktemethode gebruiken. [V] = (d[S])/(d[t]) en [a] = (d[V])/(d[t]). Omrekenen van at naar vt: [V] = ∫[a] · d[t]. Omrekenen van vt naar st: [S] = ∫[V] · d[t].

(Afbeelding: Animatie voor Bewegingsdiagrammen omzetten)

Terug naar overzicht Meld je aan

BiNaS

Informatie uit BiNaS halen

In de Binas vind je onder andere formules, meetwaardes en natuurconstanten. Hier is een algemeen stappenplan voor het werken met de Binas:

1. Ga naar het register en vind wat je zoekt.
2. Ga naar de tabel.
3. Vind de formule of waarde die je zoekt.
4. Let op de eenheden.

(Afbeelding: Animatie voor Informatie uit BiNaS halen)

Terug naar overzicht Meld je aan

Bohrmodel

Bohrmodel concept

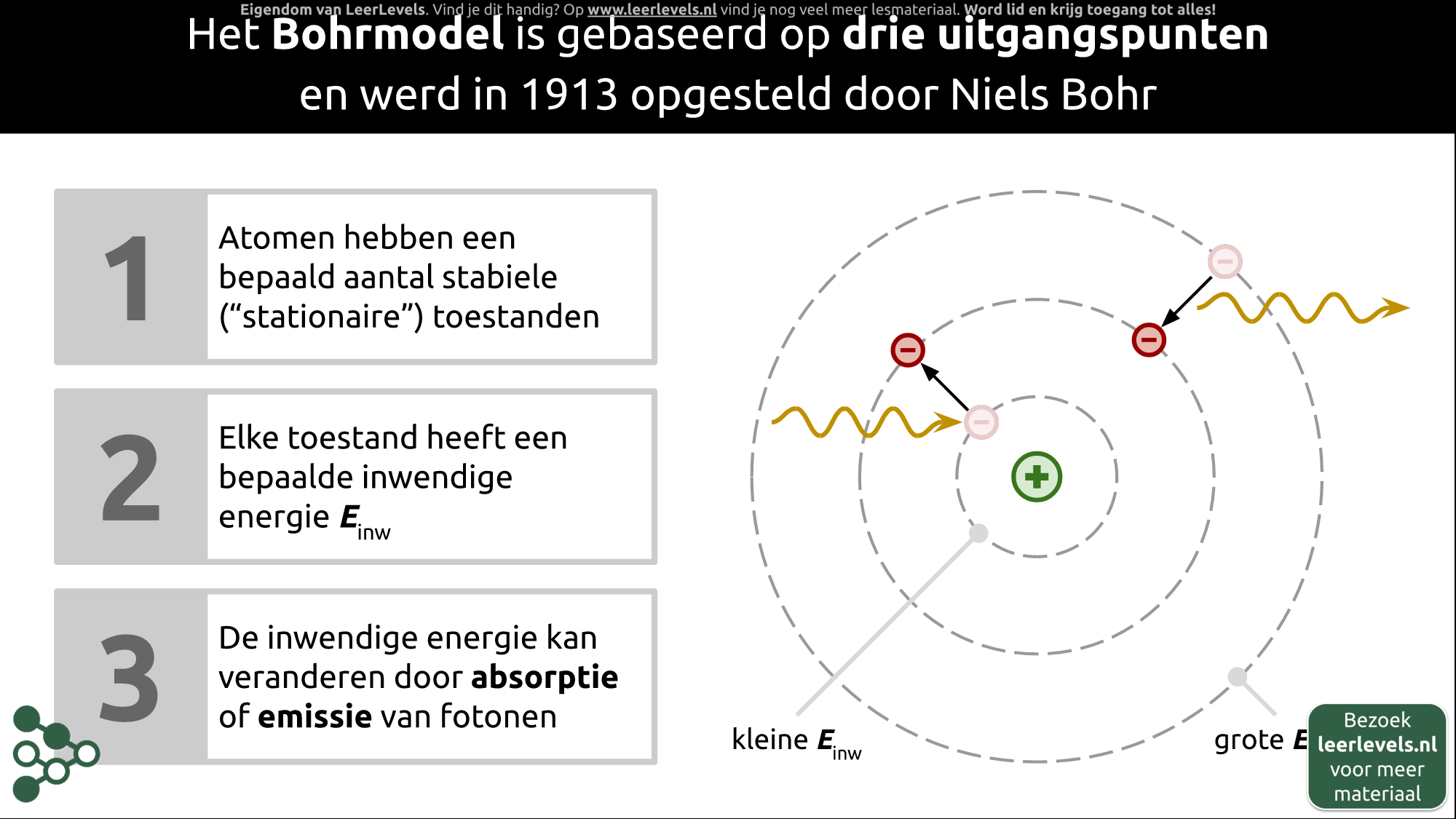
Het Bohr-model gaat over hoe atomen er van binnen uitzien. Het model heeft drie belangrijke ideeën.

Ten eerste kunnen atomen in bepaalde stabiele toestanden zijn, die "stationaire toestanden" worden genoemd. Een waterstofatoom kan bijvoorbeeld verschillende van deze toestanden hebben, afhankelijk van waar het elektron zich bevindt.

Ten tweede heeft elke toestand een bepaalde inwendige energie. Als een elektron dicht bij de kern zit, heeft het weinig energie. Als het verder weg zit, heeft het meer energie.

Ten derde kan de inwendige energie veranderen als er fotonen worden opgenomen of uitgestraald. Dit kan gebeuren als het elektron van de ene naar de andere toestand gaat.

Dit is een eenvoudige samenvatting van het Bohr-model.

(Afbeelding: Animatie voor Bohrmodel concept)

Terug naar overzicht Meld je aan

Boventonen

Boventonen formule afleiden

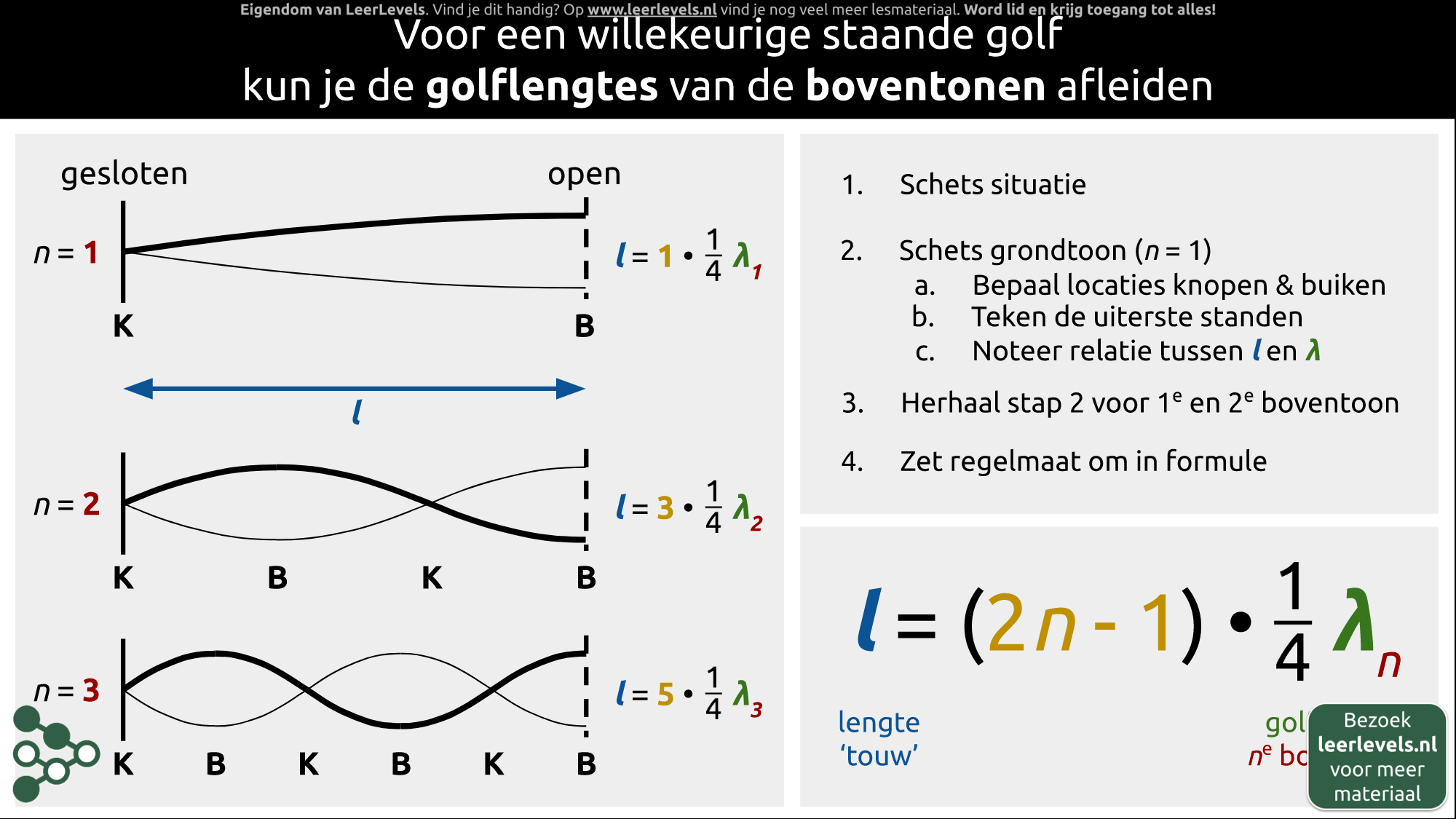
Als je een staande golf hebt, kun je de golflengtes van de boventonen berekenen door deze stappen te volgen:

1. Maak een schets van de situatie. Bijvoorbeeld een buis met een gesloten en een open uiteinde.

2. Schets de grondtoon, wat de laagste toon is met het minste aantal knopen en buiken. Bij het gesloten uiteinde zit een knoop, bij het open uiteinde altijd een buik. Noteer de relatie tussen lengte van de buis en golflengte van de grondtoon.

3. Herhaal stap 2 voor de eerste en tweede boventoon. Bij de eerste boventoon (n = 2) is de lengte van de buis gelijk aan 3/4 keer de golflengte van de boventoon. Bij de tweede boventoon (n = 3) is de lengte van de buis gelijk aan 5/4 keer de golflengte van de boventoon.

4. Maak een algemene formule om de lengte van de buis te berekenen: l = (2 n-1) · 1/4 · λn, waarbij l de lengte van de buis is in meter, n de index van de boventoon (lopend vanaf 1 voor de grondtoon) en λn de golflengte van de n-de boventoon in meter.

(Afbeelding: Animatie voor Boventonen formule afleiden)

Boventonen formules

Als je een instrument bespeelt, zoals een trompet of een dwarsfluit, dan weet je dat er verschillende tonen uitkomen als je verschillende noten speelt. Deze tonen worden 'boventonen' genoemd. De formule om de golflengte van deze boventonen te berekenen hangt af van het soort instrument dat je hebt. Als je bijvoorbeeld een buis hebt met twee gesloten of twee open uiteinden, dan is de formule l = n · ½ · λn. Hierbij staat l voor de lengte van de buis in meters, λn voor de golflengte van de n-de boventoon, en n is het nummer van de boventoon waar je naar kijkt (1 voor de laagste toon, 2 voor de volgende toon, enzovoort). Als je een buis hebt met één gesloten en één open uiteinde, dan ziet de formule er anders uit: l = (2n-1) · 1/4 · λn.

(Afbeelding: Animatie voor Boventonen formules)

Terug naar overzicht Meld je aan

Brandpunt lens

Brandpunt van een lens

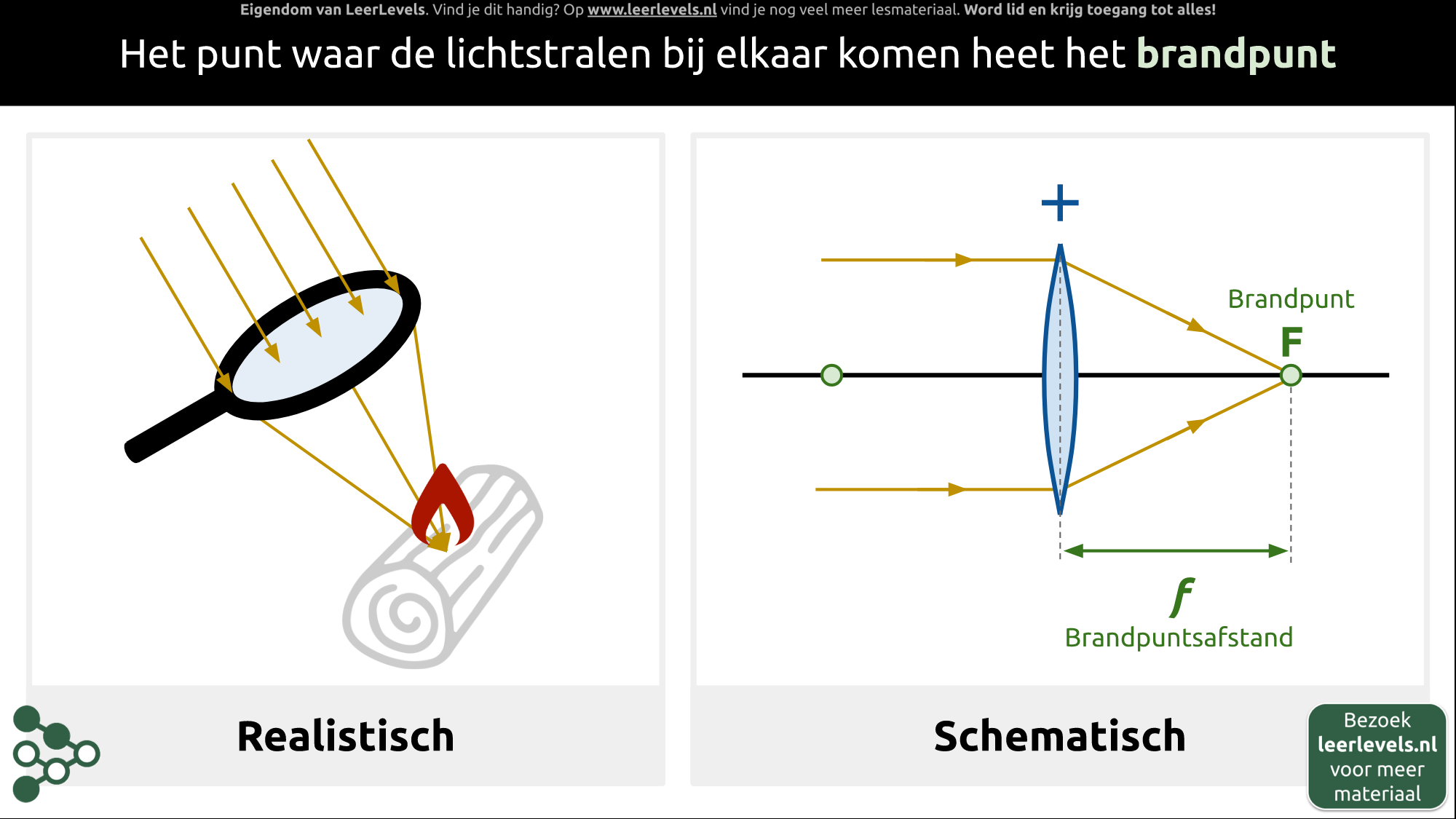
Het punt waar lichtstralen samenkomen, wordt het brandpunt genoemd. Wanneer je een vergrootglas gebruikt om zonlicht op te vangen, worden de evenwijdige lichtstralen gefocust in het brandpunt. Op die plek komt alles samen, waardoor het zeer warm wordt; dit is handig als je een vuurtje wilt maken. Schematisch werkt het als volgt: een positieve lens laat evenwijdige lichtstralen binnenkomen en focust deze op één punt. Dit punt noemen we het brandpunt, aangeduid als F. De afstand tussen het brandpunt en de lens noemen we de brandpuntsafstand, f.

(Afbeelding: Animatie voor Brandpunt van een lens)

Terug naar overzicht Meld je aan

Brandstof

Fossiele brandstof

Fossiele brandstoffen zijn een beperkte bron van chemische energie die al miljoenen jaren in de grond zijn opgeslagen. Voorbeelden van fossiele brandstoffen zijn olie voor transport, aardgas voor verwarming en kolen voor industriële toepassingen. Omdat deze voorraden eindig zijn, moeten we ervoor zorgen dat we snel overstappen op hernieuwbare energiebronnen om klimaatverandering te verminderen.

(Afbeelding: Animatie voor Fossiele brandstof)

Terug naar overzicht Meld je aan

Brekingsindex

Brekingsindex concept

De brekingsindex n laat zien hoe goed licht door een doorzichtige stof heen gaat. Als een lichtstraal van de zon van lucht naar water gaat, verandert de brekingsindex. Dit komt doordat de snelheid van licht in lucht anders is dan in water. Hoe hoger de brekingsindex, hoe moeilijker het is voor licht om door de stof te bewegen. De lichtsnelheid is alleen constant in een vacuüm en verandert in andere materialen. De brekingsindex vertelt dus hoe makkelijk of moeilijk het is voor licht om door een bepaalde stof te gaan.

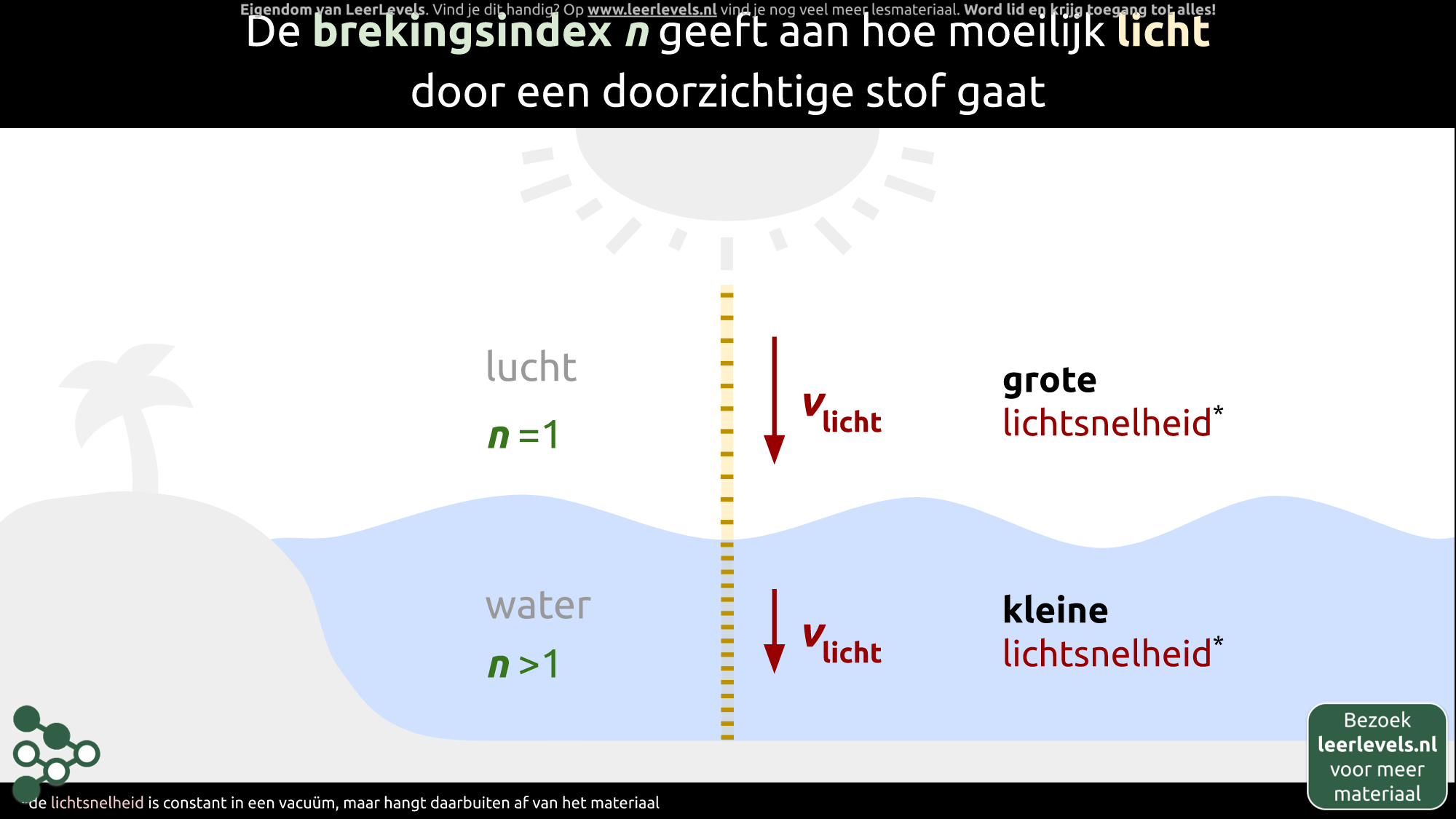
(Afbeelding: Animatie voor Brekingsindex concept)

Brekingsindex formule

De brekingsindex van een stof is de verhouding tussen de lichtsnelheid in vacuüm en de lichtsnelheid in de stof. Je kunt de brekingsindex berekenen door de lichtsnelheid in vacuüm te delen door de lichtsnelheid in de stof:

n = c/v

waarbij n de brekingsindex is, c de lichtsnelheid in vacuüm, en v de lichtsnelheid in de stof. Omdat zowel c als v in de eenheid meter per seconde (m/s) worden gemeten, is de brekingsindex eenheidsloos.

(Afbeelding: Animatie voor Brekingsindex formule)

Terug naar overzicht Meld je aan

Breuken

Betekenis van een breuk

Bij een breuk doe je wat er boven de streep staat keer elkaar en wat er onder de streep staat deel je hierdoor. Als je bijvoorbeeld A keer B gedeeld door C keer D hebt, dan wordt dit A keer B keer D gedeeld door C. Als je 7 keer 1 gedeeld door 4 plus 3 keer 4 hebt, dan kun je de 7 boven de breuk zetten. Omdat er ook een 7 onder de breuk staat, kun je deze wegdelen en houd je 4 over.

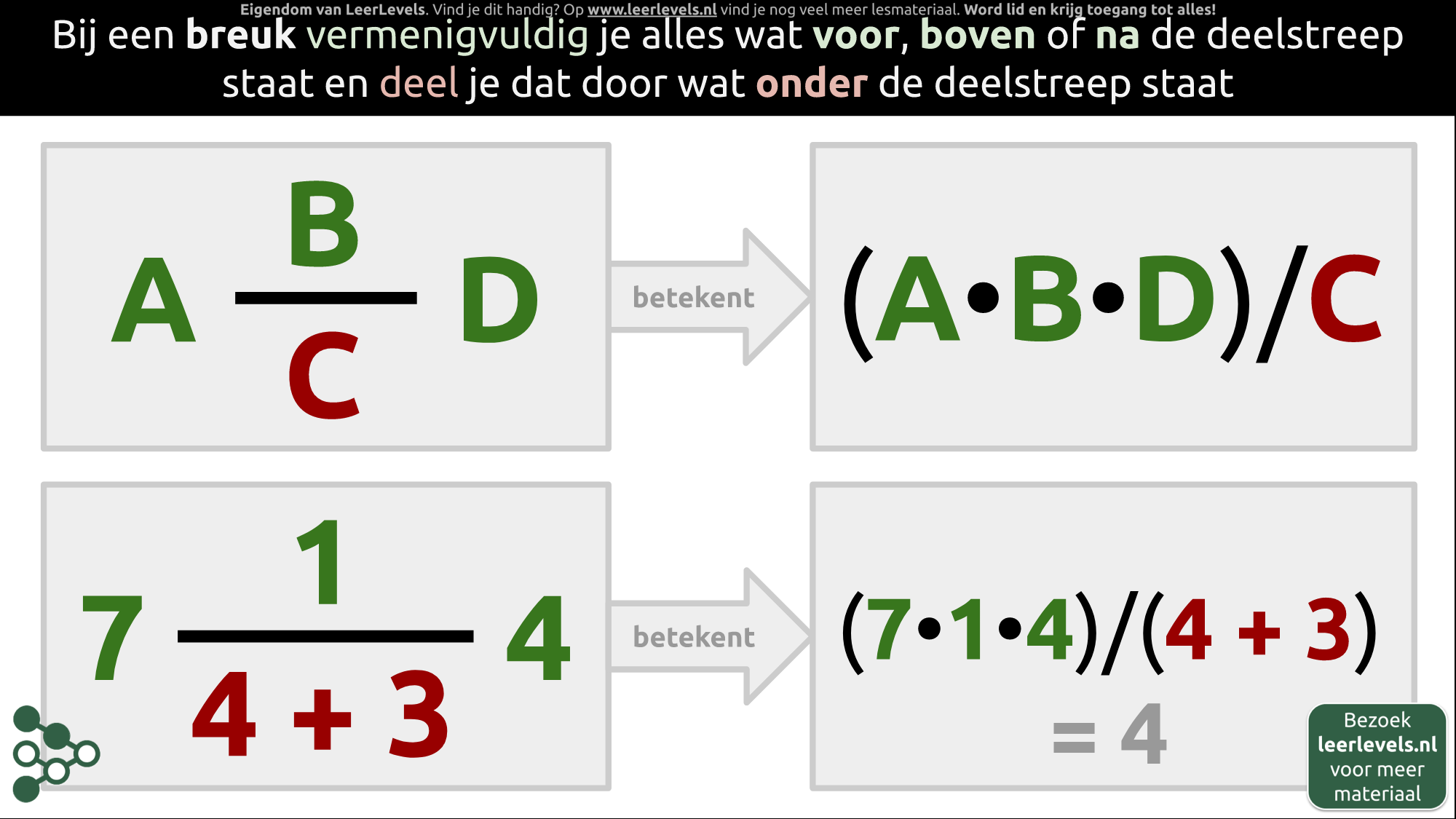
(Afbeelding: Animatie voor Betekenis van een breuk)

Vormen van een breuk

Breuken kunnen op verschillende manieren geschreven worden en toch dezelfde waarde hebben. Bijvoorbeeld, 4/2 kan ook geschreven worden als 8/4, met de schuine deelstreep op dezelfde regel. De breuk 10/5 is gelijk aan 2.

Daarnaast betekent 200% eigenlijk 200 gedeeld door 100. Als iets dus 200% is, heeft het een waarde van 2.

De notatie 2,0 is afgerond naar hele getallen en heeft de waarde van 2.

Al deze verschillende vormen, waarvan de meeste eigenlijk stiekem een breuk zijn, hebben dezelfde waarde. Het is dus belangrijk om deze verschillende vormen goed te herkennen en te begrijpen. Ze worden vaak door elkaar gebruikt, maar hebben allemaal dezelfde waarde.

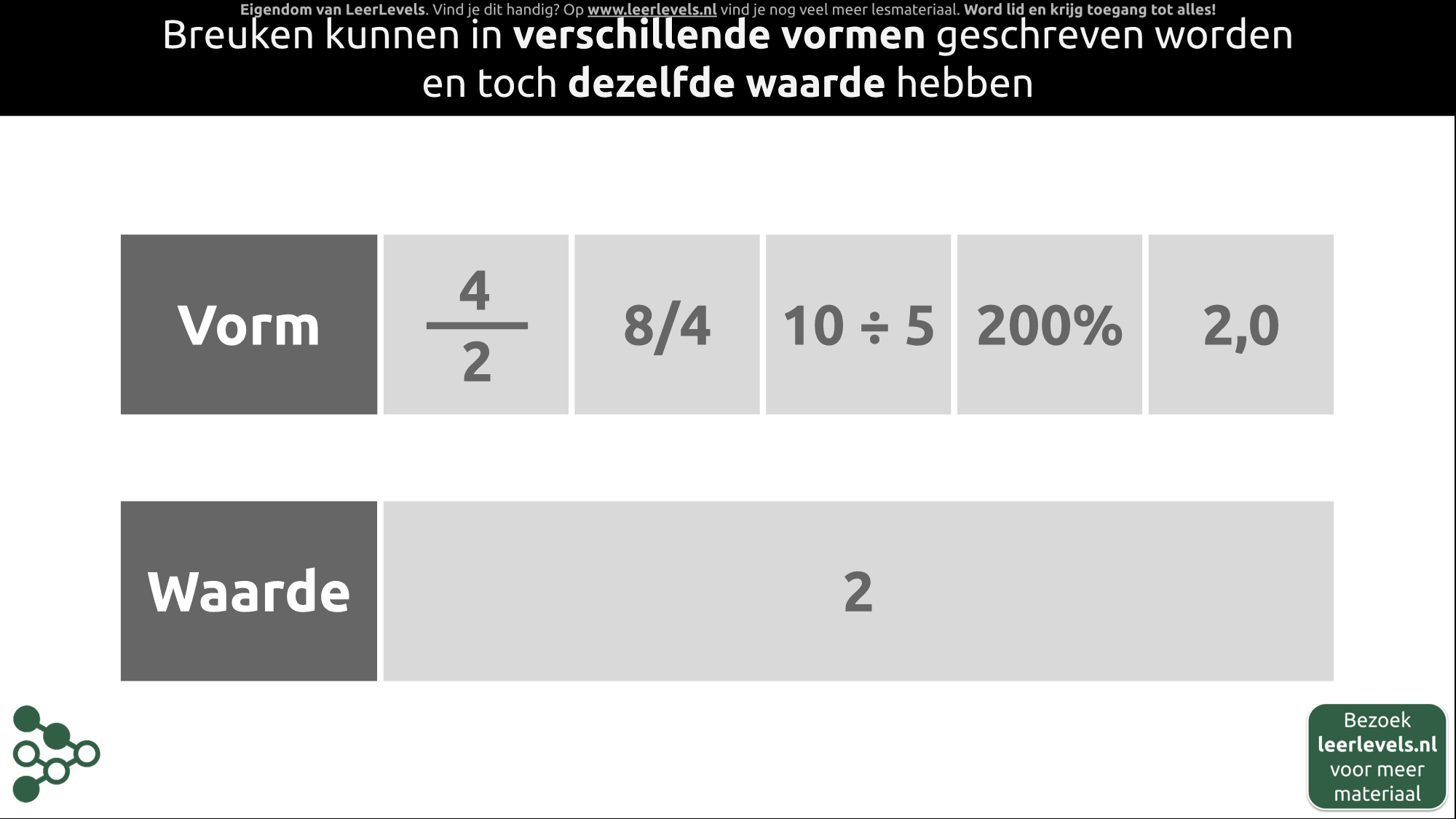
(Afbeelding: Animatie voor Vormen van een breuk)

Manipuleren van een breuk

De waarde van een breuk verandert niet als je zowel de teller als de noemer vermenigvuldigt of deelt met hetzelfde getal. Bijvoorbeeld:

2/3 = (2 · 4)/(3 · 4) = (8)/(12)

Hier zijn zowel de teller als de noemer vermenigvuldigd met 4. Een ander voorbeeld:

(6)/(10) = (6/2)/(10/2) = 3/5

In dit geval zijn zowel de teller als de noemer gedeeld door 2.

Dit principe geldt alleen voor vermenigvuldigen en delen. Als je hetzelfde getal optelt bij of aftrekt van zowel de teller als de noemer, verandert de waarde van de breuk wel. Bijvoorbeeld:

½ \neq (1 + 1)/(2 + 1) = 2/3

en

2/4 \neq (2 - 1)/(4 - 1) = 1/3

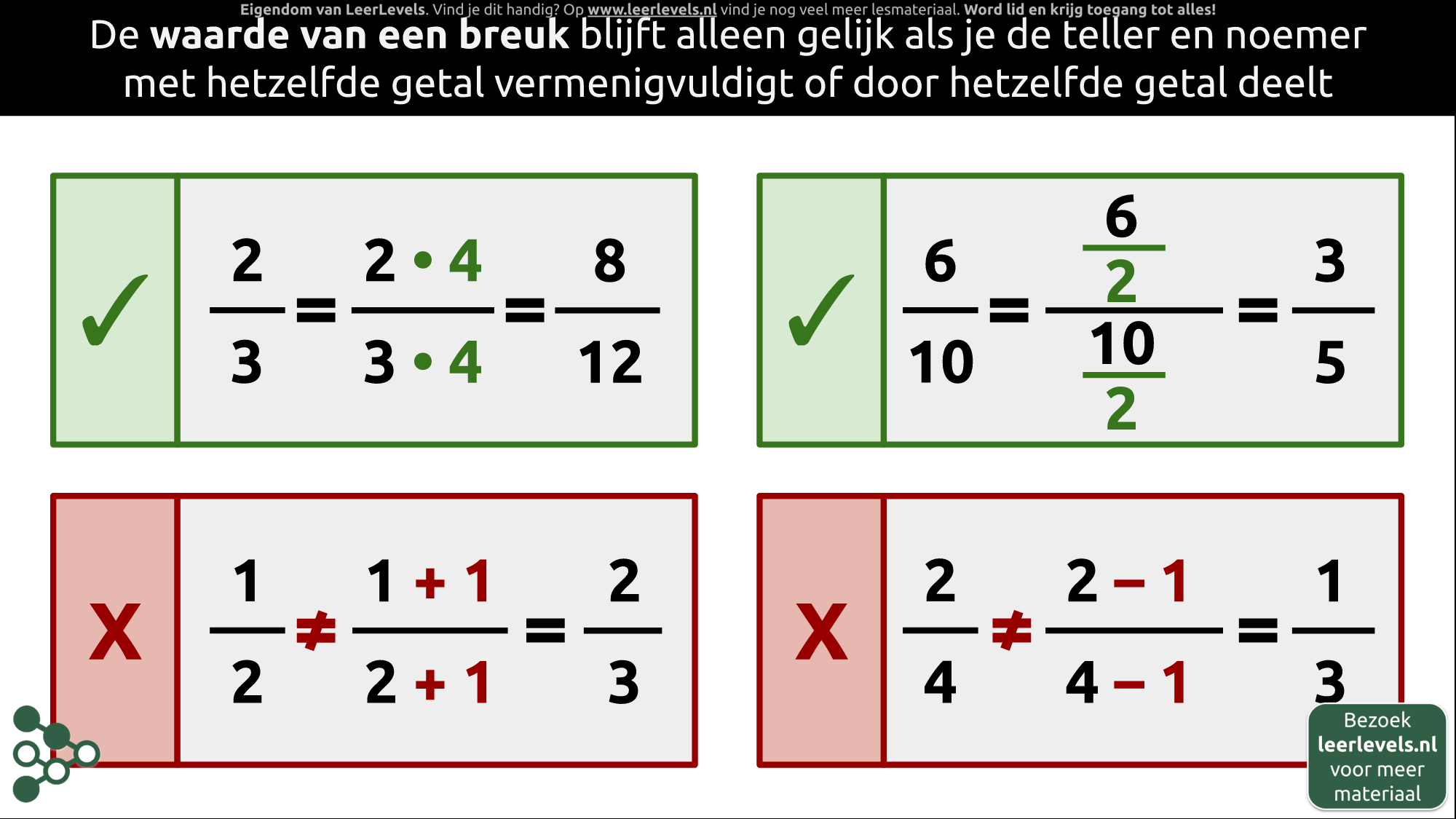
(Afbeelding: Animatie voor Manipuleren van een breuk)

Terug naar overzicht Meld je aan

Calorie

Eenheid calorie

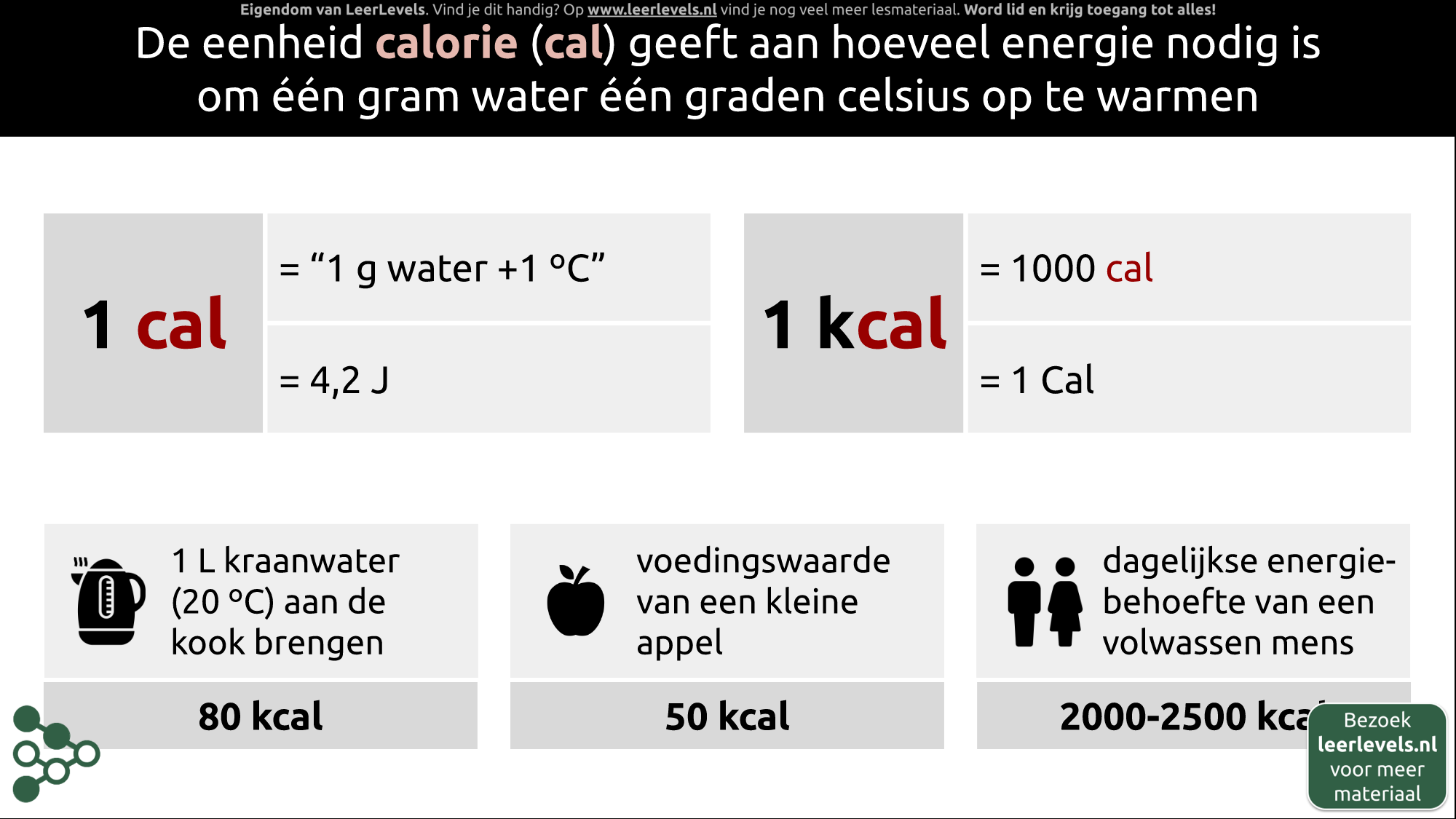
De eenheid 'calorie' geeft aan hoeveel energie er nodig is om één gram water met één graad Celsius te verwarmen. Dit is geen SI-eenheid. Een calorie (1 cal) is ongeveer gelijk aan 4,2 Joule. In de praktijk wordt naast de 'calorie' ook vaak gebruikgemaakt van de kilocalorie (kcal), wat gelijkstaat aan 1000 calorieën. Op voedingsmiddelen wordt dit vaak aangeduid als Cal met een hoofdletter C. Veel voedingsmiddelen hebben een bekend aantal calorieën, zoals een kleine appel die ongeveer 50 Cal bevat. Voor een volwassen mens is gemiddeld zo'n 2000 tot 2500 Cal per dag nodig. Dit komt neer op ongeveer 40 tot 50 appels per dag, al is het natuurlijk niet gezond om zoveel van hetzelfde te eten.

(Afbeelding: Animatie voor Eenheid calorie)

Terug naar overzicht Meld je aan

Cardiogram

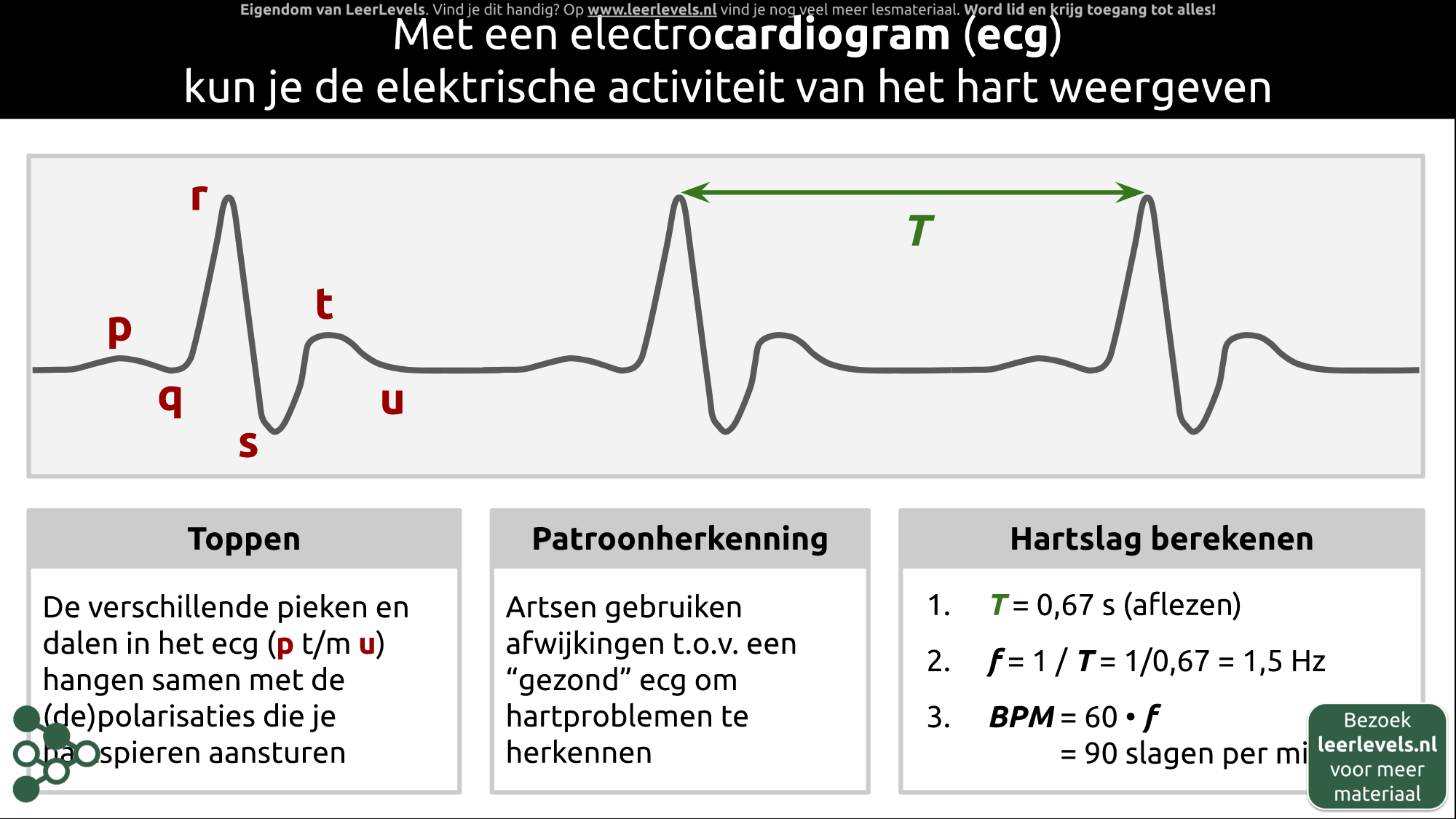
Met een elektrocardiogram (ECG) kun je zien hoe het hart elektrisch werkt. Het ECG meet pieken en dalen die iets zeggen over de aansturing van de hartspieren. Artsen kunnen aan de hand van deze metingen afwijkingen ontdekken en op die manier hartproblemen vaststellen. Ook kunnen ze op basis van het ECG de hartslag berekenen door de tijd tussen twee pieken te meten. De hartslag wordt meestal uitgedrukt in beats per minute (bpm) en kan worden berekend door de frequentie te vermenigvuldigen met 60.

(Afbeelding: Animatie voor Cardiogram)

Terug naar overzicht Meld je aan

Carnotcyclus

Carnotcyclus concept

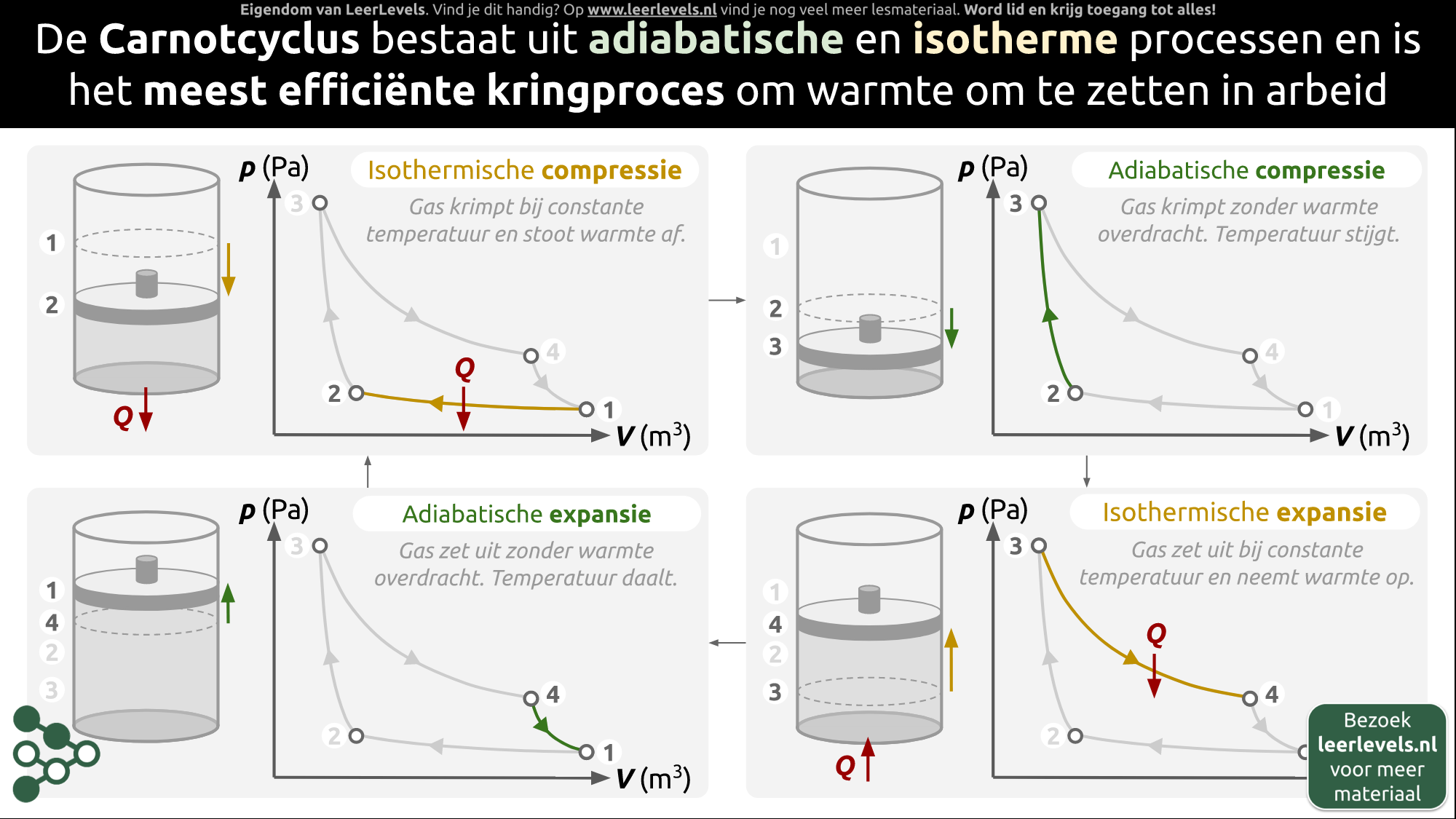
De Carnotcyclus is een kringproces waarbij warmte wordt omgezet in arbeid. De Carnotcyclus is het meest efficiënte kringproces en is daarmee een theoretische maximum van hoeveel warmte omgezet kan worden in arbeid. De cyclus bestaat uit adiabatische en isotherme processen die achter elkaar plaats vinden. De processen verlopen als volgt:

1. Isothermische compressie (Punt 1 naar Punt 2):
- Het gas krimpt bij constante temperatuur, waarbij het warmte afstaat.
- Op het (p,V)-diagram verloopt deze toestandsverandering langs de isotherm van de minimale temperatuur van het proces tussen punt 1 en punt 2.

2. Adiabatische compressie (Punt 2 naar Punt 3):
- Het gas krimpt zonder warmte uit te wisselen met de omgeving. De toegenomen druk zorgt ervoor dat de temperatuur toeneemt.
- Op het (p,V)-diagram loopt deze toestandsverandering vanaf de isotherme van de minimale temperatuur tot de isotherm van de maximale temperatuur tussen punt 2 en punt 3.

3. Isothermische expansie (Punt 3 naar Punt 4):
- Het gas zet uit bij constante temperatuur en neemt daarbij warmte op.
- Op het (p,V)-diagram verloopt deze toestandsverandering langs de isotherm van de maximale temperatuur van het proces tussen punt 3 en punt 4.

4. Adiabatische expansie (Punt 4 naar Punt 1):
- Het gas zet uit zonder warmte uit te wisselen. De afname in druk druk zorgt ervoor dat de temperatuur daalt.
- Op het (p,V)-diagram loopt deze toestandsverandering vanaf de isotherme van de maximale temperatuur tot de isotherm van de minimale temperatuur tussen punt 4 en punt 1.

(Afbeelding: Animatie voor Carnotcyclus concept)

Terug naar overzicht Meld je aan

Cirkel

Cirkel eigenschappen

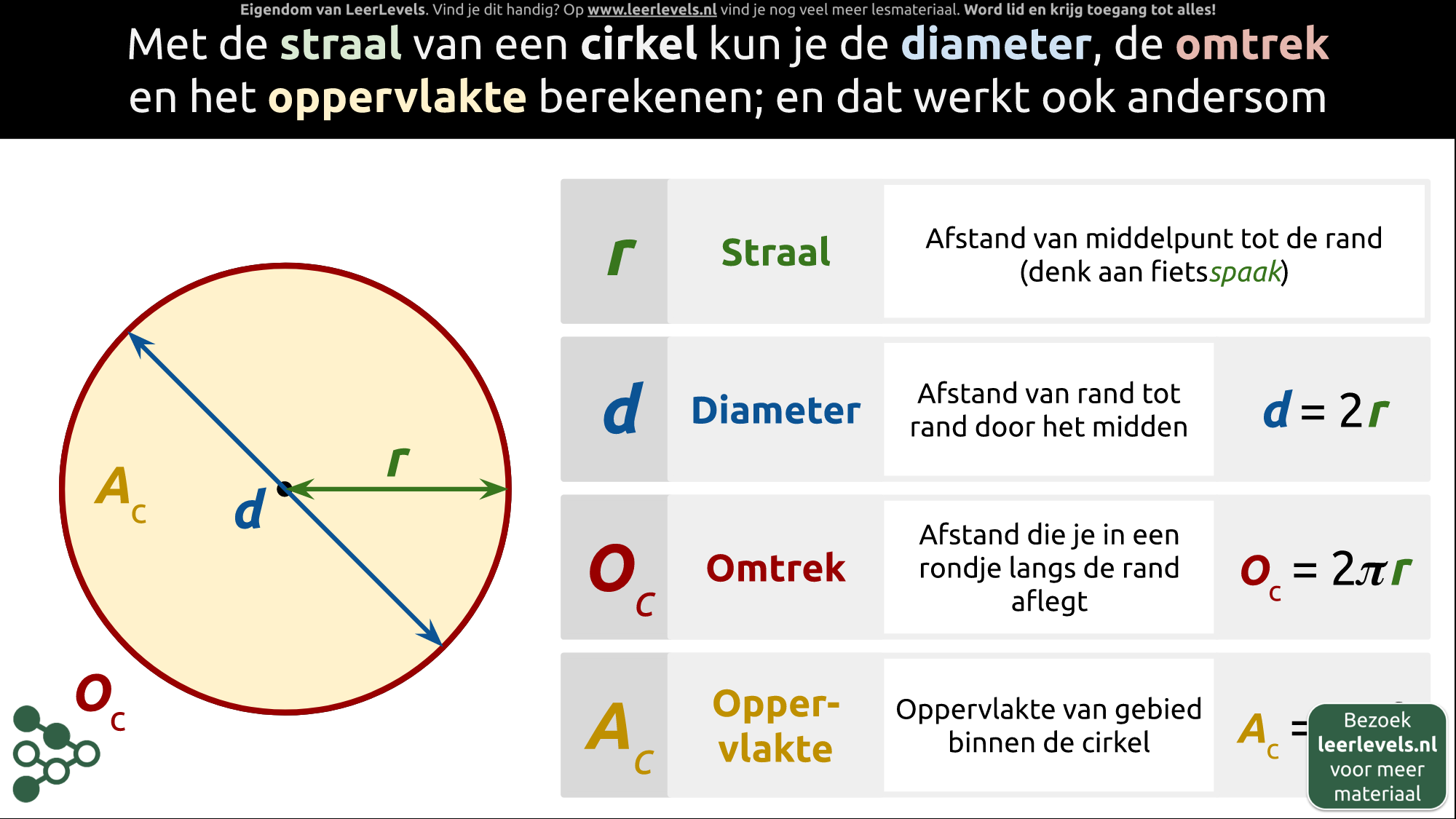
Een cirkel heeft een straal, diameter, omtrek en oppervlakte. De straal is de afstand tussen het middelpunt en de rand van de cirkel. De diameter is de afstand tussen twee tegenoverliggende punten op de rand, waarbij de lijn door het middelpunt gaat. De straal is altijd de helft van de diameter. De omtrek is de lengte van een touw dat om de cirkel gaat. Dit wordt berekend met de formule O = 2π r, waarbij π ongeveer 3 is. De oppervlakte van een cirkel wordt berekend met de formule A = π r². Een voorbeeld van een straal is de spaak in een fietswiel. In formules schrijven we de omtrek als O en de oppervlakte als A.

(Afbeelding: Animatie voor Cirkel eigenschappen)

Terug naar overzicht Meld je aan

Cirkelbeweging

Eenparige cirkelbeweging concept

Een eenparige cirkelbeweging is wanneer iets in een cirkel beweegt met een constante snelheid en constant versnelt naar het middelpunt. Stel je een draaimolen voor die tegen de klok in draait. De persoon die erop zit, vliegt met gestrekte armen rond. Op een bepaald moment bevindt de persoon zich op de plek van de stippellijn en even later op de plek van het grijze vlak erachter. Het verschil in snelheid (dv) tussen deze posities wordt veroorzaakt door een versnelling (a) die loodrecht staat op de snelheid (v) van de persoon. De locatievector van de persoon (r) loopt parallel aan de versnelling (a) op alle plekken in de cirkelbaan. In het figuur zie je dat de snelheid naar rechts wijst, de versnelling naar boven en de locatievector naar beneden toe.

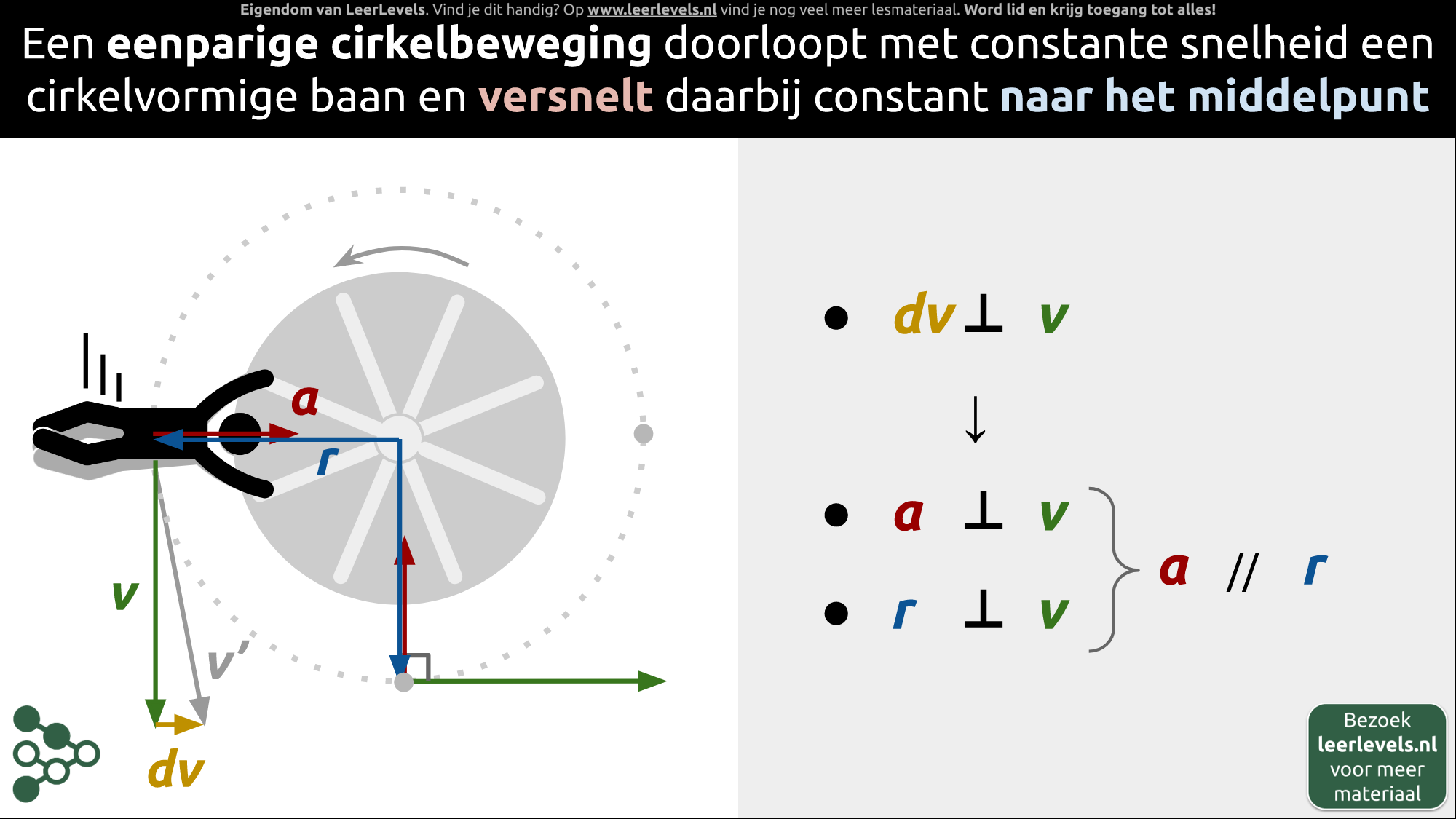
(Afbeelding: Animatie voor Eenparige cirkelbeweging concept)

Baansnelheid eenparige cirkelbeweging formule

Een eenparige cirkelbeweging is een beweging waarbij je steeds op dezelfde afstand blijft van een vast punt (bijvoorbeeld het middelpunt van een cirkel) en waarbij je met een constante snelheid beweegt. Hoe groot de snelheid is, hangt af van hoe groot de cirkel is en hoe lang je over een rondje doet. De afstand die je aflegt in één rondje noemen we de omtrek van de cirkel, en die kun je uitrekenen met de formule 2πr. Als je weet hoe groot de cirkel is en hoe snel je beweegt, kun je uitrekenen hoe lang je over een rondje doet. Dit noemen we de trillingstijd (T). De frequentie (f) van de beweging is het omgekeerde van de trillingstijd: f = 1/T. De baansnelheid (v) is gelijk aan de omtrek van de cirkel gedeeld door de trillingstijd: v = 2πr/T. Dit kun je ook schrijven als v = 2πrf. Baansnelheid wordt uitgedrukt in meter per seconde, baanstraal (r) in meter, trillingstijd (T) in seconde en frequentie (f) in hertz.

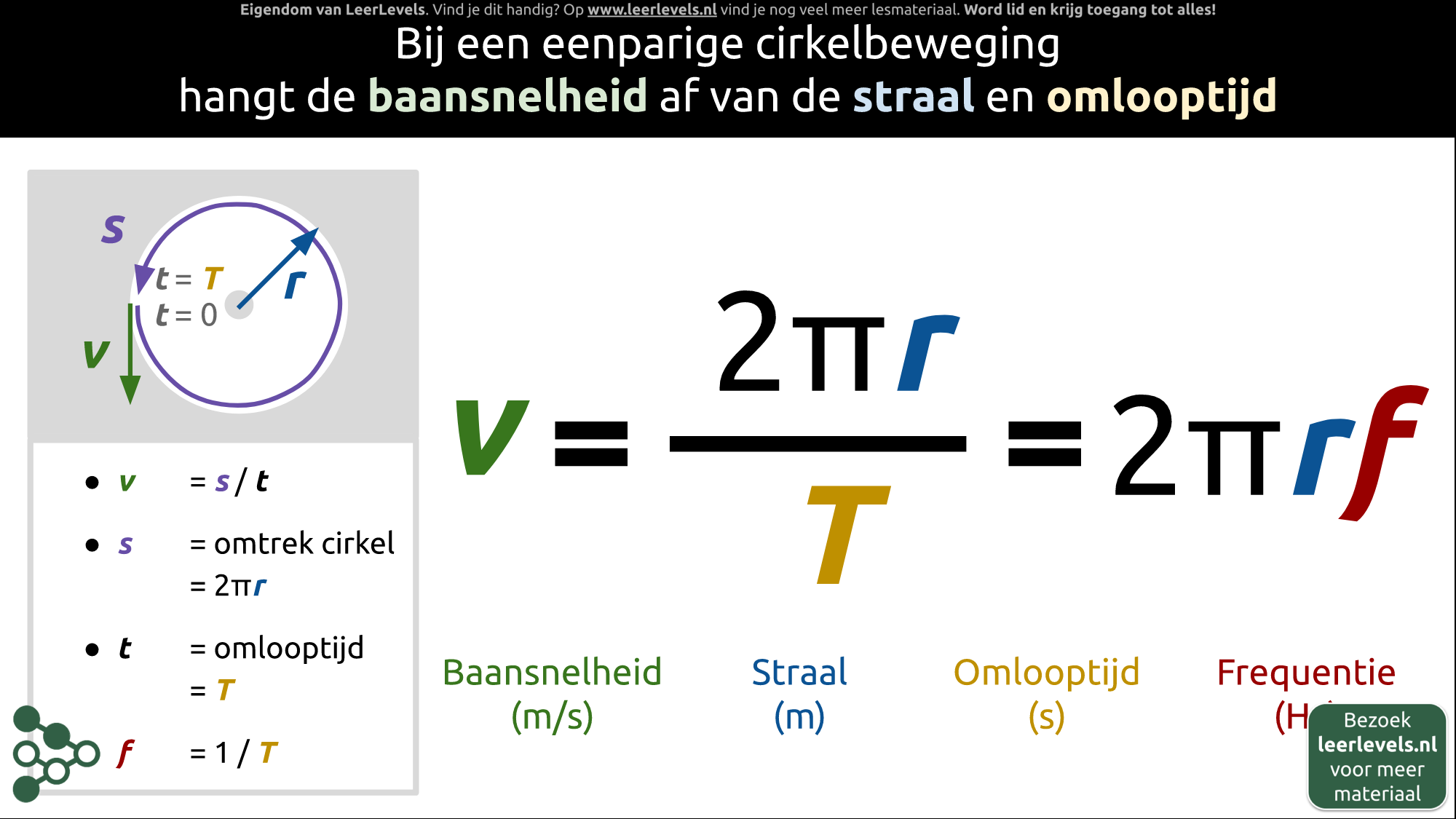
(Afbeelding: Animatie voor Baansnelheid eenparige cirkelbeweging formule)

Terug naar overzicht Meld je aan

Combinatielenzen

De totale sterkte van meerdere lenzen achter elkaar is gelijk aan de som van de sterktes van de afzonderlijke lenzen.

Wanneer je meerdere lenzen combineert, zoals twee positieve lenzen, een negatieve lens en nog een positieve lens, zonder enige tussenruimte, vormen deze lenzen samen één combinatielens met dezelfde sterkte als de optelsom van alle afzonderlijke lenzen. De sterkte van deze combinatielens Sc wordt gegeven door de formule

Sc = ∑i Si

waarin Sc de sterkte van de combinatielens in dioptrie is en Si de sterkte van de individuele lenzen in dioptrie.

Een vergelijkbare formule geldt voor de brandpuntsafstand van de combinatielens. Deze wordt gegeven door de formule

(1)/(fc) = ∑i (1)/(fi)

waarin fc de brandpuntsafstand van de combinatielens is en fi de brandpuntsafstand van de individuele lenzen.

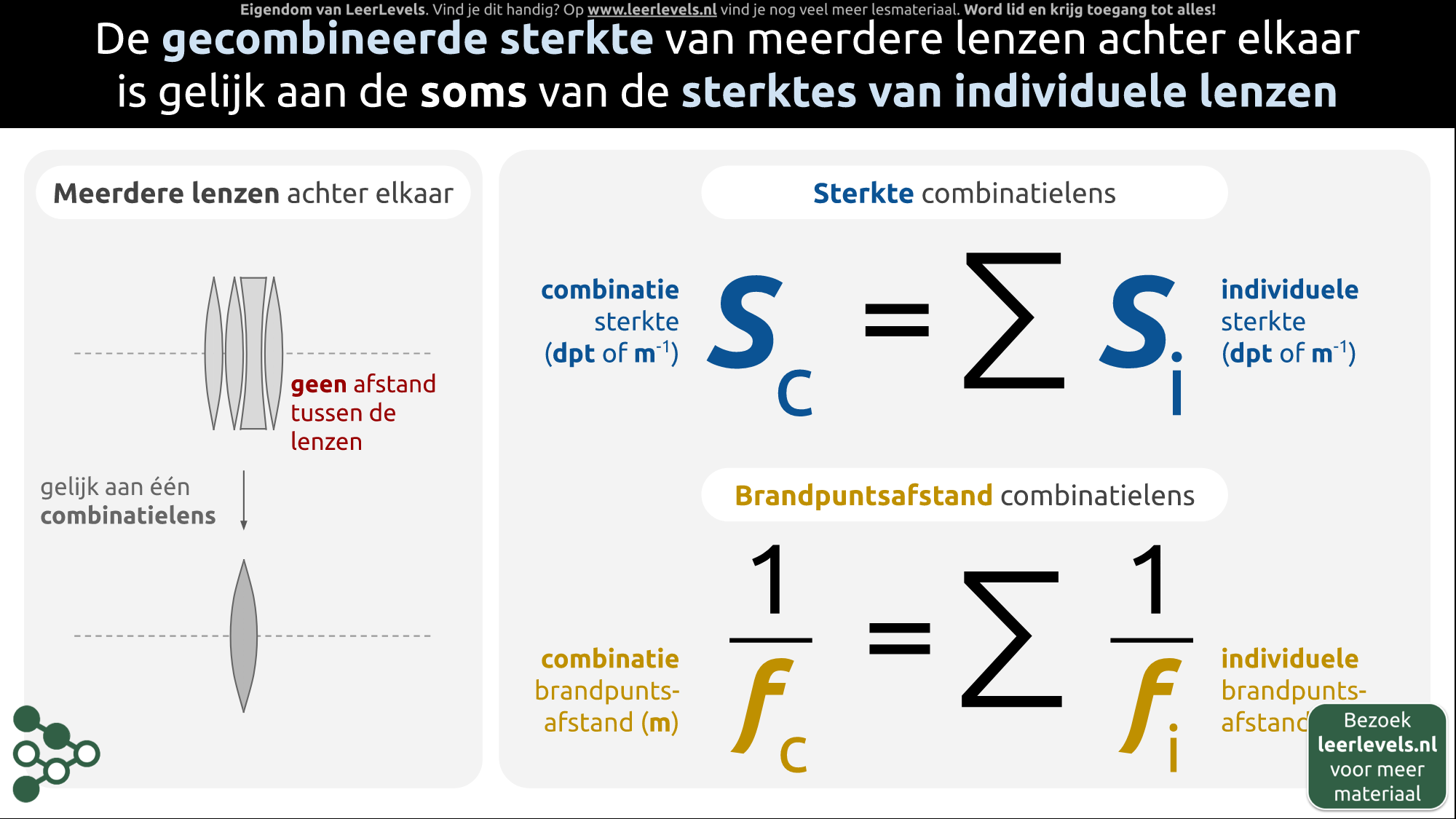
(Afbeelding: Animatie voor Combinatielenzen)

Terug naar overzicht Meld je aan

Commutator

Commutator werking

Een commutator is een onderdeel dat ervoor zorgt dat de stroomrichting in een draaiende machine elke 180 graden verandert. Het bestaat uit twee helften van een cirkel die verbonden zijn met een enkele draad. Het geheel kan ronddraaien terwijl er twee contactpunten aan de zijkant blijven zitten die niet meedraaien. Als er een batterij op wordt aangesloten, kan de stroom van de pluspool via de ene helft van de cirkel naar de andere helft stromen en zo een circuit vormen. Als de commutator draait, kunnen de contactpunten langs de helften van de cirkel bewegen, waardoor de stroomrichting verandert. Dit kan worden gebruikt om een elektromotor te maken.

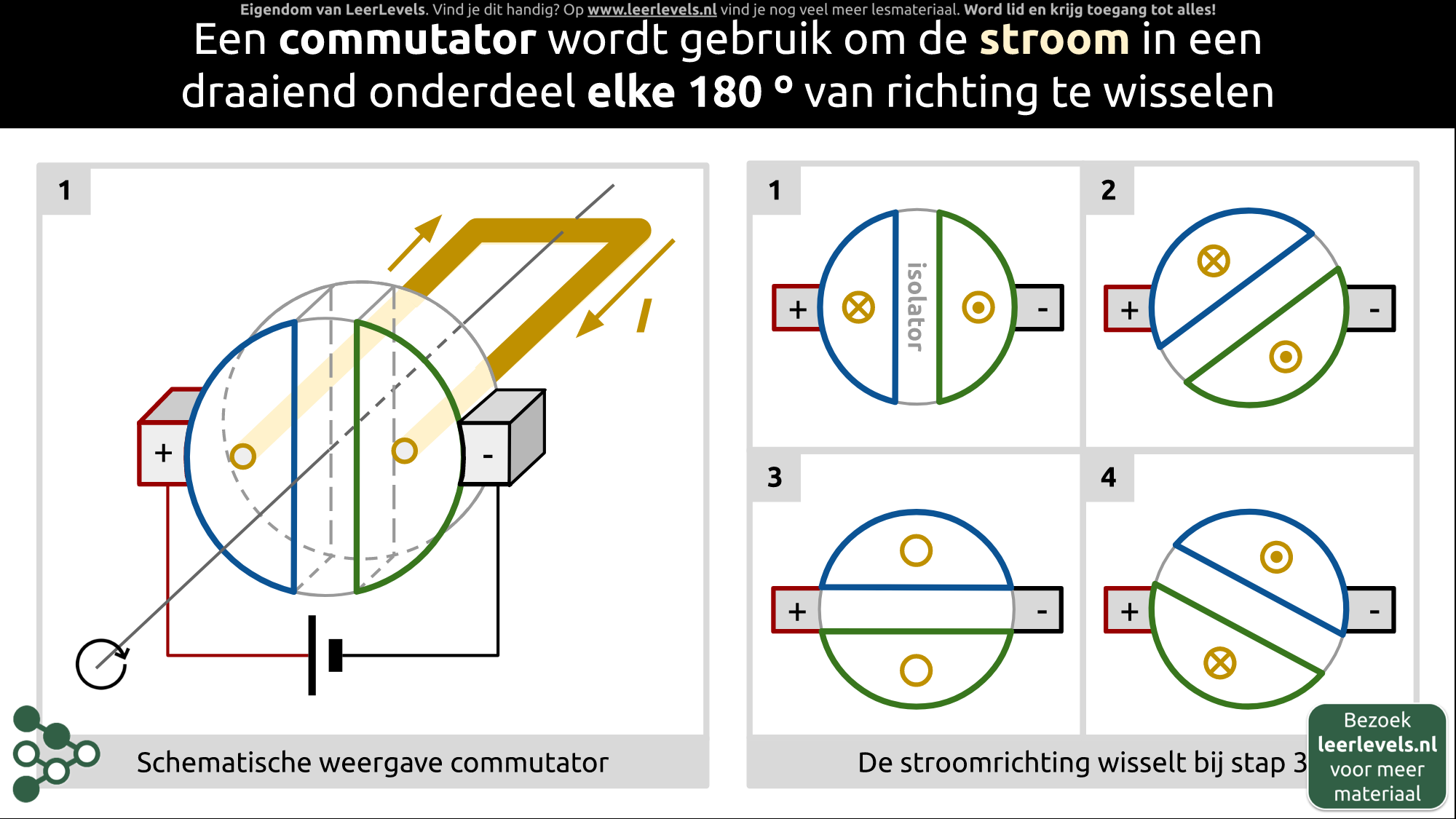
(Afbeelding: Animatie voor Commutator werking)

Terug naar overzicht Meld je aan

Complimentariteit

Complimentariteit concept

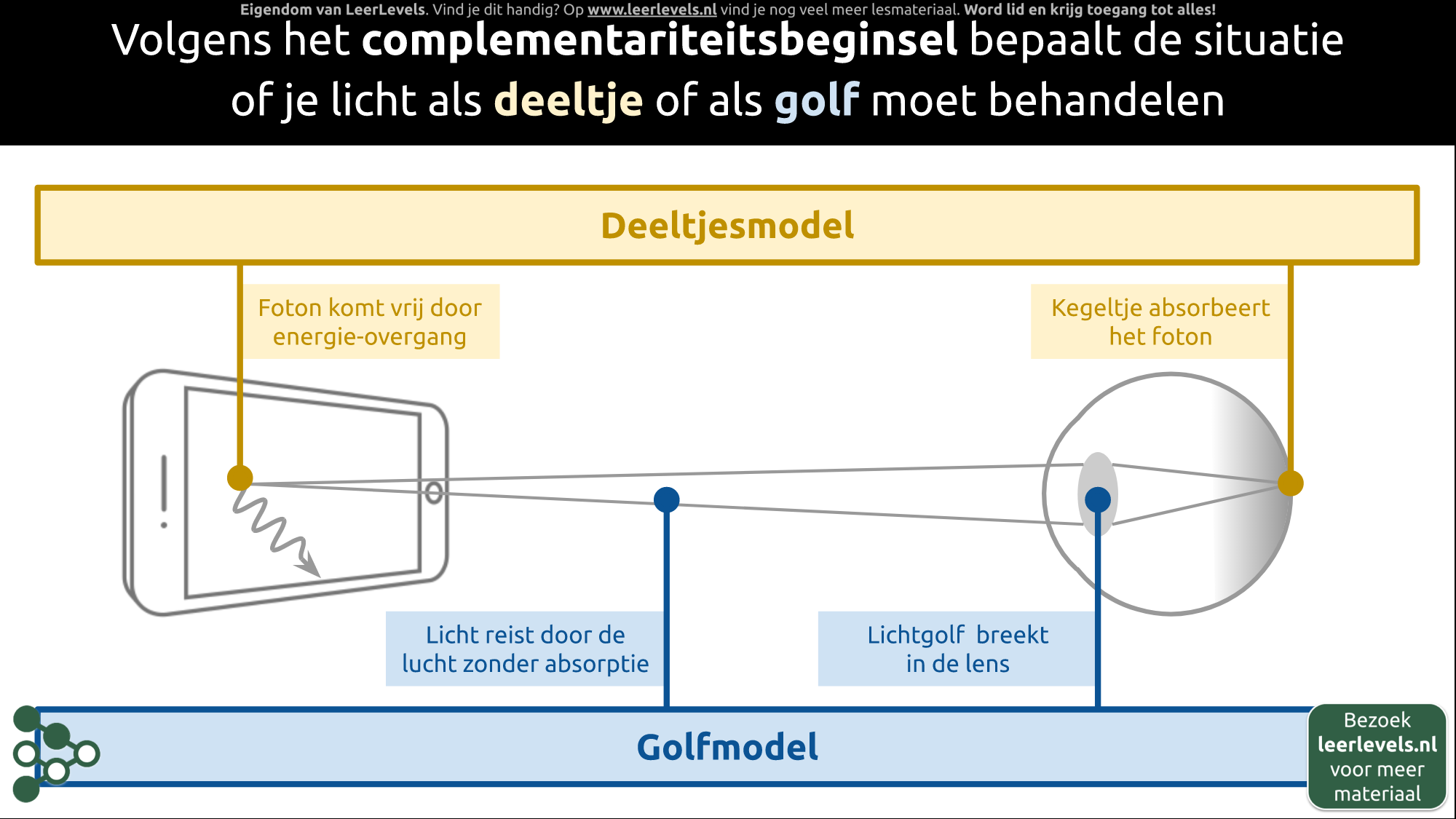
Volgens het complementariteitsbeginsel bepaalt de omgeving of je licht als een deeltje of als een golf moet beschouwen. In ons dagelijks leven, bijvoorbeeld bij het kijken naar een scherm, speelt deze dualiteit een rol. Licht reist naar onze lens en wordt afgebogen naar ons netvlies, zodat we het kunnen zien. In dit proces moet je licht soms als een deeltje en soms als een golf behandelen.

Laten we eens enkele fasen bekijken. Aan het begin, wanneer het foton vrijkomt, moeten we het als een deeltje zien. Het foton komt namelijk vrij door een energieovergang in het scherm, wat alleen verklaard kan worden met het deeltjesmodel. Wanneer het licht naar ons toe beweegt, zonder dat het onderweg met andere deeltjes in de lucht botst, behandelen we het als een golf. Op het moment dat het licht door onze lens breekt, beschouwen we het eveneens als een golf. Breking is immers een golfverschijnsel. En als het licht uiteindelijk in ons netvlies wordt waargenomen, moeten we het weer als deeltjes beschouwen. De kegeltjes en staafjes in ons netvlies absorberen fotonen stuk voor stuk, wat een interactie tussen deeltjes is.

Dus zelfs voor een eenvoudig proces als het bekijken van een scherm moeten we zowel naar het deeltjesmodel als het golfmodel kijken. Waarom dit precies zo werkt en hoe de natuur 'beslist' wat wanneer geldt, is nog onbekend.

(Afbeelding: Animatie voor Complimentariteit concept)

Terug naar overzicht Meld je aan

Constante van Planck

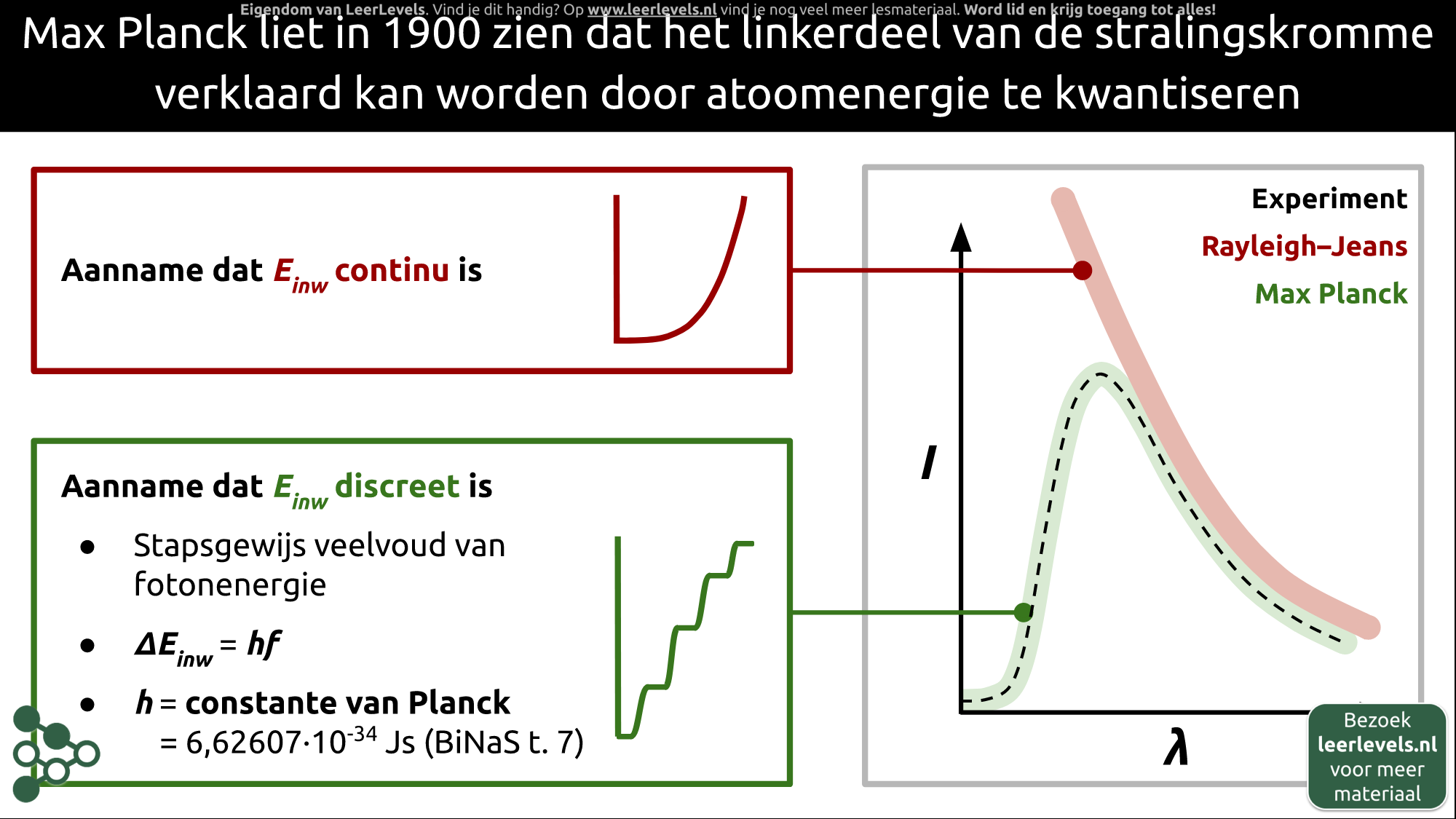
In 1900 ontdekte Max Planck dat atomen energie op een bepaalde manier uitstralen. Hij zag dat de intensiteit van uitgestraald licht van een zwarte straler bij elke golflengte anders was. Hij merkte op dat de energie van atomen niet continu, maar discreet was. Dit betekent dat de energie in kleine stappen wordt verdeeld, die veelvouden zijn van een constante (h) vermenigvuldigd met de frequentie (f) van het licht. Einstein kwam later tot de conclusie dat deze energiestappen eigenschappen waren van fotonen.

(Afbeelding: Animatie voor Constante van Planck)

Terug naar overzicht Meld je aan

Constructie beeld

Constructie beeld positieve lens

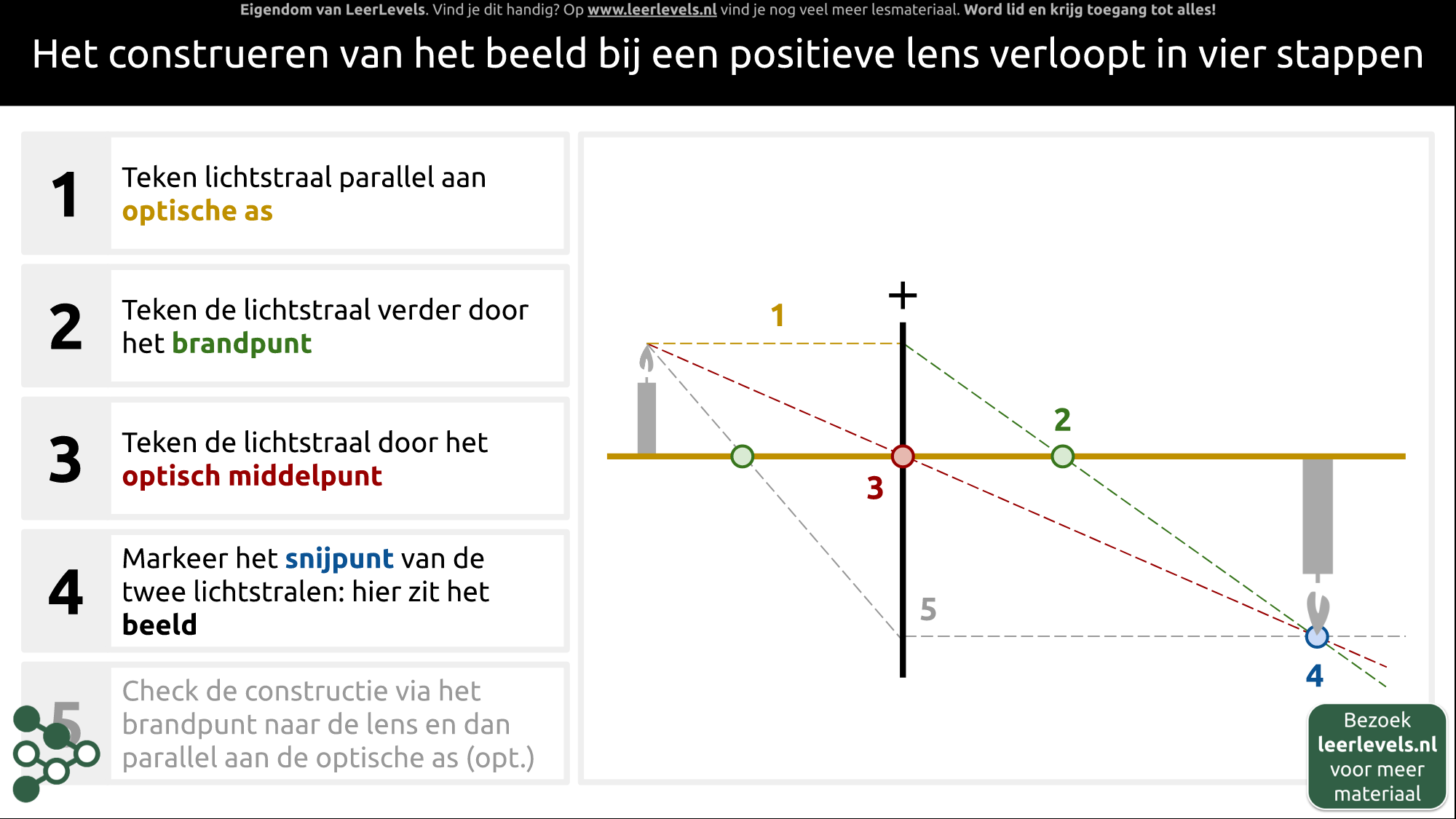
Bij het maken van een beeld met een positieve lens volg je vier stappen. Neem bijvoorbeeld een positieve lens met een optische as en een groen brandpunt. De eerste stap is een lichtstraal tekenen die parallel loopt aan de optische as. De tweede stap is deze lichtstraal te verlengen tot aan het groene brandpunt. De derde stap is de lichtstraal tekenen die door het optisch middelpunt loopt. Tot slot markeer je het snijpunt van deze twee lichtstralen als het beeldpunt. In deze situatie zal het beeldpunt daar liggen waar de vlam van de kaars is.

(Afbeelding: Animatie voor Constructie beeld positieve lens)

Terug naar overzicht Meld je aan

Constructiestralen

Constructiestralen positieve lens

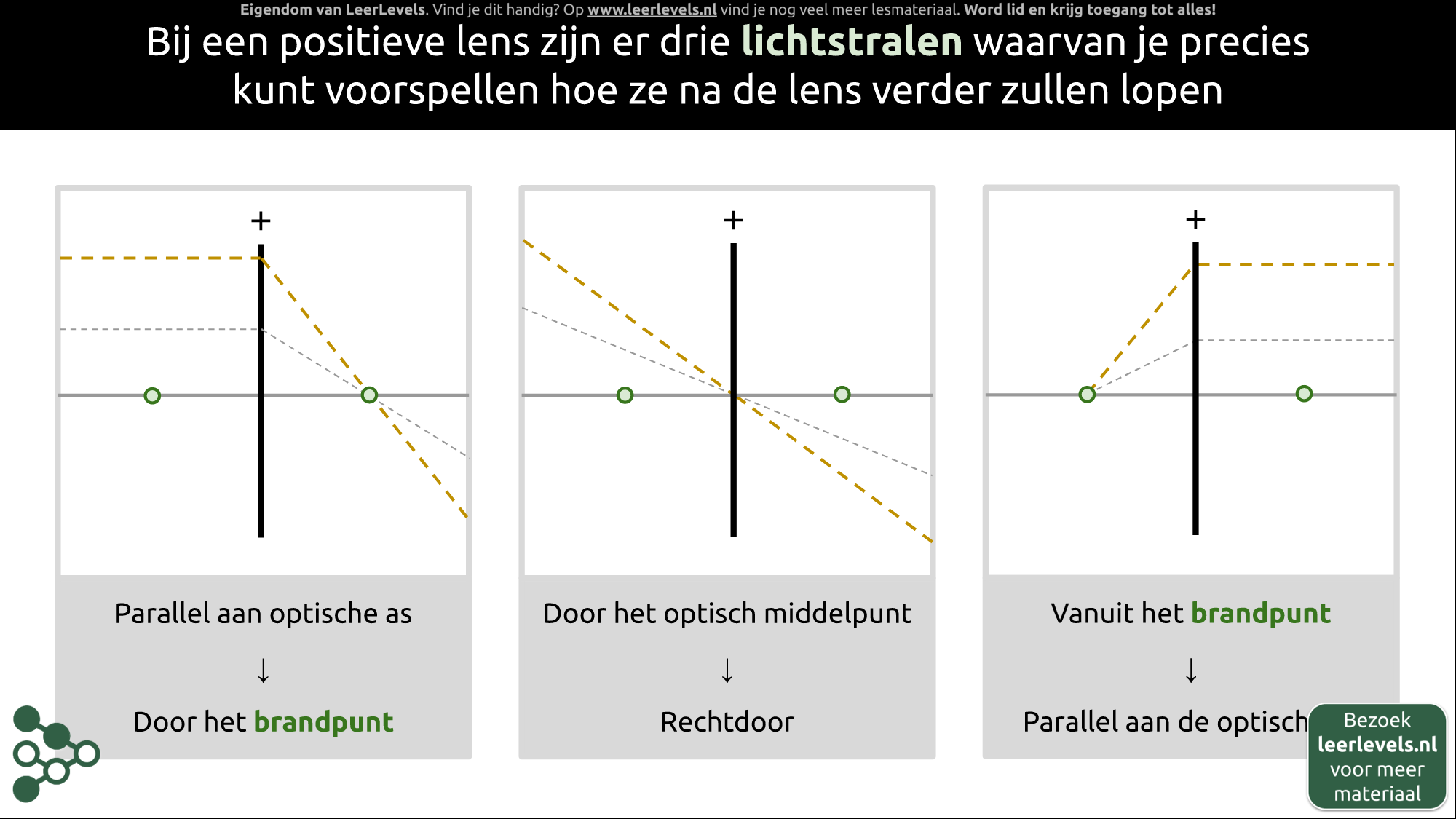
Bij een positieve lens zijn er drie lichtstralen waarvan je precies kunt voorspellen hoe ze na de lens verder zullen lopen:

1. De eerste straal loopt parallel aan de optische as. Deze straal zal door het brandpunt gaan nadat hij door de lens is gegaan. Het maakt hierbij niet uit hoe hoog de straal binnenkomt, zolang hij maar parallel aan de as is.

2. De tweede constructiestraal is de straal die precies door het optisch midden van de lens gaat. Als deze straal recht op de lens invalt, dan gaat hij zonder te buigen rechtdoor.

3. De derde constructiestraal is de straal die uit het brandpunt komt. Na de lens zal deze straal rechtdoor gaan, dus parallel aan de optische as.

(Afbeelding: Animatie voor Constructiestralen positieve lens)

Constructiestralen negatieve lens

Een negatieve lens buigt lichtstralen weg van de rechte lijn in het midden van de lens. Als er een lichtstraal parallel aan deze rechte lijn binnenkomt, dan buigt deze af door de lens en lijkt het alsof de gebogen straal afkomstig is uit een denkbeeldig groen punt. Dit denkbeeldige punt noemen we het virtuele brandpunt. De locatie van dit virtuele brandpunt helpt ons bij het tekenen van hoe lichtstralen zich gedragen als ze door de lens gaan.

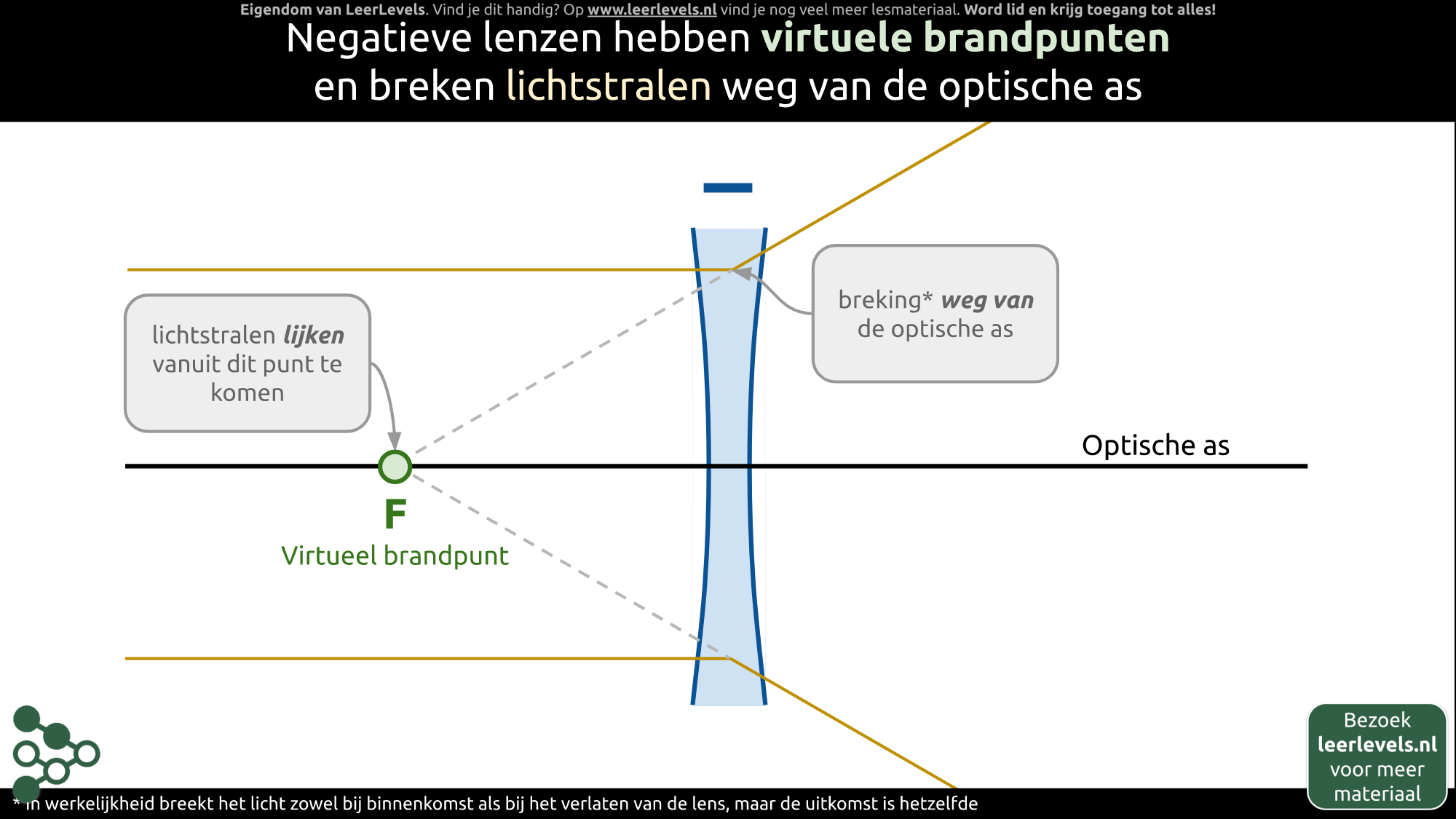
(Afbeelding: Animatie voor Constructiestralen negatieve lens)

Terug naar overzicht Meld je aan

Controle

Antwoord-check

FALSE is een handige manier om te onthouden welke vijf stappen je aan het eind van een opdracht moet controleren. De F staat voor Formule, zorg dat je deze altijd opschrijft. De A staat voor Antwoord, controleer of je de vraag goed hebt beantwoord. De L staat voor Logisch, bekijk of je antwoord logisch is. De S staat voor Significantie, let op het juiste aantal significante cijfers. De E staat voor Eenheid, controleer of je de juiste eenheid hebt gebruikt. Bijvoorbeeld: schrijf niet alleen Fz = 800N, maar ook de formule Fz = m · g. Als de vraag is of iets binnen één minuut lukt, schrijf dan niet dat het 59 seconde duurt, maar beantwoord duidelijk dat het binnen één minuut lukt. Als je berekening aangeeft dat iemand 3 km/s rent, is er waarschijnlijk een fout gemaakt, bijvoorbeeld door een factor van 1000 te vergeten. 3 m/s voor het rennen van iemand is logischer. Let op de significantie, bijvoorbeeld, schrijf 2 · 3 niet als 6,000, maar gewoon als 6. En geef de juiste eenheid, bijvoorbeeld, schrijf niet alleen 10, maar 10 meter. Kortom, controleer altijd de stappen van FALSE aan het eind van een opdracht.

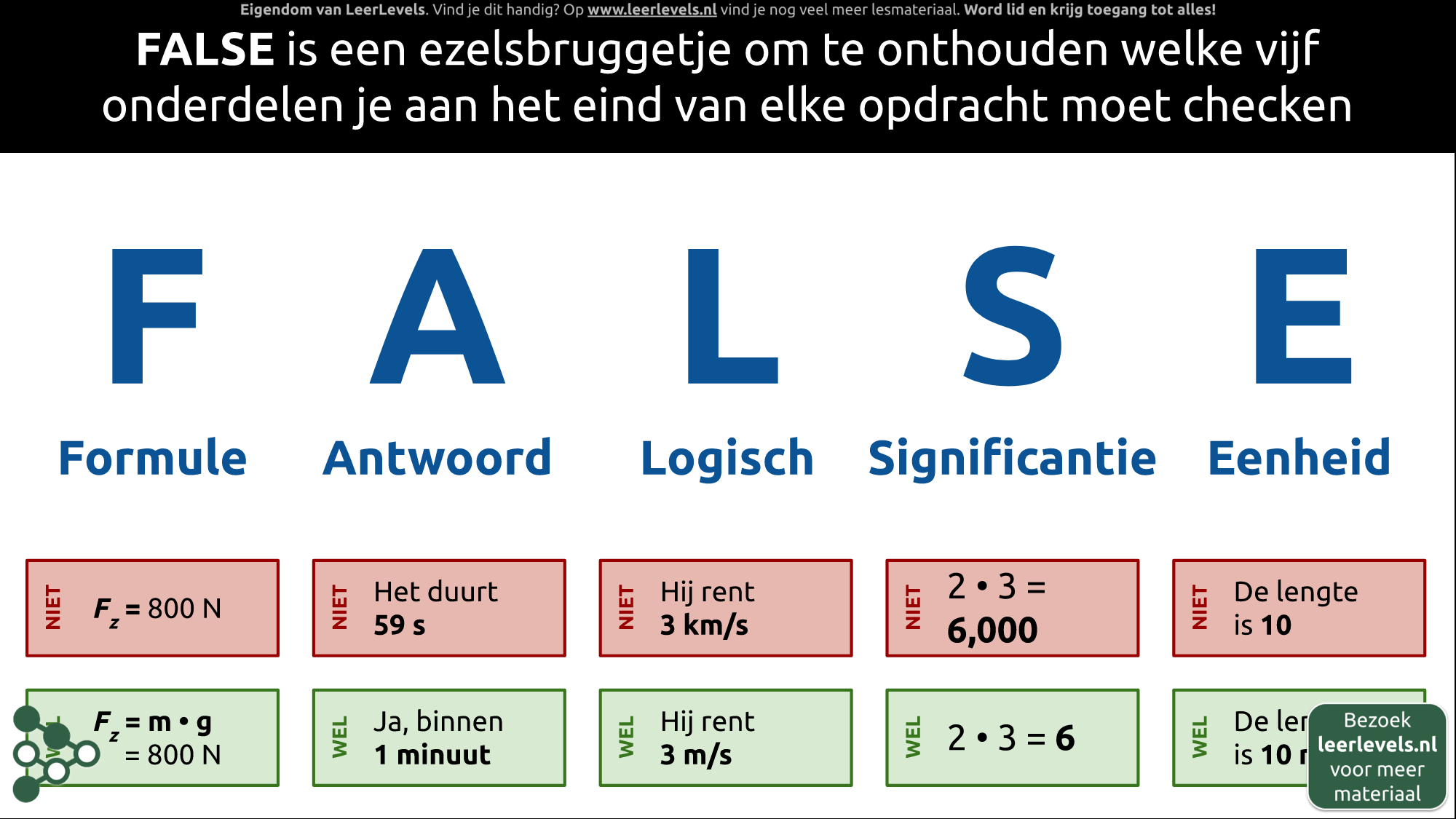
(Afbeelding: Animatie voor Antwoord-check)

Terug naar overzicht Meld je aan

Coulomb

Eenheid Coulomb

De Coulomb (C) is de standaard eenheid van lading en is gelijk aan de lading van ongeveer 6 × 10¹⁸ protonen. De formule voor lading (Q) is Q = I × t, waarbij Q de lading is in Coulomb, I de stroom in Ampère en t de tijd in seconden. Dit betekent dat C (Coulomb) gelijk is aan A (Ampère) vermenigvuldigd met s (seconde). Een Coulomb is dus gelijk aan een Ampère keer een seconde. Ampère is het aantal protonen per seconde. Dus als we dat vermenigvuldigen met een seconde, krijgen we dat een Coulomb gelijk is aan de lading van 6,24 × 10¹⁸ protonen. Nauwkeuriger gezegd is 1 Coulomb gelijk aan 1/e protonen, waarbij e staat voor het elementaire ladingsquantum.

(Afbeelding: Animatie voor Eenheid Coulomb)

Terug naar overzicht Meld je aan

Coördinatentransformatie

Coördinatentransformatie concept

Om een formule af te leiden uit meetgegevens heb je meestal een coördinatentransformatie nodig. Stel dat je deze gegevens in een tabel hebt staan, dan kun je daar een diagram van maken. Als dit diagram een rechte lijn zonder afwijkingen toont, kun je direct de evenredigheidsconstante bepalen: de helling van de grafiek. Hieruit kan je de formule y = a · x afleiden, waarbij a de helling en dus de evenredigheidsconstante is.

Als de lijn niet recht is, moet je een coördinatentransformatie vinden die ervoor zorgt dat er wel een rechte lijn ontstaat. Wanneer de coördinatentransformatie is toegepast, kun je op dezelfde manier als bij een rechte lijn de evenredigheidsconstante bepalen. De constante is dan echter niet altijd meer Δ y / Δ x, maar kan bijvoorbeeld impliceren dat x wordt vervangen door 1/x of door x². Door deze stappen te volgen, kun je uiteindelijk een formule afleiden uit de meetgegevens.

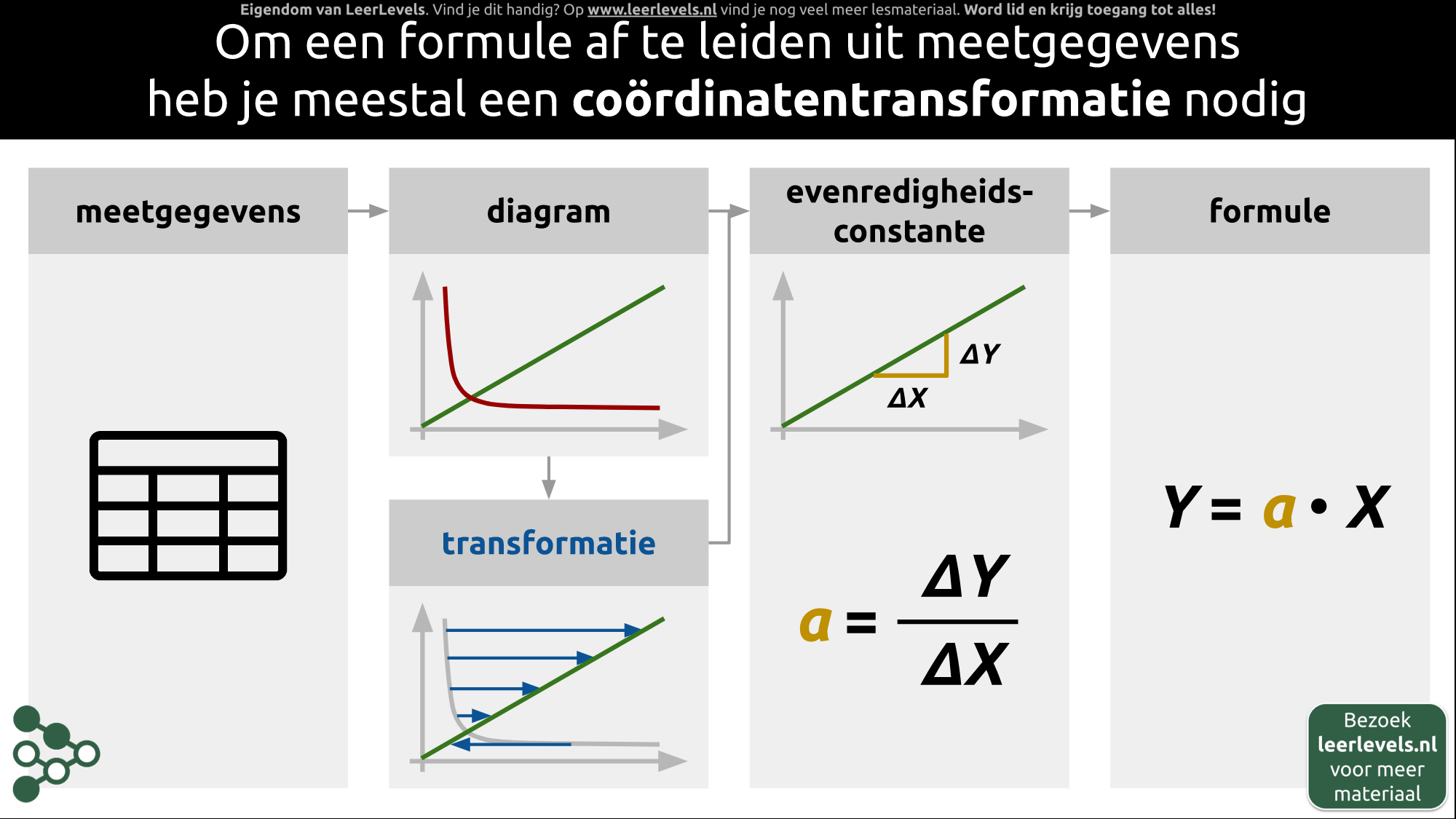
(Afbeelding: Animatie voor Coördinatentransformatie concept)

Coördinatentransformatie omgekeerde evenredigheid

Bij de coördinatentransformatie voor een omgekeerde evenredigheid vervang je x door 1/x. Stel dat je meetgegevens van druk en volume hebt. Een verandering in het volume zorgt vaak voor een verandering van de druk, mits er geen gasdeeltjes bij komen of verdwijnen. Als je deze meetgegevens in een grafiek plaatst, met volume op de x\-as en druk op de y\-as, zie je dat het verband niet recht evenredig is. We kunnen dus niet direct de evenredigheidsconstante bepalen. Wat we gaan doen, is een coördinatentransformatie toepassen, waarbij we niet V op de x\-as zetten, maar 1/V. Dit doen we door in de tabel voor elk meetpunt V om te rekenen naar 1/V. Als we daarna 1/V op de x\-as plaatsen en de bijbehorende waarden van druk op de y\-as, verschuiven alle punten en krijgen we keurig een rechte lijn. Met deze rechte lijn kunnen we de evenredigheidsconstante bepalen. In dit geval, als je twee punten op de lijn kiest, kun je berekenen dat de evenredigheidsconstante een waarde van 2 Pascal kubieke meter heeft. De formule is dus p = a · 1/V. De constante a hebben we bepaald na de transformatie. Dus de formule is dan p = 2 · 1/V of p = 2/V.

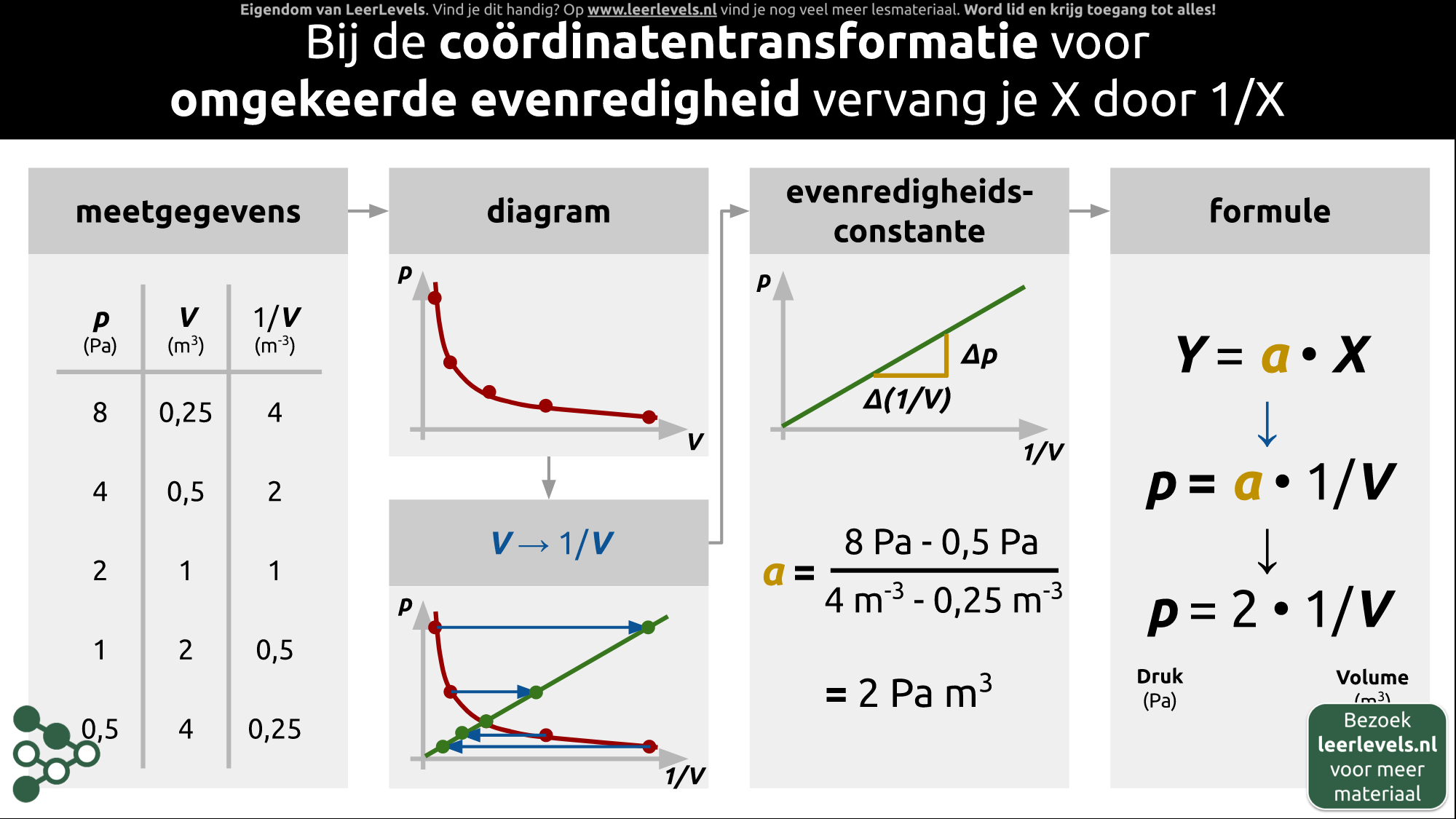
(Afbeelding: Animatie voor Coördinatentransformatie omgekeerde evenredigheid)

Overzicht coördinatentransformaties

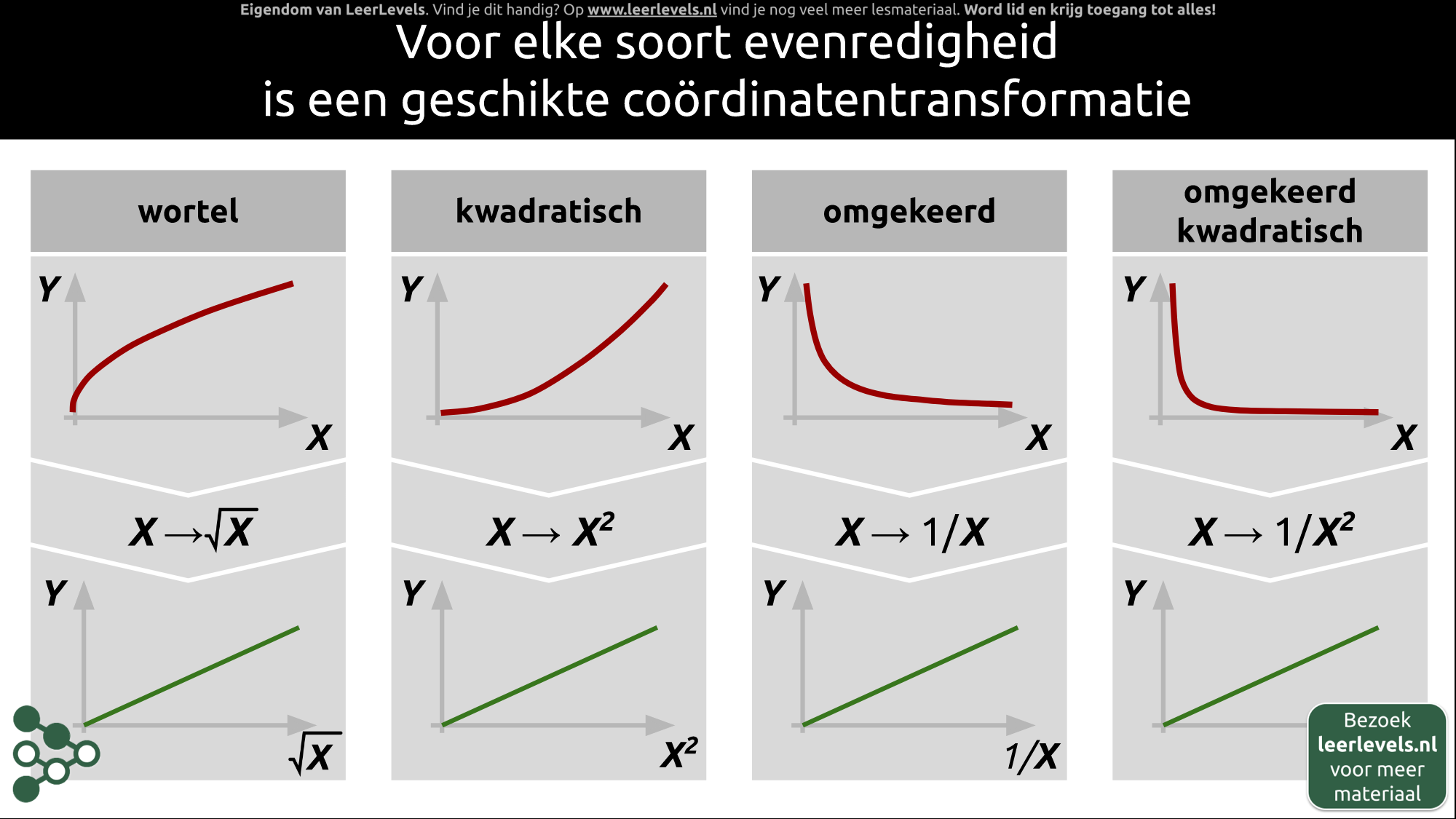
Voor elke soort evenredigheid is er een geschikte coördinatentransformatie. De belangrijkste die je moet kennen zijn het wortelverband, kwadratische verband, omgekeerd verband en omgekeerd kwadratisch verband. Bij elk van deze evenredigheden hoort een andere grafiek. Wanneer je een grafiek hebt die een verband legt tussen twee grootheden, moet je deze verbanden herkennen.

Voor de coördinatentransformatie van een wortelverband vervang je x door √(x). Bij het kwadratische verband vervang je x door x². Voor het omgekeerde verband vervang je x door 1/x , en bij het omgekeerd kwadratisch verband vervang je x door (1)/(x²).

Wanneer je de juiste transformatie toepast, krijg je in alle gevallen een rechte lijn. Deze lijn kun je gebruiken om de evenredigheidsconstante te bepalen en daarmee de formule op te stellen die het verband beschrijft tussen de twee grootheden.

(Afbeelding: Animatie voor Overzicht coördinatentransformaties)

Terug naar overzicht Meld je aan

De Broglie golflengte

De Broglie golflengte concept

In 1884 voorspelde De Broglie dat alle deeltjes golfeigenschappen vertonen en daarom een bepaalde golflengte hebben. Deze golflengte werd later bekend als de De Broglie-golflengte. De theorie van De Broglie ontstond uit de ontdekking dat licht, dat voorheen als een golf werd beschouwd, ook deeltjeseigenschappen vertoont. Toen dacht De Broglie: als golven deeltjeseigenschappen kunnen vertonen, dan kunnen deeltjes misschien ook wel golfeigenschappen vertonen. Hij veronderstelde dat deze golflengte gerelateerd was aan impuls.

Neem bijvoorbeeld een deeltje met een zeer lage impuls, zoals een elektron dat wordt weggeschoten met 1% van de lichtsnelheid. Dit elektron heeft een kleine impuls, waardoor een grote golflengte wordt verwacht. Volgens De Broglie's schatting zou deze ongeveer 10⁻¹⁰ meter moeten zijn, wat later experimenteel werd bevestigd. Deze golflengte is in dezelfde ordegrootte als de afstand tussen atomen, dus kan er golfgedrag (zoals breking) optreden wanneer elektronen door een materiaal (bijvoorbeeld een kristal) bewegen.

Bij deeltjes met een hogere impuls, zoals een waterstofion (of proton) dat met hoge snelheid wordt afgeschoten, resulteert dit in een De Broglie-golflengte van ongeveer 10⁻¹⁵ meter, wat veel kleiner is. Het is moeilijker om deze kleine golflengtes via interferentie te meten.

Bij "objecten" waar je als mens in het dagelijks leven mee te maken hebt, zoals een fietser die met 10 meter per seconde fietst, is de De Broglie golflengte ontzettend klein. Hoewel de snelheid kleiner is dan het eerder genoemde proton, is de massa veel groter dan die van een rondvliegend proton. De De Broglie-golflengte van een fietser blijkt ongeveer 10⁻³⁶ meter te zijn. In ons dagelijks leven zullen we dus nooit zelf golfeigenschappen vertonen, omdat de golflengtes van objecten waarmee we omgaan zo klein zijn dat er geen interferentie optreedt.

Kortom, in 1884 voorspelde De Broglie dat alle deeltjes golfeigenschappen hebben, maar vanwege de grote impuls van deeltjes in ons dagelijks leven zullen we hier niets van merken.

(Afbeelding: Animatie voor De Broglie golflengte concept)

De Broglie golflengte formule

De De Broglie-golflengte van een materiedeeltje is omgekeerd evenredig met de impuls. De formule is als volgt: λDB = h/p . Dit betekent dat de De Broglie-golflengte recht evenredig is met h en omgekeerd evenredig met p. Hierbij is λDB de De Broglie-golflengte in meter, h de constante van Planck, en p de impuls in Newton-seconde. Impuls kan worden geschreven als p = m · v, waarbij m de massa is in kilogram en v de snelheid in meter per seconde. Naarmate de impuls groter wordt, wordt de De Broglie-golflengte kleiner.

(Afbeelding: Animatie voor De Broglie golflengte formule)

Terug naar overzicht Meld je aan

Derde wet van Kepler

Derde wet van Kepler concept

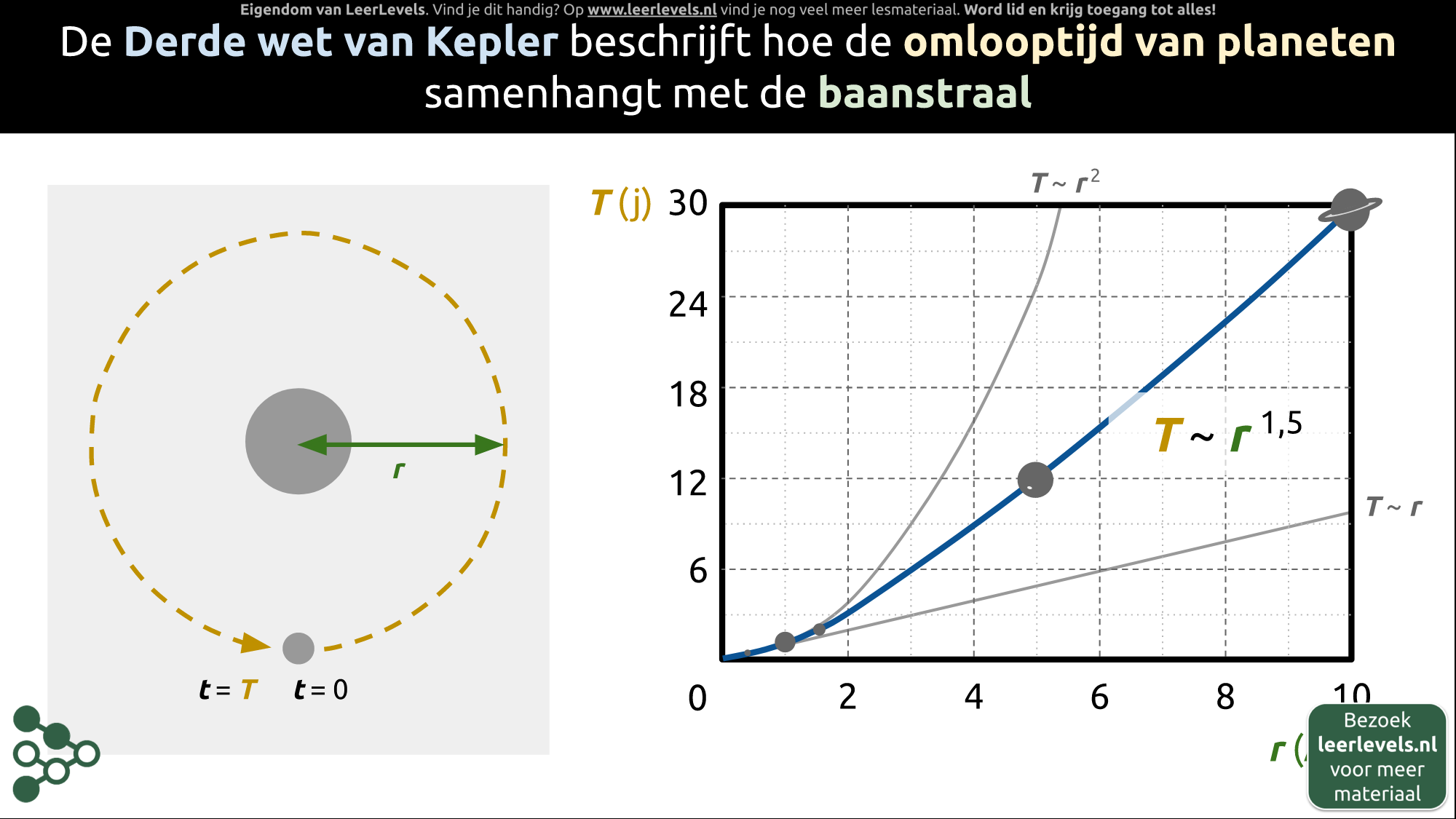
De derde wet van Kepler laat zien hoe lang het duurt voor planeten om rond een centrale massa, zoals de zon, te draaien. Deze tijd is afhankelijk van hoe ver de planeet van de centrale massa vandaan is. Als je deze afstand uitdrukt in astronomische eenheden en de tijd in jaren, dan zie je dat het verband tussen afstand en tijd niet rechtlijnig is. Het verband wordt met macht uitgedrukt, zoals tot de macht anderhalf. Kepler ontdekte dit verband en beschrijft het in zijn derde wet.

(Afbeelding: Animatie voor Derde wet van Kepler concept)

Derde wet van Kepler afleiding

De derde wet van Kepler zegt dat de verhouding tussen de kubus van de afstand van een planeet tot zijn ster en het kwadraat van de omlooptijd constant is. Dit betekent: r³/T² = constant. Hierbij is r de afstand van de planeet tot de ster in meters, T de omlooptijd van de planeet in seconden, en de constante is (GM)/(4π²), waarbij G de gravitatieconstante is en M de massa van de ster. Deze wet kan worden afgeleid uit twee formules voor de baansnelheid, namelijk v² = GM/r en v² = 4π²r²/T², door ze aan elkaar gelijk te stellen en enkele wiskundige bewerkingen toe te passen.

(Afbeelding: Animatie voor Derde wet van Kepler afleiding)

Derde wet van Kepler formule

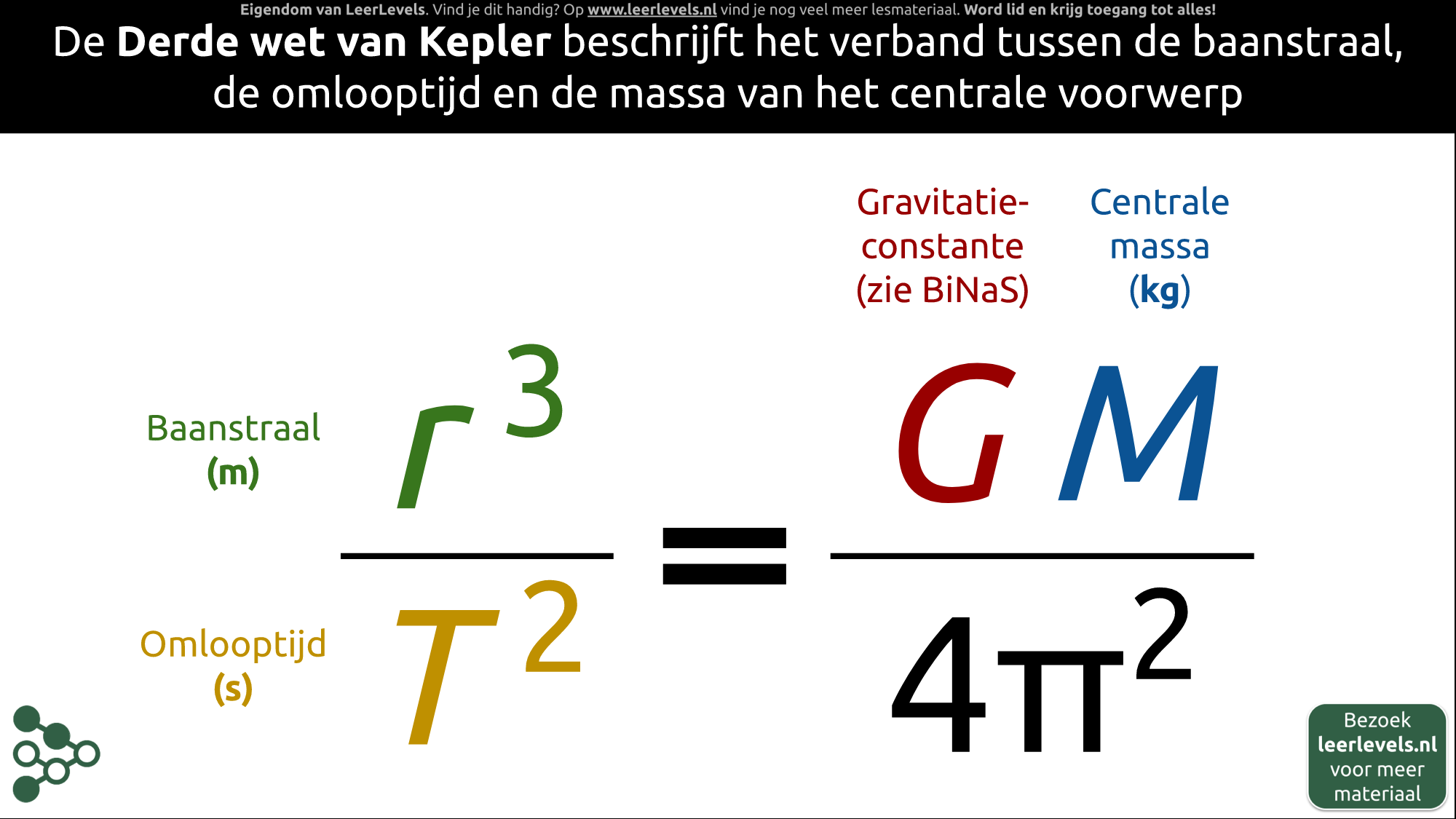
De derde wet van Kepler legt uit hoe de grootte van een baan, hoe lang het duurt om eromheen te draaien en de massa van het centrale object met elkaar te maken hebben. Dit wordt weergegeven in deze formule: r³ / T² = (G · M)/(4π²). Waarbij "r" de grootte van de baan in meter is, "T" de duur van de omloop in seconden is, "G" een constante is die zwaartekracht vertegenwoordigt en "M" de massa van het object waar omheen gedraaid wordt is. Om deze formule te gebruiken, moet je de grootte van de baan van het object dat om het centrale object draait pakken, de omlooptijd van dat object en de massa van het centrale object zelf.

(Afbeelding: Animatie voor Derde wet van Kepler formule)

Terug naar overzicht Meld je aan

Derde wet van Newton

Derde wet van Newton concept

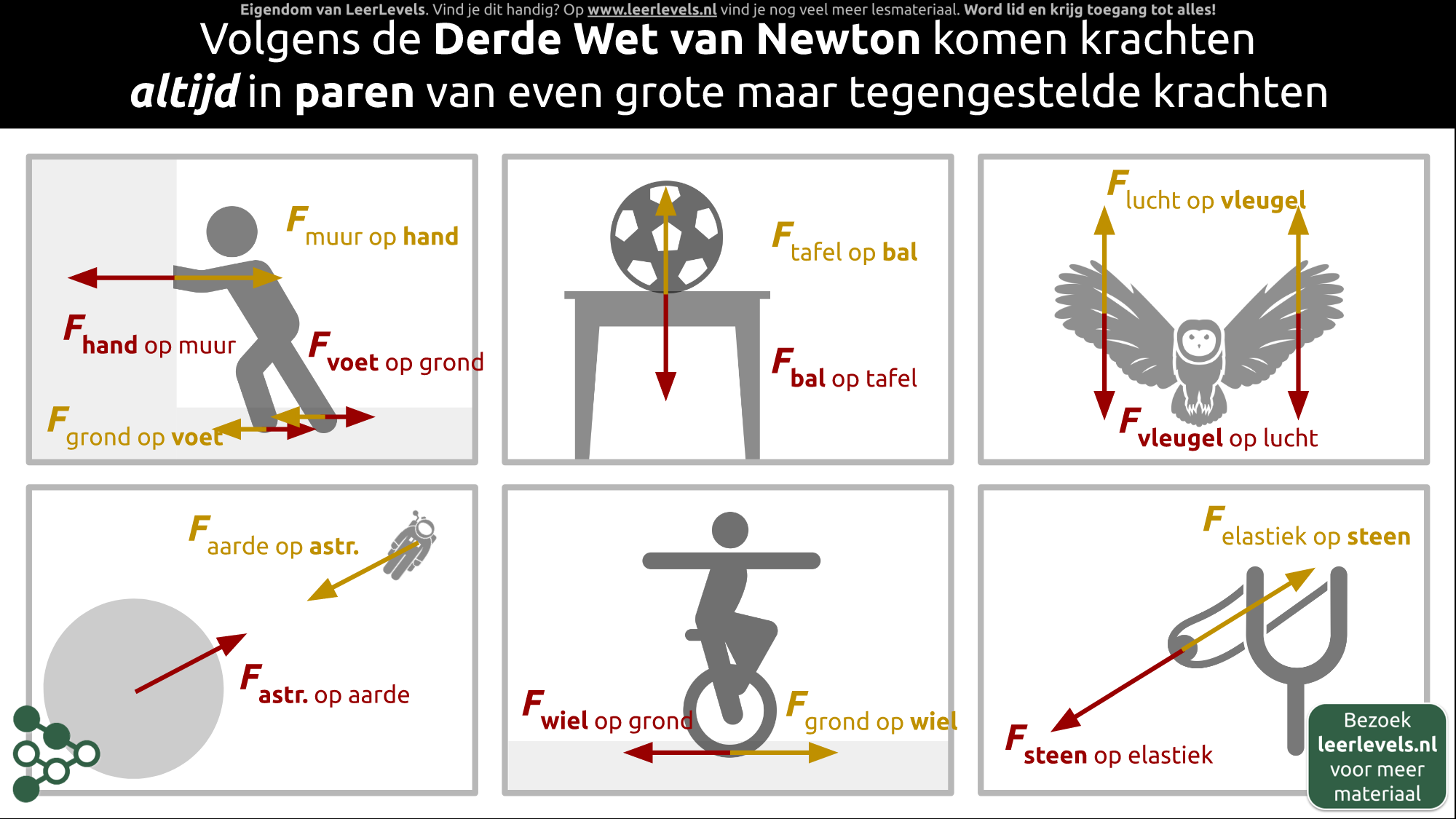
Volgens de derde Wet van Newton bestaan krachten altijd uit paren van even grote, maar tegengestelde krachten. Laten we enkele voorbeelden bekijken om dit te verduidelijken.

Stel dat er een bal op een tafel ligt. Er is een krachtenpaar bestaande uit de zwaartekracht die de bal op de tafel uitoefent en de kracht die de tafel op de bal uitoefent, ook wel de normaalkracht genoemd. Deze krachten zijn even groot.

Als je tegen een muur duwt, oefent de muur ook een kracht op jou uit. De kracht van je hand op de muur gaat gepaard met een gelijke en tegengestelde kracht van de muur op je hand.

Een ander voorbeeld is een eenwieler. Wanneer je met het wiel een kracht naar achteren op de grond uitoefent, oefent de grond een gelijke kracht naar voren uit op het wiel. Hierdoor beweeg je naar voren.

Bij een katapult is de kracht van de steen op het elastiek gelijk en tegengesteld aan de kracht van het elastiek op de steen.

Wanneer een vogel vliegt, duwen de vleugels de lucht naar beneden. De kracht van de vleugel op de lucht is gelijk aan de kracht van de lucht op de vleugel. Hierdoor blijft de vogel in de lucht.

Bij een astronaut die door de ruimte reist, is er ook sprake van een krachtenpaar, maar op afstand. De kracht waarmee de astronaut aan de aarde trekt is even groot als de kracht van de aarde op de astronaut. In dit laatste voorbeeld werken de twee krachten niet op hetzelfde punt in, in tegenstelling tot de andere voorbeelden.

(Afbeelding: Animatie voor Derde wet van Newton concept)

Derde wet van Newton toepassen

De derde wet van Newton wordt vaak toegepast om de resultante kracht of de versnelling van een massa te bepalen. Stel je bijvoorbeeld voor dat iemand tegen een muur duwt terwijl hij stilstaat. Hierbij is er een kracht van de handen op de muur en een gelijke, tegengestelde kracht van de muur op de handen. Ook oefent deze persoon met zijn voeten een kracht uit op de grond. Daarnaast is er de zwaartekracht van de aarde op de persoon, en een tegengestelde kracht van de persoon op de aarde. Omdat de aarde niet zichtbaar kan worden geschetst, kunnen we deze kracht niet zien en lijkt de persoon naar de grond te worden getrokken. Als we ons alleen richten op de krachten die op de persoon inwerken, namelijk die van de muur, de vloer, de voeten, de aarde en de grond, en we tellen deze allemaal bij elkaar op, dan is de totale kracht in dit geval nul. Dit betekent dat er geen versnelling is. We weten niet precies hoe groot alle krachten zijn, maar we kunnen aannemen dat er geen versnelling plaatsvindt.

Een voorbeeld van een situatie waarin er wel sprake is van versnelling, is wanneer een skydiver richting de aarde versnelt. Hier is er een kracht van de aarde op de persoon en een even grote, tegengestelde kracht van de persoon op de aarde. Op de skydiver werkt een resultante kracht, wat leidt tot versnelling. Om de versnelling te berekenen, deel je de kracht Fg door de massa m van de persoon. Voor een skydiver is de massa m relatief klein, waardoor de versnelling groot is. Voor de aarde daarentegen is de massa m zeer groot, dus is de versnelling van de aarde verwaarloosbaar klein.

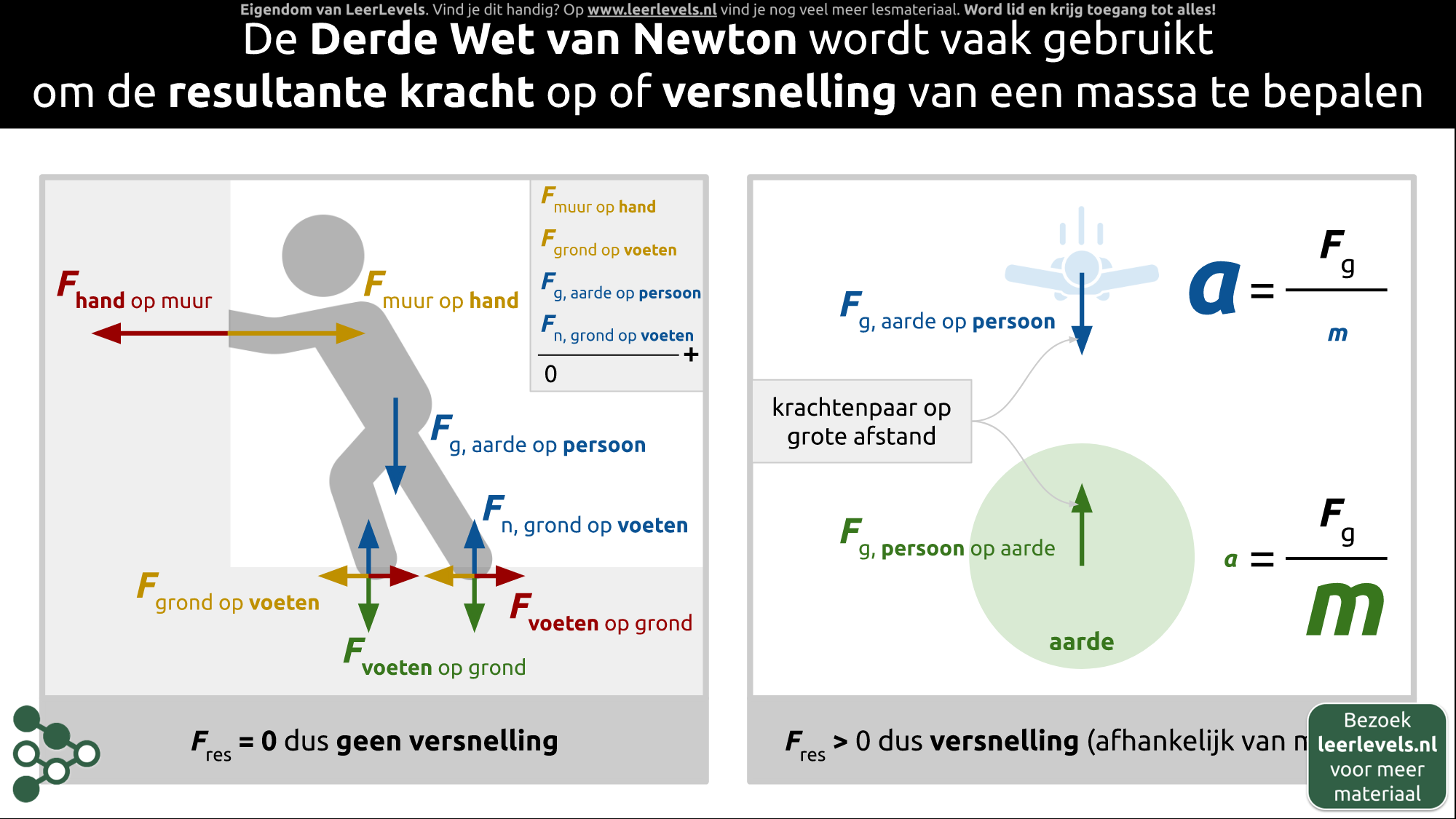
(Afbeelding: Animatie voor Derde wet van Newton toepassen)

Derde wet van Newton formule

De derde wet van Newton beschrijft het verband tussen twee krachten binnen een krachtenpaar. De kracht die object A uitoefent op object B is gelijk in grootte, maar tegengesteld in richting aan de kracht die object B uitoefent op object A. De kracht van A op B wordt 'actie' genoemd, terwijl de kracht van B op A als 'reactie' bekendstaat. Dit principe kan worden weergegeven met de formule:

FAB = -FBA

In woorden kun je deze formule lezen als: 'actie is gelijk aan min reactie'.

(Afbeelding: Animatie voor Derde wet van Newton formule)

Terug naar overzicht Meld je aan

Dichtheid

Dichtheid concept

Dichtheid geeft aan hoeveel massa er in een bepaald volume zit. Als we bijvoorbeeld 8 deeltjes in een kubus hebben, dan is de dichtheid normaal. Als we meer massa toevoegen, worden de deeltjes dichter op elkaar gepakt en wordt de dichtheid groter. Als we het volume vergroten, verspreiden de deeltjes zich en wordt de dichtheid kleiner. Het is mogelijk om zowel het volume als de massa te vergroten, zodat de dichtheid hetzelfde blijft. We kunnen de dichtheid aanpassen door het aantal deeltjes, de massa of het volume te veranderen. Dichtheid wordt uitgedrukt in massa (m) per volume (V) en de eenheid is kilogram per kubieke meter (kg/m³).

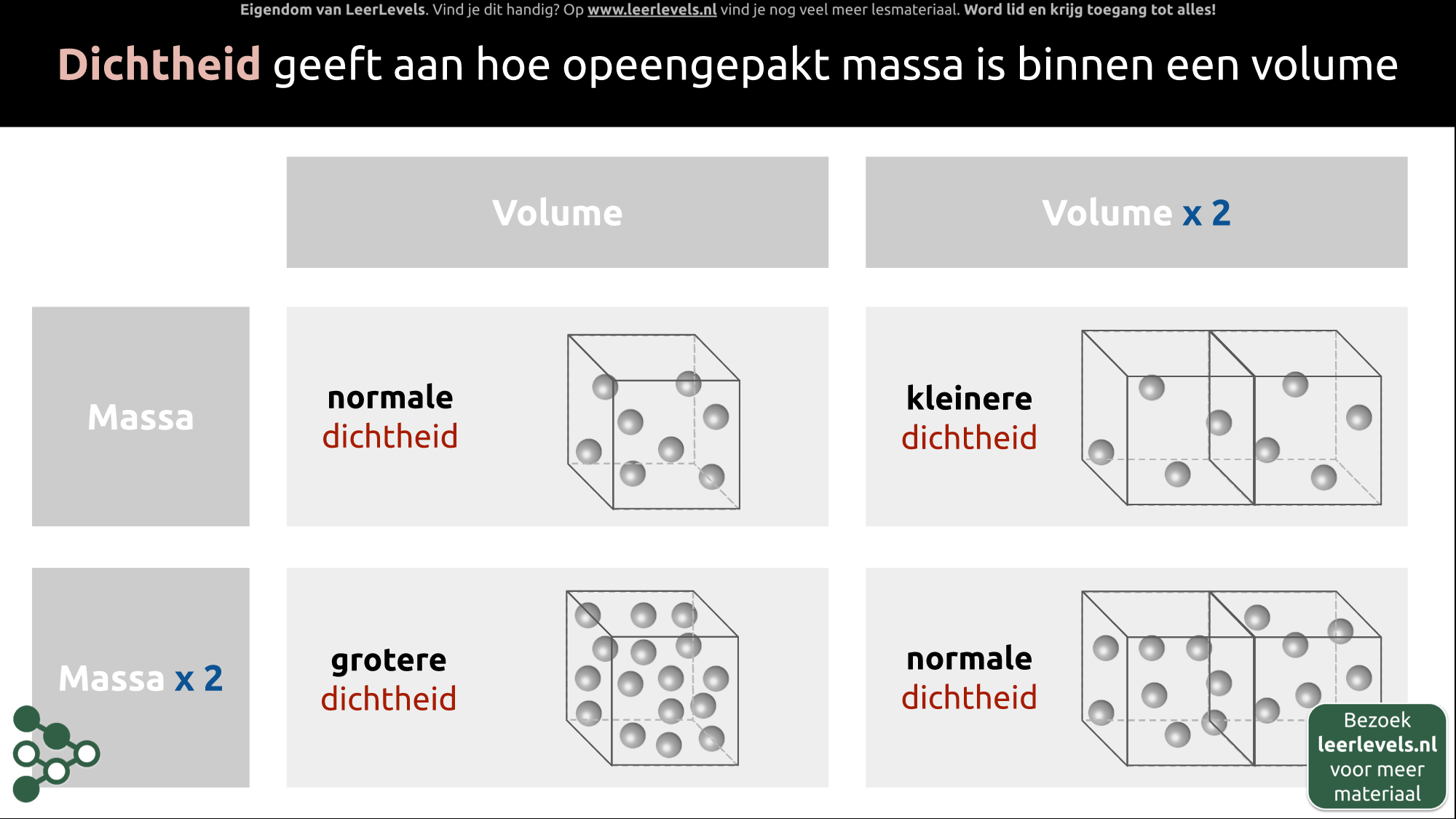
(Afbeelding: Animatie voor Dichtheid concept)

Dichtheid formule

De dichtheid van een voorwerp is recht evenredig met de massa en omgekeerd evenredig met het volume. Het symbool voor dichtheid is de Griekse letter ρ, en de formule voor dichtheid is:

ρ = m/V

waarbij m de massa is in kilogram en V het volume in kubieke meter. De eenheid van dichtheid is dus kg/m³.

(Afbeelding: Animatie voor Dichtheid formule)

Onderdompelmethode

Met de onderdompelingsmethode kan je het volume bepalen van objecten met onregelmatige vormen. Je hebt hiervoor een maatcilinder of maatbeker nodig met streepjes om het volume af te kunnen lezen. Het proces begint met alleen een vloeistof in de cilinder of beker. De hoeveelheid vloeistof die je afleest noemen we de beginstand. Vervolgens voeg je het object toe aan de vloeistof door het onder te dompelen. Nu lees je de hoeveelheid vloeistof inclusief het object af. Dit noemen we de eindstand. Het verschil tussen de eindstand en de beginstand geeft het volume van het object. Deze formule kan als volgt genoteerd worden: Vobject = Veind - Vbegin, waarbij V staat voor volume en object, eind en begin voor respectievelijk het volume van het object, de eindstand en de beginstand.

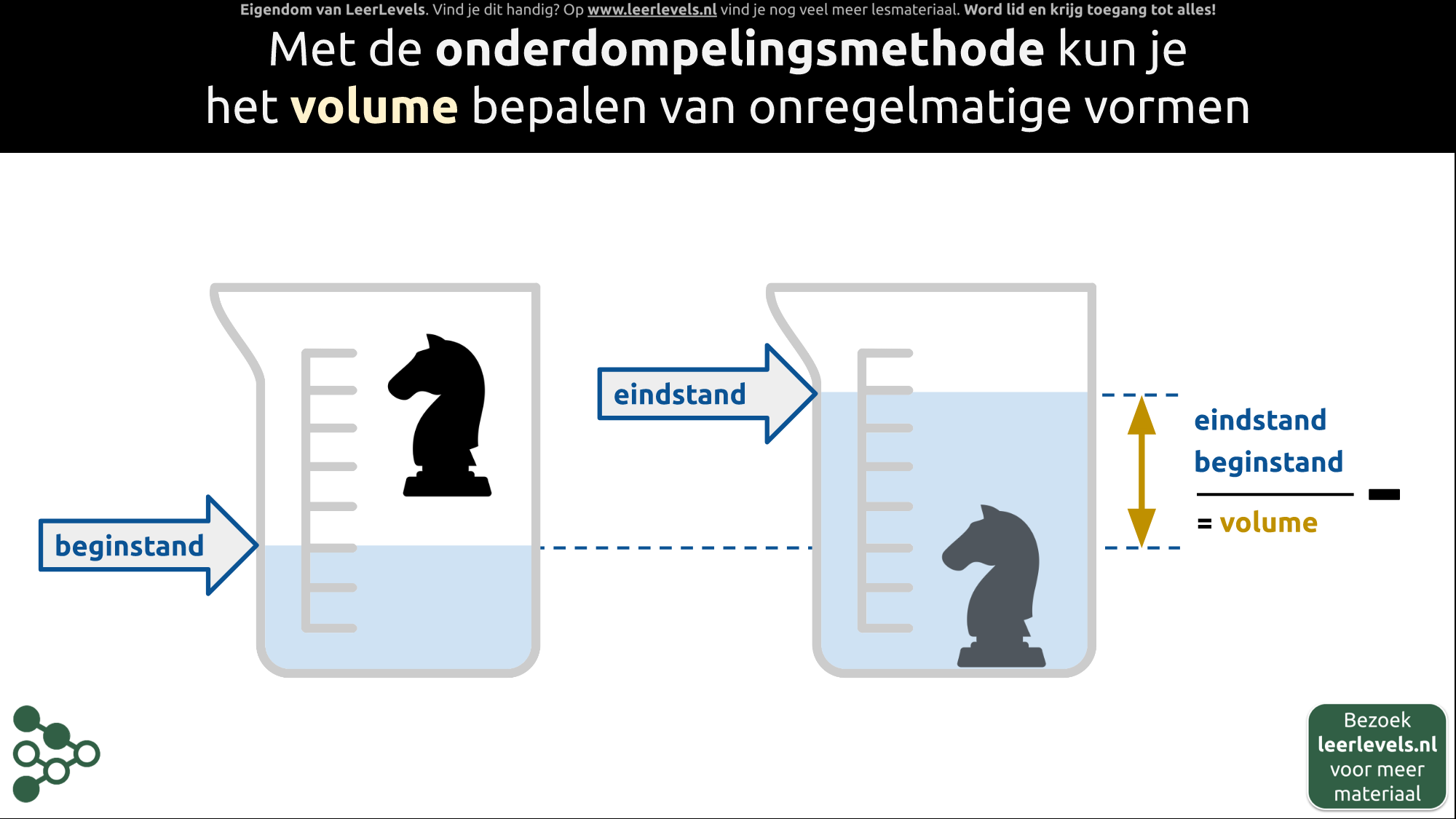
(Afbeelding: Animatie voor Onderdompelmethode)

Terug naar overzicht Meld je aan

Diffractie

Diffractie golven

Diffractie is het buigen van golven bij een kleine opening of voorwerp.

Stel dat je een redelijk grote opening hebt en er komt een golf aan. Die golf gaat gewoon recht door de opening, behalve op de plekken waar hij wordt tegengehouden. Als de opening veel groter is dan de golflengte, vindt er geen buiging plaats.

Als de grootte van de opening vergelijkbaar is met de golflengte, blijkt dat de golven na de opening een kleine bocht maken. Dit betekent dat als de golven netjes parallel aankomen, ze iets uitwaaieren na de opening. Buiging vindt dan met name plaats aan de randen.

Als je de opening nog kleiner maakt, ontstaat er een puntbron. De golf verspreidt zich dan in alle richtingen, vergelijkbaar met het gooien van een steentje in het water op de plek van de opening. Dit resulteert in cirkelvormige kringen. Dit buigingseffect staat bekend als diffractie: het buigen van golven bij een opening of voorwerp wanneer de afmeting ervan klein genoeg is in verhouding tot de golflengte.

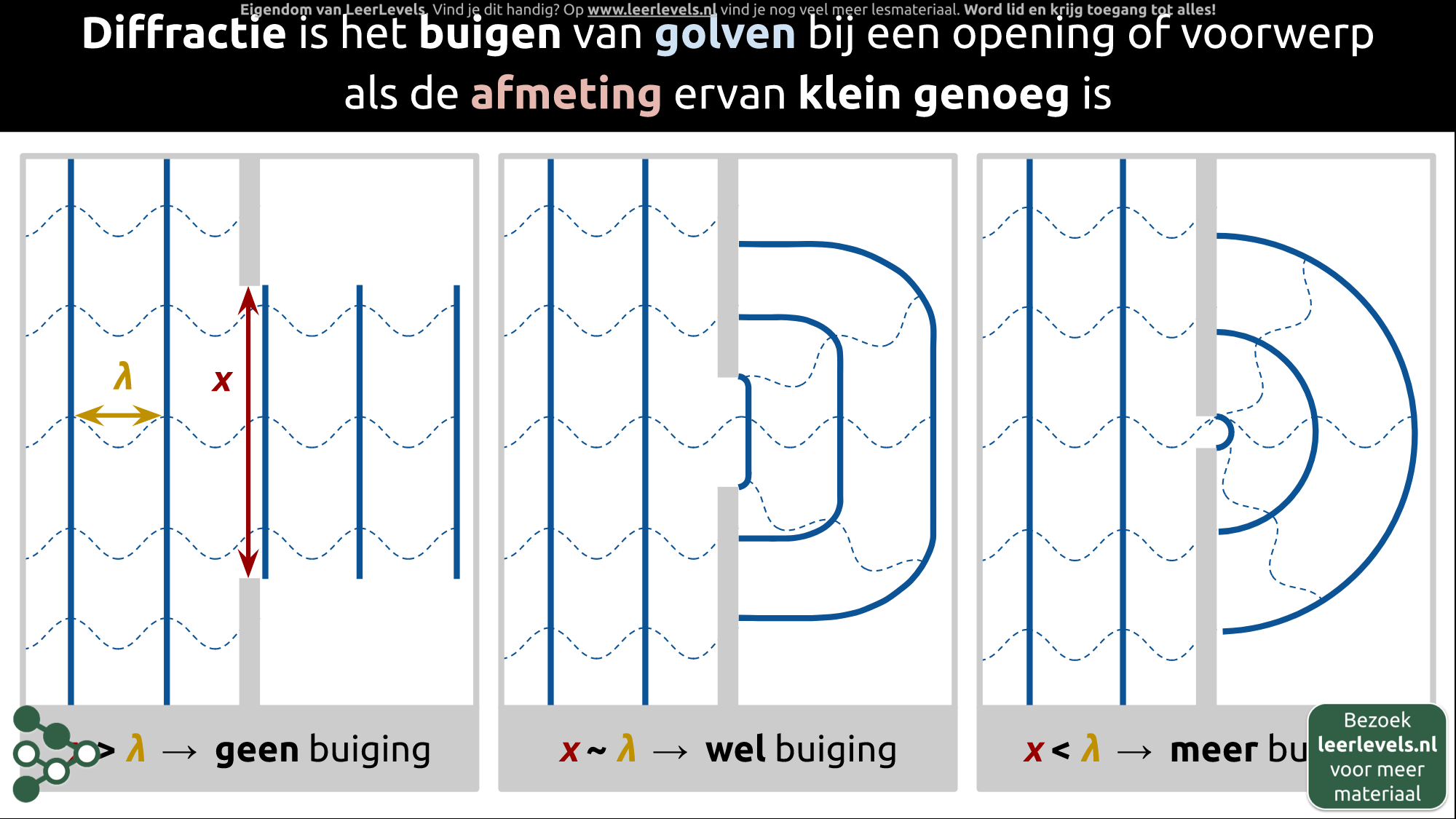
$Afbeelding voor Diffractie golven$

(Afbeelding: Animatie voor Diffractie golven)

Terug naar overzicht Meld je aan

Diode

Diode concept

Een diode is een elektrisch onderdeel dat stroom slechts in één richting doorlaat. Deze richting wordt de doorlaatrichting genoemd. Wanneer de stroom in dezelfde richting als de doorlaatrichting gaat, loopt er stroom en zal het lampje branden. Sluit je de diode in de tegenovergestelde richting aan, de sperrichting, dan loopt er geen stroom en blijft het lampje uit.

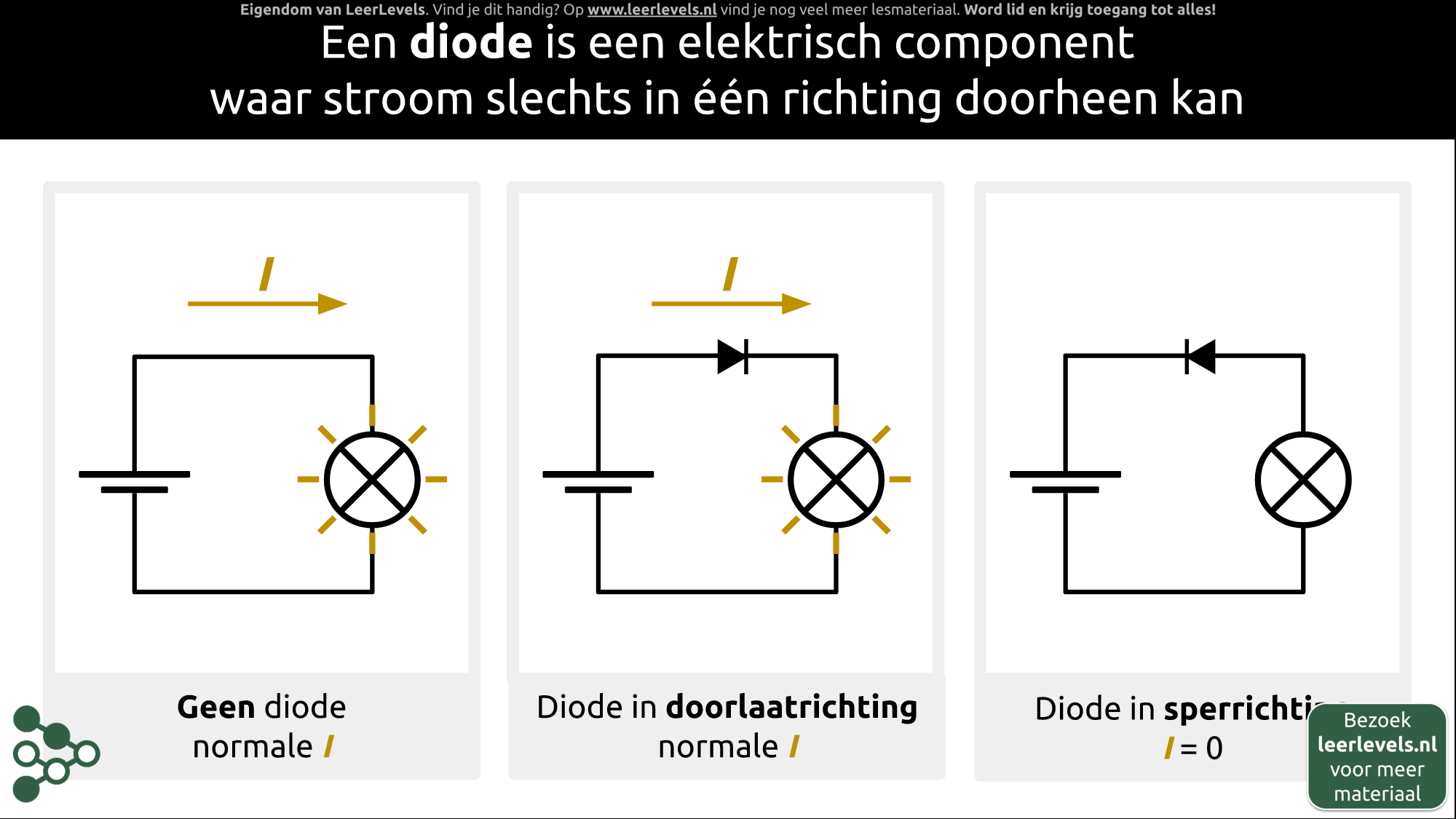
(Afbeelding: Animatie voor Diode concept)

Diode (I,U)-diagram

Een diode heeft eigenschappen die worden weergegeven in een (I,U)-diagram. Op de horizontale as staat de spanning en op de verticale as de stroom. Er zijn verschillende gebieden in dit diagram die informatie geven over de eigenschappen van een diode. Als de stroom negatief is, dan is de geleidbaarheid 0 en de weerstand oneindig groot. Als de stroom positief is, dan heeft de lijn een kleine helling en is de geleidbaarheid klein. Vanaf de drempelwaarde wordt de helling van de grafiek groot en is de geleidbaarheid groot en de weerstand klein. Aan de hand van het (I,U)-diagram kan je de eigenschappen van een diode zien.

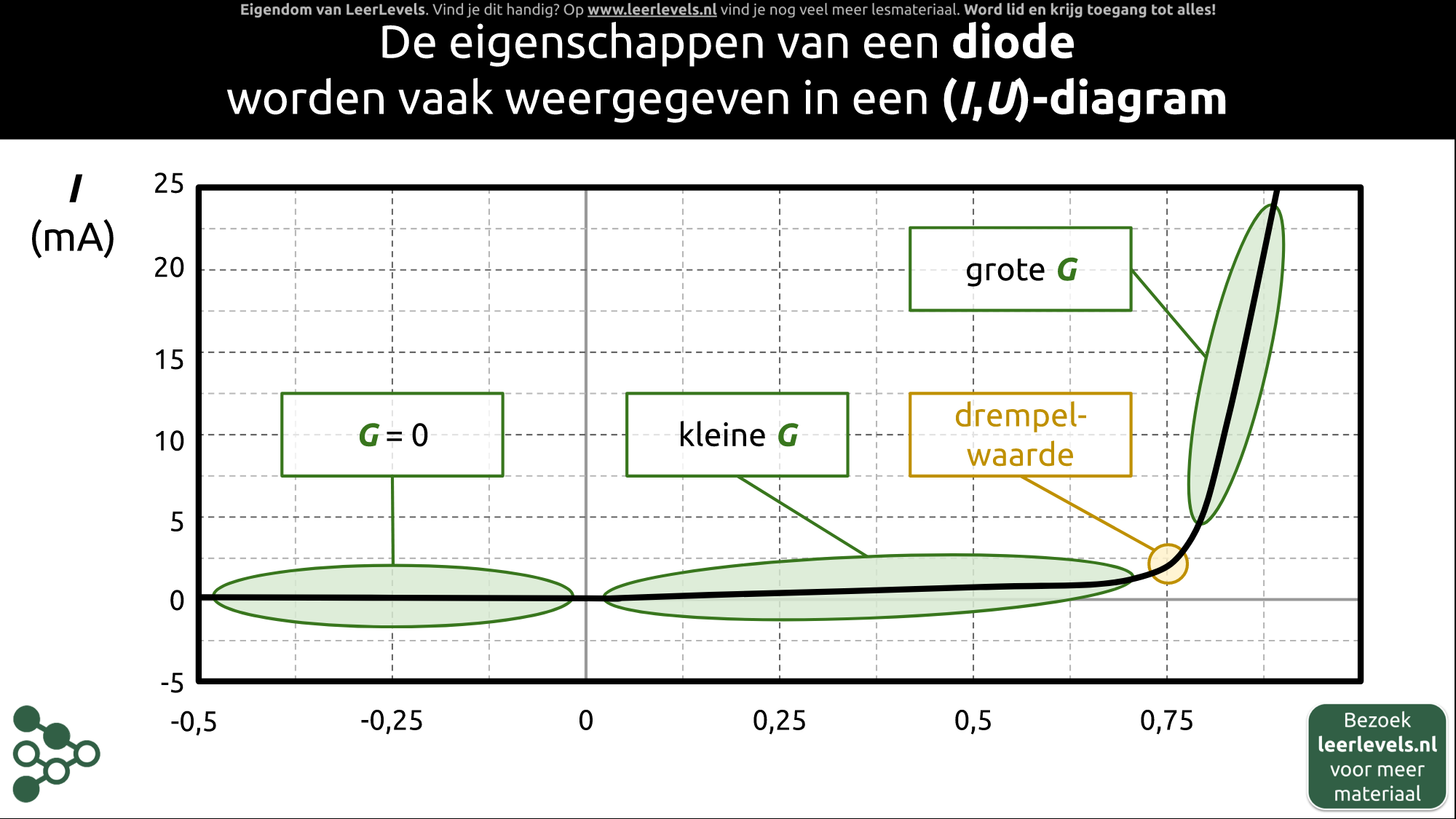
(Afbeelding: Animatie voor Diode (I,U)-diagram)

Terug naar overzicht Meld je aan

Doordringend vermogen

Het doordringend vermogen, ook wel dracht genoemd, geeft aan hoe ver straling door een materiaal kan gaan voordat het wordt geabsorbeerd. Dit vermogen verschilt per type straling. Dit verschil in doordringend vermogen hangt onder andere af van de massa van het deeltje en de lading ervan.

Alfastraling heeft een laag doordringend vermogen; wanneer alfastraling op een materiaal stuit, wordt het gemakkelijk geabsorbeerd en kan het slechts een kleine afstand doordringen voordat het volledig wordt geabsorbeerd.

Bètastraling heeft een matig doordringend vermogen en kan iets verder in het materiaal doordringen, maar wordt nog steeds relatief eenvoudig geabsorbeerd.

Daarentegen heeft gammastraling een hoog doordringend vermogen en kan in sommige gevallen zelfs dwars door een materiaal heen gaan, waardoor het moeilijker te absorberen is.

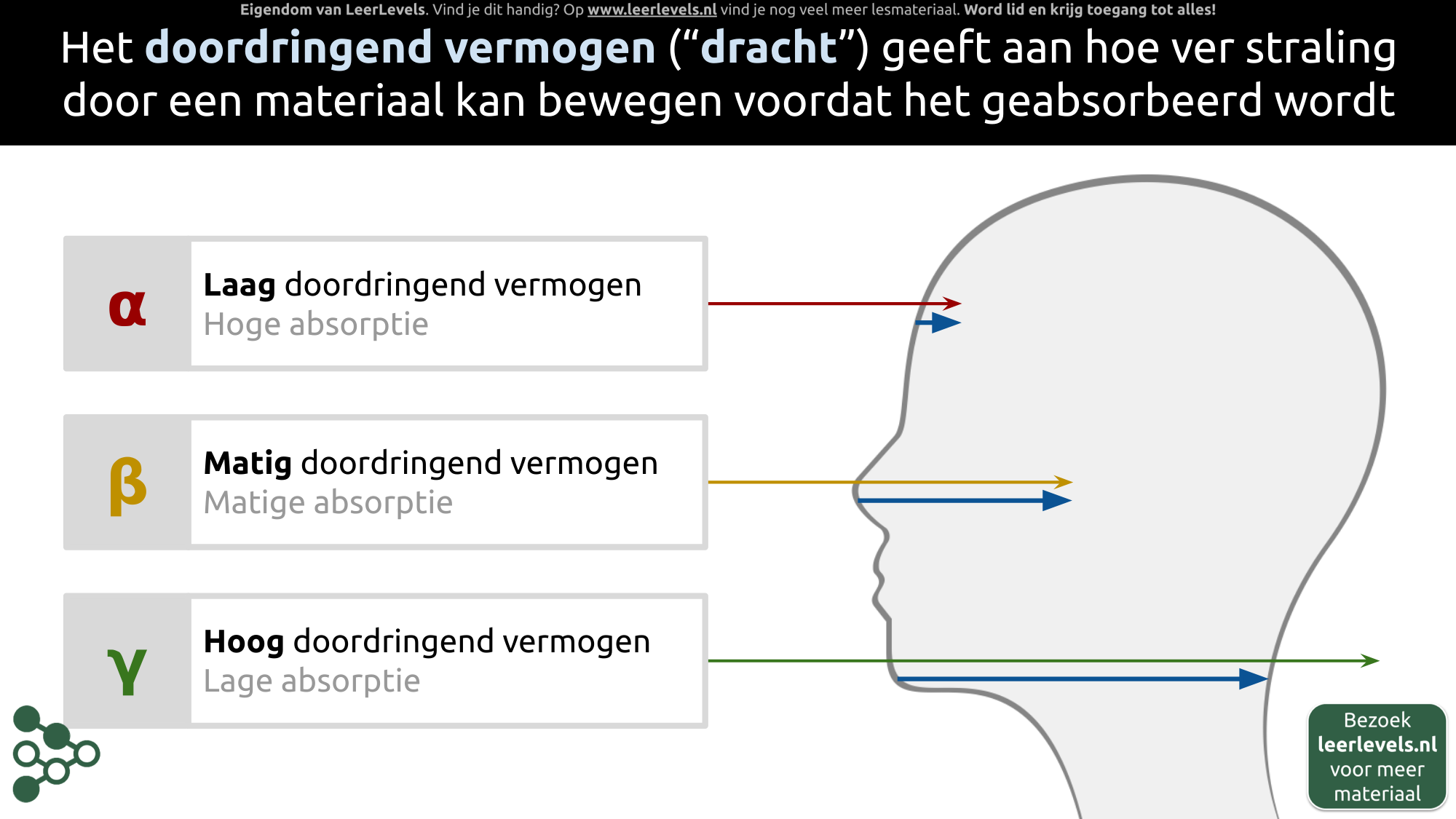
(Afbeelding: Animatie voor Doordringend vermogen)

Terug naar overzicht Meld je aan

Dopplereffect

Dopplereffect concept

Het dopplereffect is een term voor wanneer een stilstaand persoon een andere frequentie hoort of ziet dan iemand die beweegt. Dit geldt voor geluid en licht. Bijvoorbeeld als een ambulance naar een hond rijdt, hoort de hond een hogere toon dan wanneer de ambulance wegrijdt. Dit geldt ook voor licht, als een ster naar ons toe beweegt, lijkt het licht blauwer, en als de ster van ons af beweegt, lijkt het licht roder. Er worden geen formules, grootheden, of eenheden gebruikt in deze uitleg.

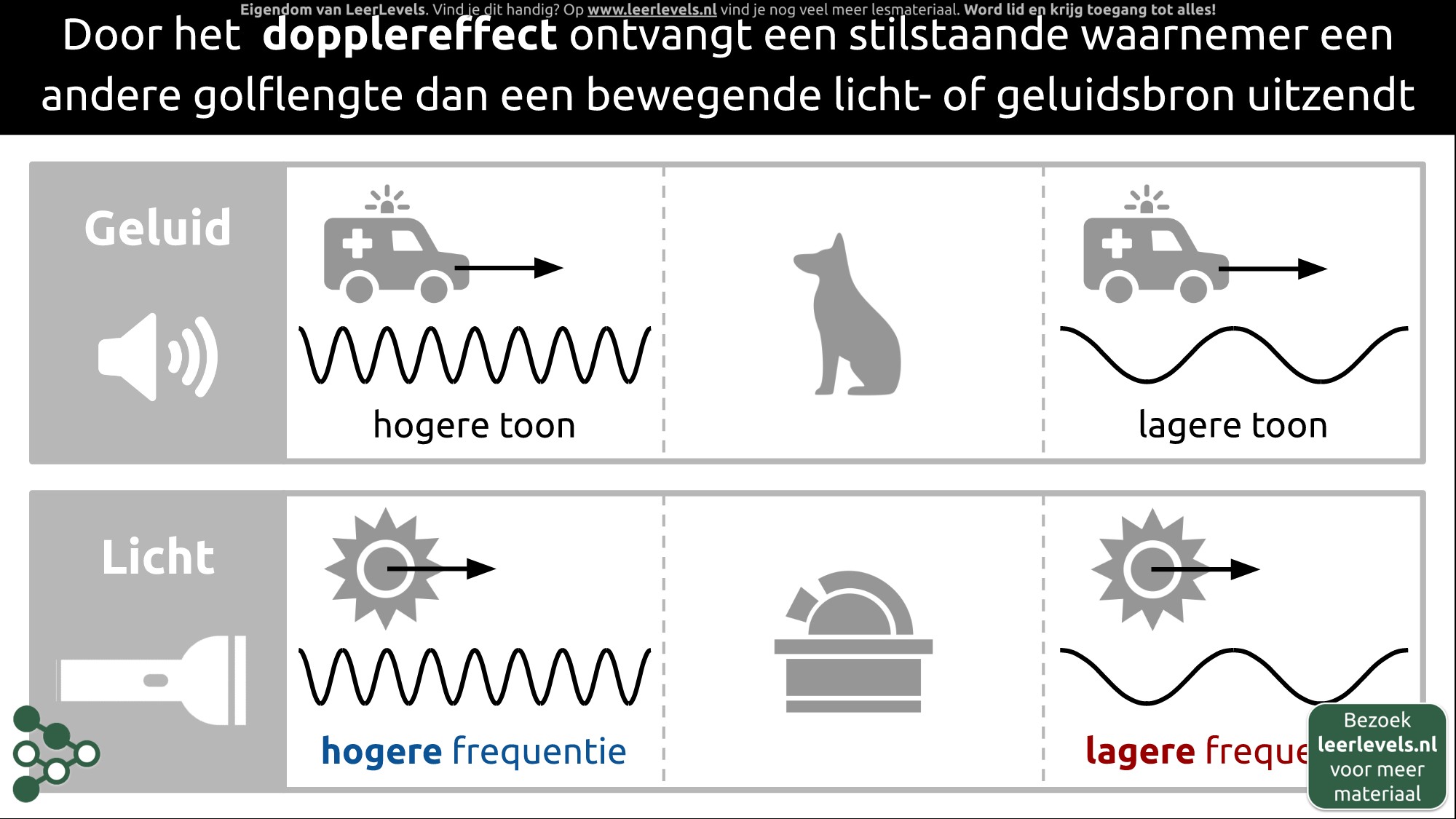
(Afbeelding: Animatie voor Dopplereffect concept)

Dopplereffect verklaring

Het dopplereffect betekent dat geluid of licht anders lijkt als de bron beweegt. Als de bron stilstaat, lijken de golven op regelmatige afstanden van elkaar te zijn. Maar als de bron beweegt, worden golven dichter op elkaar gedrukt als de bron naar iets toe beweegt en uit elkaar getrokken als de bron van iets af beweegt.

Dit komt omdat een golffront (een top in de golf) minder ver van de bron verwijderd is als het kort na een ander golffront wordt gemaakt. Als de bron beweegt, is het golffront dat later is gemaakt hoger of lager dan het golffront dat eerder is gemaakt. Golven die hoger bij elkaar komen, maken kortere golflengtes en golven die verder uit elkaar komen, maken langere golflengtes.

Dit is vergelijkbaar met kringen die zich vormen in een meer als je er een steentje in gooit. De afstand tussen de kringen is de golflengte en dit blijft hetzelfde als de bron stilstaat. Als de bron beweegt, worden de kringen dichter op elkaar geduwd in de richting van de beweging en uitgerekt in de tegenovergestelde richting.

Het dopplereffect kan worden gebruikt om te bepalen of een object van ons weg beweegt of naar ons toe komt door de golflengten van het licht te meten dat we van dat object zien.

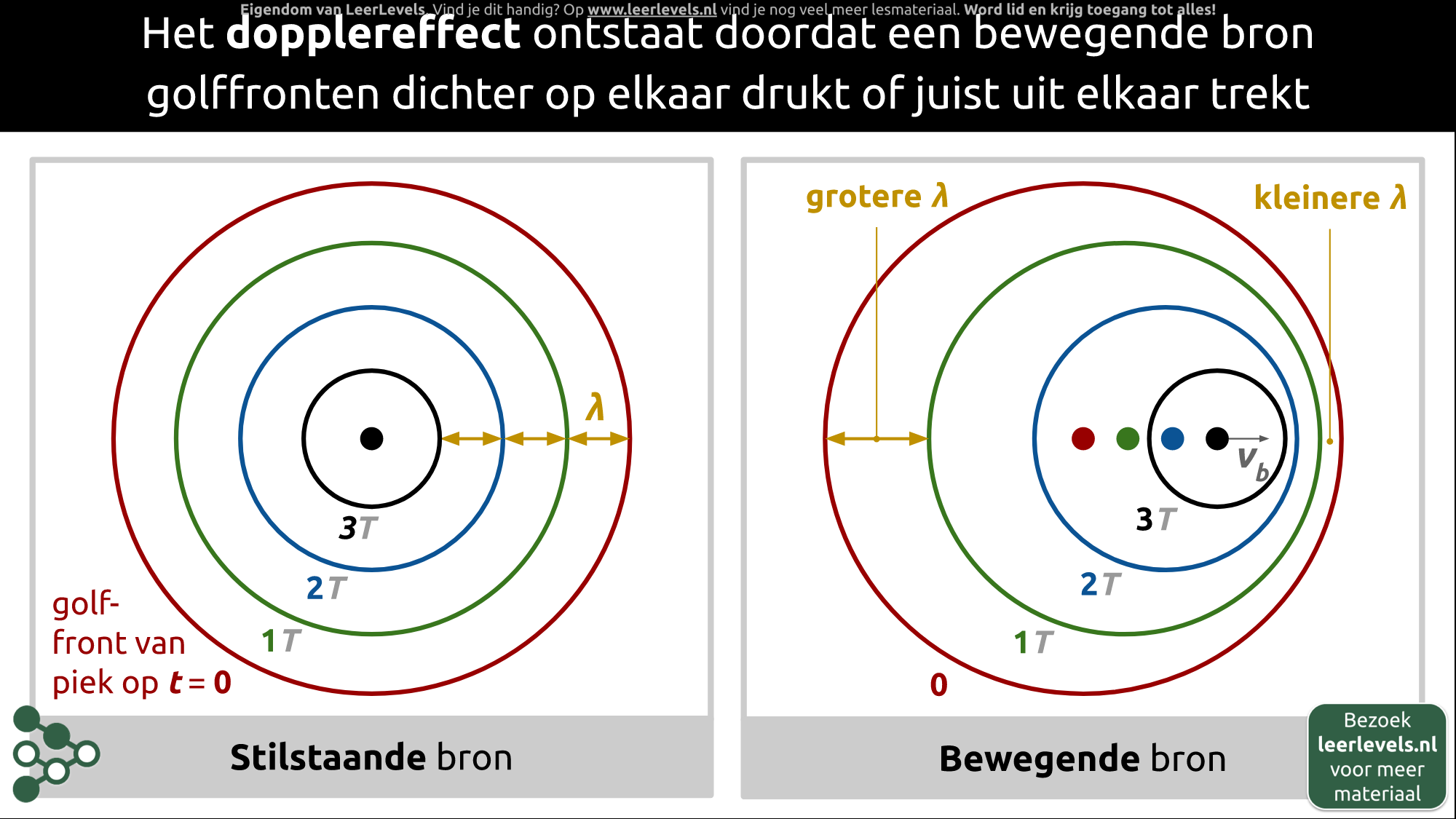
(Afbeelding: Animatie voor Dopplereffect verklaring)

Dopplereffect formule

Het Doppler-effect laat het geluid anders klinken als de bron of de luisteraar beweegt. Om te berekenen hoe de frequentie verandert, moet je weten hoe snel de bron en de luisteraar bewegen en wat de oorspronkelijke frequentie van het geluid is. De formule is fw = fb · ((v + vw)/(v-vb)), waarbij fw de waargenomen frequentie is, fb de oorspronkelijke frequentie in Hertz, v de snelheid van het geluid en vw en vb de snelheid van de luisteraar en de bron in meters per seconde. Als de snelheid positief is, beweegt iemand in de richting van de bron, als de snelheid negatief is, beweegt hij er vanaf.

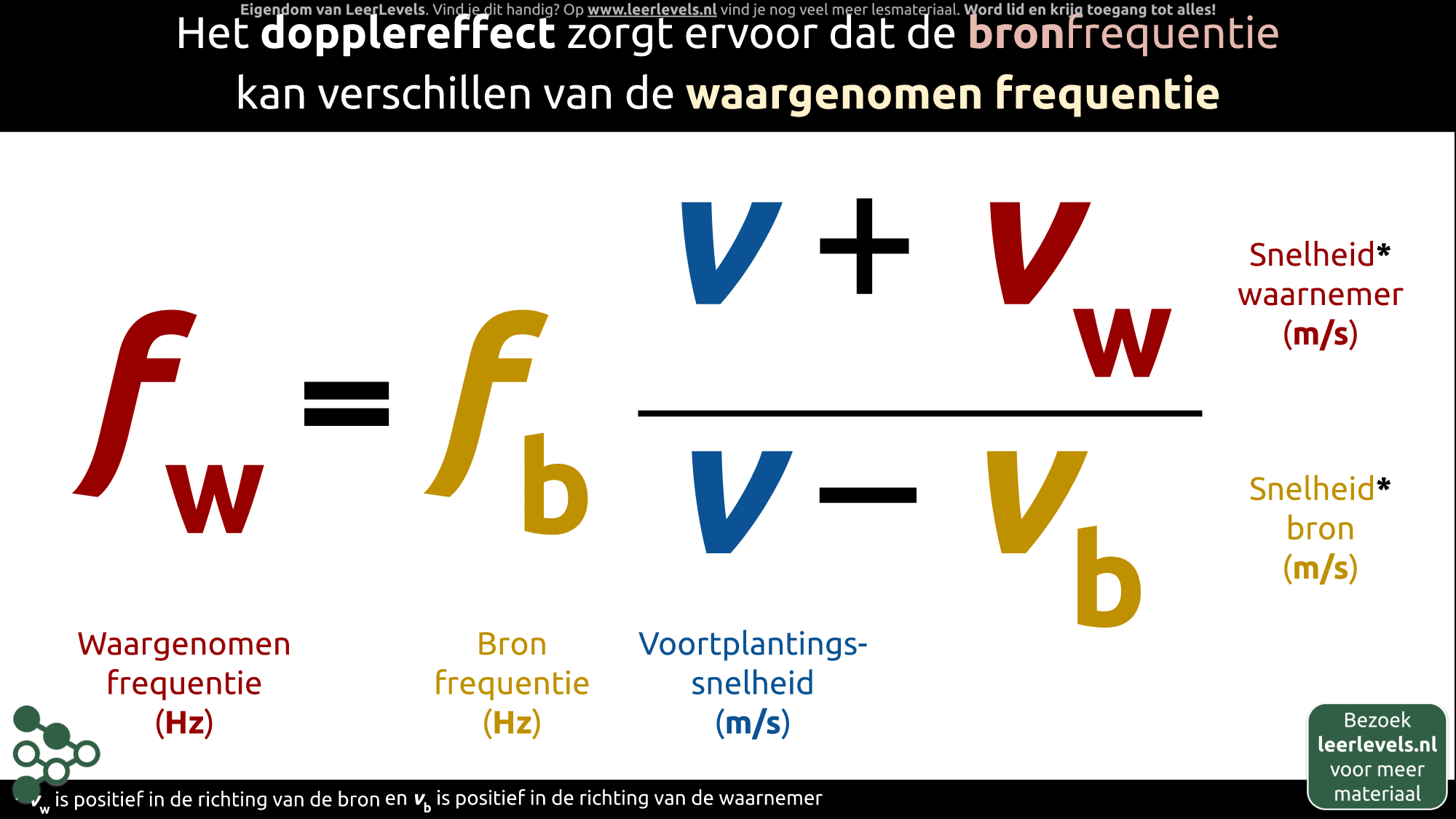
(Afbeelding: Animatie voor Dopplereffect formule)

Terug naar overzicht Meld je aan

Dosis

Dosis concept

Als een heel groot persoon een kleine hoeveelheid stralingsenergie opneemt, is dat niet zo gevaarlijk als wanneer een klein kind dezelfde hoeveelheid straling opneemt. Dit komt doordat een klein kind minder massa heeft dan een groot persoon, waardoor er bij hetzelfde stralingsniveau een grotere dosis wordt opgenomen. Er zijn ook tussenvarianten mogelijk, bijvoorbeeld een kleine dosis voor een klein kind of een grote dosis voor een groot persoon. Stralingsenergie wordt gemeten in eenheden van gray (Gy).

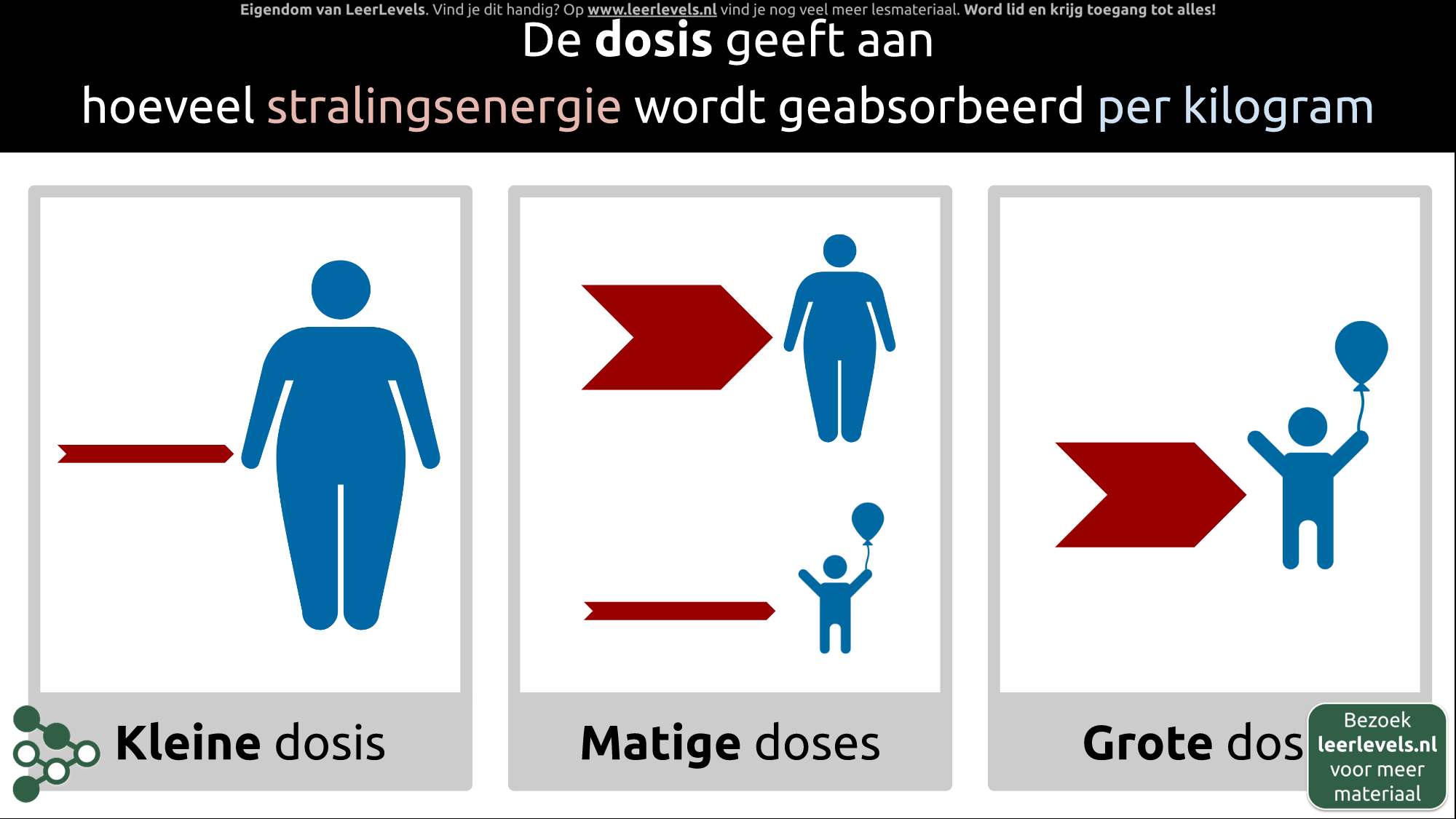
(Afbeelding: Animatie voor Dosis concept)

Dosis formule

De geabsorbeerde dosis (D) is recht evenredig met de stralingsenergie (E) en omgekeerd evenredig met de massa (m), wat kan worden weergegeven als

D = E/m

Hierin is D de dosis in gray, die verrassend genoeg wordt afgekort als Gy. Deze eenheid is vernoemd naar de wetenschapper Louis Harold Gray. Verder is E de energie in J en m de massa in kg

(Afbeelding: Animatie voor Dosis formule)

Terug naar overzicht Meld je aan

Drijven, zweven en zinken

Zinken, zweven en drijven

Of een object zinkt, drijft of zweeft, hangt af van de dichtheid van het object en het medium waarin het zich bevindt. Als de dichtheid van het object gelijk is aan die van het medium, zweeft het. Een zeepaardje zweeft omdat zijn dichtheid ongeveer gelijk is aan die van water. Als de dichtheid van het object groter is dan die van het medium, zinkt het. Bijvoorbeeld, staal zinkt omdat de dichtheid van staal (7,8 {kg}/{L}) groter is dan die van water (1 {kg}/{L}). Als het object een kleinere dichtheid heeft dan het medium, drijft het. De meeste houtsoorten drijven omdat hun dichtheid kleiner is dan die van water. Om te bepalen of een object zinkt, drijft of zweeft, moet je de dichtheid van zowel het object als het medium kennen.

(Afbeelding: Animatie voor Zinken, zweven en drijven)

Terug naar overzicht Meld je aan

Druk

Eenheden van druk

Er zijn verschillende eenheden om druk te meten. De belangrijkste eenheid is de Pascal (Pa), 1 Pascal is gelijk aan 1 Newton per vierkante meter. Dit is de standaard eenheid voor druk in het internationale SI-stelsel. Een andere veelgebruikte eenheid is de bar, 1 bar is gelijk aan 100,000 Pa. Dit wordt vooral gebruikt in de meteorologie. De atmosfeer (atm) is de gemiddelde luchtdruk op zeeniveau en is gelijk aan ongeveer 101,325 Pa. In de medische wereld wordt soms de millimeter kwik (mm Hg) gebruikt. 1 mm Hg is gelijk aan 133 Pa. In Engelstalige landen wordt soms de pounds-force per square inch (psi) gebruikt. 1 psi is gelijk aan 6,895 Pa. Deze waarden en hun symbolen staan allemaal in tabel 5 van het BiNaS-boek.

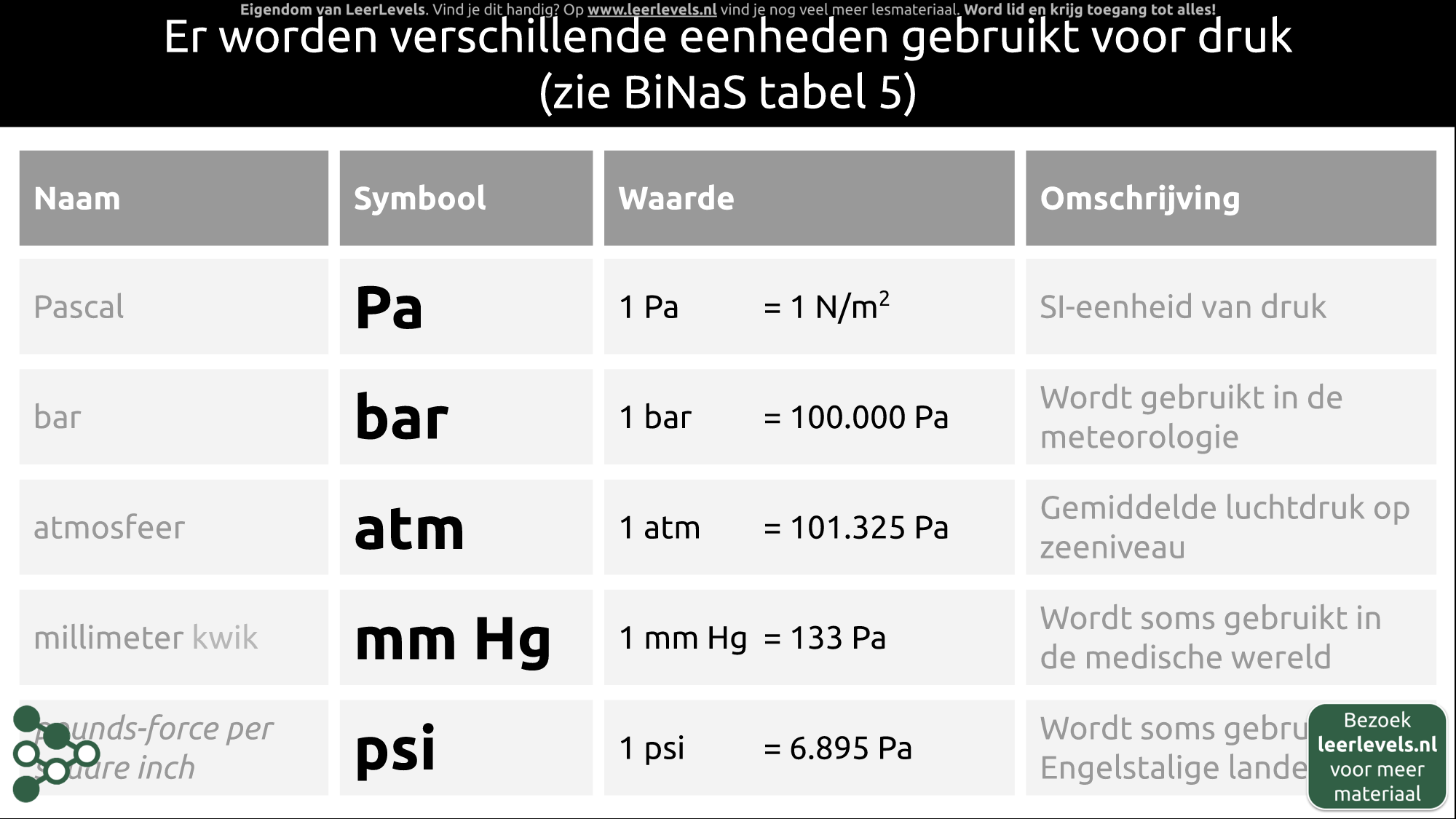
(Afbeelding: Animatie voor Eenheden van druk)

Overdruk en onderdruk

Als er meer druk is binnenin een voorwerp dan buiten, noemen we dat overdruk. Als er minder druk is binnenin dan buiten, noemen we dat onderdruk. Als je bijvoorbeeld een bal oppompt, wordt de druk binnenin hoger en moet je meer lucht in de bal blazen dan de buitenluchtdruk, om de bal harder op te pompen. Bij het drinken van water via een rietje, maak je een onderdruk in het deel van het rietje bij de mond door te zuigen, waardoor het water omhoog stroomt. Overdruk en onderdruk zijn relatieve begrippen ten opzichte van de buitenluchtdruk.

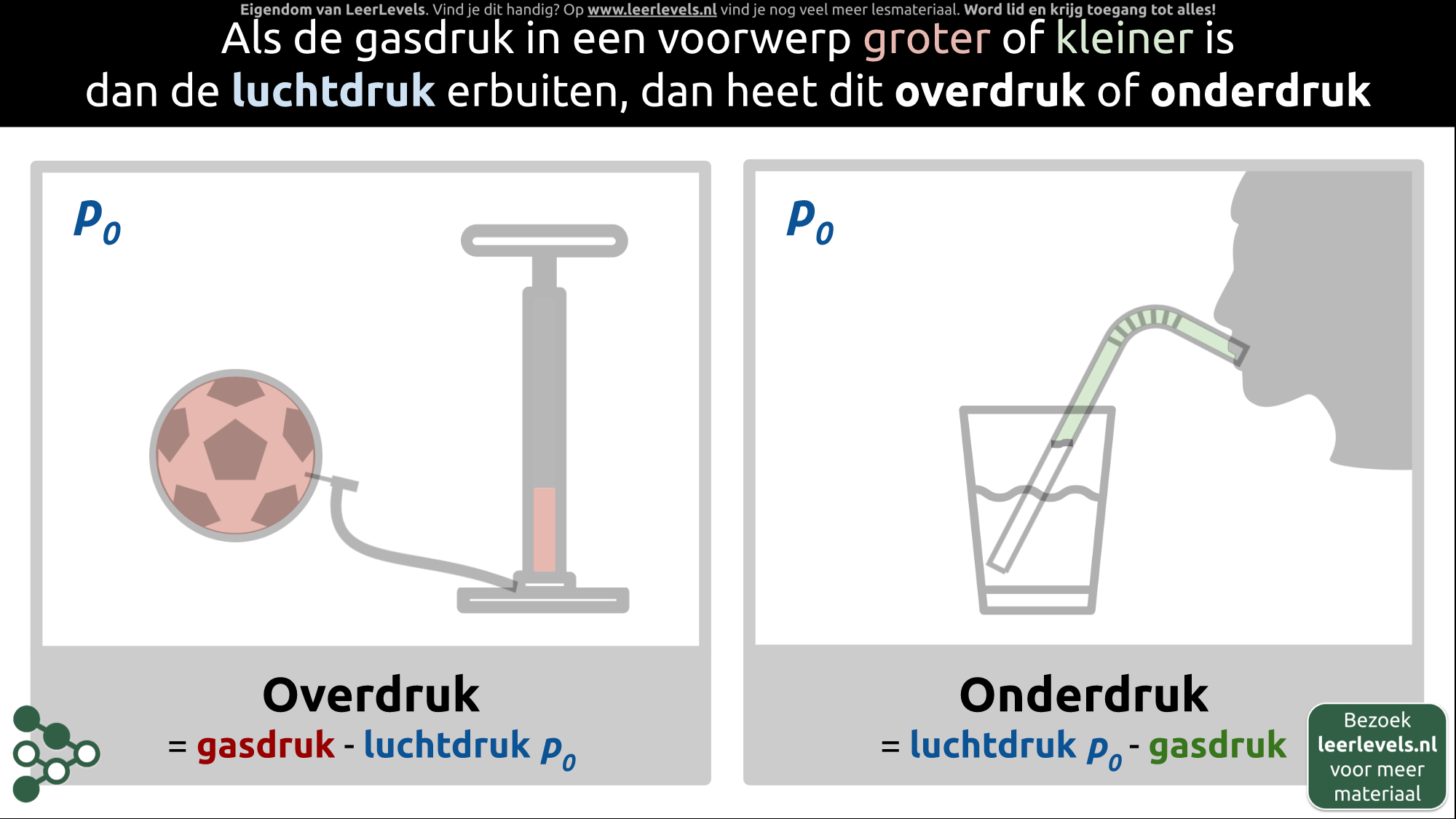
(Afbeelding: Animatie voor Overdruk en onderdruk)

Druk concept

Druk geeft aan hoeveel kracht er per oppervlakte-eenheid wordt uitgeoefend. Stel dat we een blokje op een oppervlak hebben staan. Als de kracht over een relatief groot oppervlak wordt verspreid, is de druk laag. Wanneer we meerdere blokjes naast elkaar plaatsen, wordt de kracht nog steeds over een groot oppervlak verdeeld, waardoor de druk laag blijft. Maar als we in plaats daarvan de blokjes op elkaar stapelen, wordt de totale kracht van de vier blokjes geconcentreerd op een kleiner oppervlak. Hierdoor is er een grotere kracht op een kleiner totaaloppervlak, wat resulteert in een hoge druk.

Dit principe ervaren we ook in het dagelijks leven. Stel dat je een spijker in de muur wilt duwen. Aan de kant waar je de kracht uitoefent, is het oppervlak groot en de druk dus klein. Maar aan de andere kant, waar het scherpe puntje zit, is het oppervlak klein en de druk groot. Als je dit omdraait, leidt het tot problemen: de hoge druk zit nu aan de kant van je vinger, en de lage druk aan de kant van de muur, waardoor de spijker niet in de muur gaat.

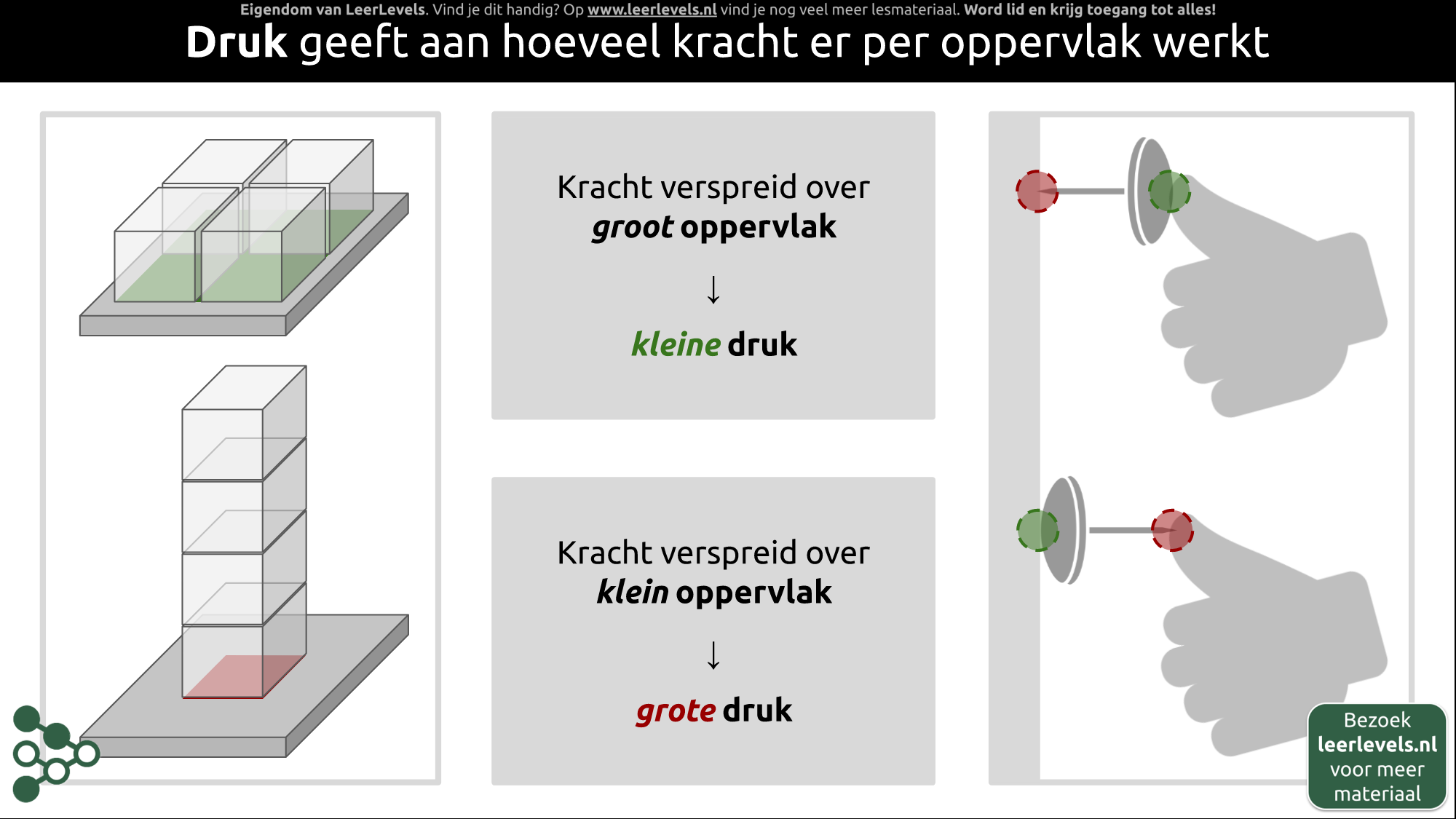
(Afbeelding: Animatie voor Druk concept)

Druk formule

Druk is hoe hard iets op iets anders drukt. Het hangt af van de kracht en de grootte van datgene waar de kracht op wordt uitgeoefend. Als je bijvoorbeeld op een klein gebied drukt, wordt de druk groter dan wanneer je op een groot gebied drukt. Druk wordt gemeten in Pascal (Pa), wat betekent Newton per vierkante meter (N/m²). De formule om druk te berekenen is: p = F/A waarbij p de druk is, F de kracht en A de grootte van het gebied waar de kracht op wordt uitgeoefend. Als je de kracht verdubbelt, wordt de druk ook twee keer zo groot, maar als je het gebied verdubbelt, wordt de druk juist twee keer zo klein.

(Afbeelding: Animatie voor Druk formule)

Druk rekenvoorbeeld uitdagend

Soms moet je een formule aanpassen of eenheden omrekenen om druk te berekenen. Bijvoorbeeld, als je een veiligheidsglas raam met een veiligheidshamer kapot maakt, barst het glas bij een druk van 2 gigapascal. Als je de ruit ziet barsten bij een kracht van 400 N, moet je oppervlakte berekenen waarop de hamer de ruit raakt. Om dit te doen, gebruik je de formule A = F / P, waarbij F de kracht is en P de druk. In dit geval is de kracht 400 N en de druk 2 gigapascal, maar je moet gigapascal eerst omschrijven naar een miljard. Dit schrijf je als 10⁻⁹. Vervolgens bereken je dat het oppervlak van de hamer 0,2 vierkante millimeter is. Om deze berekening uit te voeren, moet je de formule omschrijven en het voorvoegsel 'giga' vertalen naar macht van 10.

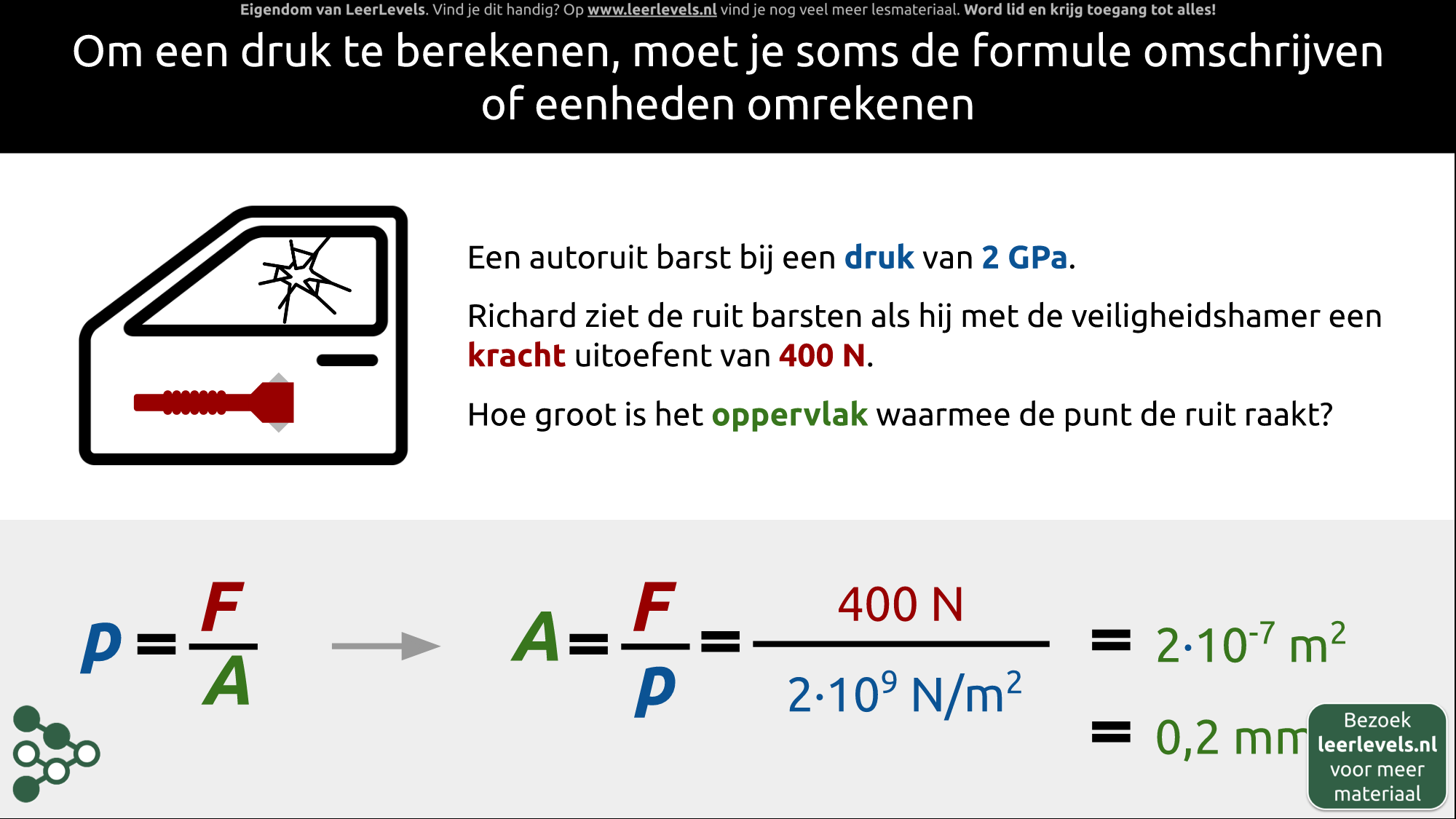
(Afbeelding: Animatie voor Druk rekenvoorbeeld uitdagend)

Druk in gas of vloeistof

De druk van gas of vloeistof wordt bepaald door alles wat er boven zit. Op een berg is er weinig lucht boven, dus de luchtdruk is laag. Op zeeniveau is er meer lucht boven, dus de luchtdruk is hoger. Onder water is er zowel lucht als water boven, dus is de druk groot door de zwaartekracht. De druk wordt hoger als er meer massa boven het punt aanwezig is. P staat voor druk en wordt bepaald door alles wat er boven je zit.

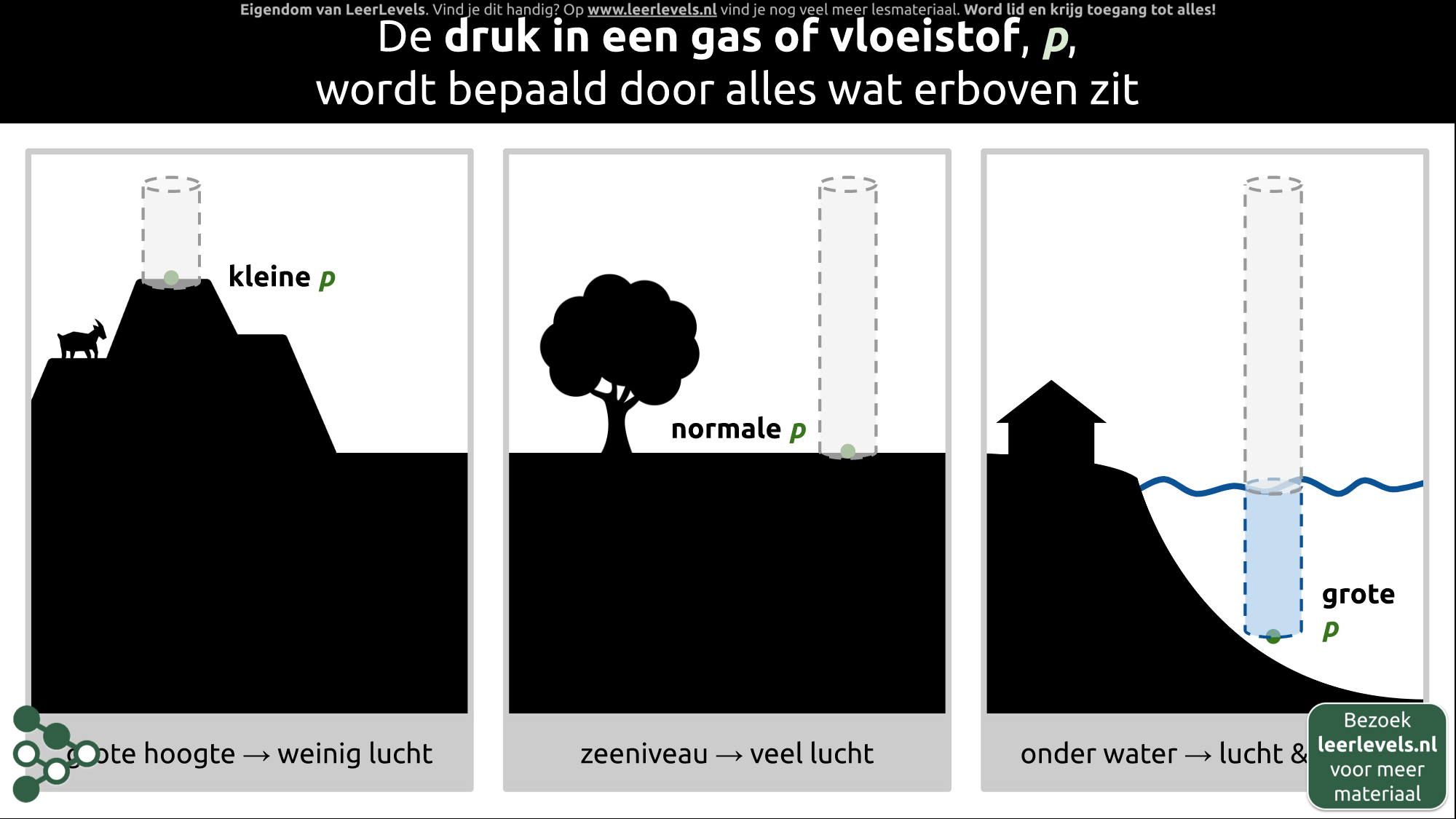
(Afbeelding: Animatie voor Druk in gas of vloeistof)

Druk rekenvoorbeeld eenvoudig

Om de druk te berekenen, gebruik je de formule: p = F/A . Hierbij staat p voor de druk in N/m² (of pascal), F voor de kracht in newton en A voor het oppervlak in m².

Stel, een blok met een massa van 1,5 kg oefent een kracht van 15 N uit op een oppervlak van 5 m². Dan vul je de formule in: p = (15 N)/(5 m² = 3 N/m² (of 3 pascal).

Als je vier blokken op elkaar stapelt, wordt de kracht vier keer zo groot (60 N). De druk wordt dan: p = (60 N)/(5 m² = 12 N/m².

Om de druk te berekenen, schrijf je dus eerst de formule op en vul je die daarna in met de gegeven waarden.

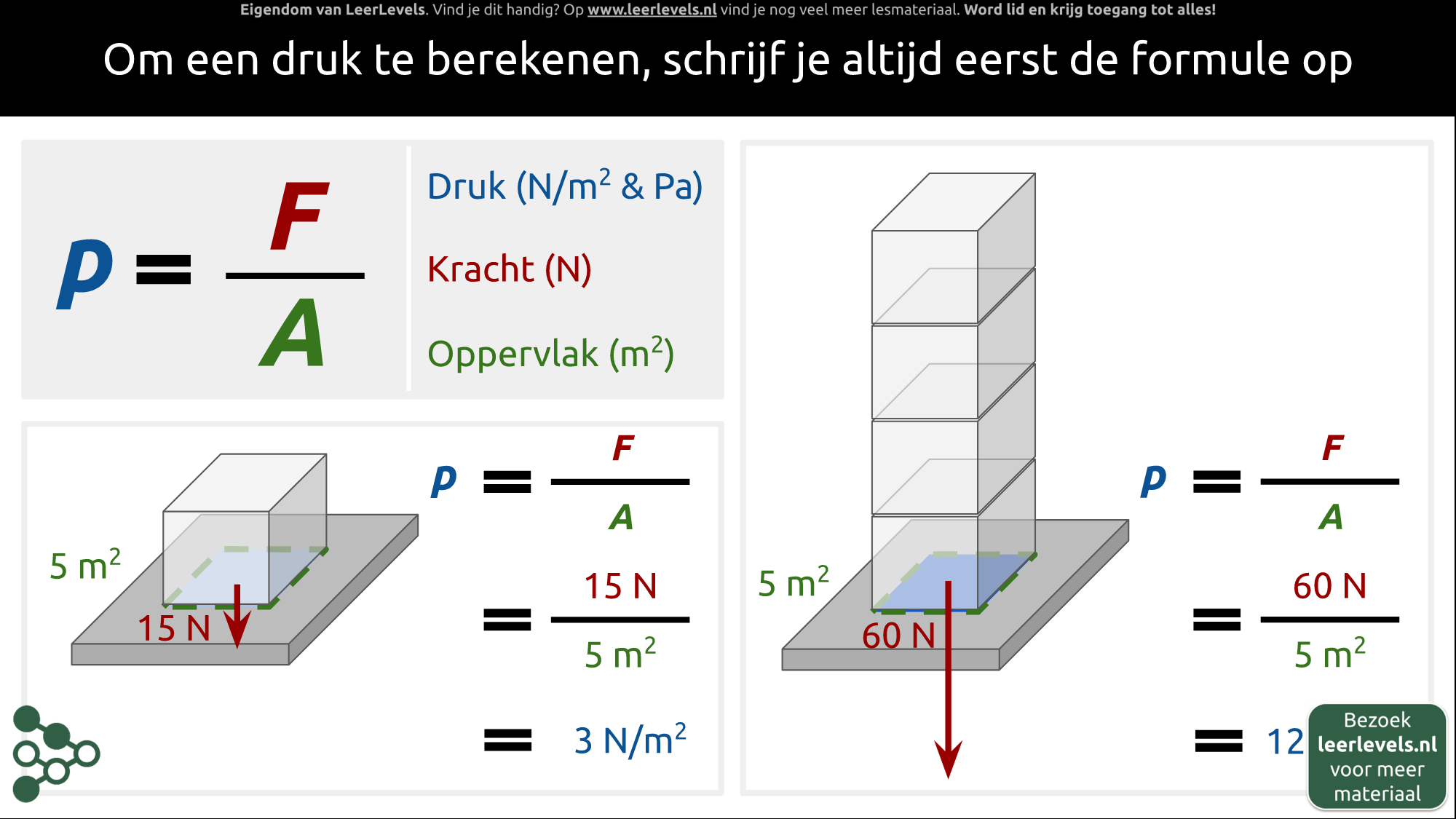
(Afbeelding: Animatie voor Druk rekenvoorbeeld eenvoudig)

Terug naar overzicht Meld je aan

Drukverschil

Drukverschil formule afleiding

Fase-overgangen verlopen bij een constante temperatuur, omdat alle energie wordt gebruikt voor de overgang. Stel dat we ijsklontjes hebben en warmte toevoegen. De temperatuur begint onder nul en neemt toe. Bij nul graden smelt een deel van het ijs en blijft de temperatuur constant, omdat de overgang van vast naar vloeibaar warmte kost. Wanneer alles gesmolten is, wordt de warmte gebruikt om het water te verwarmen. Bij 100 graden blijft de temperatuur weer constant, omdat de overgang van vloeibaar naar gas warmte kost. Nadat alles is verdampt, hebben we alleen gasvormig water over. Maar die kan nog verder worden opgewarmd. Tijdens fase-overgangen is de temperatuur constant, omdat alle energie nodig is voor de overgang.

(Afbeelding: Animatie voor Drukverschil formule afleiding)

Drukverschil formule

Het drukverschil in een vloeistof hangt af van de dichtheid van de vloeistof, de zwaartekracht en het hoogteverschil. Dit wordt weergegeven met de formule Δ p = ρ g h, waarbij Δ p het drukverschil is in pascal (of Newton per vierkante meter), ρ de dichtheid is in kilogram per kubieke meter, g de zwaartekrachtversnelling is in meter per seconde kwadraat en h de hoogte is in meter. Soms lijken de letters p en ρ op elkaar in handschriften.

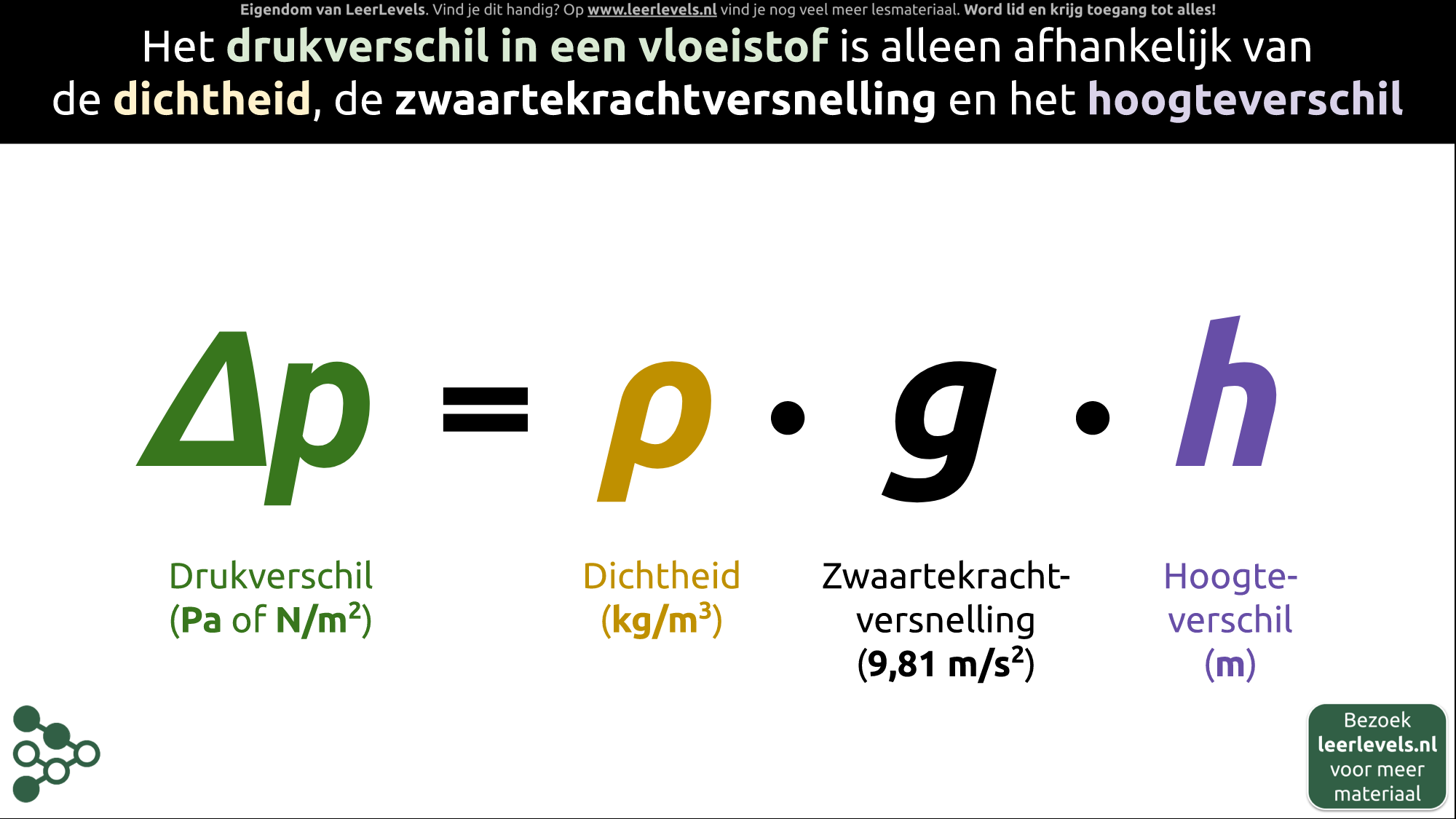
(Afbeelding: Animatie voor Drukverschil formule)

Terug naar overzicht Meld je aan

Dubbelspleetexperiment

Dubbelspleetexperiment enkele fotonen

Bij het dubbelspleetexperiment met enkele fotonen wordt stap voor stap het interferentiepatroon gecreëerd. Het experiment lijkt sterk op wat je al kent: een laser, een dubbelspleet en een scherm. Echter, in dit geval gebruiken we een laser met een zeer zwakke lichtintensiteit. Deze intensiteit is zelfs zo zwak dat er slechts één foton per keer in de opstelling aanwezig is. Pas wanneer een foton het scherm raakt, wordt de volgende foton uit de laser uitgezonden. In vergelijking met een standaard laserpointer, waarbij miljoenen fotonen gelijktijdig worden uitgezonden, is deze lasersetting dus extreem zwak afgesteld. Elk foton creëert een stip op het scherm en de locaties waar ze terechtkomen lijken willekeurig. Maar is dat wel echt zo? Bij herhaaldelijk uitvoeren van het experiment en het observeren van de stippen, ontstaat na verloop van tijd toch een patroon. Er zijn gebieden waar geen enkel foton, zelfs na vele metingen, terechtkomt. Dit zijn de minima. Daarnaast zijn er duidelijk zichtbare strepen, waar veel fotonen terechtkomen. Dit zijn de maxima. Het lijkt erop dat de kans groot is dat een foton op deze plekken terechtkomt. Bij herhaling van dit experiment miljoenen keren, wordt dit patroon zichtbaar. De pieken in het patroon duiden op de plaatsen waar veel fotonen worden gemeten (de maxima) en de dalen zijn de plaatsen waar geen fotonen terechtkomen (de minima). Dit patroon wordt een interferentiepatroon genoemd, maar wat interfereren er dan precies? Aangezien fotonen niet met elkaar kunnen interfereren omdat er slechts één foton tegelijk aanwezig is, moet het wel zo zijn dat het foton, dat als een golf gezien kan worden, tegelijkertijd door beide spleten heen golft en daardoor met zichzelf interfereert. Op deze manier wordt stap voor stap het interferentiepatroon opgebouwd bij het dubbelspleetexperiment met enkele fotonen.

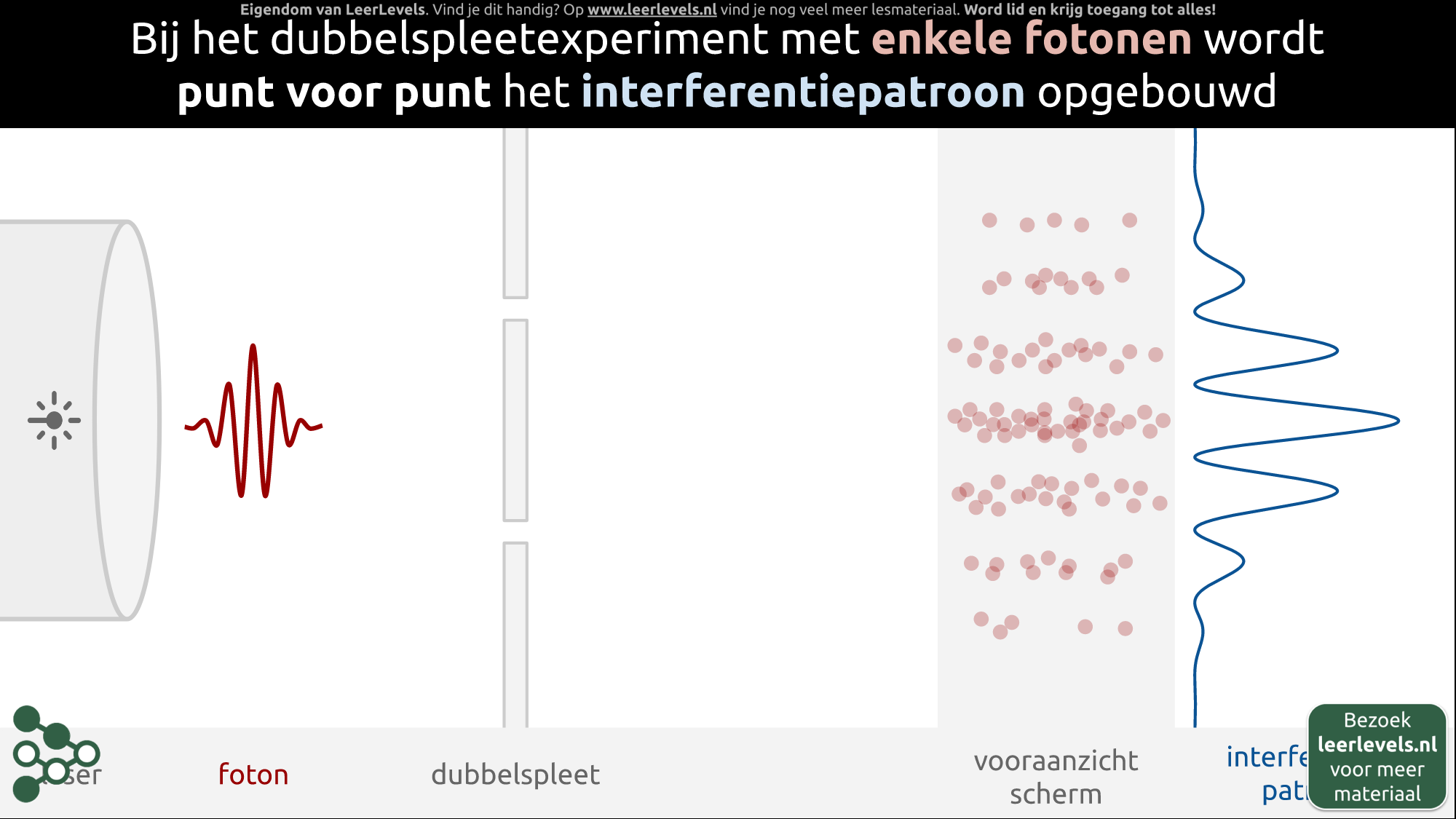
(Afbeelding: Animatie voor Dubbelspleetexperiment enkele fotonen)

Dubbelspleet-experiment concept

Bij het dubbelspleet-experiment van Young wordt er één lichtbron gebruikt om interferentie (het overlappen van lichtgolven) te veroorzaken. Dit experiment wordt nu gedaan met een laser. Het laserlicht wordt op een dubbele spleet geschoten en er ontstaan lichte en donkere vlekken onder bepaalde hoeken na de spleet. Sommige hoeken veroorzaken versterking van de golven (constructieve interferentie) en andere hoeken veroorzaken verzwakking van de golven (destructieve interferentie). Als je de fotonen van het laserlicht in detail bekijkt, zie je dat ze allemaal in dezelfde fase zijn. De spleten worden gedragent als puntbronnen en de halve cirkels laten het golffront zien. Op de plekken waar de pieken van de golven samenvallen, versterken ze elkaar en bij tussenliggende hoeken doven ze elkaar uit.

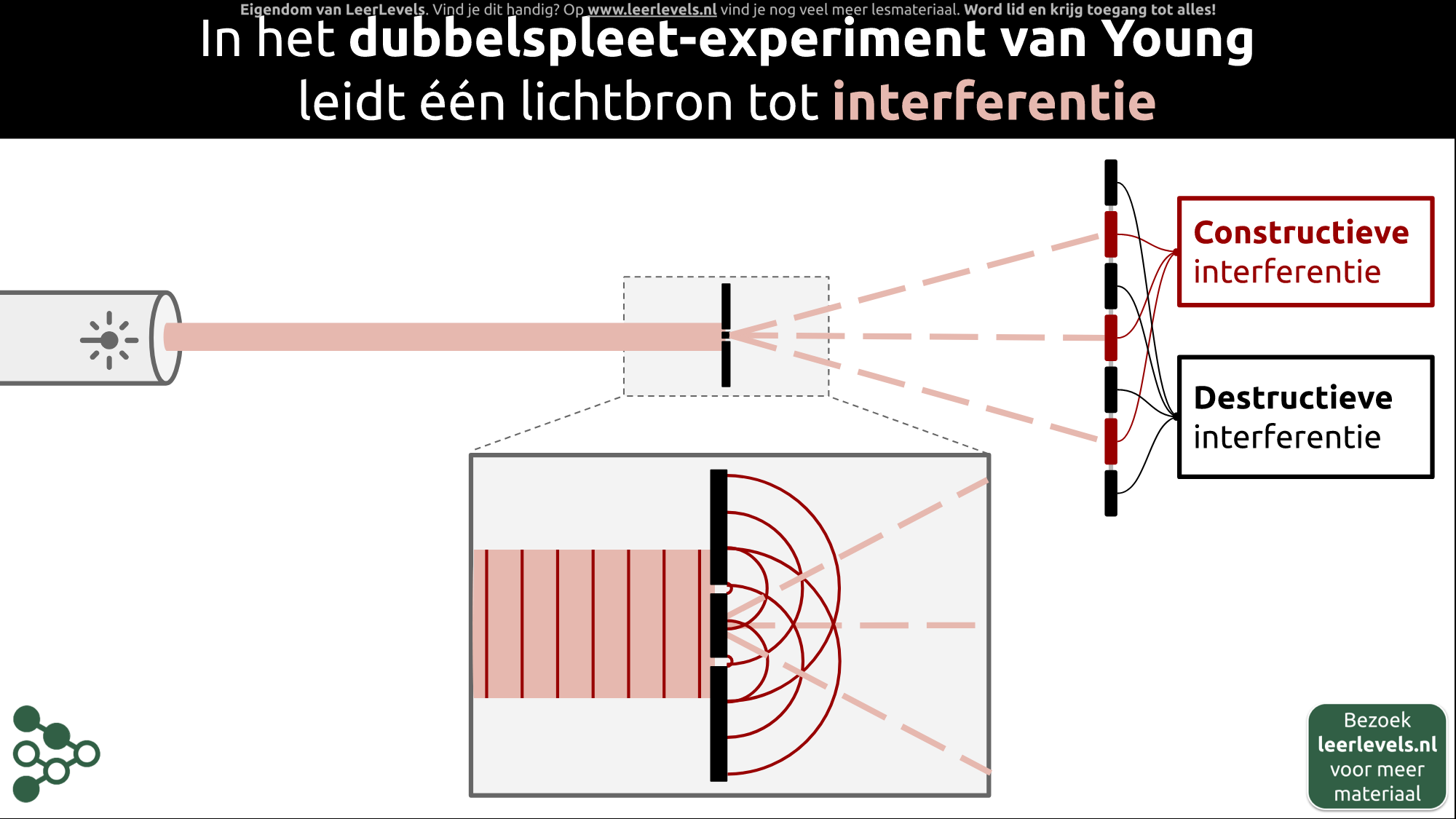
(Afbeelding: Animatie voor Dubbelspleet-experiment concept)

Dubbelspleet-experiment verklaring

In het dubbelspleet-experiment leidt diffractie onder bepaalde hoeken tot constructieve interferentie. Stel dat we een golf hebben die van links komt en door een dubbele spleet gaat. De spleten gedragen zich als puntbron die golven in alle richtingen uitzenden. Bij bepaalde hoeken treedt constructieve interferentie tussen deze golven op, zoals wanneer de golf rechtdoor gaat. Tussen deze hoeken van constructieve interferentie vindt destructieve interferentie plaats.

Laten we eerst kijken naar de golfbundel die rechtdoor gaat. Het onderlinge faseverschil van deze lichtstralen is nul. Wanneer de ene golf een piek heeft, heeft de andere dat ook. Het gereduceerde faseverschil is nul. Door de golven op te tellen, worden de pieken hoger en de dalen dieper. Dit is constructieve interferentie.

Als je onder een bepaalde kleine hoek kijkt en een loodrechte lijn trekt, zie je dat de golven precies in tegenfase zijn. De onderste golf heeft een halve golflengte extra afgelegd. Op de plek waar de bovenste golf een dal heeft, heeft de onderste een piek. Wanneer je deze optelt, doven ze elkaar uit. Het gereduceerde faseverschil is nul. Dit is destructieve interferentie.

Als je de hoek verder vergroot, kan het weglengteverschil weer precies één golflengte worden. Ook dan is het gereduceerde faseverschil nul, en zal er weer constructieve interferentie optreden.

Kortom, bij een gereduceerd faseverschil van nul (Δ φr = 0) treedt constructieve interferentie op en bij een gereduceerd faseverschil van een half (Δ φr = ½) treedt destructieve interferentie op.

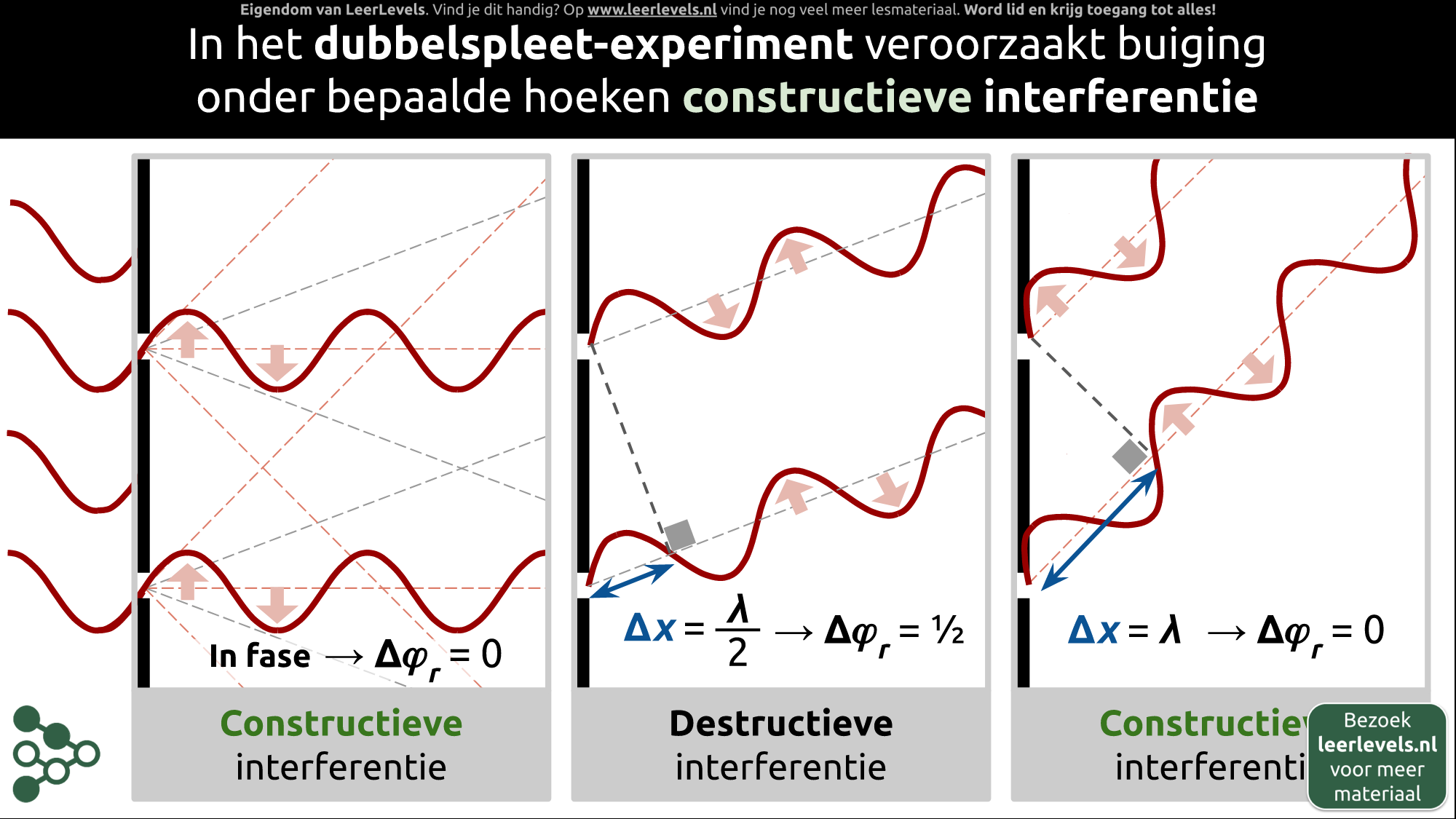
(Afbeelding: Animatie voor Dubbelspleet-experiment verklaring)

Dubbelspleet-experiment met elektronen

In 1961 werd het dubbele-spleetexperiment uitgevoerd met elektronen. Zelfs wanneer de elektronen één voor één door de spleten gingen, ontstond er een interferentiepatroon.

Laten we eerst kijken wat er gebeurt als je verfkogels door een dubbele spleet schiet. Bij grote objecten, zoals verfkogels, verwacht je dat ze een rechte lijn volgen als ze door een opening gaan. Als we de kogels één voor één afvuren en ze soms een spleet raken, ontstaat er achter de spleten een duidelijk patroon.

Als je echter verfkogels vervangt door elektronen, gebeurt er iets merkwaardigs. De elektronen spreiden zich bij aankomst niet willekeurig over het scherm uit, maar er ontstaat een interferentiepatroon. Het patroon is vergelijkbaar met licht dat door een dubbelspleet gaat en interfereert. Elektronen gedragen zich dus net als fotonen en vertonen golfgedrag door te interfereren. Zelfs als je één elektron per keer afschiet, gedraagt dat elektronen zich alsof het een golf is die met zichzelf interfereert.

Het wordt nog vreemder als je de elektronen niet alleen op het scherm detecteert, maar ook meet door welke spleet elk elektron gaat. Door die extra metingen gaan de elektronen zich plotseling weer als verfkogels gedragen: het interferentiepatroon verdwijnt.

Dit experiment is een van de belangrijkste redenen om aan te nemen dat elektronen zich soms als golven en soms als deeltjes gedragen, afhankelijk van de observatie. Dit gecombineerde gedrag wordt ook wel golf-deeltje-dualiteit genoemd.

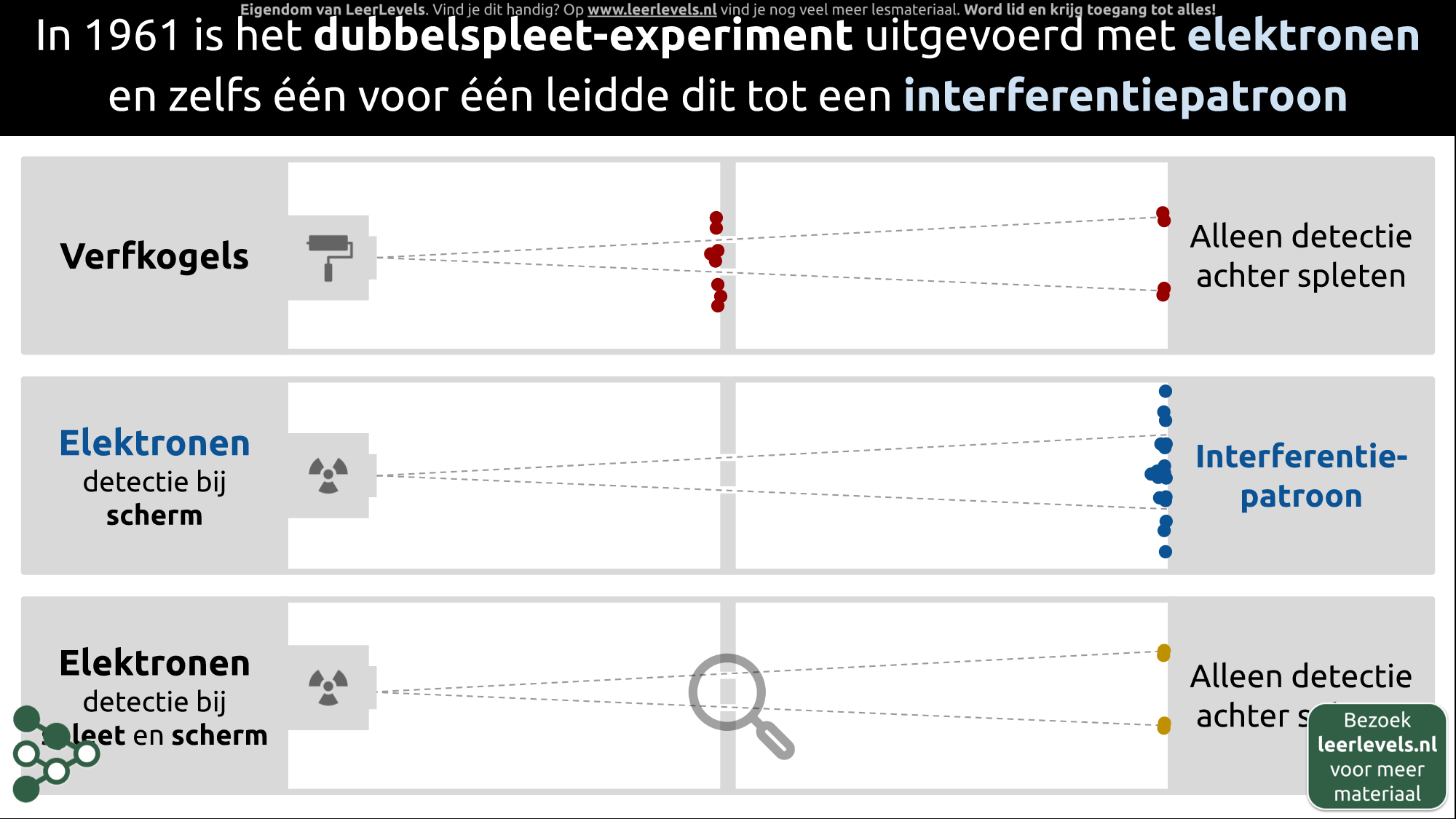
(Afbeelding: Animatie voor Dubbelspleet-experiment met elektronen)

Terug naar overzicht Meld je aan

Echo

Echo concept

Dit is bijna netjes, maar nog niet helemaal.

nog experimenteel

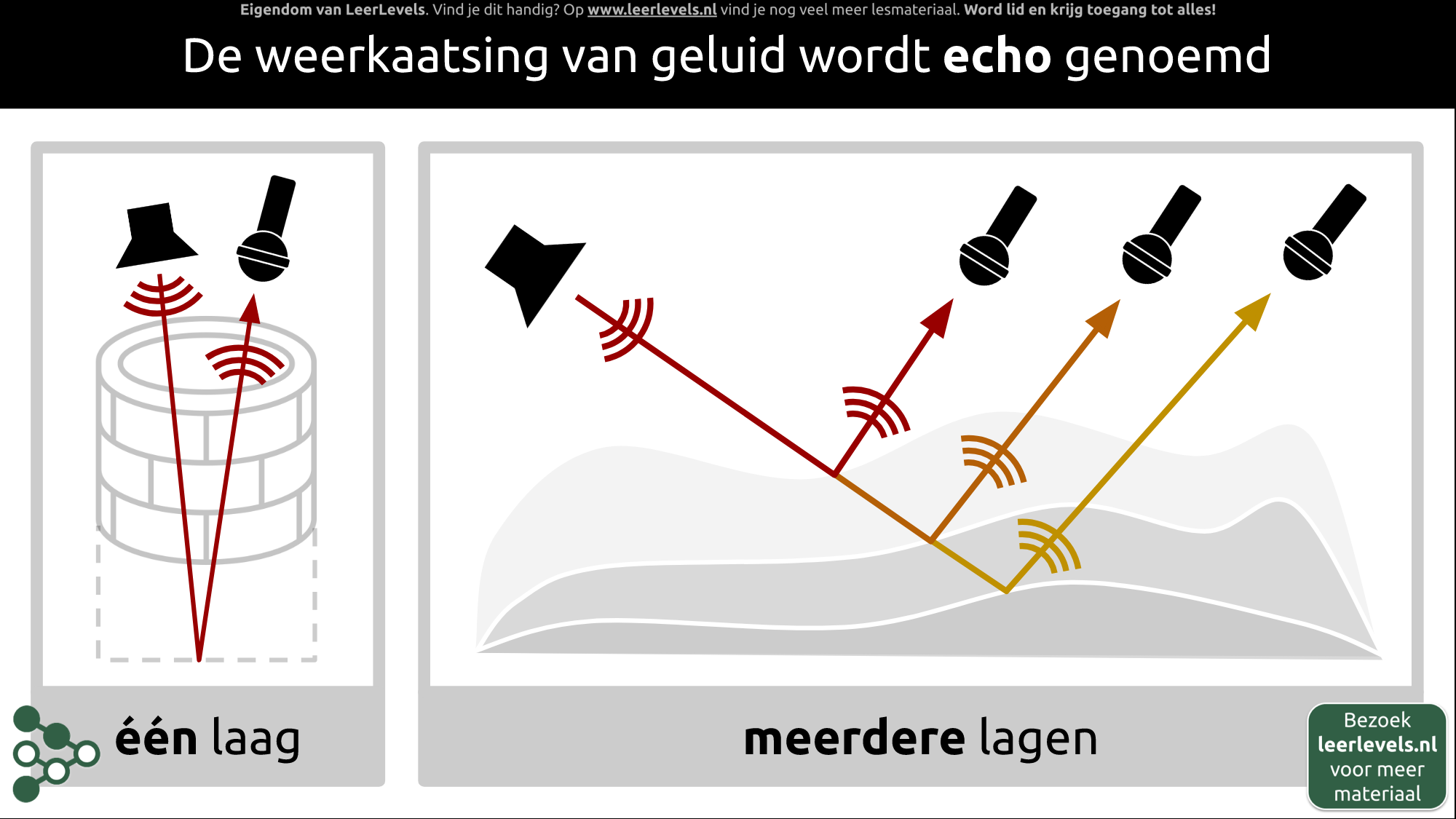
(Afbeelding: Animatie voor Echo concept)

Echo berekening

Met een echo kan je meten hoe ver iets bij jou vandaan is door de tijd te meten. Op een schip kan je bijvoorbeeld met een echo meten hoe hoog je boven de grond zit. Je stuurt geluid naar beneden en kijkt wanneer het terugkaatst met een microfoon. Met de formule v × t = s kan je dan de afstand berekenen. Hierbij is v de snelheid van het geluid in meter per seconde, s de afstand in meter en t de tijd in seconden. De snelheid van geluid in water is ongeveer 1500 meter per seconde, sneller dan in de lucht waar het 343 meter per seconde is. Dit komt door de dicht op elkaar zittende moleculen in water. Om de hoogte te berekenen deel je de afstand die het geluid aflegt door twee. De hoogte is dus de helft van de afstand. Zo kan je bijvoorbeeld bepalen dat de modem 600 m diep is. Zo kan het schip veilig eroverheen varen.

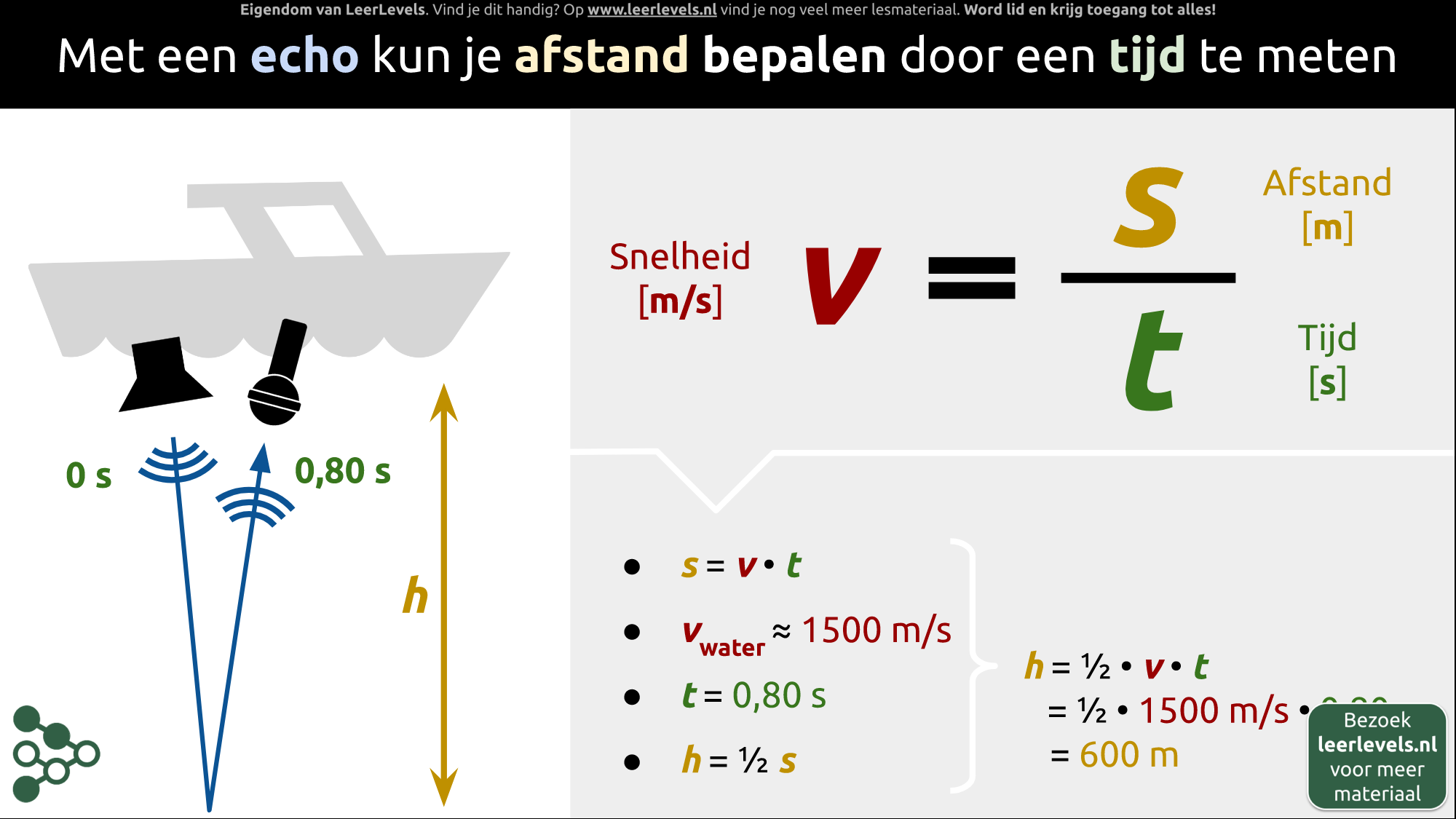
(Afbeelding: Animatie voor Echo berekening)

Terug naar overzicht Meld je aan

Eenheden

Grootheid invullen met eenheden

Bij het invullen van natuurkundige formules vervang je grootheden altijd door een combinatie van getal en eenheid. Stel dat je de formule hebt:

v = s/t

Het heeft geen zin om dit te herschrijven als:

v = (4500)/(1,5)

omdat je geen idee hebt wat die 4500 en 1,5 betekenen. Ook al komt daar 3000 uit, weet je nog steeds niet wat dat betekent.

Het is nuttiger om bijvoorbeeld 4,5 km in te vullen en 1,5 uur. Dan krijg je:

v = (4,5 km)/(1,5 uur) = 3 km/h

Of, als je het eerst omrekent naar meter en seconde, krijg je:

v = (4500 meter)/(5400 seconden) = 0,83 m/s

Het zijn dezelfde waarden, maar in een andere eenheid. Door de grootheden in te vullen als een getal met eenheid, weet je zeker dat het eindantwoord een betekenis heeft.

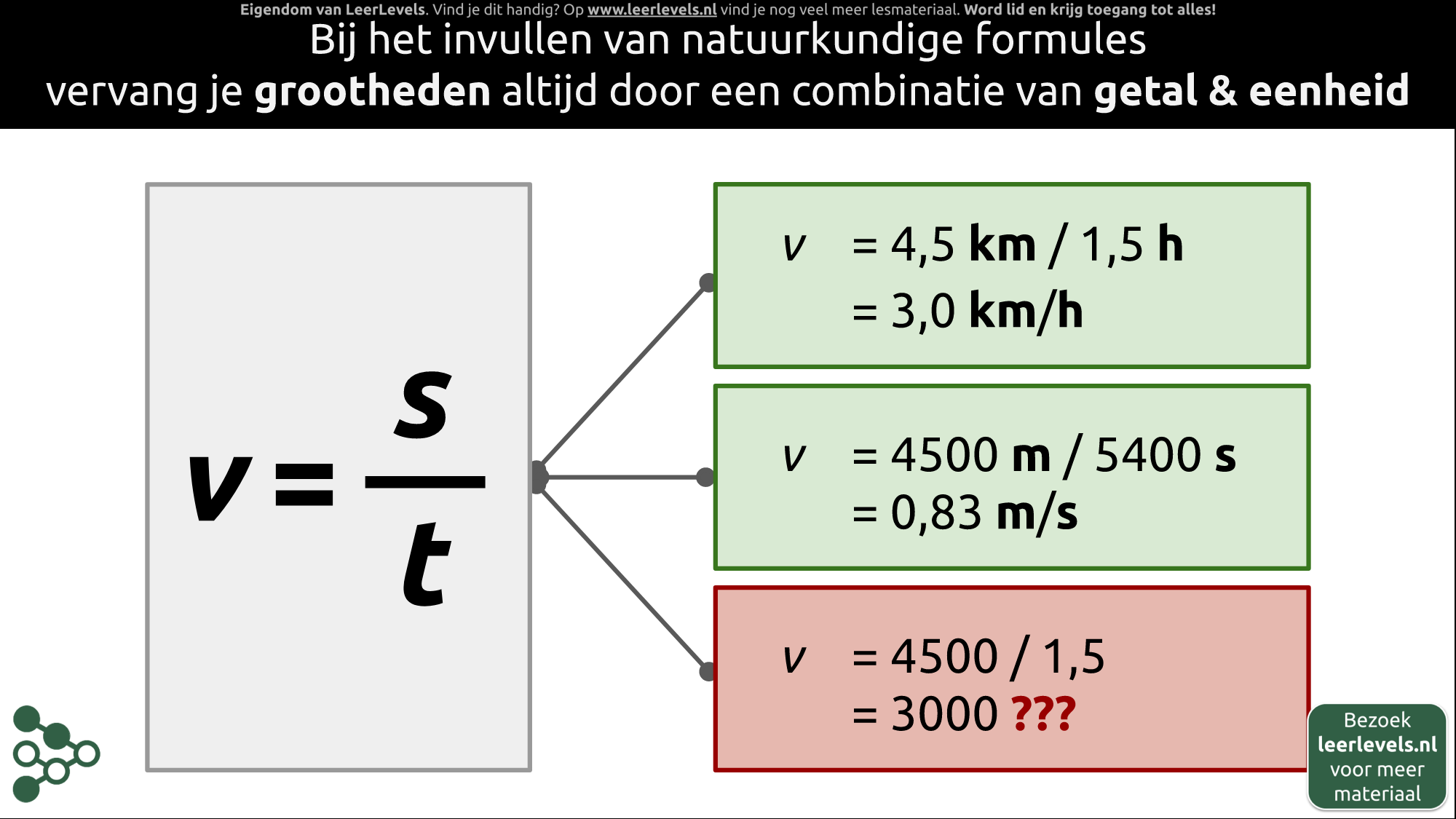
(Afbeelding: Animatie voor Grootheid invullen met eenheden)

Rekenen met eenheden

Een tekst over hoe je moet rekenen met eenheden. Het werkt hetzelfde als normale getallen. Bijvoorbeeld 6 meter gedeeld door 3 seconde is 2 meter per seconde. Kilo plus kilo is gewoon 2 kilo. Je kunt ook aftrekken, bijvoorbeeld twee seconden min één seconde is gewoon één seconde. Het is wiskunde. Je kunt ook vermenigvuldigen, bijvoorbeeld meter keer meter keer meter is meter tot de derde. Je kunt ook delen, bijvoorbeeld 10 graden Celsius gedeeld door 2 graden Celsius is alleen de getalwaarde 5. Dit betekent dat 5 een verhouding tussen twee temperaturen weergeeft en geen temperatuur zelf is.

(Afbeelding: Animatie voor Rekenen met eenheden)

Rekenen met afgeleide eenheden

Je kunt met formules berekenen hoeveel verschillende dingen met elkaar te maken hebben. Bijvoorbeeld, als je de formule F = m · a hebt, weet je dat kracht, massa en versnelling met elkaar te maken hebben. Een newton is gelijk aan een kilogram keer meter per seconde kwadraat. Als je alleen kilogram wilt weten, deel je de newton door meter per seconde kwadraat. Een andere formule is R = U / I, waarbij weerstand gelijk is aan voltage gedeeld door stroomsterkte. Als je beide kanten van de vergelijking vermenigvuldigt met ampère, krijg je volt = ampère keer ohm. Als je dan beide kanten deelt door ohm, krijg je: ampère = volt gedeeld door ohm.

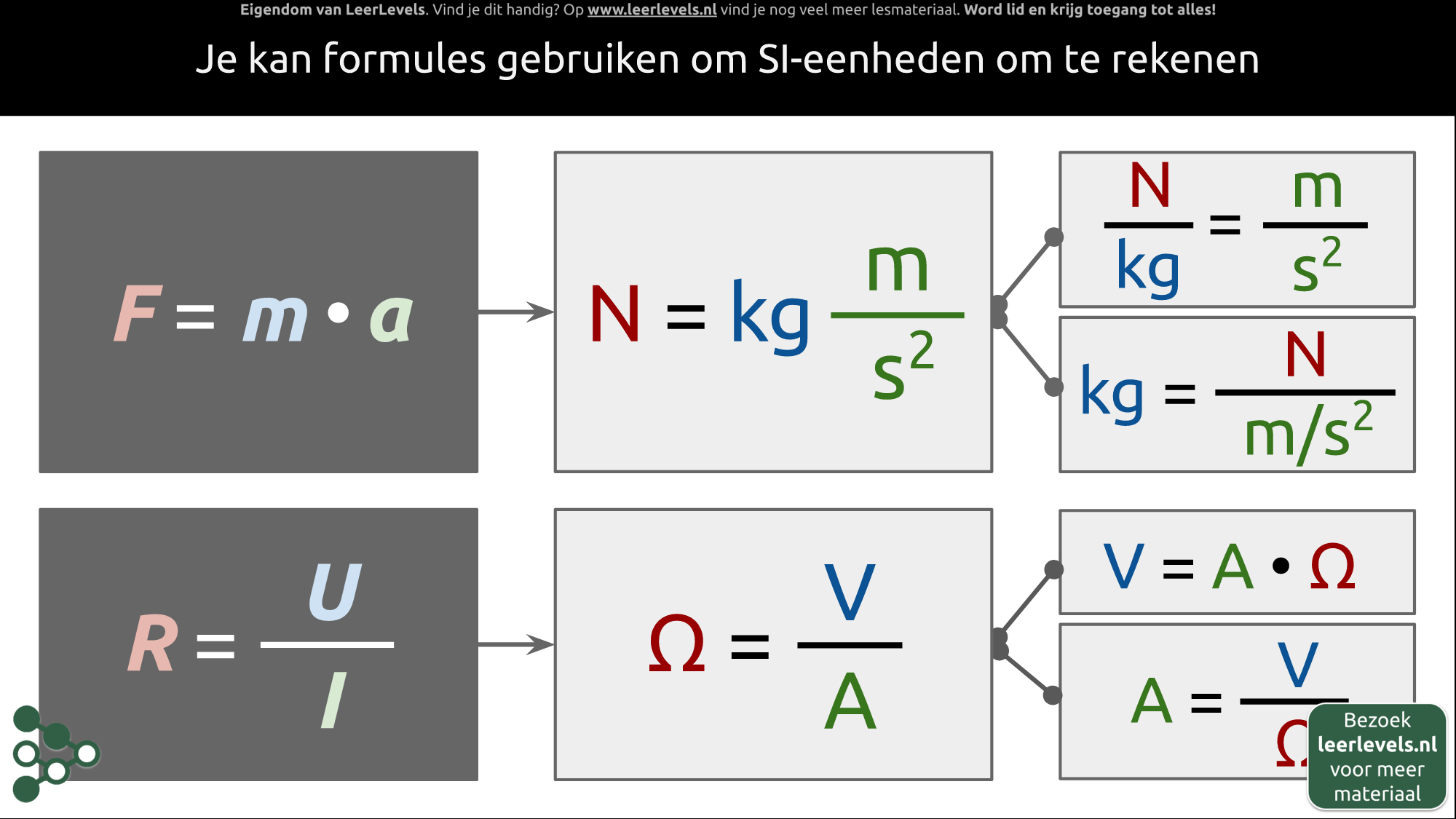
(Afbeelding: Animatie voor Rekenen met afgeleide eenheden)

SI-eenheden

In de hele wereld worden er standaardeenheden gebruikt in formules. De belangrijkste zeven worden basiseenheden genoemd: meter (m) voor afstand, seconde (s) voor tijd, mol (mol) voor hoeveelheid, kilogram (kg) voor massa, kelvin (K) voor temperatuur, ampère (A) voor elektrische stroom, en candela (cd) voor lichtsterkte. Alle andere eenheden kunnen worden uitgedrukt in deze basiseenheden. Bijvoorbeeld, snelheid wordt uitgedrukt in m/s en dichtheid in (kg)/(m³).

Sommige afgeleide eenheden hebben hun eigen naam gekregen, zoals Newton (N) voor kracht. Als je getallen invult in formules, moet je altijd de eenheden waarin ze staan meenemen. In spreektaal worden soms andere eenheden gebruikt, maar deze kunnen verkeerde resultaten opleveren in formules. Bijvoorbeeld, de eenheid inch voor afstand wordt nog weleens gebruikt in some Engelssprekende landen, maar in formules moet meter worden gebruikt.

Wanneer je formules invult, gebruik dan altijd de standaardeenheid die bij die grootheid hoort volgens het SI-systeem. Sommige natuurkundige grootheden zoals graden Celsius en calorie zijn geen standaardeenheden in het SI-systeem.

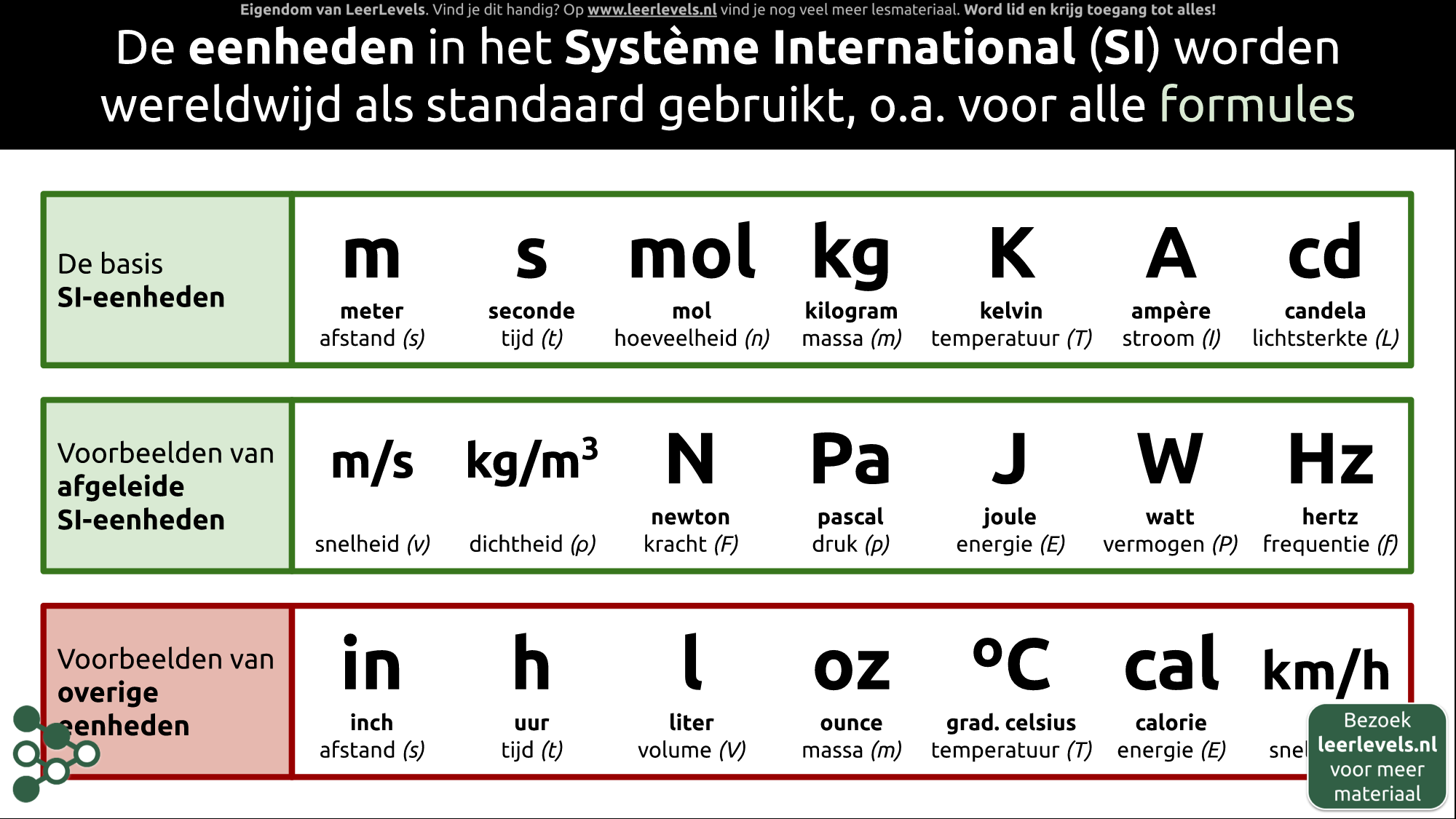
(Afbeelding: Animatie voor SI-eenheden)

Terug naar overzicht Meld je aan

Eenheden omrekenen

Eenheden omrekenen met BiNaS

Met BiNaS tabel 5 kun je verschillende eenheden omrekenen naar de bijbehorende standaardeenheid. De tabel bevat informatie over verschillende eenheden, waaronder:

- Astronomische eenheid (AE) = de gemiddelde afstand tussen de aarde en de zon = 1,496 × 10¹¹ meter.
- Massa-eenheid = 1/12 van de massa van een C-12 atoomkern = 1,661 × 10⁻²⁷ kilogram.
- Energie-eenheden, zoals kilowattuur (kWh) = het gebruiken van een uur lang vermogen van 1 kilowatt = 3,6 × 10⁶ joule, en elektronvolt (eV) = het energieverschil van een elektron voor 1 volt = 1,602 × 10⁻¹⁹ joule.
- Calorie (cal) = de energie om 1 gram water met 1 ºC op te warmen.

De tabel bevat ook informatie over verschillende grootheden, waaronder afstand, massa en energie. BiNaS tabel 5 maakt het mogelijk om deze eenheden en grootheden om te zetten naar de bijbehorende standaardeenheid.

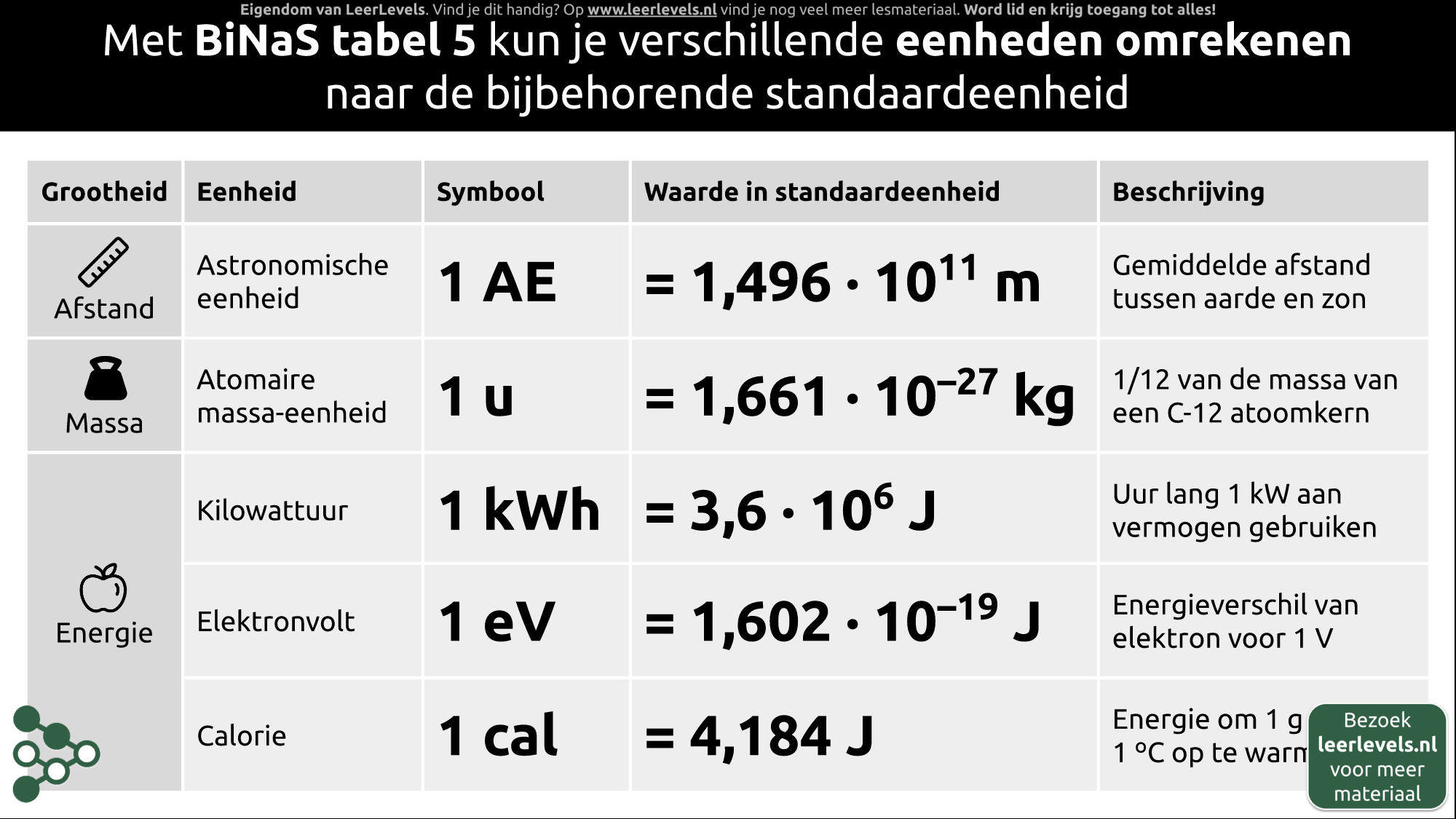
(Afbeelding: Animatie voor Eenheden omrekenen met BiNaS)

Terug naar overzicht Meld je aan

Eenparige beweging

Een eenparige beweging is een beweging waarbij je een constant en rechtlijnig pad aflegt, zonder af te remmen of bochten te maken. Een voorbeeld is fietsen op een rechte weg met dezelfde snelheid. Een manier om dit te zien is aan de hand van een vt-diagram, waarbij een horizontale lijn hoort bij een eenparige beweging. Ook in een at-diagram zal de versnelling altijd 0 zijn, omdat de snelheid constant is. In een st-diagram zal de afstand lineair toenemen, dus met een rechte lijn.

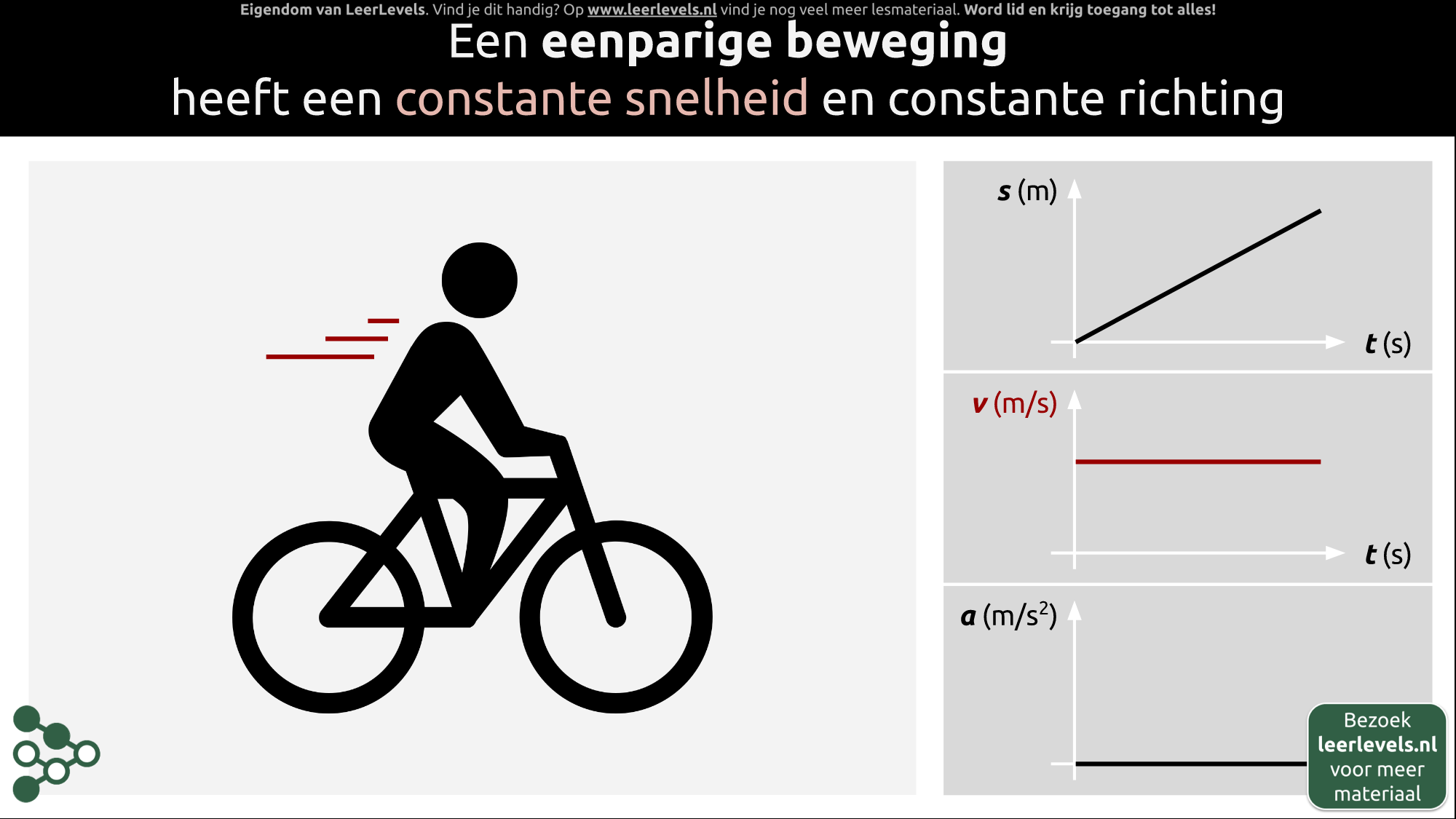
(Afbeelding: Animatie voor Eenparige beweging)

Afgelegde weg eenparig versnelde beweging formules

Als je beweegt met een constante versnelling, kun je gebruik maken van formules om in één keer de afgelegde weg te berekenen. Wanneer je een constante snelheid hebt, oftewel a = 0 m/s², is de afgelegde weg gelijk aan de rechthoek onder de (v,t)-diagram, oftewel s = v0 · t waarbij s de afstand is in meters, v0 de beginsnelheid in meter per seconde en t de tijd in seconden.

Wanneer de beginsnelheid of de eindsnelheid nul is, maar de versnelling constant blijft, wordt de totale verandering in snelheid Δ v genoemd en kan de afgelegde weg worden bepaald door het oppervlak van de driehoek onder de grafiek te berekenen: s = 0,5 · Δ v · t, waarbij Δ v gelijk is aan de versnelling a vermenigvuldigd met de tijd t.

In het geval van een bekende beginsnelheid en een constante versnelling, kan de afgelegde weg worden berekend door het oppervlak onder de grafiek op te delen in twee stukken en deze bij elkaar op te tellen: s = v0 · t + 0,5 · a · t². Hierin is a de versnelling in meter per seconde kwadraat.

---
Deze uitleg is experimenteel en wordt nog verder verbeterd.

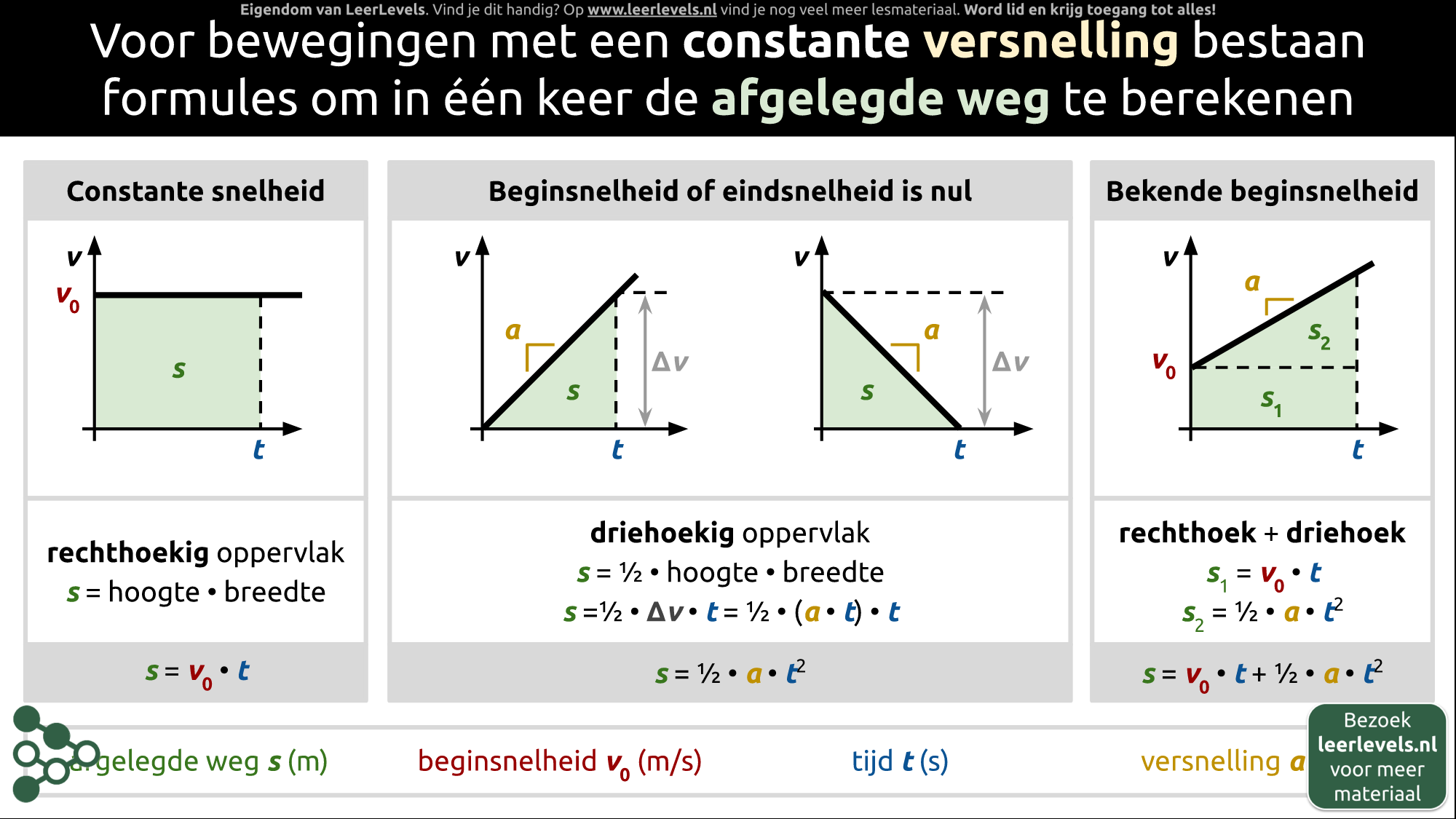
(Afbeelding: Animatie voor Afgelegde weg eenparig versnelde beweging formules)

Terug naar overzicht Meld je aan

Eerste wet van Newton

Eerste wet van Newton concept

Volgens de eerste wet van Newton hebben voorwerpen traagheid. Dit betekent dat hun snelheid alleen verandert wanneer er een resulterende kracht op hen inwerkt. Een voorbeeld hiervan is een satelliet die door de ruimte zweeft. Zonder dat er een kracht op de satelliet werkt, zoals luchtwrijving of stuwkracht, blijft de snelheid constant.

Laten we een raket als voorbeeld nemen. Een raket beweegt voort doordat hij gas naar achteren uitstoot, wat zorgt voor een duwkracht naar voren. In dit geval is er inderdaad een resulterende kracht aanwezig. Hierdoor zal de snelheid van de raket veranderen in de richting van die kracht.

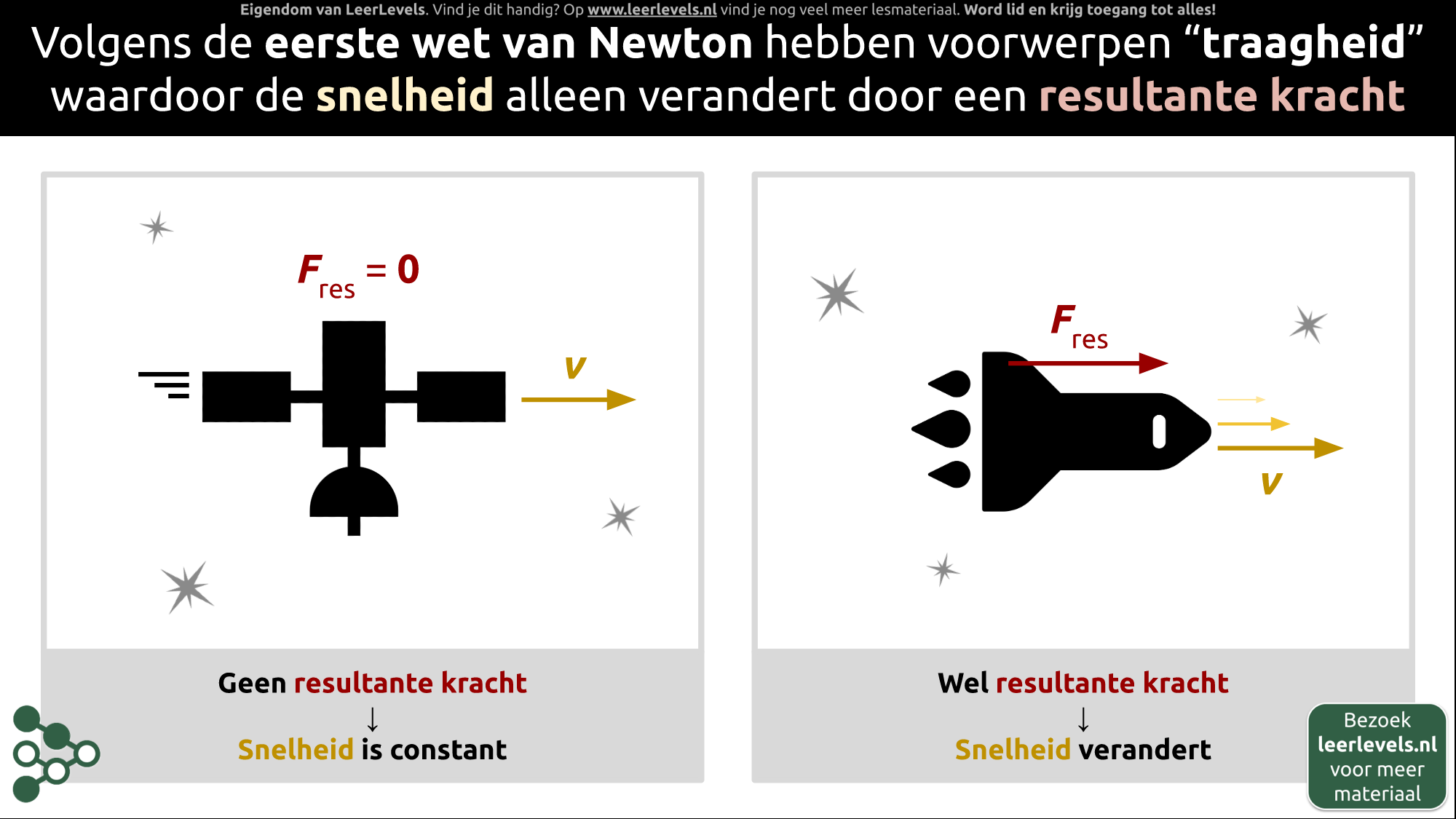
(Afbeelding: Animatie voor Eerste wet van Newton concept)

Eerste wet van Newton formule

Volgens de eerste wet van Newton, ook wel de traagheidswet genoemd, leidt alleen een resulterende kracht tot een verandering in snelheid. In formulevorm kan dit als volgt worden weergegeven:

Fres = 0 \quad\leftrightarrows \quad v = constant

Dit betekent dat als de resulterende kracht op een object nul is, het object in rust is of met constante snelheid blijft bewegen. Omgekeerd geldt dat als de versnelling nul is, de snelheid constant moet zijn, en daaruit volgt dat de resulterende kracht nul moet zijn.

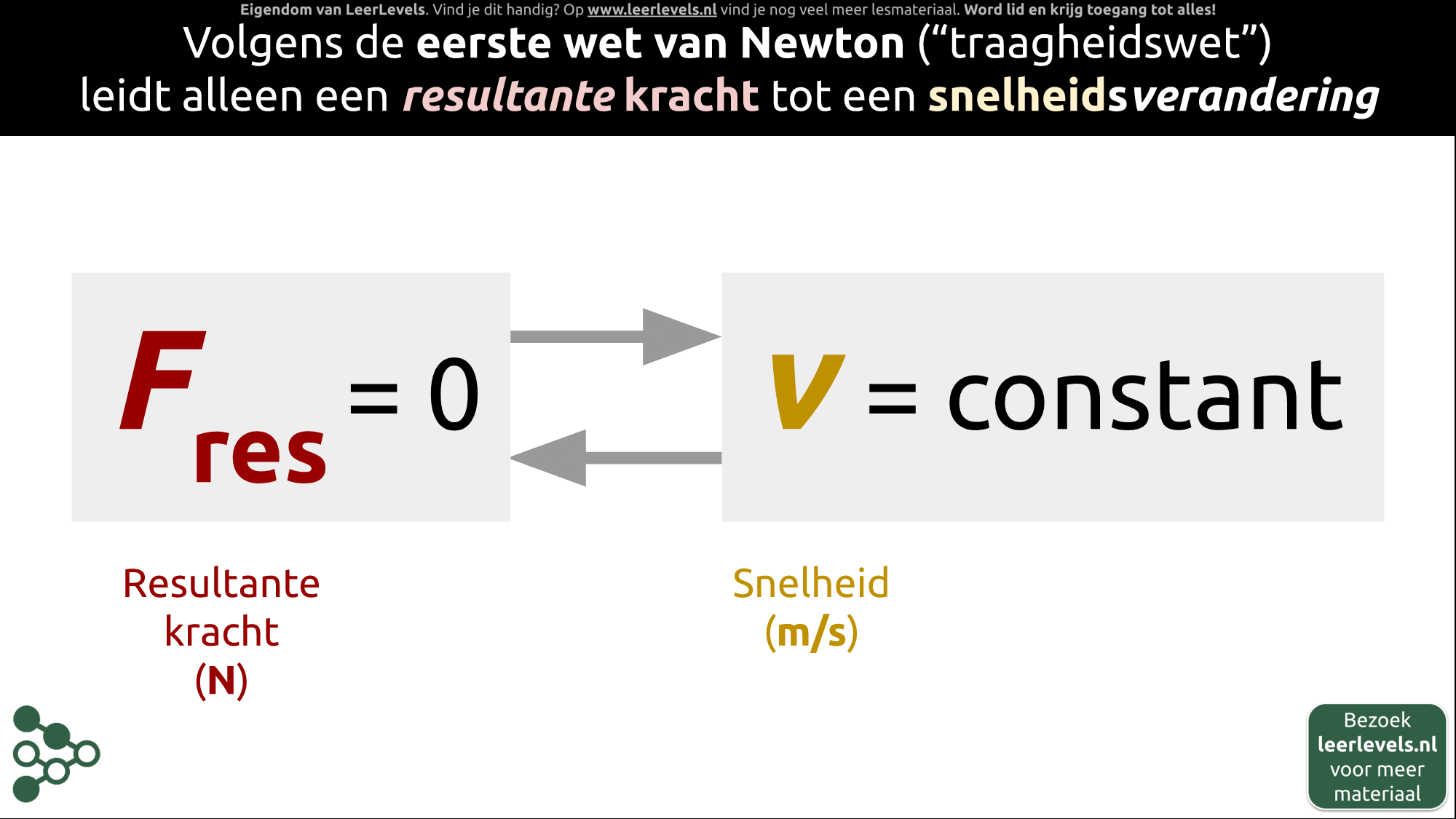
(Afbeelding: Animatie voor Eerste wet van Newton formule)

Terug naar overzicht Meld je aan

Eigenfrequentie

De eigenfrequentie is de frequentie waarmee een object begint te trillen wanneer het uit zijn evenwichtstoestand wordt gebracht en vervolgens wordt losgelaten. Overweeg een object met een lage eigenfrequentie, zoals een schommel. Als je op een schommel zit en jezelf een duwtje geeft, beweeg je langzaam heen en weer, omdat de schommel een lage eigenfrequentie heeft.

Bij objecten met een hoge eigenfrequentie gebeurt alles veel sneller. Een voorbeeld hiervan is een stemvork. Wanneer je deze aanslaat, begint hij zeer snel te trillen en produceert hij een zuivere, precieze toon.

Een voorbeeld van iets met een gemiddelde eigenfrequentie is een pogo-stick. Deze stuitert sneller dan een schommel, maar langzamer dan een stemvork. De frequentie waarmee het trilt wanneer je erop op en neer springt, is de eigenfrequentie.

(Afbeelding: Animatie voor Eigenfrequentie)

Terug naar overzicht Meld je aan

Elasticiteitsmodulus

Elasticiteitsmodulus concept

Elasticiteitsmodulus is een eigenschap van een materiaal die meet hoeveel spanning het kan weerstaan voordat het permanent vervormt. Het wordt uitgedrukt in Pascal (Pa). Als een materiaal elastisch is, kan het theoretisch tot twee keer zo lang worden uitgerekt onder mechanische spanning. Er zijn twee manieren om de elasticiteitsmodulus te berekenen. De eerste manier is visueel: het is de mechanische spanning die nodig is om een elastische rek van 100% te bereiken. Als de spanning bijvoorbeeld 2500 Pa is, dan is de elasticiteitsmodulus 2500 Pa. De tweede manier is door middel van een grafiek. Het hellingsgetal van het rechtevenredige deel van een (spanning,rek)-diagram geeft de elasticiteitsmodulus weer. Bijvoorbeeld, als de helling van het rechtevenredige deel van het diagram 2500 Pa is, dan betekent dit dat bij 100 Pa spanning een rek van 4% wordt veroorzaakt.

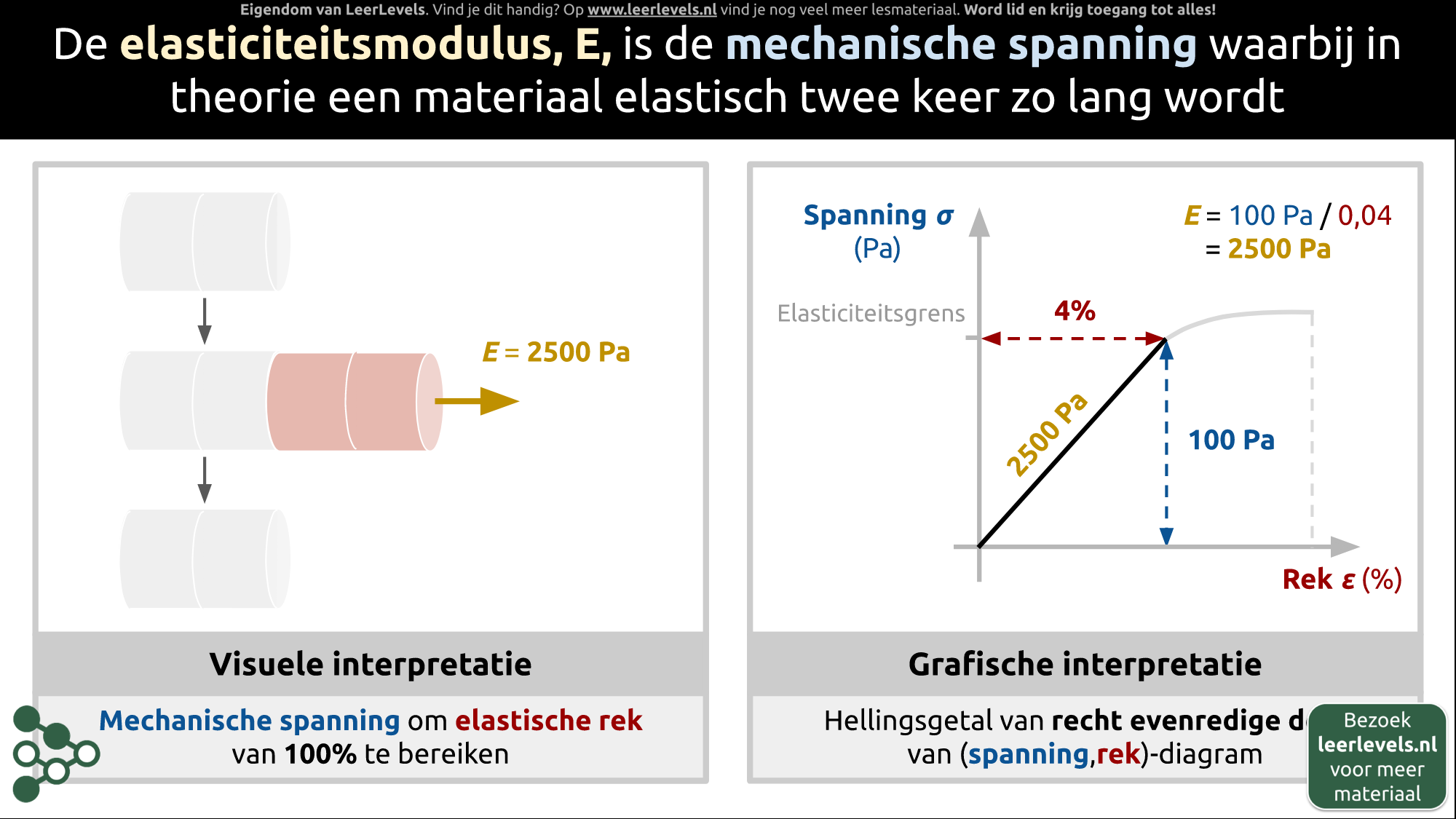
(Afbeelding: Animatie voor Elasticiteitsmodulus concept)

Elasticiteitsmodulus formule

De elasticiteitsmodulus van een materiaal geeft de verhouding weer tussen de mechanische spanning en de rek die in het materiaal optreedt. De formule hiervoor is:

E = (σ)/(ε)

waarbij E de elasticiteitsmodulus in pascal (Pa) aangeeft. De mechanische spanning σ wordt eveneens uitgedrukt in pascal, en ε is de rek als een dimensieloze grootheid. Het is belangrijk te weten dat ε als factor moet worden ingevoerd en niet als percentage. Dit betekent dat een rek van 4\% procent ingevoerd moet worden als 0,04.

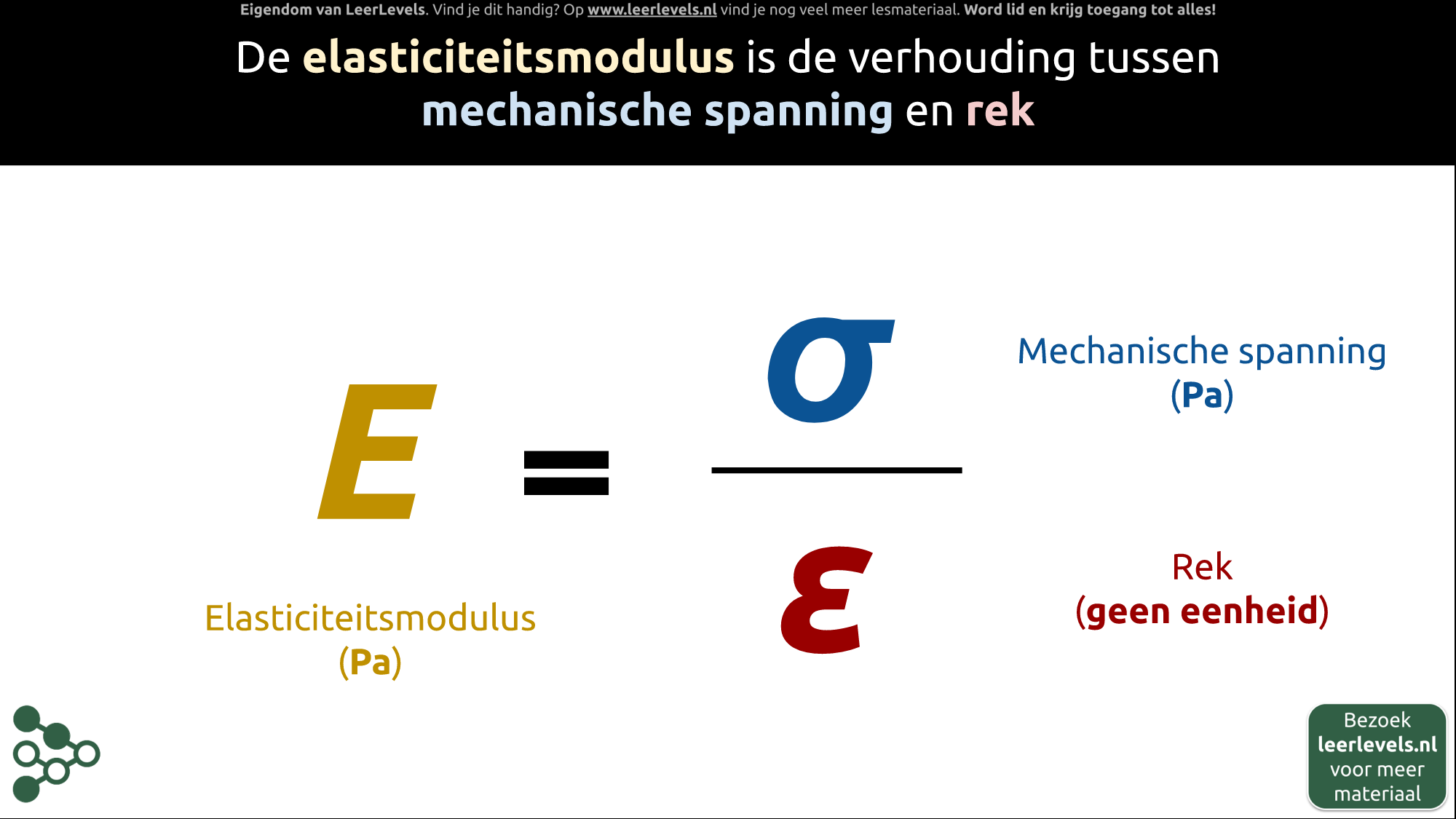
(Afbeelding: Animatie voor Elasticiteitsmodulus formule)

Terug naar overzicht Meld je aan

Elektrisch veld

Elektrisch veld concept

Het elektrische veld E geeft op elk punt in de ruimte aan welke elektrische kracht op een kleine, positieve testlading zou werken. Stel dat we een positieve lading hebben en we plaatsen een kleine testlading in de buurt; dan geldt dat positieve ladingen elkaar afstoten. Wanneer de ladingen dicht bij elkaar zijn, is de afstotende kracht groot. Als we een andere testlading verder weg plaatsen, neemt de afstotende kracht af. In alle gevallen wijst de kracht van de grote positieve lading af.

Het elektrische veld laat voor alle punten in de ruimte zien in welke richting de kracht op een testlading zou werken. Dit elektrische veld heeft enkele eigenschappen: hoe dichter de veldlijnen bij elkaar liggen, hoe groter de kracht. Bij een negatieve lading verandert de richting van de elektrische veldlijnen. Een positieve testlading wordt dan aangetrokken, waardoor de veldlijnen naar de negatieve lading wijzen.

Als je te maken hebt met twee verschillende ladingen, ontstaat er een complexere situatie. Voor iedere testlading spelen zowel de afstoting door de positieve lading als de aantrekking door de negatieve lading een rol. Naarmate de afstand toeneemt, vermindert het effect van deze krachten. Het resultaat is een ingewikkeld patroon waarbij de veldlijnen van de positieve naar de negatieve lading lopen. De veldlijnen zijn het dichtst opeengepakt direct tussen de twee ladingen, waar de veldsterkte het grootst is.

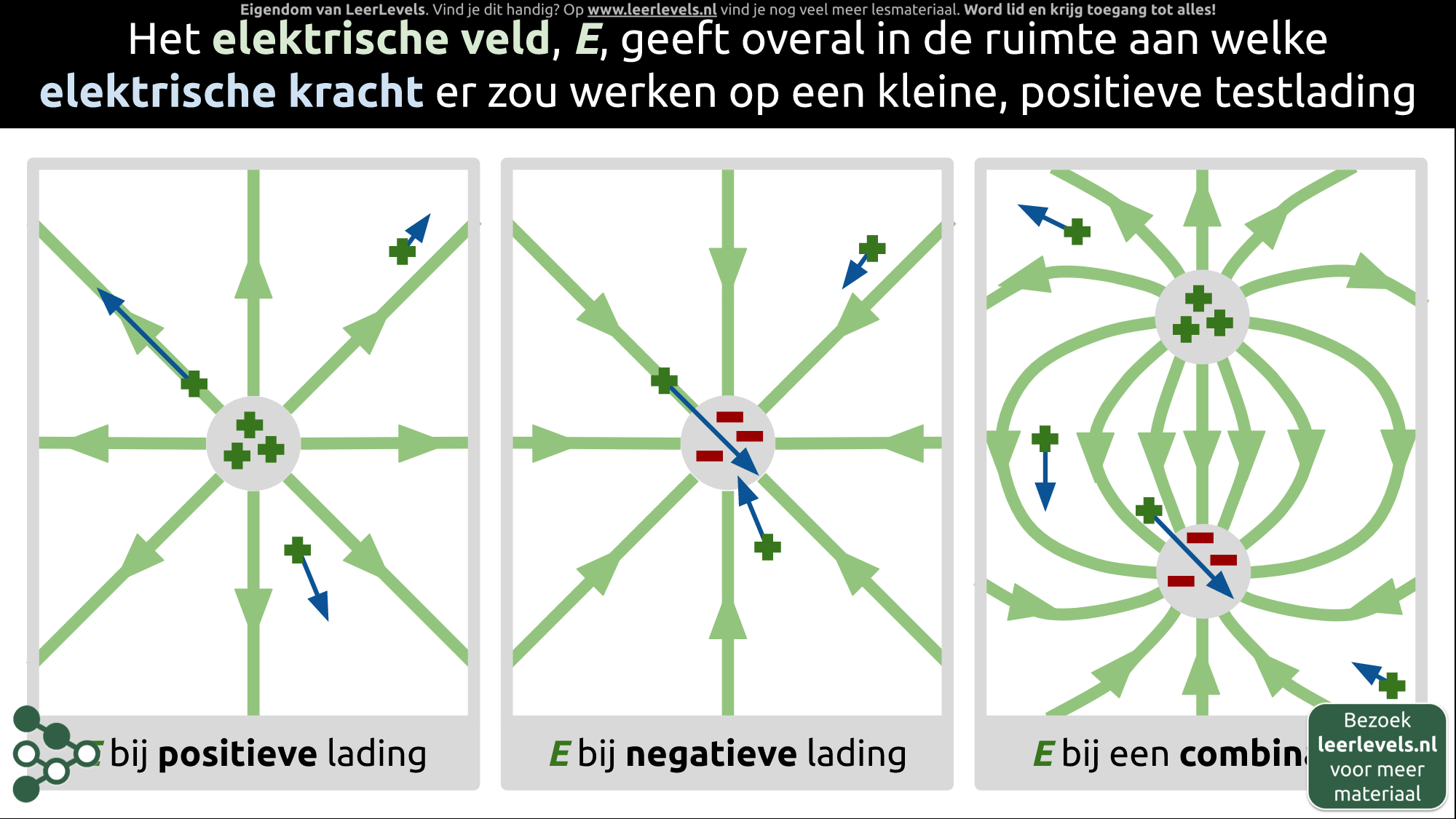
(Afbeelding: Animatie voor Elektrisch veld concept)

Elektrisch veld eigenschappen

De eigenschappen van het elektrische veld bepalen de regels voor elektrische veldlijnen. Positieve testladingen ervaren een grotere kracht wanneer ze dichter bij een positieve lading zijn. Hierdoor is de veldlijndichtheid daar het grootst. Elektrische veldlijnen lopen vrijwel altijd van positief naar negatief omdat positieve testladingen worden aangetrokken door negatieve ladingen. Een andere regel is dat de veldlijnen altijd loodrecht op geleiders staan. Dit betekent dat wanneer een veldlijn een geleider raakt, deze loodrecht moet staan.

Als er twee positieve ladingen aanwezig zijn, ontstaat er ook een elektrisch veld, wat leidt tot een complexer patroon. Een belangrijke regel is dat veldlijnen elkaar nooit mogen snijden. Als veldlijnen elkaar zouden kruisen, zou het onduidelijk zijn in welke richting de kracht op een lading wijst wanneer deze zich op het kruispunt van twee veldlijnen bevindt.

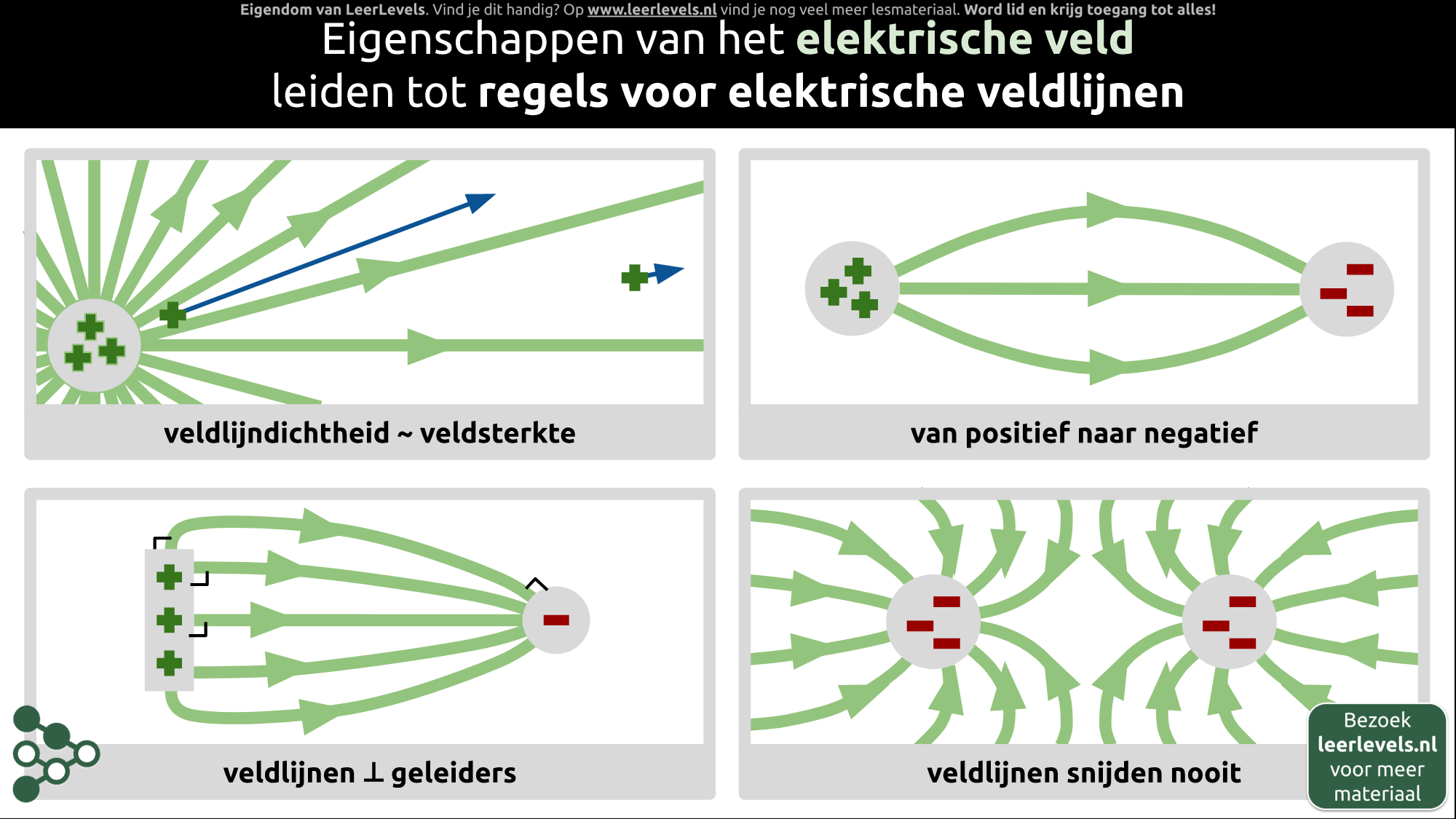
(Afbeelding: Animatie voor Elektrisch veld eigenschappen)

Elektrisch veld formule

De elektrische veldsterkte op een punt is gerelateerd aan de elektrische kracht op een testlading op dat punt. Stel dat we een positieve lading hebben en we bekijken de elektrische kracht en het elektrische veld bij een positieve testlading. De veldsterkte wordt uitsluitend bepaald door de grote positieve lading die we hebben geplaatst. Het veld wijst hier naar linksboven. Om te bepalen hoe groot de elektrische kracht op die testlading is, moet je naast het elektrische veld ook de grootte van de testlading meenemen. Omdat het een positieve testlading betreft, wijst de richting van de kracht in dezelfde richting als het elektrische veld. De grootte van de kracht is nog onbekend, omdat deze afhangt van de grootte van de ladingen, waardoor we de wet van Coulomb nog niet kunnen toepassen.

Wanneer je onderin een negatieve testlading plaatst, zie je dat het veld nog steeds wegwijst van de grote positieve lading, dus naar rechtsonder. De richting van de elektrische kracht is hier echter tegengesteld aan het elektrische veld, omdat de negatieve lading door de grote positieve lading in het midden wordt aangetrokken.

Als je de grootte van het elektrische veld wilt berekenen, kun je de volgende formule gebruiken: E = (Fel)/(q). Hierin is E de grootte van het elektrische veld in Newton per Coulomb, Fel de elektrische kracht in Newton en q de grootte van de testlading in Coulomb. Deze formule kun je ook gebruiken om de elektrische kracht te berekenen: Fel = E × q. Voor de richting van de kracht moet je zelf bepalen of het gaat om gelijke of tegengestelde ladingen.

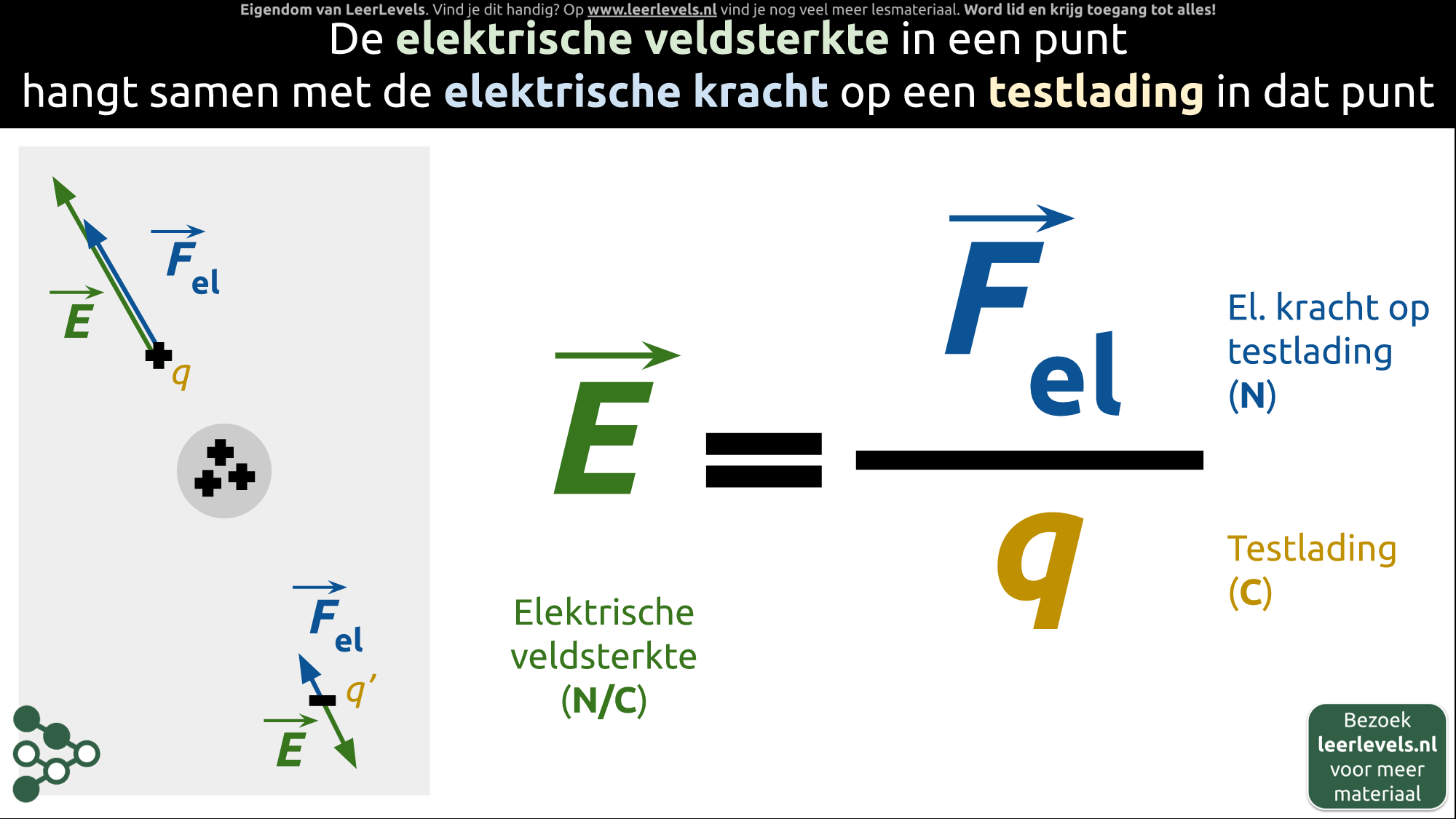
(Afbeelding: Animatie voor Elektrisch veld formule)

Homogeen elektrisch veld

In een homogeen elektrisch veld is de veldsterkte overal gelijk. Stel dat we een spanningsbron aansluiten op twee geleidende platen; deze combinatie wordt een condensator genoemd. De bovenste plaat krijgt positieve ladingen, omdat deze verbonden is met de positieve pool van de spanningsbron, terwijl de onderste plaat negatief geladen is. Tussen de platen ontstaat dan een elektrisch veld, en in het lichtgroene gebied is dit veld homogeen.

Als je de afstand tussen de platen d kent, kun je de grootte van de veldsterkte berekenen. Deze is gelijk aan de spanning U gedeeld door d, oftewel E = U/d . Stel je voor dat je een positieve testlading in dit gebied plaatst. In een homogeen elektrisch veld zijn de veldlijnen overal even ver van elkaar verwijderd, en de elektrische kracht op deze positieve testlading is naar beneden gericht. Dit komt doordat de definitie van een elektrisch veld aangeeft dat het de richting van de kracht op een positieve testlading aangeeft.

Wanneer we de positieve testlading in dit gebied plaatsen, zal de kracht naar beneden wijzen. Als we dezelfde lading hier plaatsen, bevindt deze zich dichter bij de negatieve plaat. De negatieve plaat zal meer aantrekkingskracht uitoefenen, maar tegelijkertijd is de lading verder verwijderd van de positieve plaat. Omdat de afstand precies hetzelfde is, is de kracht aan beide zijden precies even groot en wordt deze alleen bepaald door de hoeveelheid lading. De hoogte of positie van de lading heeft geen invloed op de kracht. De kracht is overal gelijk aan E · q. Let op: buiten het condensatorgebied is er geen homogeen elektrisch veld.

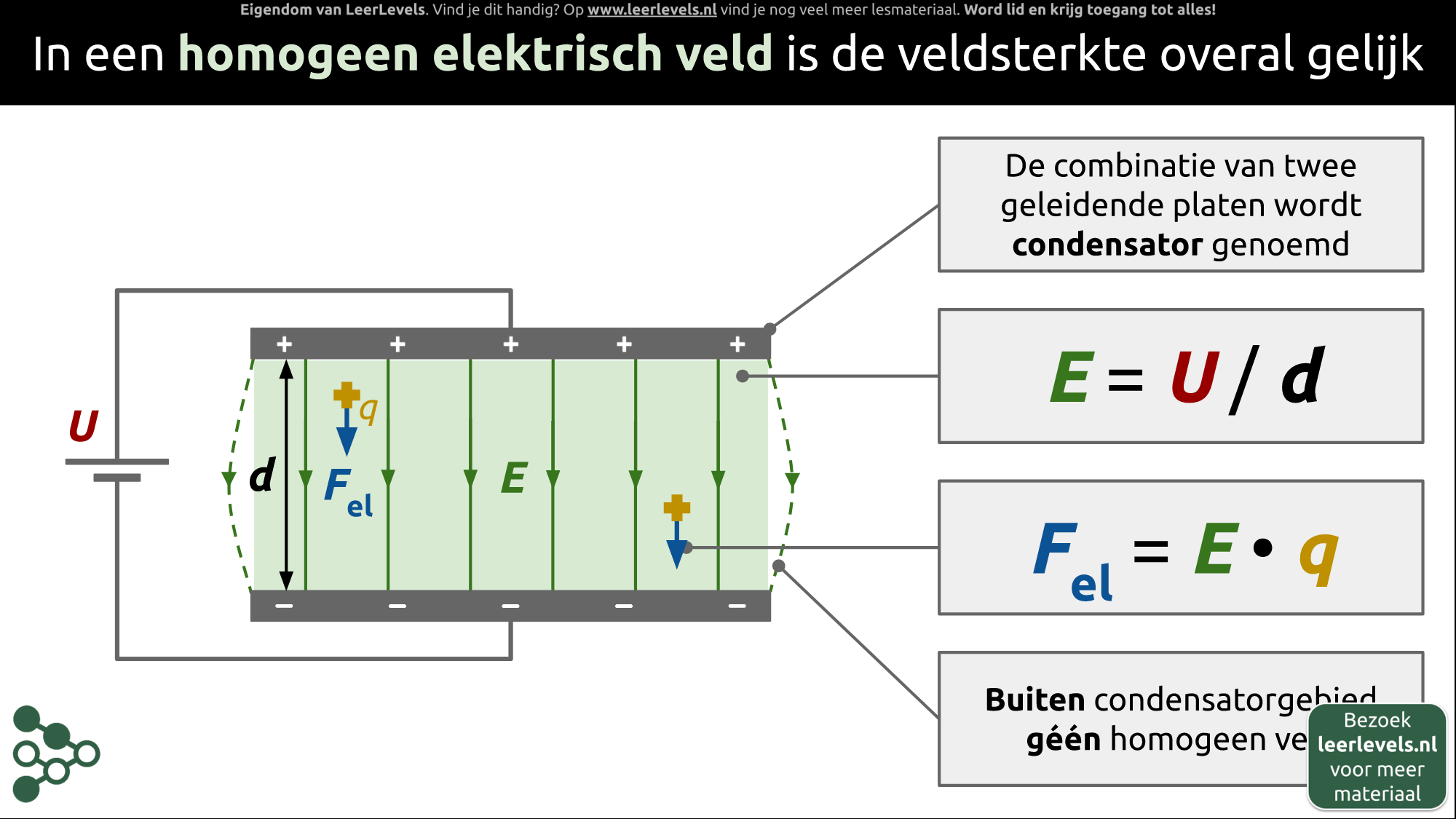
(Afbeelding: Animatie voor Homogeen elektrisch veld)

Afbuiging in elektrisch veld

Om te kijken hoe een elektrisch veld een lading buigt, moet je eerst de horizontale en verticale snelheden apart bekijken. Stel je voor dat er een homogeen elektrisch veld is met breedte w en dat er op tijd t0 een positieve test in het veld wordt gestuurd met een startsnelheid v1 alleen in de horizontale richting. Onder invloed van het elektrische veld zal er een kracht werken op de positieve lading naar beneden, waardoor de snelheid wat naar beneden buigt en er dus ook een kleine verticale snelheid vy ontstaat. Dit gaat zo door, waardoor de eindsnelheid v2 ontstaat met zowel horizontale als verticale componenten. Er werkt geen kracht op de lading in de horizontale richting en de enige kracht in de verticale richting is de elektrische kracht van boven naar beneden.

Om v2 te berekenen, moet je het tijdsverschil tussen twee punten berekenen en de versnelling berekenen met de elektrische kracht. Je weet hoe lang het veld is en wat de beginsnelheid is, dus je kunt het tijdsverschil berekenen. Vervolgens kun je de versnelling berekenen door de elektrische kracht te delen door de massa. Omdat er geen kracht werkt in de hoogterichting, is v2x = v1x. Om de eindsnelheid te berekenen, gebruik je de Pythagoras-formule om de vectoren van de horizontale en verticale snelheid te combineren. Dit resulteert in de lengte van de vector die gelijk is aan de wortel van het kwadraat van de horizontale en verticale snelheid. Op deze manier kun je de eindsnelheid berekenen door de horizontale en verticale snelheid afzonderlijk te behandelen.

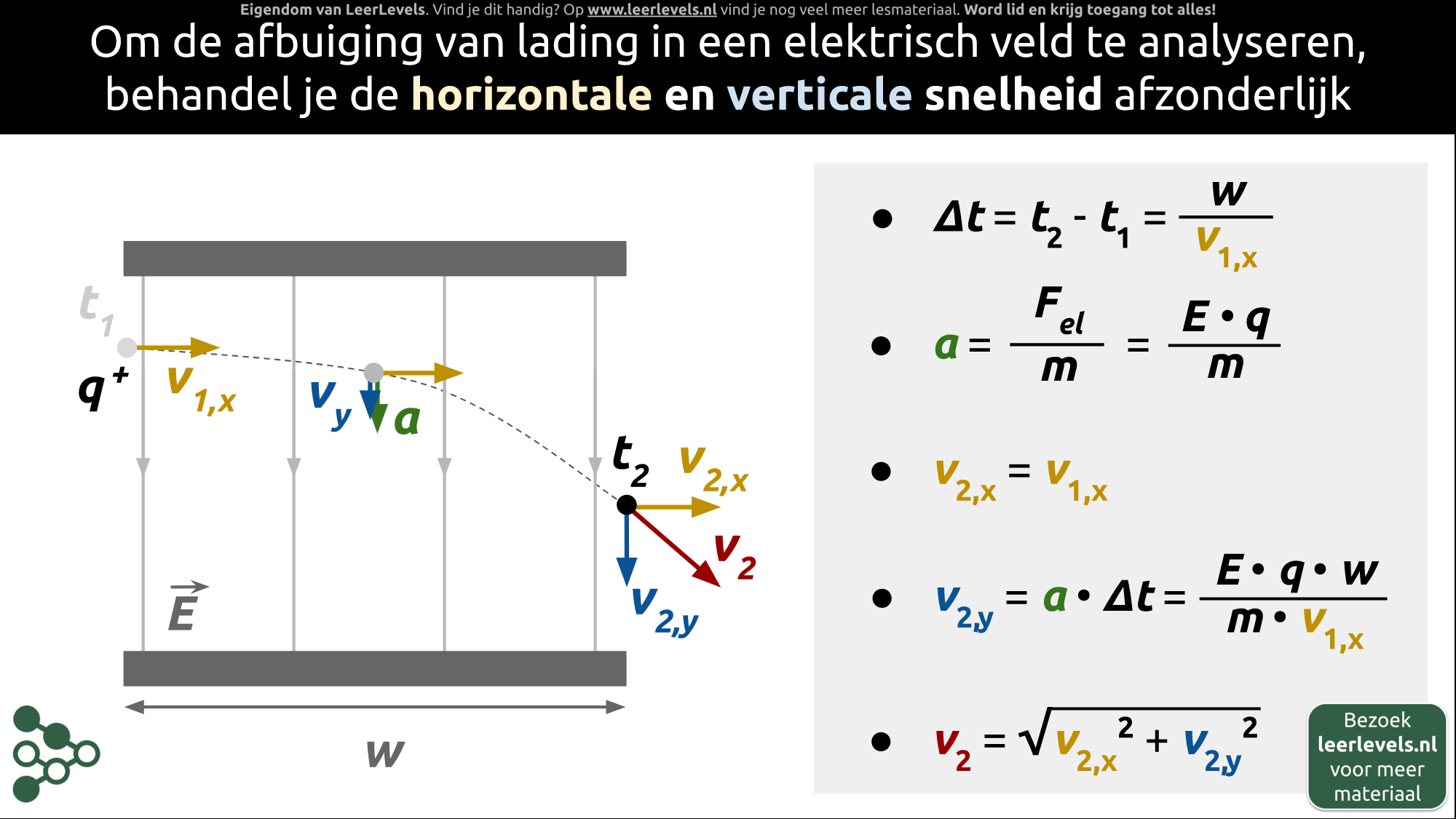
(Afbeelding: Animatie voor Afbuiging in elektrisch veld)

Elektrische veldvectoren en veldlijnen

Bij het beschrijven van een elektrisch veld zijn er twee manieren: veldvectoren en veldlijnen. Een veldvector is een pijl die aangeeft in welke richting het elektrisch veld op één punt wijst. De lengte van de pijl geeft de grootte van de veldsterkte weer. Vlakbij een positieve lading is de pijl langer en wijst hij van plus naar min. Het tekenen van veldvectoren geeft informatie over één punt. Veldlijnen vormen daarentegen een patroon en geven informatie over een gebied. De richting van de veldlijnen laat zien in welke richting het elektrisch veld wijst. Hoe dichter de veldlijnen bij elkaar zitten, hoe sterker het elektrisch veld is. Bij veldlijnen heeft de lengte van een pijl geen betekenis, omdat ze gesloten kringen vormen of oneindig ver doorlopen.

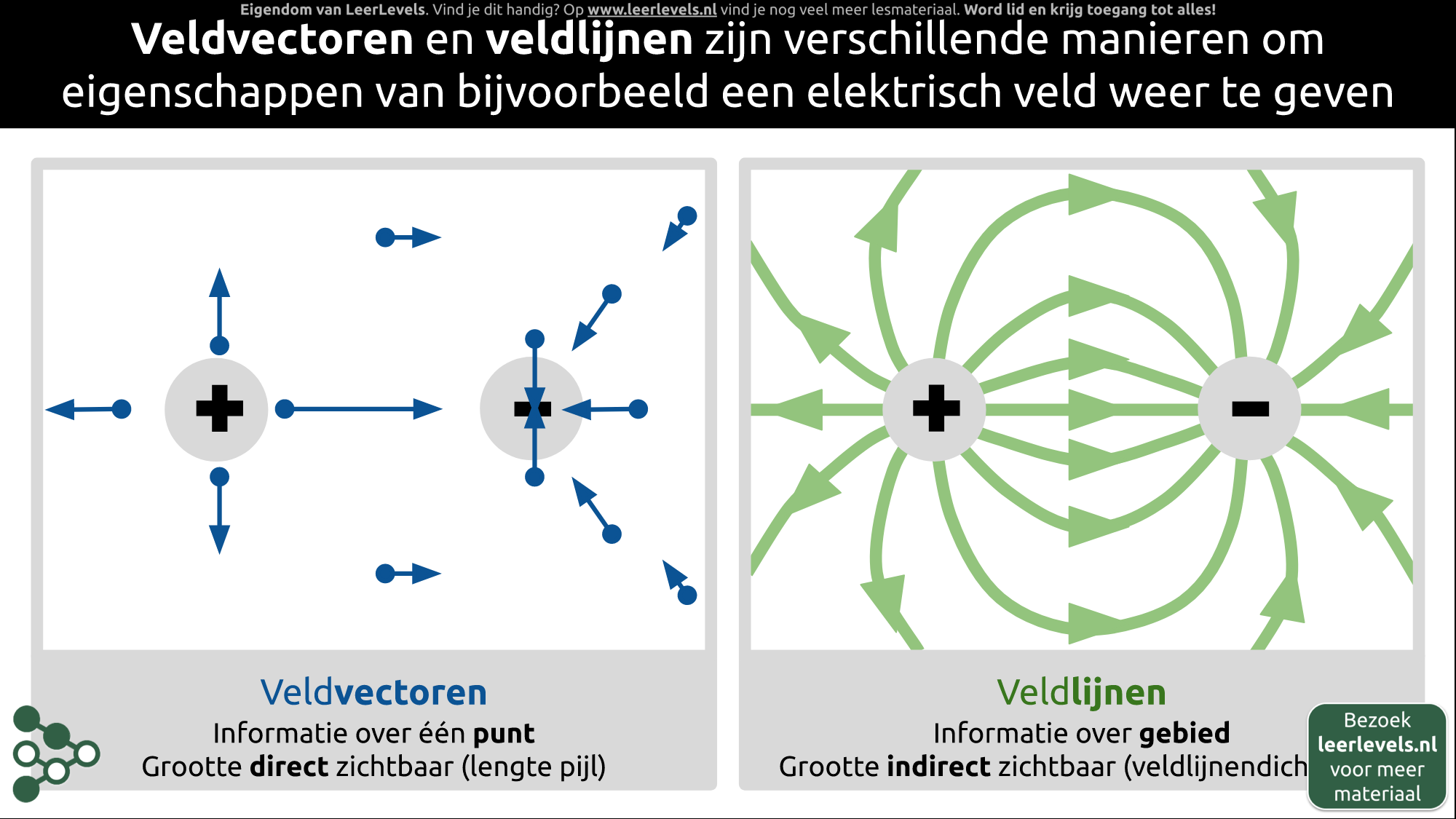
(Afbeelding: Animatie voor Elektrische veldvectoren en veldlijnen)

Terug naar overzicht Meld je aan

Elektrisch vermogen

Elektrisch vermogen formule

Elektrisch vermogen (P) hangt af van spanning (U) en stroomsterkte (I), dus P = U · I. Het vermogen kan berekend worden met deze formule. Het kan echter verwarrend zijn dat spanning in volt (V) wordt gemeten en stroomsterkte in ampère (A), omdat volt eigenlijk betekent hoeveel energie per coulomb lading is en ampère betekent hoeveel lading per seconde stroomt. De formule is wel correct, maar de eenheden horen anders. Vergeet niet dat vermogen in watt (W) gelijk is aan spanning in V · stroomsterkte in A. Als je rekening houdt met de juiste eenheden, zal het altijd goed gaan.

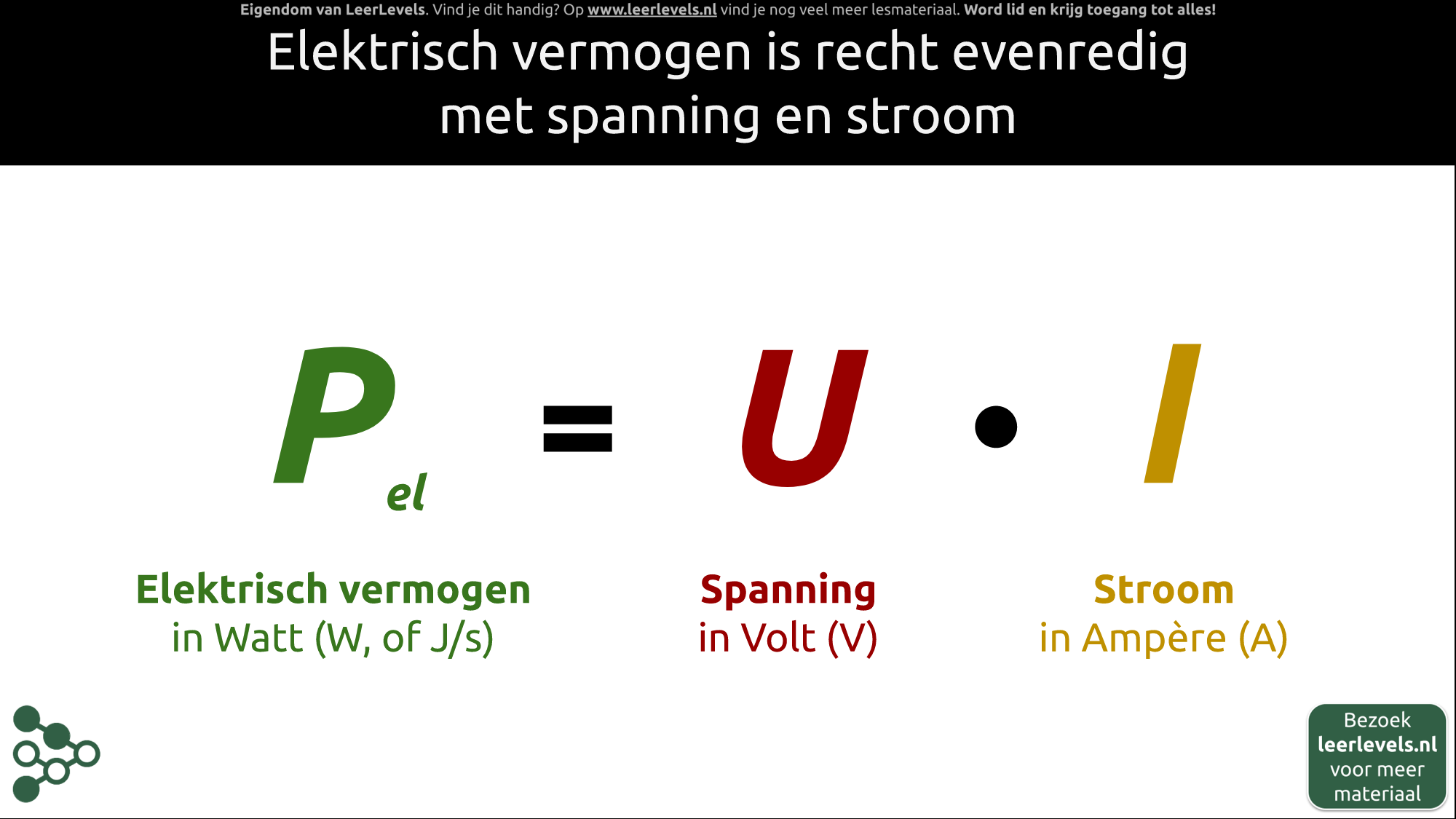
(Afbeelding: Animatie voor Elektrisch vermogen formule)

Elektrisch vermogen concept

Het elektrisch vermogen van een apparaat is hoeveel energie het per seconde gebruikt en hangt af van de spanning en stroom. Als de spanning hoog is, hebben elektronen veel energie en is er laag energieverbruik per seconde. Als de stroom hoog is, gaan veel elektronen per seconde door en is er hoog energieverbruik per seconde. Als beide hoog zijn, is er hoog energieverbruik per seconde en als beide laag zijn, is er laag energieverbruik per seconde. Anders is het normaal vermogen. Het vermogen van een apparaat wordt aangegeven in de eenheid watt (W).

(Afbeelding: Animatie voor Elektrisch vermogen concept)

Elektrisch vermogen en weerstand

Je kunt het elektrische vermogen van een weerstand berekenen als je de spanning of stroom weet. Het vermogen (P) wordt berekend door de spanning (U) te vermenigvuldigen met de stroom (I) of door de stroom in het kwadraat te vermenigvuldigen met de weerstand (R). De eenheden zijn Joule per seconde (J/s) voor vermogen, Ohm voor weerstand, Ampere voor stroom en volt voor spanning. De wet van Ohm stelt dat spanning gelijk is aan stroom keer weerstand (U = IR). Als je dat combineert met de formule voor vermogen, kun je het vermogen berekenen met behulp van de weerstand en de stroom (P = I² R). Je kunt de wet van Ohm ook schrijven als stroom gelijk aan spanning gedeeld door weerstand (I = U/R). Als je dat combineert met de formule voor vermogen, kun je het vermogen berekenen met behulp van de spanning en de weerstand (P = U²/R). Deze formules kun je gebruiken om in één keer het vermogen te berekenen, bijvoorbeeld in een serieschakeling met een stroom van 2 Ampere en een weerstand van 4 Ohm, of in een parallelschakeling met een spanning van 10 volt en een weerstand van 25 Ohm.

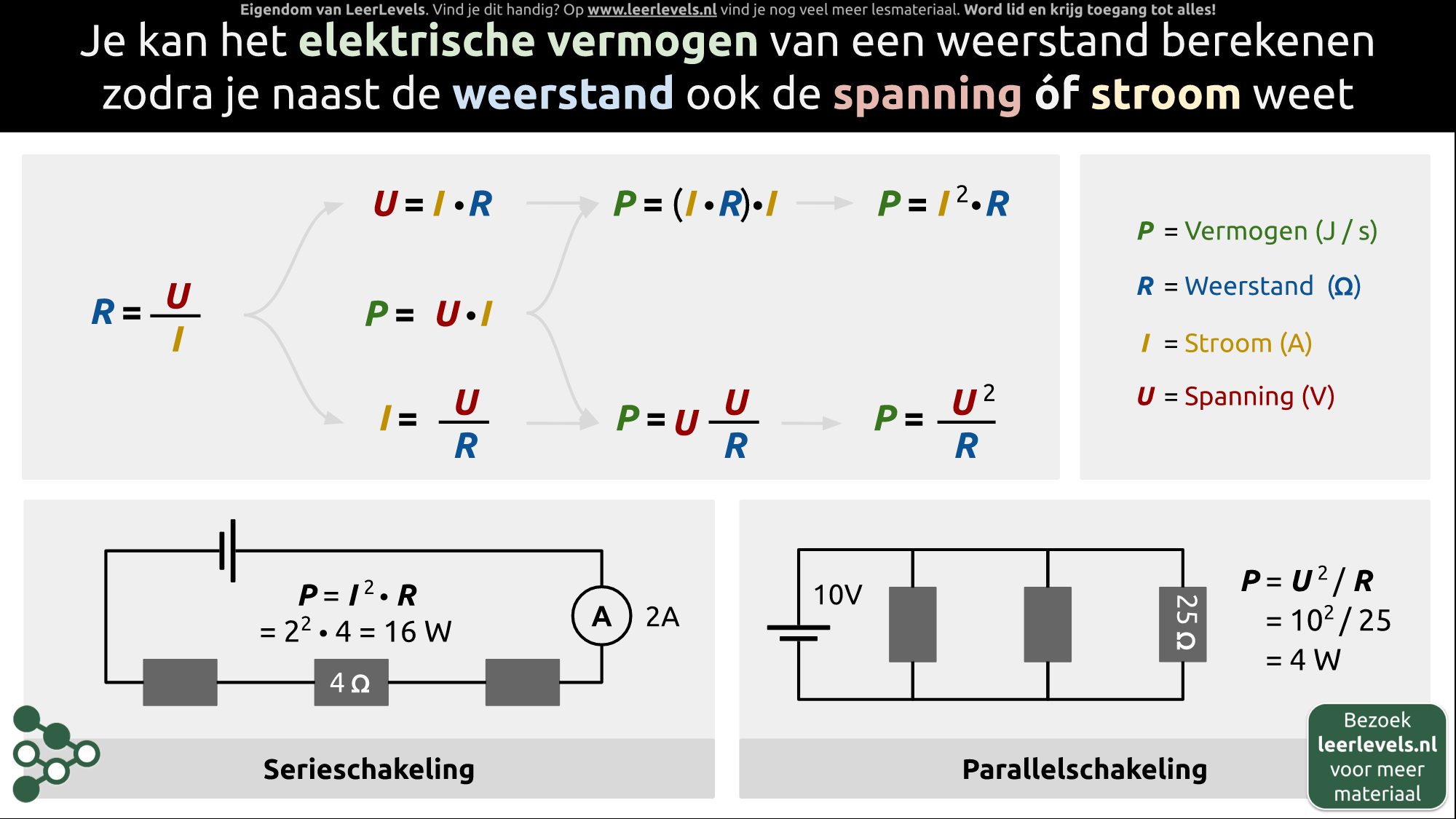
(Afbeelding: Animatie voor Elektrisch vermogen en weerstand)

Terug naar overzicht Meld je aan

Elektrische apparaten

Elektrische apparaten hebben energie nodig om te werken. Sommige apparaten hebben veel energie nodig, dit noemen we groot elektrisch vermogen. Gloeilampen hebben bijvoorbeeld een vermogen van ongeveer 50 watt, wat betekent dat ze per seconde 50 joule aan elektrische energie gebruiken om licht en warmte te maken. LED-lampen hebben minder energie nodig, maar zetten meer daarvan om in licht. Een koelkast gebruikt veel meer energie, namelijk 250 watt per seconde, om warmte van binnen naar buiten te verplaatsen en ons eten koel te houden. Deze energie komt van de energiecentrale, die als een grote spanningsbron werkt door kolen te verbranden of zonnecellen te gebruiken. Onze stopcontact verbindt onze apparaten serieus met de energiecentrale, zonder dat we het kunnen zien. Als we meer energie willen gebruiken, zoals bij het gebruik van een föhn, hebben we een vermogen van wel 1500 watt per seconde nodig. Dit laat zien dat het gebruik van elektrische apparaten veel energie kost.

(Afbeelding: Animatie voor Elektrische apparaten)

Terug naar overzicht Meld je aan

Elektrische energie

Elektrische energie concept

Elektrische energie en elektrische kracht zijn op een vergelijkbare manier gerelateerd als zwaartekracht en zwaarte-energie. Laten we eerst naar zwaarte-energie kijken. Een voorwerp dat zich hoog boven de grond bevindt, bezit veel zwaarte-energie en heeft daardoor veel potentieel om te vallen. Als het voorwerp langzaam beweegt, heeft het weinig kinetische energie (Ek). Tijdens het vallen, onder invloed van zwaartekracht, wordt arbeid verricht op het voorwerp. De zwaartekracht trekt het voorwerp naar beneden en tijdens de val neemt de zwaarte-energie af, terwijl de kinetische energie toeneemt.

Een soortgelijk proces vindt plaats in elektrische systemen. Neem een condensator met een plus- en minpool als voorbeeld. Als we een positieve lading bij de positieve pool plaatsen, heeft deze lading veel elektrische energie. Wanneer de lading richting de negatieve pool beweegt, verricht de elektrische kracht positieve arbeid op de lading. Daardoor versnelt de lading en legt uiteindelijk een afstand Δ h af. Naarmate de lading dichter bij de negatieve pool komt, neemt haar elektrische energie af, omdat deze energie wordt omgezet in kinetische energie.

Net zoals zwaarte-energie een potentieel om te vallen vertegenwoordigt, is elektrische energie een potentieel om dichter bij de negatieve pool te komen. Zo zijn elektrische energie en elektrische kracht op dezelfde manier gerelateerd als zwaartekracht en zwaarte-energie.

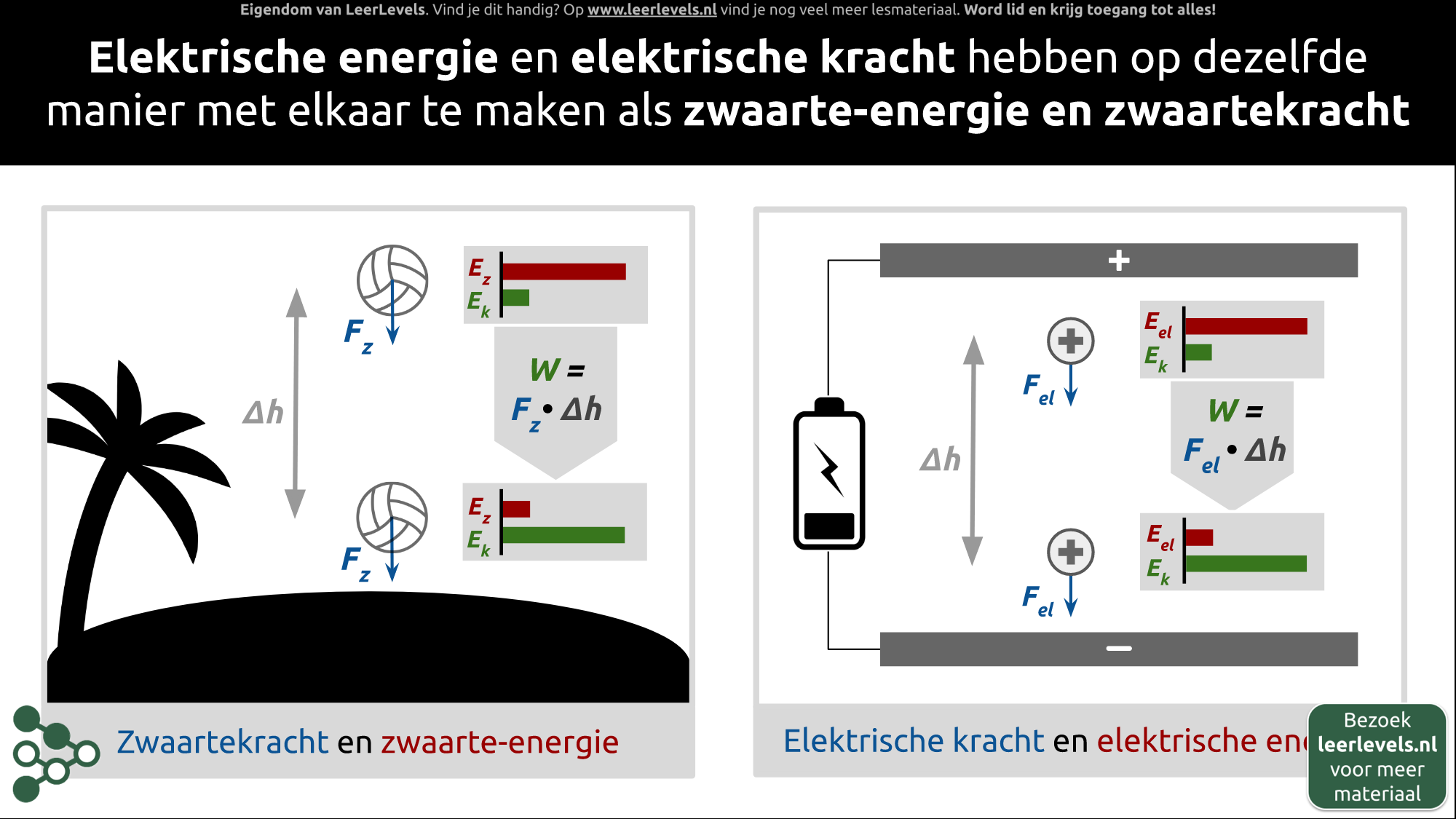
(Afbeelding: Animatie voor Elektrische energie concept)

Elektrische energie formule

De elektrische energie die wordt omgezet is recht evenredig met het spanningsverschil en de lading van het bewegende deeltje. Stel dat we een condensator hebben met een positieve testlading die zich beweegt in een homogeen elektrisch veld. De afstand tussen de platen is d. Er werkt een elektrische kracht op de positieve lading, welke we als volgt kunnen berekenen.

De elektrische veldsterkte is E = U/d , dus U = E · d. De elektrische energie die een deeltje kwijtraakt als het een bepaalde afstand d verplaatst, kan berekend worden door te kijken naar de arbeid die de elektrische kracht verricht. We weten dat arbeid W gegeven wordt door W = F · s. In dit geval betreft het de elektrische kracht Fel en de afstand d, dus Δ Eel = Fel · d. We weten ook dat Fel = E · q. Door dit te combineren vinden we: Δ Eel = E · q · d.

De twee rechterformules, U = E · d en Δ Eel = E · q · d, hebben overlap; in beide formules komt E · d voor. Je kunt dus E · d vervangen door U. Een kortere versie van de omgezette elektrische energie is dan: Δ Eel = Δ U · q. Hierin is Δ Eel de omgezette elektrische energie in Joule, Δ U de doorlopen spanning in Volt, en q de lading in Coulomb.

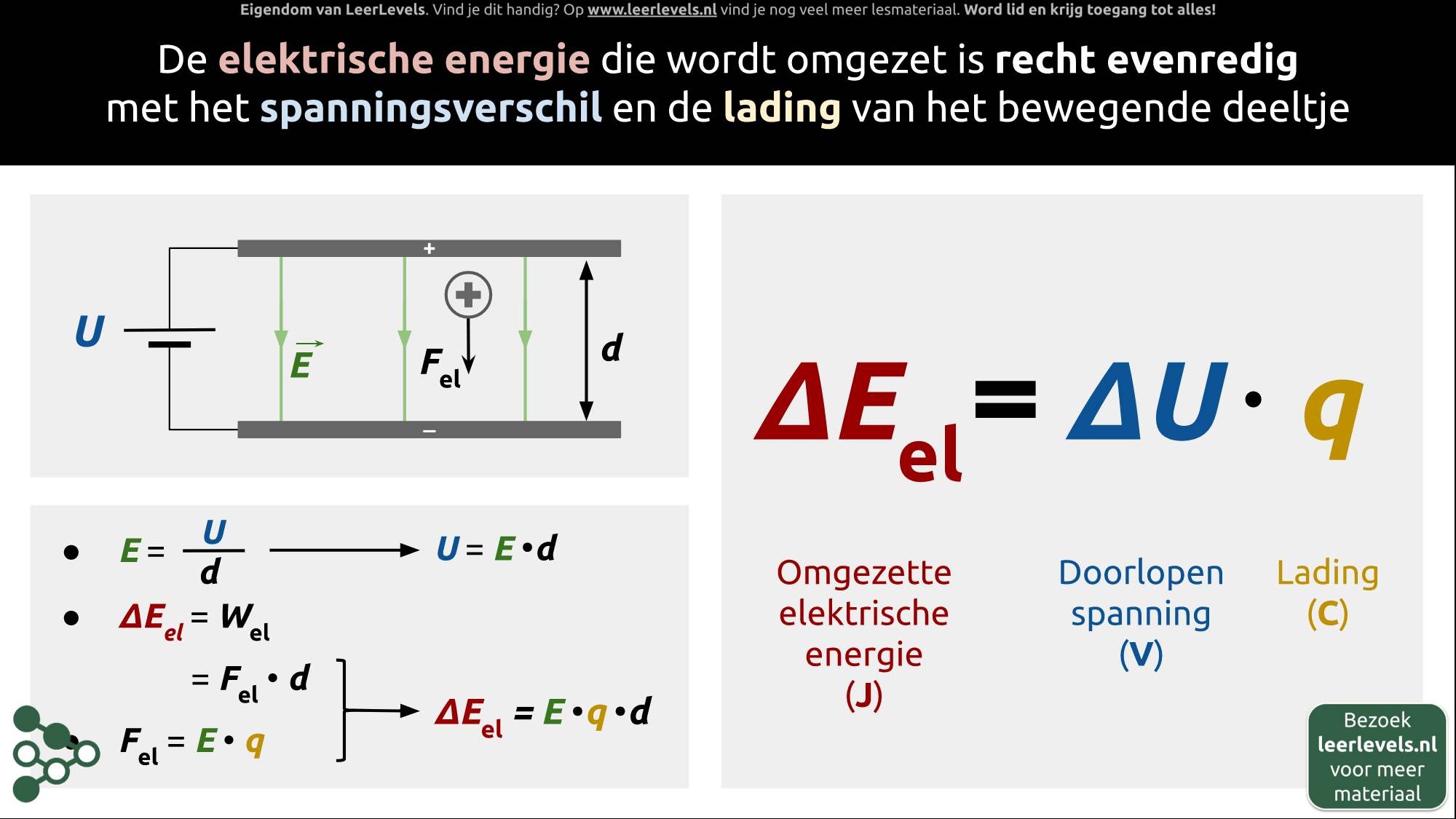
(Afbeelding: Animatie voor Elektrische energie formule)

Terug naar overzicht Meld je aan

Elektrische grootheden

Elektrische grootheden en eenheden

Er zijn verschillende grootheden en eenheden die te maken hebben met elektriciteit. Hieronder staan de namen, symbolen en beschrijvingen van enkele belangrijke grootheden en eenheden:

- Coulomb (C) staat voor lading (Q) en beschrijft de eigenschap die het gedrag van deeltjes in een elektrisch en magnetisch veld beïnvloedt.
- Ampère (A) staat voor stroomsterkte (I) en beschrijft hoeveel lading er per seconde door een bepaald punt passeert.
- Volt (V) staat voor spanning (U) en beschrijft de hoeveelheid energie die per lading wordt overgedragen.
- Ohm (Ω) staat voor weerstand (R) en beschrijft hoe 'moeilijk' stroom ergens doorheen loopt.
- Siemens (S) staat voor geleidbaarheid (G) en beschrijft hoe 'gemakkelijk' stroom ergens doorheen loopt.
- Soortelijke weerstand (ρ, in Ωm) beschrijft de weerstand van een materiaal met standaardafmetingen.

Deze grootheden en eenheden zijn belangrijk bij het beschrijven van lading, stroom, spanning, weerstand en geleidbaarheid in elektrische circuits.

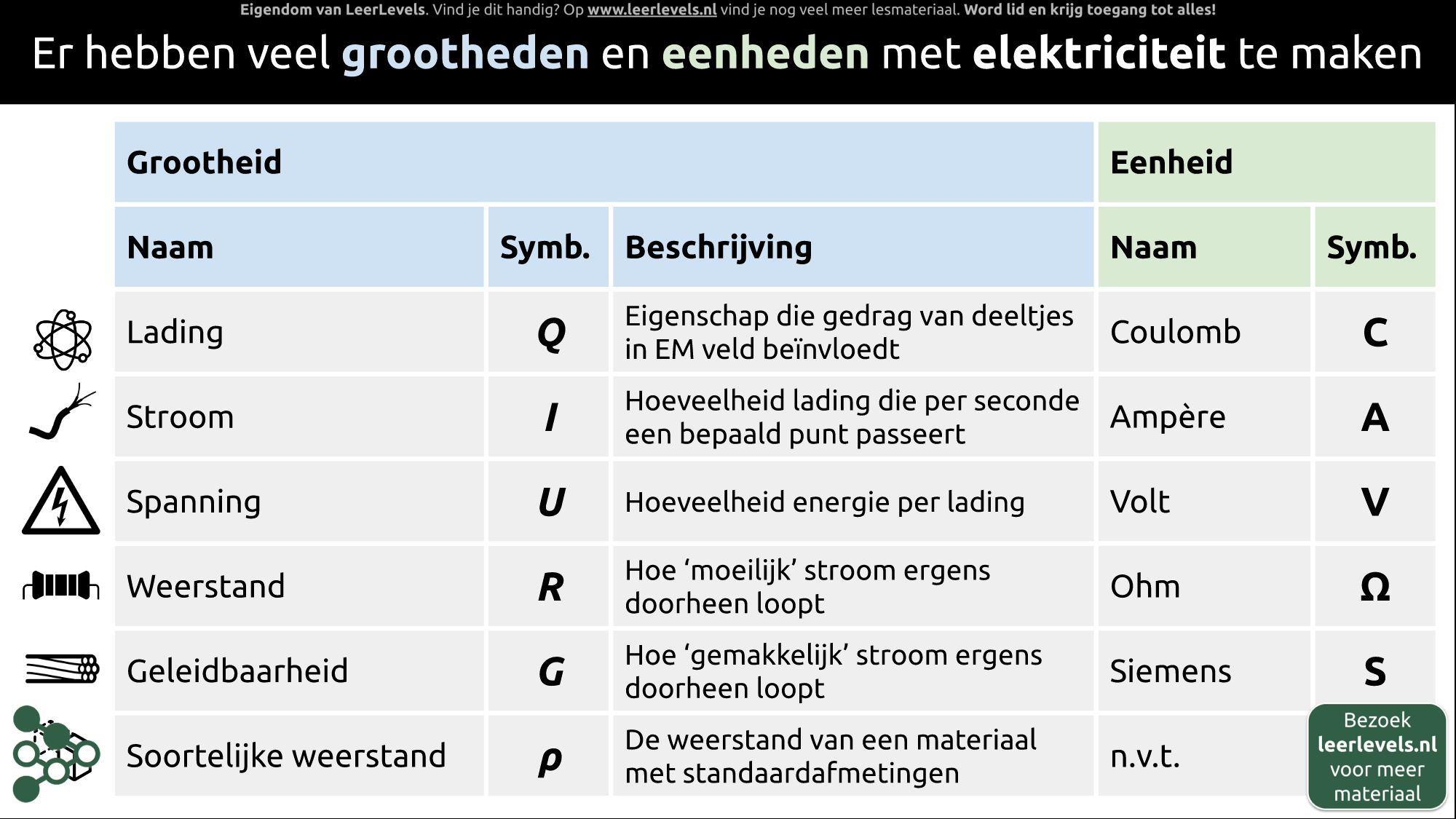
(Afbeelding: Animatie voor Elektrische grootheden en eenheden)

Terug naar overzicht Meld je aan

Elektrische kracht

Elektrische kracht concept

Geladen voorwerpen kunnen elektrische krachten op elkaar uitoefenen. Laten we kijken naar twee voorwerpen: voorwerp A heeft een grote positieve lading en voorwerp B heeft een negatieve lading. Er ontstaat een kracht tussen deze voorwerpen. Voorwerp A oefent een kracht uit op voorwerp B en andersom. Deze krachten zijn gelijk in grootte maar tegengesteld in richting.

Als je twee positief geladen voorwerpen dicht bij elkaar brengt, wordt de afstotende kracht groter naarmate de ladingen toenemen. Dit betekent dat de grootte van de lading de grootte van de kracht beïnvloedt. Positief geladen voorwerpen stoten elkaar dus af, net zoals negatief geladen voorwerpen. Het type lading bepaalt de richting van de kracht.

Ten slotte, als een positief geladen voorwerp en een negatief geladen voorwerp op een bepaalde afstand van elkaar worden geplaatst, zullen ze elkaar aantrekken. Wanneer je de afstand tussen hen vergroot, neemt de aantrekkingskracht af. Met andere woorden, een grotere afstand resulteert in een kleinere aantrekkingskracht. Dit zijn enkele belangrijke principes met betrekking tot de krachten tussen geladen voorwerpen.

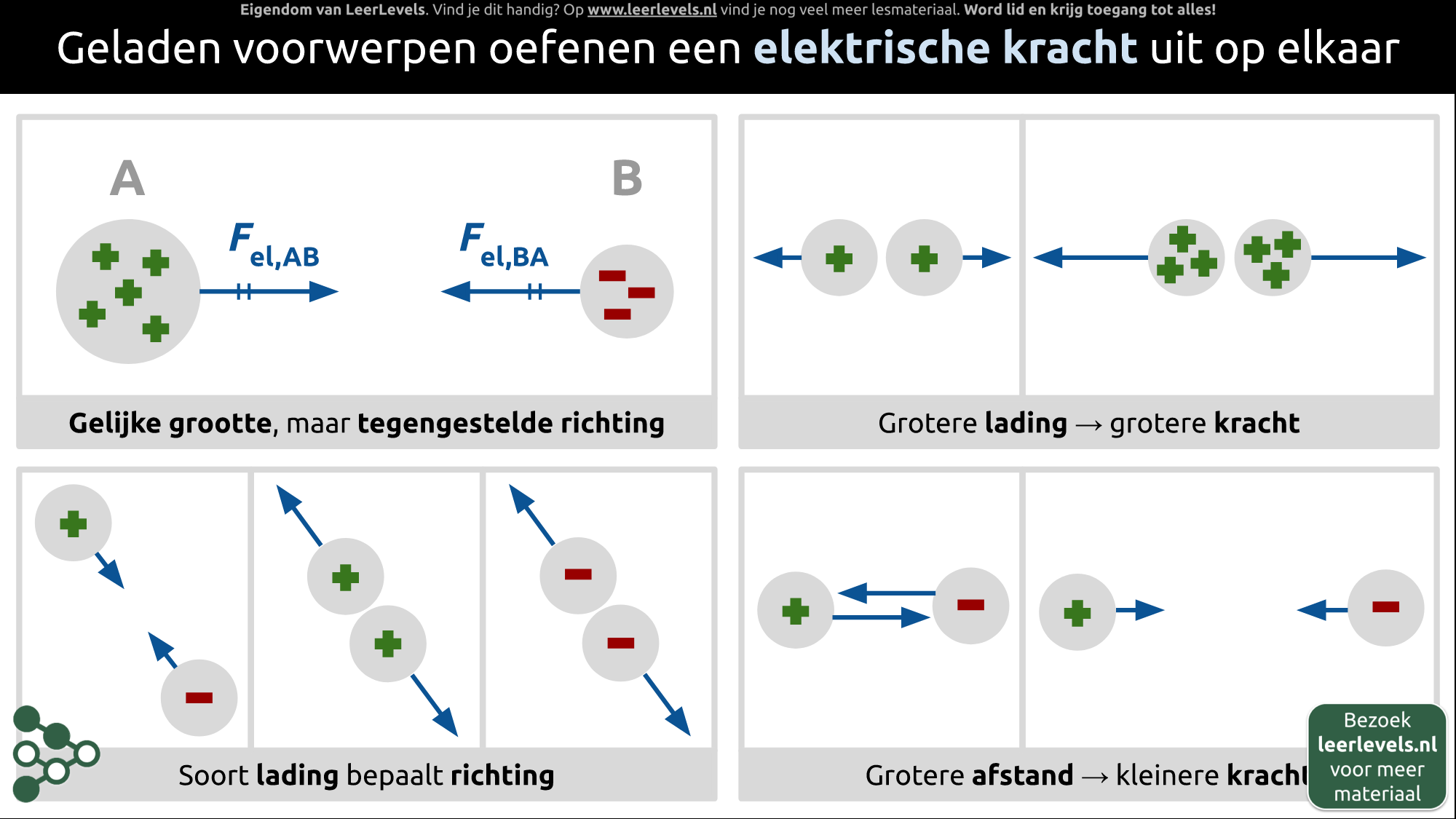
(Afbeelding: Animatie voor Elektrische kracht concept)

Elektrische kracht formule

De elektrische kracht tussen twee ladingen is recht evenredig met het product van de ladingen en omgekeerd kwadratisch evenredig met hun onderlinge afstand. Dit betekent dat de elektrische kracht te berekenen is door een constante, aangeduid met f, te vermenigvuldigen met het product van de ladingen. Deze ladingen worden vaak aangeduid met de letters q en Q, waarbij q staat voor de lading van het ene voorwerp en Q voor de lading van het andere. De kracht is ook kwadratisch afhankelijk van hun onderlinge afstand. De formule om deze elektrische kracht te berekenen is:

Fel = f · (q · Q)/r²)

Dit is beter bekend als de wet van Coulomb. Hierin is Fel de kracht in N (newton), f is de constante van Coulomb met een waarde van 8,98755 × 10⁹ N · m² · C⁻², q en Q zijn de ladingen in C (coulomb), en r is de afstand in m (meter).

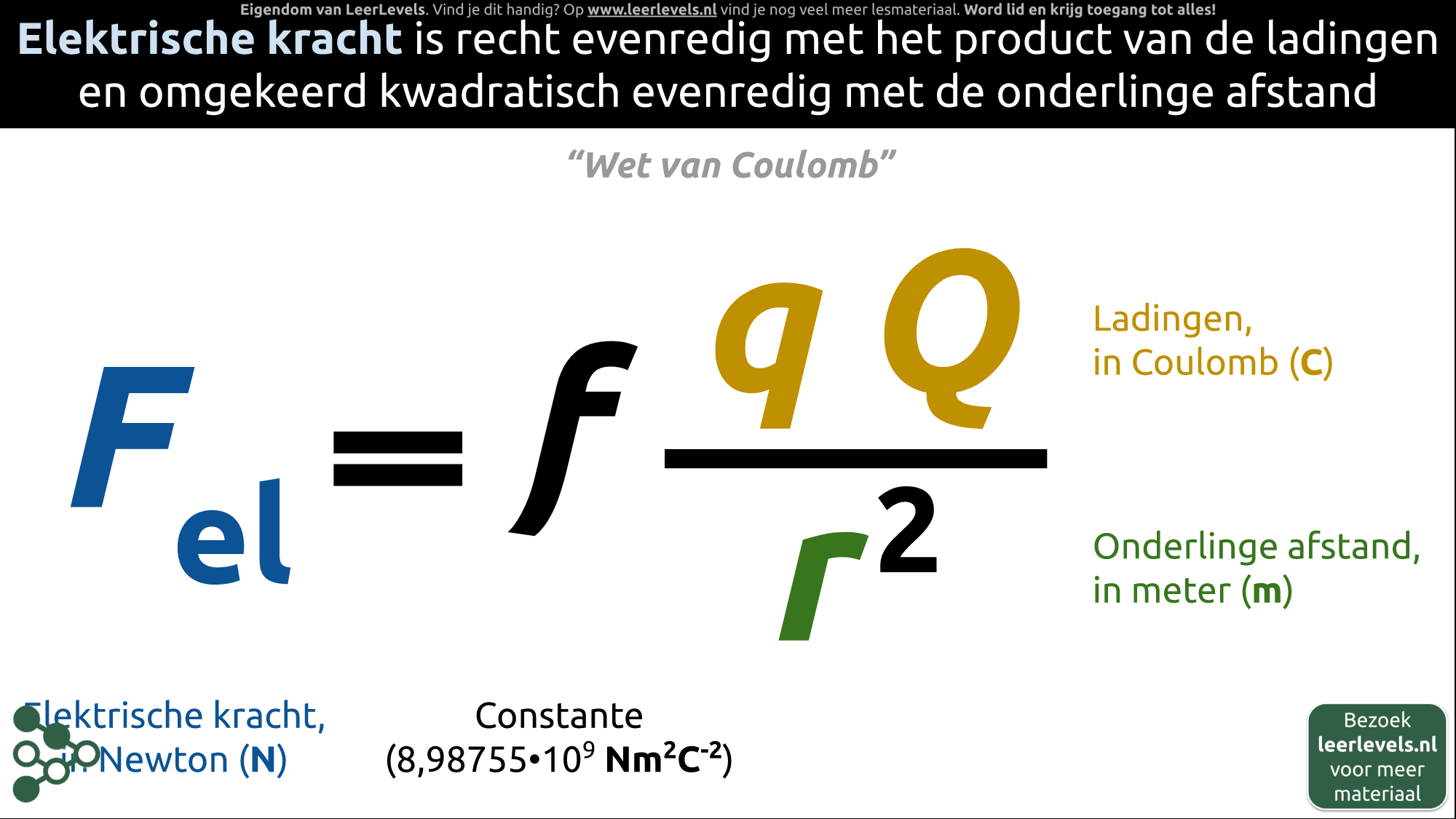
(Afbeelding: Animatie voor Elektrische kracht formule)

Terug naar overzicht Meld je aan

Elektrische potentiaal

De elektrische potentiaal V geeft aan hoeveel elektrische energie een lading heeft op een specifieke plek. Er is vaak verwarring tussen de grootheid elektrische potentiaal V en de eenheid volt. In de notatie kun je het verschil zien doordat de grootheid vaak dikgedrukt en/of cursief wordt geschreven.

Laten we een voorbeeld bekijken waarbij twee condensatorplaten zijn aangesloten op een spanningsbron: de positieve kant is verbonden met de bovenste plaat en de negatieve met de onderste plaat. Er wordt een spanning van 10 V aangewend. Deze spanning is eigenlijk een potentiaalverschil, namelijk het verschil tussen punt A (bij de bovenste plaat) en punt C (bij de onderste plaat). Hierbij geldt VA = 10 J/C en VC = 0 J/C, dus het verschil is 10 V. Wat betekent dit?

Stel dat we boven een proton plaatsen, met een lading van 1 e, de elementaire lading. De potentiaal helpt ons te berekenen hoeveel elektrische energie de lading op die plek heeft. We gebruiken de formule Eel = q · V, dus 1,602 × 10⁻¹⁹ C · 10 J/C = 1,602 × 10⁻¹⁸ J = 10 eV. Als het proton naar beneden beweegt, wordt het door het elektrisch veld versneld. Halverwege heeft het proton 5 eV aan elektrische energie, omdat dan de helft is omgezet in kinetische energie. Onderin is er geen elektrische energie meer, maar vlak voordat de plaat wordt geraakt, is er wel een hoge kinetische energie. Halverwege de platen is de potentiaal 5 J/C.

Waarom is dit handig? We kunnen hetzelfde doen voor een ander deeltje. Een alfadeeltje heeft een lading van 2e, dus bovenin heeft het een Eel van 20 eV, halverwege 10 eV, en onderin 0. De elektrische energie Eel geeft informatie over een specifieke lading op een specifieke plek. De potentiaal V vertelt ons op een specifieke plaats wat de energie per lading is. Het potentiaalverschil heeft dezelfde eenheid als de elektrische potentiaal, maar geeft informatie over de energie tussen twee plaatsen. Het potentiaalverschil U staat beter bekend als spanning.

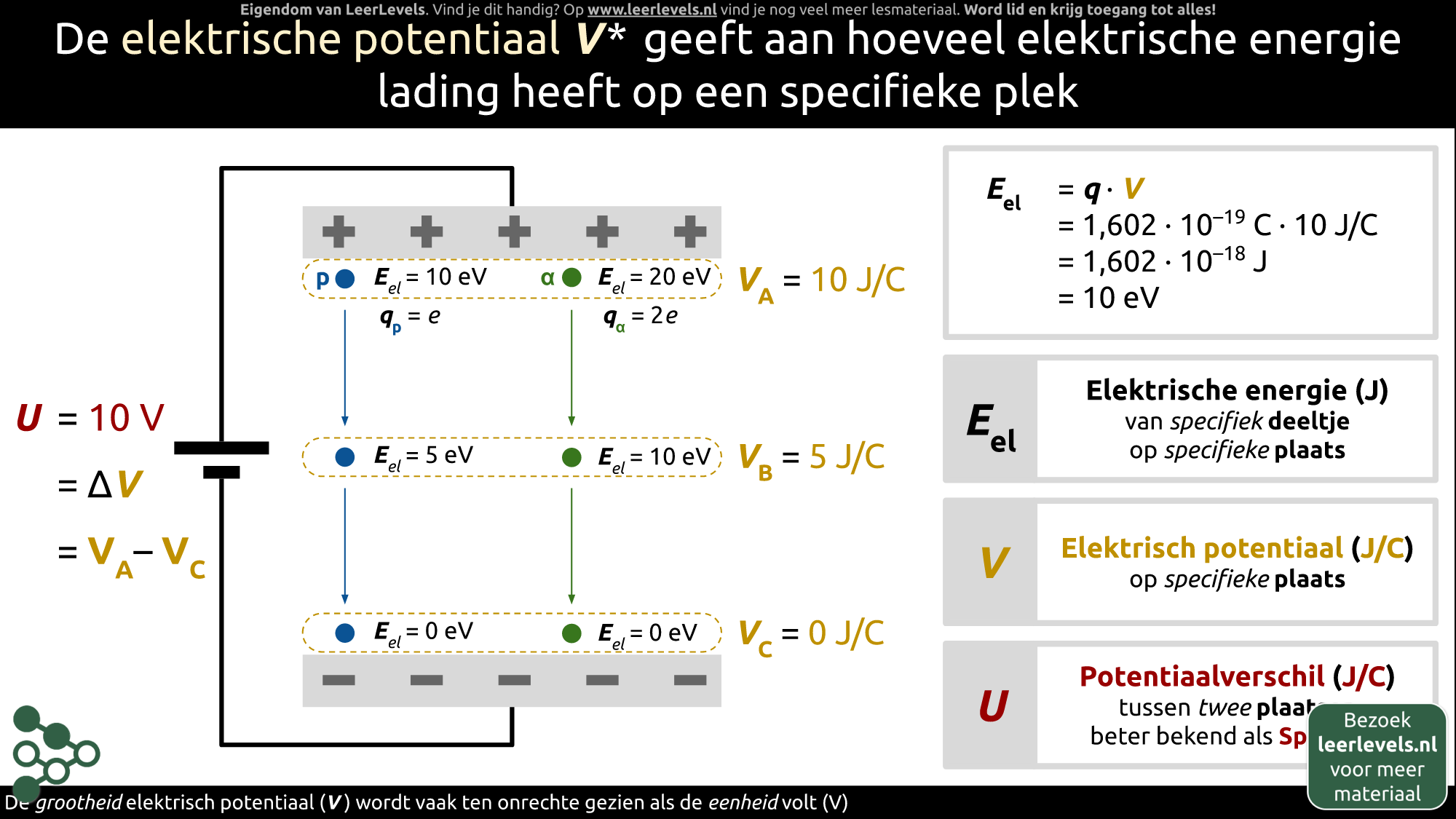
(Afbeelding: Animatie voor Elektrische potentiaal)

Terug naar overzicht Meld je aan

Elektrische schakelingen

Elektrische schakelingen stappenplan

Sommen over elektrische schakelingen volgen allemaal hetzelfde stappenplan. We doorlopen dit stappenplan aan de hand van een voorbeeld waarbij we de spanning U3 moeten berekenen.

Stap 1: Maak een schets. Zelfs als er al een afbeelding is gegeven in de opdracht, is het waardevol om zelf een schets te maken waar je extra informatie aan kunt toevoegen. Het helpt ook om beter te begrijpen hoe de schakeling werkt.

Stap 2: Voeg alle beschikbare gegevens toe aan de schets.

Stap 3: Kijk of je vervangingsweerstanden kunt berekenen.

Stap 4: Kijk of je de stroomwet van Kirchhoff kunt toepassen ("stroom stroomt").

Stap 5: Kijk of je de wet van Ohm kunt toepassen (R = U/I ).

Stap 6: Kijk of je de spanningswet van Kirchhoff kunt toepassen ("spanning fietst").

Deze stappen 3 t/m 6 herhaal je totdat je alle benodigde informatie hebt. In dit voorbeeld kunnen we eerst de vervangingsweerstand R12 berekenen:

R12 = R1 + R2 = 3 Ω + 2 Ω = 5 Ω

Daarna kunnen we de spanningswet van Kirchhoff toepassen. In het rode circuit kunnen we de volgende vergelijking gebruiken:

U0 - I1 · R12 = 0

Hieruit volgt:

I1 = (U0)/(R12) = (10 V)/(5 Ω) = 2 A

Dit kan ook direct worden berekend door te begrijpen dat het een parallelschakeling is waarbij de bronspanning over de vervangingsweerstand R12 staat. Deze 2 A voegen we toe aan de schets. Hierdoor kunnen we stap 4 toepassen:

I3 = I0 - I1 = 2,33 A - 2 A = 0,33 A

Dit voegen we ook toe aan de schets. Nu weten we de stroom I3 door R3. Nu kunnen we stap 5 toepassen, de wet van Ohm:

U3 = I3 · R3 = 0,33 A · 25 Ω = 8 V

Hiermee is de opdracht voltooid. Er zijn nog twee extra stappen die soms van toepassing kunnen zijn.

Stap 7: Het toepassen van de formule voor elektrisch vermogen, P = U · I.

Stap 8: Berekenen van een specifieke weerstand met de formule R = ρ · l/A .

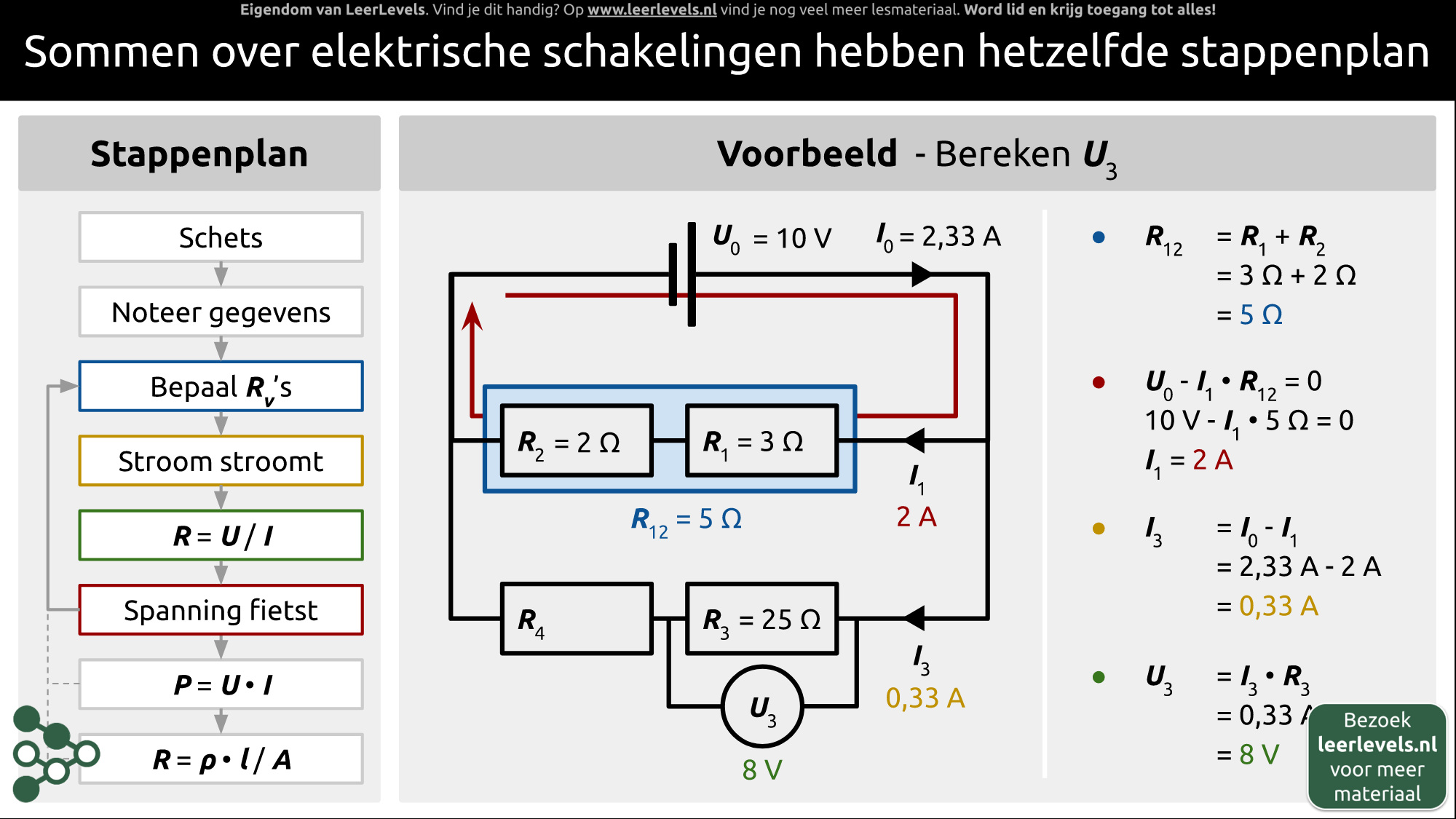
(Afbeelding: Animatie voor Elektrische schakelingen stappenplan)

Terug naar overzicht Meld je aan

Elektrische stroom

Elektronenstroom en elektrische stroom

De richting van de stroom van elektriciteit is vroeger verkeerd begrepen. Wanneer we een simpele schakeling hebben met een batterij en een lampje, loopt de stroom van de positieve naar de negatieve pool van de batterij. Dit noemen we de elektrische stroom omdat wetenschappers vroeger dachten dat de positieve deeltjes deze richting op bewogen. Maar later ontdekten ze dat de elektronen, negatief geladen deeltjes, eigenlijk de lading transporteert. Deze bewegen van de negatieve naar de positieve pool van de batterij, wat we de elektronenstroom noemen. De elektronenstroom is dus de echte richting waarin de stroom beweegt.

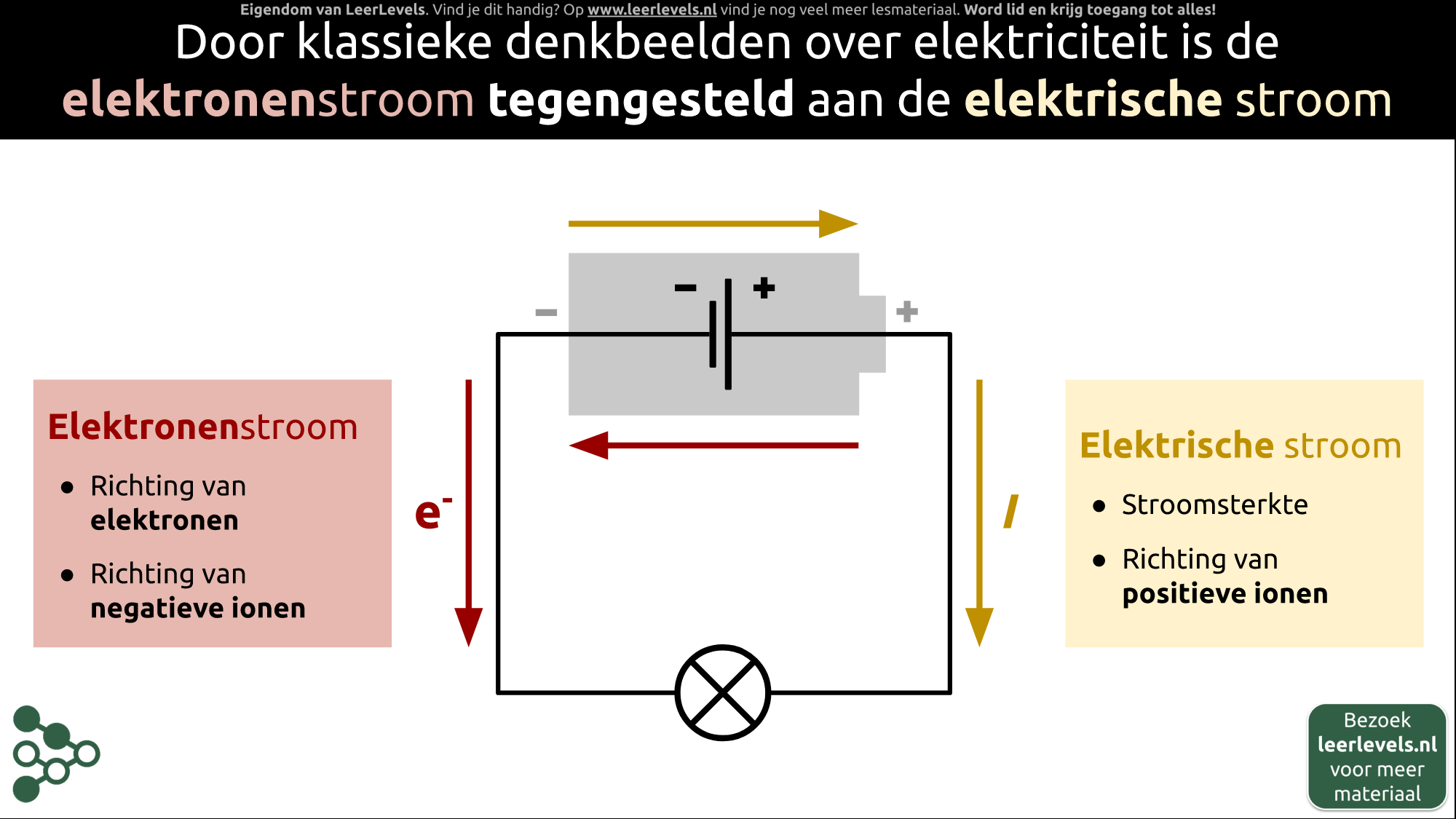
(Afbeelding: Animatie voor Elektronenstroom en elektrische stroom)

Terug naar overzicht Meld je aan

Elektromagnetisch spectrum

EM-spectrum

Zichtbaar licht vormt slechts een klein deel van het elektromagnetische (EM) spectrum. De pijl die hier te zien is, vertegenwoordigt het gehele spectrum. Het zichtbare licht is slechts een heel klein segment daarvan. Als je in het spectrum naar links gaat, naar lagere energie per foton, kom je bij infrarood (IR). Dit wordt uitgezonden door warme objecten die niet heet genoeg zijn om licht te geven. Een kaars wordt zo warm dat het zichtbaar licht uitstraalt, maar een verwarming is niet warm genoeg daarvoor. Ga je nog verder naar lagere energie, dan bereik je microgolfstraling, die wordt gebruikt in een magnetron. Met voldoende microwave-straling kun je water zeer efficiënt verwarmen. Met nog lagere energieën kom je bij radio- en wifi-straling. Gelukkig hebben deze stralingen weinig energie per foton, want ze zijn overal om ons heen aanwezig.

Als je kijkt naar stralingssoorten met meer energie per foton dan wij kunnen zien, kom je bij ultraviolet (UV) terecht. Onze zon zendt veel UV-fotonen uit, en daarom moeten we zonnebrandcrème gebruiken om onze huid te beschermen. Röntgenstraling heeft nog meer energie per foton. Deze straling dringt door vele materialen heen en kan worden gebruikt om foto's van botten te maken of voor detectiepoortjes. Bij nog hogere energie vind je gammastraling, een van de drie soorten radioactieve straling. De andere twee soorten radioactieve straling (Alfa- en bètastraling) bestaan uit deeltjes in plaats van fotonen. Gammastraling bestaat uit fotonen met zoveel energie dat ze een serieus gezondheidsrisico vormen.

Als je naar de bijbehorende frequenties kijkt, bevindt zichtbaar licht zich tussen 3,4 × 10¹⁴ en 7,5 × 10¹⁴ Hz. Deze schaal is logaritmisch, en je kunt zien dat wifi een frequentie heeft die ongeveer een miljoen keer kleiner is dan wat wij met het blote oog kunnen zien. We kijken ook vaak naar golflengtes in het EM-spectrum. Golflengte en frequentie van fotonen zijn omgekeerd evenredig met elkaar. Een hogere frequentie betekent dus een kleinere golflengte. Zichtbaar licht ligt tussen 400 nanometer (paars) en 700 nanometer (rood).

Al deze soorten straling zijn onderdeel van het elektromagnetisch spectrum. Ze vallen onder hetzelfde natuurverschijnsel, maar door de verschillende energieën worden ze voor uiteenlopende toepassingen gebruikt. In de spreektaal bedoelen we met "licht" vaak alleen het zichtbare licht. Als je echter met "licht" het volledige EM-spectrum bedoelt, dan is wifi ook een vorm van licht.

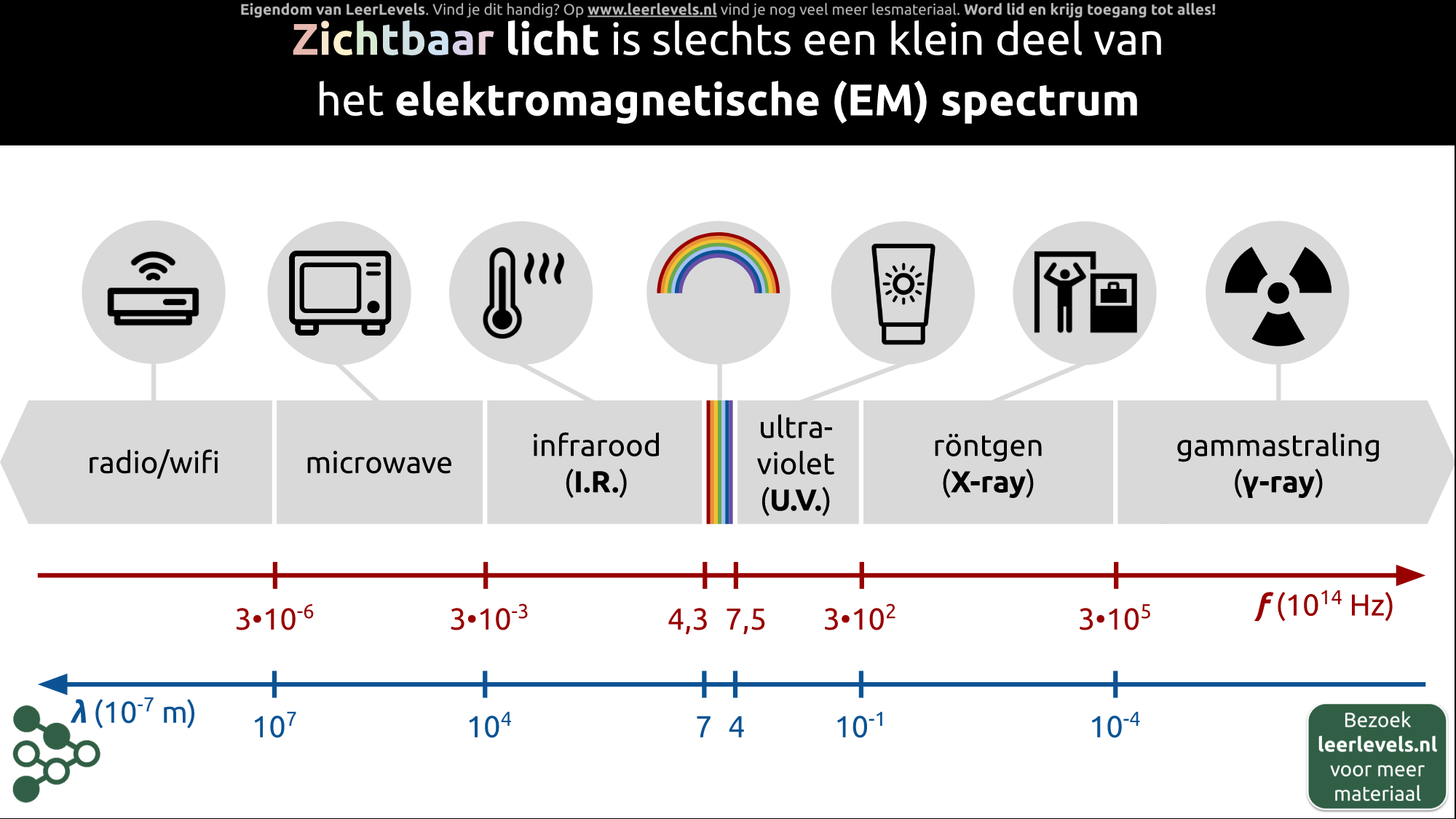
(Afbeelding: Animatie voor EM-spectrum)

Terug naar overzicht Meld je aan

Elektromagnetische straling

Zichtbaar licht bestaat uit een elektrisch veld, E, dat in de x-richting golft op en neer. Loodrecht daarop, bijvoorbeeld in de z-richting naar ons toe, bevindt zich een magnetisch veld, B. De precieze relatie tussen deze twee velden is complex, maar elke vorm van straling, inclusief zichtbaar licht, bestaat uit bewegende elektrische en magnetische velden.

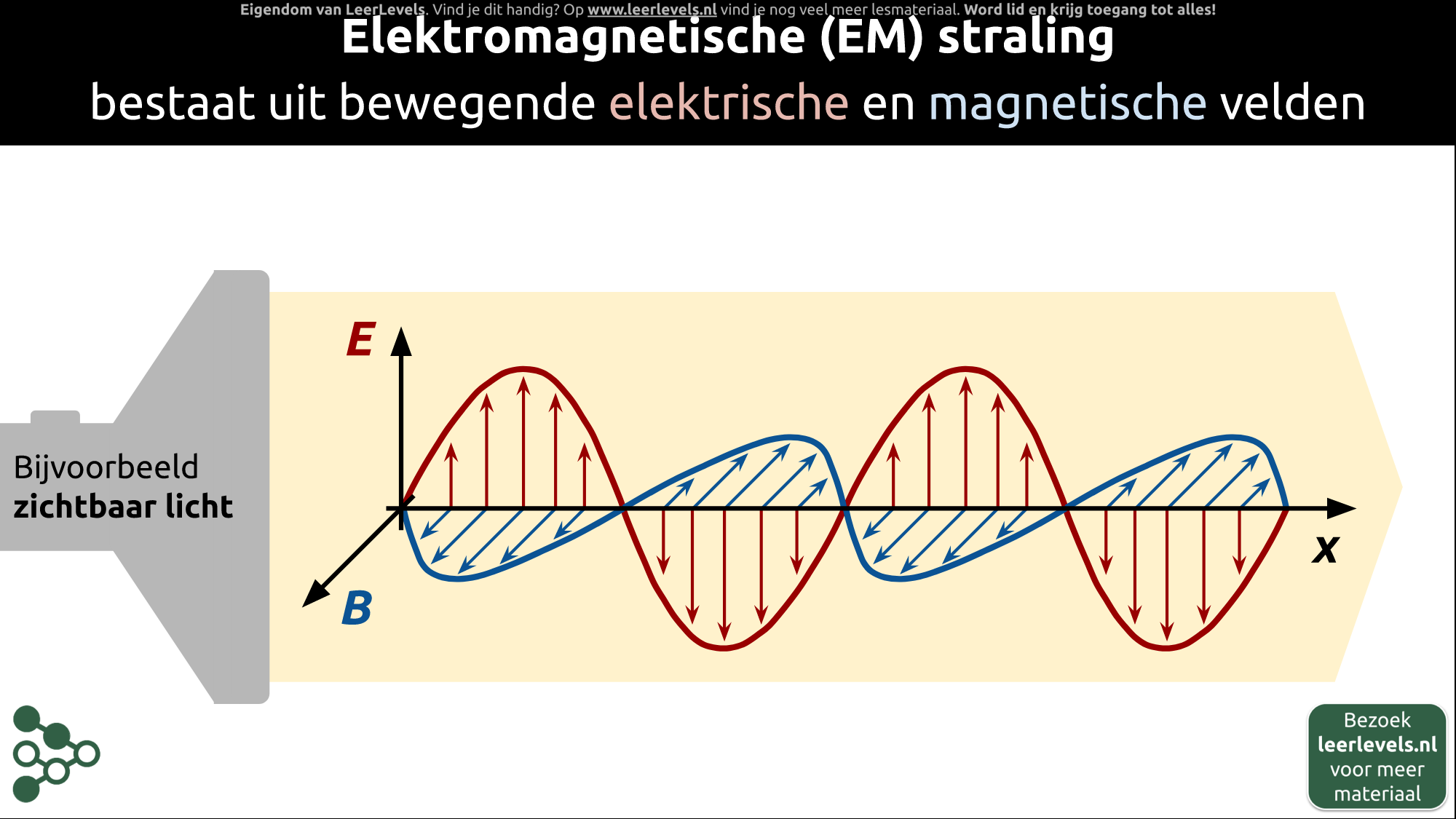
(Afbeelding: Animatie voor Elektromagnetische straling)

Terug naar overzicht Meld je aan

Elektromotor

Elektromotor werking

Een elektromotor zet elektrische spanning om in een draaiende beweging. Het werkt ook andersom: de motor kan omgekeerd als dynamo worden gebruikt. Een magnetisch veld bestaat uit een noord- en zuidpool. Door een commutator vast te zetten aan een stroomkring en te laten draaien om de paarse as, kunnen we spanning van een batterij gebruiken om het systeem te laten draaien. Loentzkrachten zorgen voor een moment waardoor het systeem gaat draaien en de spanning wordt omgezet in beweging. We kunnen ook een dynamo maken door de spanningsbron te vervangen door een spanningsmeter en zelf te zorgen voor beweging. In dat geval wekken we juist een spanning op.

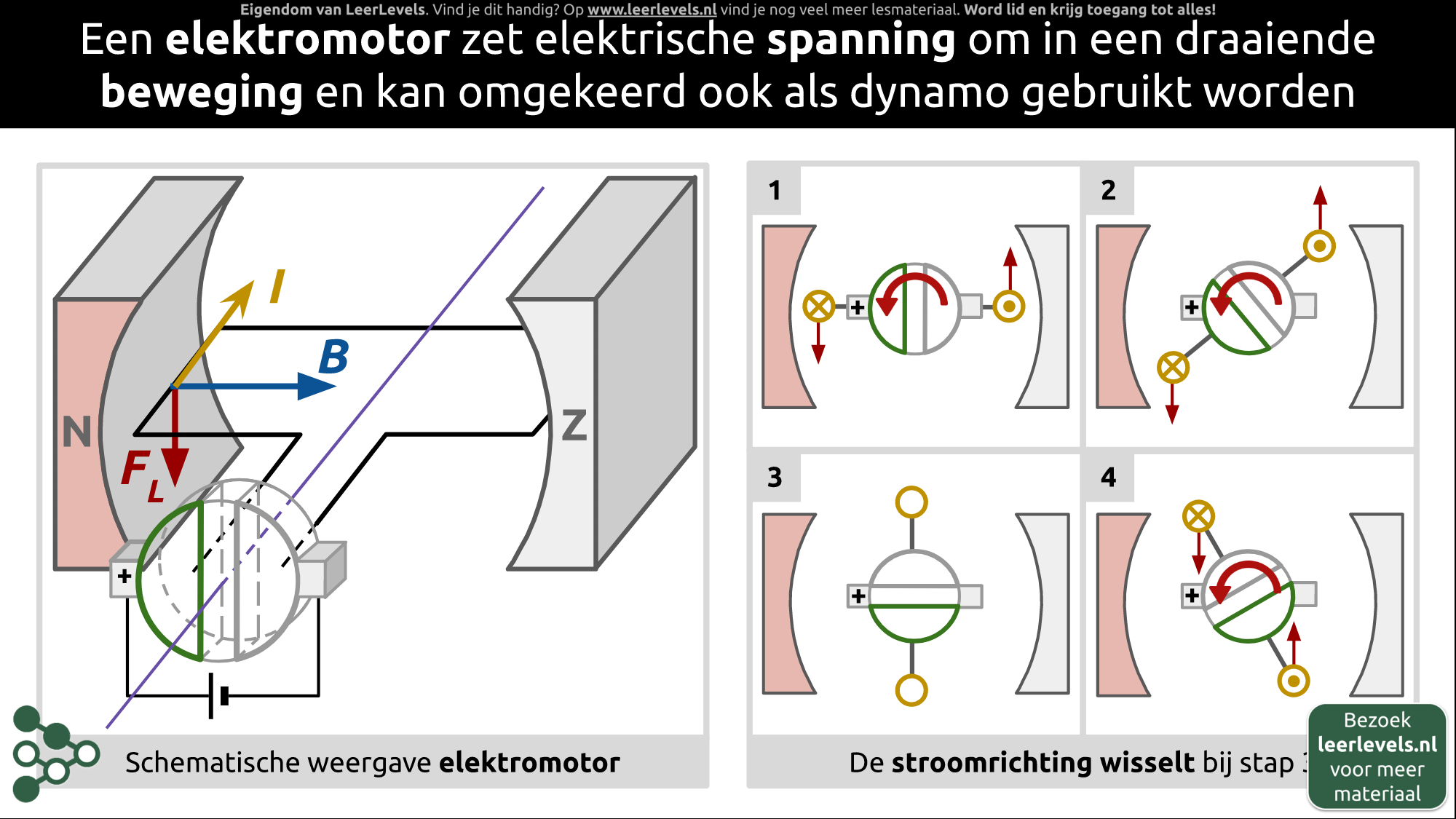
(Afbeelding: Animatie voor Elektromotor werking)

Terug naar overzicht Meld je aan

Elektronen

Elektronen zijn de kleinste onderdelen van een atoom. Als je bijvoorbeeld inzoomt op een spijker, zie je dat deze uit verschillende heel kleine deeltjes bestaat: atomen. Zoom je verder in op een atoom, dan ontdek je dat het uit verschillende onderdelen bestaat. In het midden bevindt zich de kern, met daarin protonen, die positief geladen deeltjes zijn, en neutronen, die neutraal geladen deeltjes zijn. Rondom de kern bewegen elektronen, die negatief geladen zijn. Deze drie deeltjes, protonen, neutronen en elektronen, vormen samen een atoom. Elektronen zijn daarbij de kleinste onderdelen van het atoom.

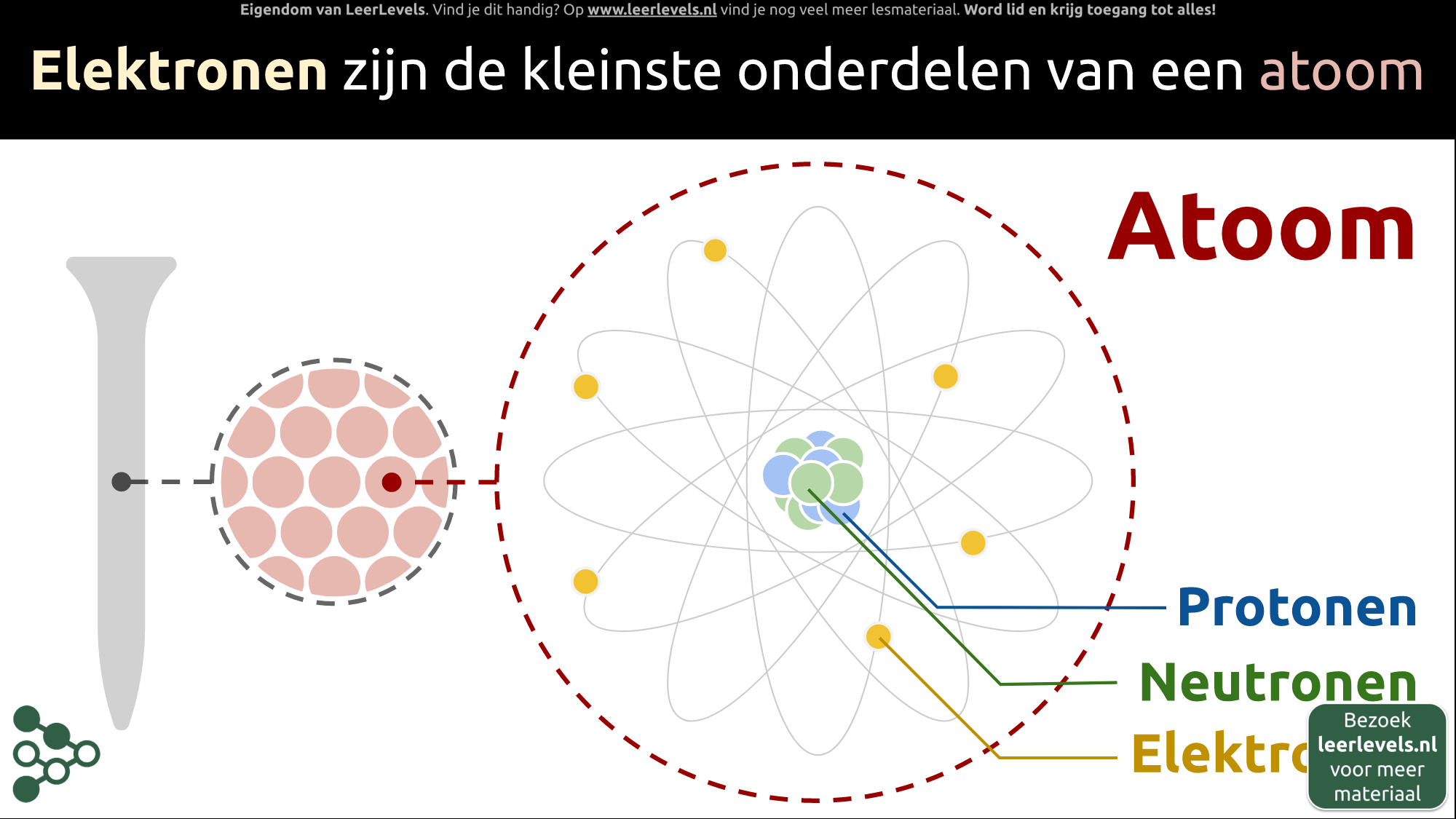
(Afbeelding: Animatie voor Elektronen)

Vrije elektronen

Elektriciteit kan door materialen zoals metalen stromen omdat ze veel vrije elektronen bevatten die niet gebonden zijn aan atomen in het materiaal. Wanneer er spanning wordt aangesloten op een metalen rooster, zorgt dit ervoor dat de elektronen bewegen van de ene kant naar de andere kant, van de negatieve naar de positieve pool. Dit zorgt voor een elektronenstroom, wat we kennen als stroom of elektriciteit. Het is echter belangrijk om te weten dat elektrische stroom in feite in de tegenovergestelde richting loopt door een historische fout bij het definiëren ervan. Maar in elk geval bevatten materialen zoals metalen veel vrije elektronen die voor de elektronenstroom zorgen.

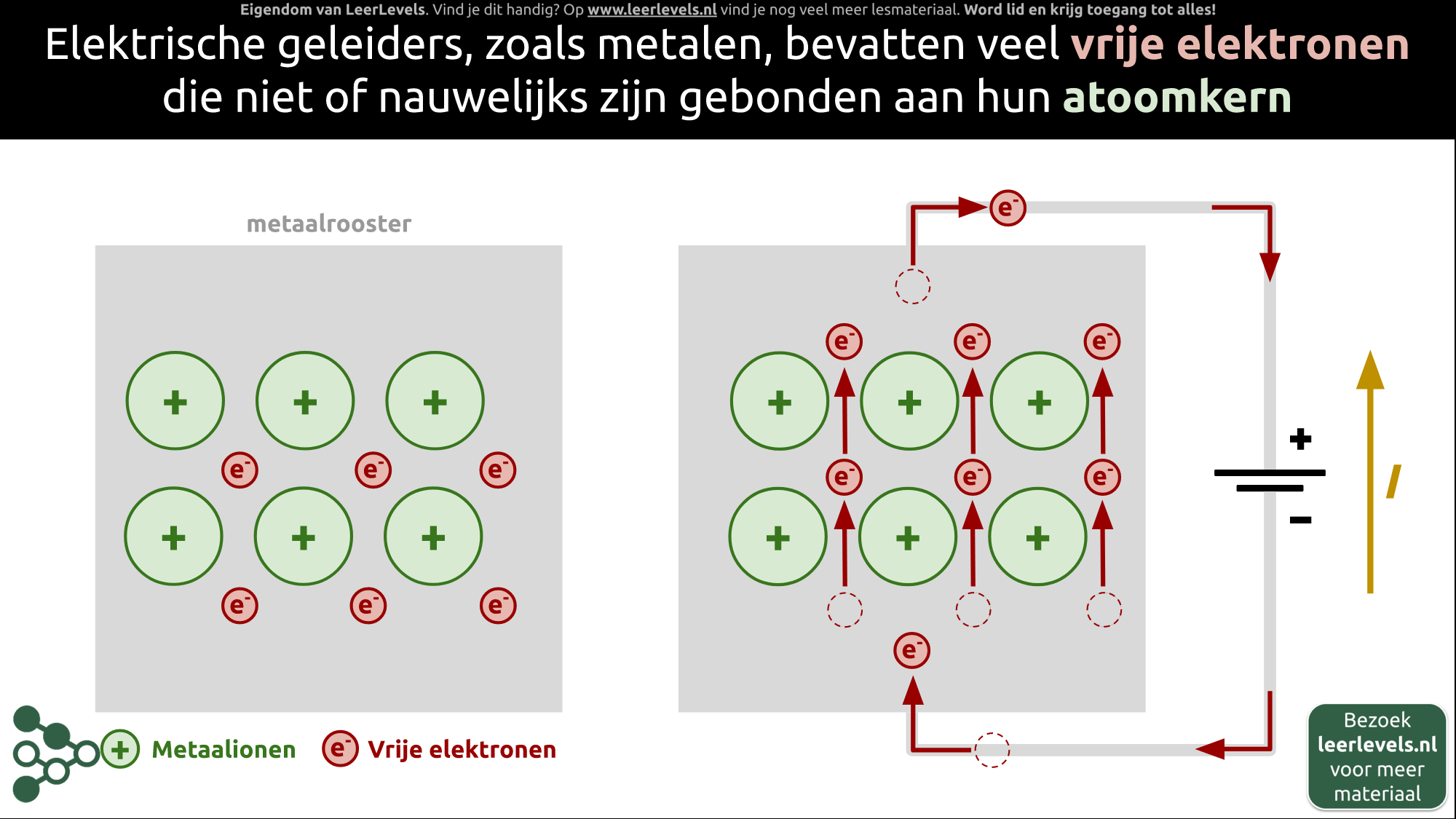
(Afbeelding: Animatie voor Vrije elektronen)

Terug naar overzicht Meld je aan

Elektronspin

Elektronspin als magneetje

De magnetische eigenschap van een elektron heeft twee waarden: spin up en spin down.

Het Stern-Gerlach-experiment heeft aangetoond dat deeltjes een gekwantiseerde magnetische eigenschap hebben, zoals elektronen. Je kunt een elektron voorstellen als een magneetje, waarbij de magnetische richting ook wel 'spin' wordt genoemd. Er zijn twee mogelijke waarden voor de spin van een elektron: spin up (noordpool omhoog) en spin down (noordpool omlaag). Schematisch wordt dit soms weergegeven als een pijl naar boven of naar beneden.

Vanuit het perspectief van de klassieke mechanica is dit een vreemd concept. Men zou verwachten dat de magnetische richting van een elektron in alle richtingen zou kunnen wijzen, net zoals een kompasnaald. Desondanks laten experimenten consistent zien dat de spin van een elektron slechts twee waarden kan hebben: up en down.

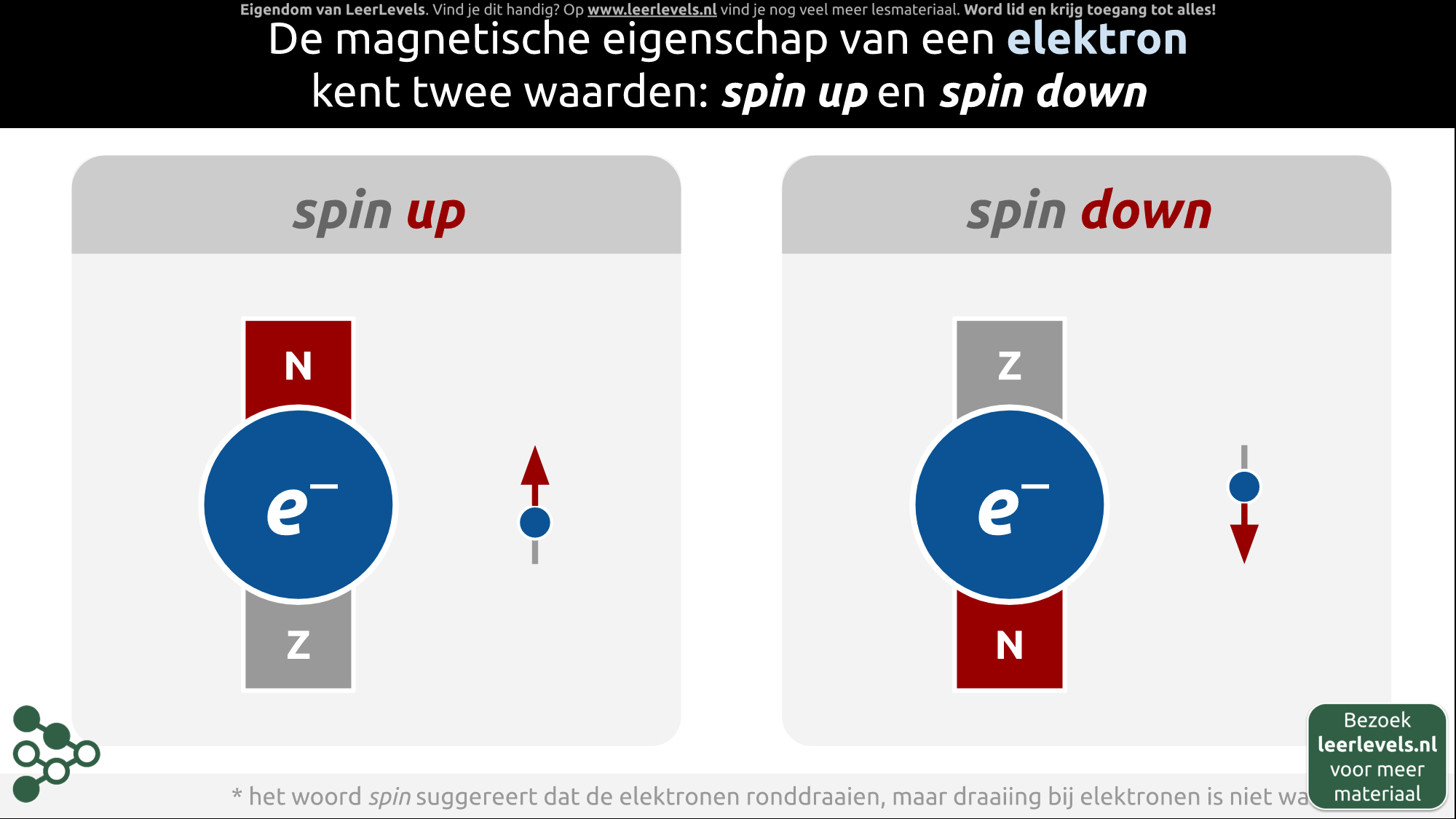
(Afbeelding: Animatie voor Elektronspin als magneetje)

Terug naar overzicht Meld je aan

Elektronvolt

Een elektronvolt (eV) is de energie die een elektron verkrijgt bij een spanning van 1 V. Stel dat we een condensator hebben met twee platen die verbonden zijn met een spanningsbron. Aan de negatieve kant bevindt zich een vrij elektron. Dit elektron wil naar de positieve kant bewegen, omdat het wordt aangetrokken door de positieve lading. De kinetische energie die het elektron uiteindelijk krijgt, is gelijk aan één elektronvolt. Dit kun je ook berekenen met de formule: Δ E = q · Δ U. Hierin is q de lading van het elektron, oftewel e, wat staat voor het elementaire ladingsquantum: 1,602 × 10⁻¹⁹ coulomb. Δ U is hier 1 volt, oftewel 1 joule per coulomb. Wanneer je deze twee waarden vermenigvuldigt, krijg je 1,602 × 10⁻¹⁹ joule. Dit is de waarde van 1 elektronvolt.

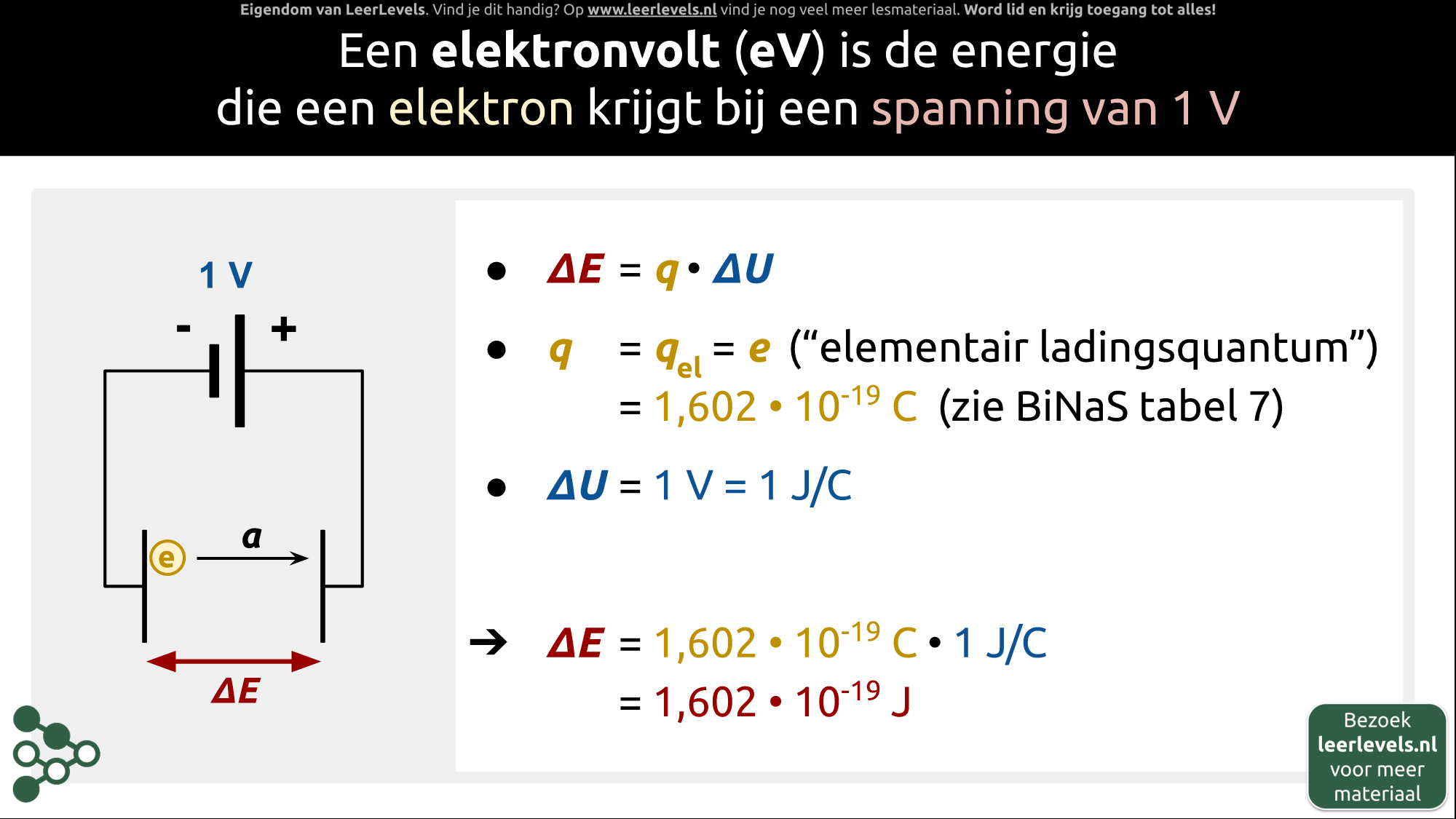
(Afbeelding: Animatie voor Elektronvolt)

Terug naar overzicht Meld je aan

Elektroscoop

Elektroscoop concept

Een elektroscoop maakt netto lading zichtbaar doordat de elektrische kracht de pootjes uit elkaar duwt. De elektroscoop bestaat uit verschillende onderdelen, zoals een geleidende kop, een behuizing, zeer lichte pootjes en soepele scharnieren.

Wanneer de netto lading nul is, zijn er evenveel positieve als negatieve ladingen en is er geen afstoting. Als er iets minder negatieve lading is, ontstaat er een kleine positieve lading, wat leidt tot lichte afstoting. De pootjes worden dan elk een beetje positief geladen en stoten elkaar af. Bijna alle ladingen worden aangeduid met een netto lading, die zowel positief als negatief kan zijn.

Als je alle negatieve ladingen verwijdert, ontstaat een grote positieve lading, wat resulteert in sterke afstoting. Maar als er juist veel negatieve ladingen aanwezig zijn, veroorzaakt dit ook afstoting. Voor de afstoting maakt het niet uit of beide pootjes positief of negatief geladen zijn, zolang ze maar dezelfde lading hebben. Zolang de netto lading niet nul is, zullen de pootjes elkaar afstoten.

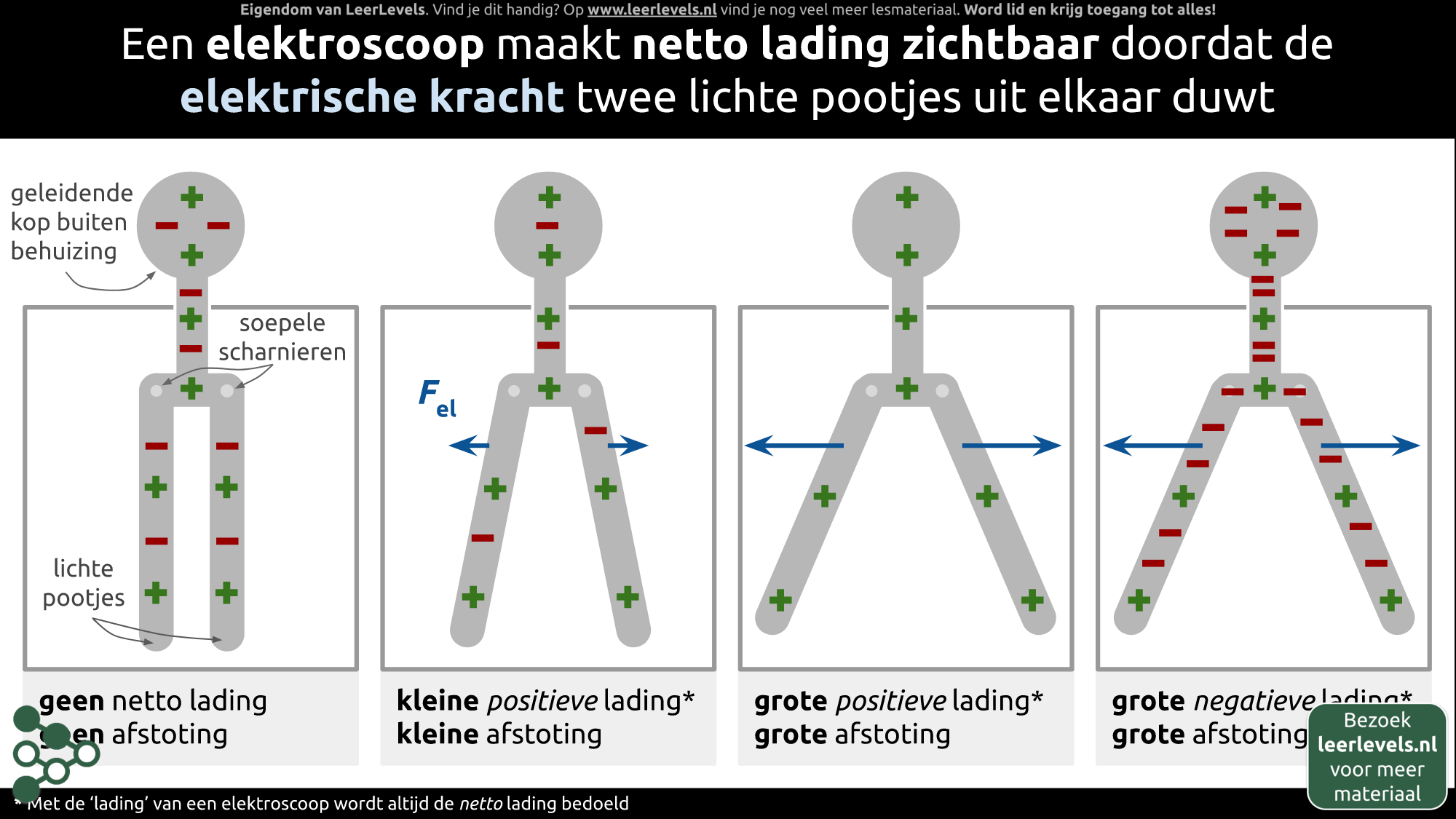
(Afbeelding: Animatie voor Elektroscoop concept)

Elektroscoop opladen

Een elektroscoop kan worden opgeladen met een geladen geleider. In stap 1 hebben we een neutrale elektroscoop met een gelijk aantal protonen en elektronen, wat resulteert in een netto lading van nul. In stap 2 brengen we een negatief geladen object dichtbij. Door influentie worden er relatief veel elektronen van de kop naar de pootjes geduwd. De pootjes krijgen hierdoor een negatieve lading en stoten elkaar af, terwijl de netto lading van de elektroscoop nog steeds nul blijft.

In stap 3 raken de pootjes het geladen object aan, waardoor elektronen van het object naar de pootjes vloeien. Dit proces gaat door totdat de netto lading van het object gelijk is aan die van de elektroscoop. Beide ladingen worden zo -3, met wat meer elektronen op beide plaatsen. Hierdoor bewegen de pootjes verder uit elkaar. Wanneer je het object weghaalt, verspreiden de ladingen zich gelijkmatig binnen de elektroscoop. De pootjes worden daardoor minder negatief, waardoor de uitwijking afneemt.

Je kunt ook een geladen isolator gebruiken in plaats van een geleider. In dit geval bestaat de ladingsoverdracht in stap 3 echter alleen uit de oppervlaktelading van het object.

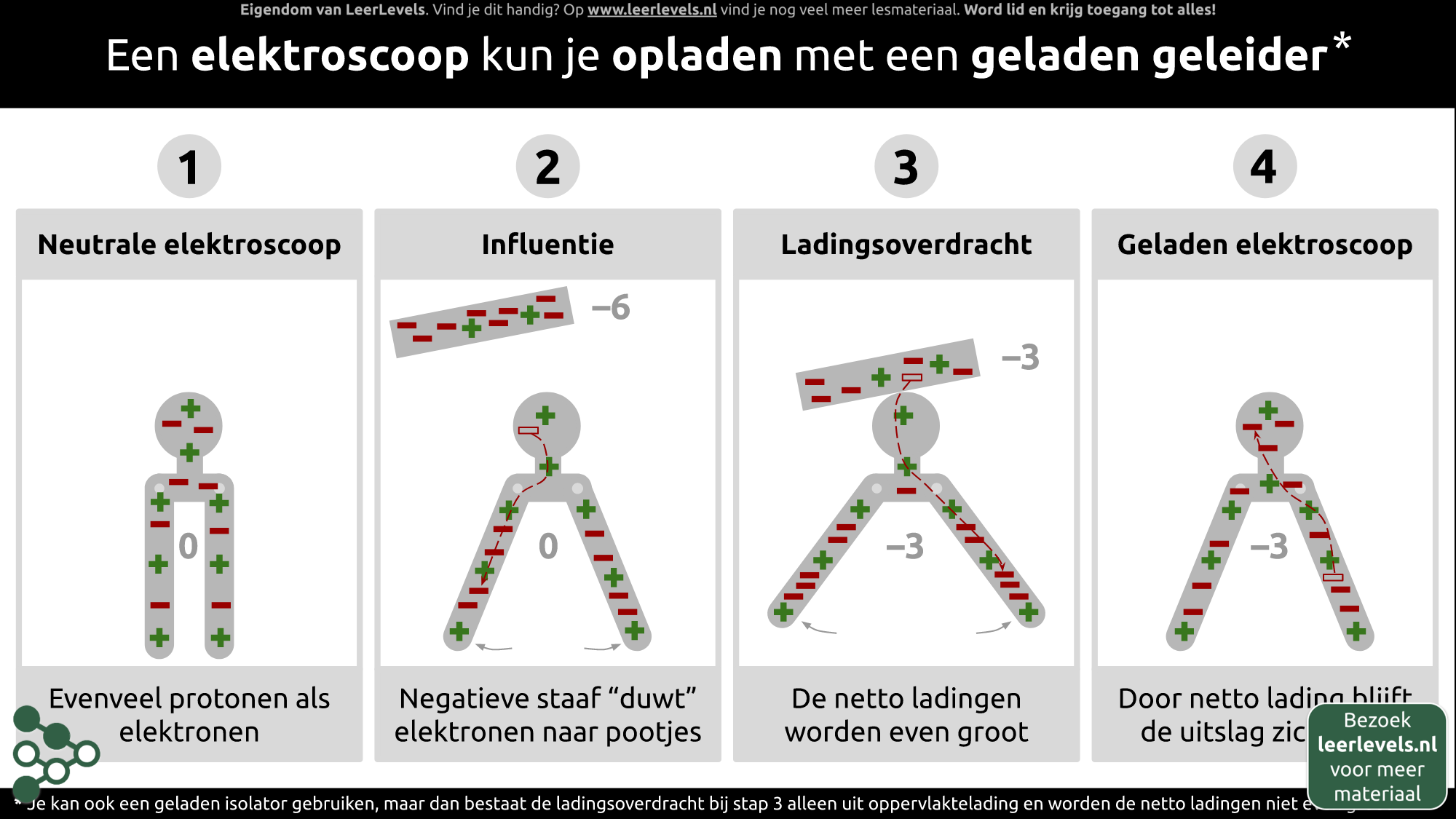
(Afbeelding: Animatie voor Elektroscoop opladen)

Terug naar overzicht Meld je aan

Elementaire lading

Elementair ladingsquantum

Het elementaire ladingsquantum, e, is de kleinste ladingseenheid in de natuur en is gerelateerd aan de lading van protonen en elektronen. Het symbool e vertegenwoordigt een lading in Coulomb, zoals vastgesteld door veel metingen. In een atoomkern bevinden zich neutronen en protonen; neutronen zijn ongeladen, terwijl protonen een positieve lading dragen, aangegeven met een plusteken ( + ). Elektronen daarentegen hebben een negatieve lading, aangeduid met een minteken (−). Er bestaat een uiterst klein verschil tussen de lading van protonen en elektronen, maar dit verschil is verwaarloosbaar klein.

(Afbeelding: Animatie voor Elementair ladingsquantum)

Terug naar overzicht Meld je aan

Energie

Energiesoorten formules

In een energiebalans bekijken we kinetische energie, zwaartekrachtenergie en arbeid. Het is nuttig om de bijbehorende formules uit je hoofd te kennen.

Zwaarte-energie

De formule voor zwaarte-energie is

Ez = m · g · h

Hierin is Ez de zwaarte-energie in J, m voor massa in kg, g voor zwaartekrachtversnelling in m/s² en h voor hoogte in m

Kinetische energie

Ook wel bewegingsenergie genoemd. De formule voor zwaarte energie is

Ek = ½ · m · v²

Hierin is Ek de kinetische energie in J, m de massa in kg en v voor snelheid in m/s.

Veerenergie

De formule voor veerenergie is

Ev = ½ · c · u²

Hierin is Ev de veerenergie in J, c de veerconstante in N/m en u de uitrekking van de veer ten opzichte van de evenwichtsstand in m.

Arbeid

Is een maat voor het verschil in energie. De formule voor arbeid is

W = F · s

Hierin is F de kracht in N en s de afstand in m

Vaak zijn veranderingen in energie gerelateerd aan zwaartekrachtenergie (Ez), veerenergie (Ev), kinetische energie (Ek), of potentiële energie. Met deze vier formules kun je de meeste energiebalansen oplossen.

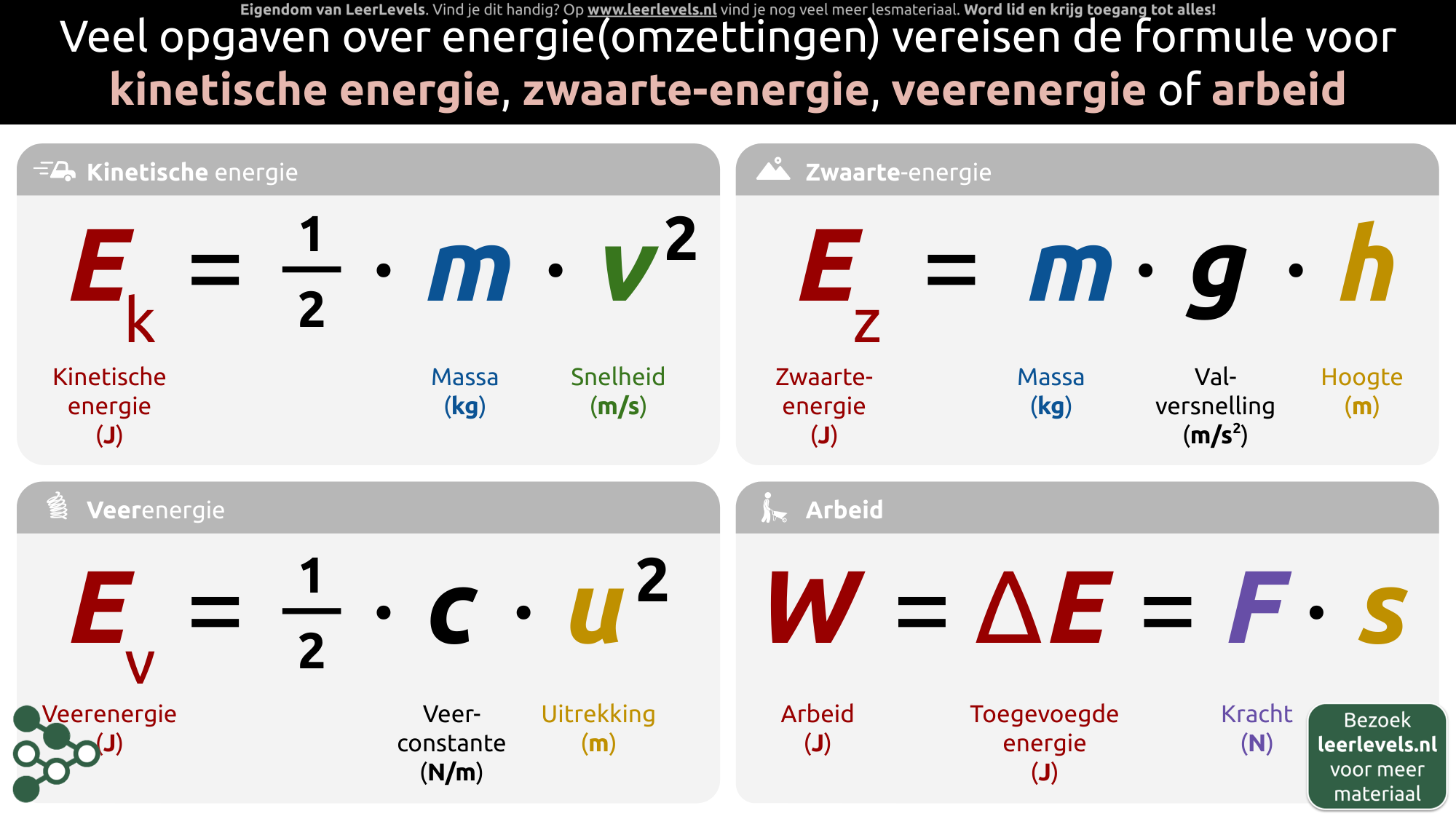
(Afbeelding: Animatie voor Energiesoorten formules)

Typen energie

Er zijn veel verschillende vormen van energie. Bijvoorbeeld, chemische energie en bewegingsenergie, die ook wel kinetische energie wordt genoemd. Wanneer je een trap oploopt, ontwikkel je hoogte-energie, ook bekend als potentiële energie. Bij het vervormen van een object gebruik je veerenergie. Alles wat met elektriciteit te maken heeft, valt onder elektrische energie. Licht dat wordt geproduceerd, noemen we lichtenergie of stralingsenergie. Als we het hebben over warmte afkomstig van vuur, gebruiken we simpelweg de term warmte, wat ook een vorm van energie is. Tot slot, wanneer er veranderingen plaatsvinden in een atoomkern, komt er energie vrij die we kernenergie noemen. Dit zijn allemaal voorbeelden van energie.

(Afbeelding: Animatie voor Typen energie)

Energie concept

Om werk te kunnen verrichten, is energie nodig. Energie is misschien wel de belangrijkste grootheid in de natuurkunde, maar het is moeilijk om precies te definiëren omdat er zoveel verschillende vormen van bestaan zijn. Neem bijvoorbeeld chemische energie: hiermee kun je werk verrichten door iets te versnellen of op te tillen. Als je een appel eet, kun je bijvoorbeeld de trap oplopen of een voorwerp vervormen. Er zijn talloze andere manieren om energie te gebruiken voor het verrichten van werk. Voor alle vormen van werk heb je echter energie nodig.

(Afbeelding: Animatie voor Energie concept)

Eenheid kilowattuur

Een kilowattuur is een eenheid van energie. Dit betekent hoeveel energie er in een bepaalde tijd wordt gebruikt. Het is opgebouwd uit drie dingen: kilo (duizend), watt (hoeveelheid energie per seconde) en uur (tijd). Als we deze samenvoegen, krijgen we 3,6 miljoen joules per seconde keer seconden. Dit kan ook worden geschreven als 3,6 keer 10 tot de 6de macht. Als we dit delen door seconde keer seconden, krijgen we joules, wat ook een eenheid van energie is. Dit kan worden geschreven als 3,6 megajoules. Dus kilowattuur is een eenheid van energie en betekent niets anders dan 3,6 megajoules.

(Afbeelding: Animatie voor Eenheid kilowattuur)

Energiecentrale

Een energiecentrale zet (fossiele) brandstof om in elektrische energie via verschillende stappen en energiesoorten. Een standaard energiecentrale begint met de verbranding van fossiele brandstof, wat warmte genereert; dit is een andere vorm van energie. We hebben hiermee brandstof omgezet in warmte. Deze warmte wordt gebruikt om stoom te produceren, die een bepaalde beweging heeft. De stoom wordt vaak ergens doorheen geperst, zet sterk uit, en kan daardoor onder hoge druk bewegen.

De bewegende stoom drijft de turbine aan. De turbine is verbonden met een as, die weer gekoppeld is aan een dynamo. Uit deze dynamo wordt elektriciteit opgewekt.

De verschillende vormen van energie in deze omzetting zijn: van brandstof naar warmte, naar bewegende stoom, naar een draaiende as, en uiteindelijk naar elektrische energie. Dit zijn de noodzakelijke omzettingen om fossiele brandstof in elektrische energie om te zetten in een energiecentrale.

(Afbeelding: Animatie voor Energiecentrale)

Duurzame energie

Duurzame energiebronnen zijn onuitputtelijk en hebben geen negatieve gevolgen voor toekomstige generaties. Voorbeelden van duurzame energie zijn zonne-energie, windenergie en waterkracht. Zonne-energie wordt direct opgevangen door zonnepanelen en indirect via windenergie, omdat de zon de lucht in beweging brengt. Windenergie wordt opgewekt met behulp van windturbines. Waterkrachtcentrales maken gebruik van stromend water, dat wordt aangedreven door de zon, die rivieren doet ontstaan. Zo zijn alle vormen van duurzame energie afhankelijk van de zon en kunnen we ze blijven gebruiken zolang deze blijft schijnen. Over het algemeen hebben duurzame energiebronnen geen negatieve effecten op toekomstige generaties.

(Afbeelding: Animatie voor Duurzame energie)

ADH energie

De aanbevolen dagelijkse hoeveelheid (ADH) energie verschilt per persoon. Een gemiddelde volwassen vrouw heeft ongeveer 2000 kcal per dag nodig, terwijl een gemiddelde volwassen man 2500 kcal per dag nodig heeft. Als je deze energie over de dag verdeelt, kom je als gemiddelde volwassen man uit op ongeveer 100 kcal per uur.

Dit verandert natuurlijk wanneer je gaat sporten. Tijdens golfen verbruik je bijvoorbeeld 250 kcal per uur. Voor het lopen van een marathon is dat zelfs 1000 kcal per uur. Als je dus 2 uur gaat hardlopen, verbruik je bijna net zoveel energie als je normaal op een hele dag nodig hebt. Daarom is het belangrijk om bij sporten rekening te houden met de extra energiebehoefte.

(Afbeelding: Animatie voor ADH energie)

Energiegebruik organen

Onze organen verdelen de energie die we uit ons voedsel halen. Wanneer we kijken waar de meeste energie naartoe gaat, zien we dat bijvoorbeeld 22% van de energie die we binnenkrijgen naar onze spieren gaat, aangezien skeletspieren veel energie verbruiken. Ons brein daarentegen gebruikt eveneens een aanzienlijk deel van de energie; hoewel het een orgaan is dat niet fysiek beweegt, is het wel de plek waar al onze emoties en gedachten plaatsvinden. Het brein verbruikt namelijk 20% van de binnengekomen energie. Dit maakt het tot een echte energieslurper. De lever is ook een grootverbruiker, met een energieverbruik van 18%. Het hart is een relatief klein orgaan, maar gebruikt toch 9% van de totale energie. Onze nieren verbruiken 8%, ander weefsel 6%, en alle overige kleine organen nemen samen ongeveer 19% van de energie voor hun rekening. Wanneer we dit op een rijtje zetten, zien we dat onze skeletspieren, ons brein en onze lever samen al meer dan de helft van al onze energie verbruiken.

(Afbeelding: Animatie voor Energiegebruik organen)

Terug naar overzicht Meld je aan

Energie-omzetting

Bij een energieomzetting verandert energie van de ene vorm naar een andere, maar blijft de totale hoeveelheid energie gelijk. Dit gebeurt overal om ons heen. Denk bijvoorbeeld aan een klassieke auto met een verbrandingsmotor. Als je chemische energie in de auto stopt, gaat deze rijden en wordt er warmte geproduceerd. De chemische energie wordt omgezet in bewegingsenergie en warmte.

Een ander voorbeeld is een elektrische auto. Hierbij wordt geen chemische energie gebruikt, maar elektrische energie. Daarbij ontstaat vooral beweging en minder warmte, wat elektrische auto's efficiënter maakt dan auto's met een verbrandingsmotor.

Elk proces dat je om je heen ziet, is eigenlijk een vorm van energieomzetting. Een bloem bijvoorbeeld zet licht om in chemische energie en warmte. Zelfs een vallende steen lijkt op het eerste gezicht simpel, maar is eigenlijk een vorm van energieomzetting: van zwaarte-energie naar voornamelijk beweging, met wat warmteontwikkeling door luchtwrijving.

Andere voorbeelden zijn een zonnecel, waar geprobeerd wordt om zo veel mogelijk licht om te zetten in elektrische energie, en een lift, waarbij elektrische energie zo veel mogelijk wordt omgezet naar zwaarte-energie.

Kortom, er zijn talloze processen waarbij energie van vorm verandert, en dit gebeurt echt overal om ons heen.

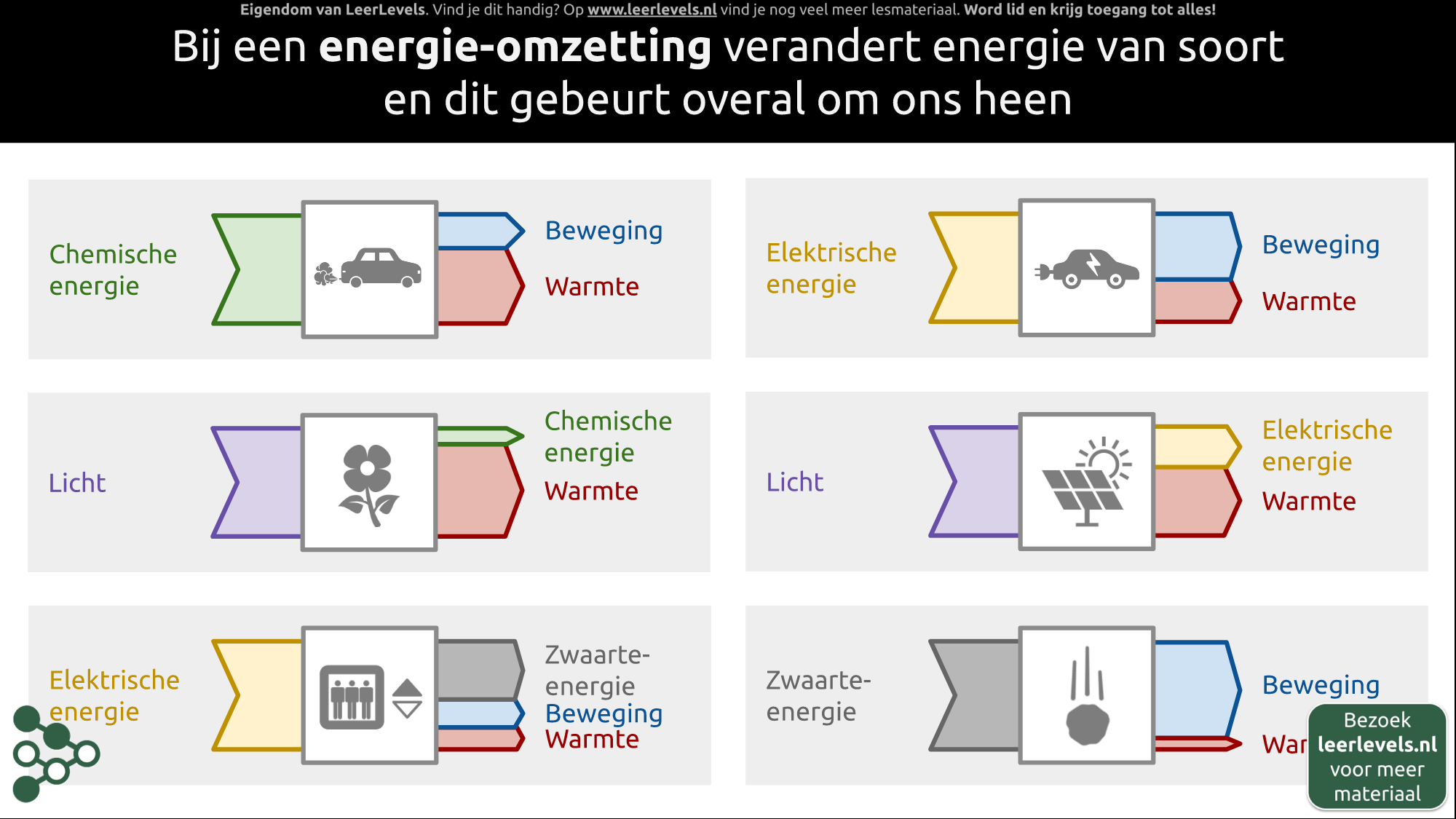
(Afbeelding: Animatie voor Energie-omzetting)

Terug naar overzicht Meld je aan

Energiebalans

Gesloten energiebalans concept

Energie kan niet uit het niets ontstaan of verdwijnen in een systeem, dus de totale hoeveelheid energie blijft altijd hetzelfde. Laten we een bal als voorbeeld nemen. Als de bal stilstaat op een bepaalde hoogte, heeft hij alleen zwaarte-energie omdat hij een hoogte heeft maar geen snelheid. Omdat we in dit geval niks doen met een veer, is er geen sprake van veerenergie. Als de bal van positie verandert en dus van hoogte verandert, wordt er energie omgezet van zwaarte-energie naar kinetische energie. Zolang er geen energie verloren gaat door wrijving of op een andere manier, blijft de totale hoeveelheid energie in het systeem constant.

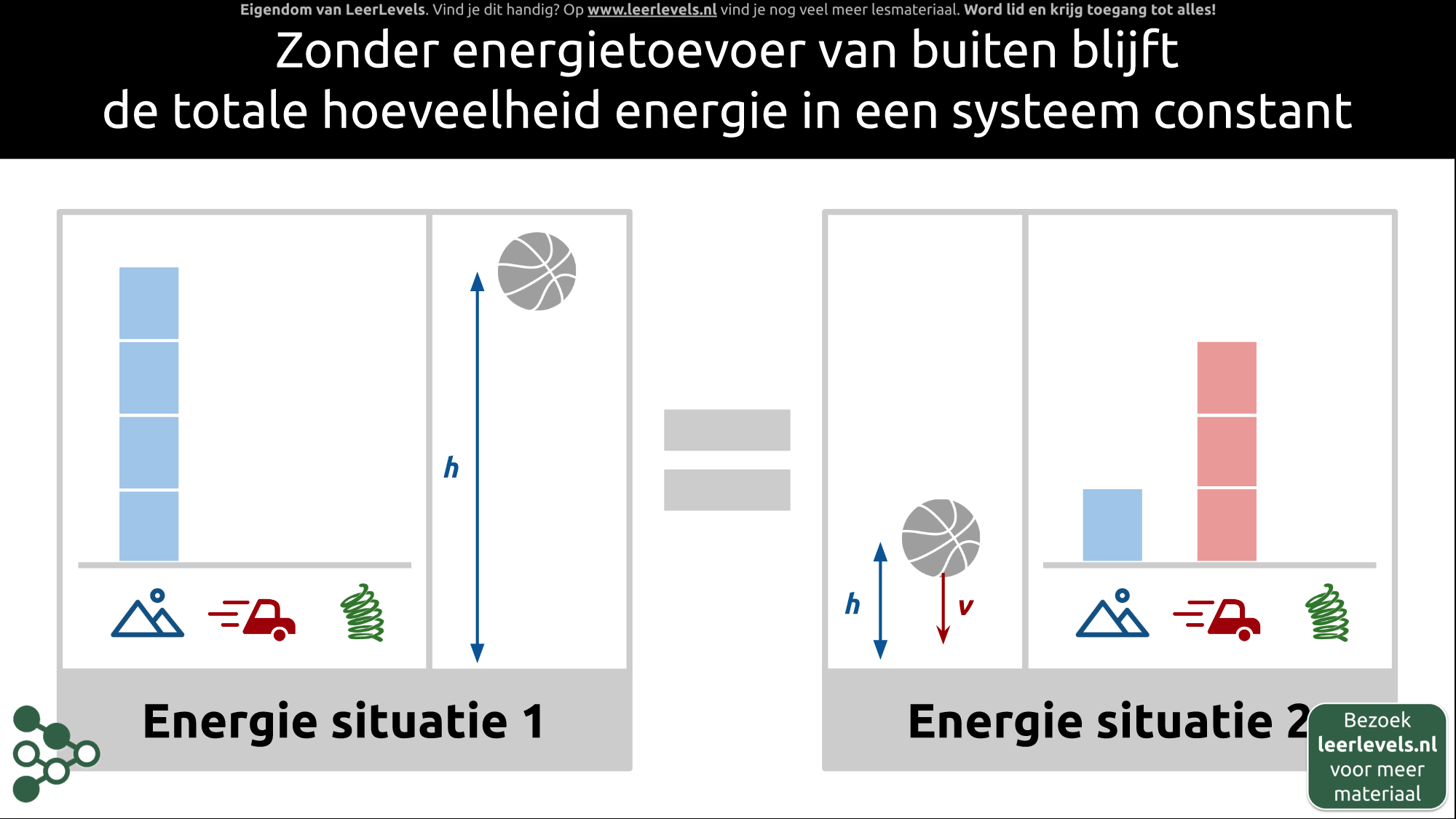
(Afbeelding: Animatie voor Gesloten energiebalans concept)

Gesloten energiebalans formule

De som van zwaarte-energie, kinetische energie en veerenergie blijft gelijk wanneer er geen arbeid op het systeem wordt verricht. Als we naar twee situatie kijken dan is de som van alle energie in situatie 1 gelijk aan de som van alle energie in situatie 2. Dus

∑ E1 = ∑ E2

Soms gebruiken we ook "voor" en "na" in plaats van situatie 1 en situatie 2. In dat geval wordt de formule

∑ Evoor = ∑ Ena

In beide situaties kan een voorwerp zwaarte-energie (Ez,1), kinetische energie (Ek,1) en veerenergie (Ev,1) hebben. Dus de formule wordt

Ez,1 + Ek,1 + Ev,1 = Ez,2 + Ek,2 + Ev,2

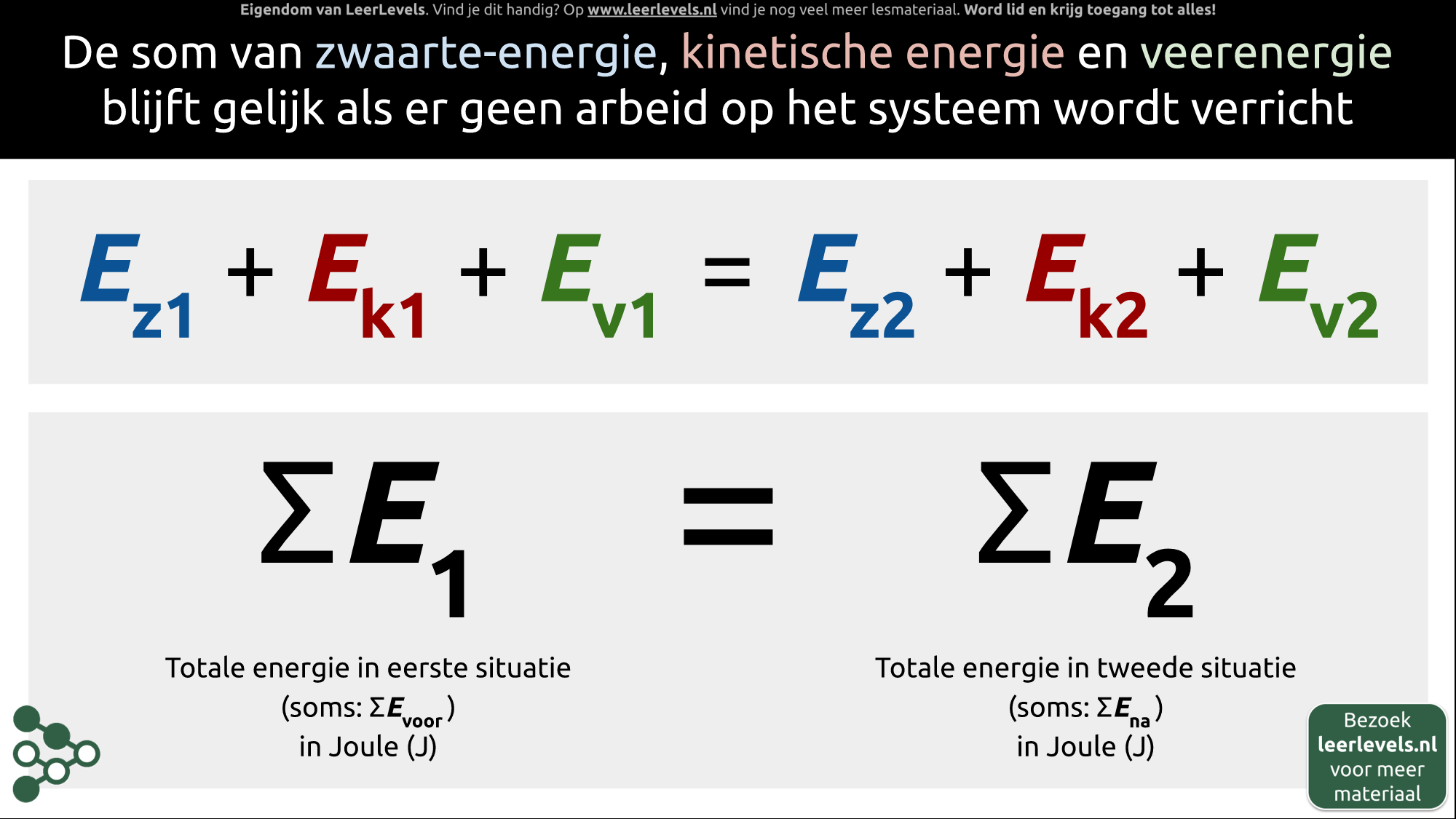
(Afbeelding: Animatie voor Gesloten energiebalans formule)

Open energiebalans concept

De totale energie in een systeem kan veranderen wanneer er arbeid wordt verricht. Laten we bijvoorbeeld een honkbal bekijken die op de grond ligt. Zolang de bal stil op de grond ligt, heeft hij geen zwaarte-energie, geen kinetische energie en geen veerenergie.

Wanneer een pitcher de honkbal gooit, verricht hij arbeid door een kracht op de bal uit te oefenen. Op het moment dat de bal wordt losgelaten en door de lucht vliegt, bezit hij zowel zwaarte-energie als kinetische energie.

We kunnen deze situatie beschrijven met een energiebalans. Stel dat er 5 eenheden arbeid op de bal is verricht, en via de hoogte weten we dat er 2 eenheden zwaarte-energie in de bal aanwezig zijn. Dit betekent dat er nog 3 eenheden energie overblijven die volledig in kinetische energie moeten zitten.

Het belangrijkste inzicht is dat de arbeid die wordt verricht, de totale energie in het systeem kan veranderen. Soms neemt de energie toe, zoals in situatie 2, en soms neemt de energie af, bijvoorbeeld door wrijving. Wat altijd geldt, is dat de energie in situatie 1 plus de verrichte arbeid gelijk is aan de energie in situatie 2.

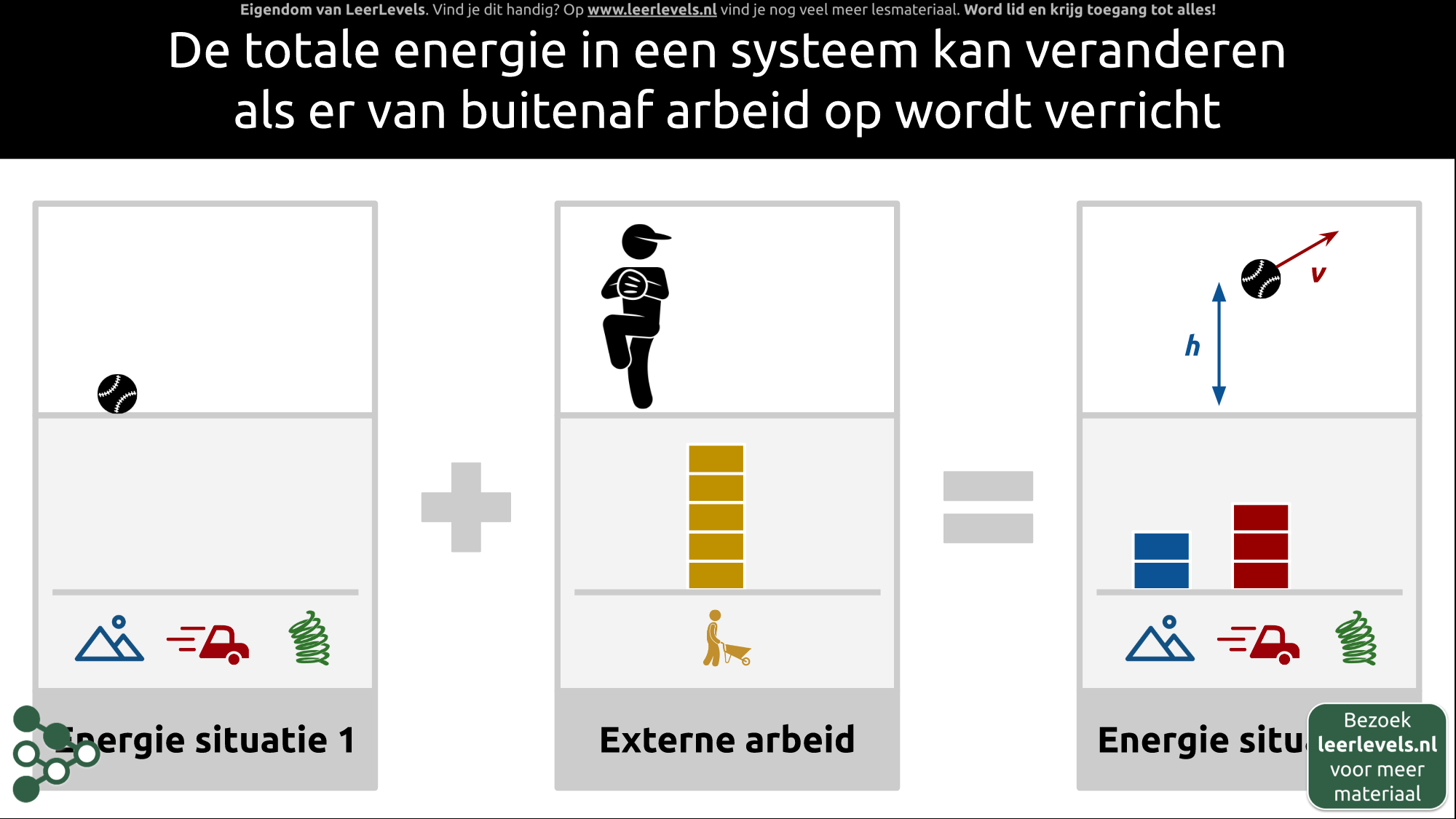
(Afbeelding: Animatie voor Open energiebalans concept)

Open energiebalans formule

In een open energiebalans moet ook de externe arbeid worden meegenomen. De totale hoeveelheid energie aan het begin van het proces, samen met de externe arbeid die op het systeem wordt verricht, moet gelijk zijn aan de totale hoeveelheid energie aan het einde. Dit kan worden uitgedrukt in de formule:

∑ E1 + ∑ W = ∑ E2

Hierin staat ∑ E1 voor de totale energie aan het begin, ∑ W voor de totale externe arbeid, en ∑ E2 voor de totale energie aan het einde, allen uitgedrukt in joules (J).

Het is daarbij belangrijk om op te merken dat arbeid zowel positief als negatief kan zijn. Wanneer energie aan het systeem wordt toegevoegd, zoals wanneer een werper een bal gooit, spreken we van positieve arbeid. Aan de andere kant kan energie door wrijving aan het systeem worden onttrokken en omgezet in warmte, wat als negatieve arbeid wordt aangeduid. Het is cruciaal dat alle vormen van energie in een energiebalans worden opgenomen.

(Afbeelding: Animatie voor Open energiebalans formule)

Terug naar overzicht Meld je aan

Energiebanden

Energieband concept

Wanneer atomaire golffuncties overlappen, ontstaan er splitsingen in energieniveaus, wat resulteert in energiebanden in een vaste stof.

Bij een enkel atoom ontstaan energieniveaus doordat de atoomkern kan worden voorgesteld als een kleine energieput. Het buitenste elektron wordt aangetrokken door de positieve atoomkern. Door te kijken naar welke golffuncties van dit elektron passen in de put, zoals de grondtoestand, kan de energiewaarde worden bepaald. Maar hoe werkt dit in een vaste stof, waar er niet slechts één atoom is, maar vele atomen dicht bij elkaar? Bijvoorbeeld, in een stukje koperdraad van 1 cm lang en 1 mm dik zijn er al ongeveer 10²² atomen aanwezig!

Om dit te begrijpen, is het handig om eerst te kijken wat er gebeurt wanneer je twee atomen dicht bij elkaar brengt. Dan heb je geen enkel, maar twee energieputjes. Het interessante is dat het uiteinde van de golffunctie van het ene atoom zich verspreidt tot in het putje van de buurman, waardoor elk elektron kan 'tunnelen' naar het andere atoom. Hierdoor kan niet langer worden gezegd welk elektron bij welk atoom hoort! De twee elektronen krijgen dan één gezamenlijke golffunctie, waarbij de grondtoestand van het enkel atoom zich splitst in twee toestanden: Ψ1a en Ψ1b. Ψ1a neemt iets meer ruimte in en heeft een iets lagere energie, terwijl de golffunctie van Ψ1b iets smaller is en daarbij hoort een iets hogere energie. Deze splitsing is ook zichtbaar in het energieniveauschema, zowel bij de grondtoestand als bij de eerste en tweede aangeslagen toestand.

Nu, in een vaste stof, hebben we geen twee atomen, maar een duizelingwekkend aantal van 10²² atomen, waardoor de grondtoestand zich opsplitst in 10²² toestanden! Elk van deze toestanden heeft een iets andere energie, die zeer dicht bij elkaar liggen. De energieën van de grondtoestand vormen samen een energieband. Ook de eerste aangeslagen toestand splitst zich op in 10²² niveaus, evenals de tweede aangeslagen toestand.

Kortom, als atomaire golffuncties overlappen, splitsen energieniveaus zich op en ontstaan er energiebanden in een vaste stof.

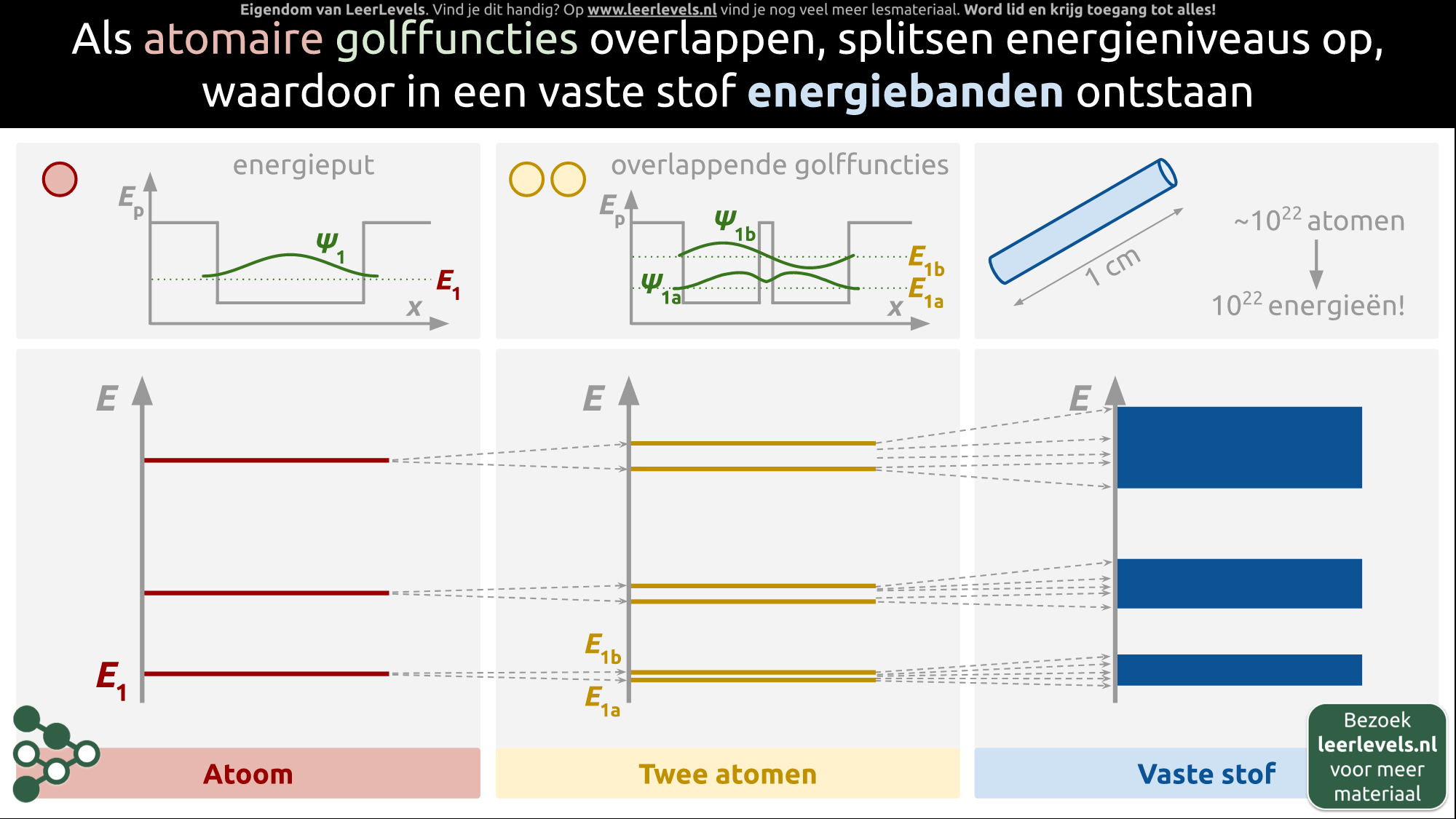
(Afbeelding: Animatie voor Energieband concept)

Valentieband en geleidingsband

De valentieband is de hoogste energieband waar elektronen in zitten T = 0 Kelvin. De geleidingsband is de laagste energieband waar geen elektronen in zitten bij T = 0 K.

In een halfgeleider is de valantieband bij T = 0 K altijd volledig gevuld. De elektronen in deze band komen uit de buitenste schil van de atomen en worden valentie-elektronen genoemd. Daarom wordt de hoogste gevulde band de valentieband genoemd.

De band direct boven de valentieband is de geleidingsband. Deze band is leeg bij T = 0K. Zodra de temperatuur boven de 0K komt, kán een elektron genoeg energie krijgen om de bandgap te overbruggen. In dat geval is de geleidingsband niet langer leeg en is de valentieband niet meer volledig gevuld. Wanneer een elektron in de geleidingsband terechtkomt, kan dat elektron vrij bewegen, waardoor de stof geleidend wordt.

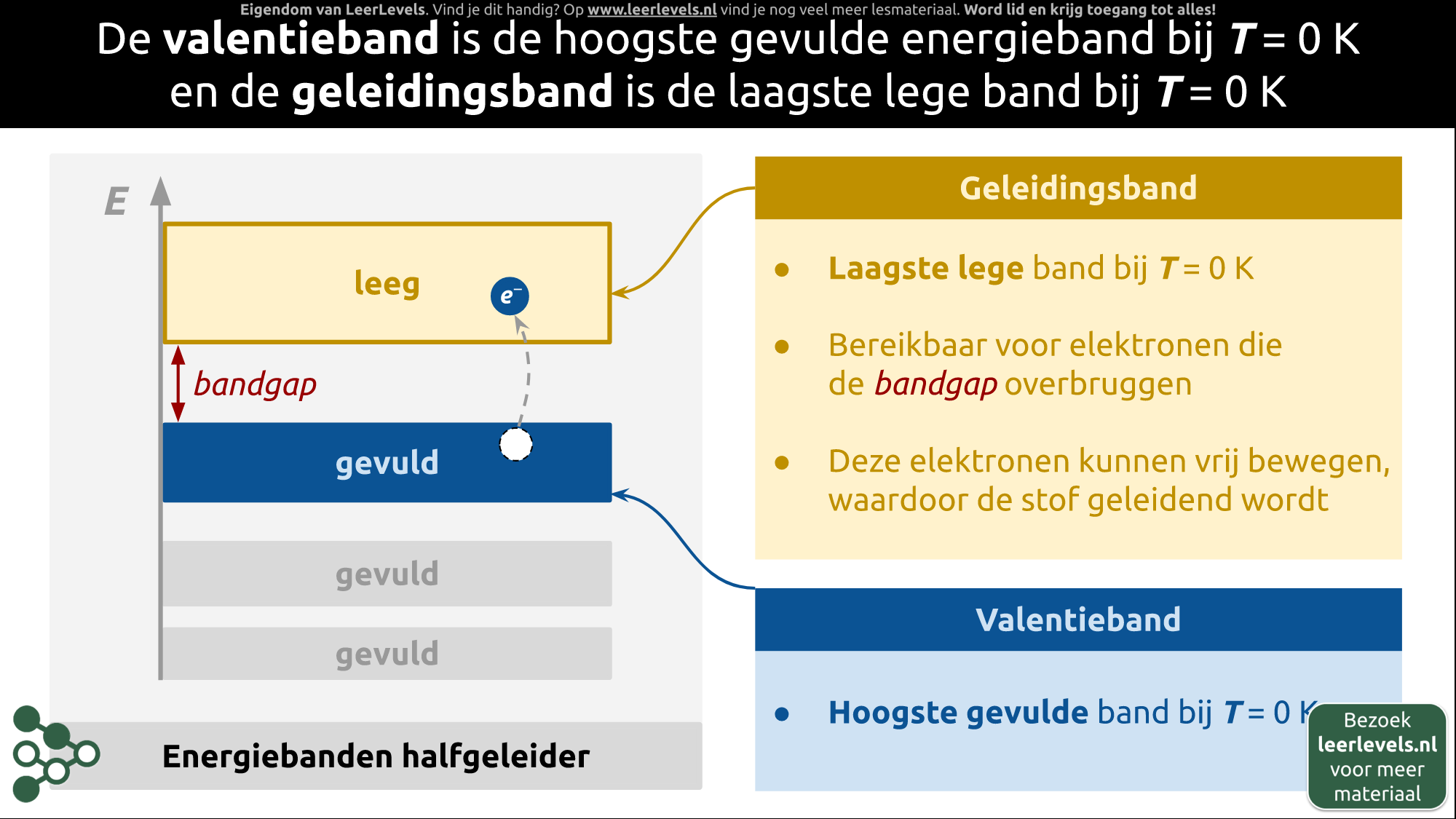
(Afbeelding: Animatie voor Valentieband en geleidingsband)

Energiebanden en geleiding

Een vaste stof geleidt elektriciteit wanneer elektronen naar een hoger energieniveau kunnen springen.

In een vaste stof zijn er energiebanden, waarin de energieniveaus worden gevuld met elektronen. Als bijvoorbeeld de laagste energieband half gevuld is, is de stof een goede geleider omdat elektronen gemakkelijk een kleine sprong omhoog kunnen maken. Deze sprong kan veroorzaakt worden door thermische fluctuaties, de bewegingen van atomen, of door het absorberen van licht of het aanleggen van een elektrische spanning.

Het kan ook voorkomen dat in een vaste stof de laagste energieband volledig gevuld is. In dit geval is het niet mogelijk om een kleine sprong omhoog te maken, omdat er geen energieniveaus beschikbaar zijn om naartoe te springen. Deze stof geleidt dus niet. Geleiding vindt alleen plaats wanneer een elektron kan springen naar een iets hoger energieniveau.

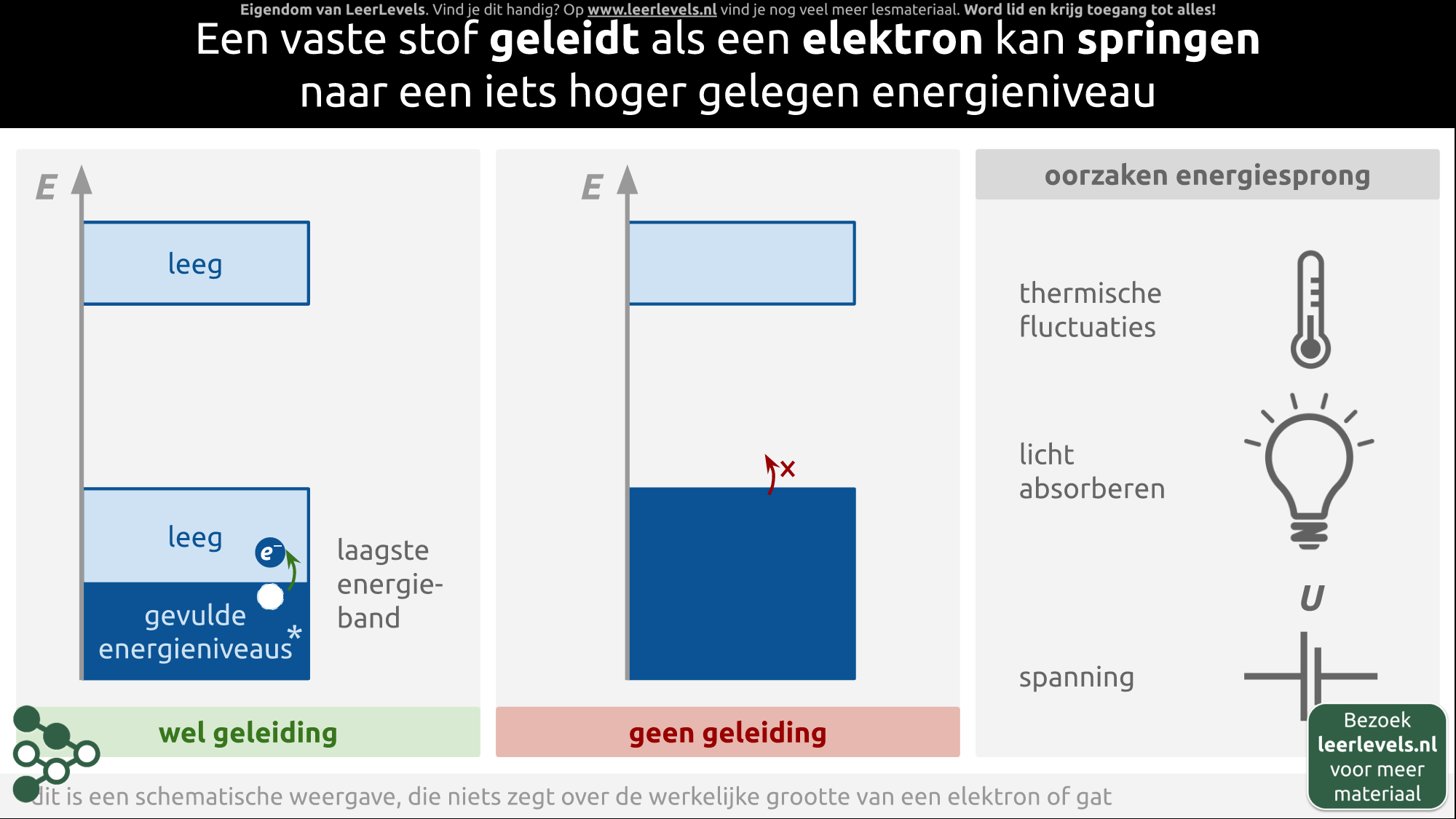
(Afbeelding: Animatie voor Energiebanden en geleiding)

Terug naar overzicht Meld je aan

Energiebehoud

Energiebehoud heelal concept

In de ruimte werkt de zwaartekracht anders dan op aarde. We gebruiken daarom gravitatie-energie in plaats van zwaarte-energie en veerenergie is niet belangrijk. Stel dat er een satelliet om de aarde draait met snelheid v en afstand r. De satelliet heeft kinetische energie Ek en gravitatie-energie Eg. De totale energie Etot is negatief. Als de satelliet dichterbij de aarde komt, wordt de gravitatie-energie negatiever. Maar de totale energie moet hetzelfde blijven, dus de kinetische energie neemt toe. Hierdoor gaat de snelheid van de satelliet omhoog. We rekenen dit uit met de formule: 2Ek - 3Eg = -1Etot.

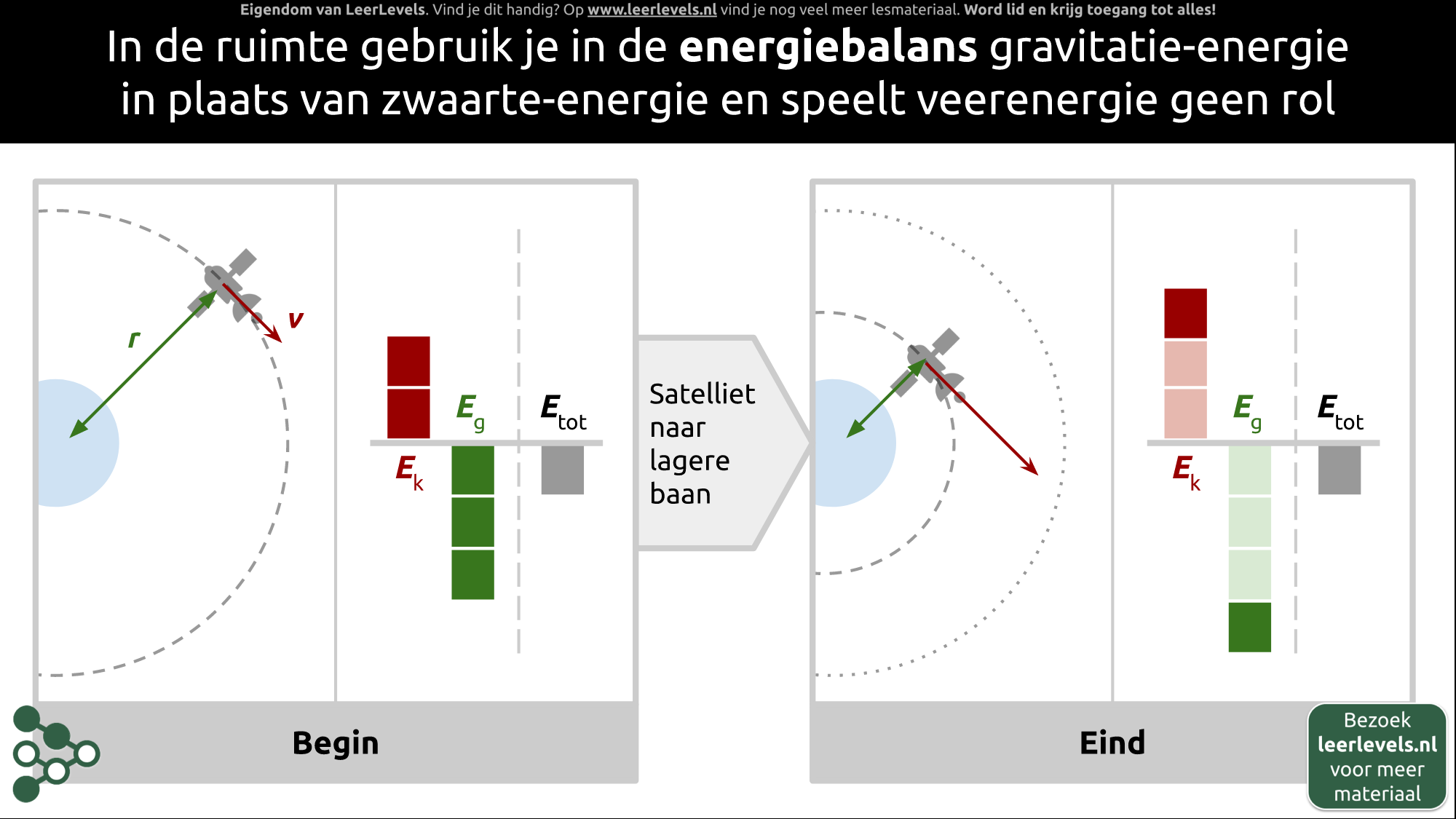
(Afbeelding: Animatie voor Energiebehoud heelal concept)

Energiebehoud heelal formule

Om energiebehoud in de ruimte te analyseren, moet je rekening houden met gravitatie-energie, kinetische energie en eventueel verrichte arbeid. De formule ziet er als volgt uit:

Eg1 + Ek1 + W = Eg2 + Ek2

Hierbij zijn Eg1 en Eg2 de gravitatie-energieën aan het begin en aan het eind, uitgedrukt in Joule. Ek1 en Ek2 representeren de kinetische energieën aan het begin en aan het eind, eveneens in Joule. Tot slot is W de arbeid die op het systeem wordt verricht, ook uitgedrukt in Joule.

(Afbeelding: Animatie voor Energiebehoud heelal formule)

Wet van behoud van energie

Volgens de wet van behoud van energie blijft de totale energie constant bij elke energieomzetting. Dit houdt in dat energie niet kan verdwijnen of spontaan worden gecreëerd. Energie kan echter wel worden omgezet, zoals van elektrische energie naar licht en warmte in een lamp. Als je naar de energieomzetting kijkt, gaat er aan de linkerkant 10 eenheden energie in. Aan de rechterkant komen er ook 10 eenheden energie uit. Van deze 10 eenheden worden er 6 omgezet in licht en 4 in warmte. Dit laat zien dat energie wel kan worden omgezet, maar niet kan verdwijnen of worden gemaakt. De totale energie blijft gelijk, en dat is precies wat de wet van behoud van energie inhoudt.

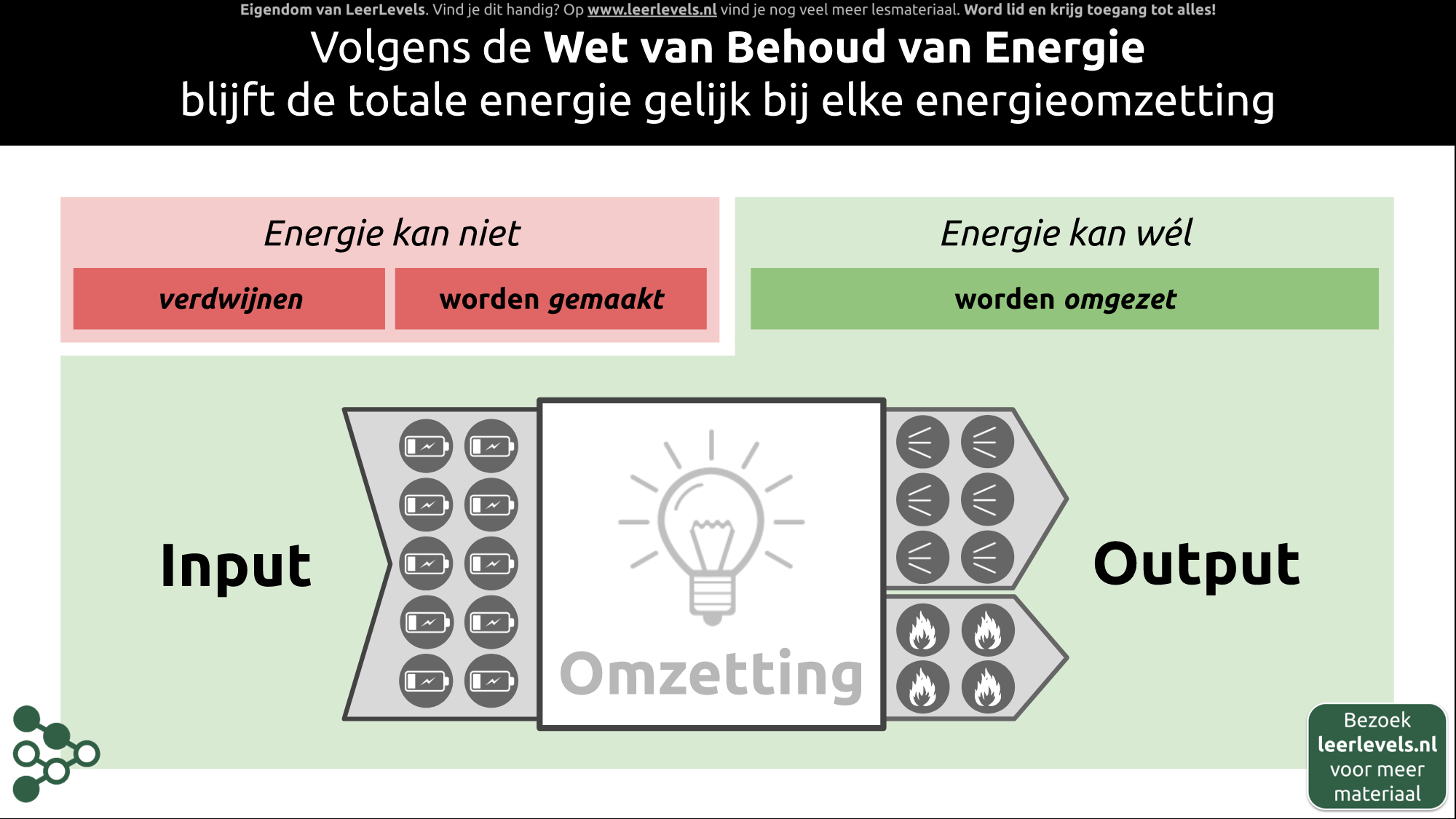
(Afbeelding: Animatie voor Wet van behoud van energie)

Terug naar overzicht Meld je aan

Energieniveaus

Energieniveau's concept

Een atoom heeft energieniveaus, vergelijkbaar met een bal die op verschillende hoogtes in een put kan zijn. Het laagste niveau is de binnenste schil, terwijl hogere niveaus een hogere energie hebben. Het energieniveauschema laat dit zien als een streepdiagram. Een waterstofatoom heeft maximaal één elektron, dat zich op verschillende niveaus kan bevinden. Naarmate de energie toeneemt, zijn er meer niveaus beschikbaar. Wanneer de energie hoger is dan nul, is het elektron vrij en wordt het atoom een ion. Het elektron krijgt energie als het naar boven beweegt, omdat de energieniveaus naar boven toe minder negatief worden.

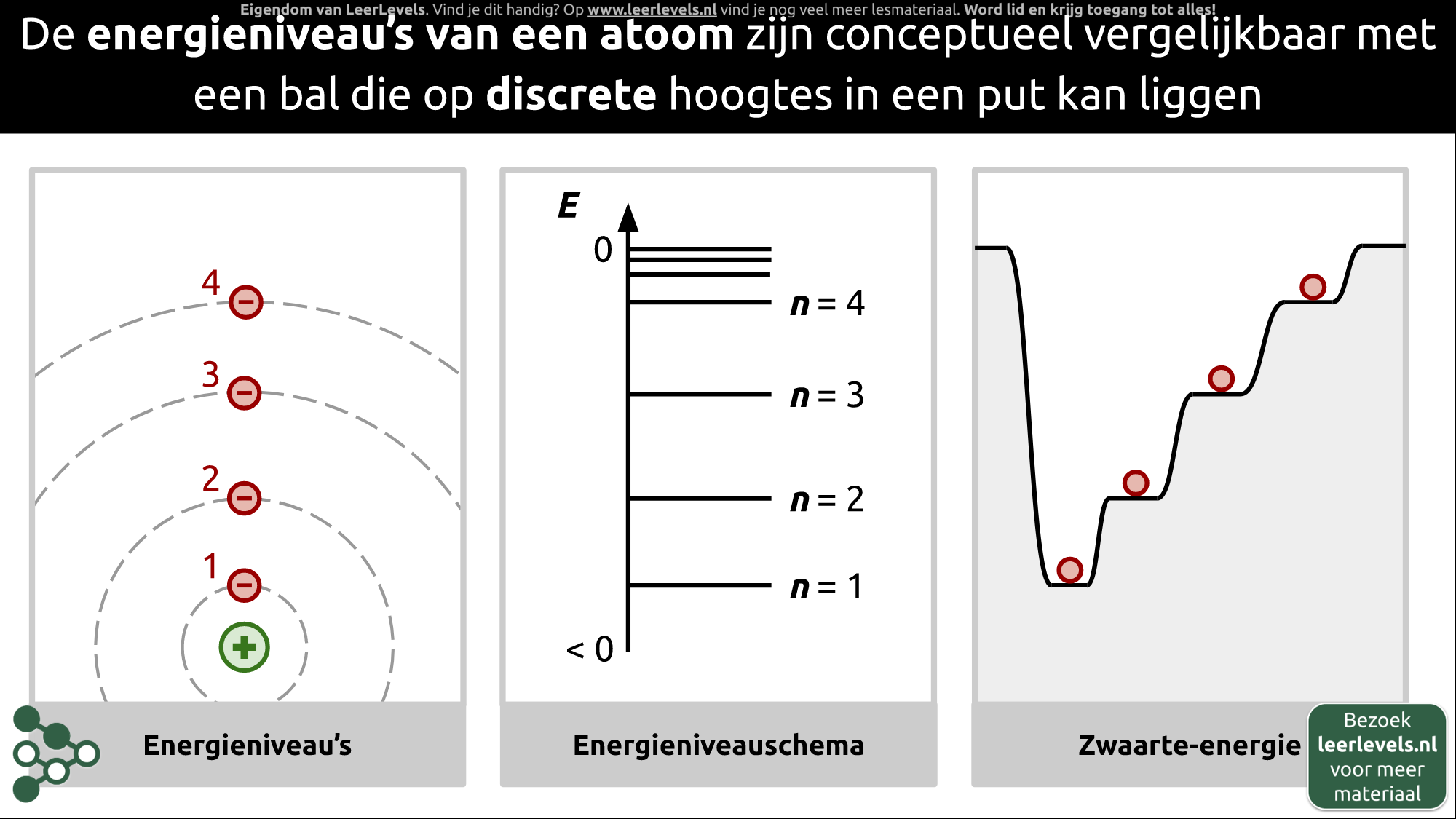
(Afbeelding: Animatie voor Energieniveau's concept)

Energieniveauschema

De energieniveaus van het waterstofatoom zijn nauwkeurig bepaald. Het energieniveauschema ziet er als volgt uit: bij n = 1 hoort een energie van -13,6 eV. Dit wordt de grondtoestand genoemd en is de laagst mogelijke energietoestand waarin het waterstofatoom kan verkeren. De index hiervoor is 1. De tweede toestand is de eerste aangeslagen toestand, met index 2. Dit is de eerste energietoestand boven de grondtoestand. Alle toestanden boven de grondtoestand worden aangeslagen toestanden genoemd. Dit zijn discrete energieniveaus. Net onder de inwendige energie Einw = 0 bevinden zich ontzettend veel mogelijke energieniveaus.

De inwendige energieën van het waterstofatoom zijn negatief gedefinieerd omdat deze het energieverschil weergeven tussen de gebonden toestand van het elektron en de toestand waarin het elektron volledig vrij is van de kern. Dit betekent dat het elektron energie moet opnemen om de binding met de kern te verbreken (ionisatie). De referentie voor Einw = 0 is de situatie waarin het elektron zich op een oneindig grote afstand van de kern bevindt en niet langer gebonden is, oftewel de vrije toestand.

Het negatieve teken geeft dus aan dat het elektron in een gebonden toestand een lagere energie heeft dan wanneer het vrij is. Dit is analoog aan een balletje dat zich in een put bevindt: zolang het in de put zit, heeft het een negatieve potentiële energie ten opzichte van de rand van de put. Pas wanneer het balletje voldoende energie krijgt om boven de rand van de put uit te komen, bereikt het een energie van 0 of hoger, en is het niet langer gebonden.

De ionisatie-energie is de energie die nodig is om het elektron van Einw = -13,6 eV naar Einw = 0 te brengen. Dit proces komt overeen met het losmaken van het elektron van de kern, waarbij het atoom positief geladen wordt en verandert in een ion. Net zoals een balletje dat over de rand van de put wordt getild, is het elektron dan niet langer gebonden aan het atoom.

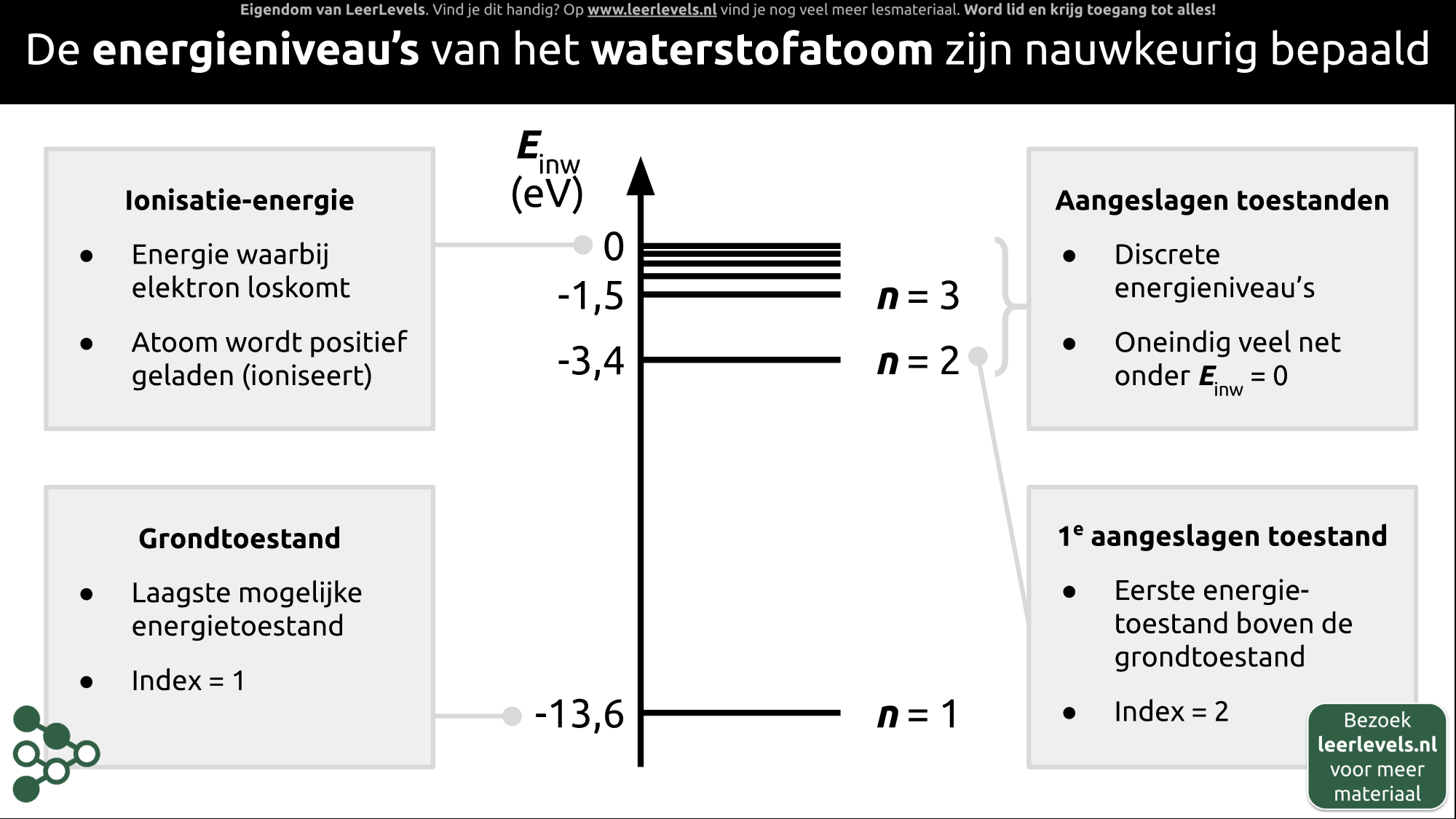
(Afbeelding: Animatie voor Energieniveauschema)

Energieniveaus waterstof formule

De energietoestanden van waterstof zijn omgekeerd kwadratisch evenredig met de index van de toestand. In formulevorm ziet dit er zo uit: En = -(13,6 eV)/(n²), waarbij n de index van de toestand is. De toestand met n = 1 wordt de grondtoestand genoemd. Wanneer deze toestand wordt geëxciteerd (of "aangeslagen"), wordt er energie geabsorbeerd en kan het atoom naar de eerste aangeslagen toestand gaan, waarvoor n = 2 geldt. De energie die vrijkomt bij de terugkeer naar de grondtoestand kan worden waargenomen als uitgezonden licht. Door naar de energietoestand van een aangeslagen toestand te kijken, kun je berekenen hoeveel energie er nodig is om naar een hogere energietoestand te gaan.

(Afbeelding: Animatie voor Energieniveaus waterstof formule)

Terug naar overzicht Meld je aan

Energiestroomdiagram

Een energiestroomdiagram illustreert de energieomzettingen binnen bijvoorbeeld een apparaat. Neem een gloeilamp als voorbeeld. Wanneer je deze aanzet, stroomt er energie in, en er worden licht en warmte uitgestraald. Zo'n diagram heeft drie kenmerken:

1. Het toont welke vormen van energie veranderen, vaak aangeduid met icoontjes of woorden.
2. De dikte van een pijl geeft aan hoeveel energie erbij betrokken is. Bij een gloeilamp komt er bijvoorbeeld veel warmte vrij en weinig licht.
3. De energie die het systeem binnengaat, moet gelijk zijn aan de energie die het systeem verlaat, volgens de wet van behoud van energie.

Een ander voorbeeld is een led-lamp, waarbij er meer licht en minder warmte vrijkomt. Of denk aan een sporter die chemische energie omzet in beweging en warmte.

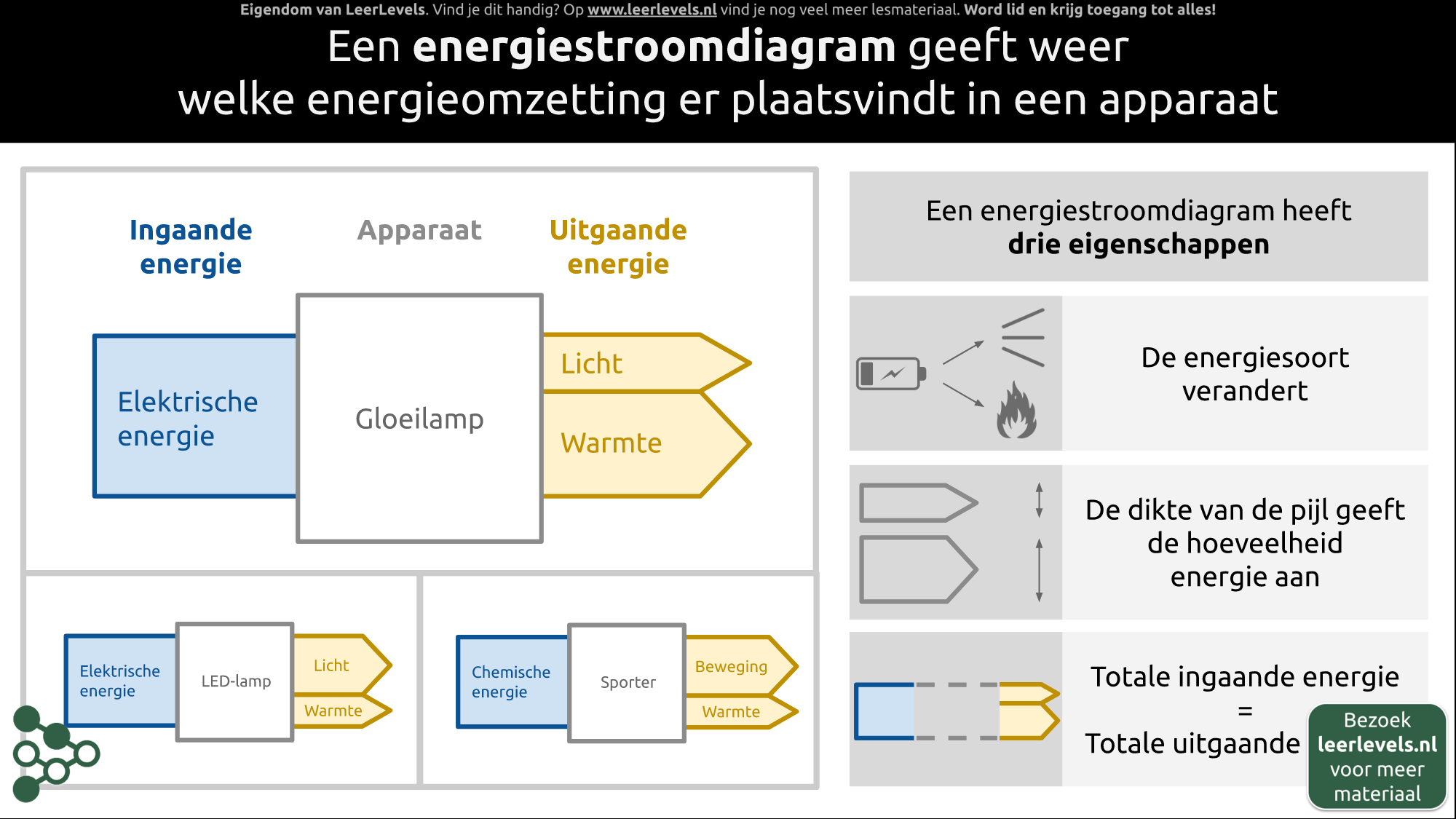
(Afbeelding: Animatie voor Energiestroomdiagram)

Terug naar overzicht Meld je aan

Equivalente dosis

Equivalente dosis concept

De equivalente dosis, weergegeven als H, corrigeert de geabsorbeerde dosis voor de biologische effecten van ioniserende straling. Bijvoorbeeld, bij blootstelling aan gammastraling is de schade beperkt, omdat gammastraling een beperkte impact op ons lichaam heeft.

Wanneer dezelfde hoeveelheid energie echter wordt overgedragen via alfastraling, wat grote heliumkernen met een hoge lading betreft, is de situatie anders. Alfastraling kan ons lichaam van binnenuit beschadigen en heeft daarom een veel nadeliger effect.

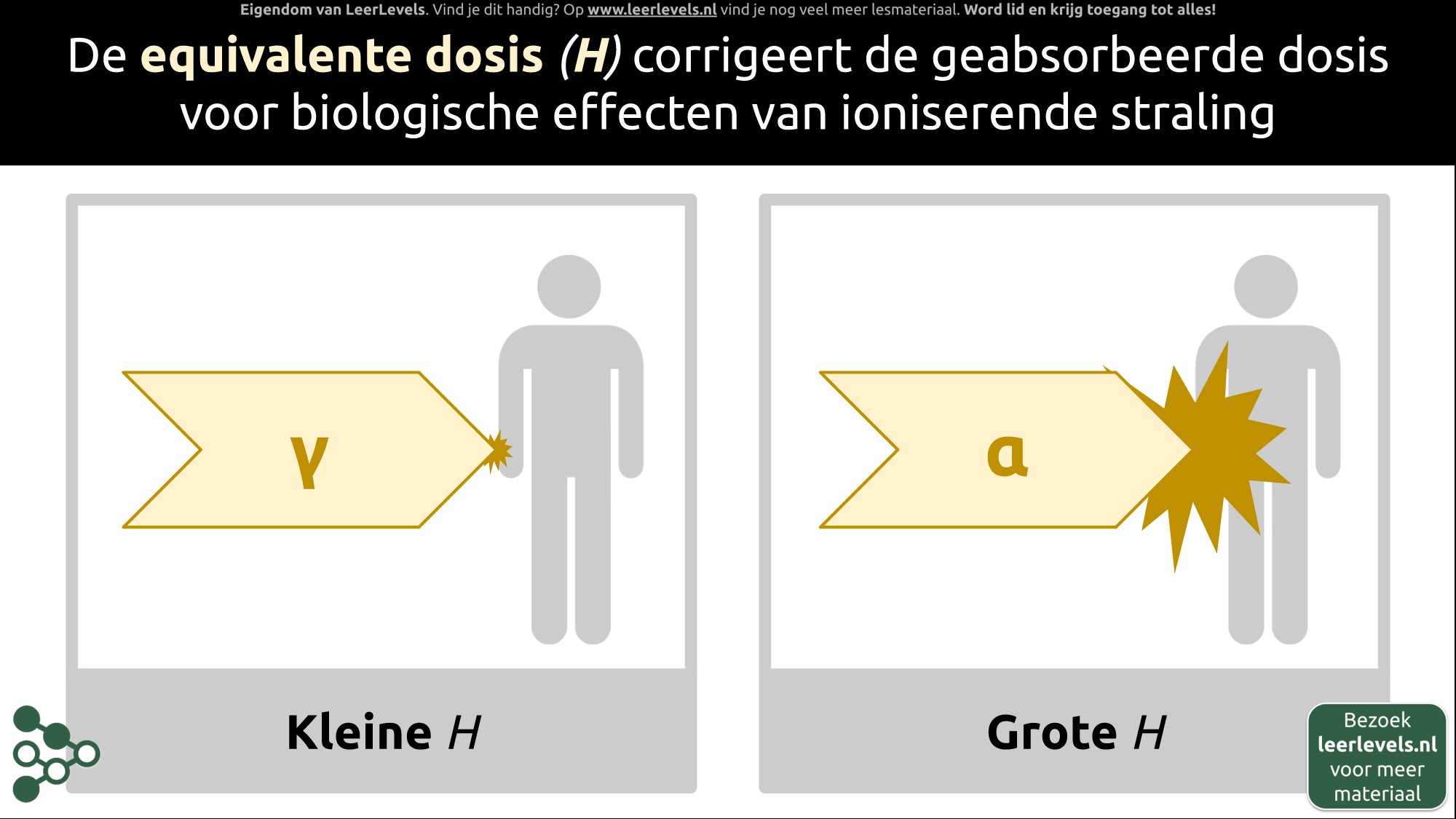
(Afbeelding: Animatie voor Equivalente dosis concept)

Equivalente dosis formule

De equivalente dosis (H) kun je berekenen door de geabsorbeerde dosis te vermenigvuldigen met een weegfactor. H wordt uitgedrukt in Sievert (Sv). D is de geabsorbeerde dosis in Gray (Gy). De weegfactor (w) kun je vinden in een boekje als BiNaS. Het kan verwarrend zijn dat H en D dezelfde eenheid hebben, dus let daarop. De waarde van de weegfactor hangt af van het type straling dat je gebruikt. Bij alfastraling is w 20, bij beta en gamma is het 1. Bij protonen ligt het rond de 10 en bij neutronen tussen de 3 en 20, afhankelijk van de locatie.

(Afbeelding: Animatie voor Equivalente dosis formule)

Terug naar overzicht Meld je aan

Evenredigheid

Evenredigheid concept

De evenredigheid tussen twee grootheden is een kwantitatieve beschrijving van een kwalitatief verband. Een kwalitatief verband is bijvoorbeeld: "Als A groter wordt, dan wordt B ook groter" of "Als A groter wordt, dan wordt B kleiner". Bij kwalitatieve verbanden geven we alleen aan of een grootheid groter of kleiner wordt, maar niet hoeveel groter of kleiner.

Bij evenredigheden daarentegen gaat het om kwantitatieve verbanden. Een voorbeeld van een kwantitatief verband is: "Als A twee keer zo groot wordt, dan wordt B twee keer zo groot". De evenredigheid die hierbij hoort, is recht evenredig.

Een ander voorbeeld is: "Als A twee keer zo groot wordt, dan wordt B vier keer zo groot". De evenredigheid die hierbij hoort, is een kwadratisch verband. We zeggen dat B kwadratisch evenredig is met A.

Een derde voorbeeld van een kwantitatief verband is: "Als A vier keer zo groot wordt, dan wordt B twee keer zo groot". Dit is een voorbeeld van een wortel-evenredigheid.

Voor recht evenredigheid, wortel-evenredigheid en kwadratische evenredigheid geldt dat als een grootheid groter wordt, een andere grootheid ook groter wordt.

Er zijn ook kwantitatieve verbanden die horen bij het kwalitatieve verband "Als A groter wordt, dan wordt B kleiner". Een voorbeeld hiervan is het verband: "Als A twee keer zo groot wordt, dan wordt B twee keer zo klein". Dit is een voorbeeld van omgekeerd evenredigheid.

Een ander voorbeeld is het verband: "Als A twee keer zo groot wordt, dan wordt B vier keer zo klein". Dit is een voorbeeld van omgekeerd kwadratisch evenredigheid.

Het herkennen van deze evenredigheden is belangrijk om het verband tussen twee of meer grootheden te kunnen voorspellen.

(Afbeelding: Animatie voor Evenredigheid concept)

Recht evenredig

Bij een recht evenredig verband leidt het verdubbelen van een grootheid tot het verdubbelen van een andere grootheid. De formule die dit beschrijft, is

y = ax

waarbij x de ene grootheid is en y de andere grootheid.

Een voorbeeld van zo'n verhouding is die tussen massa, dichtheid en volume. Wanneer het volume toeneemt, neemt ook de massa toe, afhankelijk van de constante dichtheid. Dit wordt weerspiegeld in de grafische weergave van deze verhouding, waarbij een rechte lijn kenmerkend is voor een recht evenredig verband. Als je de massa en het volume van een bepaalde stof meet en deze waarden in een grafiek weergeeft, zouden ze op een rechte lijn moeten liggen. Soms wijken de punten iets af van de lijn door meetfouten.

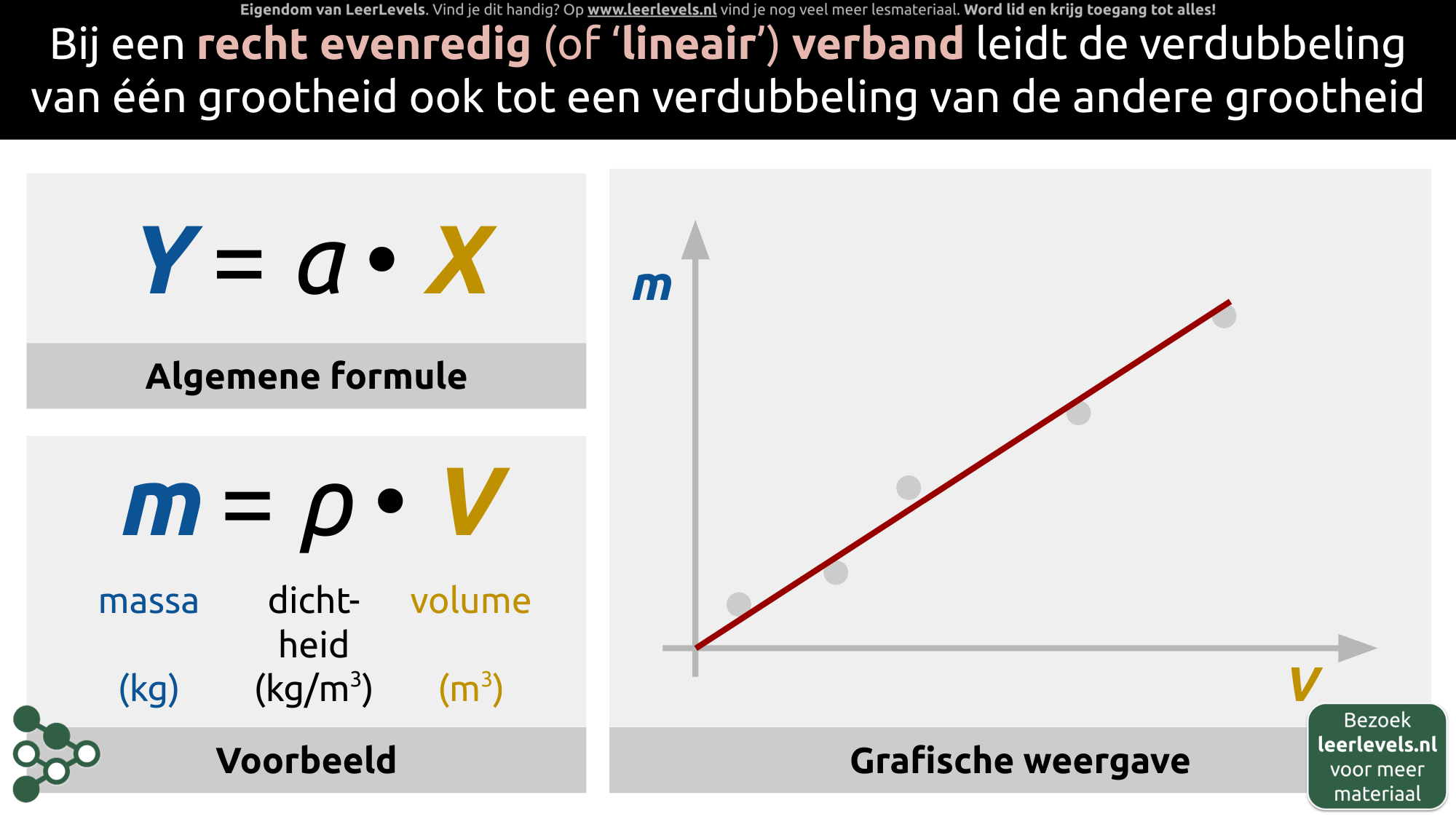
(Afbeelding: Animatie voor Recht evenredig)

Kwadratisch evenredig

Bij een kwadratisch evenredig verband zorgt verdubbeling van een grootheid voor een verviervoudiging van de andere grootheid. De formule hiervoor is y = ax². Als x twee keer zo groot wordt, wordt y 4 keer zo groot. Bijvoorbeeld bij de oppervlakte van een cirkel, waarbij de oppervlakte gelijk is aan π r². We kunnen dit weergeven in een grafiek door de straal op de x-as en de oppervlakte op de y-as te zetten. Dit geeft een kwadratische functie.

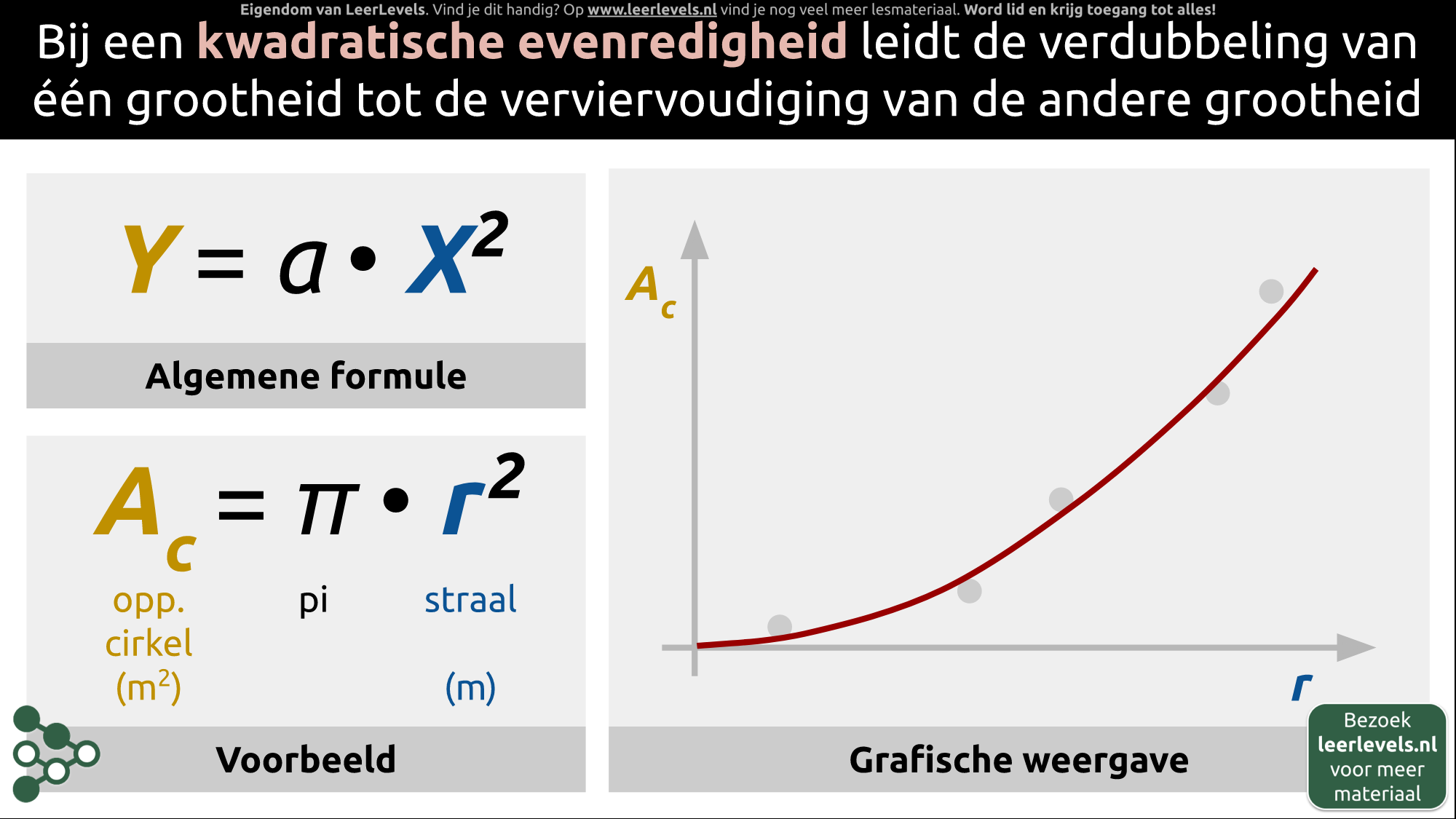
(Afbeelding: Animatie voor Kwadratisch evenredig)

Omgekeerd evenredig

Bij omgekeerde evenredigheid halveert de ene grootheid als de andere grootheid verdubbelt. De formule hiervoor is y = a · 1/x , waarbij a een constante factor is die het verband tussen y en x bepaalt. Een voorbeeld van omgekeerde evenredigheid is gravitatie-energie, die afneemt als de afstand tussen twee objecten groter wordt. De formule hiervoor is EG = c · 1/r , waarbij EG de gravitatie-energie is in Joule en r de afstand tussen de objecten in meters is. Dit kun je grafisch weergeven door de afstand op de x-as en de gravitatie-energie op de y-as te zetten. Als de afstand toeneemt, neemt de gravitatie-energie af.

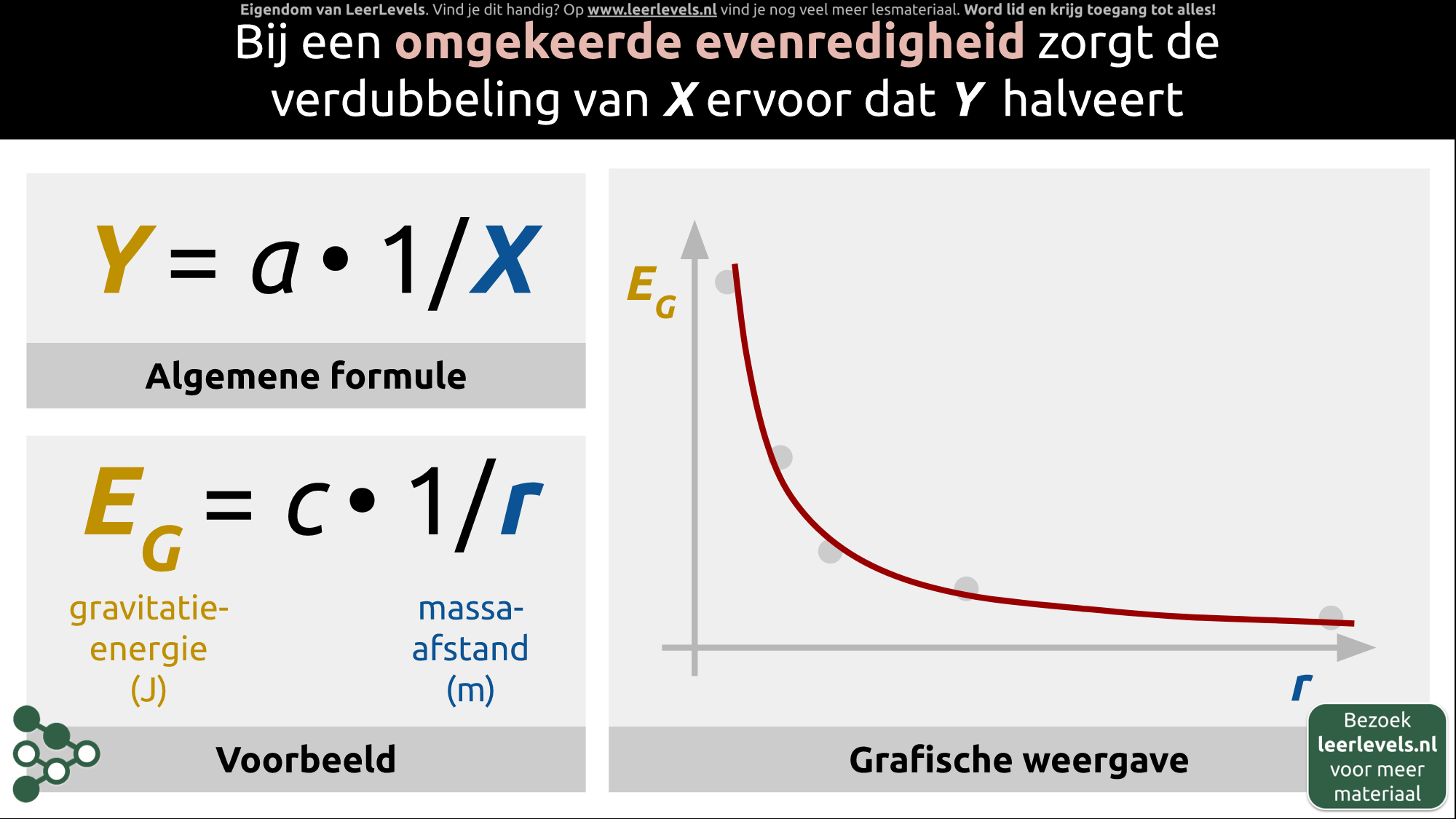
(Afbeelding: Animatie voor Omgekeerd evenredig)

Omgekeerd kwadratisch evenredig

Een omgekeerd kwadratisch verband betekent dat als een grootheid verdubbelt, de andere grootheid vier keer kleiner wordt. Dit kan worden uitgedrukt via de formule y = a · (1)/(x²). Een voorbeeld hiervan is de elektrische kracht tussen twee deeltjes, waarvoor de formule Fel = c · (1)/(r² geldt. De afstand wordt hierbij in meters gemeten en de kracht in Newton. De grafiek van een omgekeerd kwadratisch verband lijkt op die van een omgekeerd verband, maar gaat nog sneller naar beneden naarmate de afstand groter wordt.

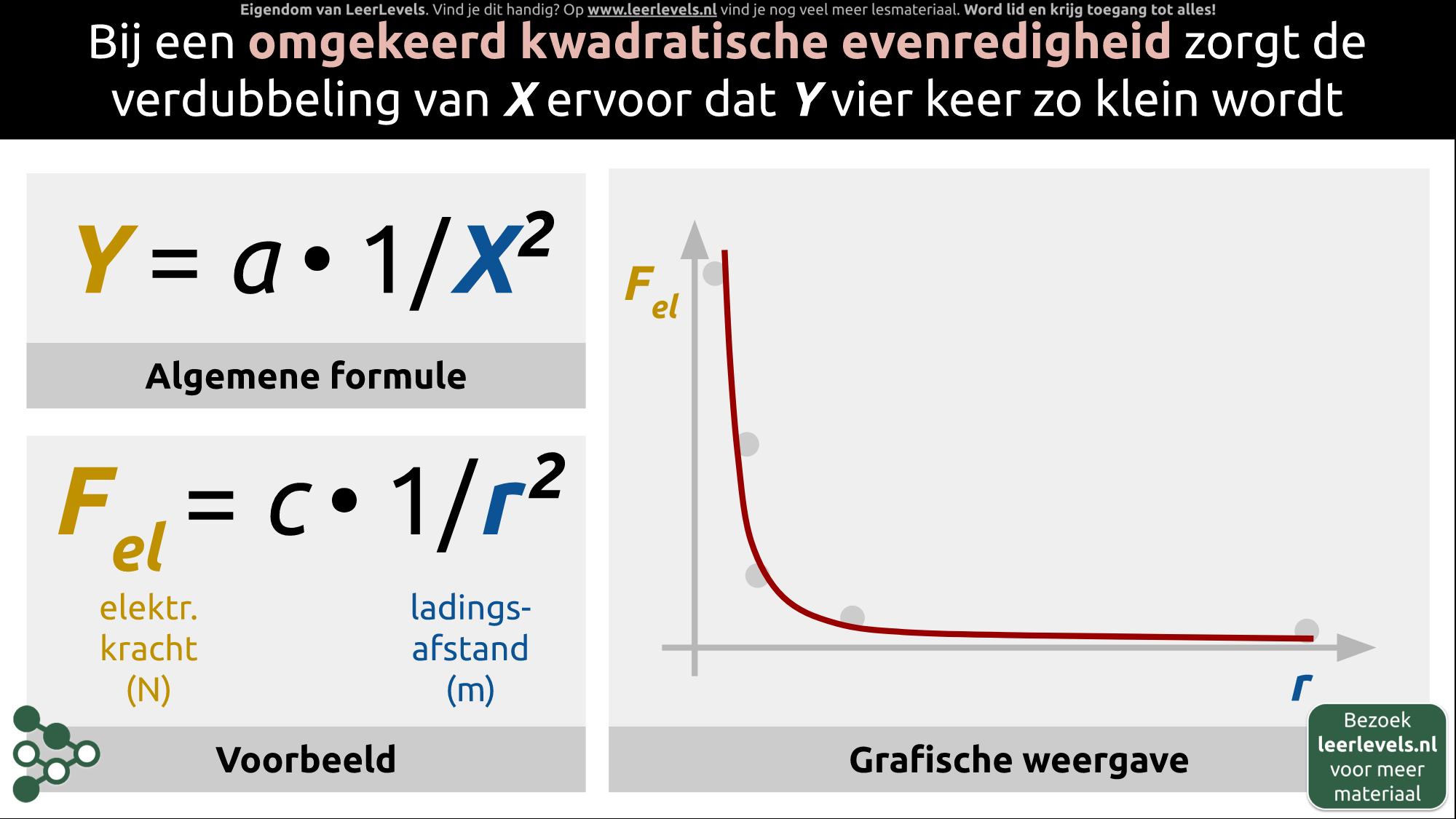
(Afbeelding: Animatie voor Omgekeerd kwadratisch evenredig)

Terug naar overzicht Meld je aan

Evenwicht

Een voorwerp is in evenwicht wanneer het zwaartepunt boven het steunvlak ligt. Dit betekent dat als je bijvoorbeeld op een stoel zit, je zwaartepunt zich ongeveer ter hoogte van je navel bevindt en het steunvlak het gebied tussen de vier poten van de stoel is. Als je rechtop zit, ligt je zwaartepunt boven het steunvlak en is er evenwicht. Als je achterover leunt, wordt het steunvlak kleiner en kan het evenwicht verstoord raken. Dit geldt ook voor andere voorwerpen, zoals een fles. Zolang het zwaartepunt boven het steunvlak ligt, is er evenwicht. Maar als het zwaartepunt verplaatst, kan het evenwicht verstoord raken en kan het voorwerp vallen. Het verplaatsen van het zwaartepunt ten opzichte van het steunvlak kan het evenwicht verstoren.

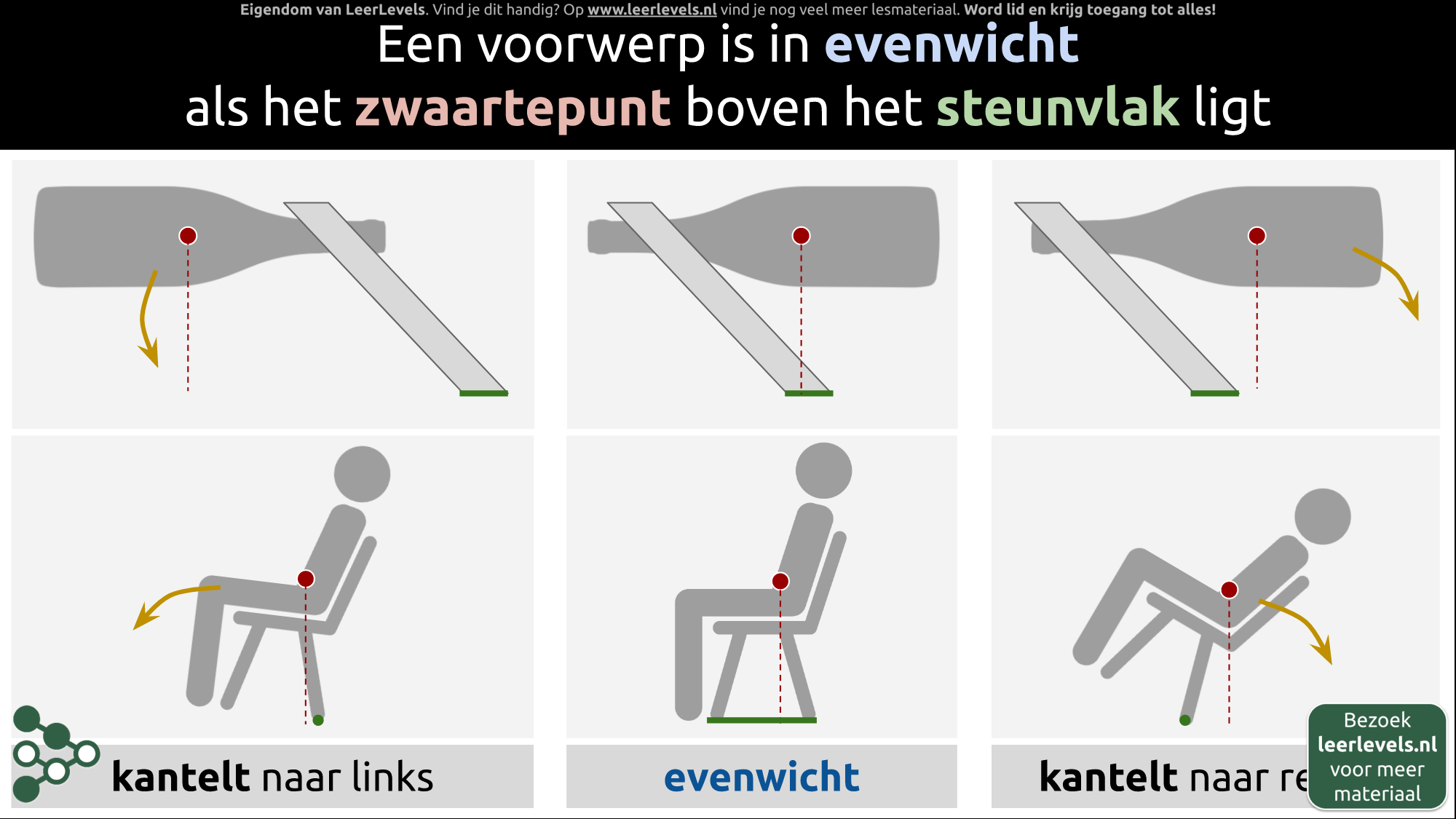
(Afbeelding: Animatie voor Evenwicht)

Terug naar overzicht Meld je aan

Examen

Examenwerkwoorden

Bij een examen natuurkunde staan er veel verschillende werkwoorden in de vragen. Elke werkwoord vraagt om een andere manier van uitwerken. Zo zijn er werkwoorden als 'toon aan of' waarbij je iets moet bewijzen en werkwoorden als 'bereken' waarbij je een som moet maken. Bij elk werkwoord horen verschillende acties die je kan doen, zoals het opschrijven van een formule of het uitleggen van je denkstappen. Elk werkwoord heeft een andere combinatie van acties. Bij sommige werkwoorden, zoals 'toon aan dat', krijg je de conclusie al aangeboden en hoef jij deze alleen maar te gebruiken. Bij 'noem' hoef je alleen maar de conclusie te noemen zonder extra uitleg.

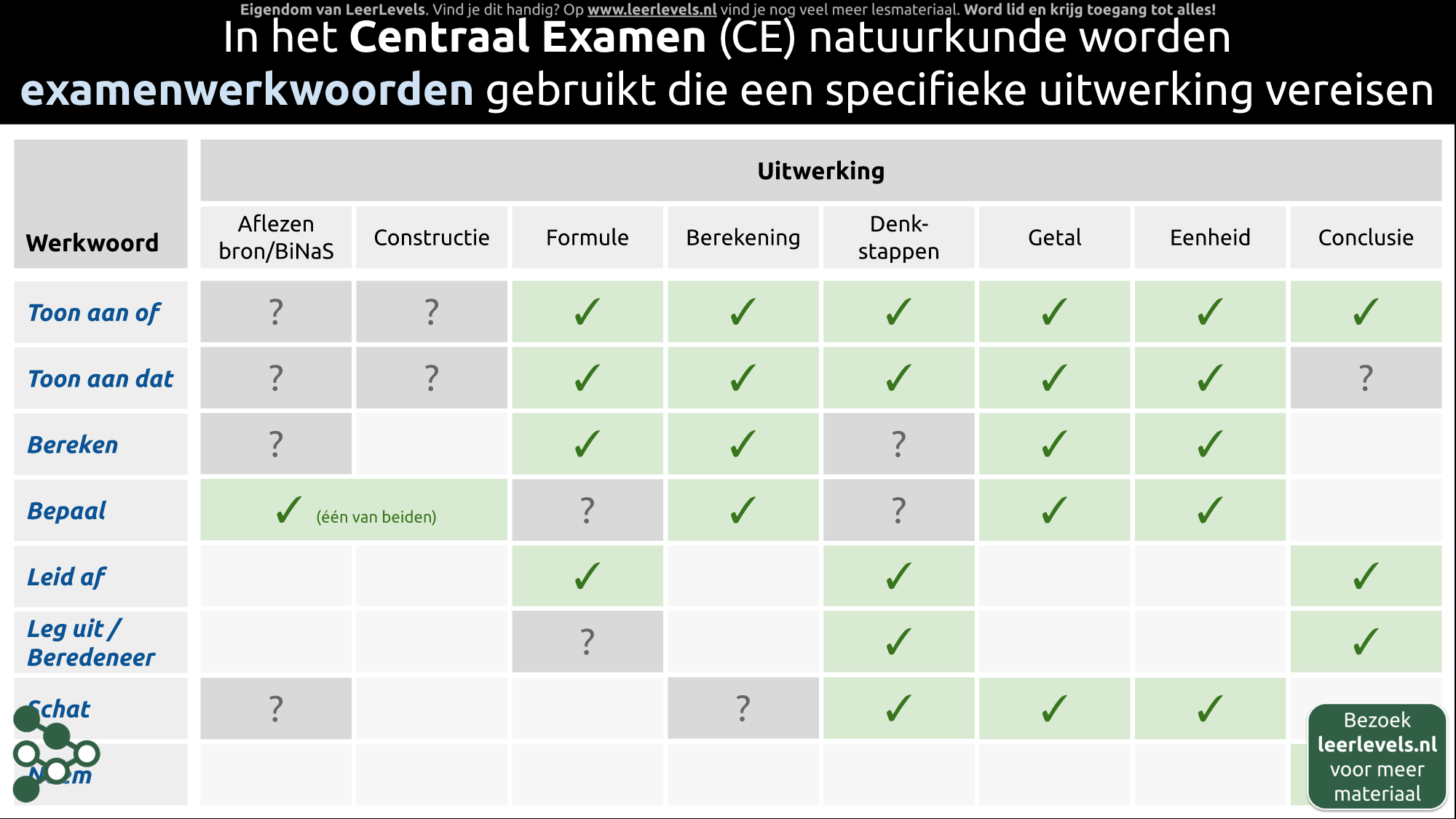
(Afbeelding: Animatie voor Examenwerkwoorden)

Terug naar overzicht Meld je aan

FIRE-methode

Met de FIRE-methode kun je in vier simpele stappen een berekening maken. De vier letters van de FIRE-methode staan voor de vier stappen: "F" staat voor Formule, "I" voor Invullen, "R" voor Rekenen en "E" voor Eenheden.

Om het makkelijker te maken, zullen we de stappen uitleggen aan de hand van een voorbeeldopdracht. We willen het volume van een gouden kroon berekenen, waarbij de dichtheid van goud 19,3 kg/L is en de kroon een massa heeft van 2,5 kg.

Stap 1 is Formule. Hier schrijven we de formule op die we nodig hebben voor de berekening. In dit geval is dat rho = m / V. Dit betekent dat de dichtheid (rho) gelijk is aan de massa (m) gedeeld door het volume (V).

Stap 2 is Invullen. Hier vullen we de bekende gegevens in de formule in. We weten dat de dichtheid 19,3 kg/L is en de massa 2,5 kg. Dus rho = 19,3 en m = 2,5.

Stap 3 is Rekenen. Nu we de formule hebben ingevuld, kunnen we het volume berekenen door de formule om te vormen tot V = m / rho. In dit geval is V = 2,5 / 19,3 = 0,13.

Stap 4 is Eenheden. We moeten nog controleren of de eenheden van onze berekening kloppen. In dit geval hebben we de eenheden kg/L en kg gebruikt. Het antwoord moet in liters (L) zijn, dus het volume is 0,13 L.

Door deze vier simpele stappen te volgen, kun je gemakkelijk een berekening maken.

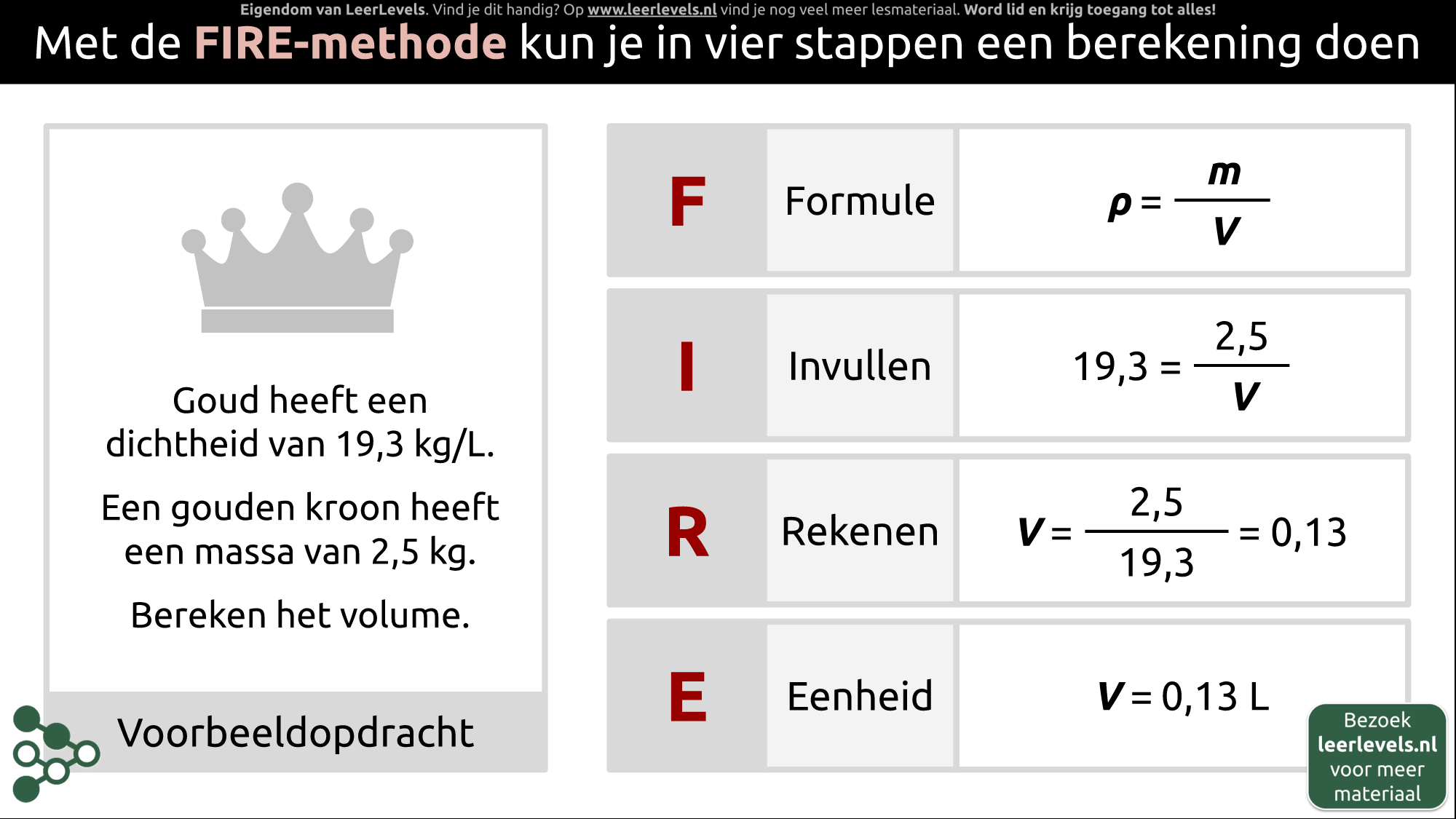
(Afbeelding: Animatie voor FIRE-methode)

Terug naar overzicht Meld je aan

Fase

Fase concept

De fase is een manier om te berekenen hoeveel keren iets heen en weer beweegt. Stel je voor dat je naar iemand op een schommel kijkt. Als de persoon stil staat, heeft hij nog geen enkele beweging gemaakt en is zijn fase 0. Na een seconde beweegt hij al een stukje, dus is zijn fase ¼. Na twee seconden is hij op het hoogste punt aan de rechterkant, dus is zijn fase ½. Na drie seconden gaat hij terug naar links en is zijn fase 0,75. Na vier seconden heeft hij één volledige beweging gemaakt, dus is zijn fase 1. Na vijf seconden is zijn fase 1,25 omdat hij alweer een stukje terug is bewogen. Dus, de fase vertelt ons hoeveel bewegingen er al zijn gemaakt. De notatie is fase = a/b , waarbij a de afgelegde afstand is en b de maximale afstand die afgelegd kan worden in een volledige beweging.

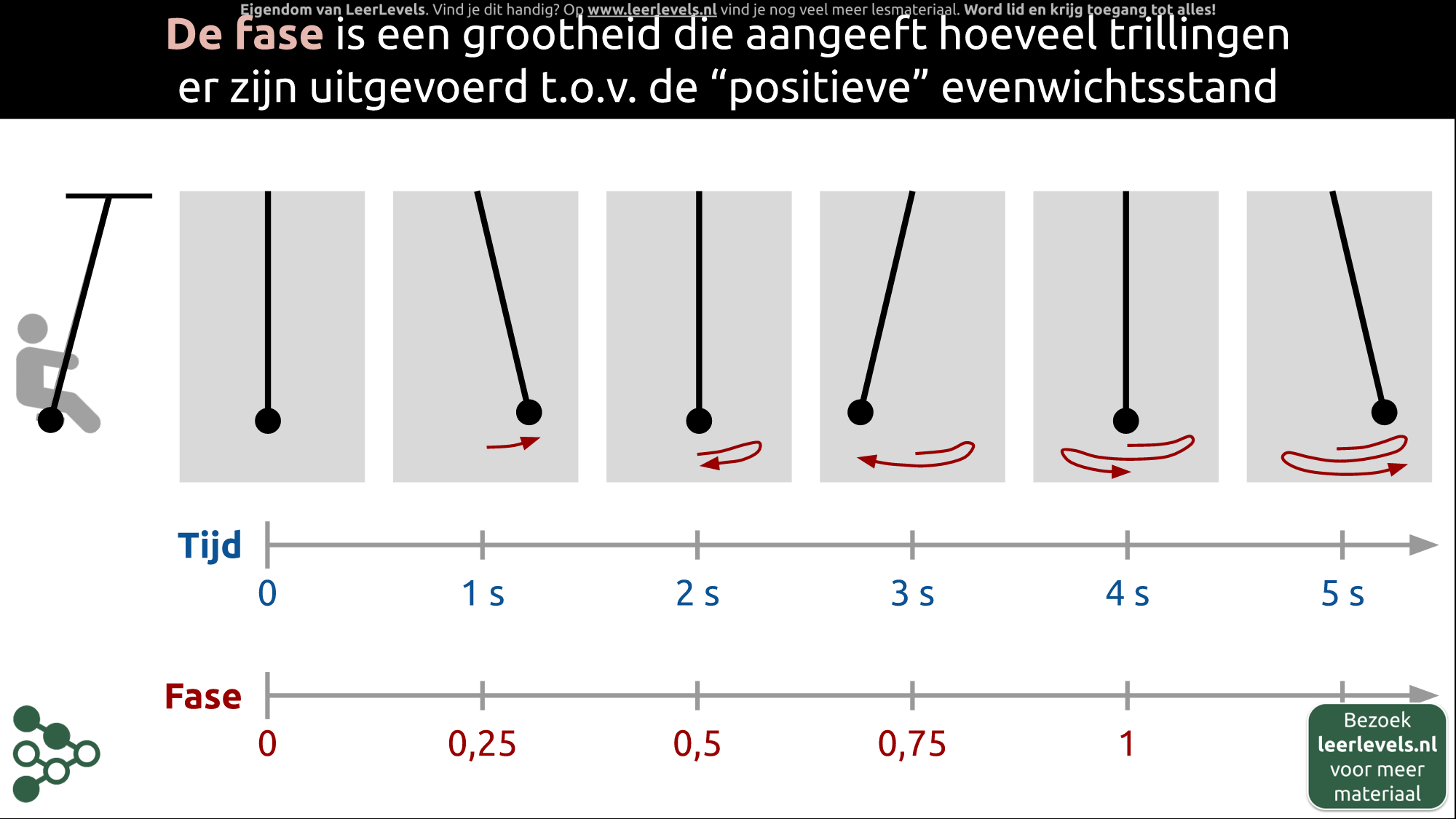
(Afbeelding: Animatie voor Fase concept)

Fase formule

Je kunt de fase berekenen door de verhouding van de verstreken tijd tot de trillingstijd te bepalen. Dit doe je door de verstreken tijd (t) te delen door de trillingstijd (T). Beide tijden zijn uitgedrukt in seconden, waardoor de fase (φ) een dimensieloos getal is:

φ = t/T

De fase vertegenwoordigt het aantal volledige trillingen dat is voltooid. Het geeft aan hoe vaak de verstreken tijd in de trillingstijd past.

(Afbeelding: Animatie voor Fase formule)

Gereduceerde fase

Als iets trilt, beweegt het heen en weer. De fase is een manier om te kijken hoe ver iets al is bewogen. Als iets bijvoorbeeld drie keer heen en weer is gegaan, dan zeggen we dat de fase drie is. Maar als we naar de "gereduceerde fase" kijken, tellen we alleen trillingen mee die nog niet helemaal zijn afgerond. Dus als iets bijvoorbeeld vier keer heen en weer gaat en dan nog een beetje verder gaat, dan zou de fase vijf zijn, maar de gereduceerde fase is dan weer nul. Dit komt doordat de situatie op dat moment heel erg lijkt op het begin. Als we dit in formules zouden schrijven, zou je kunnen zeggen dat de gereduceerde fase (φr) gelijk is aan de fase (φ) min het aantal volledig uitgevoerde trillingen.

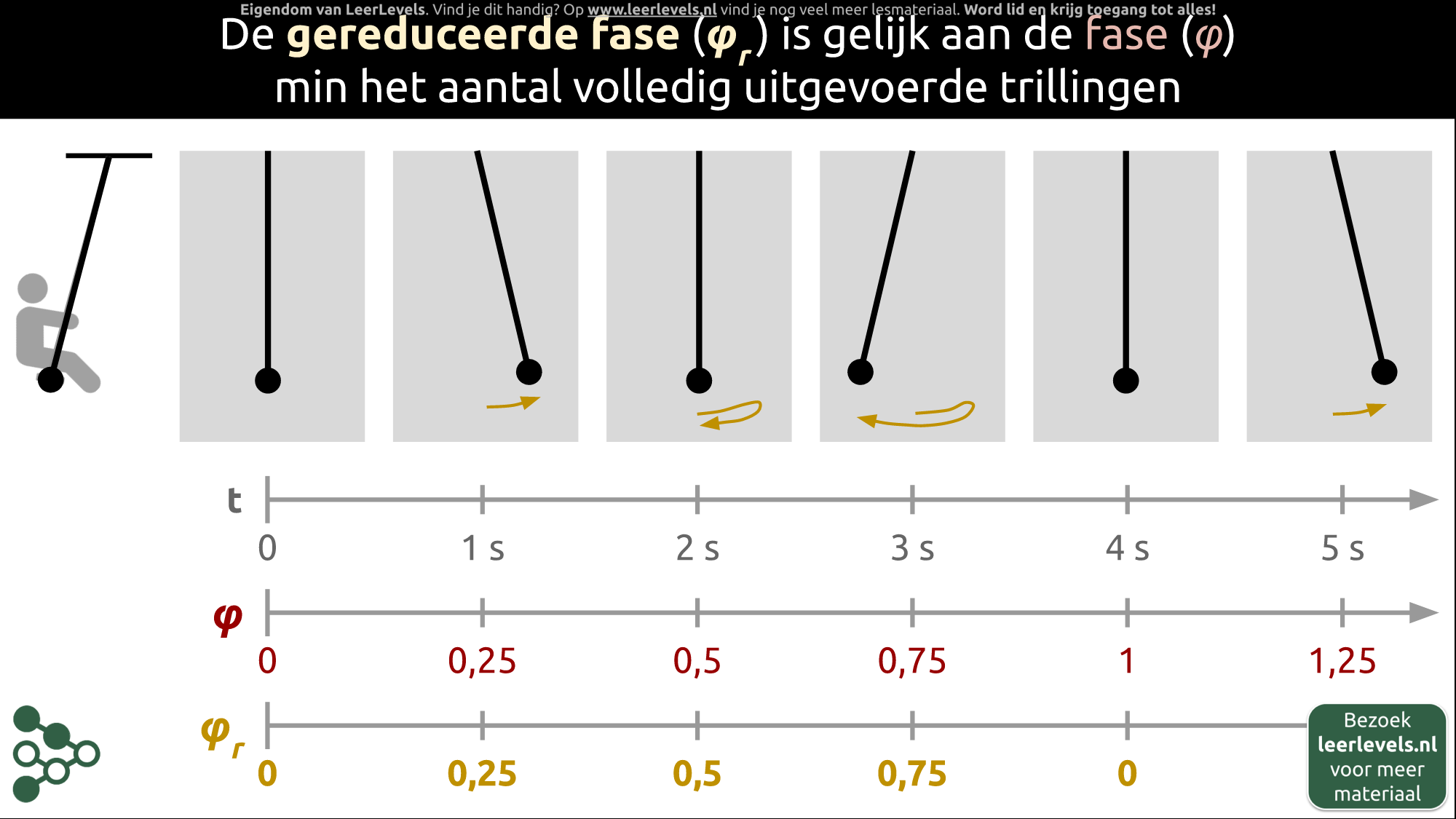
(Afbeelding: Animatie voor Gereduceerde fase)

Terug naar overzicht Meld je aan

Fase-overgang

Fase-overgangen

Bij een faseovergang van vast naar vloeibaar of van vloeibaar naar gas kan er sprake zijn van endotherme of exotherme reacties. Een endotherme reactie kost energie, zoals bij het smelten van een vast materiaal naar vloeistof. Hierbij hebben de moleculen extra energie nodig om te kunnen bewegen. Bij de overgang van vloeistof naar gas is er nog meer energie nodig. Dit noemen we ook wel een endotherme reactie. De andere kant op, van gas naar vloeistof, wordt condenseren genoemd. Bij deze overgang komt juist energie vrij. Bij stollen komt ook energie vrij. Naast deze overgangen zijn er nog twee andere reacties mogelijk: sublimeren (van vast naar gas) en rijpen (van gas naar vast). Bij sublimeren kost het veel energie en bij rijpen komt er juist veel energie vrij.

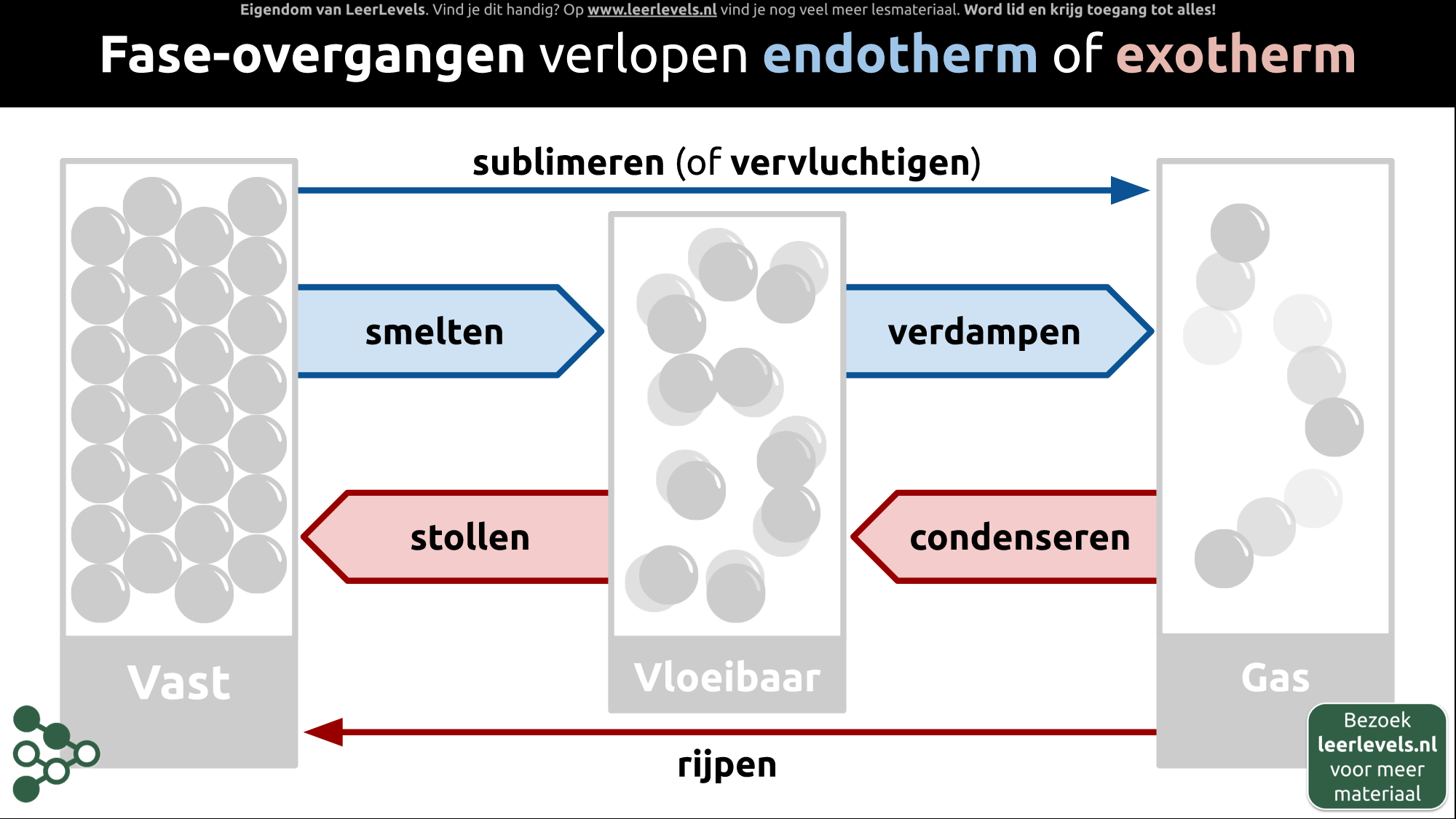
(Afbeelding: Animatie voor Fase-overgangen)

Temperatuur tijdens fase-overgang

Tijdens een fase-overgang blijft de temperatuur constant. De warmte die tijdens een fase-overgang wordt toegevoegd of onttrokken aan een materiaal, heeft alleen invloed op de fase; niet op de temperatuur. Als we bijvoorbeeld ijs van – 10 graden Celsius verwarmen, zal de temperatuur stijgen. Als het ijs 0 graden Celsius is geworden, begint de fase-overgang van vast naar vloeibaar. Tijdens deze overgang blijft de temperatuur 0 graden Celsius. Aan het begin heb je ijs van 0 graden Celsius en aan het eind van de fase-overgang heb je water van 0 graden Celsius. Pas als al het ijs water is geworden, zal nieuw toegevoegde warmte ervoor zorgen dat de temperatuur stijgt.

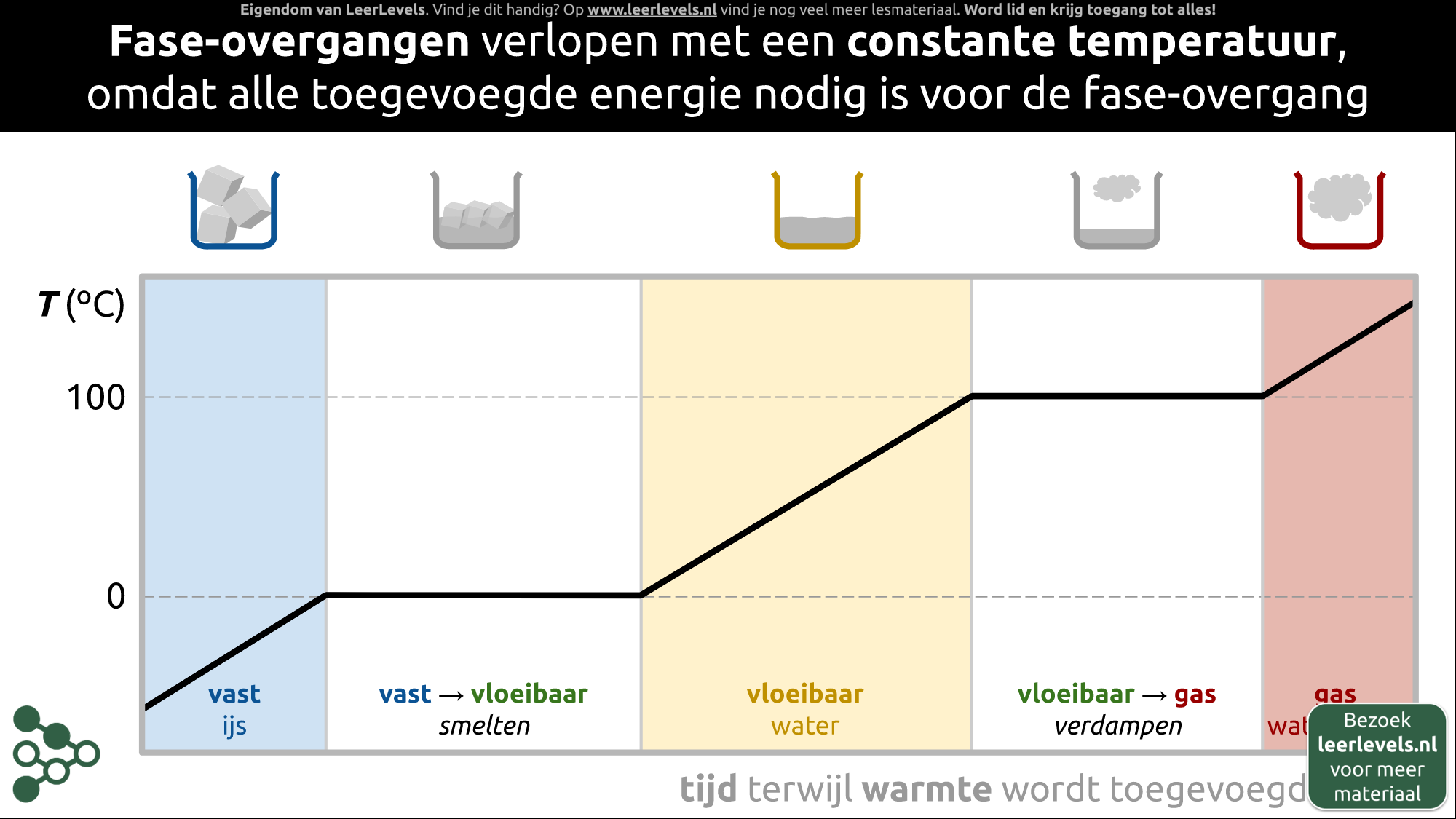
(Afbeelding: Animatie voor Temperatuur tijdens fase-overgang)

Terug naar overzicht Meld je aan

Faseverschil

Faseverschil concept

Het faseverschil Δ ψ is het aantal golflengtes tussen twee punten op een golf. Stel je voor dat je naar iemand kijkt die met een touw aan een boom vastzit en een golfpatroon maakt door te schudden met het touw. Als je kijkt naar twee punten op deze golf die dicht bij elkaar liggen, is het faseverschil tussen deze punten klein, omdat er maar weinig golven tussen deze punten liggen. Als er meer golven tussen deze punten zijn, is er juist een groot faseverschil tussen deze punten. De afstand tussen twee pieken opeenvolgende in een golf is precies één golflengte. Daar hoort een faseverschil van één bij. Als je kijkt naar de afstand tussen een piek en een dal van de golf, zit daar altijd een halve golflengte tussen en dus een faseverschil van een half.

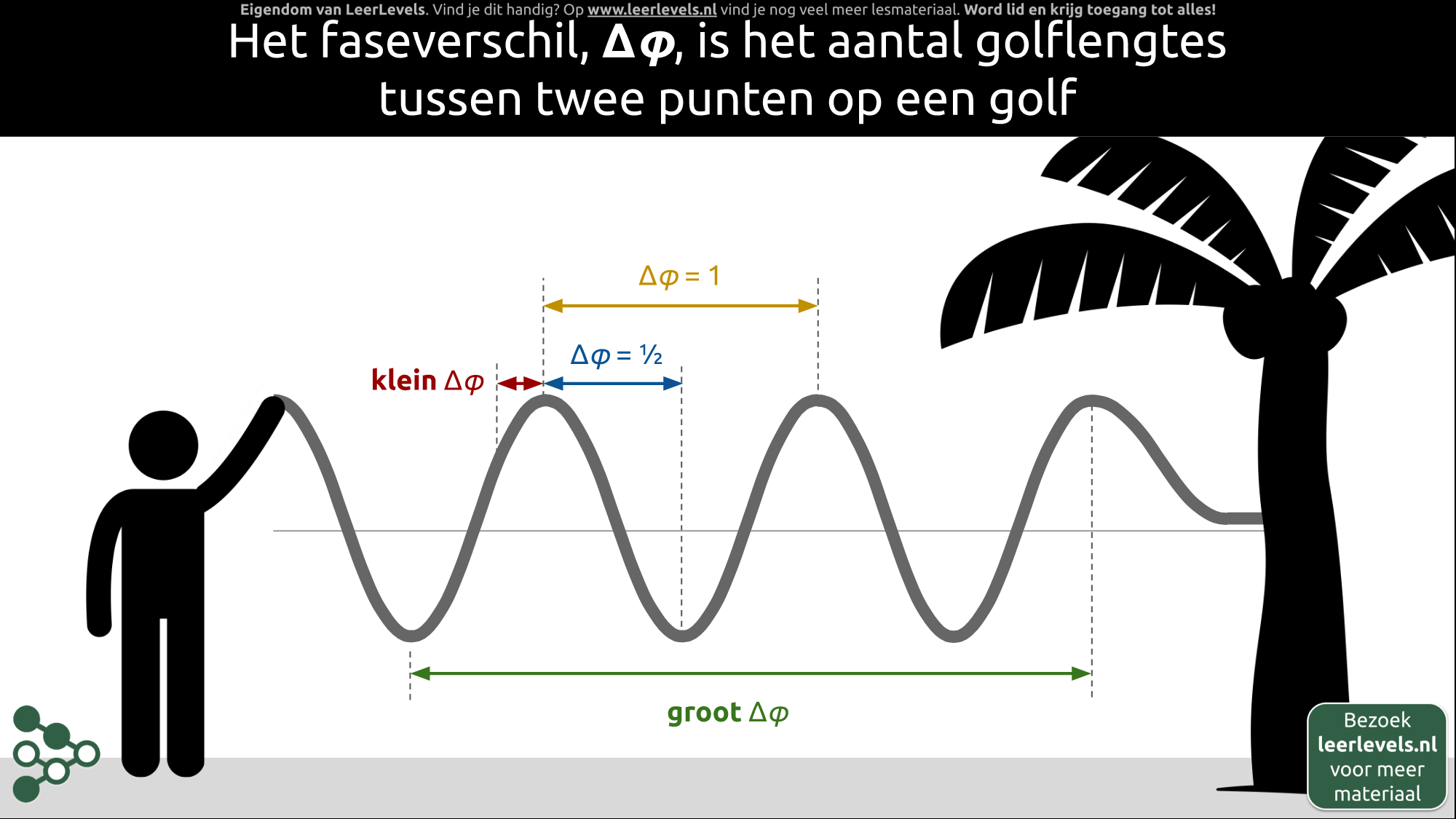
(Afbeelding: Animatie voor Faseverschil concept)

Faseverschil formule

Het faseverschil tussen twee punten op een golf is recht evenredig met de afstand tussen die punten en omgekeerd evenredig met de golflengte. Dit wordt weergegeven met de formule:

Δ φ = (Δ x)/(λ)

waarbij Δ x de afstand tussen de twee punten in meters is, en λ de golflengte in meters. Dit laat zien dat Δ φ, het faseverschil, eenheidsloos is, omdat de eenheden meters in de teller en de noemer wegvallen.

(Afbeelding: Animatie voor Faseverschil formule)

Terug naar overzicht Meld je aan

Fermi-vragen

Bij Fermi-vragen moet je schatten om het bereik van het antwoord te bepalen. Bijvoorbeeld, hoeveel HAVO-eindexamens natuurkunde zijn er elk jaar? Je kunt niet zomaar een antwoord schatten, want dat kan heel erg afwijken. Daarom moet je meerdere tussen-schattingen maken. Bijvoorbeeld, ongeveer 5% van de 17 miljoen mensen in Nederland zit op school, en daarvan doet zo'n 20% een HAVO-examen. HAVO duurt vijf jaar, dus in een bepaald jaar doet zo'n 20% een HAVO-examen. Hoeveel daarvan doet natuurkunde? Dat is lastig te schatten, misschien wel 35%, misschien wel 20% of 50%. Als je deze waardes met elkaar vermenigvuldigt, kom je uit op het antwoord. In dit geval is dat ongeveer 12,000. Maar omdat er bij alle schattingen foutmarges zijn, kan het antwoord variëren tussen de 3,6 duizend en 46 duizend. Je kunt deze fouten compenseren zodat je toch een redelijke schatting kunt maken. Zo kun je bij Fermi-vragen meerdere schattingen maken om het bereik van het antwoord te bepalen.

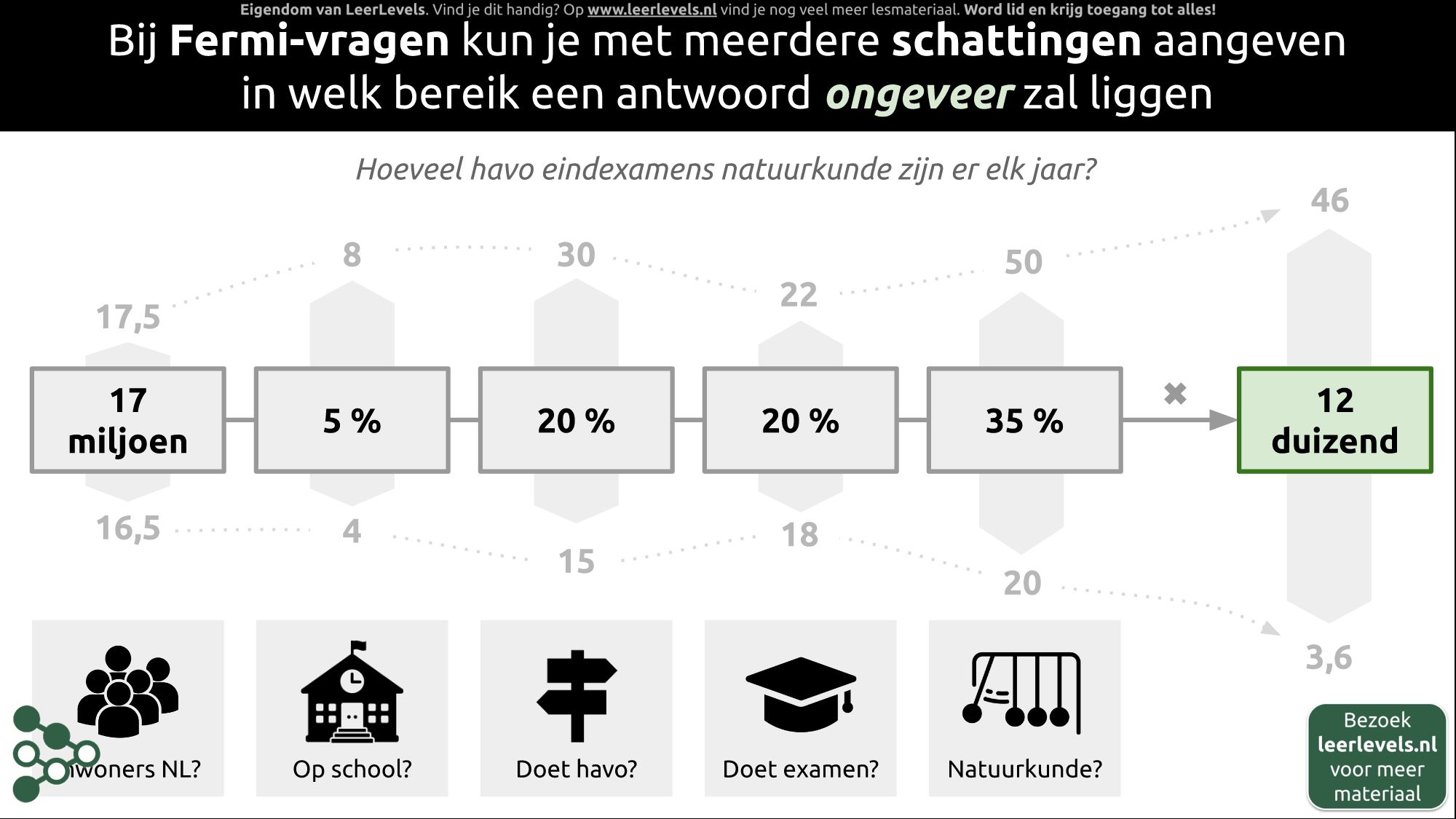
(Afbeelding: Animatie voor Fermi-vragen)

Terug naar overzicht Meld je aan

Fluoroscopie

Fluoroscopie met contrastvloeistof is een manier om een live video te maken van wat er in het lichaam van een persoon gebeurt. Dit is anders dan een röntgenfoto, waarbij alleen de botten zichtbaar zijn. Bij fluoroscopie wordt er wel een contrastvloeistof gebruikt die in de aderen van de persoon terechtkomt. Dit kan niet door de röntgenstraling heen, waardoor ook alles waar de vloeistof terechtkomt zichtbaar wordt. Deze gebieden worden in een andere kleur weergegeven dan de botten. Omdat bij fluoroscopie een lagere energie wordt gebruikt dan bij een röntgenfoto, is het niet schadelijk om meerdere foto's te maken. Artsen kunnen deze techniek gebruiken om live mee te kijken tijdens een operatie en te kijken waar de organen en bloedvaten zich bevinden.

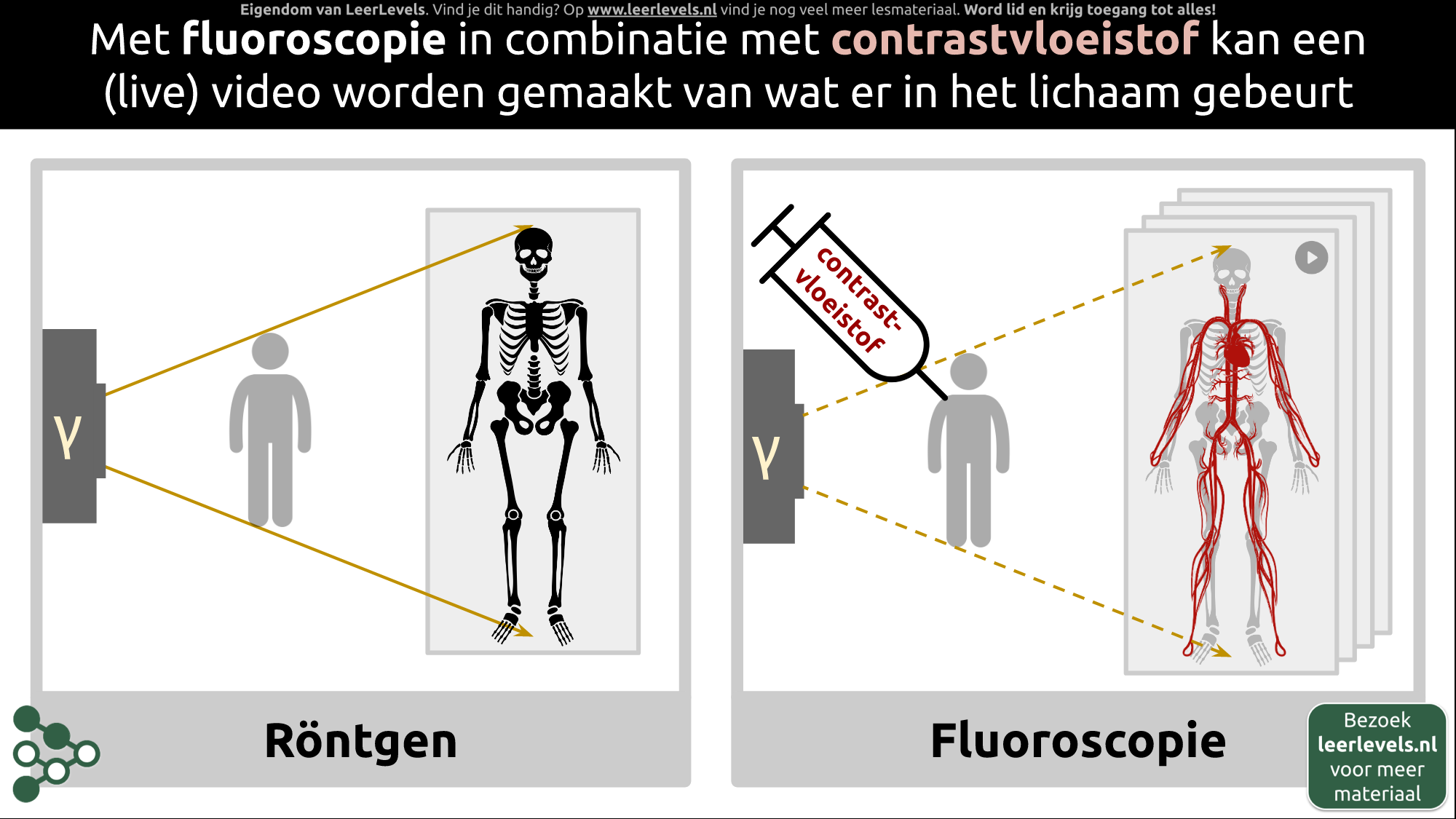
(Afbeelding: Animatie voor Fluoroscopie)

Terug naar overzicht Meld je aan

Formules

Formules invullen met eenheden

Als je formules invult, is het belangrijk om goed op te letten welke eenheden en voorvoegsels erbij horen. Ook moet je weten wat wetenschappelijke notatie is.

Als je bijvoorbeeld de weerstand van een lampje wilt berekenen en je weet de spanning (U) en stroom (I), dan gebruik je de formule R = U / I. Staat er op het lampje dat de spanning 25 V is en de stroom 10 mA, dan vul je dit in de formule in: R = 25 V / 10 mA.

Maar let op: de eenheid van stroom moet omgezet worden naar A (ampère). Dit doe je door 10 mA te vermenigvuldigen met 1 m (milli) en door 1000 te delen. Zo wordt 10 mA gelijk aan 0,01 A.

Nu kun je de rekensom uitvoeren. Uitkomst is 2,5 kΩ (kilo-ohm), oftewel 2,5 keer 1000 Ohm.

(Afbeelding: Animatie voor Formules invullen met eenheden)

Formules invullen met eenheden voor gevorderden

Deze opdracht gaat over het berekenen van weerstand van een draadje. Om dit te berekenen moet je gebruik maken van een formule R = ρ · l / A, waarbij ρ staat voor de soortelijke weerstand, l voor de lengte en A voor de doorsnede van het draadje. In dit geval is de soortelijke weerstand 1,7·10-8 Ωm, de lengte 20 cm en de doorsnede 340 (μm)2. Door deze waarden in te vullen krijg je de formule R = 10 Ω als uitkomst. Het is belangrijk om extra op te letten bij deze ingewikkelde formules omdat er gebruik wordt gemaakt van verschillende eenheden, voorvoegsels en wetenschappelijke notatie.

(Afbeelding: Animatie voor Formules invullen met eenheden voor gevorderden)

Taal omzetten in formules

Bij natuurkundige problemen moet je vaak woorden omzetten in sommen met getallen erin. Bijvoorbeeld: rode appels zijn zwaarder dan groene appels. Als je 5 rode appels en 5 groene appels bij elkaar doet, hebben ze samen een massa van 1,3 kilogram. Hoe zwaar is één groene appel? Om het antwoord te krijgen, moet je deze som oplossen:

5(mg + 30g) + 5mg = 1,3kg

Je komt uit op mg = 0,12 kg, wat betekent dat één groene appel 120 gram weegt.

(Afbeelding: Animatie voor Taal omzetten in formules)

Terug naar overzicht Meld je aan

Foto-elektrisch effect

Foto-elektrisch effect concept

Het foto-elektrisch effect legt uit hoe één foton één elektron kan vrijmaken uit een metalen oppervlak. Als we een foton met een lage frequentie op een metaal schieten, gebeurt er niets. Maar als we een foton met een hogere frequentie (energie) schieten, kan er een elektron vrijkomen met een bepaalde kinetische energie. Als we een foton met nog hogere frequentie schieten, kan er een elektron vrijkomen met meer kinetische energie. Elk foton kan slechts één elektron vrijmaken en de hoeveelheid energie waarmee het elektron vrijkomt hangt af van de frequentie (en dus de energie) van het invallende foton.

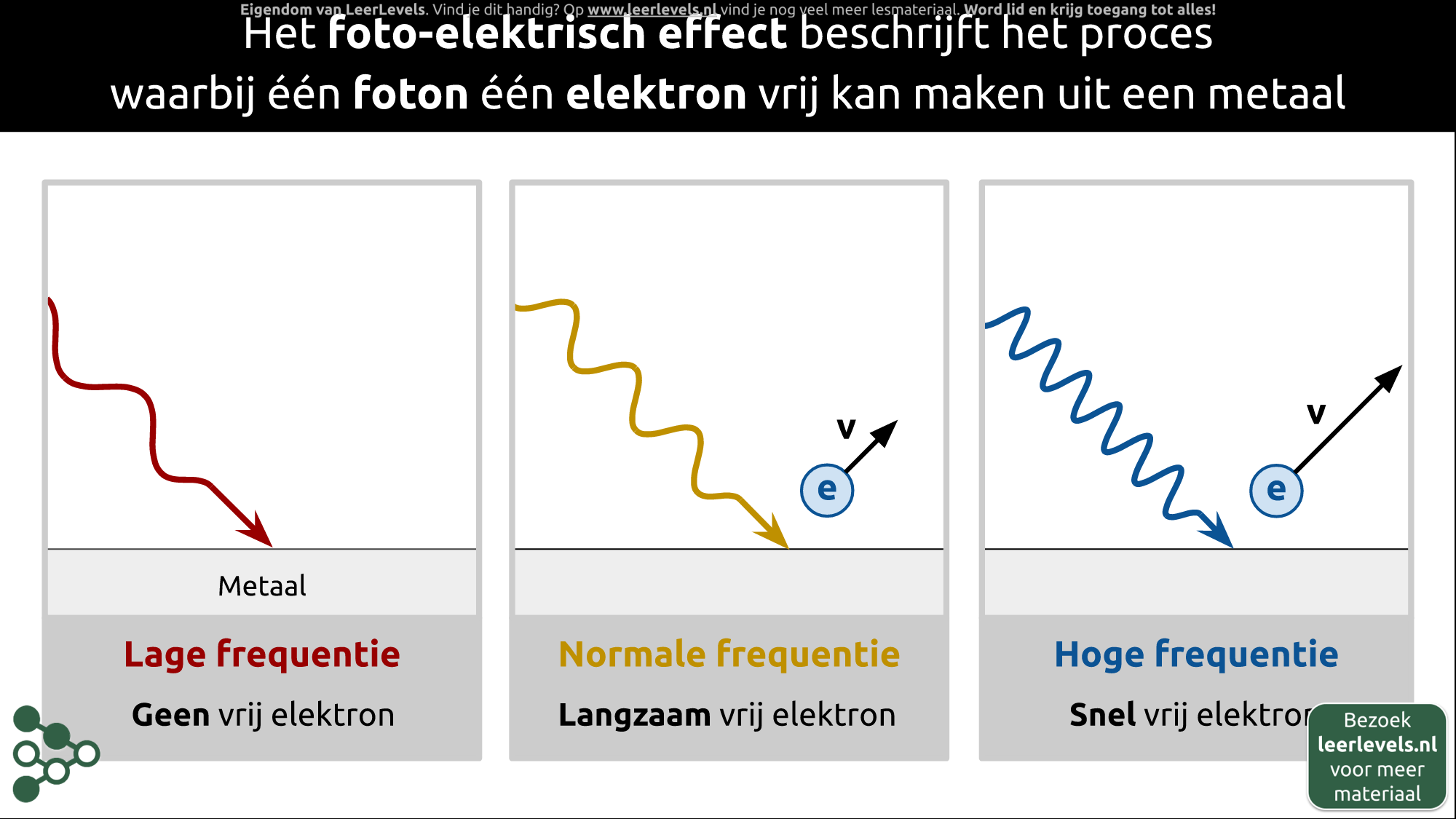
(Afbeelding: Animatie voor Foto-elektrisch effect concept)

Foto-elektrisch effect experiment

Het foto-elektrische experiment laat zien dat licht bestaat uit losse fotonen. Als je een foton op een plaat schiet en er ontstaat een stroom tussen twee platen, dan zijn er elektronen van de ene naar de andere plaat gegaan. Dit gebeurt alleen als er fotonen op de plaat vallen en elk foton genoeg energie heeft om één elektron vrij te maken. Dit is anders dan bij lichtgolven, omdat elke foton individueel genoeg energie moet hebben. Er is een bepaalde hoeveelheid arbeid nodig om één elektron vrij te maken en dit kan worden berekend met de formule W = h · fgrens, waarbij h de constante van Planck is en fgrens de grensfrequentie in Hertz. Als er meer fotonen met een grotere foton-energie worden toegevoegd, wordt de stroomsterkte recht evenredig groter. Het maakt niet uit of de fotonen boven of ver boven de grensfrequentie zaten, als de elektronen maar onder de juiste hoek vrijkomen zodat ze de overkant raken.

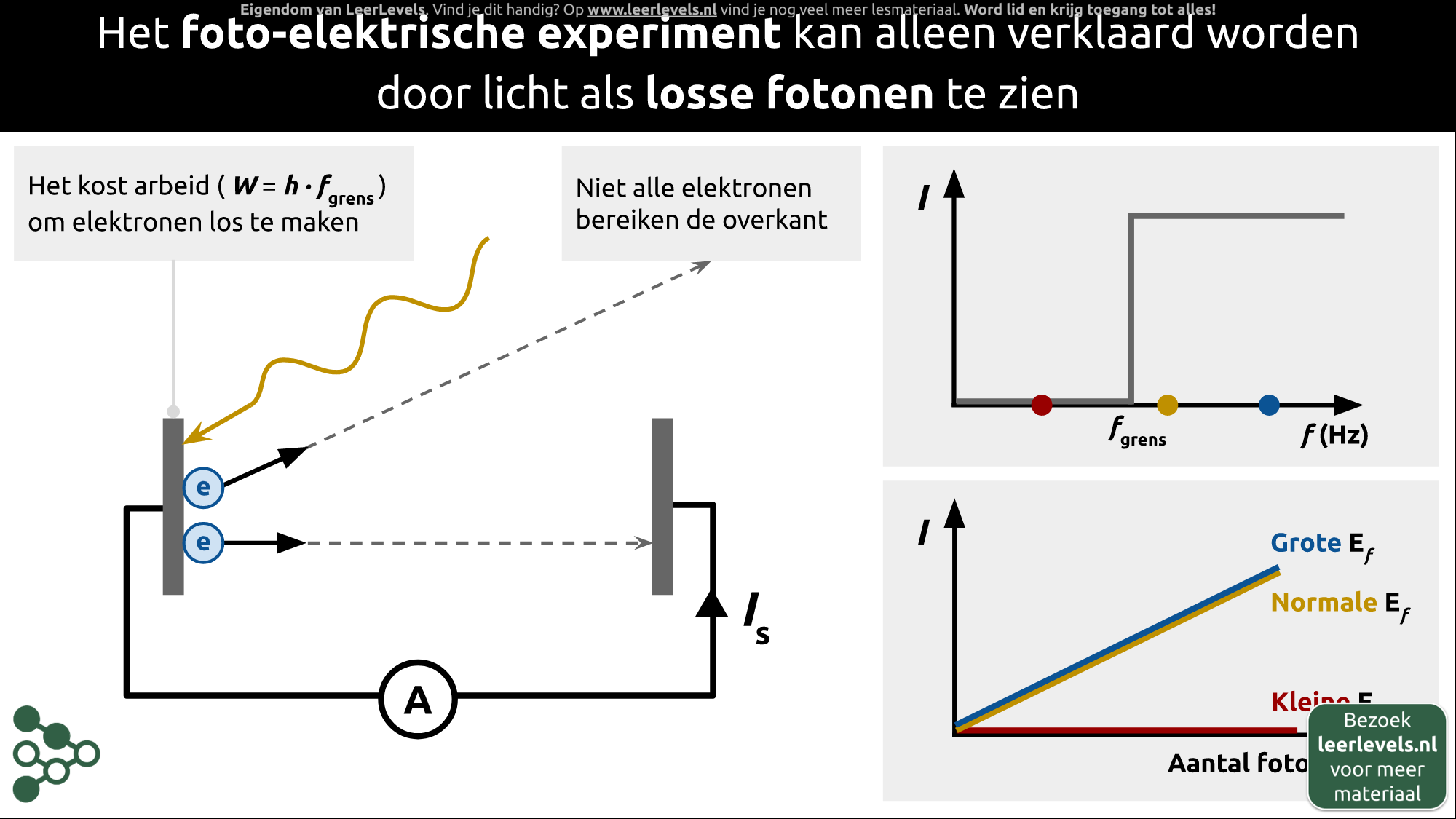
(Afbeelding: Animatie voor Foto-elektrisch effect experiment)

Terug naar overzicht Meld je aan

Foton

Een foton is een pakketje elektromagnetische straling waarvan de energie (E) wordt bepaald door de frequentie (f). Als we kijken naar zichtbaar licht, zien we dat dit bestaat uit kleine energiepakketjes met een matige frequentie. Een radiozendmast zendt radiofotonen uit, met lagere frequenties dan zichtbaar licht en dus ook een lagere energie. Aan de andere kant van het spectrum bevindt zich bijvoorbeeld een röntgenapparaat dat wordt gebruikt om tassen op verdachte voorwerpen te scannen. Een foton van een röntgenapparaat heeft een zeer hoge frequentie en veel energie. Kortom, elk foton heeft een specifieke hoeveelheid energie die afhankelijk is van de frequentie.

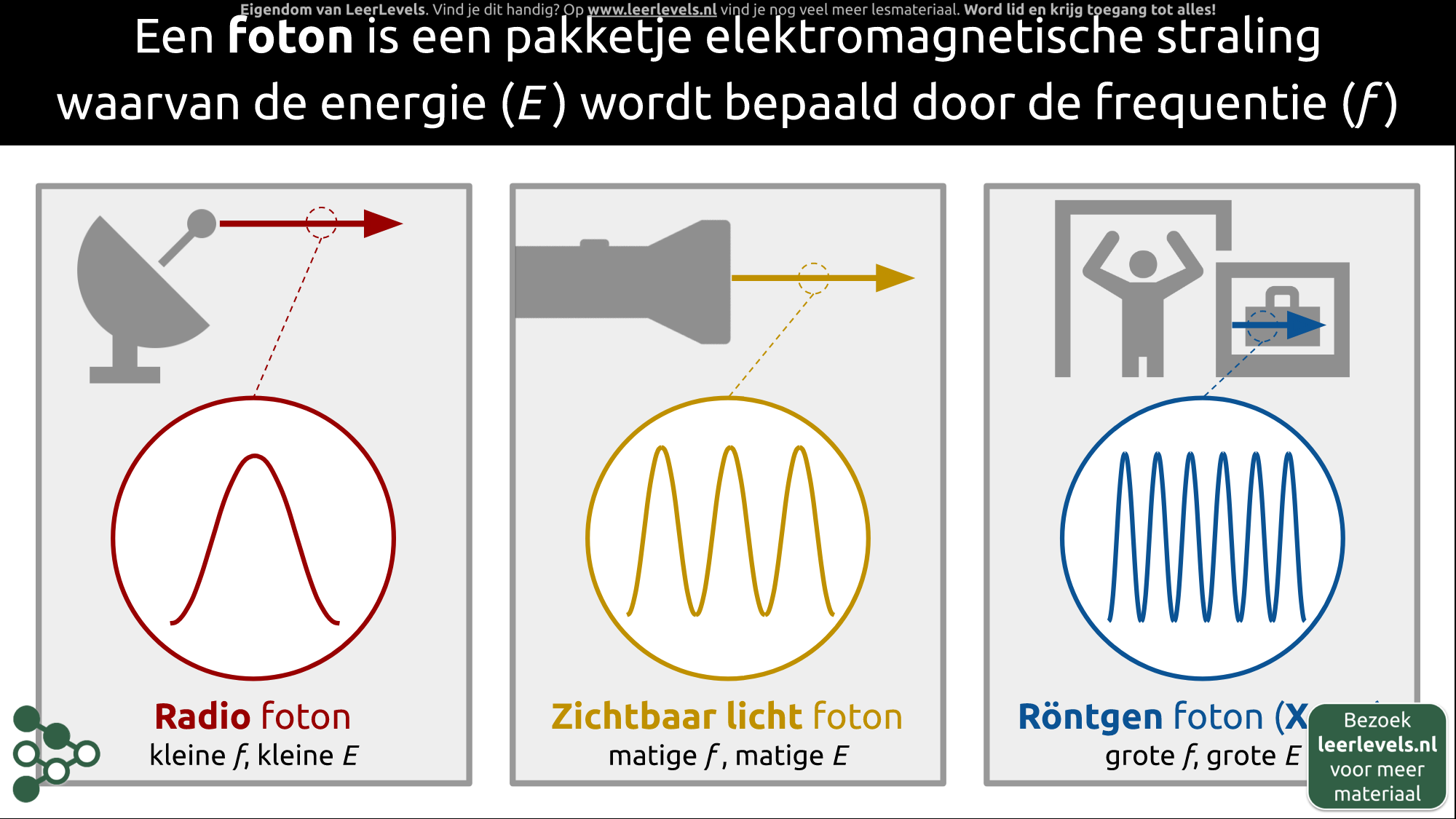
(Afbeelding: Animatie voor Foton)

Terug naar overzicht Meld je aan

Foton-impuls

Foton-impuls concept

Het Compton-effect bewijst dat fotonen een impuls hebben en voldoen aan de botsingswetten die ook gelden voor 'normale' deeltjes. Het effect is vernoemd naar een experiment waarbij röntgenstraling op een elektron werd gericht. Voor de botsing had het foton een impuls groter dan nul omdat het een snelheid had, terwijl het elektron stil stond en dus een impuls van nul had. De energie van het foton was ook groter dan nul, terwijl de kinetische energie van het elektron nul was. Tijdens de botsing gelden twee behoudswetten: impulsbehoud en energiebehoud.

Deze behoudswetten voorspellen dat na de botsing de impuls van het foton vermindert omdat een deel van de oorspronkelijke impuls is overgedragen aan het elektron, waardoor het elektron een bepaalde snelheid krijgt. Ook wordt de energie van het foton lager, omdat de energie van het elektron toeneemt. Deze voorspelling gaat ervan uit dat elektronen zich als deeltjes gedragen. Het experiment toonde aan dat deze voorspelling juist was, wat een indirect bewijs levert dat fotonen een impuls hebben en voldoen aan de botsingswetten voor "normale" deeltjes.

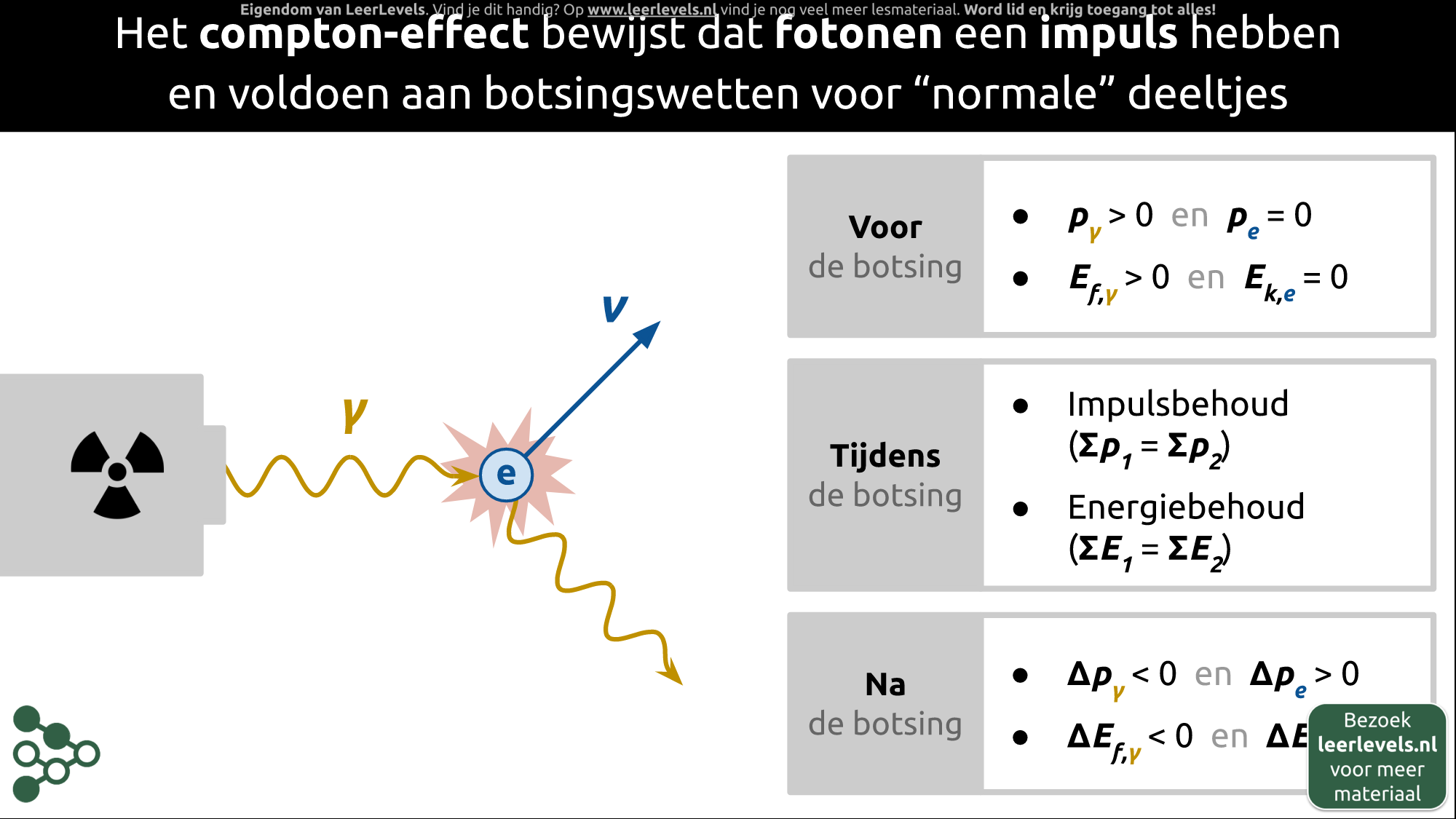
(Afbeelding: Animatie voor Foton-impuls concept)

Foton-impuls formule

Een foton heeft een impuls die omgekeerd evenredig is met de golflengte. Dit betekent dat als de golflengte groter wordt, de impuls kleiner wordt. De impuls van een foton kan worden berekend met de formule p = (h)/(λ), waarbij p staat voor de impuls in kgm/s, λ de golflengte van het foton is en h de constante van Planck is (h = 6,626 × 10⁻³⁴ Js). Deze formule kan ook worden toegepast op frequenties, waarbij blijkt dat een hogere frequentie leidt tot een grotere impuls. Beide grootheden hebben te maken met de energie in beweging van het foton.

(Afbeelding: Animatie voor Foton-impuls formule)

Terug naar overzicht Meld je aan

Fotonenergie

Fotonenergie formule

De energie van een foton is evenredig met de frequentie en omgekeerd evenredig met de golflengte. De energie van een foton, aangeduid als Ef, is gelijk aan een constante vermenigvuldigd met de frequentie:

Ef = h · f

Hierin is h de constante van Planck, met een waarde van 6,626 · 10⁻³⁴ joule-seconde. Het is niet gek dat h zo'n klein getal is, want het hangt samen met de energie van één enkel foton. De energie van een foton hangt naast h ook af van de frequentie in hertz. Als de frequentie hoger wordt, heeft het foton meer energie.

Naast frequentie kun je de energie van een foton ook uitdrukken in termen van de golflengte (λ) van het licht. Voor elke golf geldt dat het product van de frequentie en golflengte gelijk is aan de golfsnelheid (f · λ = vgolf), en voor licht is de golfsnelheid gelijk aan de lichtsnelheid (f · λ = c). Hiermee kun je de frequentie vervangen (f = (c)/(λ)) en een formule voor de fotonenergie maken:

Ef = (h · c)/(λ)

Hierin heeft c een waarde van ongeveer 3 · 10⁸ m/s (per definitie: 299792458 m/s).

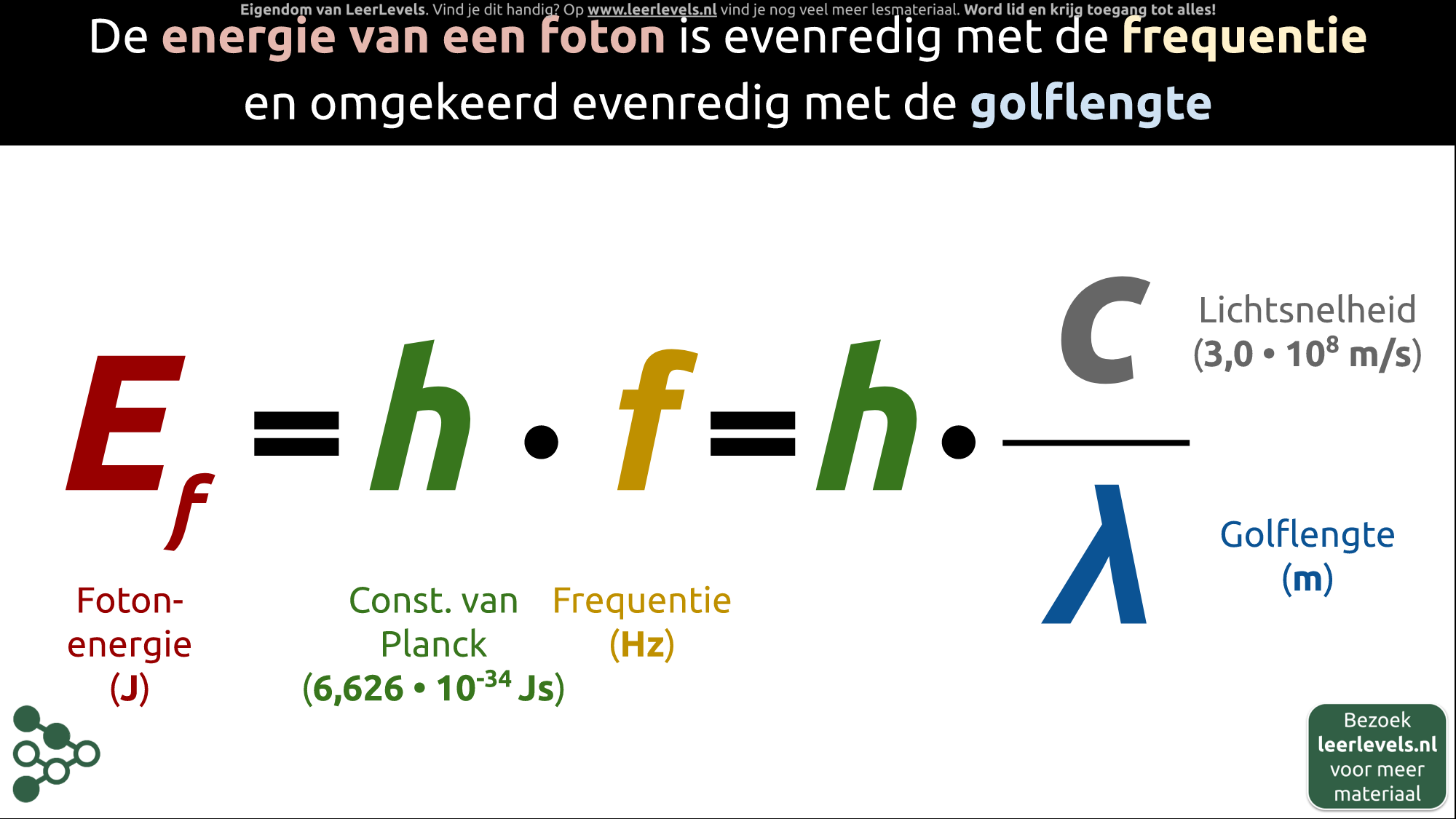
(Afbeelding: Animatie voor Fotonenergie formule)

Terug naar overzicht Meld je aan

Fraunhoferlijnen

In 1814 ontdekte een persoon genaamd Fraunhofer dat er in het zonlicht zwarte lijnen zitten. Deze lijnen tonen aan dat er waterstof aanwezig is. De zon heeft een kern en daaromheen een mantel. In de kern vindt kernfusie plaats waardoor er straling vrijkomt. Deze straling gaat door de mantel. In de kern wordt een continu spectrum uitgezonden, maar in de mantel worden specifieke golflengtes geabsorbeerd. Wat overblijft, reist via een vacuum naar de aarde en dit licht kunnen we opvangen met apparaten zoals satellieten. Vervolgens kunnen we het licht analyseren. We ontdekken dan dat er bepaalde absorptielijnen in het zonlicht zitten. Sommige van deze absorptielijnen horen specifiek bij waterstof, meer specifiek bij de Balmer-serie van waterstof. Fraunhofer concludeerde dat er waterstof in de mantel van de zon moest zitten vanwege de absorptielijnen.

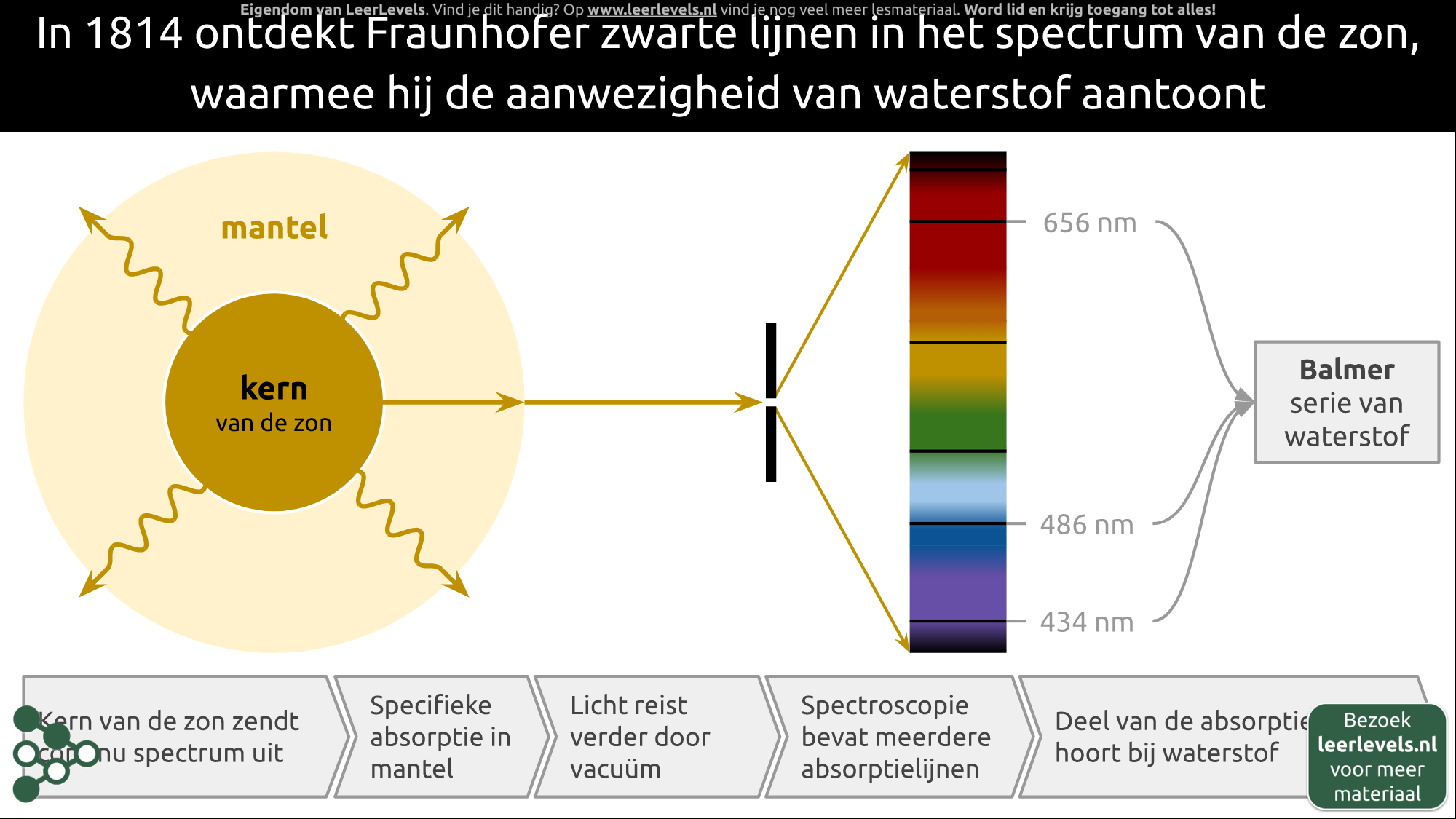
(Afbeelding: Animatie voor Fraunhoferlijnen)

Terug naar overzicht Meld je aan

Frequentie

Frequentie concept

De frequentie f duidt het aantal trillingen per seconde aan. Bij een vogel die langzaam met zijn vleugels slaat, is het aantal trillingen per seconde laag, wat resulteert in een lage frequentie. Deze lage frequentie produceert een diep geluid.

Wanneer de vleugels sneller bewegen, zoals bij een mug, is het aantal trillingen per seconde veel hoger. Dit resulteert in een hoge frequentie en produceert een hoog, zoemend geluid.

Een hogere frequentie betekent dus simpelweg meer trillingen per seconde, wat leidt tot een hoger geluid.

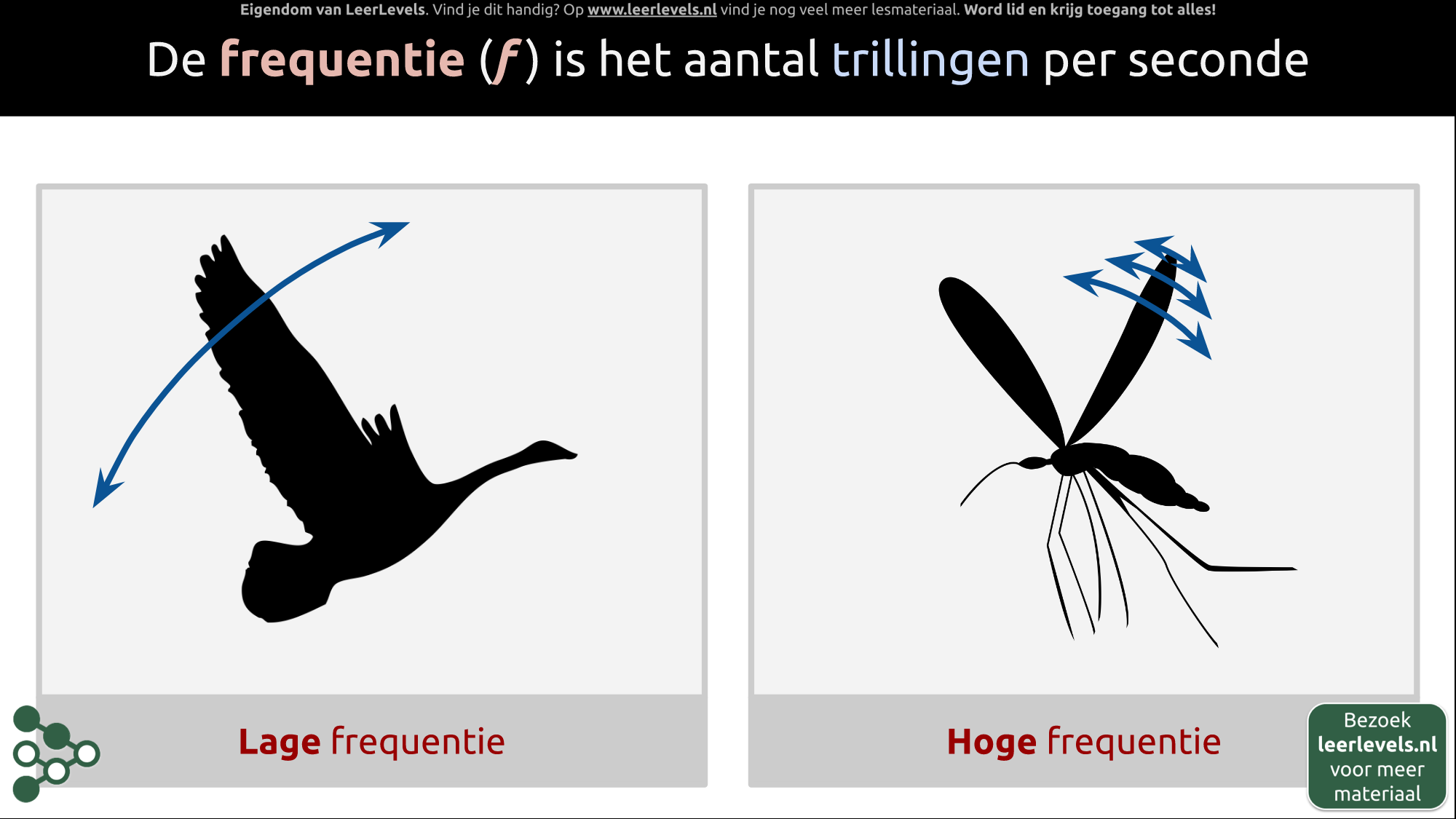
(Afbeelding: Animatie voor Frequentie concept)

Frequentie formule

Frequentie (f) en trillingstijd (T) zijn omgekeerd evenredig. Dit betekent dat als de trillingstijd toeneemt, de frequentie afneemt. Frequentie wordt gemeten in hertz (Hz) en geeft aan hoe vaak iets per seconde trilt. Dit bereken je door 1 te delen door de trillingstijd (f = 1/T ). Als de trillingstijd toeneemt, neemt de frequentie automatisch af omdat er minder trillingen per seconde plaatsvinden. Als de trillingstijd korter is, passen er meer trillingen in een seconde en neemt de frequentie toe.

(Afbeelding: Animatie voor Frequentie formule)

Terug naar overzicht Meld je aan

Frequentiespectrum

Als een geluid niet perfect klinkt, betekent dit dat het geluid is opgebouwd uit verschillende boventonen. De frequenties en amplitudes van deze boventonen worden weergegeven in een diagram, waarbij de x-as de frequentie aangeeft en de y-as de amplitude van de boventonen ten opzichte van de maximale waarde.

Om een niet-perfect geluid op te bouwen uit perfecte sinusgolven, voegen we verschillende sinusoïden toe. We beginnen met een groene sinusoïde die op de juiste plaatsen hoog en laag is, maar nog niet perfect past. Vervolgens voegen we een rode sinusoïde toe om dichterbij te komen, en de overgebleven verschillen worden opgelost met een gele sinusoïde. Als we alle geluidsgolven bij elkaar optellen, krijgen we een samengesteld geluid dat er niet meer uitziet als een perfecte sinusgolf, maar als een zaagtandvorm.

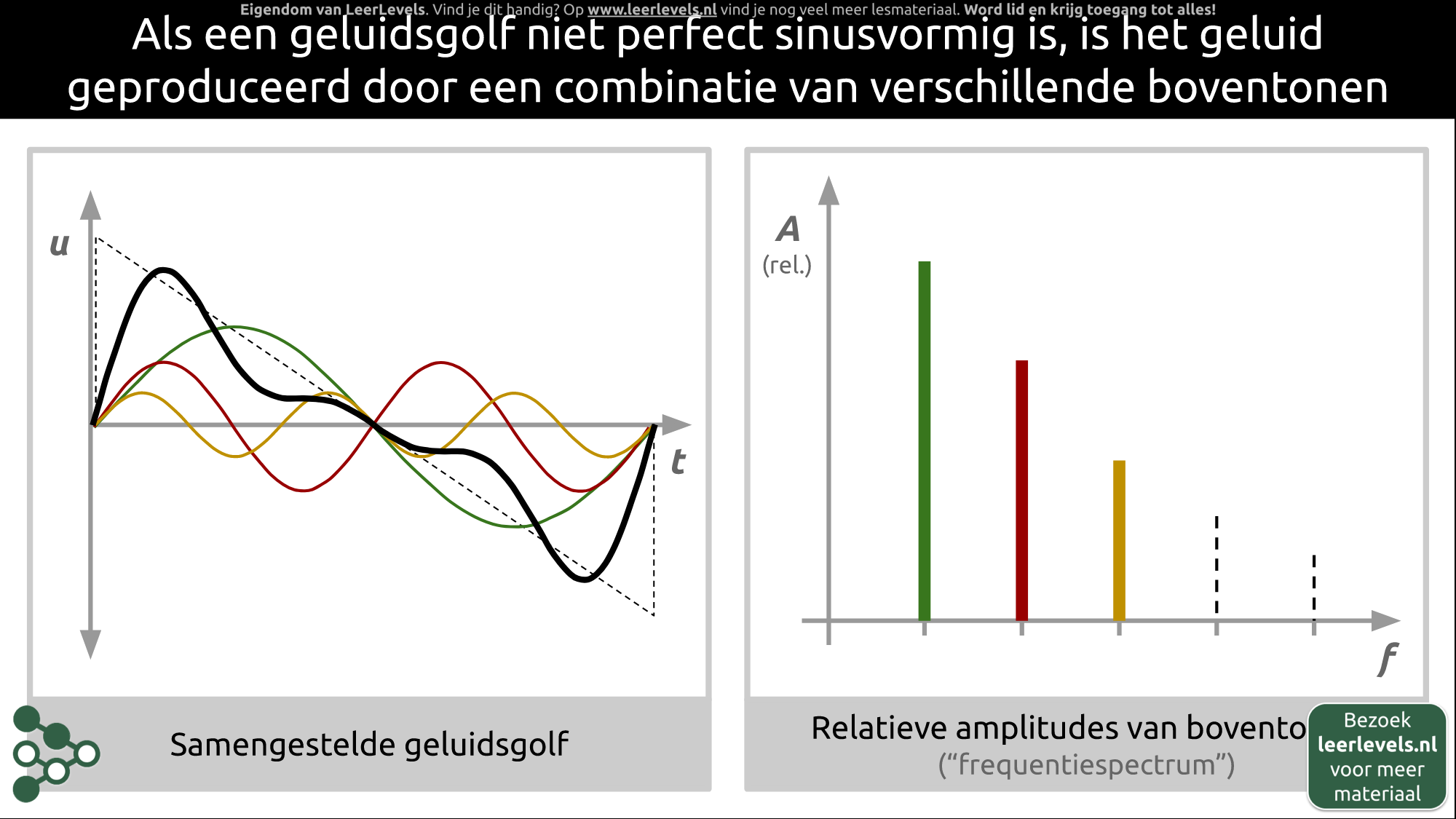
(Afbeelding: Animatie voor Frequentiespectrum)

Terug naar overzicht Meld je aan

Gasdruk

De gasdruk in een ruimte wordt veroorzaakt door talloze bewegende moleculen in het gas die voortdurend tegen de wanden botsen. Laten we een situatie bekijken met weinig moleculen en een lage temperatuur. Dit leidt tot minder botsingen per molecuul en minder kracht per botsing. In deze situatie is de gasdruk erg laag. Stel je voor dat er slechts één molecuul is; door de lage temperatuur beweegt het langzaam. Als het de muur raakt, gebeurt de botsing met een lage snelheid, waardoor er weinig kracht op de muur wordt uitgeoefend. Deze ene botsing resulteert in een zeer kleine gasdruk.

Vergelijken we dit met een situatie van hoge temperatuur, dan beweegt dat ene molecuul sneller. Hierdoor legt het in dezelfde tijd een grotere afstand af en oefent het bij elke botsing een grotere kracht uit op de wand. Het resultaat is een matige gasdruk.

Kijken we naar een situatie met lage temperatuur en veel moleculen, bijvoorbeeld drie, dan zijn er drie keer zoveel botsingen als in de situatie met weinig moleculen. De som van de krachten blijft beperkt, wat resulteert in een kleine gasdruk.

In een situatie met veel moleculen en een hoge temperatuur zijn er talrijke botsingen, waarbij elke botsing een grote kracht uitoefent. De totale kracht is groot, waardoor er een hoge gasdruk heerst.

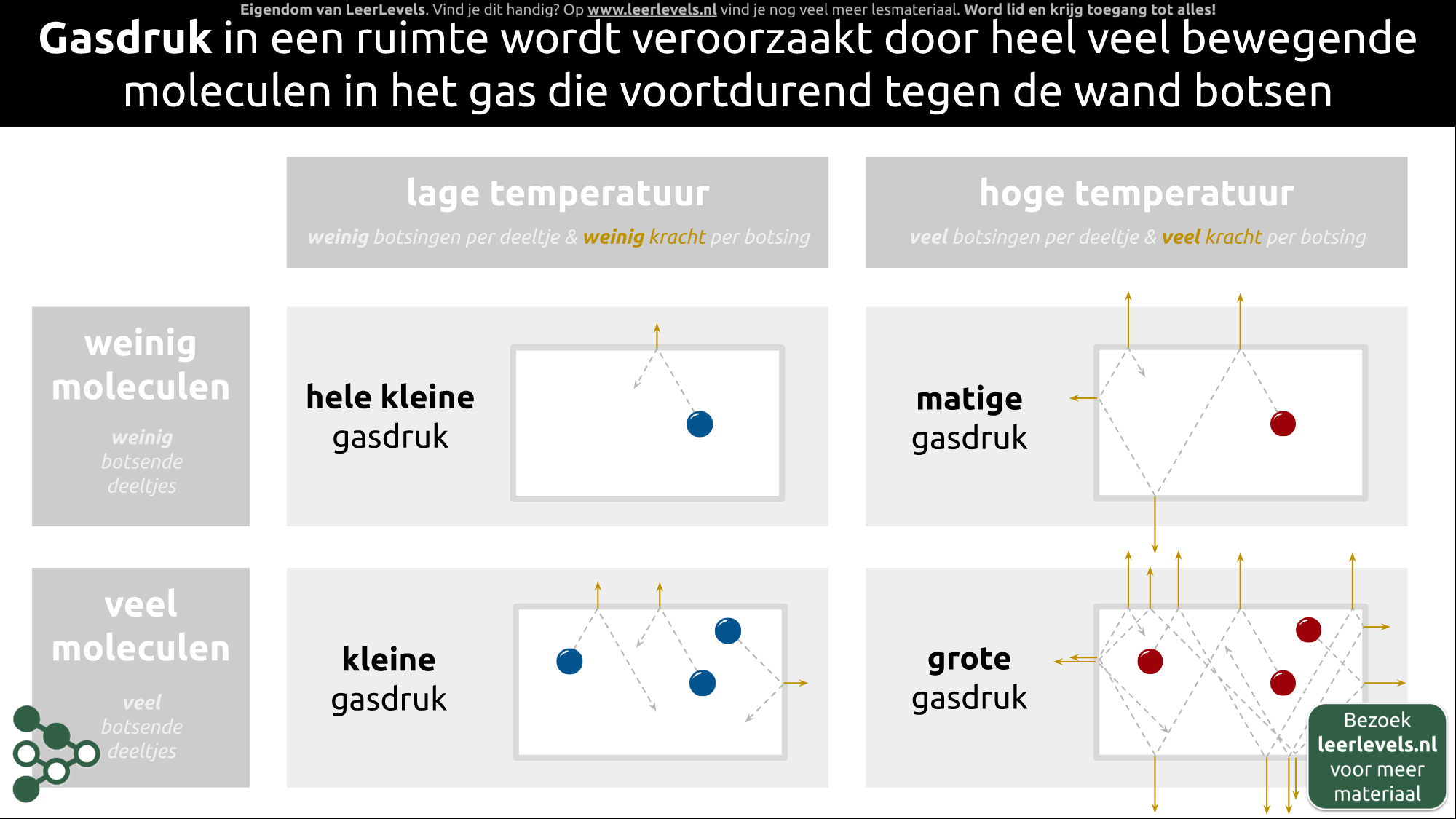
(Afbeelding: Animatie voor Gasdruk)

Terug naar overzicht Meld je aan

Geiger-mullerteller

Een Geiger-Müllerteller kan ioniserende straling detecteren en gaat hierbij door vier stappen. Als eerste wordt de straling geabsorbeerd door een telbuis. Door deze absorptie raakt het gas in de buis geïoniseerd. Omdat het gas onder hoge spanning staat, ontstaat er een elektrische stroom bij elke ionisatie. Dit wordt elektronisch versterkt. Voor elke absorptie van stralingsdeeltjes volgt een teller, die het display laat zien. Ook wordt er bij elke absorptie een signaal via de luidspreker afgespeeld. Hiermee kan radioactiviteit hoorbaar worden gemaakt, omdat mensen straling niet kunnen voelen. Hierdoor is detectie van ioniserende straling mogelijk.

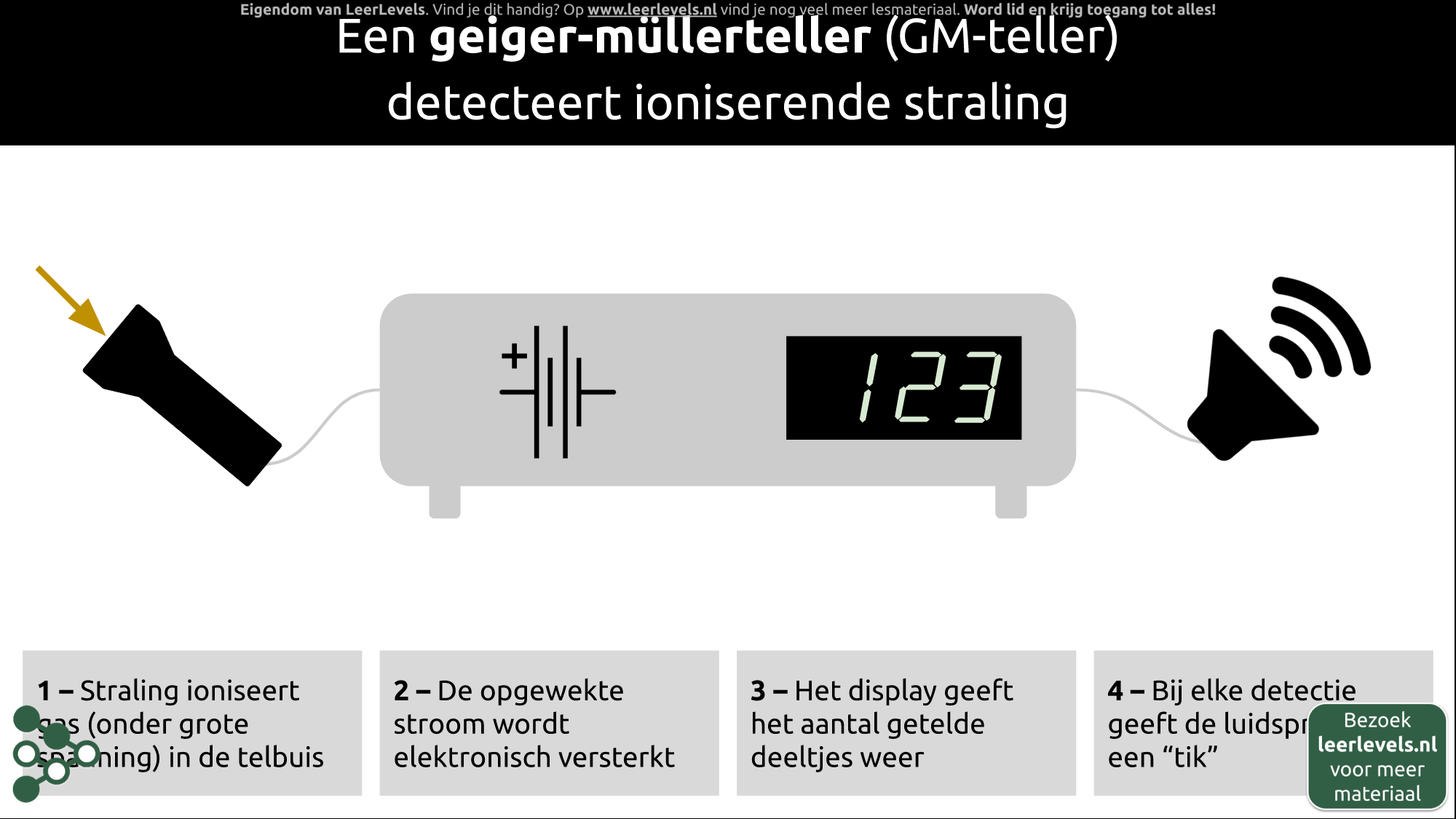
(Afbeelding: Animatie voor Geiger-mullerteller)

Terug naar overzicht Meld je aan

Gekoppeld systeem

Gekoppeld systeem concept

Een gekoppeld systeem bestaat uit meerdere massa's die gezamenlijk bewegen en dus dezelfde versnelling hebben. Een eenvoudig voorbeeld hiervan is de situatie waarin je twee blokken tegen elkaar hebt staan en een kracht naar rechts uitoefent. Hierdoor komt niet alleen blok 1 in beweging, maar ook blok 2. De totale versnelling is afhankelijk van de massa van beide blokken. Zelfs als er verschillende massa's verbonden zijn, moet je hiermee rekening houden wanneer je het geheel wilt optillen. Je moet de totale massa in beschouwing nemen, omdat het volledige systeem dezelfde versnelling krijgt.

In sommige situaties is het niet direct duidelijk wat er gebeurt. Bijvoorbeeld wanneer twee massa's verbonden zijn door middel van een katrol. Als massa 1 naar beneden wordt getrokken, zal massa 2 omhoog bewegen. Kortom, wanneer er een kracht werkt op een gekoppeld systeem, bekijk dan de totale massa van de onderdelen om te bepalen welke versnelling het systeem uiteindelijk krijgt.

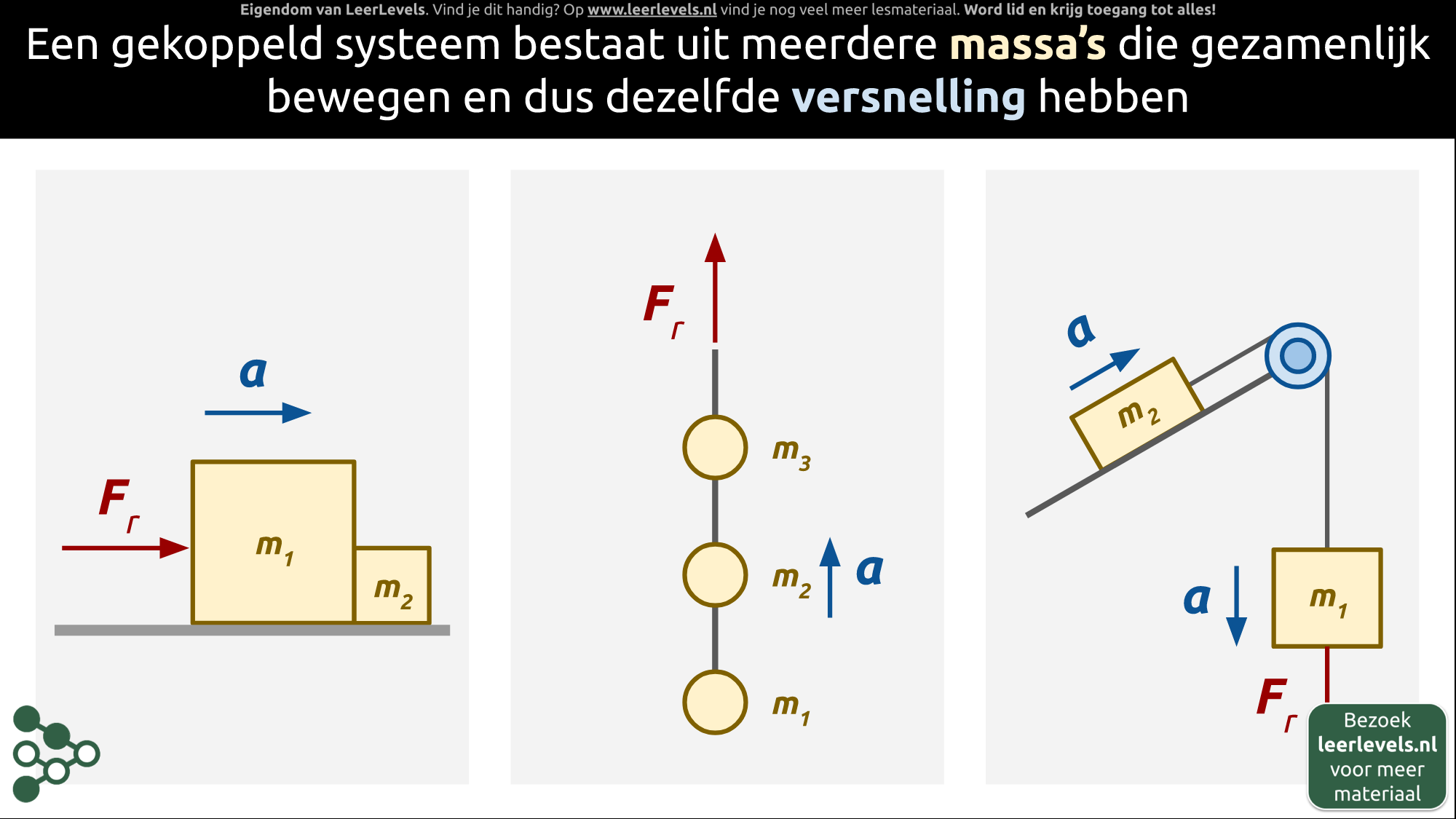
(Afbeelding: Animatie voor Gekoppeld systeem concept)

Terug naar overzicht Meld je aan

Geleidbaarheid

Geleidbaarheid concept

De elektrische geleidbaarheid vertelt ons hoe makkelijk stroom door een object gaat. Een dikke buis heeft een hoge geleidbaarheid en laat stroom makkelijk door. Een normale draad heeft een normale geleidbaarheid en laat minder makkelijk stroom door. Een lange draad heeft een kleine geleidbaarheid en laat nog minder stroom door. Weerstand is het tegenovergestelde van geleidbaarheid. Normale geleidbaarheid creëert normale weerstand en grote geleidbaarheid creëert kleine weerstand. Als stroom door iets makkelijk gaat, heeft het een hoge geleidbaarheid en weinig weerstand. Als een object een lage geleidbaarheid heeft, heeft het een hoge weerstand en laat het moeilijk stroom door. Geleidbaarheid en weerstand zijn tegenovergestelde begrippen. De formule voor geleidbaarheid is G = I/V , waarbij G de geleidbaarheid is, I de stroom en V het voltage.

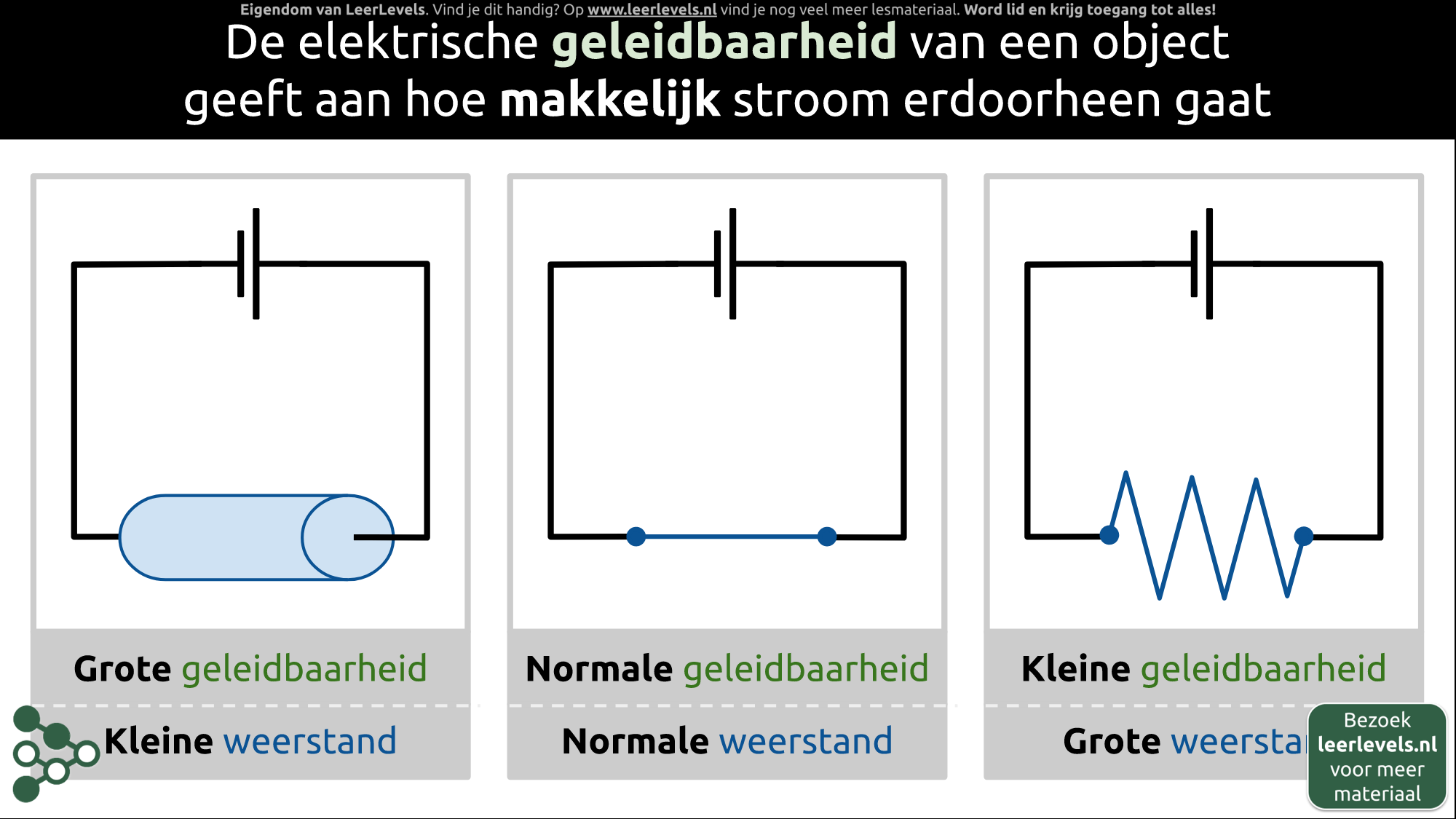
(Afbeelding: Animatie voor Geleidbaarheid concept)

Geleidbaarheid en weerstand

De geleidbaarheid en weerstand zijn omgekeerd evenredig aan elkaar. Dit betekent dat wanneer de geleidbaarheid toeneemt, de weerstand afneemt, en andersom. Beide grootheden zijn elkaars omgekeerde. Dus, als de geleidbaarheid groot is, is de weerstand klein, en vice versa. De eenheid voor geleidbaarheid is de siemens (S), terwijl de eenheid voor weerstand de ohm (Ω) is.

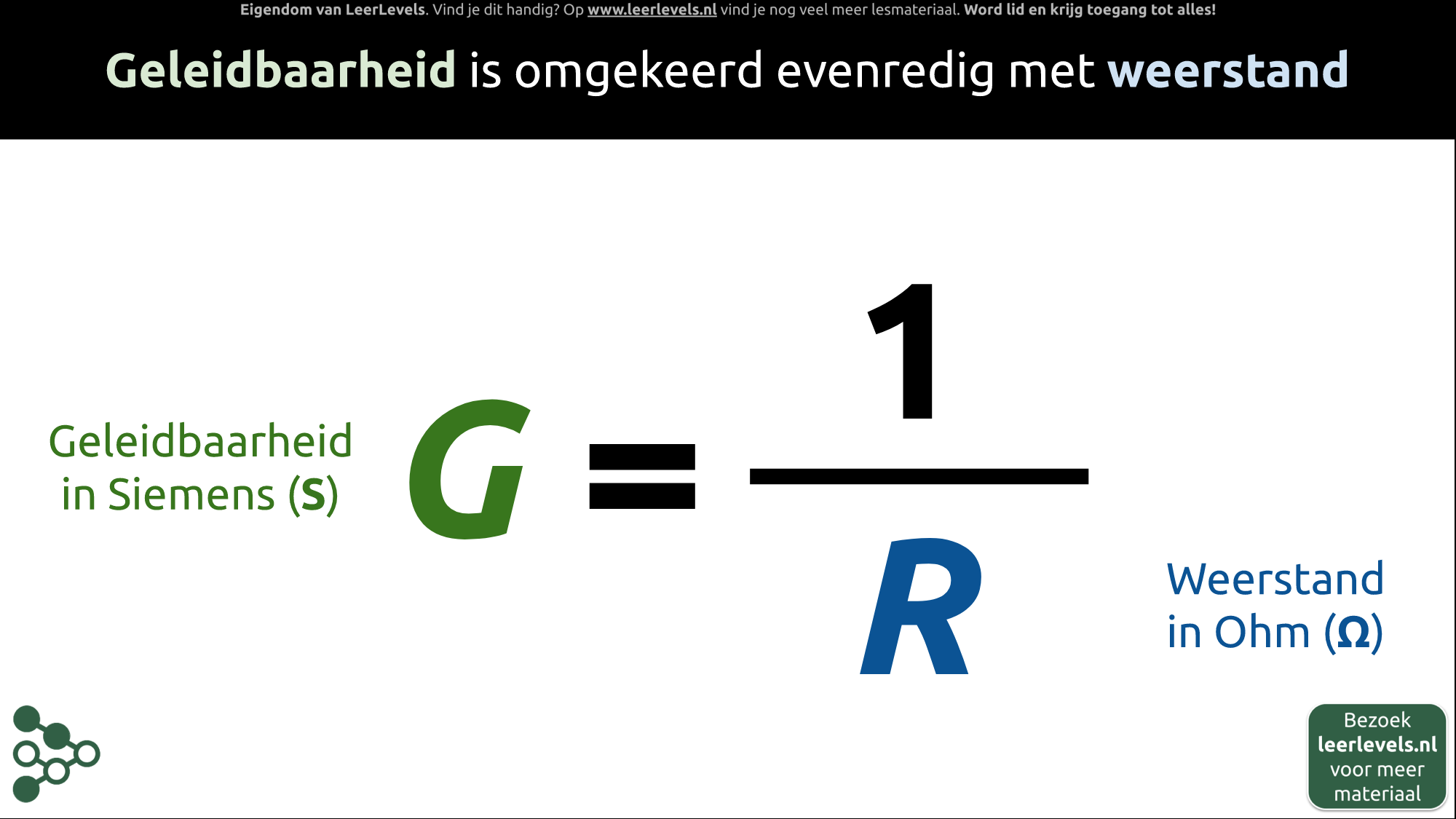
(Afbeelding: Animatie voor Geleidbaarheid en weerstand)

Geleidbaarheid formule

De elektrische geleidbaarheid is recht evenredig met de stroomsterkte door een object en omgekeerd evenredig met de spanning over dat object. Voor de geleidbaarheid G geldt daarom:

G = I/U

waarbij G de geleidbaarheid in Siemens is, I de stroomsterkte in ampère en U de spanning in volt.

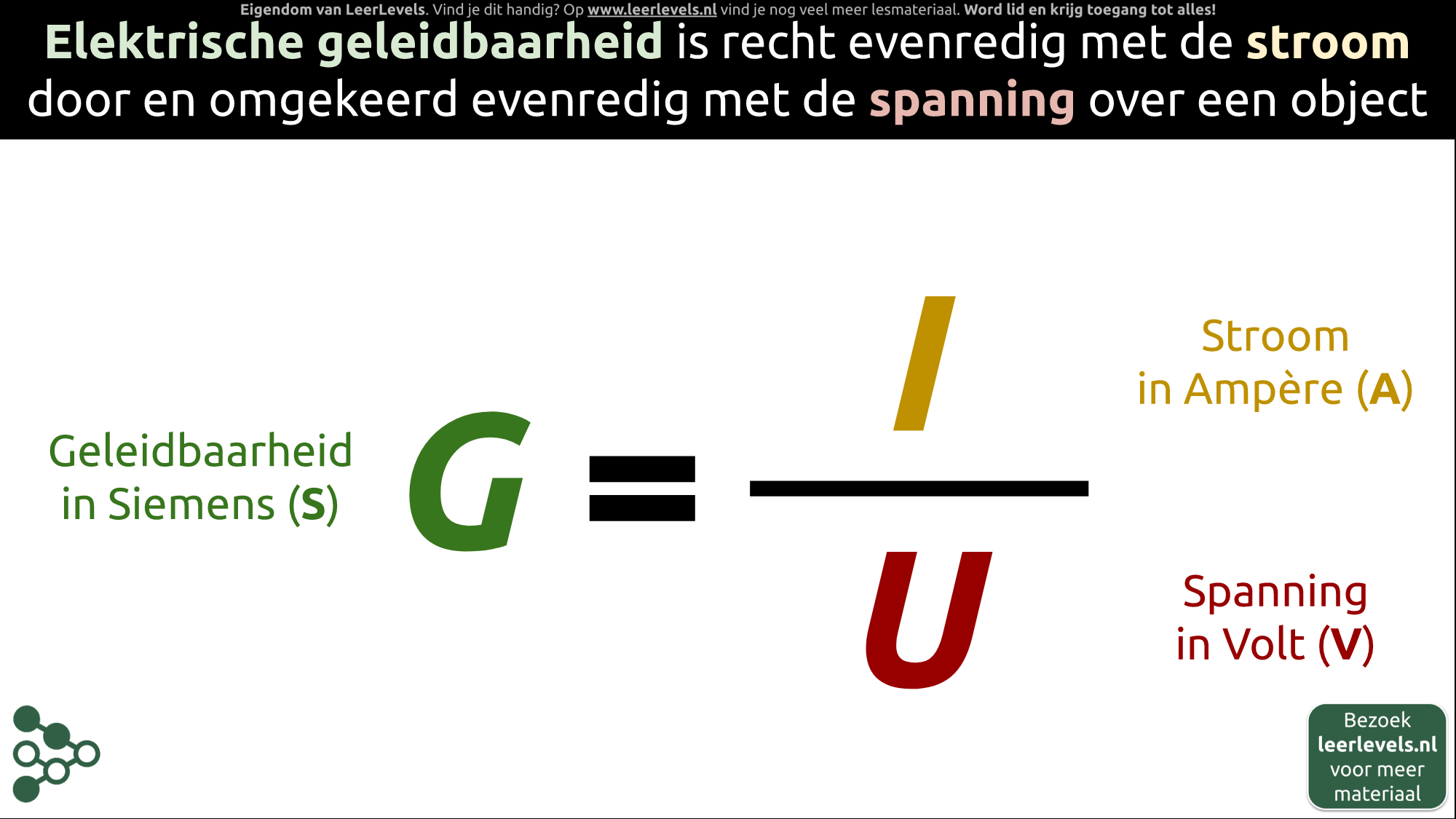
(Afbeelding: Animatie voor Geleidbaarheid formule)

Terug naar overzicht Meld je aan

Geleiders

Geleiders en isolatoren

In een geleider kunnen elektronen vrij bewegen tussen de atomen, waardoor ze gemakkelijk stroom kunnen geleiden. In een isolator zitten de elektronen echter vast, wat betekent dat ze niet kunnen bewegen, en daarom kan er geen stroom worden geleid. Bij geleiding kunnen de elektronen van het ene atoom naar het andere springen en op die manier stroom geleiden. Geleiding is dus alleen mogelijk in een materiaal waarin de elektronen vrij kunnen bewegen.

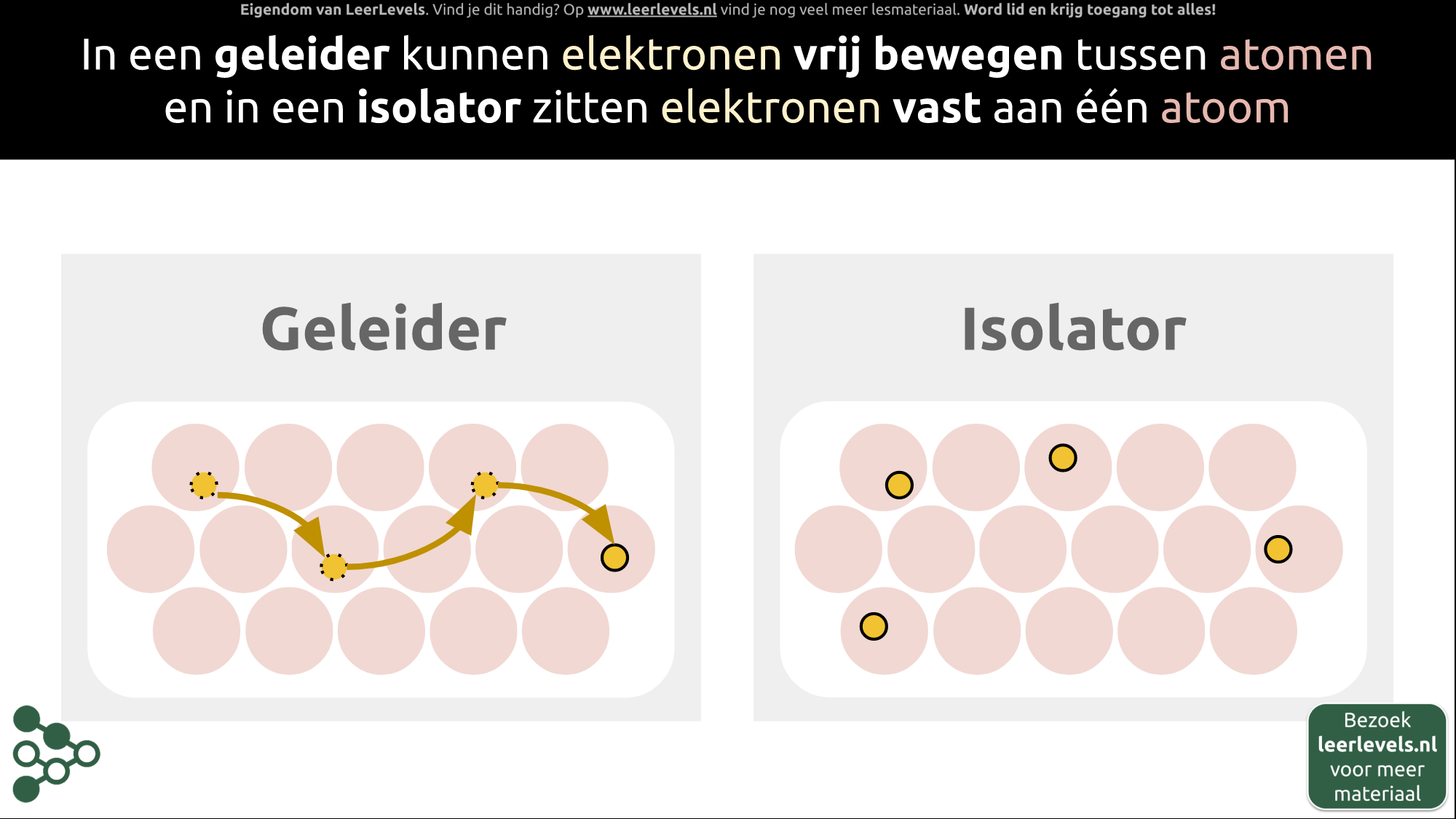
(Afbeelding: Animatie voor Geleiders en isolatoren)

Terug naar overzicht Meld je aan

Geluid

Geluid concept

Geluid is iets wat je kunt horen en ontstaat als iets beweegt en trilt. Een stemvork bijvoorbeeld gaat trillen als je er hard tegenaan slaat. Hierdoor komt er lucht in beweging en dat zorgt voor geluid. Een koptelefoon heeft een heel klein elementje dat op de juiste manier beweegt en daardoor kun je muziek horen. Bij een gitaar zijn het de snaren die trillen en bij een trompet zijn het de lippen van de bespeler die trillen, waardoor er geluid ontstaat. Kortom, geluid ontstaat als iets trilt en dit zorgt voor een drukgolf die we kunnen horen. Er worden geen formules, grootheden of eenheden genoemd.

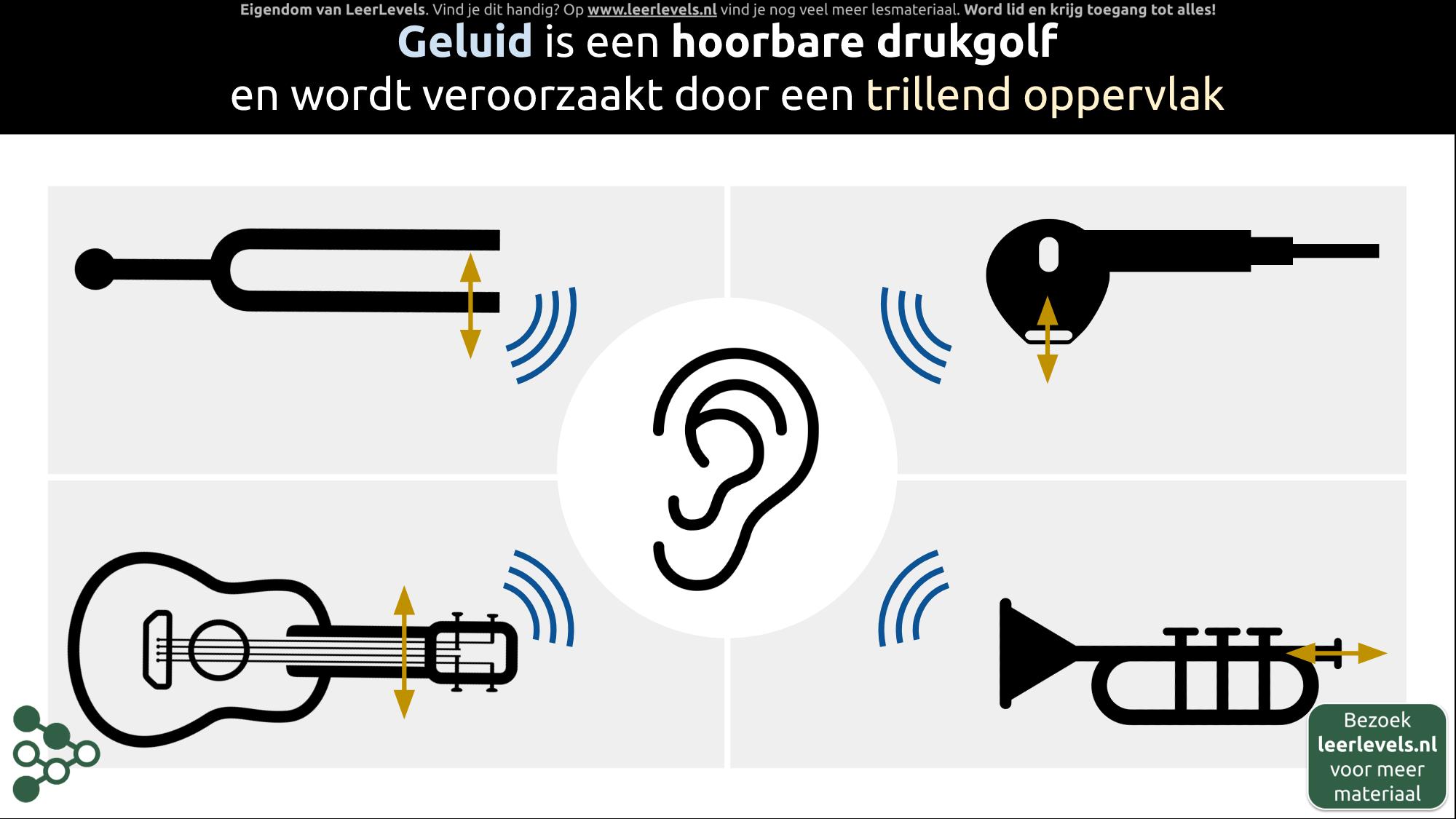
(Afbeelding: Animatie voor Geluid concept)

Voortplanting van geluid

Geluidsgolven zijn trillingen die zich met verschillende snelheden door verschillende materialen voortplanten. Meestal horen we geluid wanneer het zich door de lucht verplaatst. Lucht is een gasvormig mengsel waarin geluid zich relatief langzaam voortbeweegt, omdat de luchtmoleculen ver van elkaar verwijderd zijn en elkaar niet gemakkelijk raken. In een vloeistof, zoals water, verplaatst geluid zich veel sneller, omdat de moleculen de beweging sneller aan elkaar kunnen doorgeven. In een vaste stof reist geluid het snelst, omdat de moleculen daar dicht op elkaar zitten; als één molecuul beweegt, beweegt het volgende meteen mee. Daarom verplaatst geluid zich het snelst door een vaste stof.

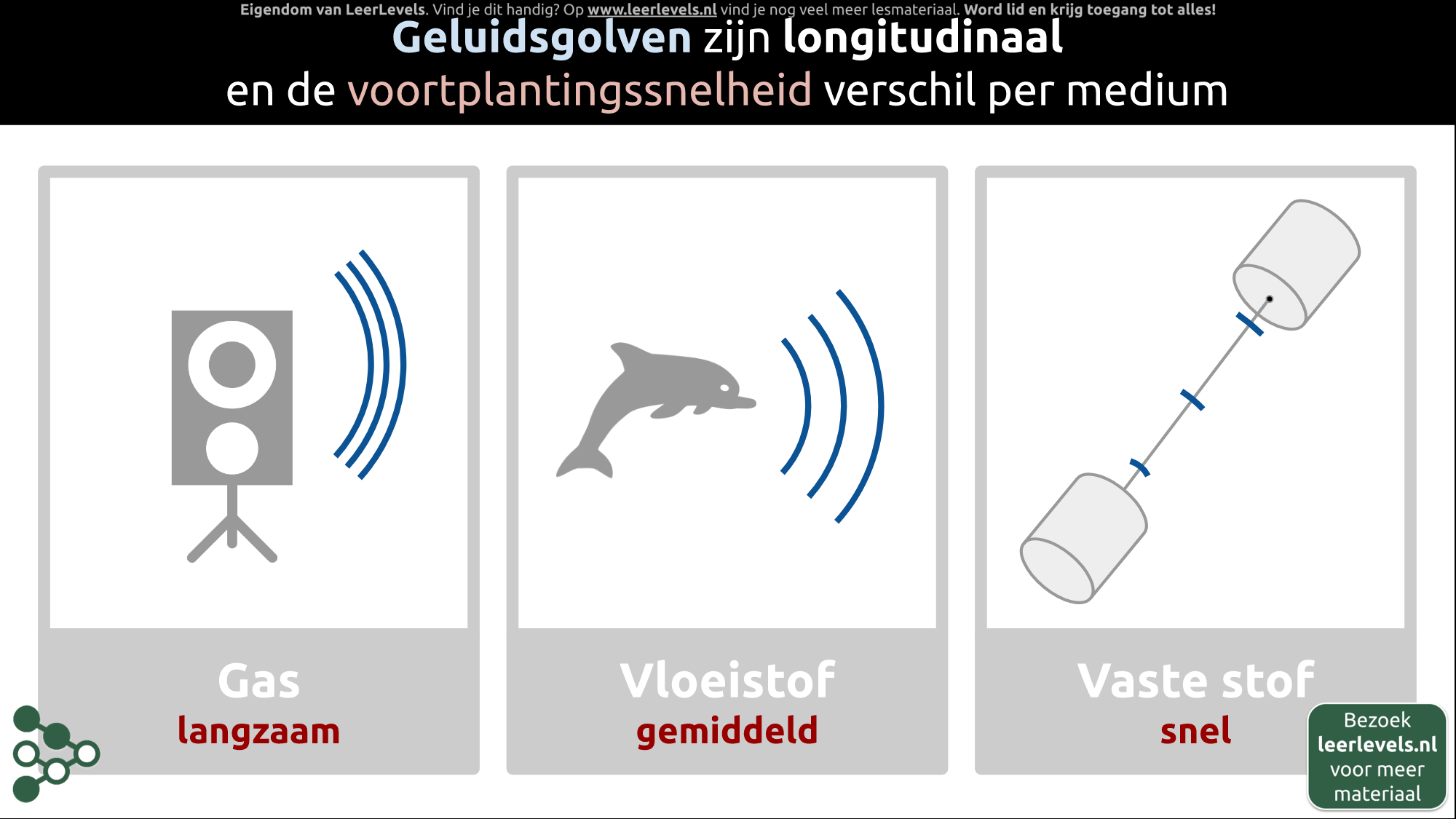
(Afbeelding: Animatie voor Voortplanting van geluid)

Geluidssterkte

De geluidssterkte is gerelateerd aan de amplitude van een geluidsgolf en wordt ook wel volume genoemd. Bij een geluidsbron met een lage geluidssterkte, zoals een koptelefoon, hoort een kleine amplitude. Daarentegen heeft een geluidsbron met een hoge geluidssterkte, zoals een krachtige stereo-installatie, een grote amplitude. Dit komt doordat de geluidsgolf een grotere amplitude heeft. Dus, de geluidssterkte informeert ons over de amplitude van de geluidsgolf, en in het dagelijks taalgebruik wordt dit aangeduid als het volume.

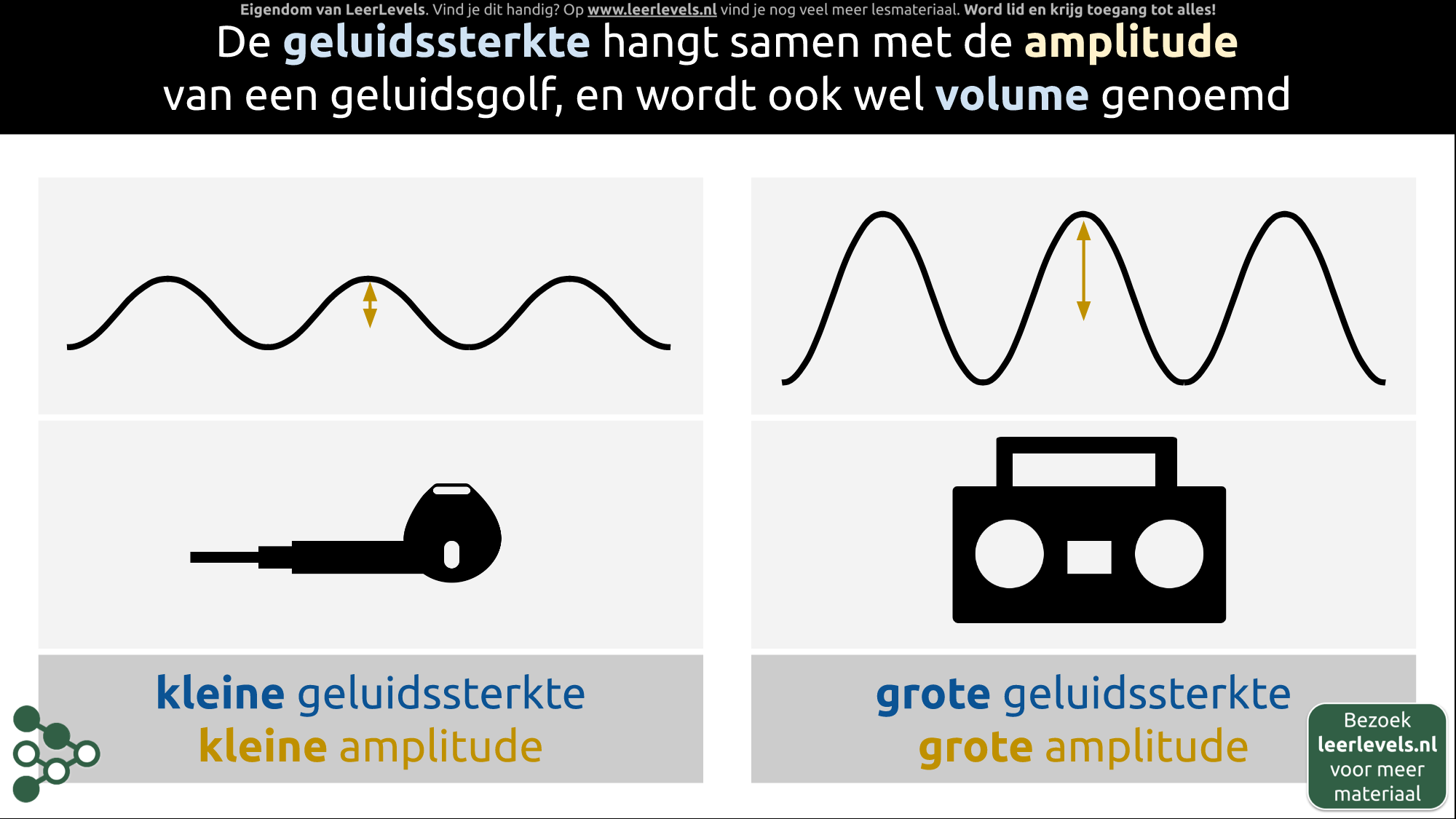
(Afbeelding: Animatie voor Geluidssterkte)

Toonhoogte

De toonhoogte van geluid wordt bepaald door de frequentie (f) van de trillingen van de geluidsbron en vaak ook door de lengte (L) van de bron. Laten we eerst kijken naar instrumenten met een hoge toon, zoals een blokfluit of een viool. Hier is de frequentie hoog, wat betekent dat de lucht snel trilt in de fluit of rondom de snaar van de viool. Bij de viool trillen de snaren heel snel, zoals te zien is met een hogesnelheidscamera. Deze instrumenten hebben een relatief korte lengte van de buis of de snaren.

Nu zullen we twee instrumenten bekijken met een lage toon, namelijk de tuba en de cello. Deze instrumenten produceren geluid met een lage frequentie, wat betekent dat de lucht langzaam trilt. De lengte van de buis of snaren is hier juist lang. Bij de cello is dit duidelijk zichtbaar, terwijl de lange buis van de tuba goed opgerold is en daarom moeilijker te zien is. Als je de buis echter volgt van het mondstuk tot de uitgang, zie je hoe lang de buis werkelijk is. Kortom, de toonhoogte van geluid wordt bepaald door de frequentie van de trillingen van de geluidsbron en over het algemeen geldt: hoe langer de buis of het instrument, hoe lager de toon.

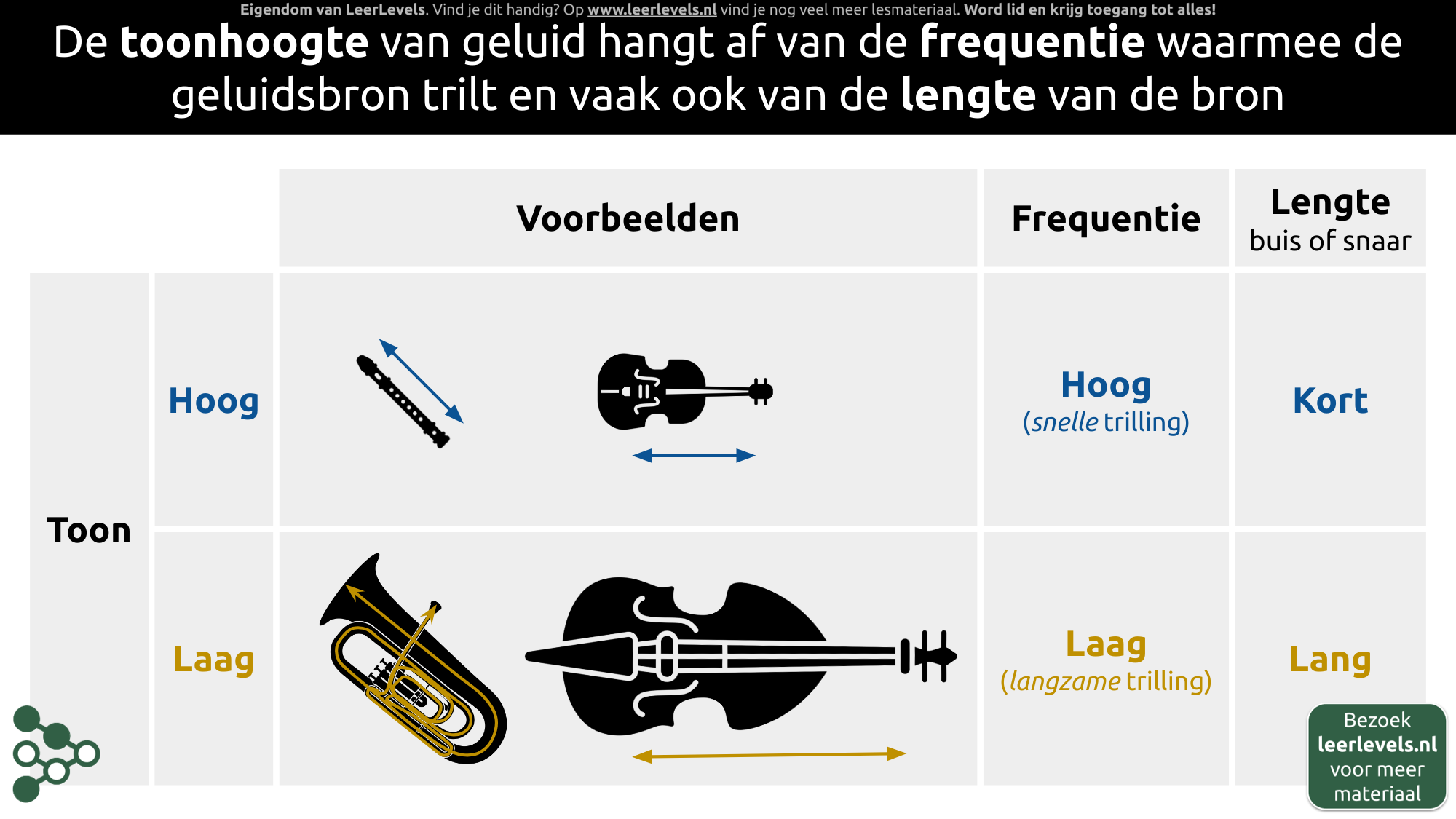
(Afbeelding: Animatie voor Toonhoogte)

Terug naar overzicht Meld je aan

Gewicht

Gewicht is de grootte van de kracht tussen jou en een steunvlak. Als je stilstaat in een lift zonder versnelling, is de kracht omhoog (normaalkracht) gelijk aan de kracht omlaag (zwaartekracht) en geeft de weegschaal je juiste massa aan. Bij versnelling naar boven wordt de normaalkracht groter en dus ook je gewicht. Bij versnelling naar beneden wordt de normaalkracht kleiner en dus ook je gewicht. Alleen als er geen verticale versnelling is, is je gewicht gelijk aan de zwaartekracht. Gewicht wordt uitgedrukt in Newton (N).

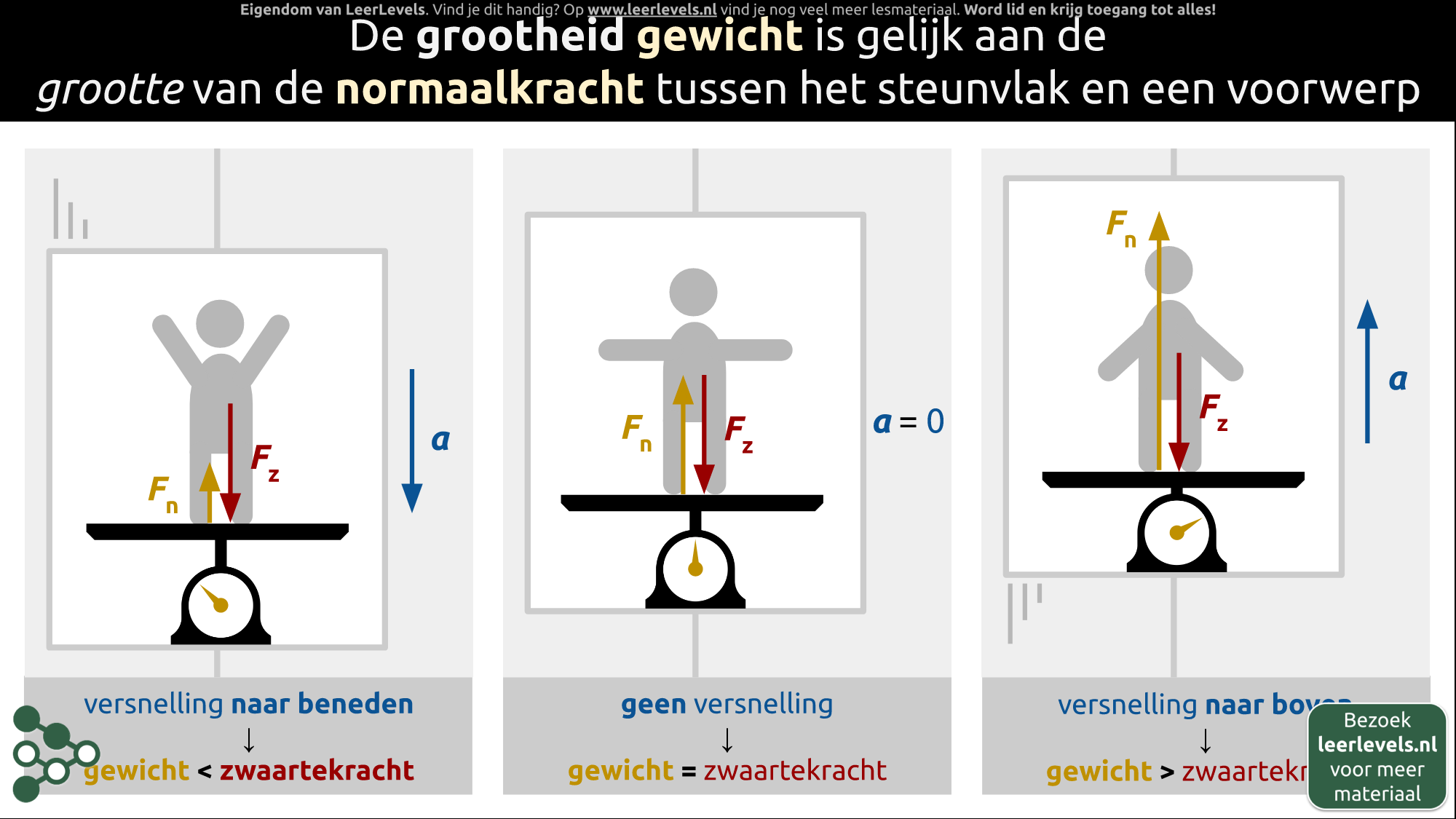
(Afbeelding: Animatie voor Gewicht)

Terug naar overzicht Meld je aan

Gezichtsveld

Het gezichtsveld omvat alle plekken van waaruit licht de ogen kan bereiken. Stel je een zeer grote ruimte voor met twee ogen. Omdat ogen niet recht opzij of naar achteren kunnen kijken, ligt een bepaald gebied, aangeduid met een groen vlak, binnen het gezichtsveld. Als er vervolgens een muur wordt geplaatst, kun je door middel van zichtlijnen bepalen welk gebied nog zichtbaar blijft. Dit doe je voor elk oog afzonderlijk. Vervolgens bepaal je welke gebieden door geen van beide ogen zichtbaar zijn; dat gebied ligt buiten het gezichtsveld. Door een spiegel te gebruiken, kan het gezichtsveld worden vergroot. Met extra zichtlijnen kun je in kaart brengen hoe het gezichtsveld wordt vergroot.

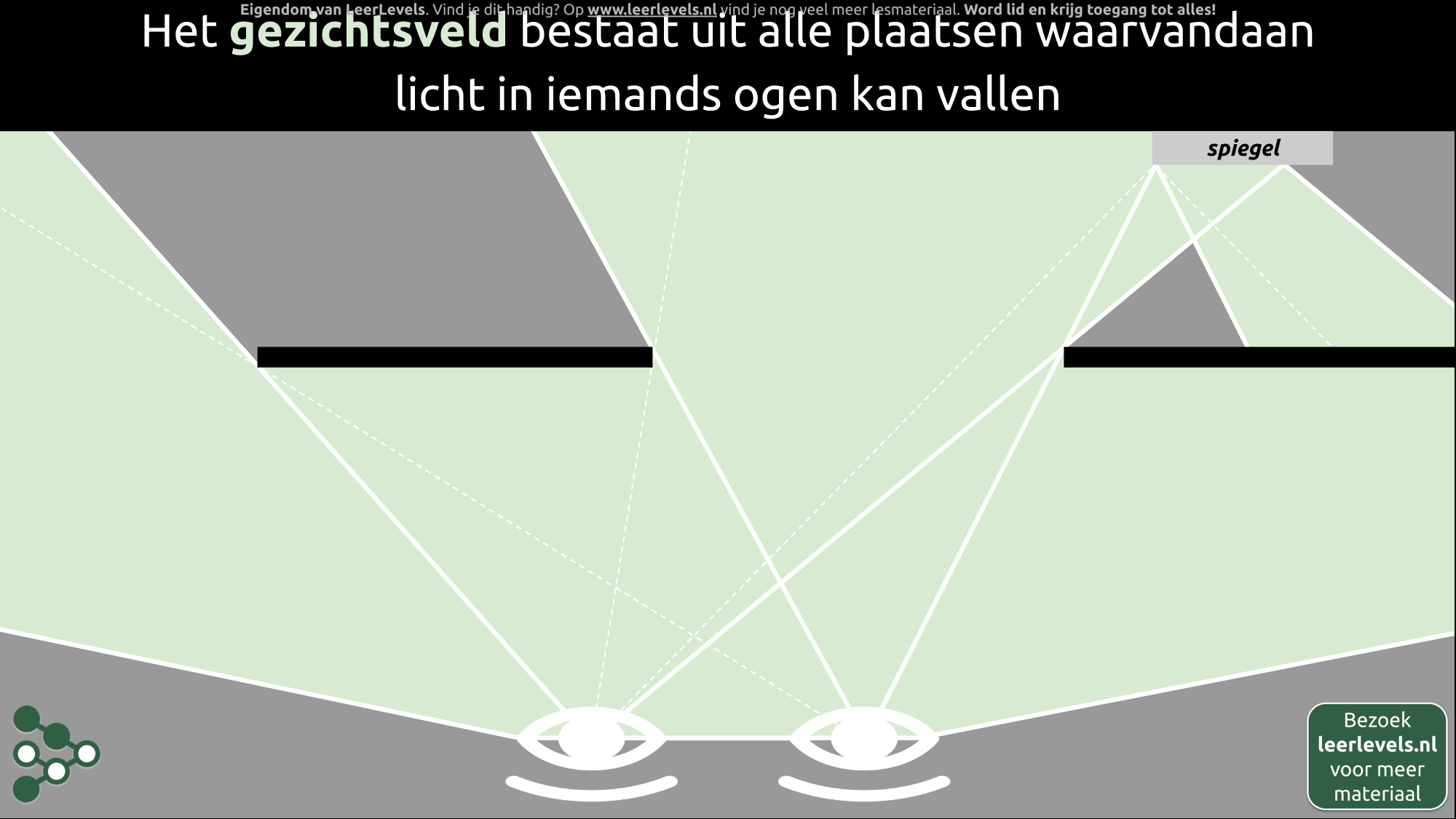
(Afbeelding: Animatie voor Gezichtsveld)

Terug naar overzicht Meld je aan

Gloeilamp

Werking gloeilamp

Een gloeilamp geeft licht doordat de gloeidraad heel heet wordt als er stroom doorheen loopt. Dit zorgt voor thermische energie, waardoor elektronen in een hogere toestand terechtkomen. Als deze elektronen weer terugvallen, stralen ze licht uit. Het licht komt dus niet voort uit het absorberen en uitstralen van fotonen, maar uit de thermische energie.

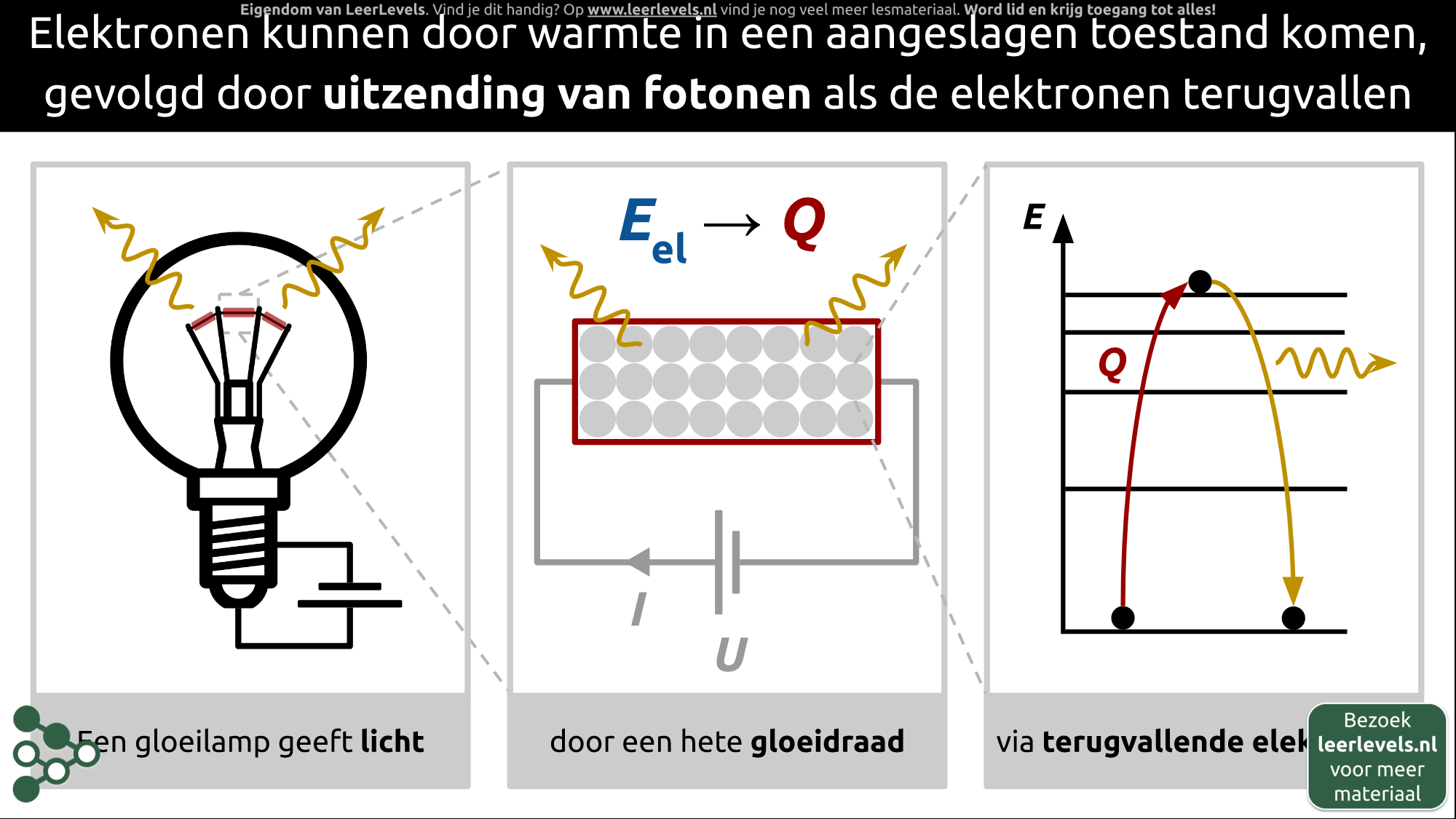
(Afbeelding: Animatie voor Werking gloeilamp)

Terug naar overzicht Meld je aan

Golf

Een golf is een trillende beweging die ontstaat doordat trillingen elkaar beïnvloeden. Een golf op een touw is een bekend voorbeeld: als je een punt omhoog trekt, gaat het volgende punt ook omhoog en verplaatst de golf zich zo. Belangrijk is dat een golf uit meerdere trillingen bestaat: elk punt op het touw trilt alleen maar op en neer, maar door de invloed van andere trillingen ontstaat er een golvende beweging. De deeltjes van het touw trillen alleen maar in combinatie met andere trillingen. Dit noemen we een golf.

(Afbeelding: Animatie voor Golf)

Golf weergeven

Een UX-diagram laat de volledige golf in één oogopslag zien, terwijl een UT-diagram de beweging van een specifiek punt op de golf in de tijd weergeeft.

Laten we deze twee diagrammen naast elkaar bekijken. Links bevindt zich het UX-diagram van de hele golf, waarbij de positie x op de x-as staat en de uitwijking op de y-as.

Rechts is het UT-diagram geplaatst, met de tijd op de x-as.

Stel dat we beginnen met een touw op tijdstip t = 0. Als we op dat moment een foto maken, zien we een recht touw. In het rechter diagram observeren we hoe één punt op dat touw in beweging komt, specifiek bij plaats x = 0. In het linker diagram is dit te zien als het punt helemaal links op het touw, met een uitwijking van 0, net als alle andere punten.

Laten we het touw na 1 seconde een beetje omhoog trekken. We maken opnieuw een foto. In het UX-diagram zie je dan de blauwe lijn. Het punt bij positie x = 0 is dan iets omhoog gegaan.

Na 2 seconden zien we dat het touw nog verder is opgetrokken. Het beginpunt (x = 0) is dan verder omhoog gegaan.

Wanneer we het touw vervolgens naar beneden trekken, verplaatst het punt x = 0 ook naar beneden. Dit proces herhaalt zich en leidt tot een golfbeweging. Aan de rechterkant ontstaat dus ook een soort golfpatroon. Als je deze beweging voortzet, ontstaat de grijze lijn. Door in de tijd één punt te volgen, krijg je een grijze sinusvorm.

In het linker diagram, het UX-diagram, maken we als het ware telkens nieuwe foto's. In het rechter diagram volgen we de positie van één punt in de tijd.

In het linker diagram is de rode pijl gelijk aan een halve golflengte. We zien slechts de helft van de golflengte.

In het rechter diagram komt de pijl overeen met een halve trillingstijd. Na deze tijd is de helft van de volledige trilling van dat specifieke punt doorlopen.

Het is essentieel om te letten op wat er op de x-as staat. Als daar positie staat, kun je uitspraken doen over de golflengte. Als er tijd staat, kun je uitspraken doen over de trillingstijd.

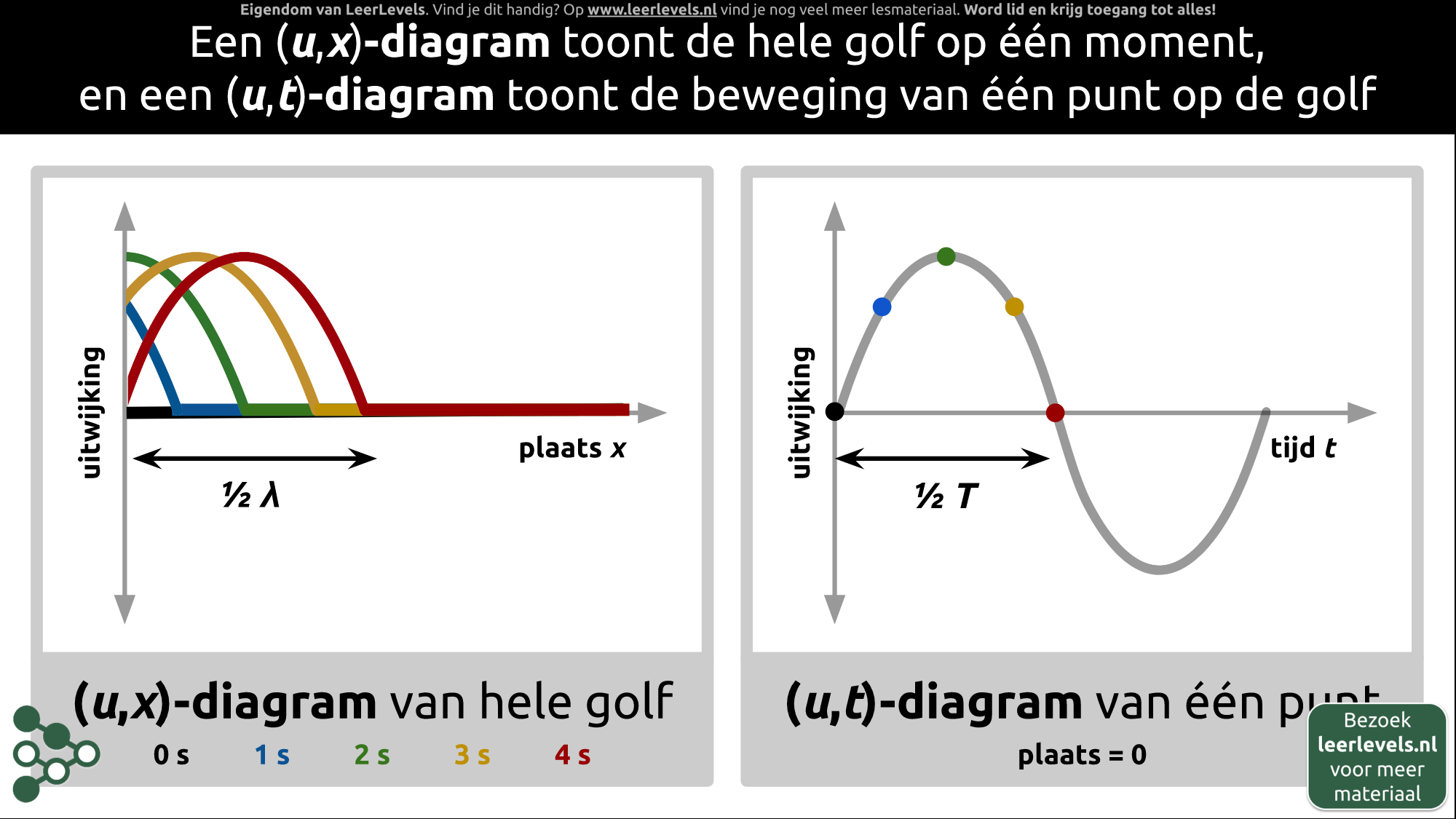
(Afbeelding: Animatie voor Golf weergeven)

Terug naar overzicht Meld je aan

Golf-deeltje dualiteit

Golf-deeltje dualiteit waarnemingen

In de geschiedenis zijn er waarnemingen gedaan die aantonen dat licht zowel golfgedrag als deeltjesgedrag vertoont.

De waarnemingen die het golfgedrag van licht illustreren, zijn over het algemeen ouder. Denk bijvoorbeeld aan breking: wanneer wit licht door een prisma gaat, breken de verschillende kleuren onder net een andere hoek. Dit fenomeen is goed te verklaren als je licht behandelt als een golf. Buiging is ook een kenmerk van golfgedrag; hierbij beweegt een golf door een kleine opening en verspreidt zich vervolgens in alle richtingen. Interferentie, zoals te zien in Young's dubbelspleet-experiment, is eveneens een verschijnsel dat bij golfgedrag hoort.

Er zijn daarnaast waarnemingen die suggereren dat licht zich als een deeltje gedraagt. Bijvoorbeeld, de Planckkromme van een zwarte straler kan alleen verklaard worden door licht te beschouwen als discrete deeltjes (fotonen). Het foto-elektrisch effect is ook bewijs dat fotonen gequantiseerd zijn: per foton kan er maar één elektron worden vrijgemaakt. Ten slotte is er het Compton-effect, dat verklaard kan worden als je fotonen beschouwt als deeltjes met een bepaalde impuls; hierdoor kunnen ze elektronen een impuls geven.

Al deze waarnemingen tezamen leiden tot de conclusie dat we licht zowel als golf als deeltje moeten behandelen.

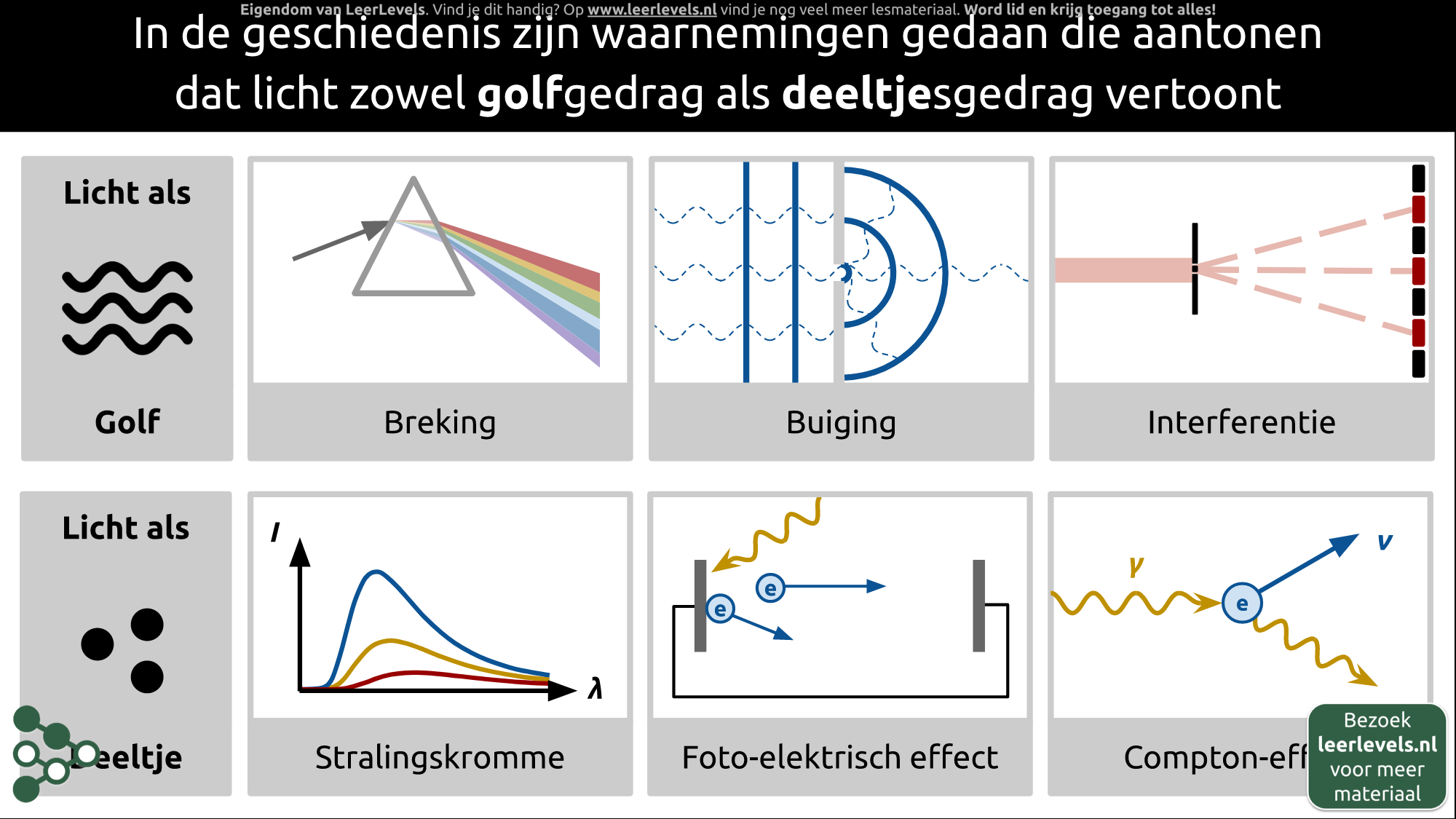
(Afbeelding: Animatie voor Golf-deeltje dualiteit waarnemingen)

Terug naar overzicht Meld je aan

Golflengte

De golflengte is hoe ver het is tussen twee pieken of twee dalen van een golf. Dit is makkelijk te zien bij transversale golven, zoals een golf in een touw of watergolven. Bij geluidsgolven in lucht is het iets lastiger, omdat er geen pieken en dalen zijn. In plaats daarvan zijn er plekken waar de lucht dichter of minder dicht is. De afstand tussen twee van deze plekken noemen we de golflengte. Kort gezegd is de golflengte de afstand tussen twee pieken of dalen van een golf. Het wordt zichtbaar bij transversale golven en door dichtheid te kijken bij longitudinale golven.

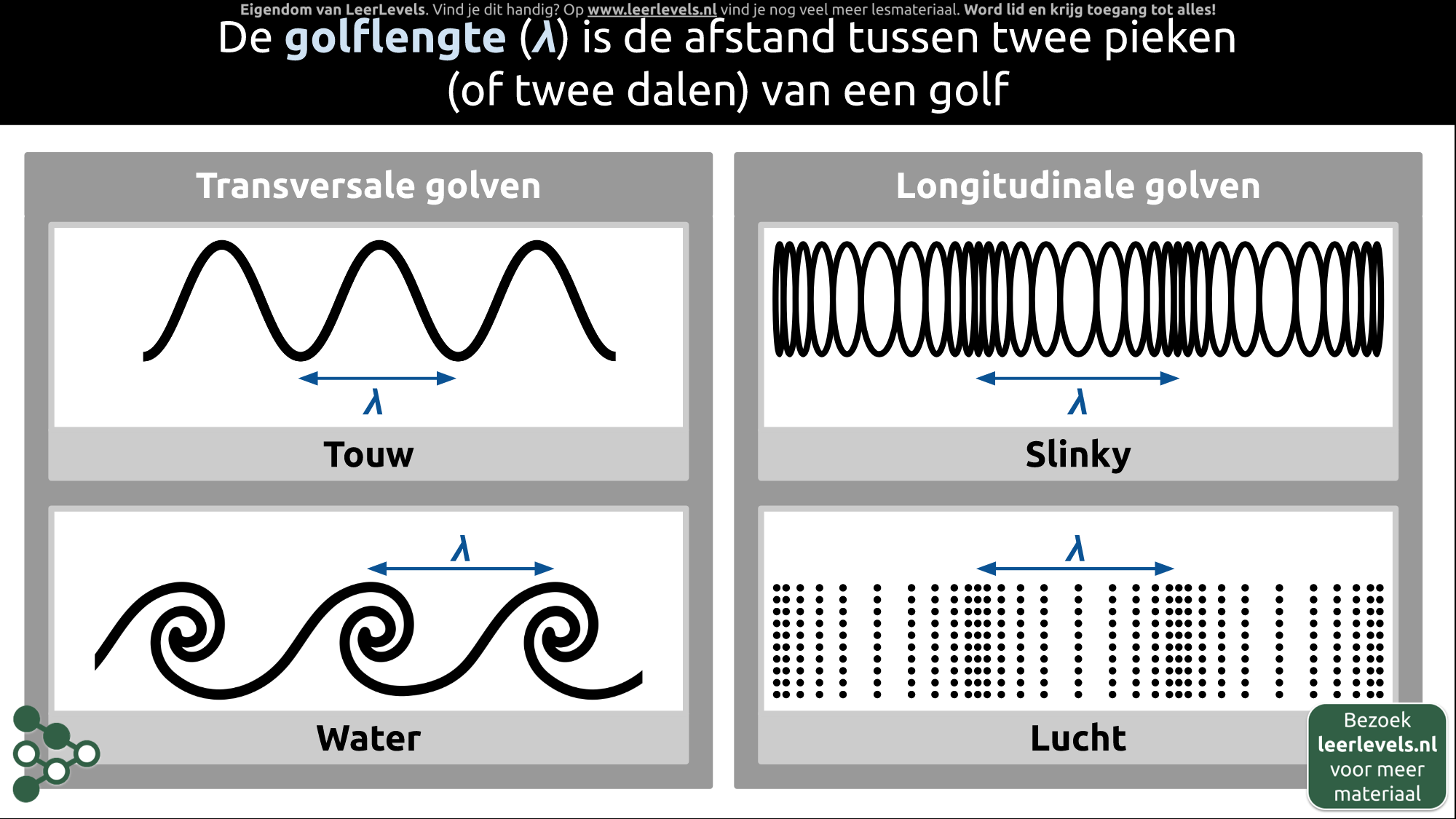
(Afbeelding: Animatie voor Golflengte)

Terug naar overzicht Meld je aan

Golfsnelheid

Golfsnelheid concept

De golfsnelheid vertelt ons hoe snel een golf zich verplaatst, maar zegt niets over hoe snel individuele punten bewegen. Als we een golf naar rechts zien bewegen, kunnen we door bepaalde punten op het touw te plaatsen zien wat er met het touw gebeurt. Na een bepaalde tijd is de golf verder naar rechts verplaatst en zien we dat sommige punten terug zijn gegaan naar de evenwichtsstand en andere punten ervan zijn afgeweken. Om de golfsnelheid te berekenen, kijken we naar de verplaatsing van de piek (of dal) en gebruiken we de formule: snelheid = verplaatsing / tijd. De verplaatsing van de piek wordt weergegeven met Delta x en de verstreken tijd in seconden met Delta t. Als we deze waarden in de formule invullen, krijgen we de golfsnelheid in meter per seconde.

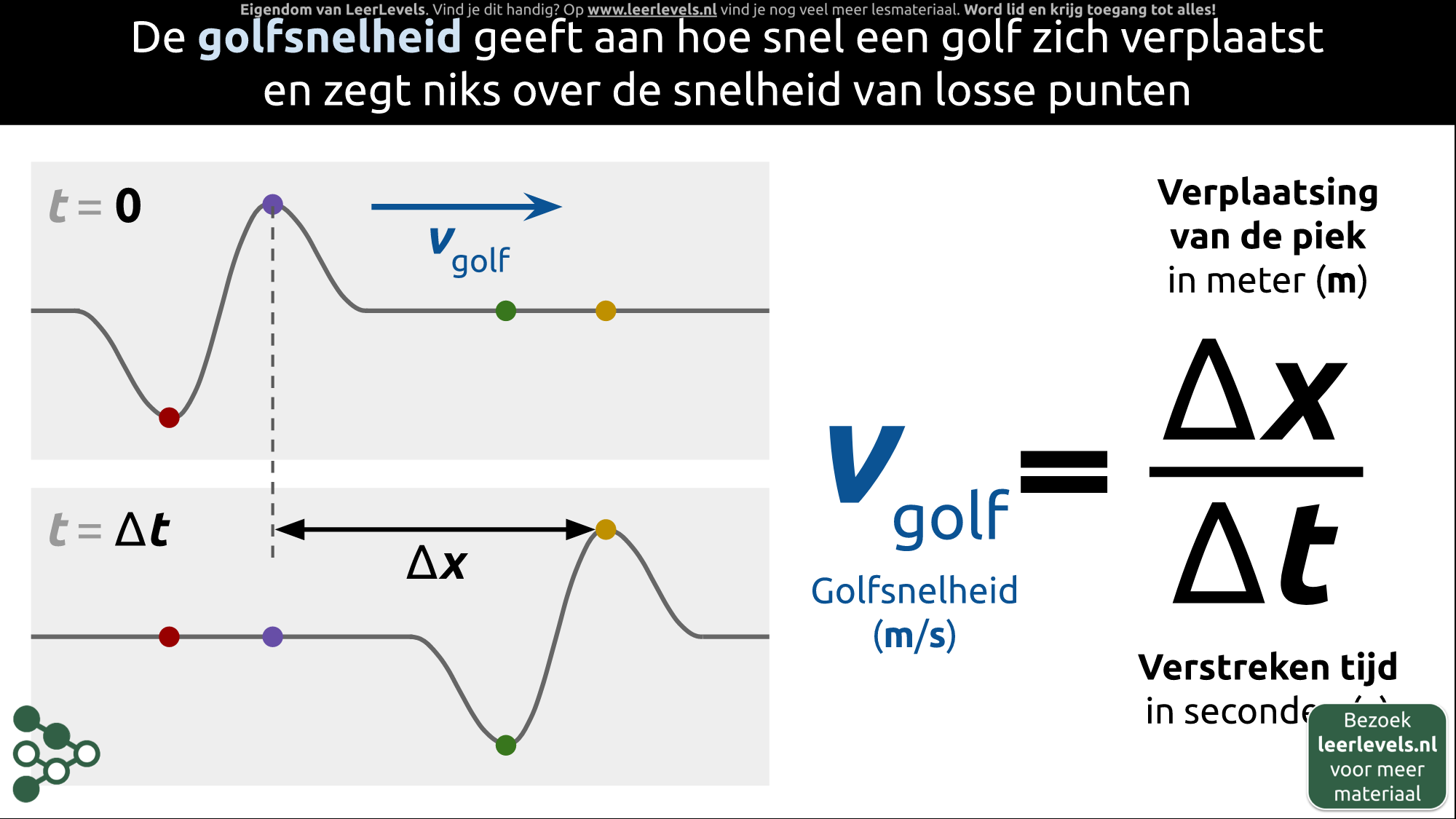
(Afbeelding: Animatie voor Golfsnelheid concept)

Golfsnelheid afleiding

Als je begrijpt wat snelheid, golflengte en frequentie zijn, kun je de formule voor golfsnelheid afleiden. Als je naar een golf kijkt die naar rechts beweegt op tijdstip t = 0 en een trillingstijd later kijkt, heeft het golffront zich precies één golflengte verplaatst. Dit betekent dat de golf een bepaalde snelheid heeft. Je kunt deze snelheid berekenen door de golflengte te delen door de trillingstijd. Dit kan ook geschreven worden als golflengte keer frequentie. Snelheid wordt gemeten in meter per seconde, de golflengte in meter en de frequentie in Hertz.

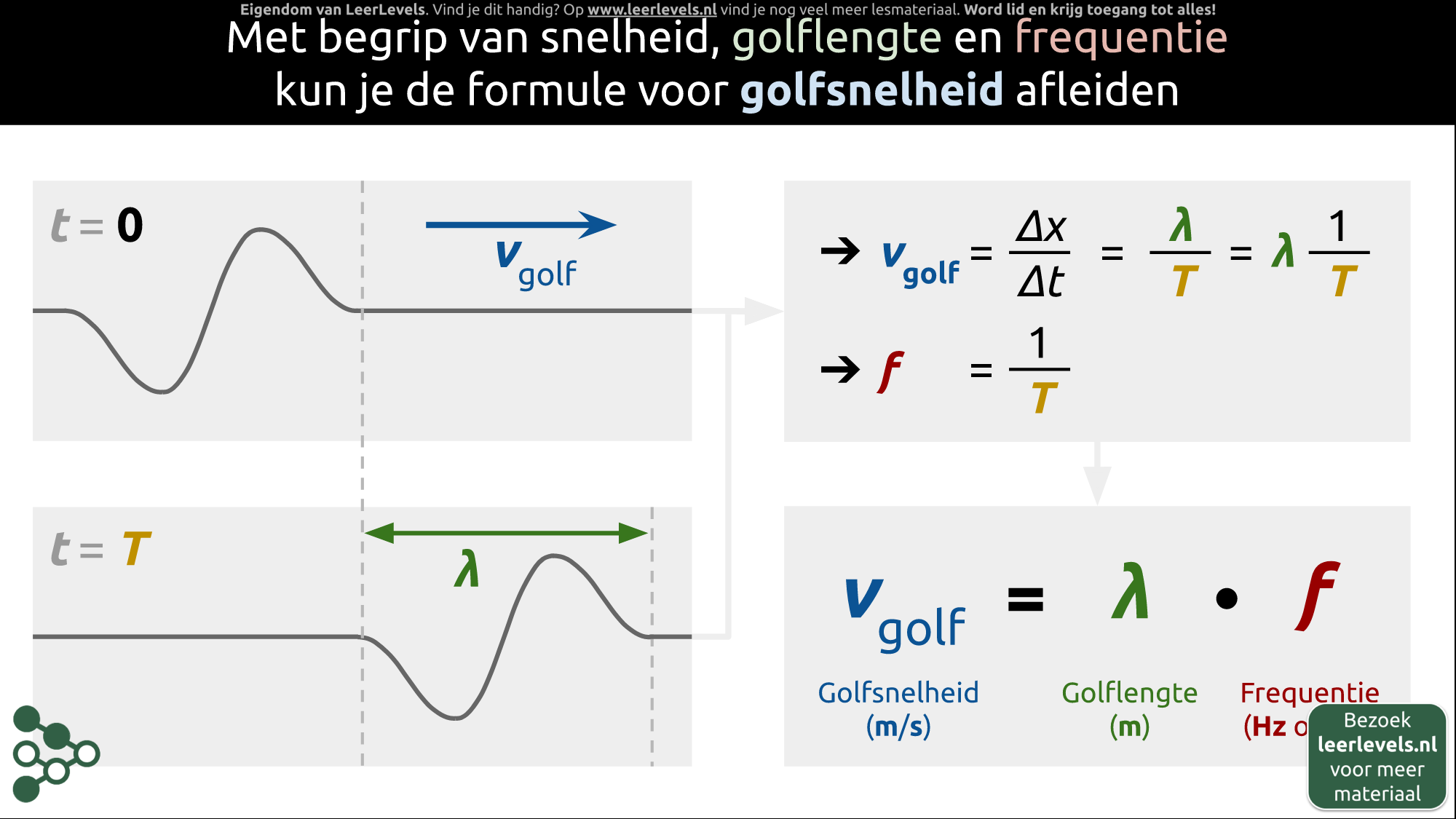
(Afbeelding: Animatie voor Golfsnelheid afleiding)

Golfsnelheid formule

De snelheid waarmee een golf beweegt is recht evenredig met de golflengte en de frequentie. Dit betekent dat de golfsnelheid gelijk is aan de golflengte λ vermenigvuldigd met de frequentie f. Wiskundig kunnen we dit als volgt schrijven:

v = λ · f

waarbij v de golfsnelheid is, λ de golflengte in meters, en f de frequentie in Hertz (aantal per seconde).

(Afbeelding: Animatie voor Golfsnelheid formule)

Terug naar overzicht Meld je aan

Golven

Transversale en longitudinale golven

Er zijn twee soorten golven: transversaal en longitudinaal. Bij een transversale golf bewegen trillingen loodrecht op de richting van de golf. Dit betekent bijvoorbeeld dat als we een veer hebben die onze golf vertegenwoordigt, onze handen op en neer zullen bewegen terwijl de golf van links naar rechts gaat. Bij een longitudinale golf bewegen trillingen parallel aan de richting van de golf. Als we een veer hebben die onze golf vertegenwoordigt, bewegen we onze handen voor en achteren. Hierdoor worden er verdikkingen en verdunningen in de veer gecreëerd die zich als een golf kunnen voortplanten. Elk stukje van de veer blijft echter op ongeveer dezelfde plek en beweegt in dit geval van links naar rechts. Er worden geen formules, grootheden of eenheden genoemd.

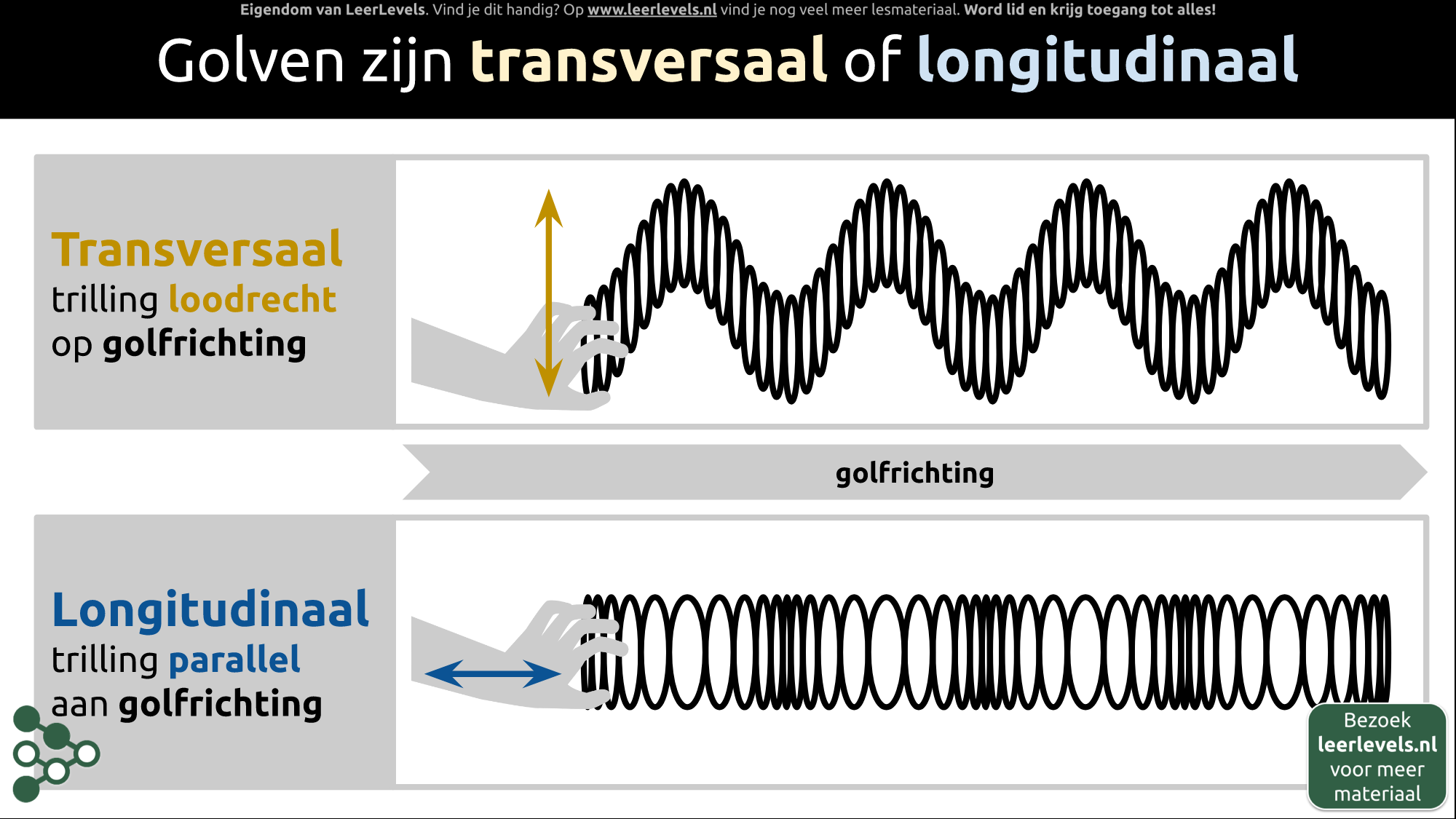
(Afbeelding: Animatie voor Transversale en longitudinale golven)

Lopende en staande golven

Het verschil tussen lopende en staande golven wordt bepaald door de uitwijking en beweging van de pieken. Laten we eerst kijken naar een lopende golf, weergegeven op verschillende tijdstippen. Lopende golven hebben twee eigenschappen: de pieken bewegen en de amplitude blijft constant.

Bij een staande golf zien we diagrammen die de uitwijking in de tijd laten zien. In het eerste beeld is de uitwijking maximaal omhoog, waarna deze kleiner wordt, nul bereikt en vervolgens naar beneden afwijkt. Dit beschrijft bijvoorbeeld de beweging van een trillende snaar.

Een staande golf heeft geen bewegende pieken. De locatie van de pieken blijft constant en de golf heeft geen constante amplitude.

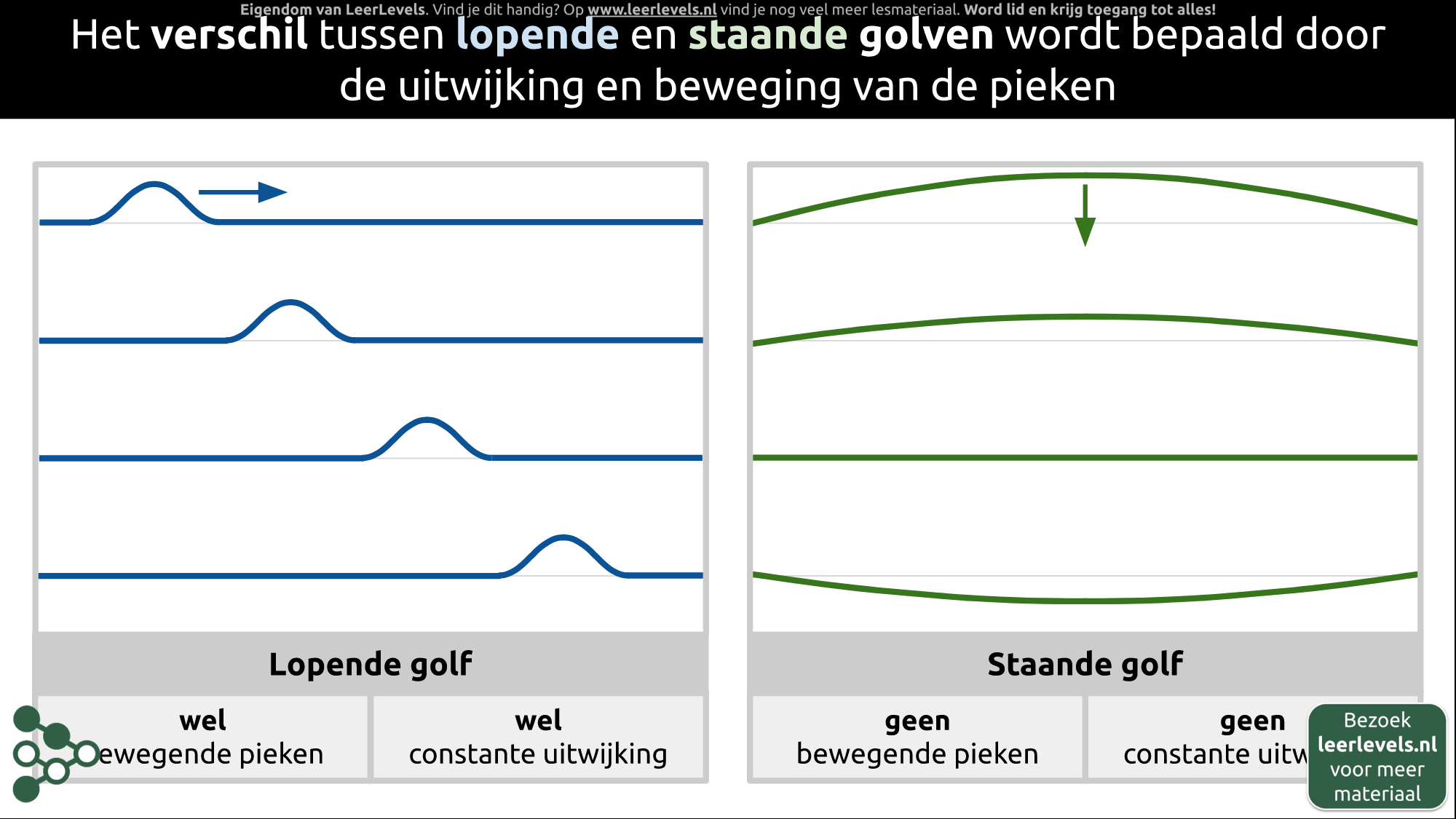
(Afbeelding: Animatie voor Lopende en staande golven)

Terug naar overzicht Meld je aan

Grafieken

Grafiek tekenen

Een grafiek bij een tabel maken doe je in vier stappen:

1. Maak een tabel waarbij je de grafiek kunt tekenen.
2. Kies de horizontale en verticale as. De horizontale as is voor de onafhankelijke variabele, bijvoorbeeld tijd, en de verticale as is voor de afhankelijke variabele, bijvoorbeeld afstand.
3. Verdeel de assen en zet de punten uit de tabel in de grafiek.
4. Trek een vloeiende lijn door de punten.

Als je deze stappen volgt, kun je van een tabel naar een grafiek komen.

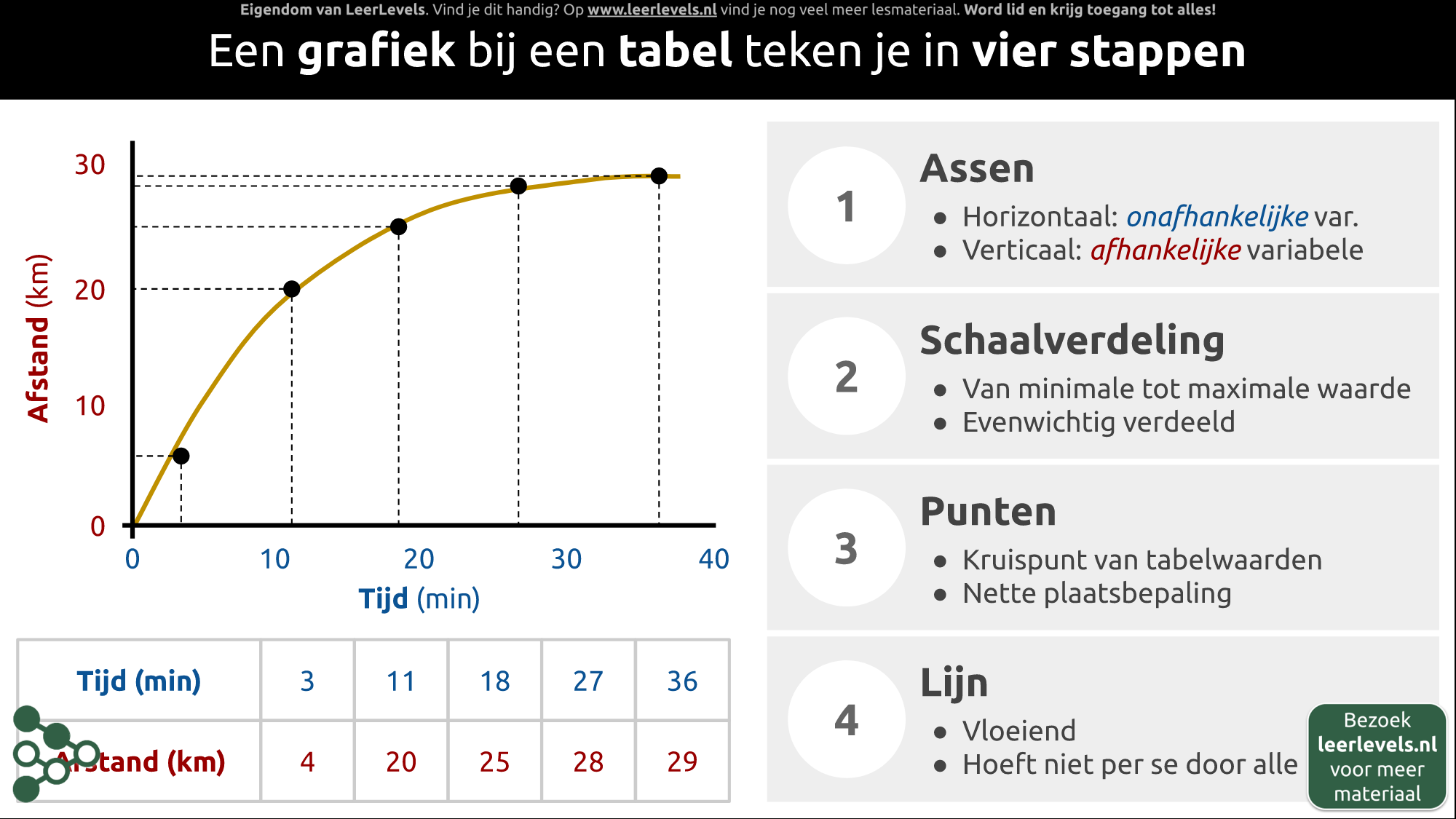
(Afbeelding: Animatie voor Grafiek tekenen)

Grafiek herkennen

Een goede grafiek heeft vaste onderdelen. Teken eerst netjes de assen met een geodriehoek of liniaal. Zet de grootheden die je meet langs de assen, met de bijbehorende eenheden van tijd (s) en afstand (m). Je kan de tijd en afstand in andere eenheden zetten, maar maak het wel duidelijk. Voeg schaalverdelingen toe, inclusief de oorsprong. Het is netjes als de grafiek bij het punt 0,0 begint. Maak duidelijke datapunten en verbind ze met een rechte of gebogen lijn. Kies voor een rechte lijn bij een recht evenredig verband en anders voor een vloeiende gebogen lijn. Door deze zeven regels te volgen, maak je altijd een goed afleesbare grafiek.

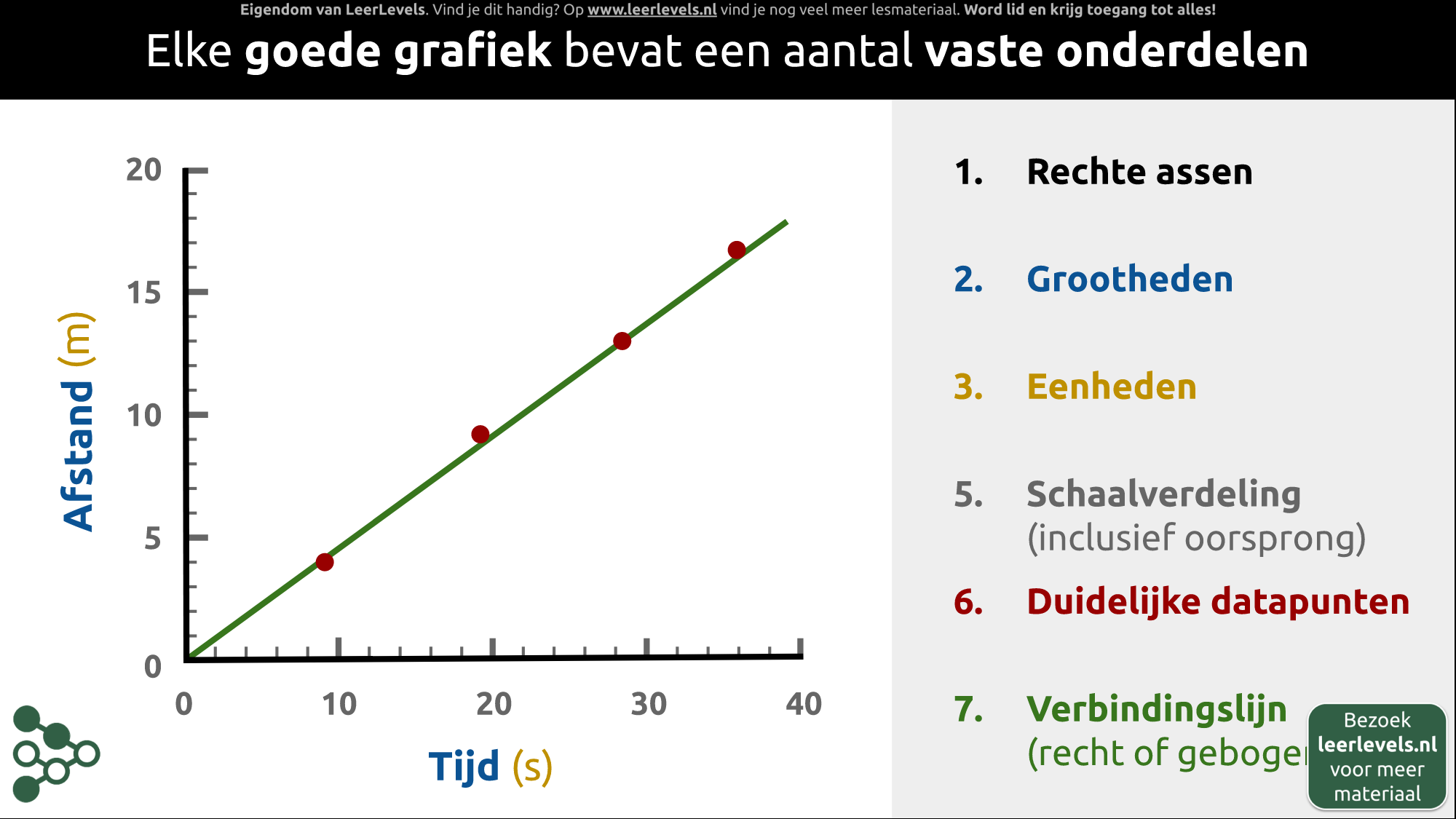
(Afbeelding: Animatie voor Grafiek herkennen)

Terug naar overzicht Meld je aan

Grafisch model

Grafisch model onderdelen

Een grafisch model bestaat uit verschillende onderdelen en is bedoeld om situaties te visualiseren. Bijvoorbeeld een emmer die gevuld wordt met water uit de kraan, waarbij er een gaatje in zit waar water uit kan stromen. De hoeveelheid water in de emmer noemen we de toestandsvariabele of groeigrootte. Deze waarde wordt bijgehouden en kan toenemen of afnemen. Bij het begin van het model moet de beginwaarde van de emmer worden ingesteld. Om het model te visualiseren, vullen we de emmer aan de ene kant met een kraan en aan de andere kant is er een klein gaatje waardoor het water langzaam wegstroomt. Voor het in- en uitstromende water hebben we twee pijlen nodig, een voor de instroomsnelheid en een voor de uitstroomsnelheid. De stroombel geeft aan hoeveel de waarde voor de toestandsvariabele per tijdseenheid moet veranderen. Deze waarde kan worden ingesteld of volgt uit andere waarden.

Een hulpvariabele die we kunnen gebruiken om alle deelstappen van een model te laten zien, is de stand van de kraan. Dit is een variabele die wordt gebruikt om het volume van de grootheid in te stellen. Om de stand van de kraan te koppelen aan andere objecten in het model, zoals de instroomsnelheid, gebruiken we relatiepijlen. Deze geven formules weer. Bijvoorbeeld: "De instroomsnelheid is gelijk aan drie keer de stand van de kraan". Het is handig als we deze variabele kunnen aanpassen als we het model later willen uitbreiden, bijvoorbeeld met een automatisch sluitende kraan.

Om de relatie tussen het water in de emmer en de uitstroomsnelheid aan te geven, trekken we ook een relatiepijl. Meer water betekent een grotere uitstroomsnelheid, maar het hangt ook af van de grootte van het gat, dat een constante variabele is. De beginwaarde van deze constante moet ook worden ingesteld door de gebruiker, omdat de grootte van het gat invloed heeft op de uitstroomsnelheid.

Dit is een simpel voorbeeld, maar de meeste modellen bevatten meer onderdelen. Hier zie je echter wel de belangrijkste onderdelen waaruit een grafisch model in Coach bestaat.

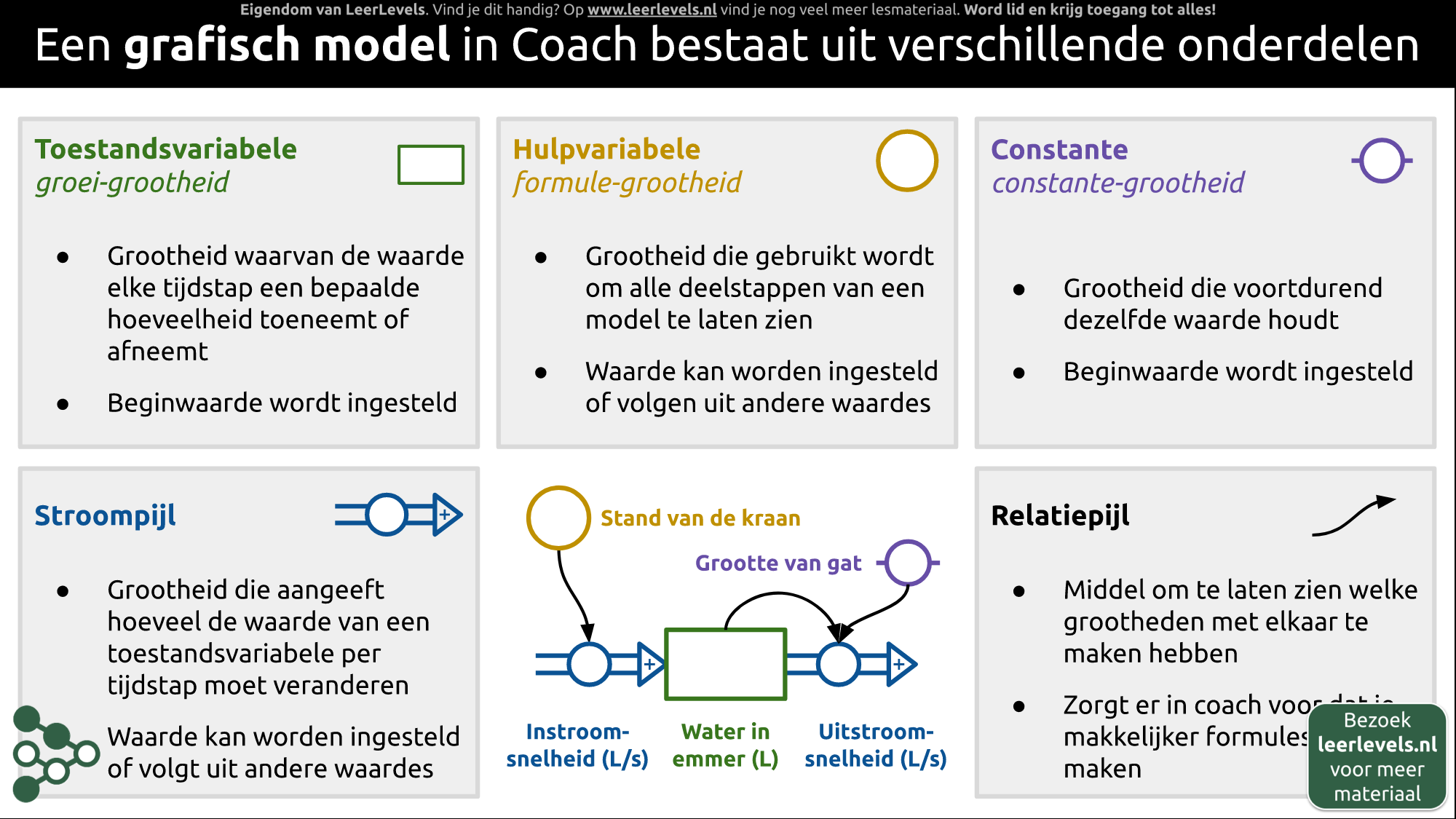
(Afbeelding: Animatie voor Grafisch model onderdelen)

Terug naar overzicht Meld je aan

Gravitatie-energie

Gravitatie-energie concept

Gravitatie-energie is de energie die twee massa's hebben als ze op een bepaalde afstand van elkaar zijn, zoals een astronaut in de ruimte en de aarde. De energie hangt af van de afstand tussen de twee massa's en is nul als de afstand oneindig is. Als de afstand kleiner wordt, neemt de gravitatiekracht toe en verricht deze arbeid. Dit zorgt ervoor dat de gravitatie-energie afneemt en in sommige gevallen negatief kan zijn. Het verschil in gravitatie-energie kan zowel negatief als positief zijn, afhankelijk van of de afstand tussen de massa's afneemt of toeneemt. Kortom, de gravitatie-energie is altijd negatief, maar het verschil kan zowel negatief als positief zijn.

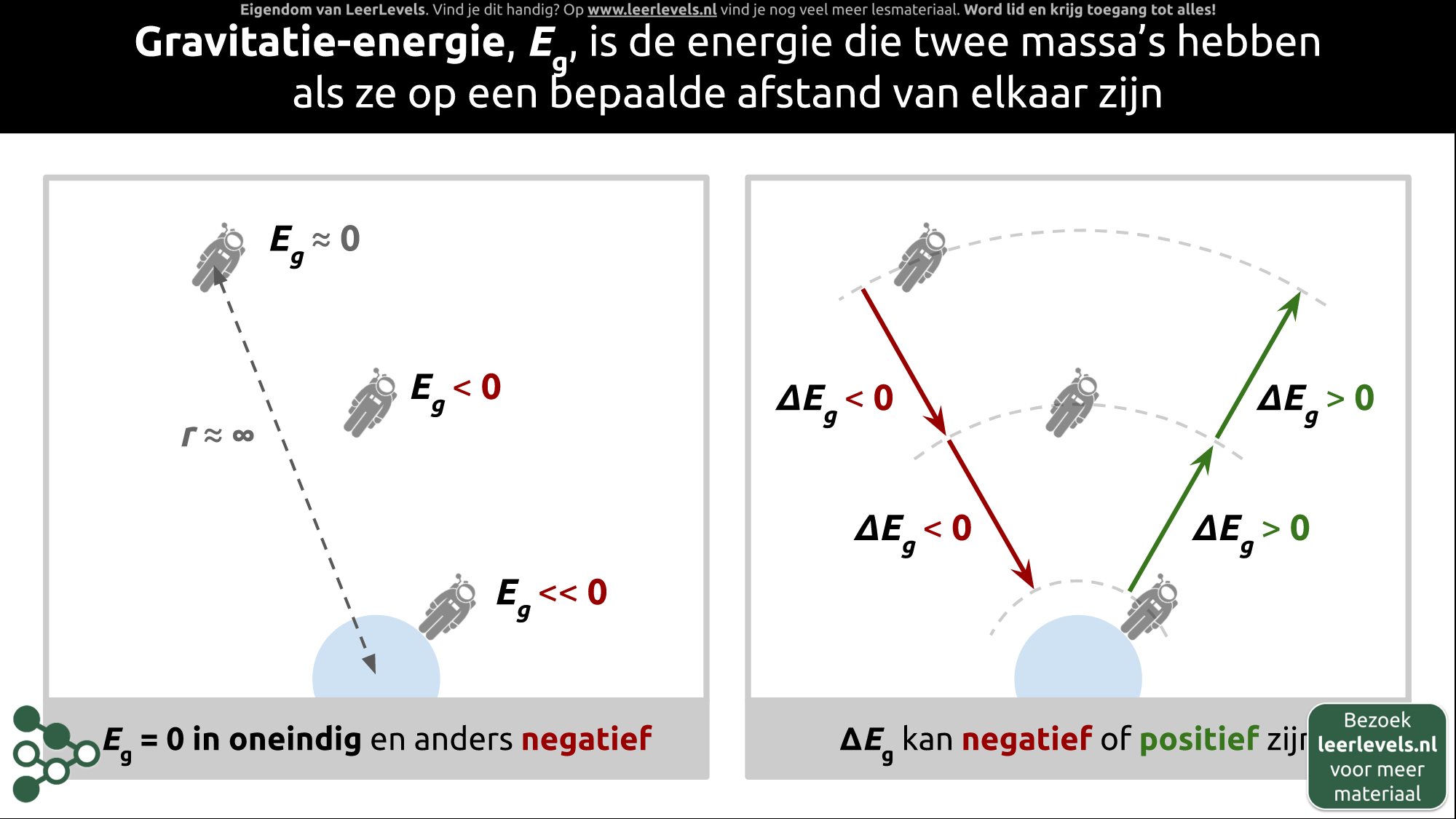
(Afbeelding: Animatie voor Gravitatie-energie concept)

Gravitatie-energie formule

Gravitatie-energie hangt af van de massa's van twee dingen en hoe ver ze van elkaar zijn. Dit wordt berekend met de formule Eg = -G (Mm)/(r), waarin G de gravitatieconstante is, M en m de massa's zijn (in kilogram) en r de afstand tussen hen (in meter). De waarde van G is 6,67 × 10⁻¹¹ Nm²/kg². Deze formule lijkt op de formule voor gravitatiekracht, maar in plaats van te delen door r² en geen min-teken te hebben, deelt deze door r en heeft een min-teken omdat gravitatie-energie negatief is.

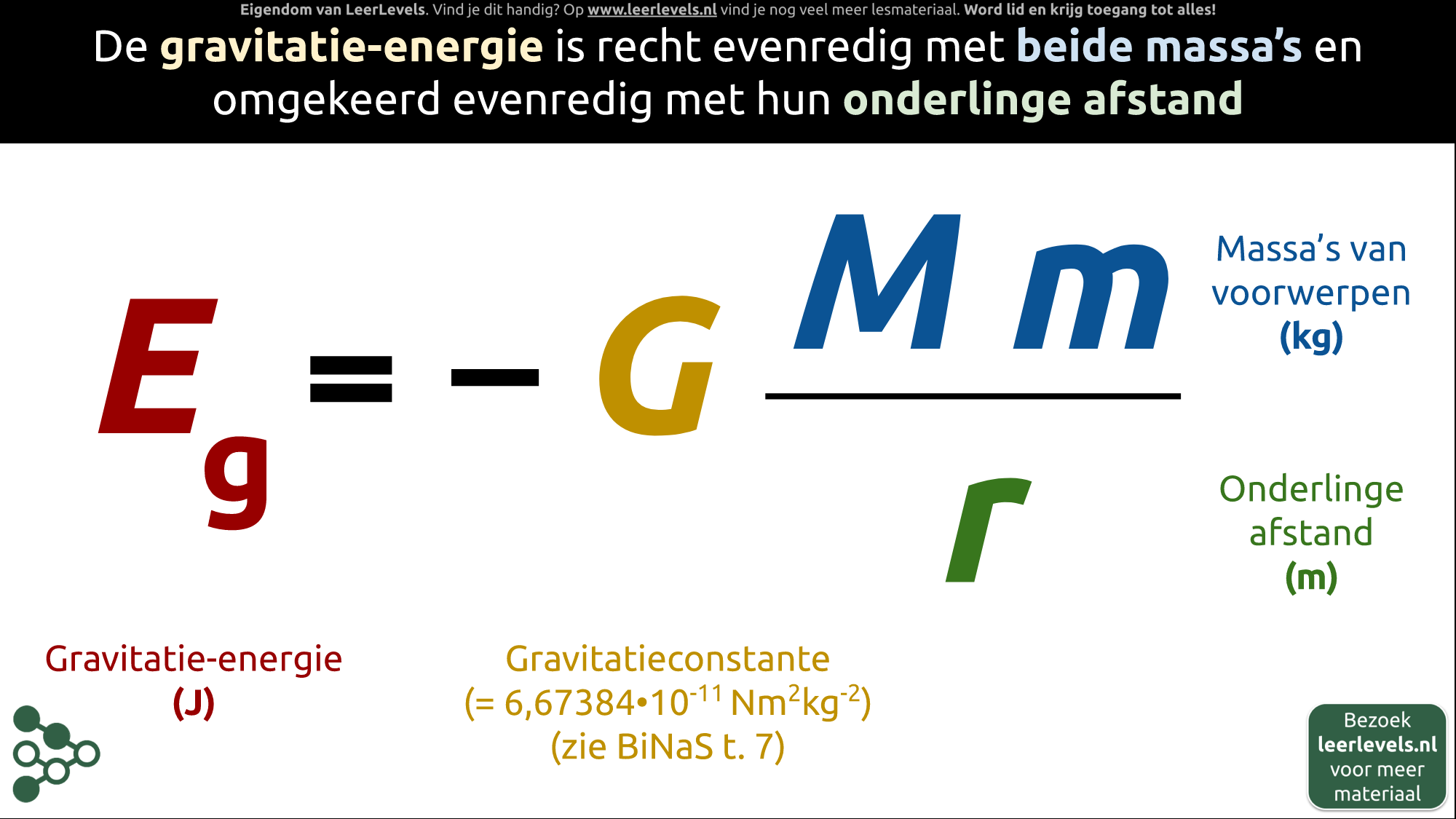
(Afbeelding: Animatie voor Gravitatie-energie formule)

Terug naar overzicht Meld je aan

Gravitatiekracht

Gravitatiekracht concept

Alles in het universum heeft een zwaartekracht en trekt elkaar aan. Dit heet de gravitatiekracht, Fg. Hoe groter de massa van een voorwerp en hoe dichterbij het andere voorwerp, hoe groter de gravitatiekracht is.

Een voorbeeld van grote gravitatiekracht is tussen de zon en de aarde. De zon trekt de aarde naar zich toe en andersom. De krachten zijn gelijk, maar omdat de zon zoveel groter is, voelt de aarde het meeste effect.

Een ander voorbeeld is tussen de aarde en een astronaut. Als de astronaut op het oppervlak van de aarde staat, is de gravitatiekracht 10³ N. Op grote afstand wordt de gravitatiekracht kleiner, omdat de afstand groter is. In de ruimte is de gravitatiekracht tussen de astronaut en de aarde heel klein, namelijk 10⁻⁹ N.

Hoe groter de afstand, hoe kleiner de gravitatiekracht. De massa blijft hetzelfde, maar de afstand heeft een grote invloed op de gravitatiekracht. De grootte van de gravitatiekracht wordt aangeduid met de eenheid N (newton).

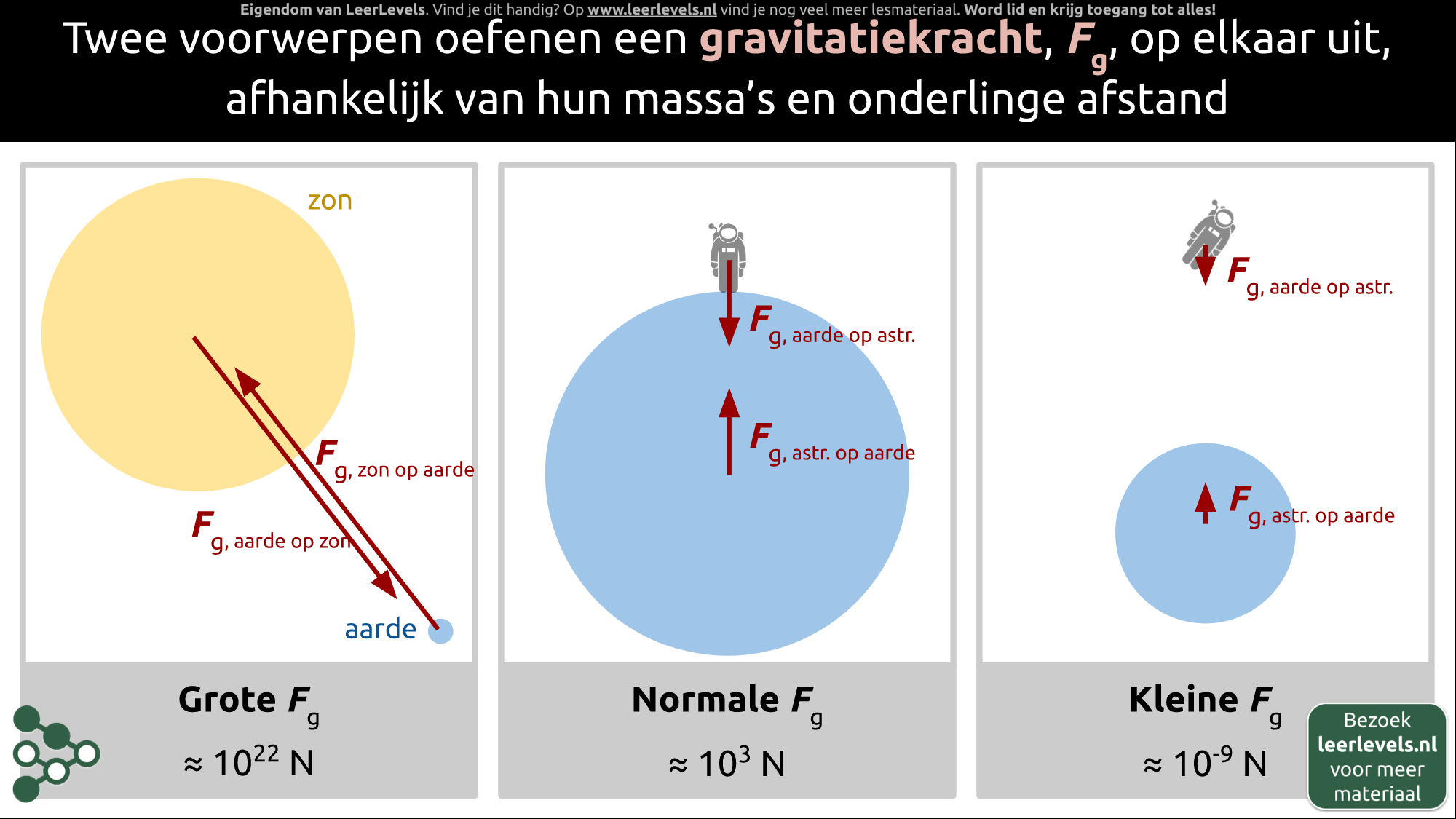
(Afbeelding: Animatie voor Gravitatiekracht concept)

Gravitatiekracht formule

De gravitatiekracht tussen twee voorwerpen is sterker als ze dichter bij elkaar zijn en zwakker als ze verder uit elkaar zijn. De formule om dit te berekenen is Fg = G · (M · m) / r², waarbij Fg de gravitatiekracht is, G de gravitatieconstante (6,67 x 10⁻¹¹ N m² / kg²), m en M de massa's van de voorwerpen zijn (in kilogram) en r de afstand tussen de voorwerpen is (in meter). Als je de afstand tussen de voorwerpen verdubbelt, wordt de gravitatiekracht vier keer zo klein. Soms wordt m1 en m2 gebruikt om de massa's aan te duiden, maar dit is niet verplicht.

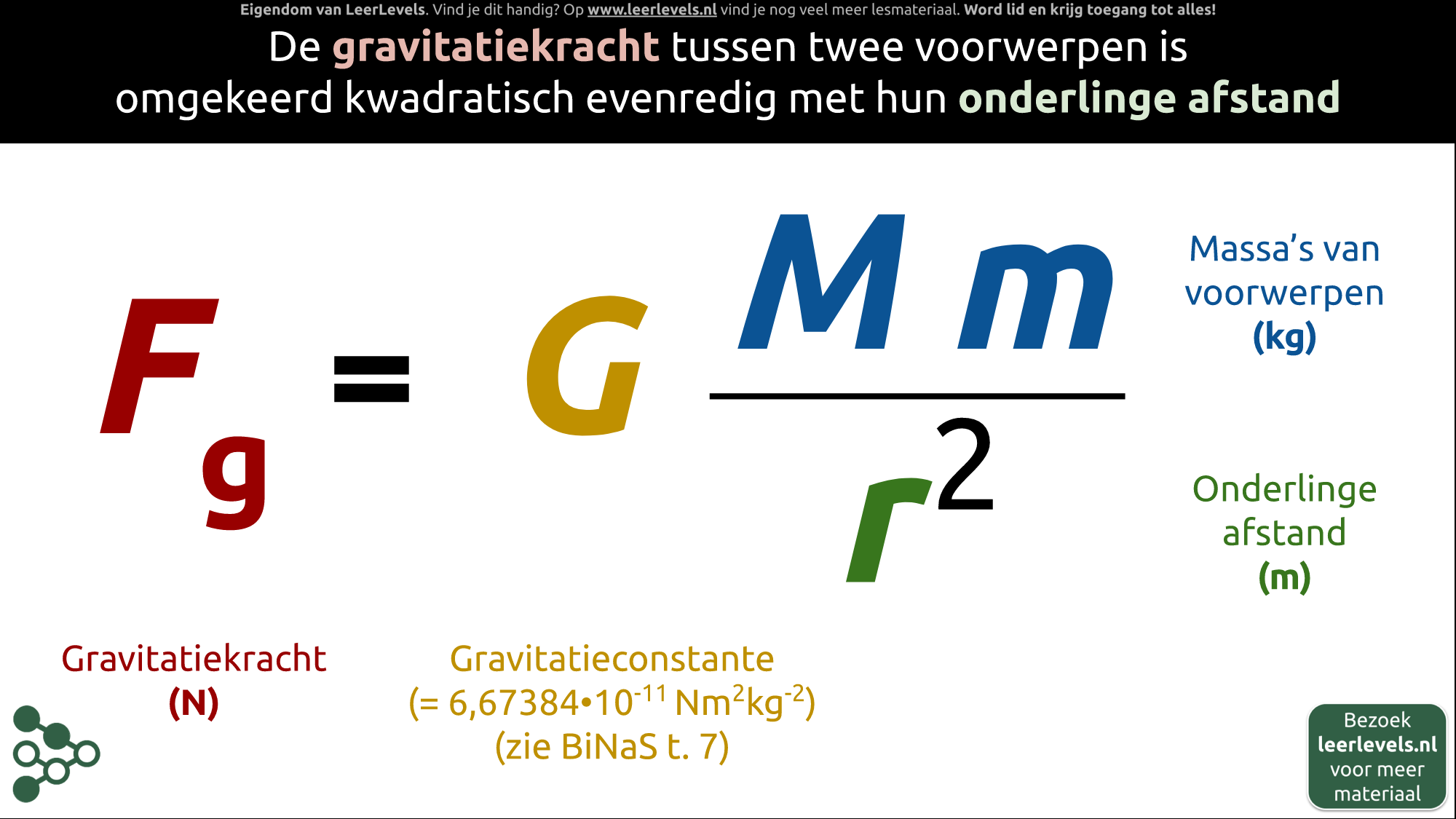
(Afbeelding: Animatie voor Gravitatiekracht formule)

Gravitatiekracht en zwaartekracht

Als je dicht bij het aardoppervlak bent, is de kracht die je voelt door de zwaartekracht bijna gelijk aan de zwaartekracht zelf. Dit geldt omdat de hoogte ten opzichte van de straal van de aarde erg klein is. Deze kracht kan worden beschreven door de formule Fz = m · g, waarbij m de massa van het object is en g de zwaartekrachtsversnelling. Voor de aarde is g ongeveer 9,81 m/s². De algemenere formule voor de gravitatiekracht is Fg = GMm/r², waarbij G de gravitatieconstante is en M en r de massa en straal van de planeet zijn. Dit kun je gebruiken om de zwaartekrachtsversnelling op andere planeten te berekenen. Kortom, de formule Fz = m · g is een speciaal geval van de algemenere gravitatiekrachtformule voor de aarde.

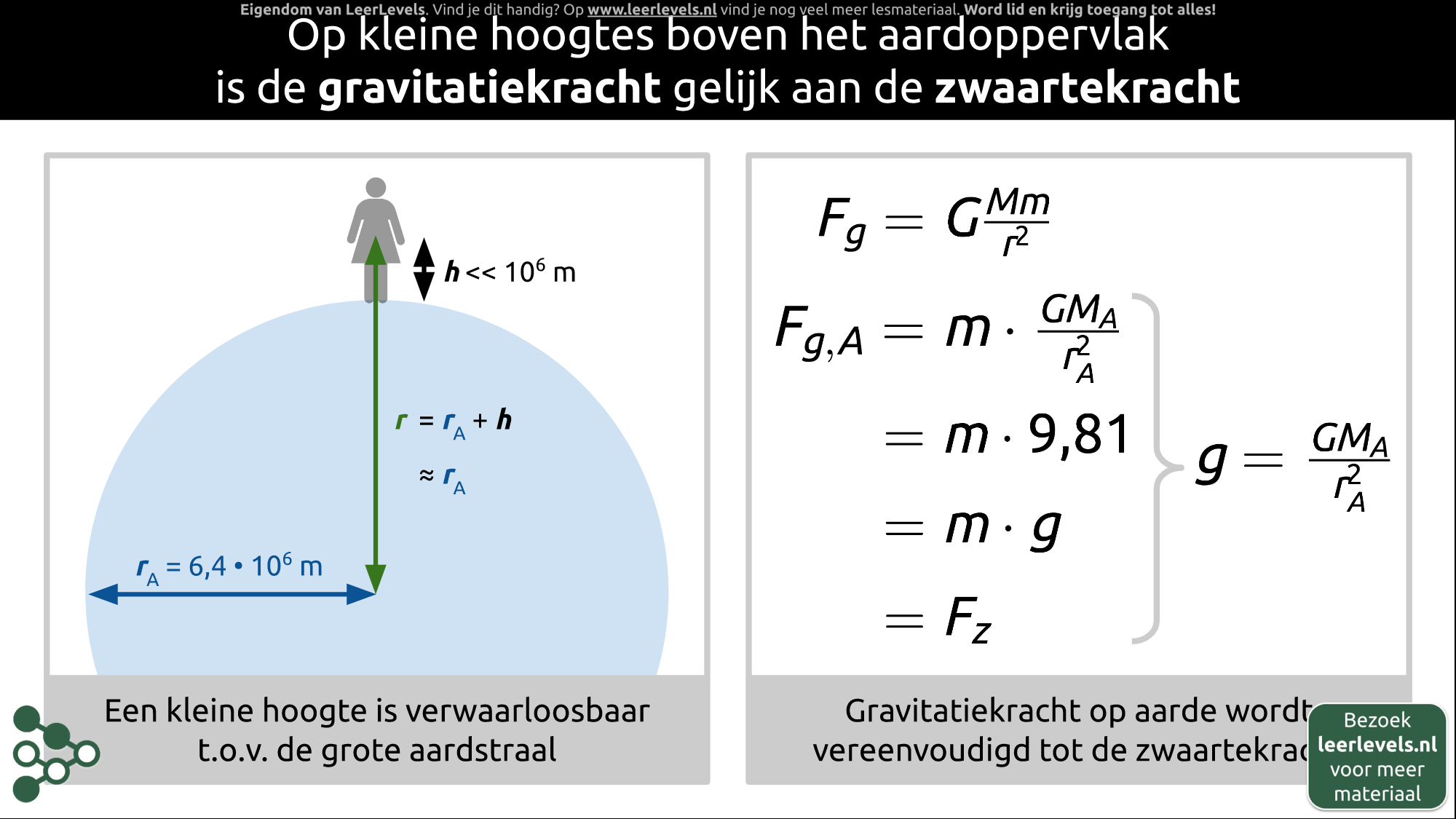
(Afbeelding: Animatie voor Gravitatiekracht en zwaartekracht)

Terug naar overzicht Meld je aan

Grondtoon

De grondtoon is de laagste toon die een object kan maken als het trilt. Dit wordt bepaald door het aantal knopen en buiken in de staande golf van het systeem. Bij een ingeklemde schaar zijn er op de zijkanten knopen en in het midden een buik, wat het kleinste aantal knopen en buiken is. Bij een latje is er een knoop waar het latje vast zit en een buik waar het maximaal uitwijkt. Bij een buis met twee openingen zijn de buiken bij de openingen en is er in het midden een knoop. Bij een buis met één opening zijn er twee knopen: één bij de opening waar de lucht veel beweegt en één aan de gesloten kant waar de dichtheid nauwelijks verandert. Dit zijn de vier situaties waarbij het aantal knopen en buiken minimaal is, wat de grondtoon bepaalt. Er worden geen formules, grootheden of eenheden gebruikt in deze uitleg.

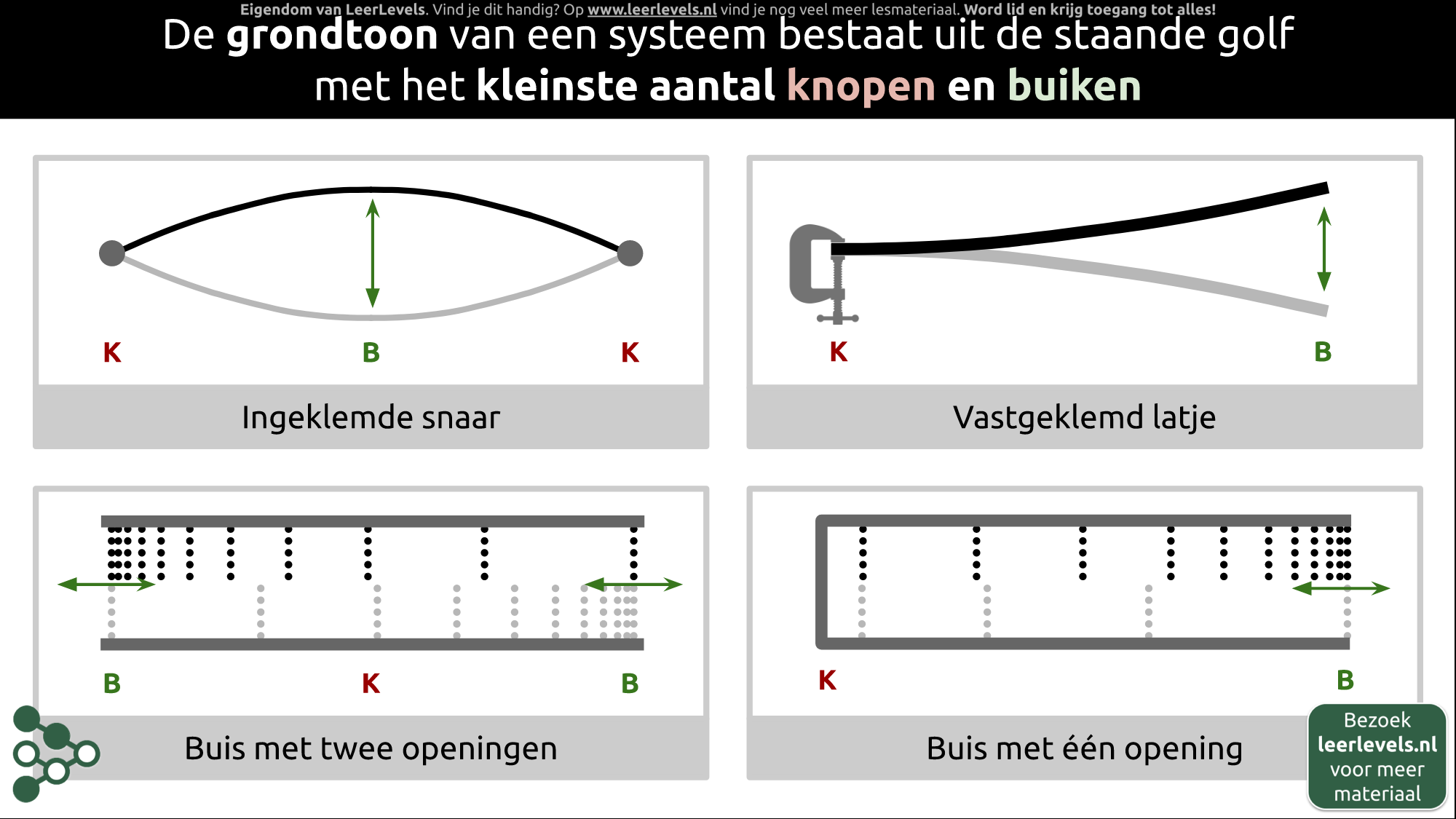
(Afbeelding: Animatie voor Grondtoon)

Terug naar overzicht Meld je aan

Grootheden

Definitie grootheid en eenheid

Alles in de natuurkunde wordt beschreven met grootheden en eenheden.

Een grootheid is iets wat je kunt meten, en de eenheid is de maat waarin je deze grootheid uitdrukt. Een voorbeeld van een grootheid is de afstand, aangeduid met s. De bijbehorende eenheid is meter, m. Een ander voorbeeld van een grootheid is de tijd, met symbool t, en de bijbehorende eenheid is seconde, s. Een laatste voorbeeld is de massa, met symbool m, en de eenheid kilogram, kg.

Het valt op dat sommige grootheden en eenheden hetzelfde symbool hebben. Bijvoorbeeld, de grootheid afstand heeft het symbool s, terwijl de eenheid seconde ook het symbool s heeft. Om onderscheid te maken tussen grootheden en eenheden, is afgesproken dat eenheden in de tekst schuingedrukt, dikgedrukt of beide worden geschreven.

(Afbeelding: Animatie voor Definitie grootheid en eenheid)

Veelvoorkomende grootheden

Er zijn ongeveer 100 dingen die natuurkundigen gebruiken om dingen te meten. Je ziet elke dag sommige van deze dingen, zoals lengte, tijd en hoeveel licht nodig is om dingen te zien. Stroom is belangrijk voor onze elektrische apparaten. Als je dingen telt, gebruik je een hoeveelheid. Als je iets optilt, merk je hoe zwaar het is. Er zijn nog veel meer dingen op de lijst, maar dit zijn er 21 die je elke dag tegenkomt.

(Afbeelding: Animatie voor Veelvoorkomende grootheden)

Grootheid en eenheid herkennen

In de zin 'Haar leeftijd is 14 jaar' wordt zowel de eenheid als de grootheid genoemd. De grootheid is de leeftijd, uitgedrukt met het getal 14. De eenheid is het jaar, dat de maat voor de grootheid (leeftijd) aangeeft. In de natuurkunde worden grootheden altijd weergegeven door middel van een combinatie van een getal en een eenheid. De eenheid is datgene waarin de grootheid wordt uitgedrukt.

(Afbeelding: Animatie voor Grootheid en eenheid herkennen)

Terug naar overzicht Meld je aan

Gulden regel

Gulden regel en katrollen

Met extra katrollen heb je minder kracht nodig om iets omhoog te tillen, maar moet je wel meer touw verplaatsen. Als je bijvoorbeeld een massa aan een touw omhoog wil tillen en niet sterk genoeg bent om de zwaartekracht te overwinnen, kan je gebruik maken van een bewegende katrol. Hierdoor heb je nog maar de helft van de oorspronkelijke kracht nodig, maar moet je wel twee keer zo veel touw verplaatsen. Door meer katrollen toe te voegen kan je deze kracht nog verder verminderen, maar moet je wel steeds meer touw verplaatsen. Het is daarom handig om lange touwen te gebruiken, zodat je dit probleem kunt vermijden. Dit systeem wordt op veel plekken gebruikt, bijvoorbeeld bij zeilschepen.

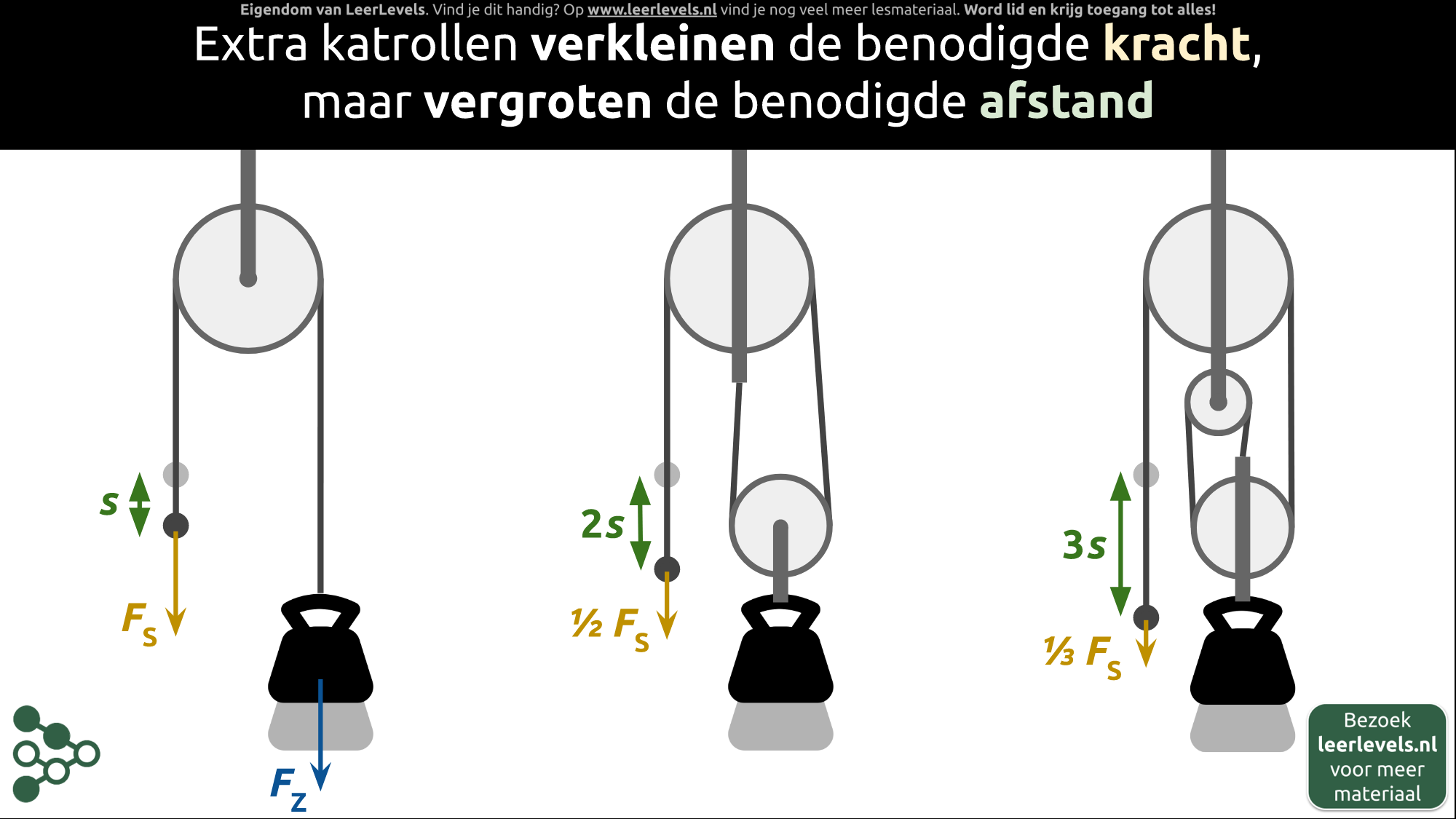
(Afbeelding: Animatie voor Gulden regel en katrollen)

Terug naar overzicht Meld je aan

Halfgeleider

Halfgeleider concept

Een halfgeleider heeft een relatief kleine bandgap en gedraagt zich afhankelijk van de situatie als een geleider of als een isolator.

Bij geleiders is de laagste energieband waar elektronen in zitten slechts deels gevuld, waardoor elektronen gemakkelijk naar een iets hoger energieniveau kunnen springen. Zelfs een kleine thermische excitatie zorgt ervoor dat sommige elektronen hun "eigen" atoom verlaten en als vrij elektron in een iets hogere energietoestand komen. Hierdoor geleidt de stof goed.

Bij isolatoren is de laagste energieband waar elektronen in zitten volledig gevuld, terwijl de band erboven helemaal leeg is. De kloof tussen deze banden, de bandgap, is zo groot dat elektronen niet naar hogere niveaus kunnen springen. In de bandgap ontbreken namelijk energieniveaus om naartoe te verplaatsen. Het gevolg is dat alle elektronen 'vast' blijf zitten aan 'hun' atomen. Hierdoor geleidt de stof niet.

Halfgeleiders bevinden zich tussen deze twee uitersten. Net als bij isolatoren geldt voor haflgeleiders dat de laagste energieband waar elektronen in zitten volledig is gevuld en dat de eerstvolgende energieband helemaal leeg is. Echter, de bandgap tussen deze twee banden is veel kleiner dan bij een isolator. Of de halfgeleider geleidt, hangt af van de beschikbare energie. Als er voldoende energie beschikbaar is, bijvoorbeeld afkomstig van licht, thermische bewegingen van de deeltjes, of een elektrische spanning, kunnen elektronen de bandgap overbruggen en geleidt de stof. Is de beschikbare energie lager dan de bandgap, dan kunnen elektronen deze sprong niet maken en geleidt de stof niet.

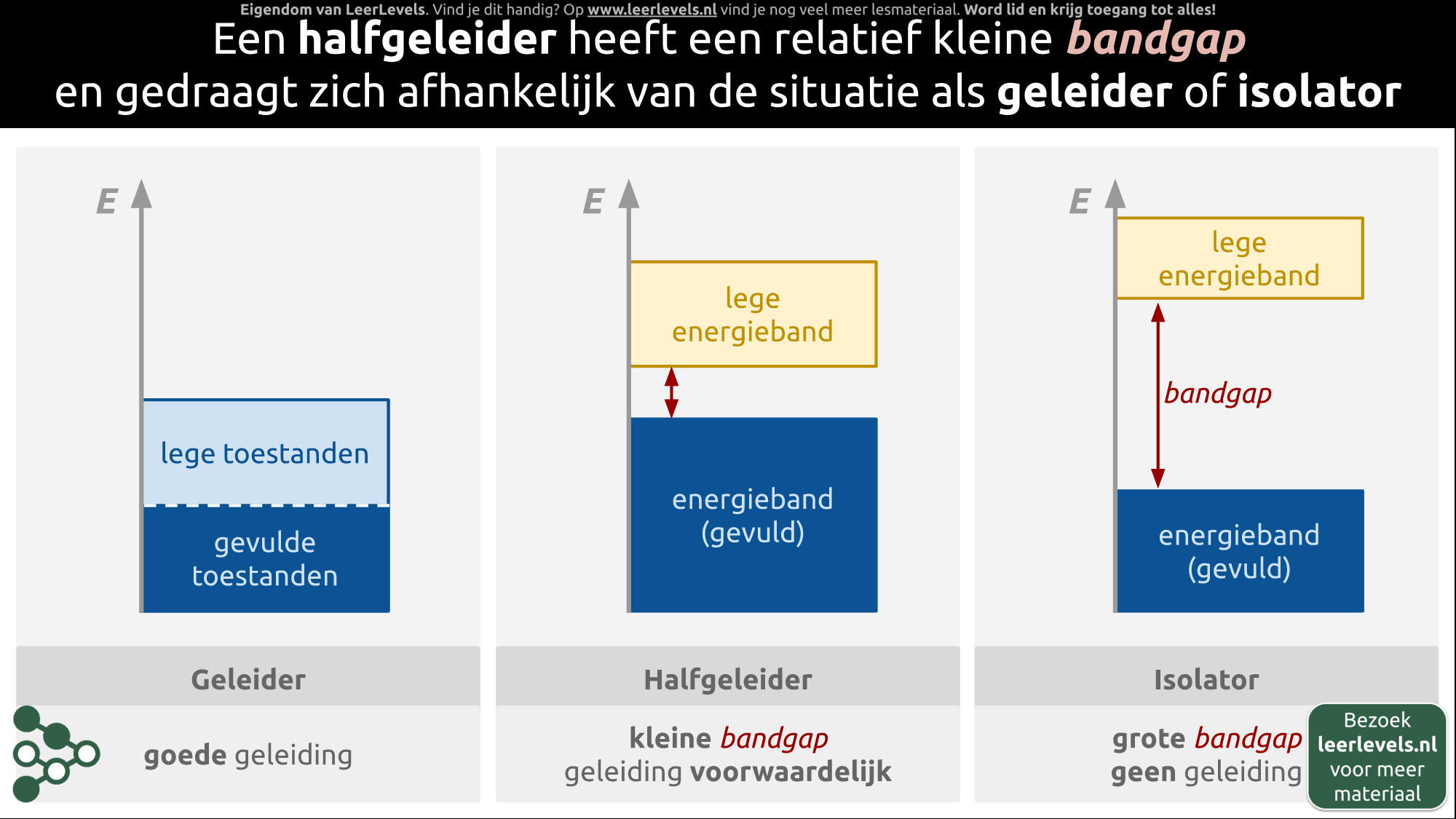
(Afbeelding: Animatie voor Halfgeleider concept)

Terug naar overzicht Meld je aan

Halveringsdikte

Halveringsdikte concept

De halveringsdikte (dhalf) laat zien hoe ver straling door een materiaal kan gaan voordat de intensiteit is gehalveerd. Als je bijvoorbeeld start met 100% intensiteit en door een materiaal gaat met precies de halveringsdikte, dan zal de intensiteit halveren tot 50%. Dit komt doordat de straling van richting verandert of omgezet wordt in warmte. Als je nog een keer door de halveringsdikte gaat, wordt de resterende 50% gehalveerd tot 25%, en zo gaat het verder.

Als je door een muur gaat die drie keer de halveringsdikte heeft, dan zal er na elke halveringsdikte gedeeltelijk verspreiding en conversie van de straling plaatsvinden. Zo zal er uiteindelijk slechts 12,5% van de oorspronkelijke intensiteit overblijven.

Je kunt ook de vermindering van straling meten voor diktes die niet gelijk zijn aan een geheel aantal halveringsdiktes. Dit kun je doen door een grafiek te maken met op de X-as de dikte als een aantal halveringsdiktes en op de Y-as het overgebleven percentage van de straling. Deze curve verloopt geleidelijk en laat de afname van straling met halve halveringsdiktes zien.

Beginnend bij 100% intensiteit, blijft er na 1 keer de halveringsdikte nog maar 50% over, na 2 keer nog maar 25% en na 3 keer nog maar 12,5%. Deze curve kan ook aangeven hoeveel procent van de straling nog overblijft bij een halve halveringsdikte.

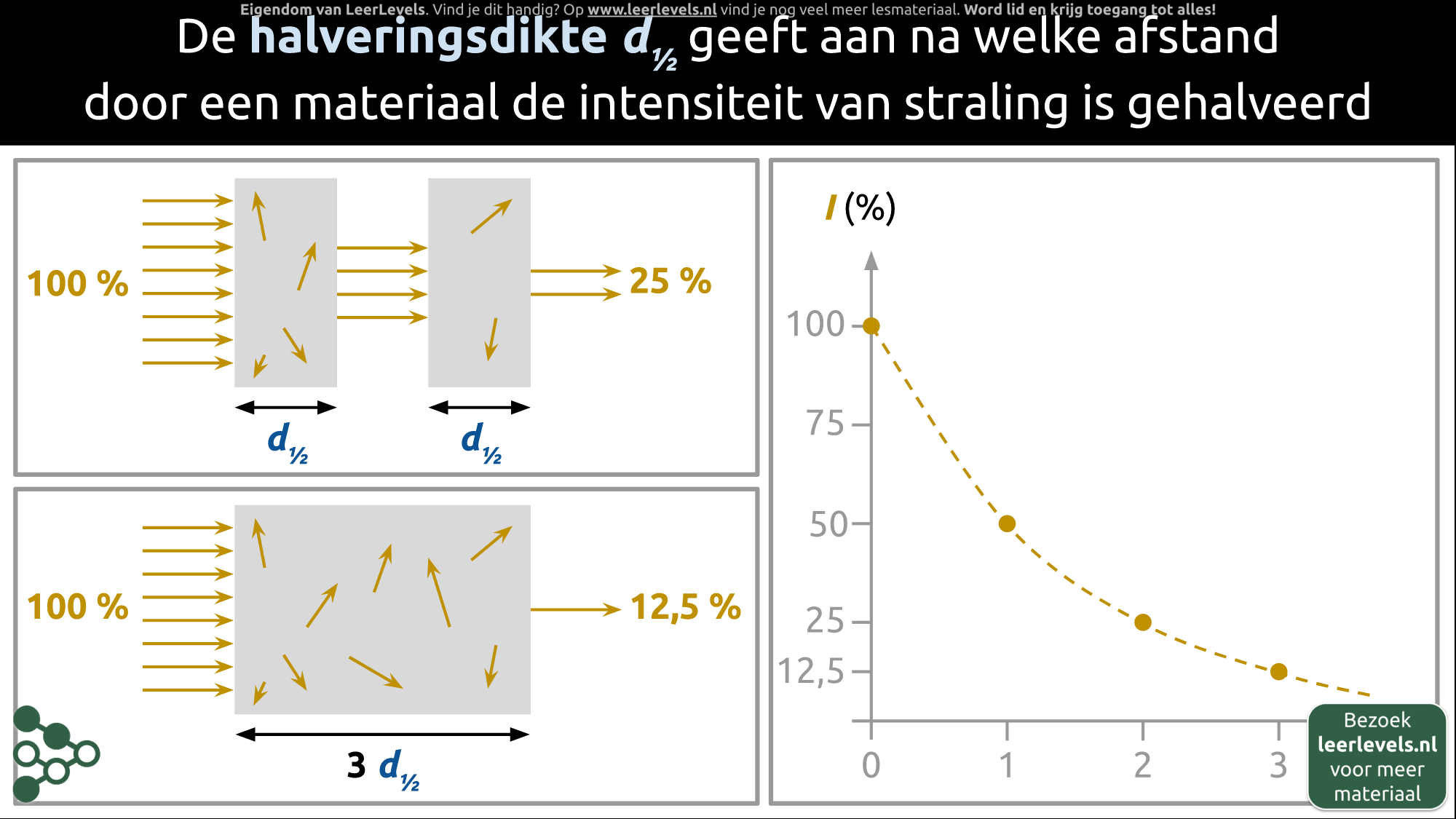
(Afbeelding: Animatie voor Halveringsdikte concept)

Halveringsdikte formule

De stralingsintensiteit verandert als het door een materiaal gaat. Dit hangt af van de beginwaarde, de dikte en de halveringsdikte van het materiaal. De stralingsintensiteit na afstand d door het materiaal is gelijk aan de beginwaarde keer een half tot de macht d/d1/2. Hierbij is d de afstand door het materiaal en d1/2 de halveringsdikte van het materiaal. Zorg dat d en d1/2 in dezelfde eenheid staan, zodat je het aantal halveringsdiktes krijgt. Bij 3 halveringsdiktes blijft er 12,5% over.

(Afbeelding: Animatie voor Halveringsdikte formule)

Terug naar overzicht Meld je aan

Halveringstijd

Halveringstijd concept

De halveringstijd van een isotoop vertelt ons hoe lang het duurt voordat de helft van de instabiele kernen is vervallen. Dit wordt weergegeven op een grafiek waarbij de x-as de tijd in halveringstijden weergeeft en de y-as het percentage instabiele kernen. Bij tijdstip 0 is er nog niets vervallen en is het percentage instabiele kernen 100%. Na één halveringstijd is de helft vervallen en blijft er 50% over. Bij twee keer de halveringstijd is er nog maar 25% over. De lijn die door deze punten loopt, kan worden gebruikt om tijden te bepalen die niet precies een veelvoud van de halveringstijd zijn. Het subscript 1/2 geeft aan dat het om de halveringstijd gaat.

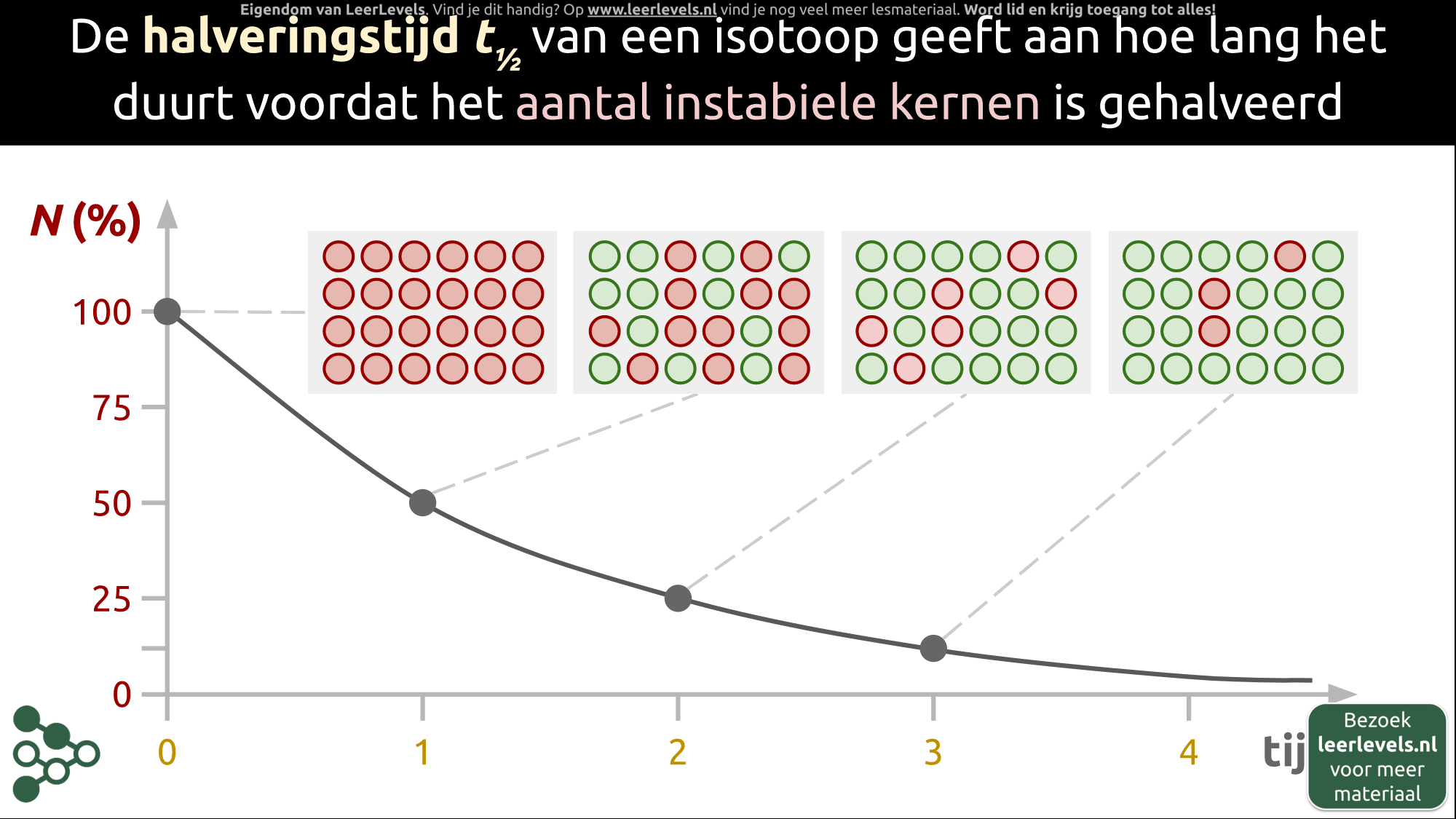
(Afbeelding: Animatie voor Halveringstijd concept)

Halveringstijd formule

Het aantal overgebleven instabiele kernen kan worden berekend met behulp van de beginwaarde en de tijd die is verstreken. Dit aantal wordt uitgedrukt als een hoeveelheid overgebleven kernen die wordt berekend door de beginwaarde te vermenigvuldigen met een exponentiële functie. De grondtal van deze functie is 1/2 en de exponent is de tijd die is verstreken gedeeld door de halveringstijd. Het is belangrijk dat de eenheden van de verstreken tijd en de halveringstijd hetzelfde zijn, bijvoorbeeld jaren of uren. Door het aantal halveringstijden te berekenen, kan het overgebleven aantal kernen worden bepaald. Dit kan als een breuk worden uitgedrukt, waarbij de teller het overgebleven aantal kernen is en de noemer het aantal kernen bij de start. Het precieze aantal overgebleven instabiele kernen kan worden berekend door deze breuk te vermenigvuldigen met de beginwaarde.

(Afbeelding: Animatie voor Halveringstijd formule)

Terug naar overzicht Meld je aan

Harmonische trilling

Harmonische trilling concept

Een harmonische trilling is een trilling waarbij de uitwijking de vorm heeft van een sinusoïde.

Als we bij de grafiek van de uitwijking geen enkele herhaling zien, dan is dat geen trilling. Soms tonen grafieken wel herhaling, maar is de vorm niet sinusoïdaal. In dat geval hebben we te maken met een trilling, maar geen harmonische trilling. Een harmonische trilling moet dus de vorm hebben van een sinusoïde. De frequentie en amplitude van de harmonische trilling kunnen variëren, afhankelijk van de toepassin

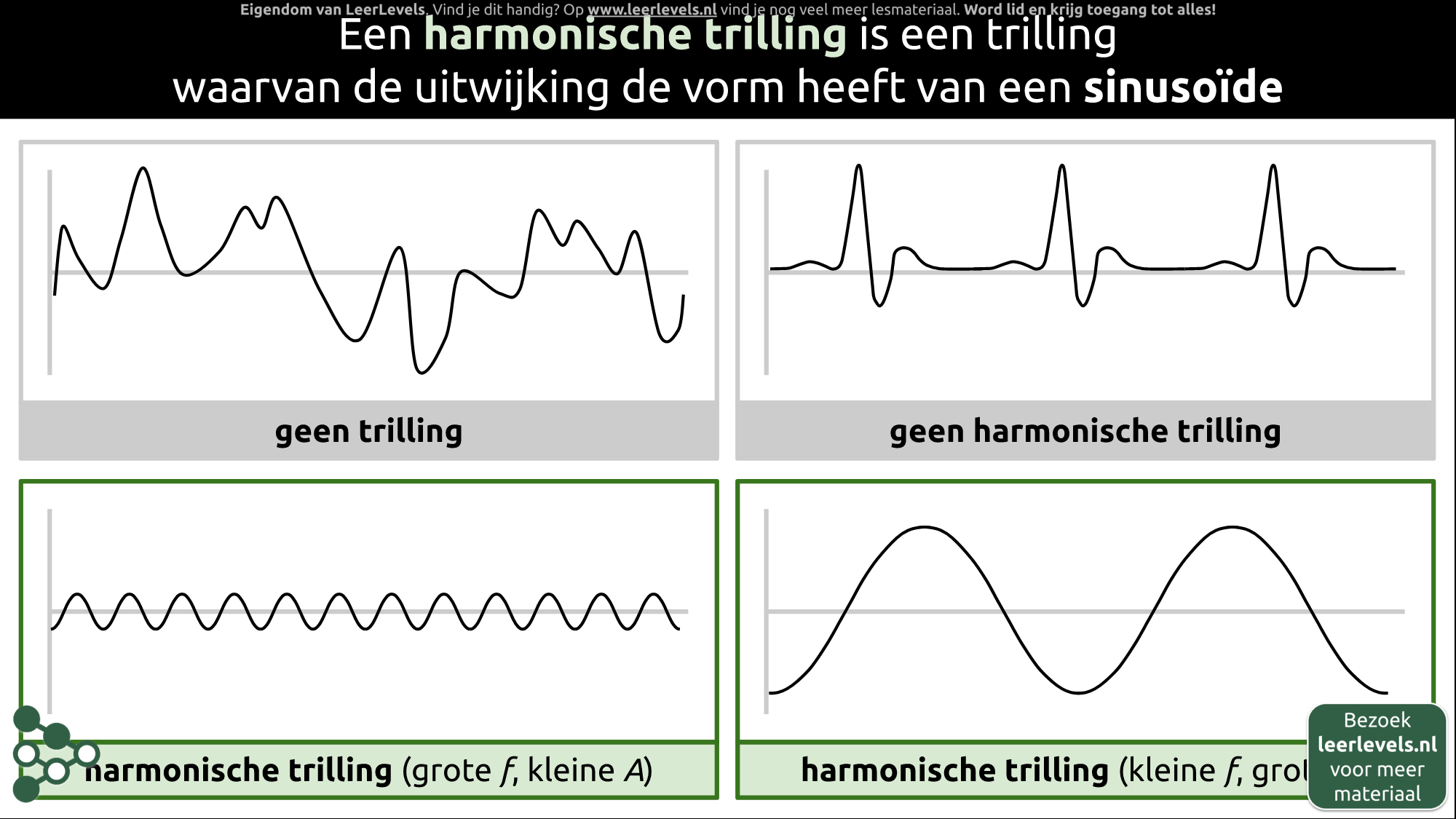
(Afbeelding: Animatie voor Harmonische trilling concept)

Harmonische trilling functie

Een harmonische trilling kan worden beschreven als een sinusvormige beweging. Dit betekent dat de beweging heen en weer gaat rond een middelpunt op een voorspelbare en regelmatige manier. De eigenschappen van deze trilling worden beschreven door de amplitude (hoe ver de beweging van het middelpunt gaat) en de trillingstijd (hoe lang het duurt om één volledige cyclus te voltooien).

Deze trillingsbeweging kan worden beschreven door een functie genaamd A keer sinus van 2 pi keer f keer t, waarbij A de amplitude in meters, f de frequentie in Hertz en t de tijd in seconden is. Dit betekent dat de beweging op een bepaald moment t kan worden voorspeld door deze formule te gebruiken.

Het is handig om de logica achter deze formule te begrijpen. Als de tijd gelijk is aan de trillingstijd, wordt het laatste deel van de formule gelijk aan 1 en staat er alleen sinus van 2 pi. Hierdoor kom je precies terug op nul en is er één volledige cyclus afgerond. Als je de tijd invoert als de helft van de trillingstijd, kom je halverwege de cyclus uit.

Kortom, de uitwijking van een harmonische trilling kan worden beschreven als een sinusfunctie met amplitude, frequentie en tijd. Door deze formule te begrijpen, kunnen we de beweging van een trilling op elk moment voorspellen.

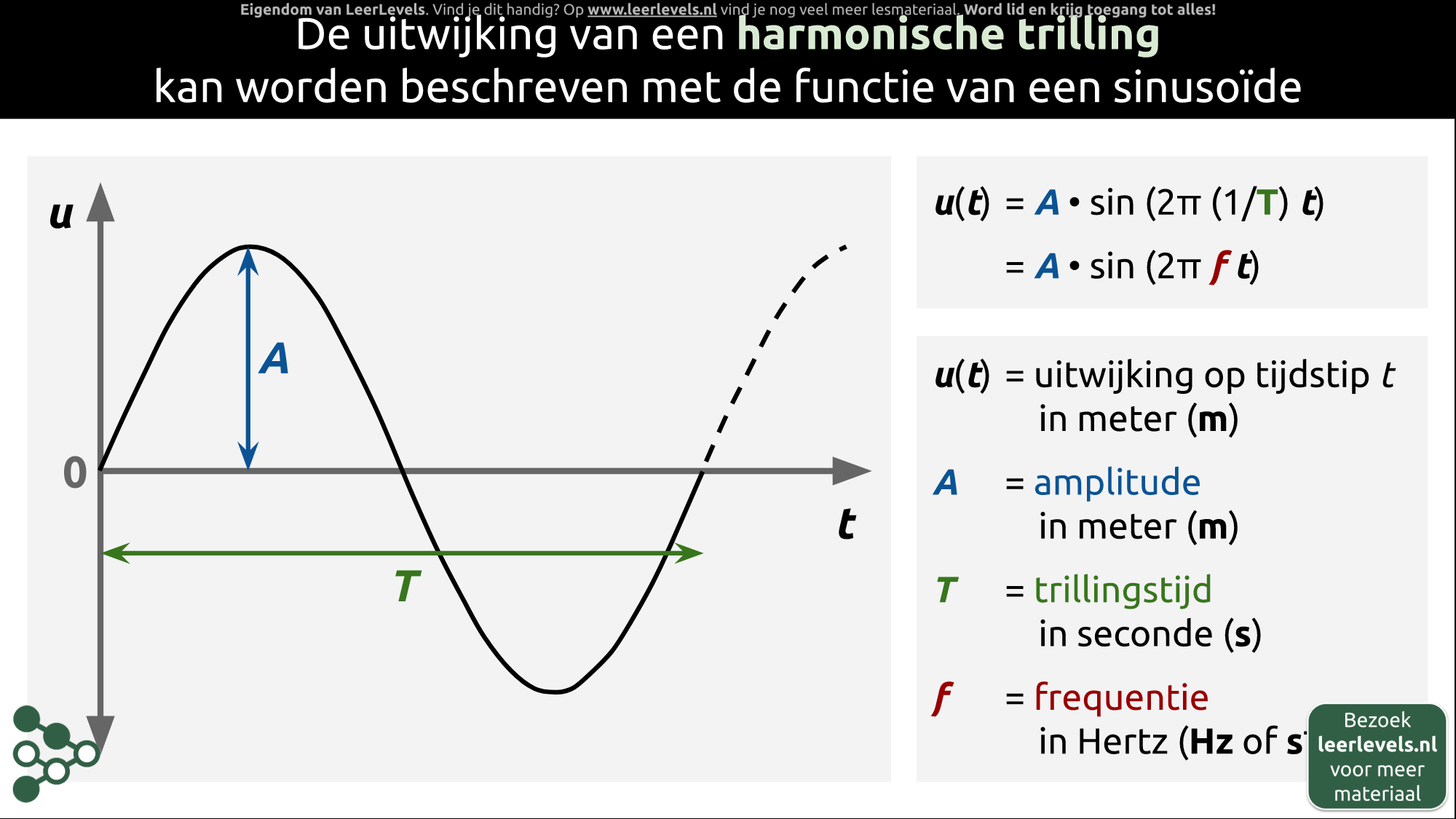
(Afbeelding: Animatie voor Harmonische trilling functie)

Maximale snelheid in harmonische trilling formule

Een trilling is de beweging van een voorwerp dat heen en weer gaat. De snelheid waarmee het voorwerp beweegt, hangt af van de grootte van de trilling en de tijd die het duurt om één volledige trilling te voltooien. Het is mogelijk om de snelheid van het voorwerp op elk punt van de trilling te berekenen. Om dit te doen, bekijk je een grafiek van de beweging van het voorwerp als functie van de tijd, genaamd ut-diagram. Hierin lees je de uitwijking af. De snelheid kan worden afgeleid uit de helling van de grafiek. Bij het hoogste punt van de uitwijking heeft het voorwerp een snelheid van nul, en bij het uiterste punt is het ook even stilstaand. De maximale snelheid kan worden berekend met de formule: vmax = 2π A / T, waarbij A de amplitude van de trilling is en T de tijd die nodig is om één volledige trilling te voltooien. Deze formule kan worden afgeleid uit de vergelijking van de uitwijking: u(t) = Asin(2π t / T) en de snelheid vergelijking: v(t) = 2π A / T · cos(2π t / T).

(Afbeelding: Animatie voor Maximale snelheid in harmonische trilling formule)

Terug naar overzicht Meld je aan

Heelal

Uitdijend heelal en oerknal

De wet van Hubble zegt dat het heelal groter wordt en we kunnen hiermee berekenen hoe oud het heelal is sinds de oerknal. Als we kijken naar sterren die verder van ons af staan, bewegen ze sneller van ons weg dan sterren die dichtbij staan. Dit komt doordat de ruimte waarin alle sterren zich bevinden, groter wordt. We kunnen dit uitleggen met het ballonmodel waarin alle sterren op de oppervlakte van een ballon zitten die opgeblazen wordt. Alle sterren hebben dezelfde snelheid vanaf een bepaald startpunt, maar afhankelijk van waar ze nu zijn, meten we verschillende snelheden. Door hun snelheid en afstand te meten, kunnen we berekenen waar de sterren vandaan kwamen en hoelang geleden de oerknal plaatsvond. Dit geeft ons een leeftijd van het heelal van ongeveer 13,9 miljard jaar. Dit is bewezen door metingen en modellen die de wet van Hubble ondersteunen. De constante van Hubble kan niet echt constant zijn, want dan zou het heelal niet ouder worden.

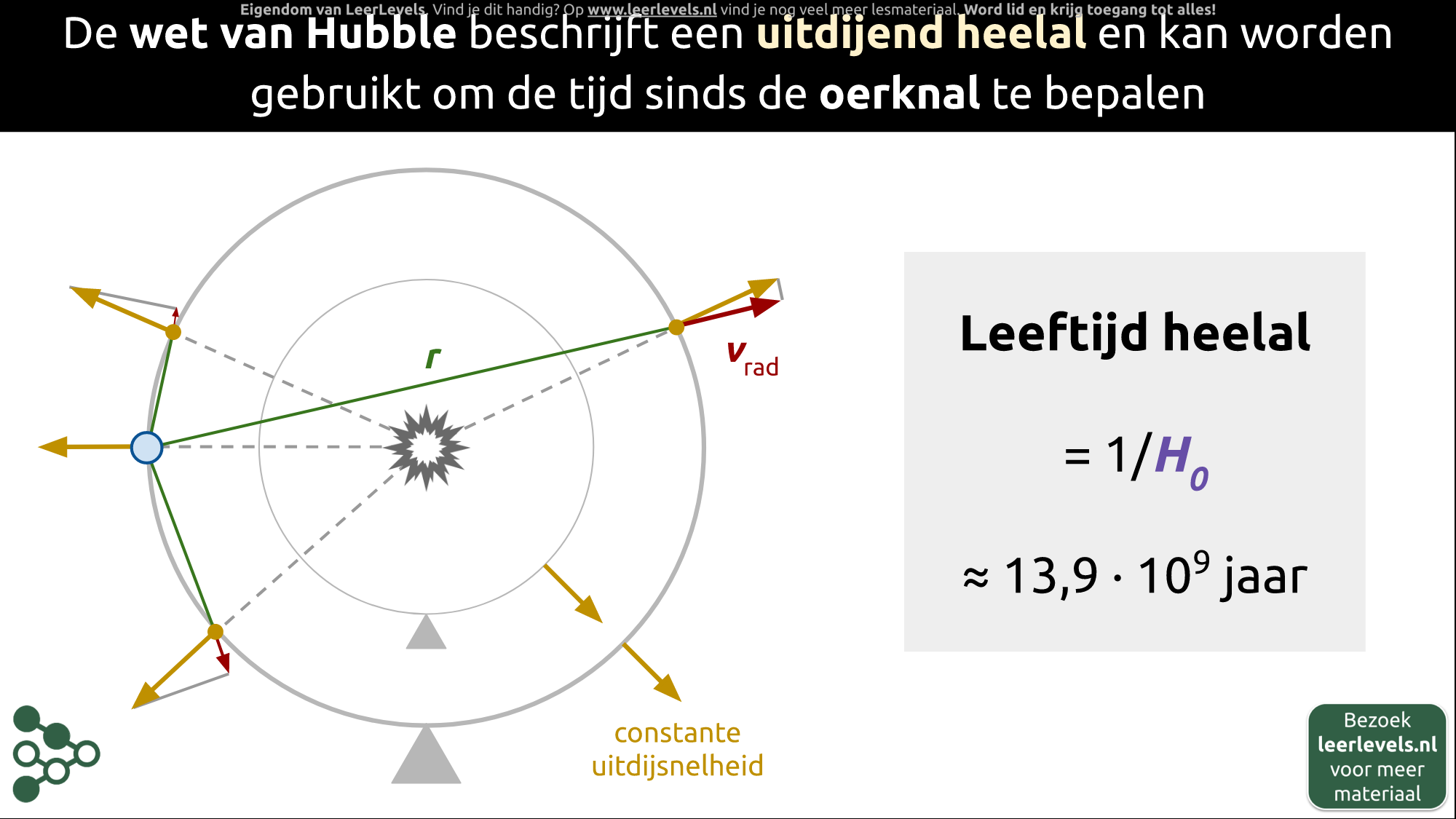
(Afbeelding: Animatie voor Uitdijend heelal en oerknal)

Terug naar overzicht Meld je aan

Hefboom

Hefboomwet

De hefboomwet zegt dat je bij het gebruik van een hefboom kracht en afstand moet inruilen. Bijvoorbeeld als je een flesje opent met een opener, hoef je niet veel kracht te gebruiken. Dit komt doordat de opener een langere arm heeft. Maar je moet wel een grotere afstand afleggen met je hand. Hetzelfde geldt voor het tillen van zware dingen. Je moet verder weg duwen om het omhoog te krijgen. Dus met een hefboom kun je veel kracht uitoefenen, maar je moet wel meer afstand afleggen. Helaas is er in de natuurkunde niets gratis.

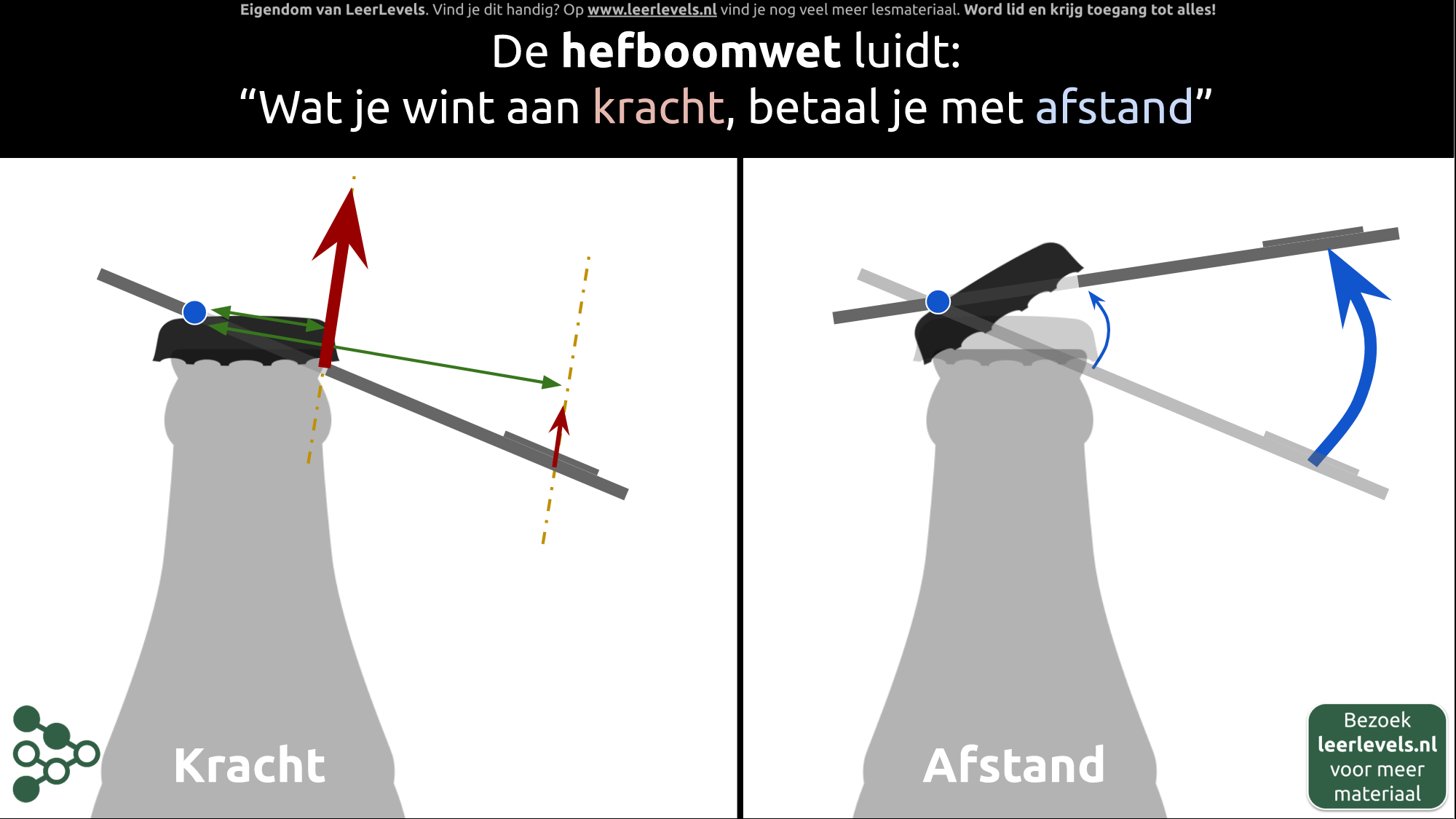
(Afbeelding: Animatie voor Hefboomwet)

Hefboom

Een hefboom kan ervoor zorgen dat een kleine kracht meer kracht heeft. Dit komt doordat de krachten een verschillende arm hebben. Als het draaipunt tussen de krachten zit, zorgt een kleine kracht naar beneden voor een grote kracht naar boven door de grote arm aan de kleine kracht kant en de kleine arm aan de grote kracht kant. Als het draaipunt aan het uiteinde zit, zorgt een kleine kracht omhoog voor meer kracht als je dichter bij het draaipunt zit door de grotere arm. Let op: bij het draaipunt tussen de krachten is de kracht van de spieren naar beneden en de werkkracht naar boven. Bij het uiteinde werken de spieren en de werkkracht in dezelfde richting. Dit komt door de hefboomwet: een kleine arm hoort bij een grotere kracht.

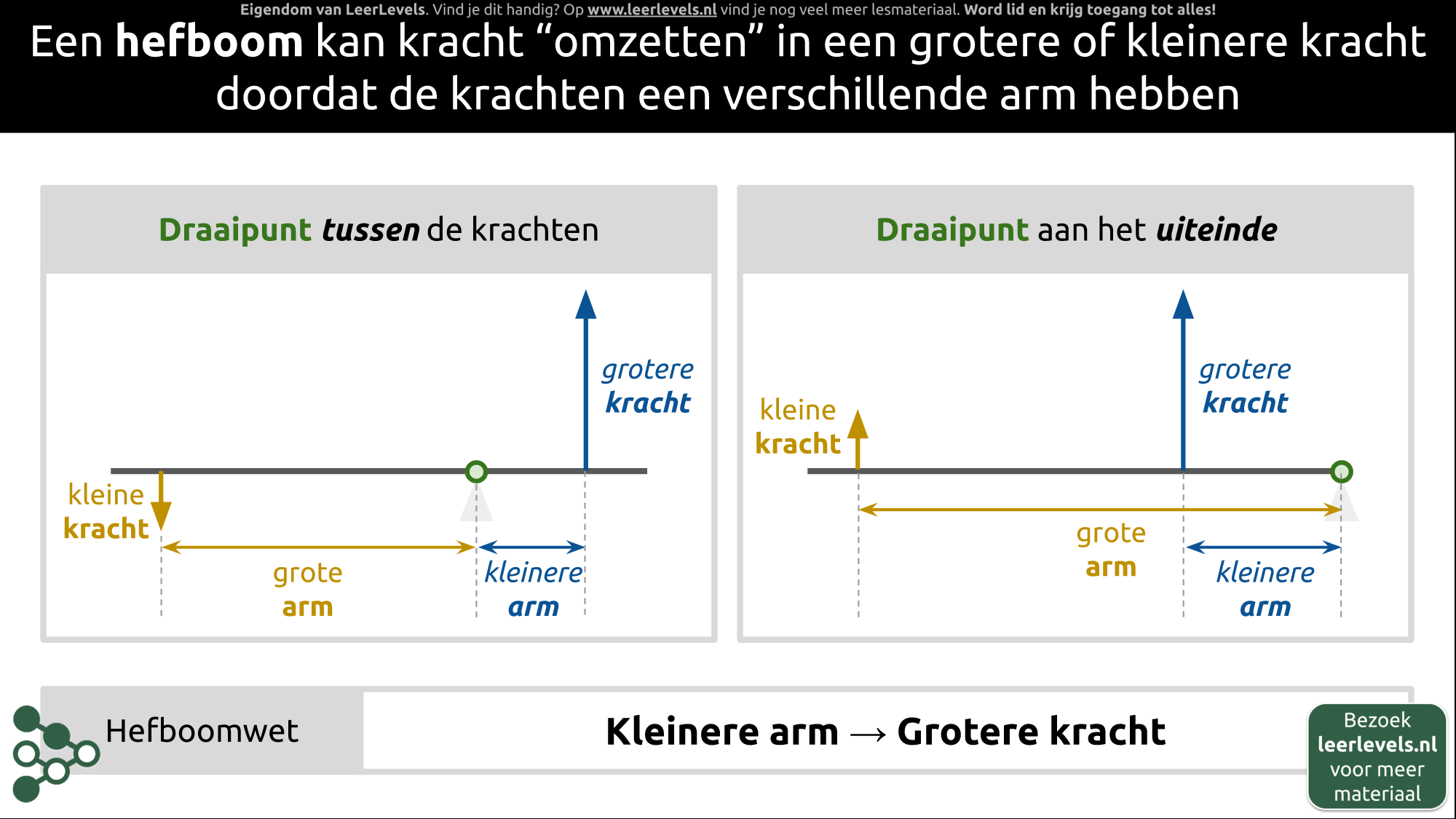
(Afbeelding: Animatie voor Hefboom)

Terug naar overzicht Meld je aan

Hefboomwerking

Hefboomwerking bij tandwielen

Als je meerdere tandwielen op dezelfde as hebt, dan kun je deze gebruiken als een hefboom om krachten groter of kleiner te maken. Een klassieke hefboom heeft een draaipunt met een kracht aan het einde die zorgt voor een grotere kracht dichter bij het draaipunt. Als je wielen op dezelfde as hebt, kun je bijvoorbeeld aan het uiteinde een kleine kracht uitoefenen, waardoor de kracht wanneer je dichterbij het draaipunt komt, hoger zal zijn.

Als het tweede wiel op een andere plek is bevestigd, kan het zijn dat je meer kracht nodig hebt om het wiel tegen te houden wanneer je langs de rand van het wiel probeert te hem tegen te houden. Dit komt omdat de afstand tussen het draaipunt en de rand van het wiel groter is. Dit effect kun je gebruiken in wat we noemen een "tandwielhefboom". Een voorbeeld hiervan is wanneer er twee wielen op elkaar zijn bevestigd aan het plafond en de persoon een touw vasthoudt dat om het gele wiel heen loopt en aan de andere kant aan het blauwe wiel is bevestigd. Hierdoor ontstaat er een hefboom en kan er een grotere kracht worden uitgeoefend.

Op deze manier kun je kracht vergroten door het gebruik van tandwielen op dezelfde as die samen een hefboom vormen. De grootte van de kracht wordt beïnvloed door de afstand van het draaipunt tot de plaats waar de kracht wordt uitgeoefend.

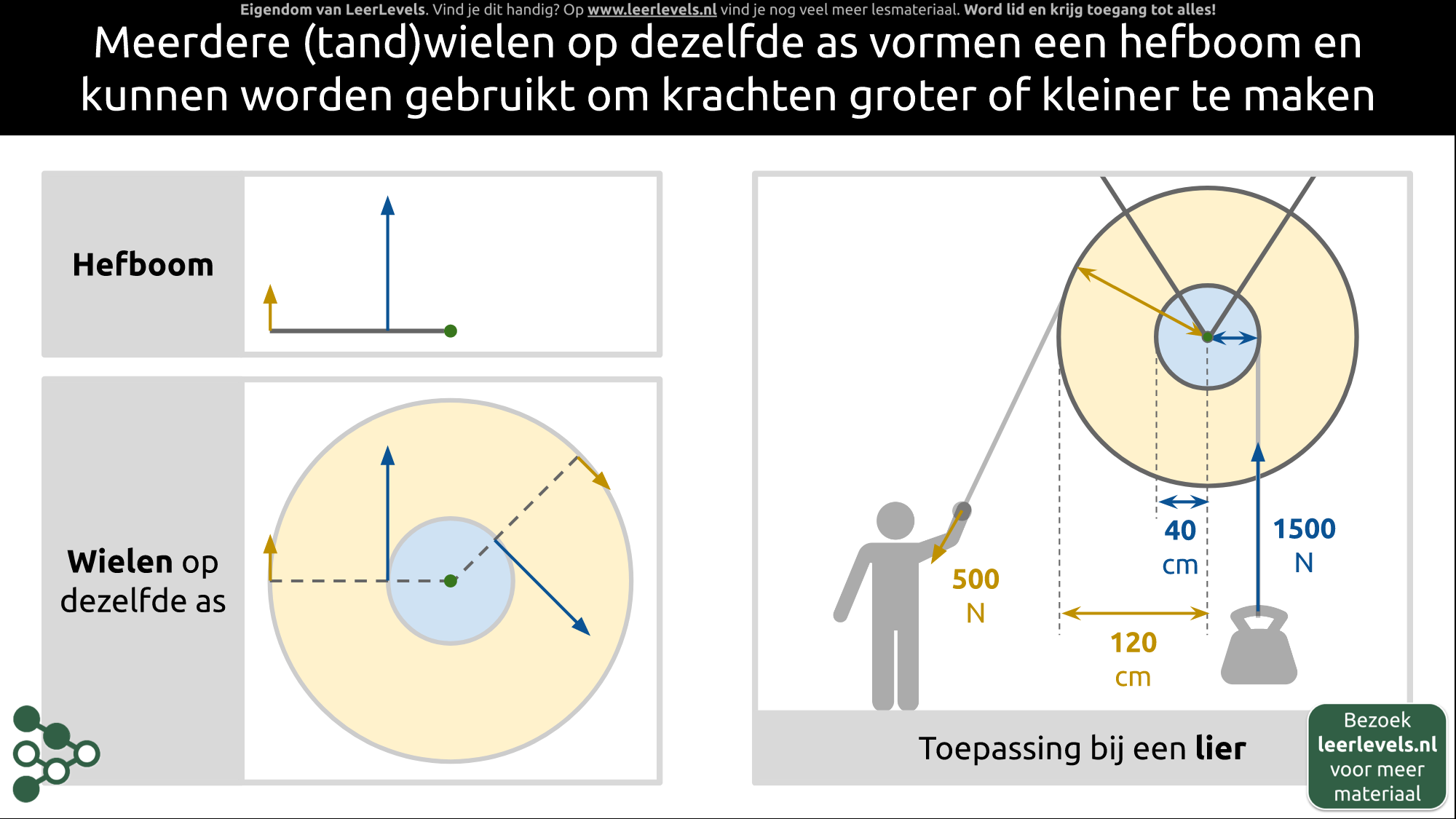
(Afbeelding: Animatie voor Hefboomwerking bij tandwielen)

Terug naar overzicht Meld je aan

Hertzsprung-Russell-diagram

Hertzsprung-Russell-diagram klassen

In het Hertzsprung-Russell-diagram kun je zien tot welke klasse een ster behoort. De eerste klasse is de zogenaamde Hoofdreeks. Daarnaast zijn er de Witte Dwergen, waartoe Sirius B behoort. In het groen zijn de Reuzen te zien, en Betelgeuze maakt deel uit van de Superreuzen. Deze klassen worden onder andere gebruikt om de levensloop van sterren te beschrijven.

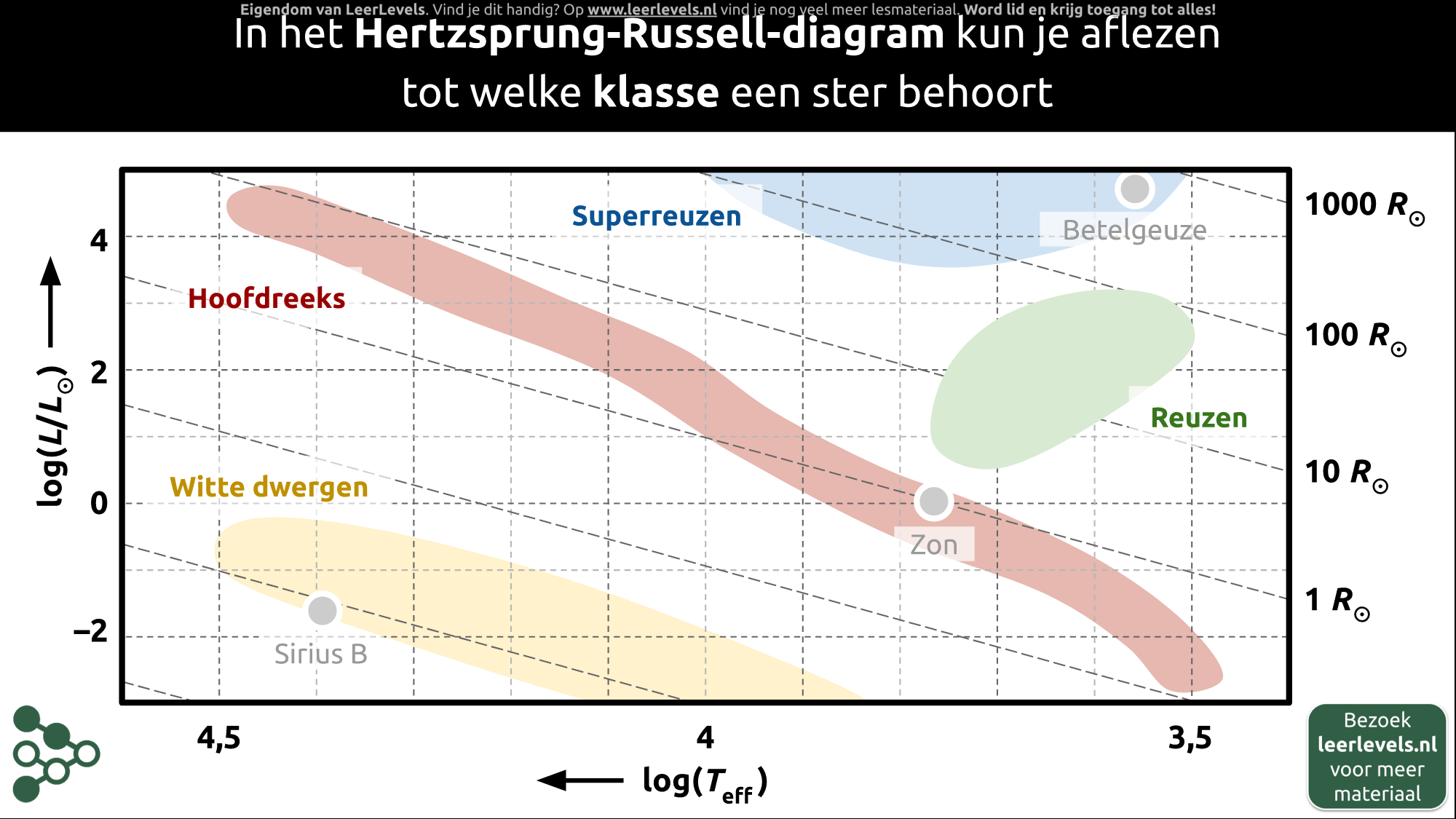
(Afbeelding: Animatie voor Hertzsprung-Russell-diagram klassen)

Terug naar overzicht Meld je aan

Hoeksnelheid

Hoeksnelheid concept

De hoeksnelheid geeft aan welke hoek er per seconde wordt afgelegd. Een voorbeeld van een kleine hoeksnelheid is de aarde, omdat de aarde ongeveer 24 uur nodig heeft om eenmaal om haar eigen as te draaien. Dit resulteert in een vrij kleine hoeksnelheid. Voor een normale hoeksnelheid kun je denken aan een draaimolen, die we met het blote oog kunnen zien draaien. Een voorbeeld van een hoge hoeksnelheid is een boormachine die op vol vermogen draait. Bij hoeksnelheid gaat het niet om de baansnelheid van een bepaald punt op het voorwerp, maar om de afgelegde hoek. Het maakt dus niet uit hoe groot of klein de cirkel is.

(Afbeelding: Animatie voor Hoeksnelheid concept)

Hoeksnelheid formule

De hoeksnelheid ω is omgekeerd evenredig met de trillingstijd of recht evenredig met de frequentie. In formulevorm wordt dit weergegeven als

ω = (2π)/(T)

waarbij T de trillingsperiode in seconden is. Dit kan ook geschreven worden als

ω = 2π f

waarbij f de frequentie is, uitgedrukt in hertz (aantal trillingen per seconde).

(Afbeelding: Animatie voor Hoeksnelheid formule)

Terug naar overzicht Meld je aan

Horizontale worp

Bij een wrijvingsloze horizontale worp blijft de snelheid in horizontale richting hetzelfde, terwijl de snelheid in verticale richting groter wordt door zwaartekracht. Als iemand een bal met 20 m/s gooit, dan blijft de horizontale snelheid 20 m/s en wordt de verticale snelheid na 1 seconde 10 m/s. De totale snelheid van de bal na 1 seconde is √(20²⁺¹⁰²) ≈ 22 m/s. Na 2 seconden is de verticale snelheid 20 m/s, en na 3 seconden is de totale snelheid √(20²⁺³⁰²) ≈ 36 m/s. Dit komt doordat er zonder wrijving geen kracht in horizontale richting werkt en de zwaartekracht alleen invloed heeft op de verticale snelheid.

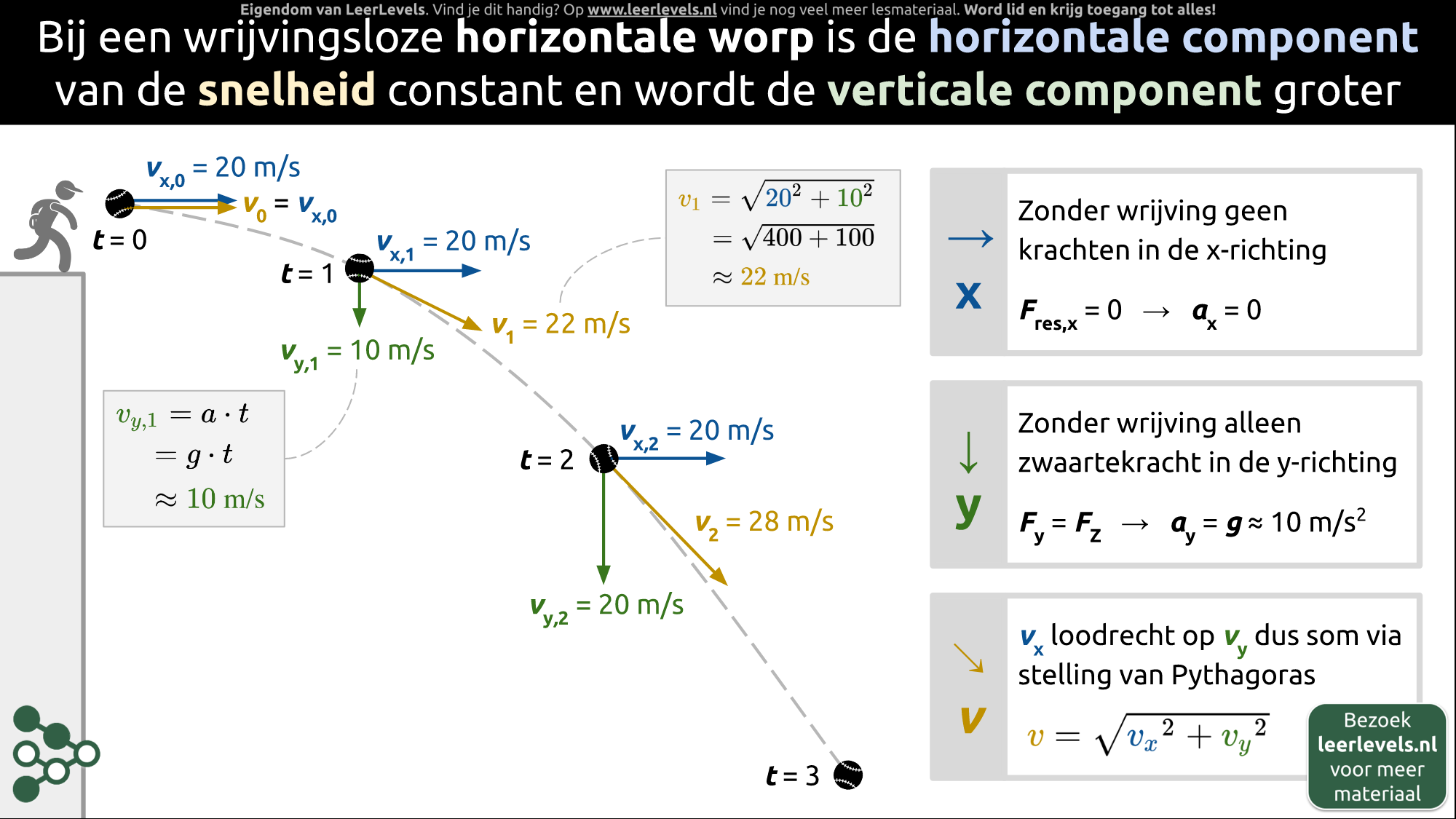
(Afbeelding: Animatie voor Horizontale worp)

Terug naar overzicht Meld je aan

Ideale gaswet

Ideale gaswet concept

De ideale gaswet zegt dat er een verband bestaat tussen het volume, aantal deeltjes, temperatuur en druk in een systeem. We kijken naar 2 ballonnen, een klein en een groot. Een manier om het volume van een ballon te vergroten is door er meer lucht in te pompen. Een andere manier is om de lucht op te warmen, waardoor de deeltjes sneller gaan bewegen en de ballon uitzet. Een derde manier is door de druk te verhogen of de buitenste druk te verlagen. Er bestaat dus een verband tussen deze factoren. De ideale gaswet beschrijft dit verband en wordt weergegeven in een formule.

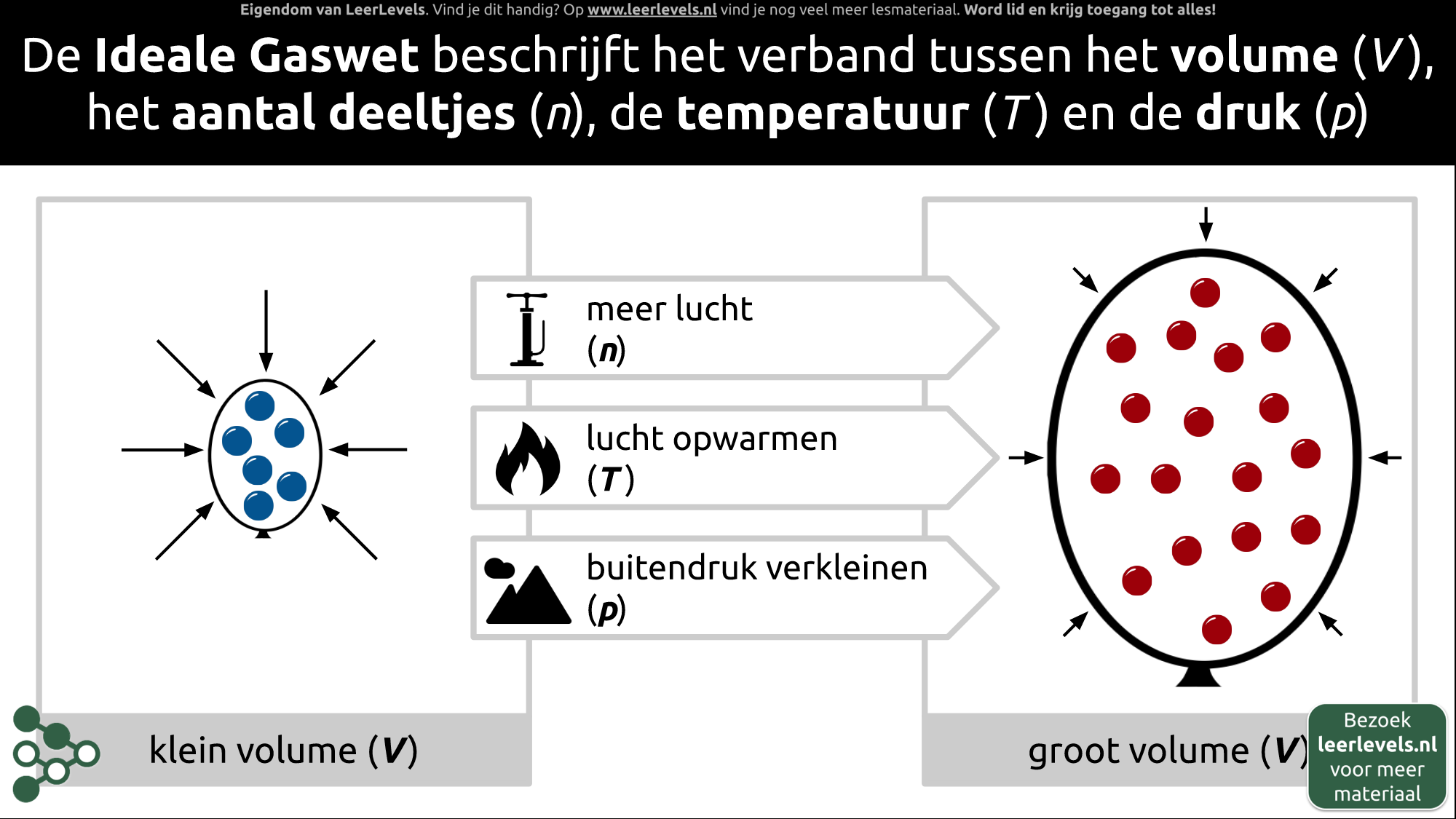
(Afbeelding: Animatie voor Ideale gaswet concept)

Ideale gaswet formule

Volgens de ideale gaswet is het product van druk en volume recht evenredig met het product van de temperatuur en het aantal deeltjes. Deze wet kan worden uitgedrukt als p · V = n · R · T, waarbij p de druk is in pascal, V het volume in kubieke meter, n het aantal deeltjes in mol, en R de gasconstante, die een experimenteel bepaalde waarde heeft. Ten slotte staat T voor de temperatuur in kelvin, niet in graden Celsius. Deze formule beschrijft de ideale gaswet en maakt diverse berekeningen mogelijk.

(Afbeelding: Animatie voor Ideale gaswet formule)

Terug naar overzicht Meld je aan

Ijkdiagram

Sensor ijkdiagram

Een ijkdiagram toont hoe een sensor een gemeten grootheid omzet in een elektrische spanning. Laten we een temperatuursensor als voorbeeld nemen; deze geeft voor elke temperatuur een specifieke sensorspanning af. Het ijkdiagram kan er als volgt uitzien: bij temperaturen van -20 ºC tot ongeveer -12 ºC is de sensorspanning nul. Vervolgens stijgt de spanning tot ongeveer 65 ºC, waarna de spanning constant blijft, ongeacht verdere temperatuurstijgingen.

Voor sensoren zijn twee grootheden van belang: het meetbereik R en de gevoeligheid. Het meetbereik omvat alle waarden van een grootheid die de sensor effectief kan meten. Volgens het ijkdiagram loopt er een rechte lijn van ongeveer 0 ºC tot 50 ºC. Binnen dit bereik levert de sensor voor elke toename van de gemeten grootheid een constante toename in spanning, wat de betrouwbaarheid vergroot. Dit heet het effectieve bereik. Als het volledige ijkdiagram in de software van een digitale temperatuursensor wordt verwerkt, kunnen temperaturen worden gemeten in een iets groter bereik, namelijk van -20 ºC tot ongeveer 65 ºC. Dit is het totale meetbereik. Voor lagere temperaturen blijft de sensorspanning nul en voor hogere temperaturen constant op 4,5 V, wat verdere meting onmogelijk maakt.

Een andere belangrijke grootheid is de gevoeligheid: de mate waarin de sensor reageert op veranderingen. Dit bekijken we alleen binnen het effectieve meetbereik, want daar is de gevoeligheid constant. Om de gevoeligheid te berekenen, bepalen we de helling van de grafiek binnen het effectieve meetbereik. We nemen twee gemakkelijk af te lezen punten op dat stuk en berekenen de helling: het verschil in spanning gedeeld door het verschil in temperatuur. Dus, Δ U / Δ T = (4,0 - 0,5) V / (50 - 0) ºC = 3,5 V / 50 ºC = 0,07 V/ºC ofwel 70 mV/ºC. Hoe steiler de grafiek, hoe hoger de gevoeligheid.

Kortom, een ijkdiagram toont hoe een sensor een gemeten grootheid omzet in een elektrische spanning, waarbij zowel het meetbereik R als de gevoeligheid van belang zijn.

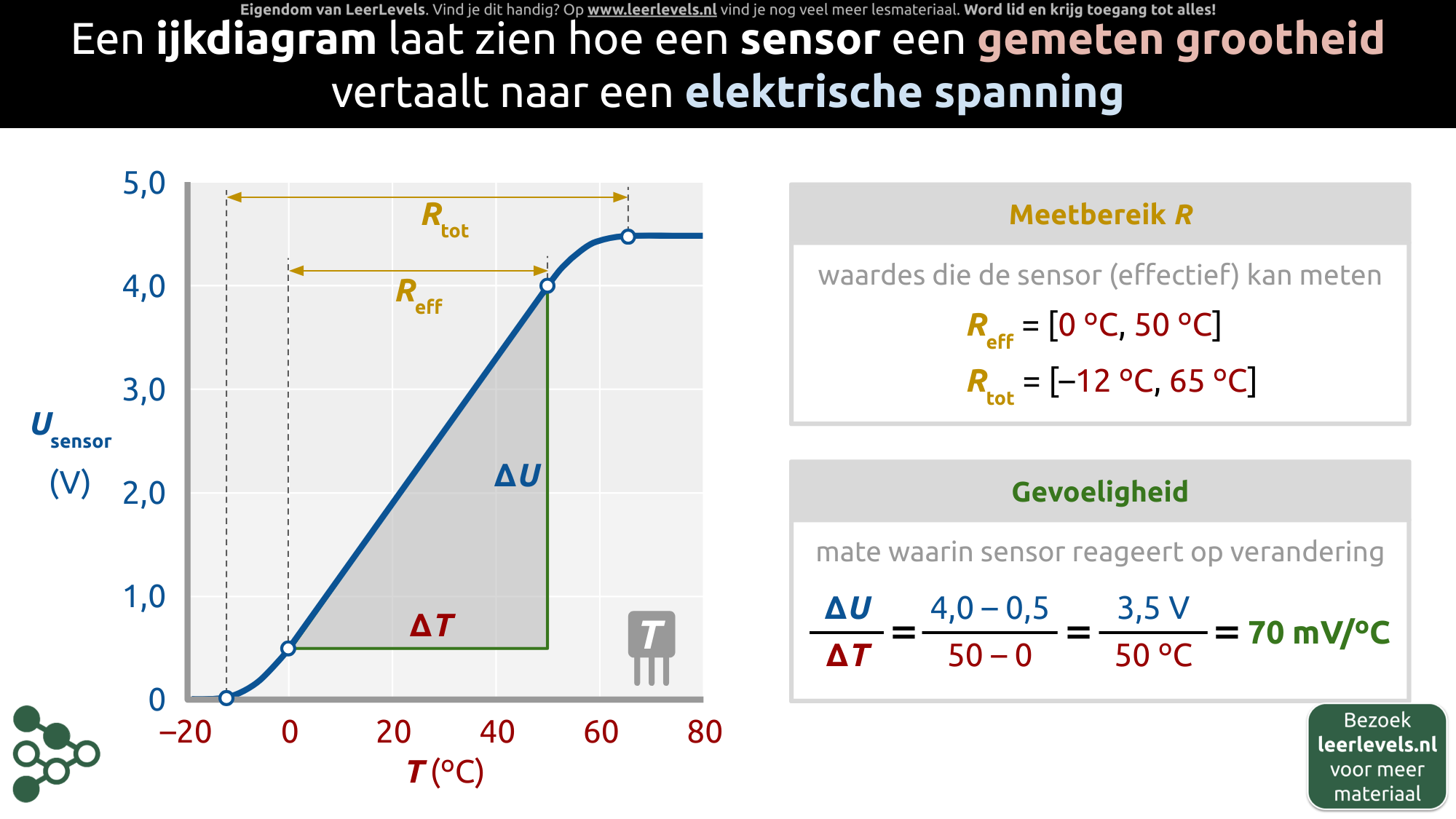
(Afbeelding: Animatie voor Sensor ijkdiagram)

Terug naar overzicht Meld je aan

Impuls

Impuls concept

Impuls is de hoeveelheid beweging van een bewegend voorwerp en wordt bepaald door de massa en de snelheid. Bij kleine voorwerpen of lage snelheden is de impuls ook klein, zoals bij een vallend blaadje. Bij grote massa's of hoge snelheden kan de impuls echter gevaarlijk zijn, zoals bij een afgevuurde kogel of een vliegende raket. Impuls kan worden berekend met de formule p = mv, waarbij p de impuls is, m de massa en v de snelheid.

(Afbeelding: Animatie voor Impuls concept)

Impuls formule

De impuls van een voorwerp is hoeveel kracht het heeft om iets anders te bewegen. Het hangt af van hoe zwaar het voorwerp is en hoe snel het gaat. De formule is p = m · v, waarbij p de impuls is in kg · m/s (of een 'Newton seconde'), m de massa is in kg en v de snelheid is in m/s. De pijltjes boven de symbolen p en v betekenen dat impuls en snelheid ook een richting hebben. Dus als je de impuls van een voorwerp berekent, moet je ook weten welke kant het beweegt. Kortom, hoe zwaarder en sneller een voorwerp is, hoe meer impuls het heeft.

(Afbeelding: Animatie voor Impuls formule)

Impuls en kinetische energie

Kinetische energie kan worden uitgedrukt in impuls en massa in plaats van snelheid en massa. Als je de impuls-functie kwadrateert en deelt door de massa, krijg je

(p²)/(m) = (m² · v²)/(m) = m · v²

dus

(p²)/(2m) = ½ · m · v²

dus

Ek = (p²)/(2m)

Dit kun je weer omschrijven naar

p = √(2 · m · Ek)

Hierdoor kun je de kinetische energie en impuls op een andere manier uitdrukken.

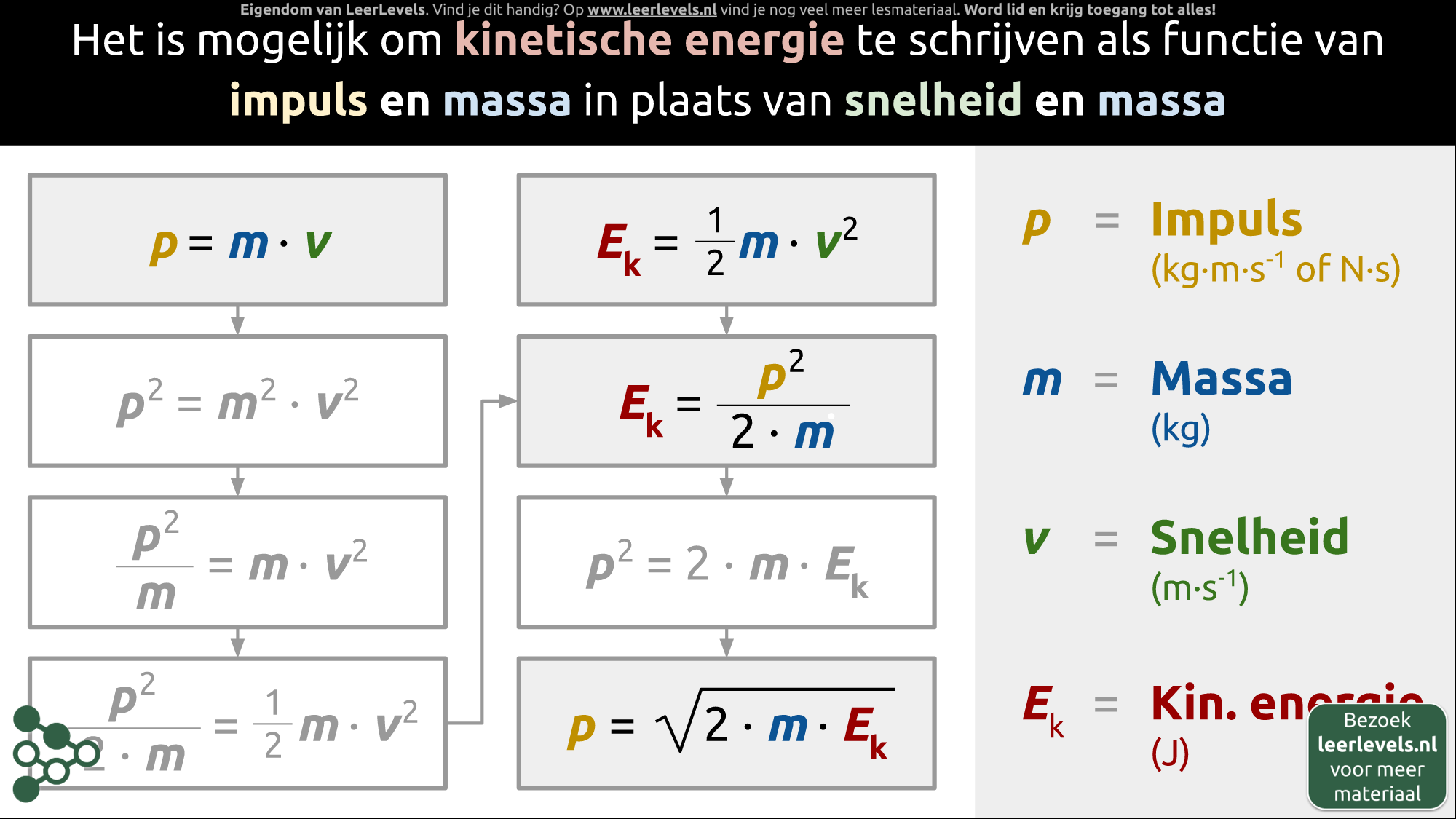
(Afbeelding: Animatie voor Impuls en kinetische energie)

Terug naar overzicht Meld je aan

Impulsmoment

Impulsmoment concept

Het impulsmoment L van een draaiend voorwerp beschrijft de "hoeveelheid rotatie beweging". Het impulsmoment hangt af van drie eigenschappen van het voorwerp: massa (m), straal (r) en hoeksnelheid (omega).

Als de massa van het voorwerp groter wordt, dan wordt het impulsmoment L ook groter. Als de straal van het voorwerp groter wordt, dan wordt het impulsmoment L ook groter. En als de hoeksnelheid van het voorwerp groter wordt, dan wordt het impulsmoment L ook groter.

Dus, het impulsmoment L van een voorwerp beschrijft de "hoeveelheid rotatie beweging" in een draaiend voorwerp.

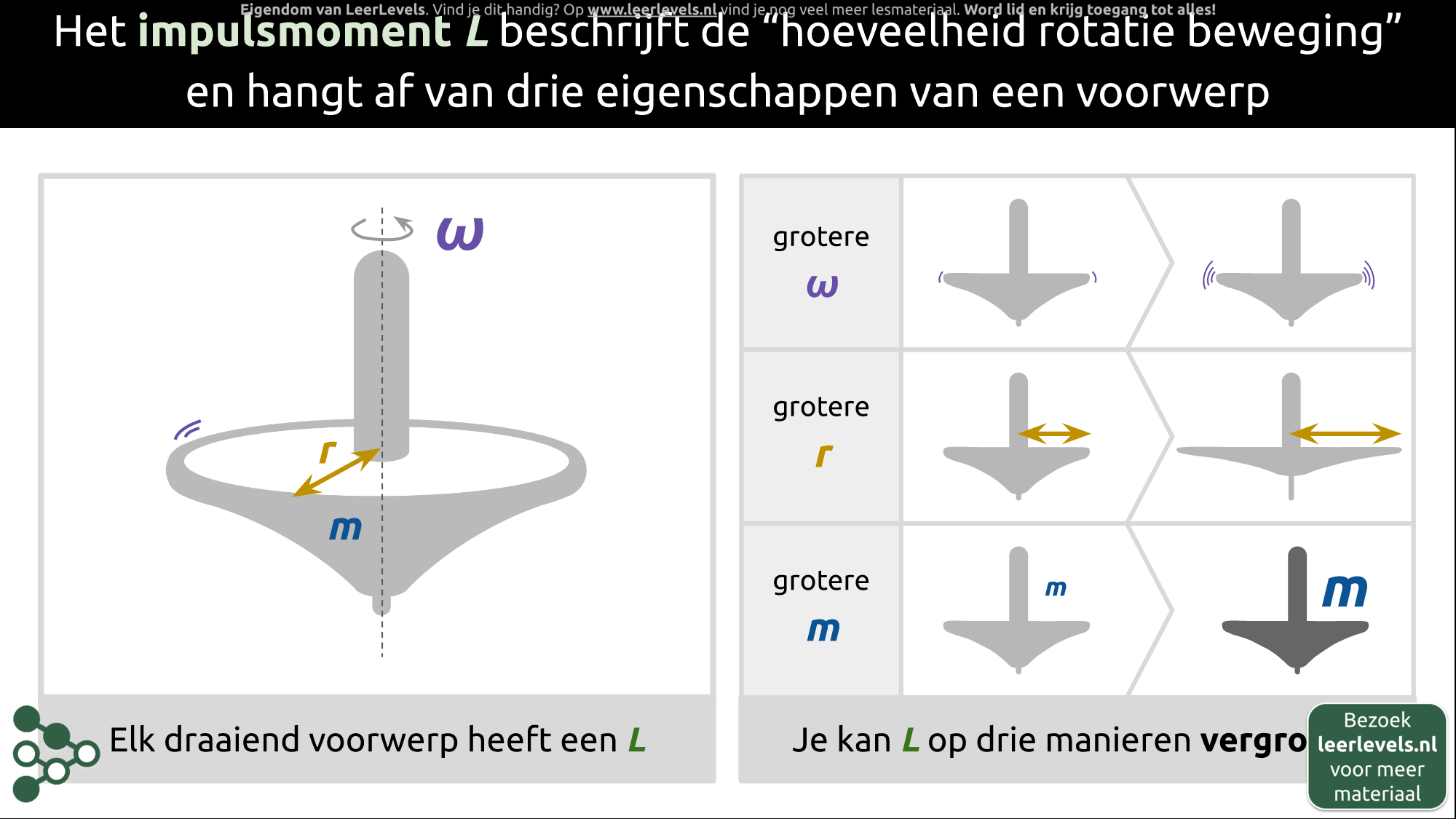
(Afbeelding: Animatie voor Impulsmoment concept)

Terug naar overzicht Meld je aan

Inductie

Inductie en deductie

Inductie en deductie zijn manieren om iets te bewijzen. Om deze methodes te gebruiken, moet je beginnen met het observeren van dingen. Bij inductie formuleer je daarna een regel op basis van deze waarnemingen. Een voorbeeld hiervan is het feit dat een appel naar beneden valt, waarmee je de regel kunt afleiden dat alle voorwerpen richting de aarde vallen in een constante versnelling, ongeacht de massa. Bij deductie werk je andersom. Hierbij gebruik je bestaande regels om voorspellingen te doen. Bijvoorbeeld: de aantrekkingskracht tussen twee objecten is omgekeerd evenredig met de afstand. Met deze regel kun je voorspellen dat de maan het getij beïnvloedt omdat water naar de maan wordt getrokken. Deze voorspellingen kun je dan weer controleren door middel van waarnemingen. Kortom, inductie en deductie zijn verschillende methoden van bewijsvoering die beginnen met waarnemingen en uitmonden in respectievelijk een nieuwe regel of voorspelling.

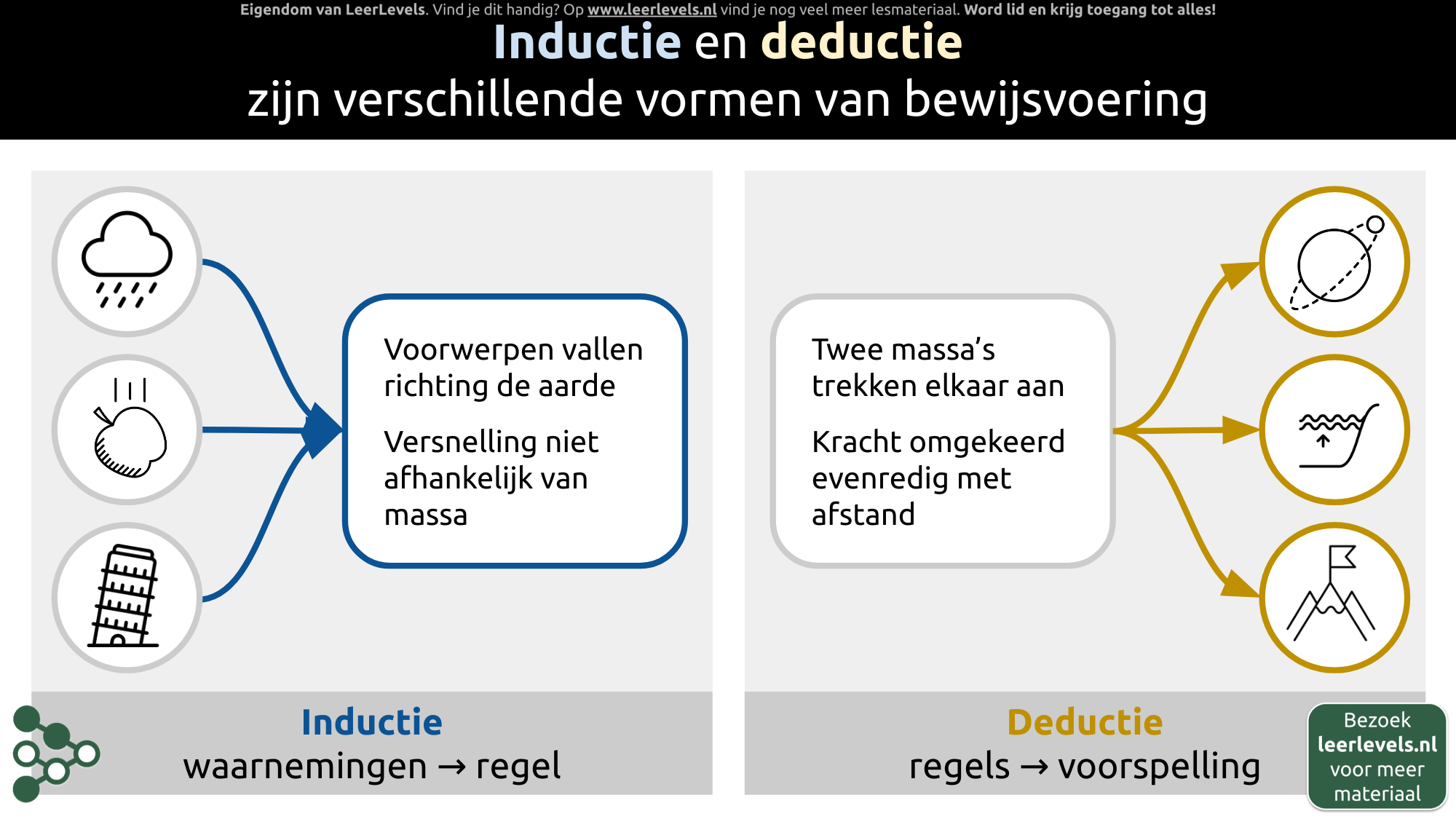
(Afbeelding: Animatie voor Inductie en deductie)

Terug naar overzicht Meld je aan

Inductiespanning

Inductiespanning concept

Als je een magneet boven een spoel laat hangen, zonder dat de magneet beweegt, gebeurt er niets en gaat er geen stroom door de spoel. Maar als je de magneet naar beneden laat bewegen, komen er steeds meer veldlijnen door de spoel heen en gaat er wel stroom door de spoel. Dit komt doordat er tijdens het veranderen van de flux (de hoeveelheid veldlijnen die door de spoel gaan) een inductiespanning ontstaat over de uiteindes van de spoel. Het lampje dat op de spoel is aangesloten, gaat dan branden. Als de magneet stilhangt boven de spoel, verandert de flux niet en ontstaat er geen inductiespanning. Het is dus alleen bij het veranderen van de flux dat er een inductiespanning ontstaat en er stroom door de spoel gaat.

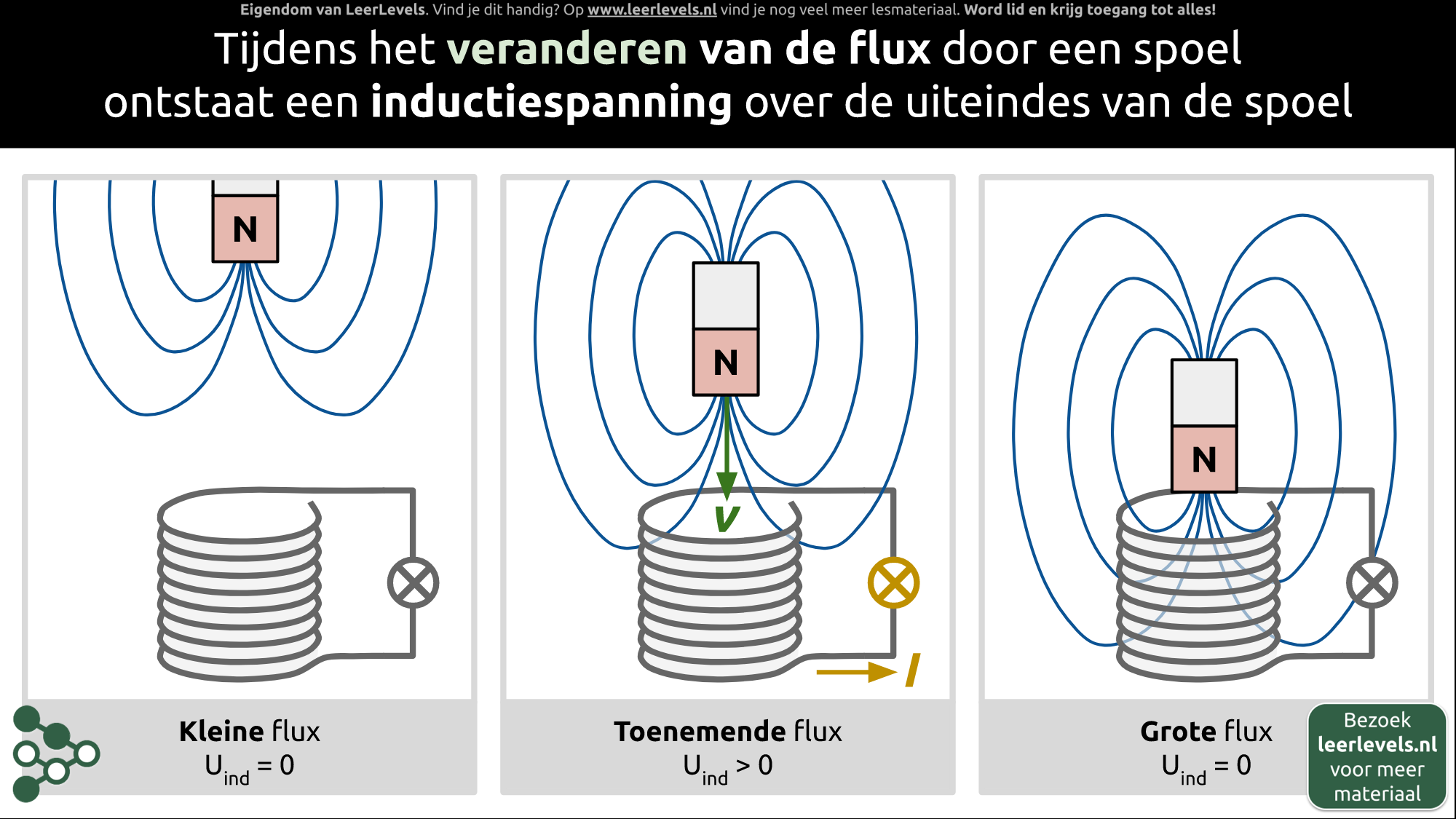
(Afbeelding: Animatie voor Inductiespanning concept)

Inductiespanning formule

De gemiddelde inductiespanning hangt af van drie dingen:

- Het aantal windingen
- De verandering van de flux
- De tijd waarin deze verandering plaatsvindt

De gemiddelde inductiespanning wordt weergegeven met een streepje erboven en is gelijk aan:

\overline{V} = {N · ΔΦ\overΔ t}

Hierbij is N het aantal windingen, ΔΦ de verandering in flux (gemeten in weber, afgekort als Wb) en Δ t de tijdsduur (gemeten in seconden). De inductiespanning wordt uitgedrukt in Volt (V) en het aantal windingen is eenheidsloos.

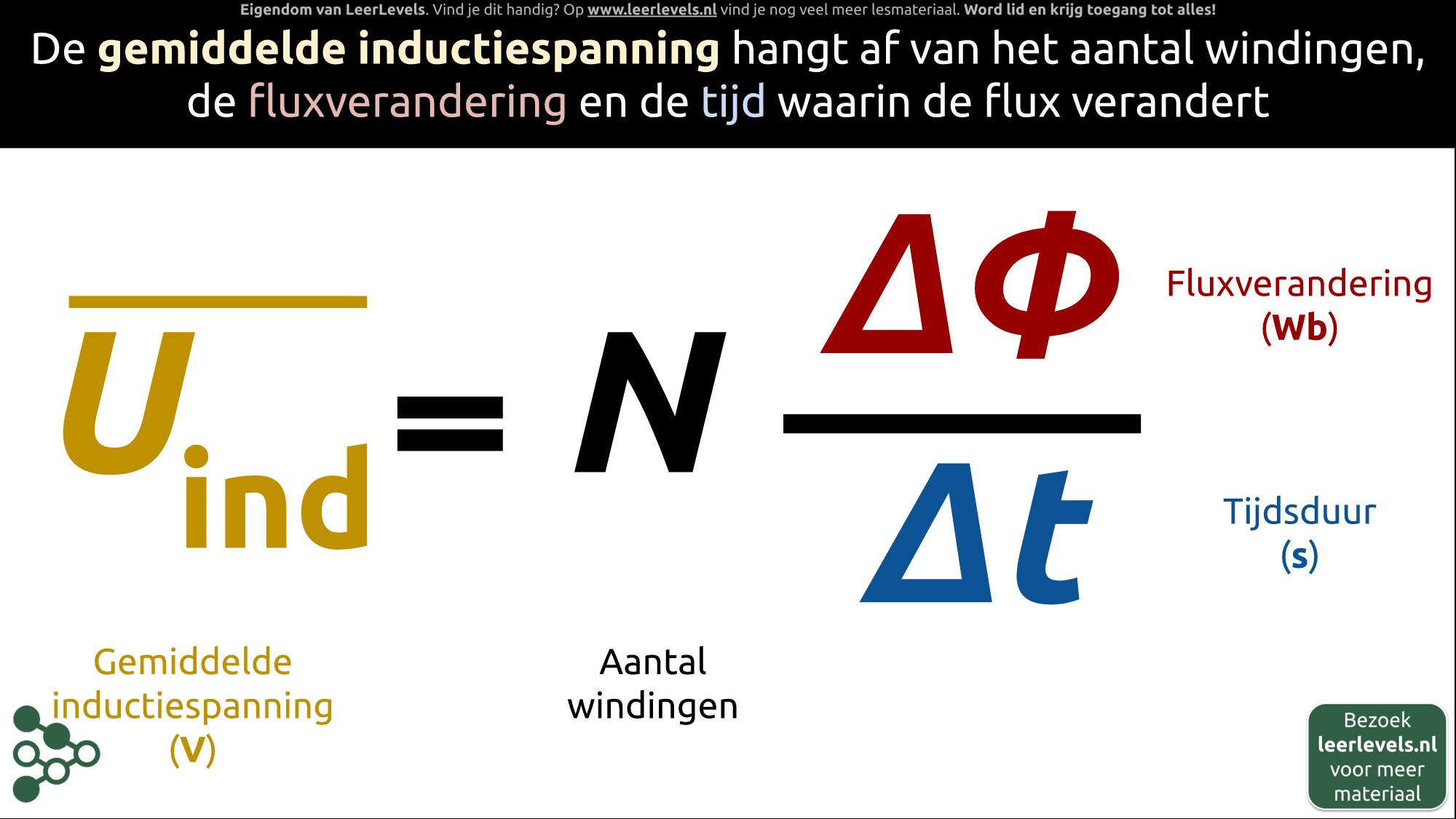
(Afbeelding: Animatie voor Inductiespanning formule)

Terug naar overzicht Meld je aan

Intensiteit

Intensiteit concept

Intensiteit betekent hoeveel kracht er op een oppervlak terechtkomt. Als er zonlicht op een oppervlak schijnt, kan de intensiteit laag zijn als het oppervlak groot is. Maar als dezelfde hoeveelheid zonlicht op een kleiner oppervlak komt, is de intensiteit hoog omdat de kracht van de zon op een kleiner gebied wordt geconcentreerd. Dit voelt anders aan op je huid. Als je je vinger links houdt, voelt het normaal aan. Maar als je het rechts houdt, voel je dat er meer kracht op een kleiner gebied valt, wat aangeeft dat de intensiteit hoger is.

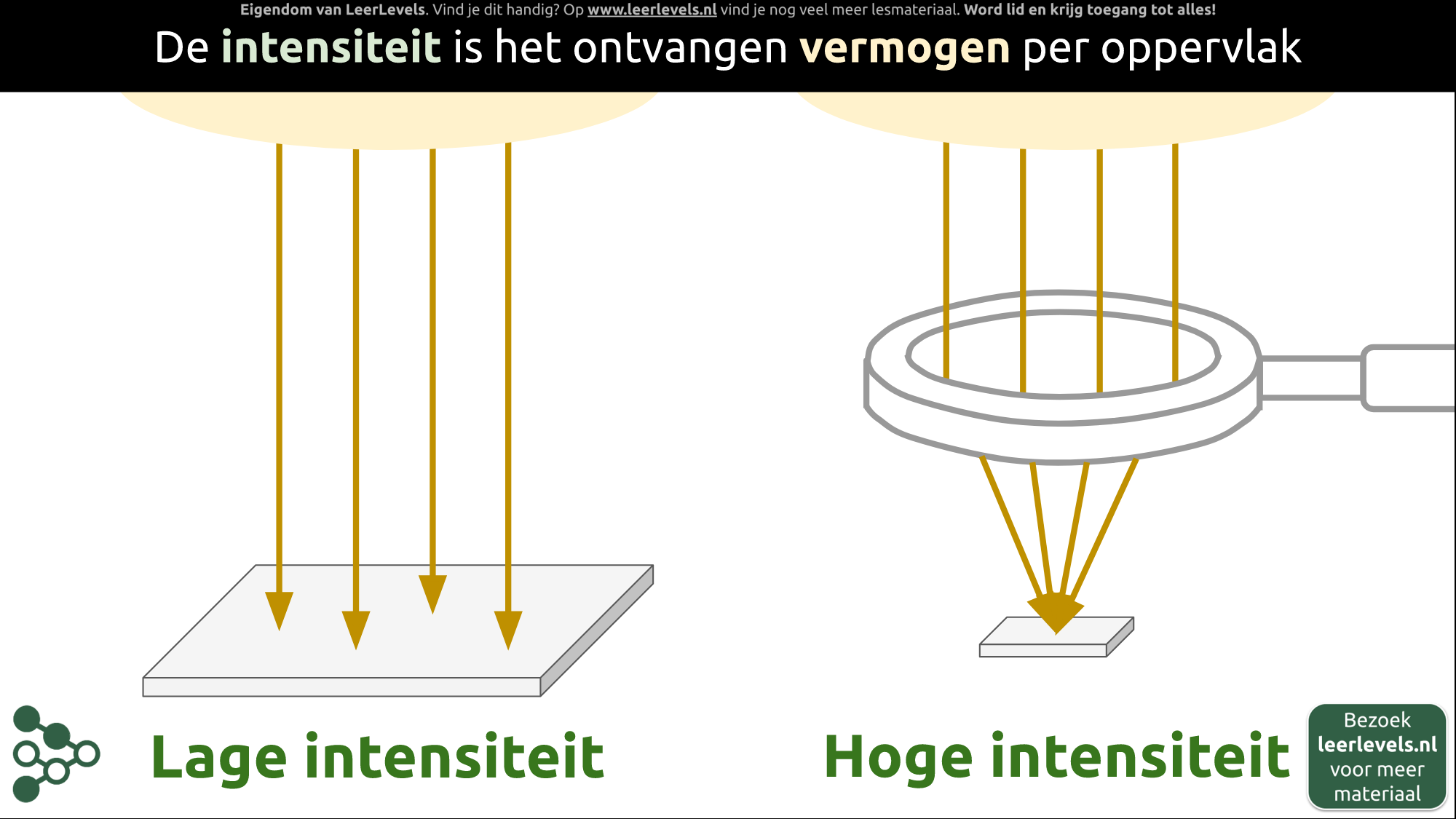
(Afbeelding: Animatie voor Intensiteit concept)

Intensiteit formule

De intensiteit is recht evenredig met het vermogen en omgekeerd evenredig met het bereikte oppervlak. In formulevorm wordt dit weergegeven als:

I = P/A

Hierin is de intensiteit (I) uitgedrukt in W/m², aangezien het vermogen (P) wordt gemeten in Watt (Joule per seconde) en het oppervlak (A) in vierkante meter. Dus, de eenheid van intensiteit is Watt per vierkante meter

(Afbeelding: Animatie voor Intensiteit formule)

Terug naar overzicht Meld je aan

Interferentie

Bij interferentie tussen golven kun je de amplitude van afzonderlijke golven optellen om de amplitude van de resulterende golf te bepalen. Laten we twee golven bij elkaar optellen en het resultaat bekijken. We voegen een blauw en een geel golfpatroon samen. Op elke positie tel je de amplitudes op, wat leidt tot de groene golf. Als twee pieken samenvallen, resulteert dit in een grotere piek. Dit versterkende effect noemen we constructieve interferentie. Het omgekeerde is ook mogelijk. Als een dal samenvalt met een top in hetzelfde blauwe patroon, zie je dat de berg en het dal elkaar opheffen. Dit uitdovende effect wordt destructieve interferentie genoemd. Een combinatie is ook mogelijk: een berg en een dal heffen elkaar op, terwijl twee bergen elkaar versterken.

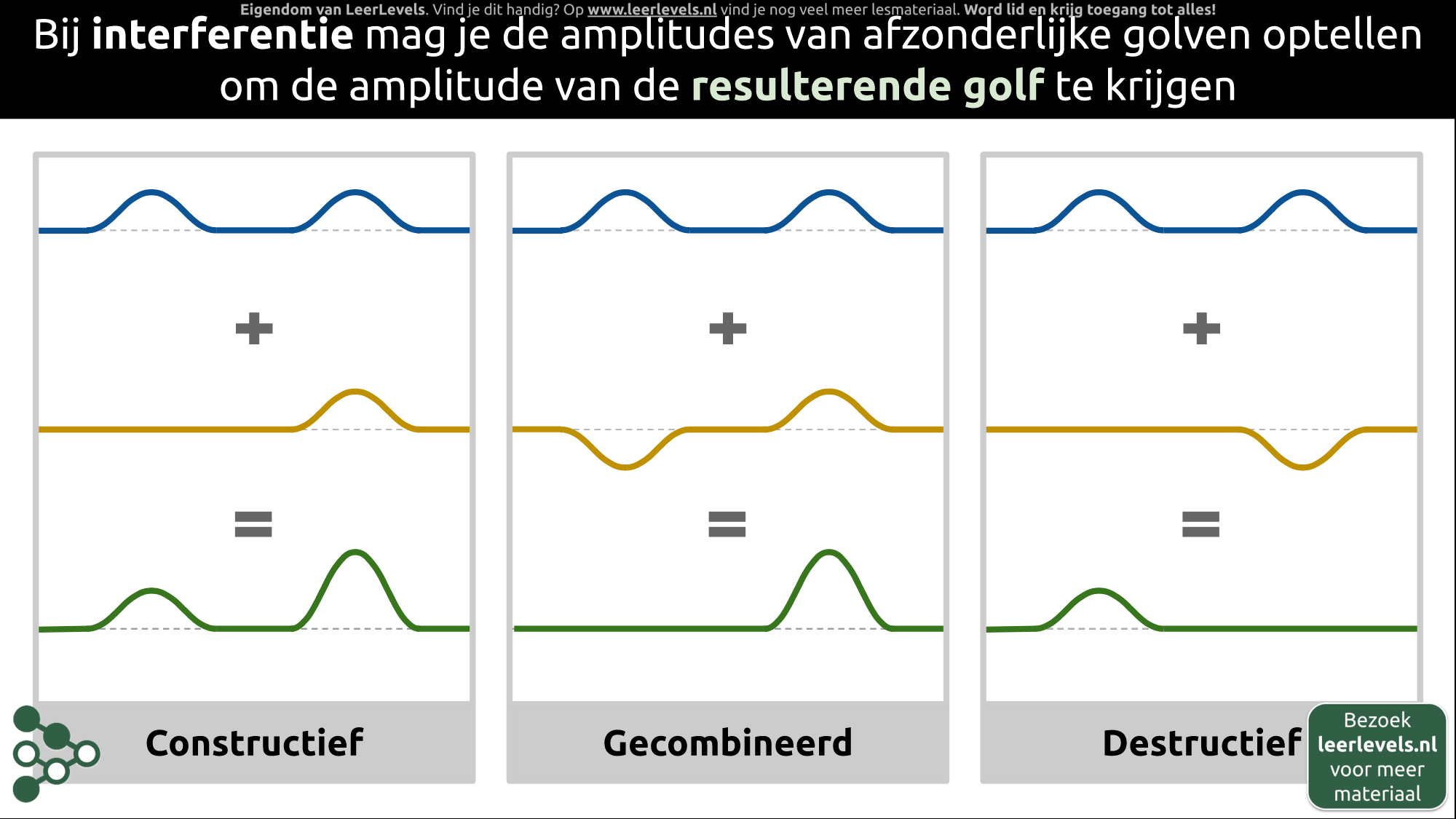
(Afbeelding: Animatie voor Interferentie)

Terug naar overzicht Meld je aan

Inzicht

Snappen wat je kan

Bij natuurkunde rekenen we niet alleen om formules en trucjes uit ons hoofd te leren. Het gaat vooral om het begrijpen van wat we doen en waarom we het doen. Door het maken van opdrachten ontdekken we wat wel en niet werkt. Er zijn verschillende trucjes, zoals "vermenigvuldigen met het omgekeerde" ( 1/x ), "driehoekjes", "kruislings vermenigvuldigen" en "naar de andere kant halen". Hoewel deze trucjes soms handig zijn bij het oplossen van een vergelijking, is het belangrijk om te begrijpen wat je doet bij deze stappen. Op die manier weet je zeker dat je ze goed gebruikt. Het belangrijkste bij rekenen in de natuurkunde is dat de vergelijking in balans moet blijven. Er zijn verschillende manieren om dit te doen, zoals het vereenvoudigen van dingen die aan de linkerkant van de vergelijking staan. Als je begrijpt wat je doet en de regels volgt, dan kun je de juiste uitkomst vinden.

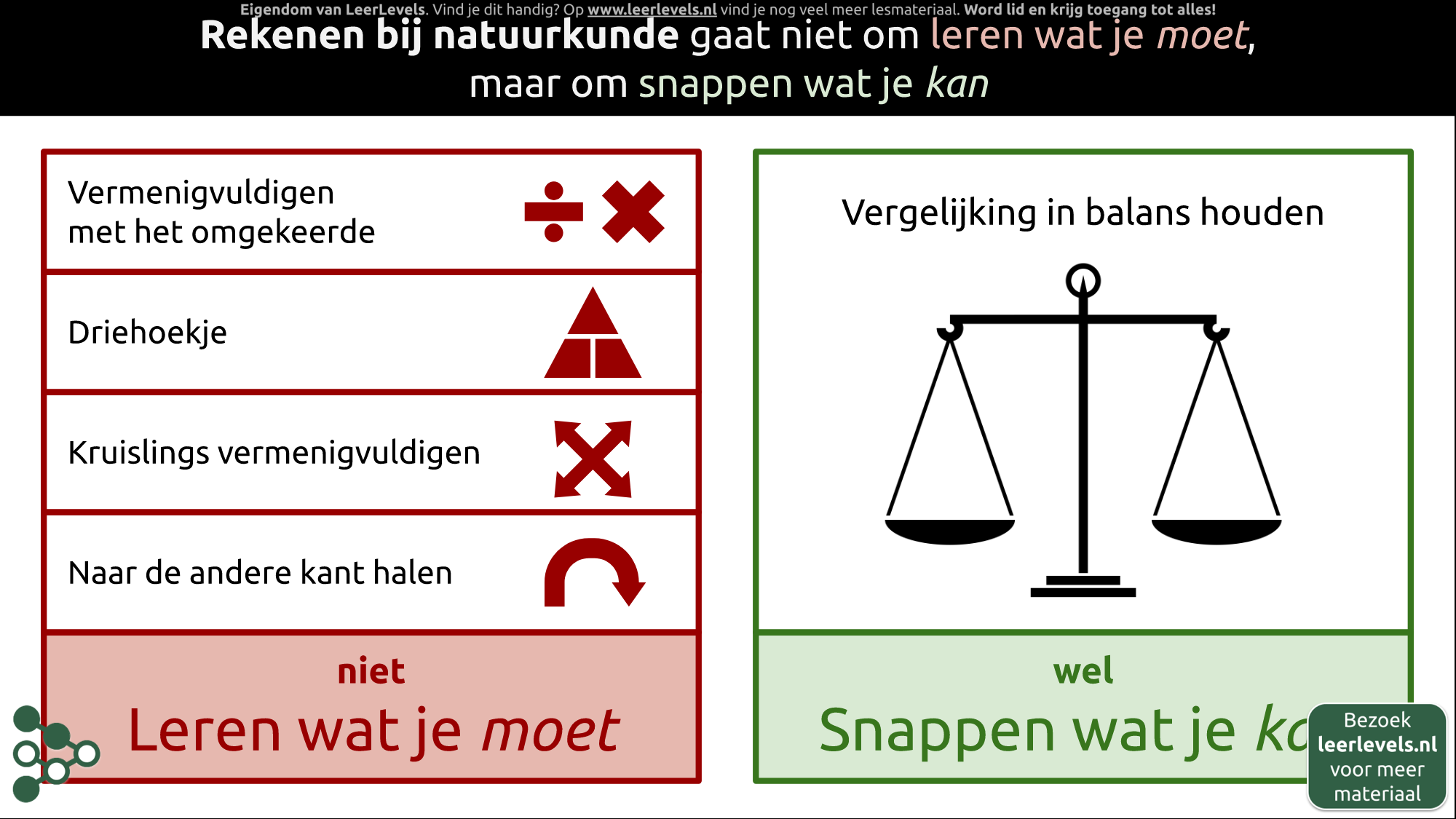
(Afbeelding: Animatie voor Snappen wat je kan)

Terug naar overzicht Meld je aan

Ion

Een ion is een geladen deeltje, dit kan een molecuul of atoom zijn. Een neutraal deeltje is geen ion, deze heeft evenveel protonen als elektronen. Een voorbeeld hiervan is helium-4 met 2 protonen, 2 neutronen en 2 elektronen. Een positief ion heeft meer protonen dan elektronen, bijvoorbeeld 4,2-He2 + waarbij er geen elektronen zijn en de netto lading 2 + is. Een negatief ion heeft minder protonen dan elektronen, bijvoorbeeld 16,8 O2- waarbij er twee elektronen teveel zijn voor het aantal protonen. Een ion kan dus een verschillende lading hebben. Als er evenveel protonen als elektronen zijn, is het geen ion.

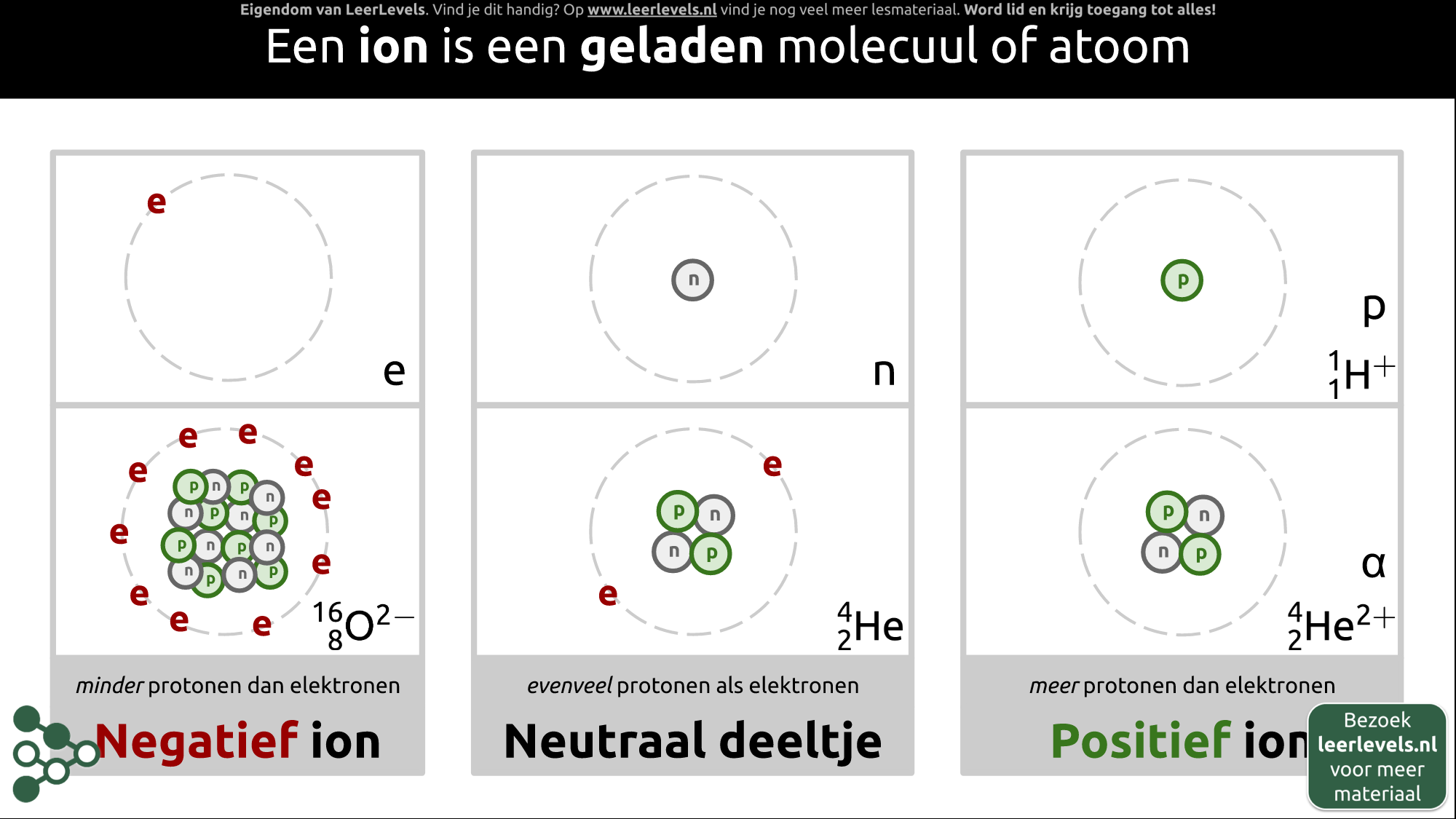
(Afbeelding: Animatie voor Ion)

Terug naar overzicht Meld je aan

Ionisatie

Ioniserend vermogen

Ioniserende straling kan atomen beschadigen door deze te ioniseren. Het ioniserend vermogen geeft aan in hoeverre dit mogelijk is. Alfastraling is hierbij het meest schadelijk, omdat het een grote positieve lading heeft en makkelijk andere deeltjes kan ioniseren. Betastraling is minder schadelijk omdat het een lading van min 1 heeft en een kleinere massa dan alfastraling. Gammastraling is nauwelijks ioniserend en kan alleen elektronen losmaken uit de baan als het foton precies de juiste energie heeft. Alleen dan is de kans op schade relatief klein. We kunnen dus concluderen dat alfastraling het meest schadelijk is, gevolgd door betastraling en tot slot gammastraling.

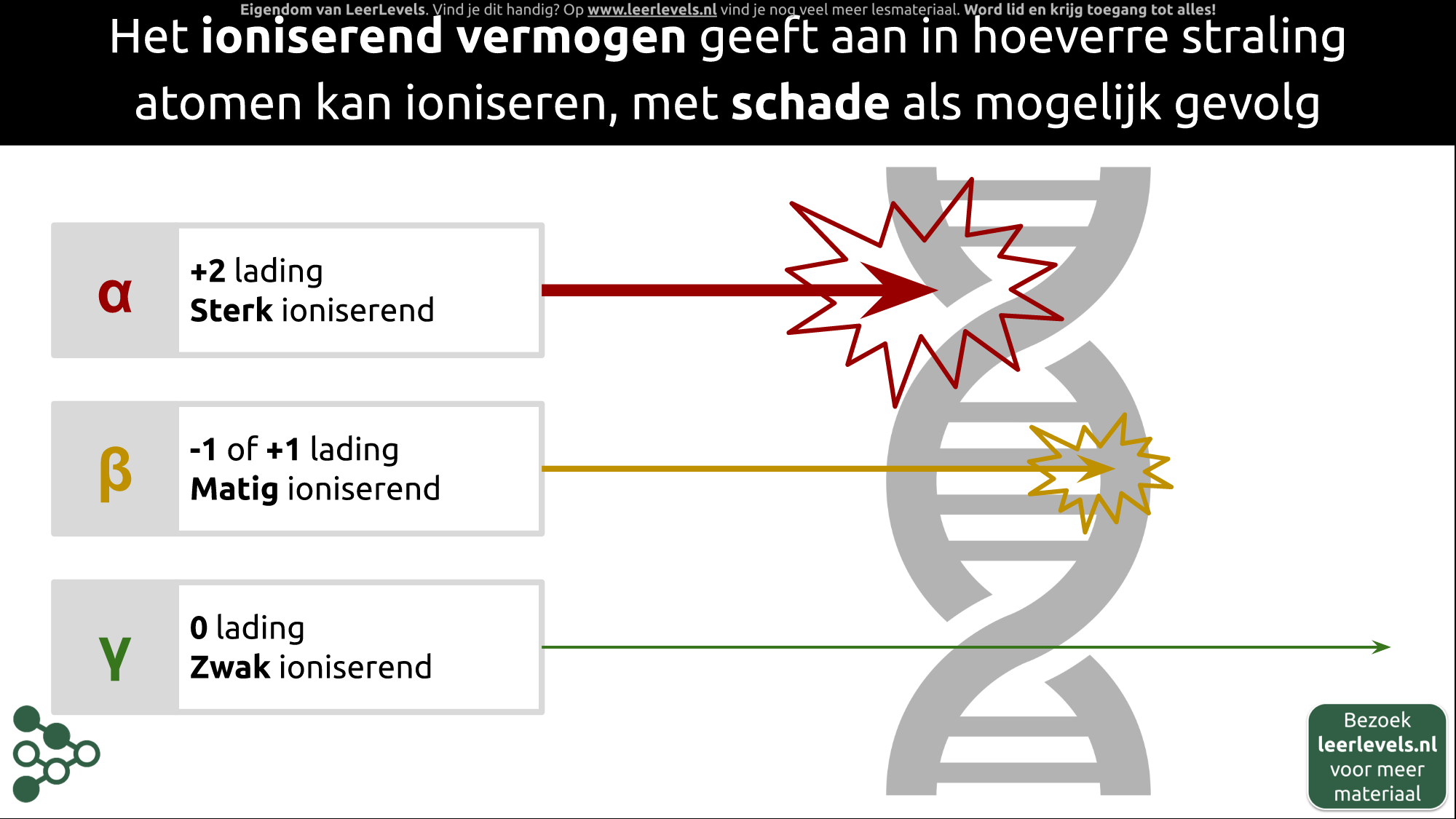
(Afbeelding: Animatie voor Ioniserend vermogen)

Terug naar overzicht Meld je aan

Isotopen

Isotopen zijn atomen van dezelfde soort, maar met een ander aantal neutronen. Waterstof is het meest eenvoudige atoom. Het heeft één proton en geen neutronen. Als er een extra neutron aan wordt toegevoegd, heet het deuterium. Deuterium heeft nog steeds één proton en één elektron, maar is zwaarder omdat het een extra neutron heeft. Het is ongeveer 2 keer zo zwaar als waterstof. Als er nog een extra neutron wordt toegevoegd, wordt het tritium. Tritium heeft 3 kerndeeltjes: 1 proton en 2 neutronen. Dit wordt geschreven als H³. Isotopen zijn dus atomen van dezelfde soort, maar met een ander aantal neutronen.

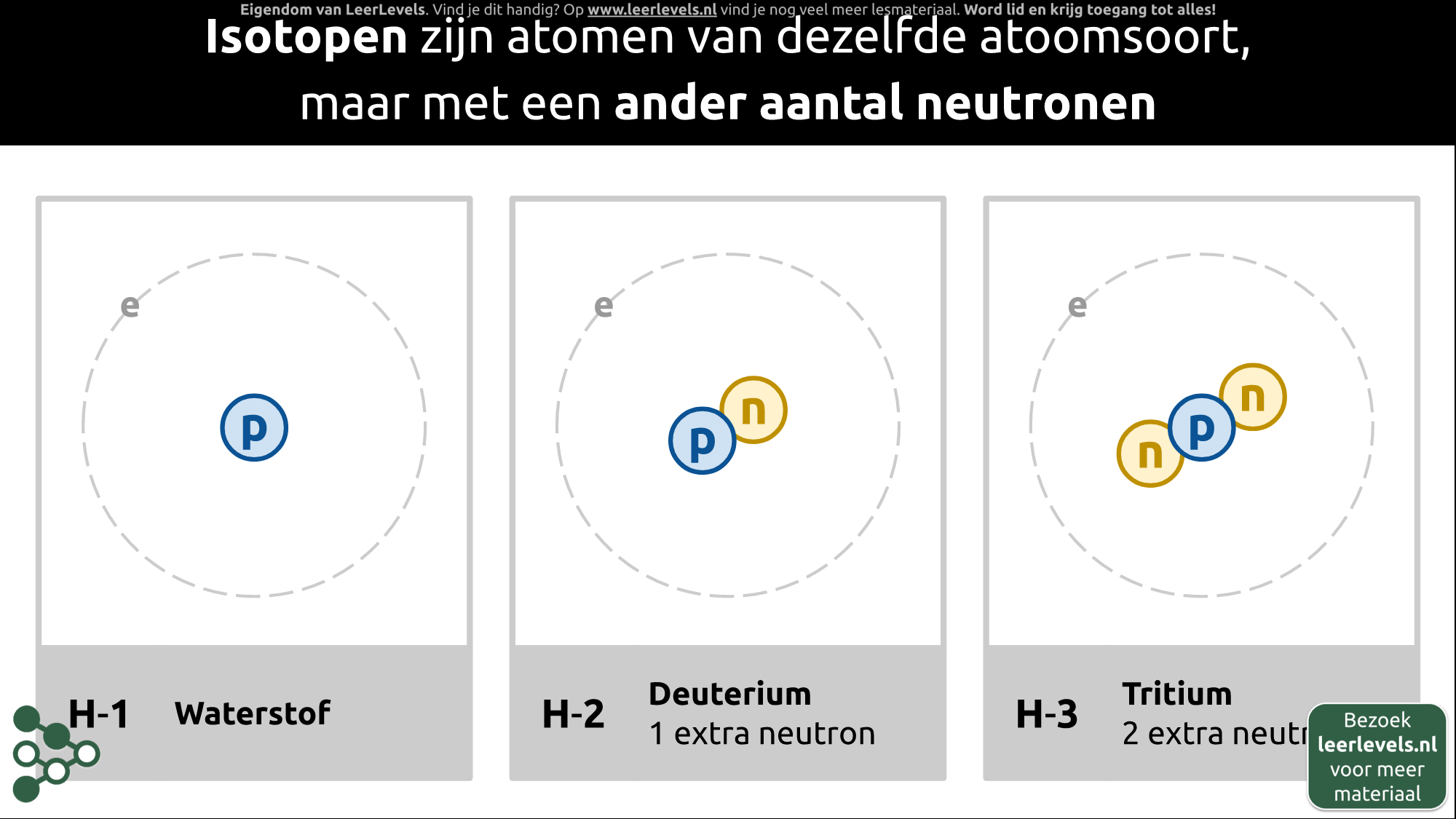
(Afbeelding: Animatie voor Isotopen)

Terug naar overzicht Meld je aan

Isotopenkaart

Isotopenkaart concept

De isotopenkaart laat zien welke isotopen er bestaan op basis van het aantal protonen en neutronen. Het aantal neutronen staat op de x-as en het aantal protonen op de y-as. Stabiele isotopen zijn zwart en de gestippelde lijn N = Z laat zien waar er evenveel neutronen als protonen zijn. Er zijn boven N = 126 geen stabiele isotopen. Het rood geeft isotopen aan die beta-plus verval hebben en het blauw geeft isotopen weer die beta-min-verval laten zien. Als een isotoop alfaverval heeft dan staat deze in het groen en een klein groepje in het geel heeft K-vangst. De isotopenkaart maakt het mogelijk om verschillende isotopen en hun eigenschappen te vergelijken.

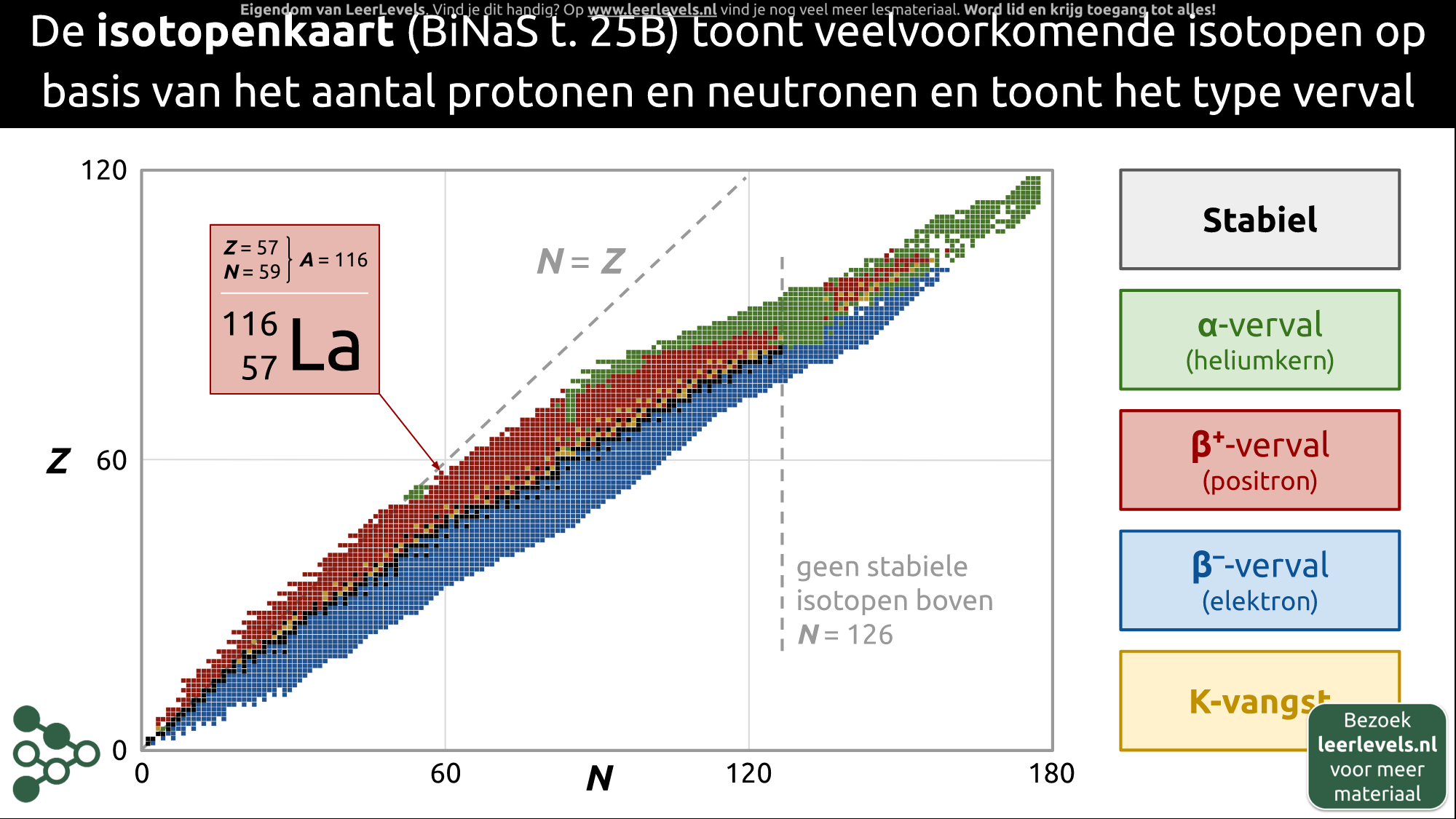
(Afbeelding: Animatie voor Isotopenkaart concept)

Isotopenkaart vervalreacties

In een isotopenkaart staan pijlen die laten zien hoe een atoomkern verandert in een andere atoomkern door radioactief verval. Een pijl gaat van de "moederkern" naar de "dochterkern". Bijvoorbeeld het atoom Be-8 vervalt tot een atoom met twee protonen en twee neutronen (een heliumkern). Het aantal neutronen en protonen verandert dus van 4 naar 2. Dit is alfa-verval en de pijl in de isotopenkaart gaat daarom naar linksonder. Bij koolstof-11 wordt een positron uitgezonden, waardoor het aantal neutronen stijgt en het aantal protonen daalt. Dit type verval wordt beta-plus-verval genoemd en de pijl in de isotopenkaart wijst naar rechtsonder. Bij lithium-9 vindt beta-min-verval plaats, wat betekent dat er een elektron wordt uitgezonden, waardoor het aantal neutronen daalt en het aantal protonen stijgt. De pijl in de isotopenkaart gaat daarom naar linksboven in de richting van Be-9.

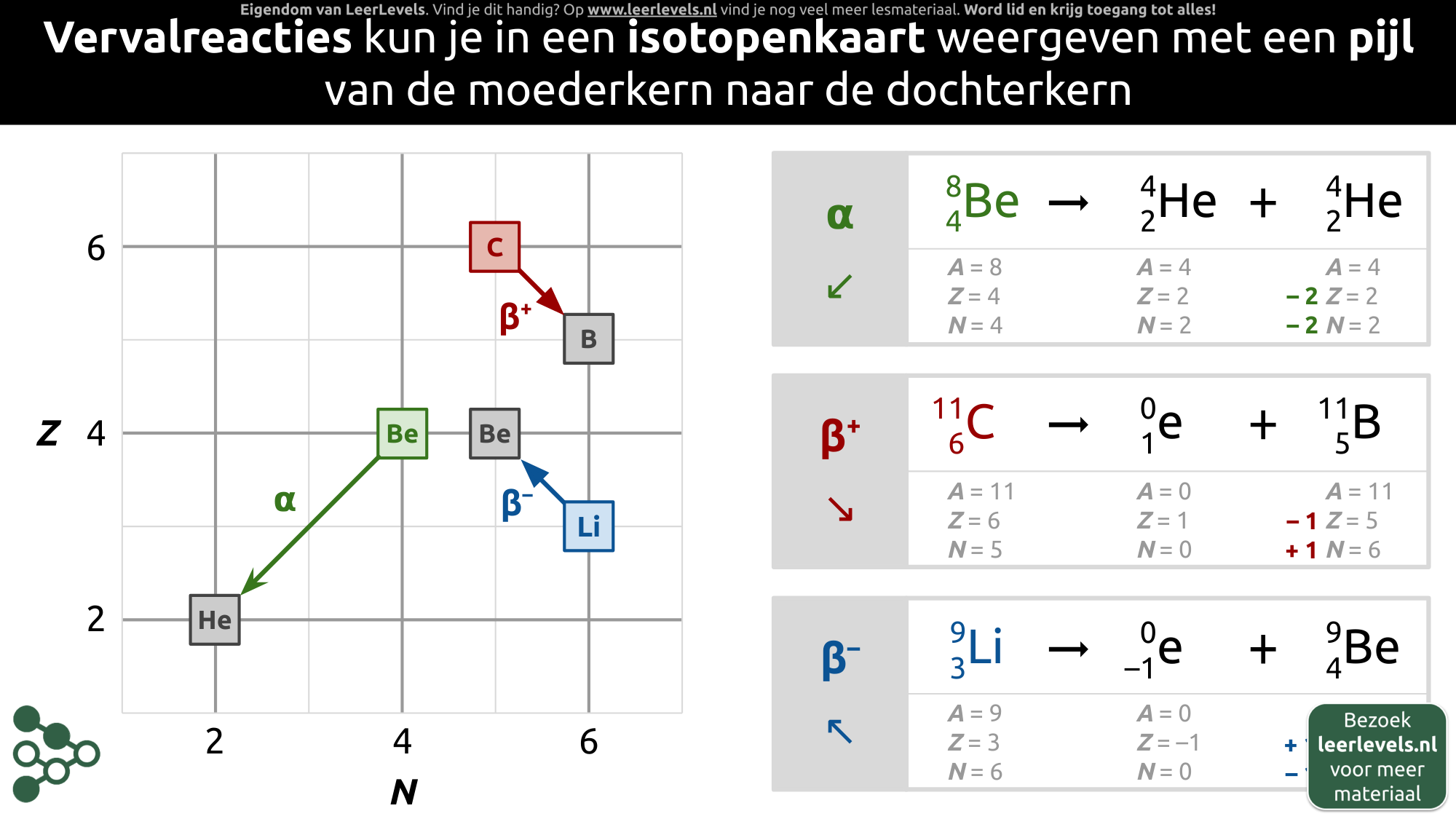
(Afbeelding: Animatie voor Isotopenkaart vervalreacties)

Terug naar overzicht Meld je aan

Joule

Eenheid joule

De Joule (J) is de standaardeenheid van energie. Met één Joule kun je ongeveer 100 gram een meter optillen. 10 megajoule (10⁷ J) is ongeveer wat je nodig hebt om een mens 24 uur te laten leven. 1 Joule is niet erg veel, want we hebben op een dag ongeveer 10 miljoen Joule (10⁷ J) nodig.

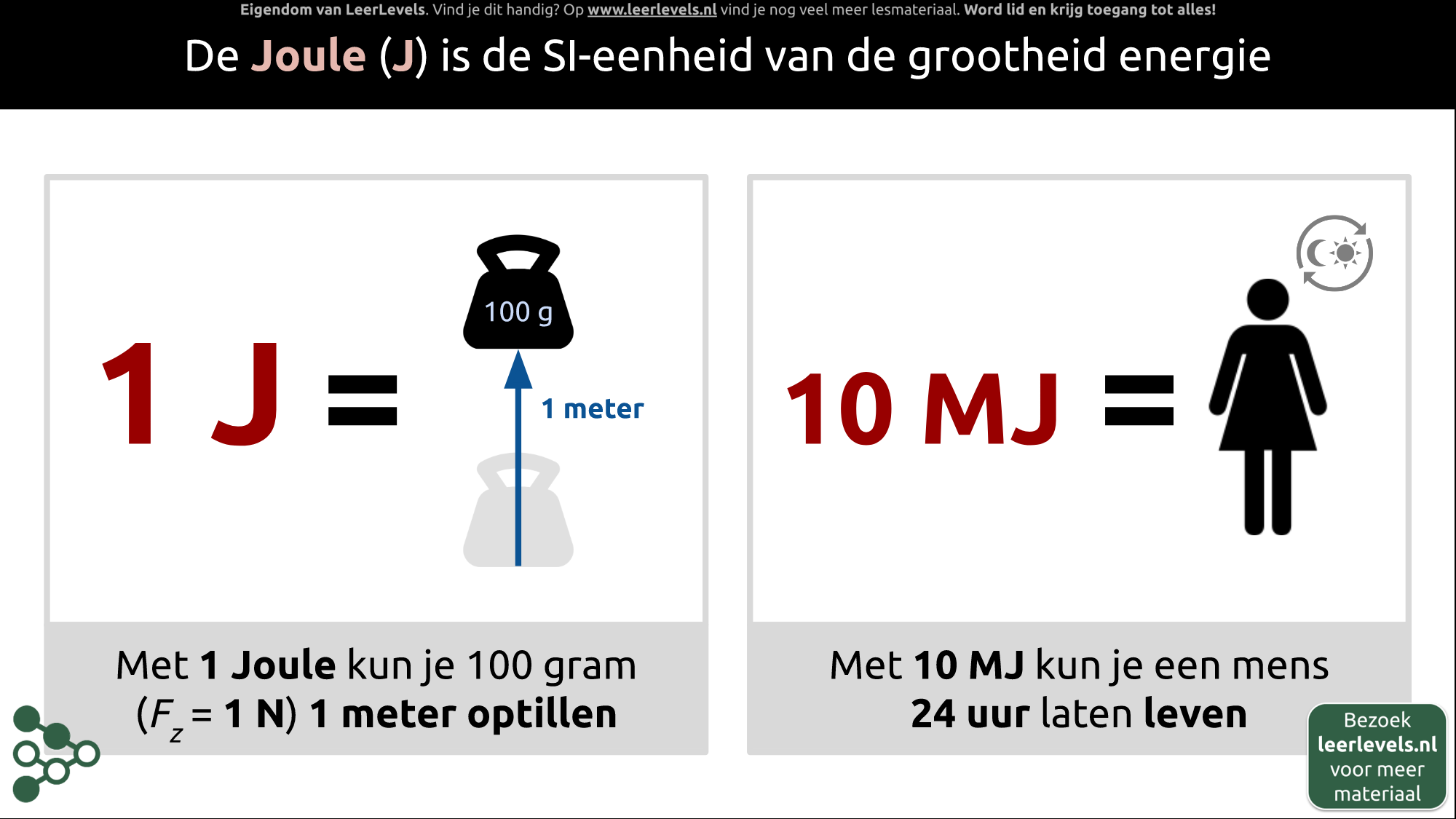
(Afbeelding: Animatie voor Eenheid joule)

Terug naar overzicht Meld je aan

K-vangst

K-vangst concept

Bij K-vangst vindt er een fusie plaats tussen een elektron en een proton, waardoor er een neutron ontstaat. Dit gebeurt bijvoorbeeld bij helium-3, waarbij een elektron in de kern valt. De massa van het neutron is vergelijkbaar met die van het oorspronkelijke proton. De vrijgekomen energie gaat naar een gamma deeltje (foton).

Om K-vangst te laten plaatsvinden, moeten drie voorwaarden worden voldaan: het aantal kerndeeltjes blijft gelijk, de totale lading blijft gelijk en de verandering van het aantal protonen resulteert in een verandering van de atoomsoort.

Notitie: In de originele tekst wordt verwezen naar 'foton', 'proton' en 'neutron', wat allemaal grootheden zijn. Er worden geen specifieke waarden of eenheden gegeven. Daarom hoefden er geen dollar-notaties van LaTeX te worden gebruikt.

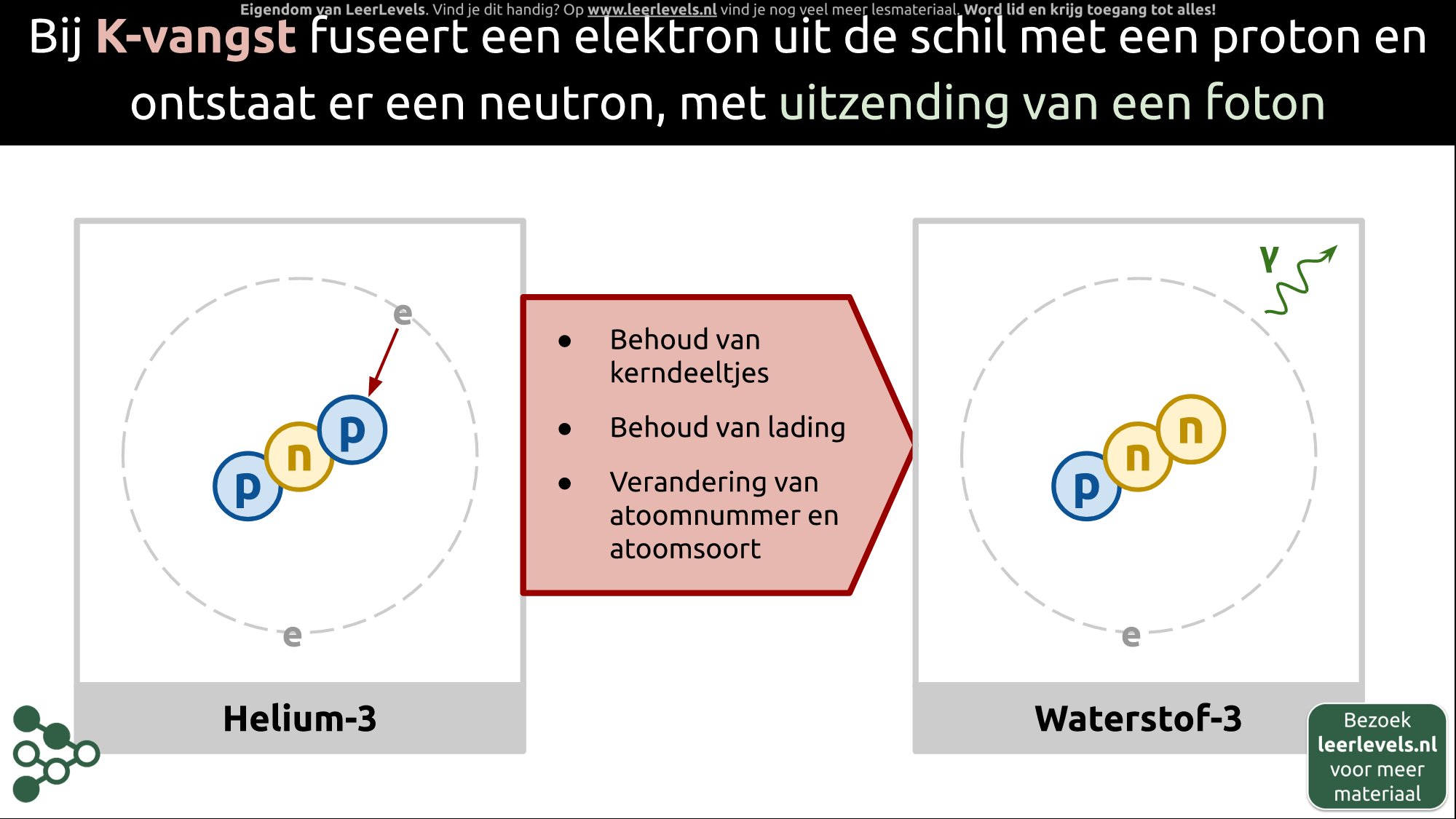
(Afbeelding: Animatie voor K-vangst concept)

K-vangst vervalvergelijking

Bij de vervalvergelijking van K-vangst wordt het opgenomen elektron vóór de pijl genoteerd. Stel dat we beginnen met ¹¹C, dat K-vangst ondergaat. We voegen daar een elektron aan toe, namelijk het elektron dat zich al in de K-schil van het koolstofatoom bevindt. Dit elektron fuseert met de kern, waardoor een ander atoom ontstaat, namelijk ¹¹B. Er wordt ook een foton uitgezonden, omdat de energie van het opgenomen elektron ergens naartoe moet. Deze vergelijking klopt, waarbij het elektron, aangeduid als e⁻, afkomstig is uit de binnenste elektronenschil, de zogenaamde K-schil, vandaar de naam K-vangst.

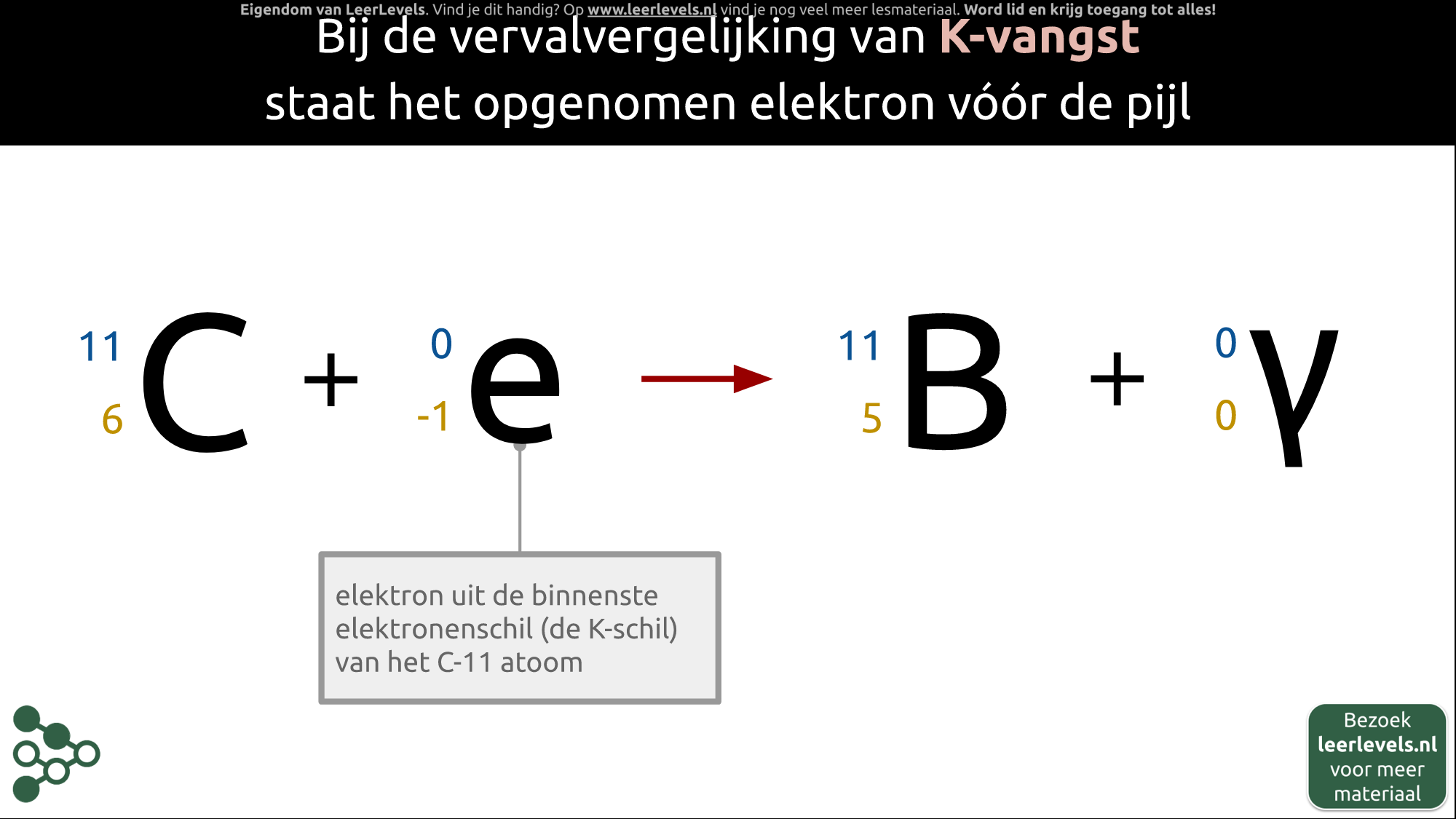
(Afbeelding: Animatie voor K-vangst vervalvergelijking)

Terug naar overzicht Meld je aan

Katrol

Vaste katrol

Een vaste katrol verandert alleen de richting van een spankracht op een blok. Als je een blok optilt en omhoog trekt met een touw, blijft de spankracht naar boven gericht en even groot als de zwaartekracht, ongeacht de lengte van het touw. Als je het moeilijk vindt om kracht naar boven te geven, kan je een vaste katrol gebruiken om de spankracht naar beneden te richten. Dit maakt het vaak gemakkelijker, zonder dat de grootte van de spankracht verandert. De formules en grootheden zijn niet relevant voor deze uitleg.

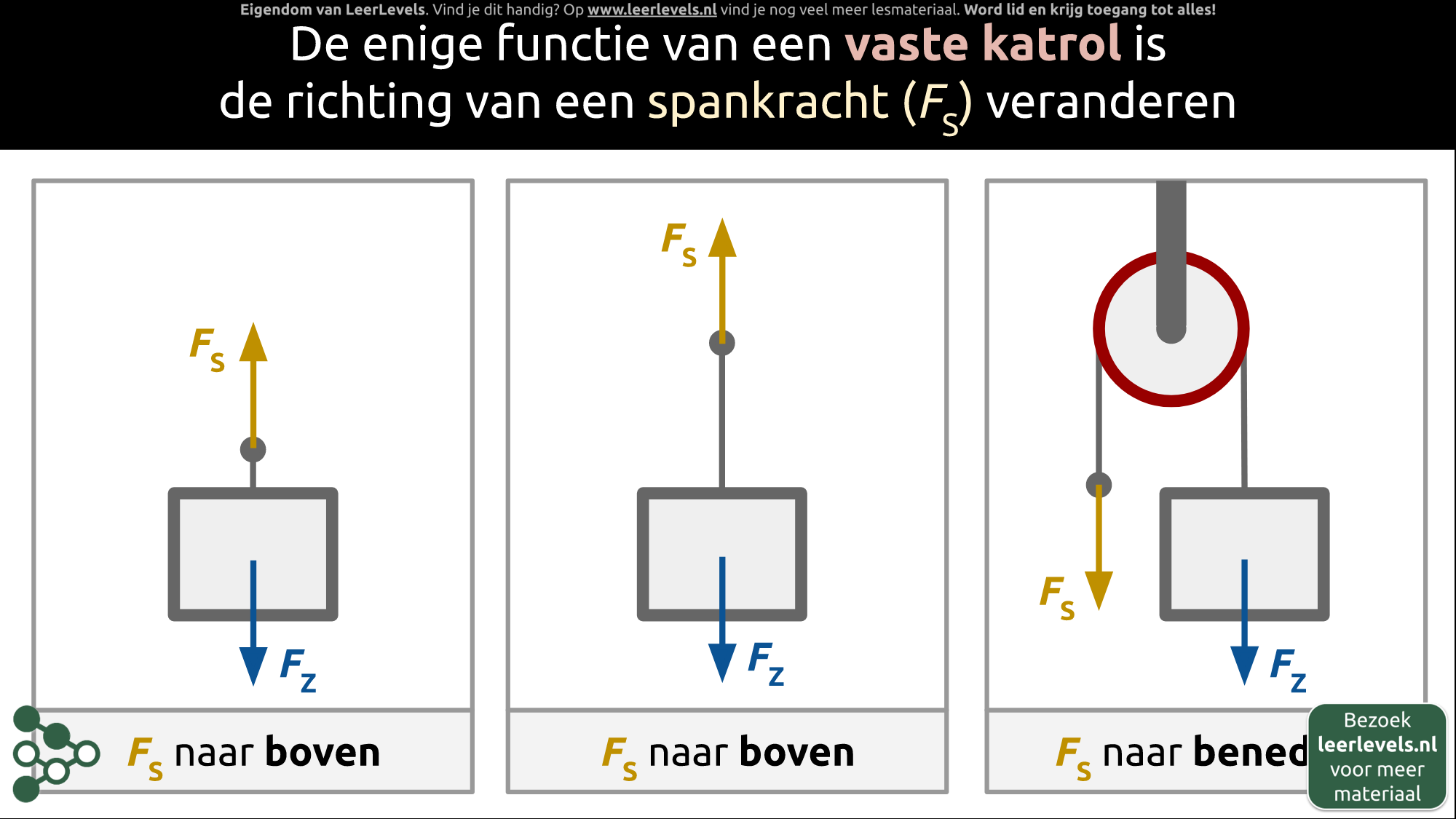
(Afbeelding: Animatie voor Vaste katrol)

Krachtverdeling bewegende katrol

Een bewegende katrol kan kracht verdelen over twee touwen. Zonder een katrol moet je net zoveel kracht gebruiken als de zwaartekracht om iets op te tillen. Met een katrol verdeel je de kracht over twee touwen, dus je hoeft minder kracht te gebruiken om elk touw vast te houden. Maar je hebt nog steeds dezelfde totale kracht nodig om iets op te tillen. Als je echter een touw aan het plafond vastmaakt en de katrol eraan bevestigt, hoef je slechts één touw omhoog te tillen en heb je slechts de helft van de zwaartekracht nodig. Door een katrol te gebruiken, kun je de totale benodigde kracht zelfs verminderen.

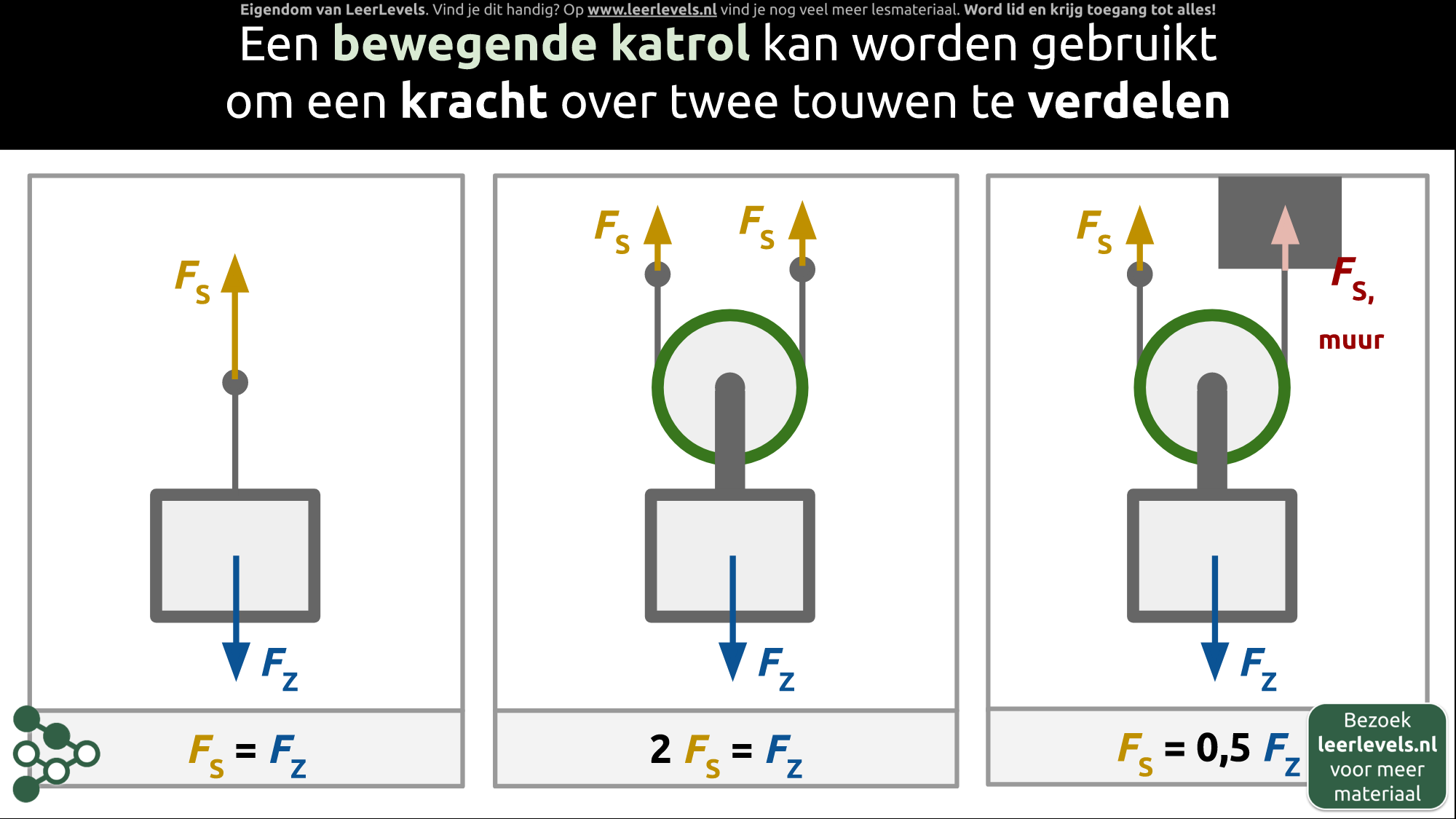
(Afbeelding: Animatie voor Krachtverdeling bewegende katrol)

Verplaatsing bewegende katrol

Bij een bewegende katrol beweegt het touw twee keer zo ver als de katrol zelf. Stel je voor dat je een blok omhoog trekt met een touw, dan zal het geheel omhoog bewegen. De plek waar het blok vast zat zal een bepaalde afstand afleggen, terwijl de plek waar jij het touw vast had zich twee keer zo ver omhoog beweegt. Dit komt doordat beide kanten van het touw korter moesten worden gemaakt om de katrol omhoog te krijgen. Geen extra informatie nodig.

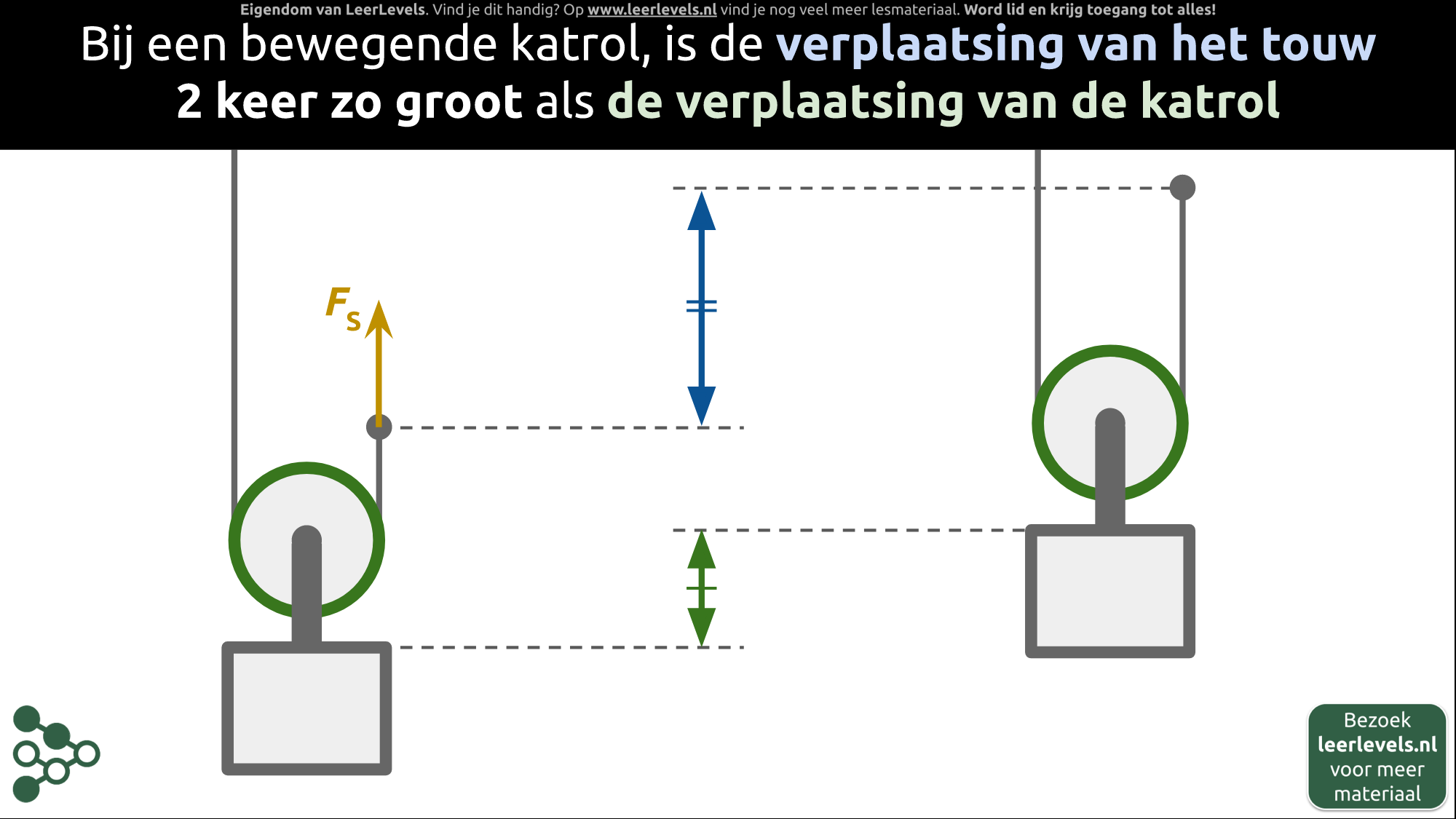
(Afbeelding: Animatie voor Verplaatsing bewegende katrol)

Terug naar overzicht Meld je aan

Kernfusie

Kernfusie in sterren

In sterren gebeurt er iets bijzonders genaamd kernfusie. Dit zorgt voor veel energie. Het gaat als volgt: als twee protonen dicht bij elkaar komen, kan er een neutron ontstaan. Er komt dan een positron en een neutrino vrij. Als er dan nog een proton bij komt, ontstaat er een element. Als dit proces twee keer gebeurt, ontstaat er helium. Bij deze reactie komen er twee protonen vrij die veel energie bevatten en met hoge snelheid wegvliegen. Dit totale proces staat bekend als 6p → He-4 + 2p + 2e + + 2ν. De vrijgekomen energie gaat vooral in de twee protonen zitten. Het gaat om 2,75 × 10⁻¹² joule, ofwel 17 miljoen elektronvolt. Dit lijkt weinig, maar het wordt veroorzaakt door maar liefst 6 protonen. Dit proces gebeurt constant in de zon, waardoor er enorm veel energie vrijkomt. Hierdoor krijgen wij op aarde warmte.

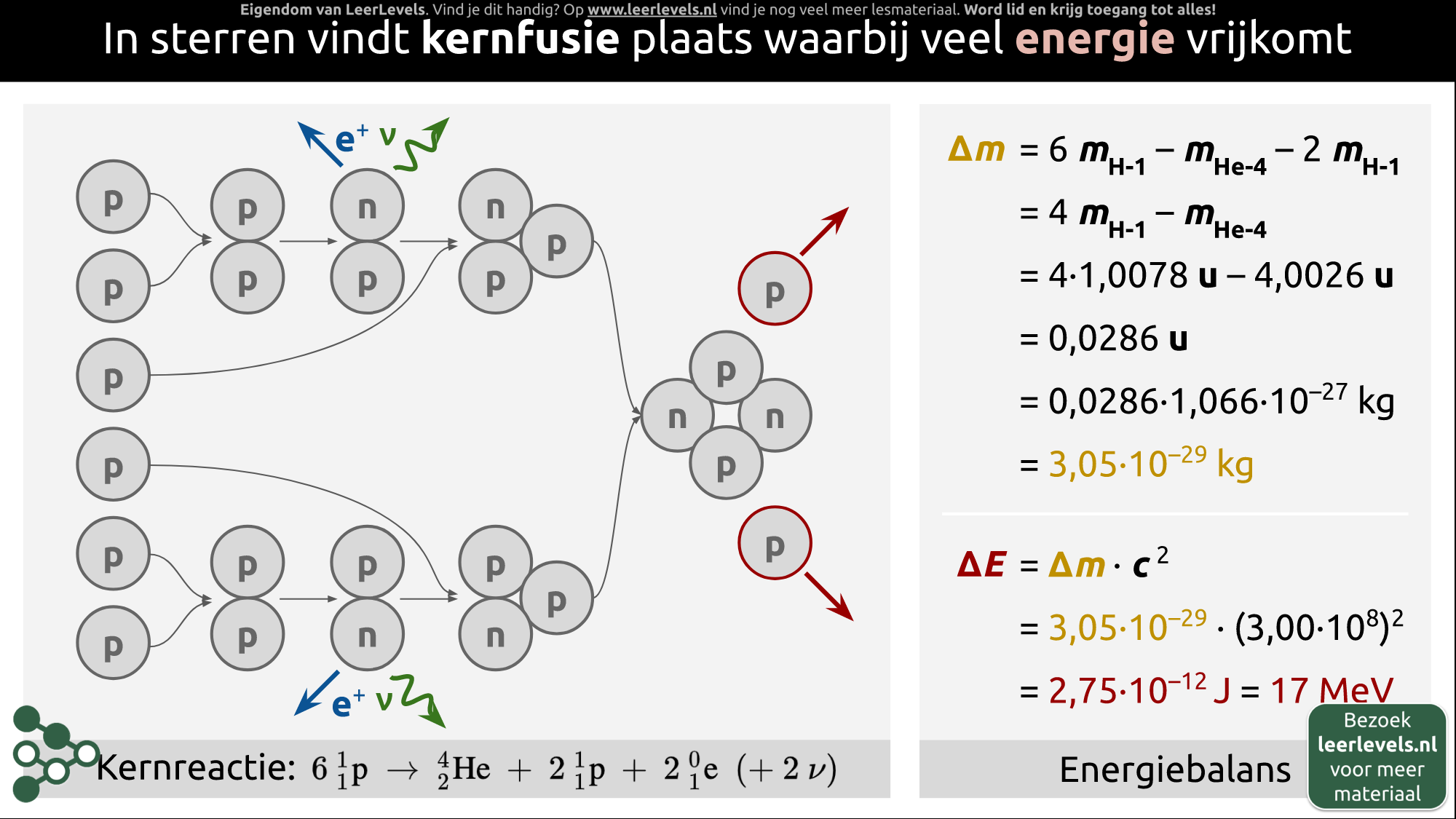
(Afbeelding: Animatie voor Kernfusie in sterren)

Terug naar overzicht Meld je aan

Kinetische energie

Kinetische energie concept

De kinetische energie van een voorwerp neemt toe naarmate de snelheid toeneemt. Wanneer een fiets stilstaat, beweegt deze niet en heeft dus een kinetische energie van nul. Als je rustig fietst, heb je een lage snelheid en bijgevolg een kleine hoeveelheid kinetische energie. Wanneer je echter sneller gaat fietsen, neemt de snelheid toe en daarmee ook de kinetische energie. Hoeveel dit is, hangt af van zowel de snelheid als de massa van het voorwerp. Bij een hoge snelheid kan de kinetische energie aanzienlijk groot zijn.

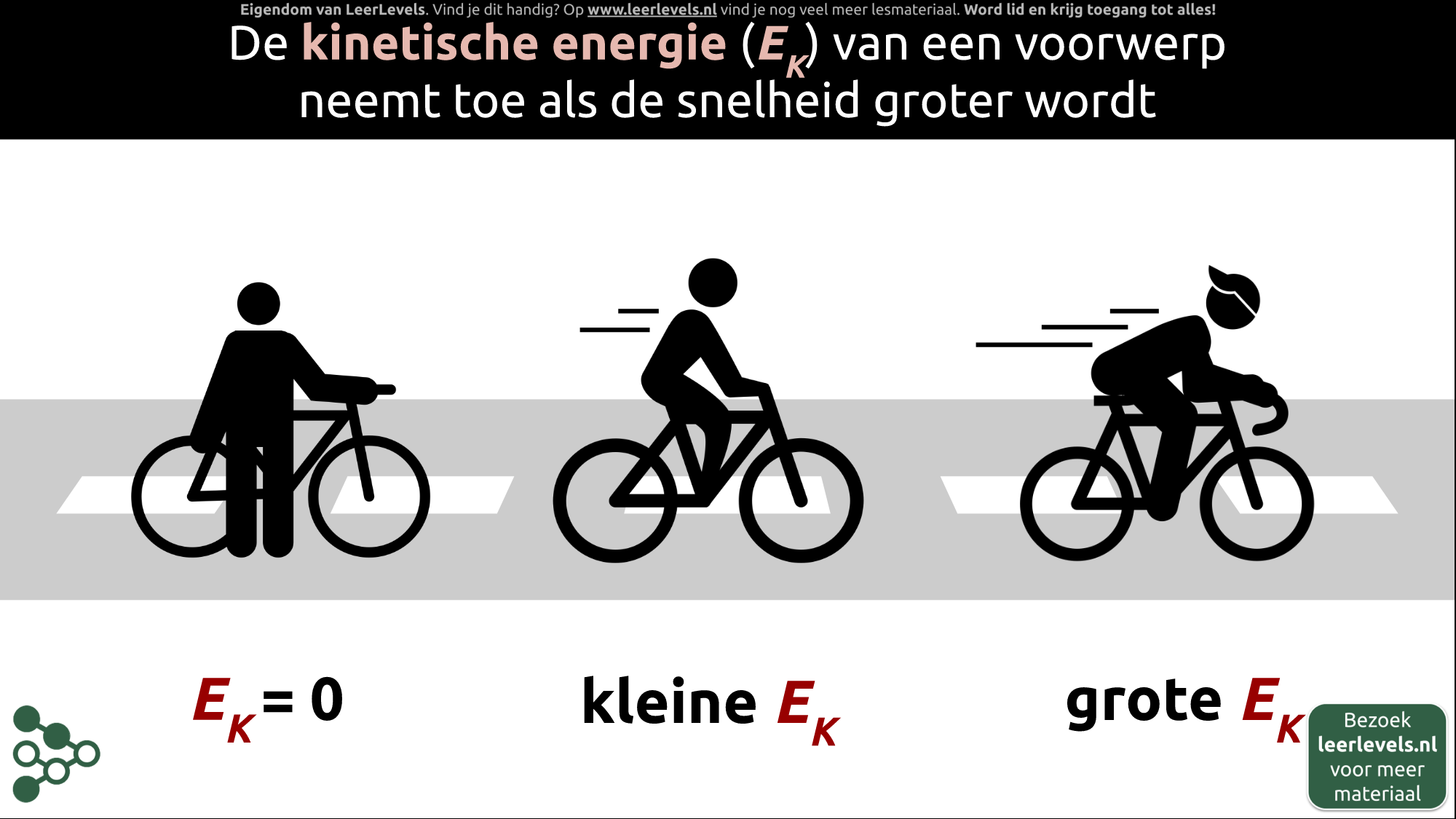
(Afbeelding: Animatie voor Kinetische energie concept)

Kinetische energie formule

De kinetische energie van een voorwerp is recht evenredig met de massa en kwadratisch evenredig met de snelheid. Dit wordt in formulevorm weergegeven als:

Ek = ½ · m · v²

Hierbij is Ek de kinetische energie in joule (J), m de massa in kilogram (kg) en v de snelheid in meter per seconde (m/s). Let op dat de snelheid moet worden omgerekend naar meter per seconde en vergeet niet het kwadraat van de snelheid te nemen.

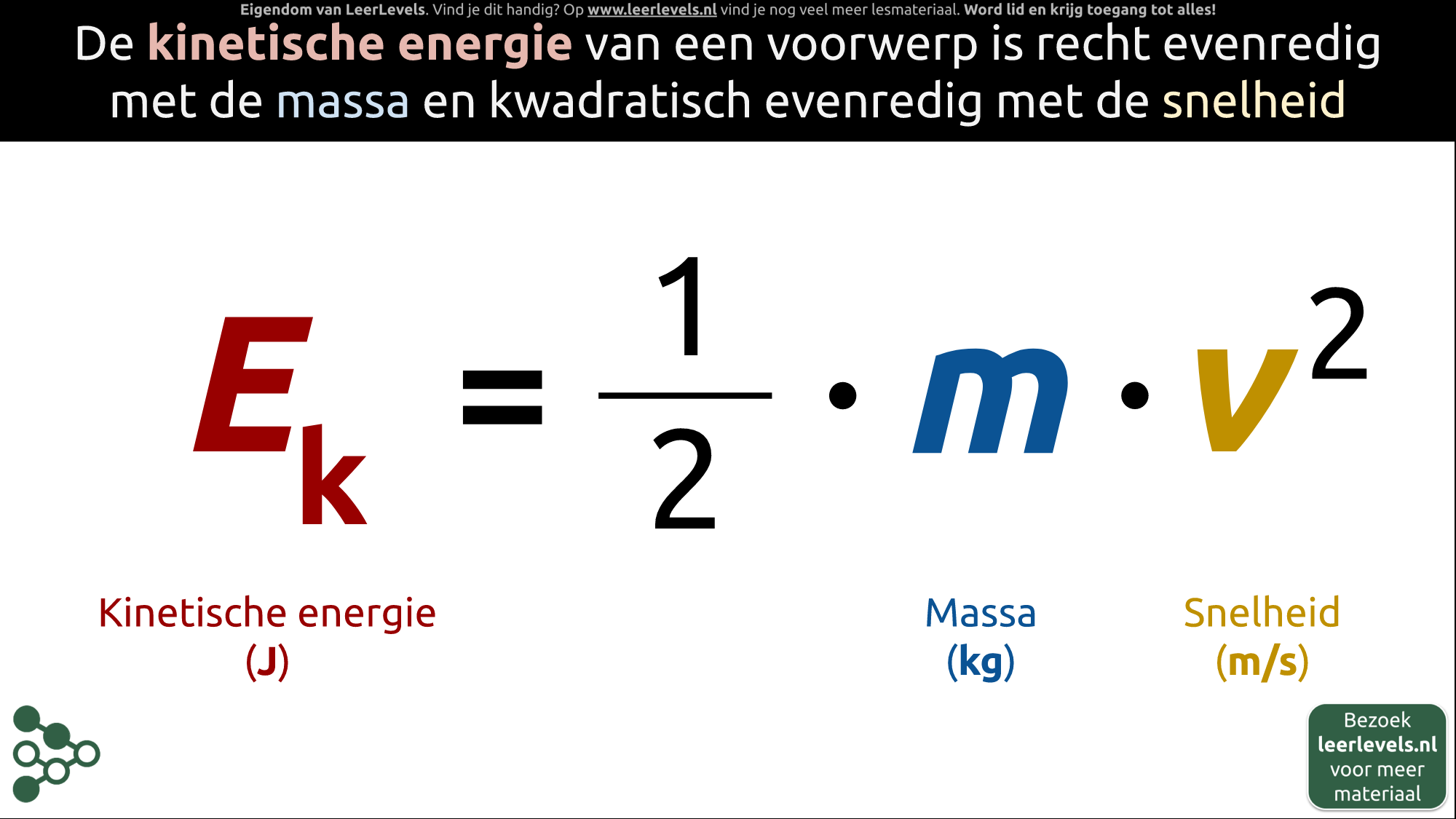
(Afbeelding: Animatie voor Kinetische energie formule)

Terug naar overzicht Meld je aan

Klankkleur

Sommige tonen bestaan uit één golfpatroon, terwijl andere tonen een bepaalde klankkleur hebben. Voorbeelden van één golfpatroon zijn onder andere stemvorken, dwarsfluiten en luidsprekers die zijn aangesloten op een toongenerator die slechts één toon produceert. Als tonen een bepaalde klankkleur hebben, dan bestaan ze uit verschillende frequenties met verschillende relatieve amplitudes. Dit lijkt voor ons gehoor nog steeds als één toon, maar als het geluid wordt gemeten, blijkt het een combinatie van verschillende frequenties te zijn. Hetzelfde geldt voor een triangel en voor zangstemmen die niet één zuivere noot zingen.

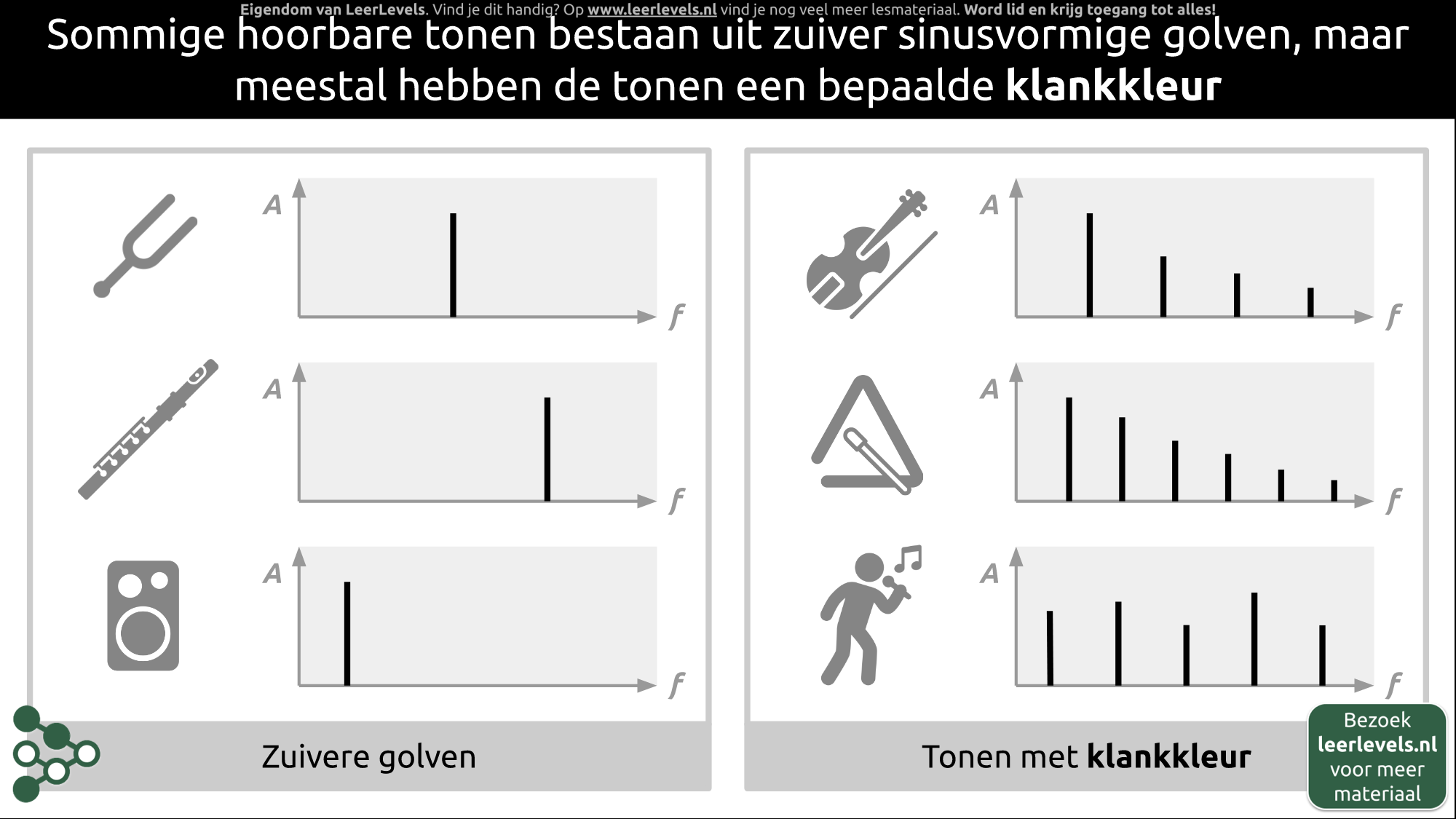
(Afbeelding: Animatie voor Klankkleur)

Terug naar overzicht Meld je aan

Kleur

Kleur voorwerp

De kleur van een voorwerp wordt bepaald door welke kleuren er worden geabsorbeerd en welke kleuren er worden gereflecteerd. Bijvoorbeeld een rode aardbei reflecteert alleen rood licht en absorbeert groen en blauw licht. Een groen blad reflecteert groen licht en absorbeert rood en blauw licht. Een blauwe vlinder reflecteert blauw licht en absorbeert rood en groen licht. De kleur die we zien is dus de kleur die wordt gereflecteerd. Dit komt doordat ons oog alleen de kleur ziet die wordt gereflecteerd.

(Afbeelding: Animatie voor Kleur voorwerp)

Terug naar overzicht Meld je aan

Kleuren mengen

Kleuren mengen licht

Onze ogen hebben kleine kegeltjes die kleuren kunnen zien. Als we verschillende kleuren licht bij elkaar laten komen, kunnen onze hersenen dit vertalen naar nieuwe kleuren. Bijvoorbeeld, als we rood en groen licht mengen, zien we geel. Dit komt doordat de kegeltjes in onze ogen zowel rode als groene lichtdeeltjes ontvangen. Zo kunnen we ook magenta zien wanneer rood en blauw licht bij elkaar komen, en cyaan wanneer groen en blauw licht bij elkaar komen. De drie primaire kleuren licht zijn rood, groen en blauw (RGB). Door combinaties van deze kleuren kan ons brein andere kleuren waarnemen. Wanneer al deze kleuren samenkomen, zien we wit licht.

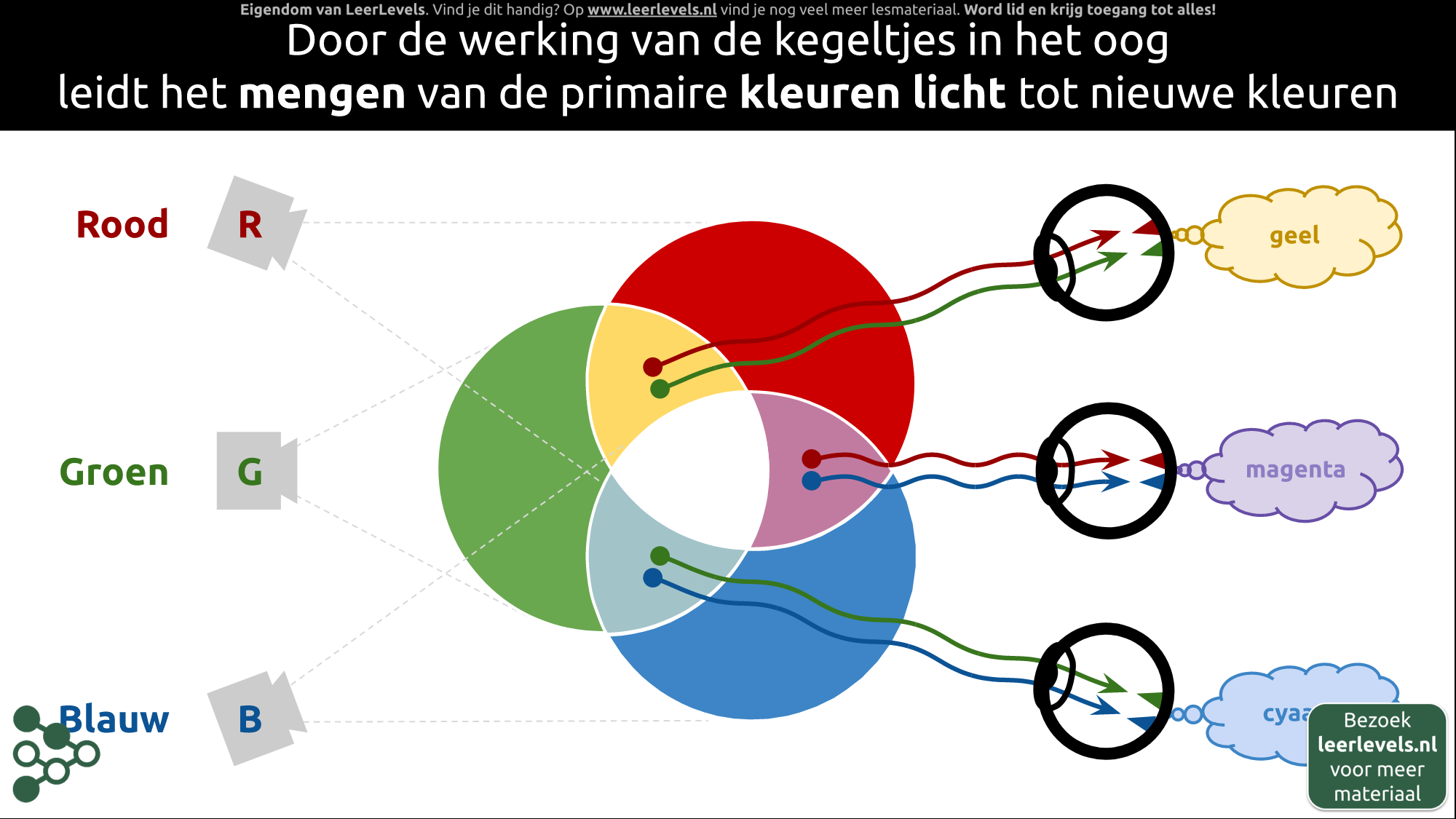
(Afbeelding: Animatie voor Kleuren mengen licht)

Kleuren mengen verf

Primaire kleuren zijn kleuren die je niet kunt maken door andere kleuren te mengen. Er zijn twee sets van primaire kleuren: kleuren van verf (CYM) en kleuren van licht (RGB). Verf absorbeert licht en een mengsel van verf absorbeert meerdere kleuren licht. Als je bijvoorbeeld gele verf op een wit papier aanbrengt, ziet het er geel uit omdat de verf de kleur blauw absorbeert. Als je geel en cyaan mengt, wordt groen gemaakt. En als je alledrie de kleuren mengt, krijg je zwart. CYM is de set primaire kleuren van verf en RGB is de set primaire kleuren van licht.

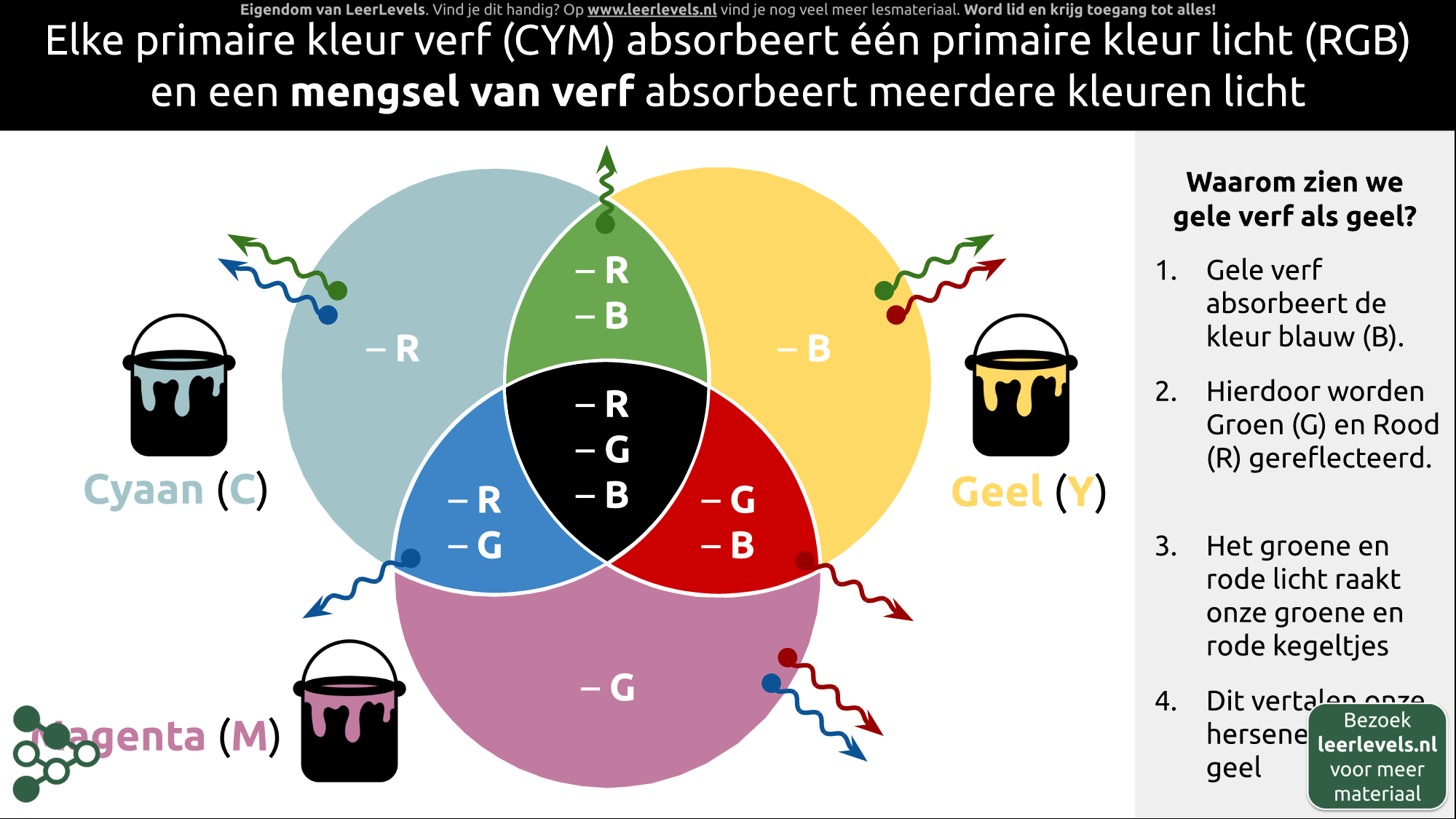
(Afbeelding: Animatie voor Kleuren mengen verf)

Terug naar overzicht Meld je aan

Kleurenspectrum

Het kleurenspectrum omvat alle kleuren van zichtbaar licht. Dit spectrum kunnen we zichtbaar maken met een lichtbron, zoals een kaarsje. Deze lichtbron straalt alle kleuren licht uit, maar we zien het als wit licht. Om het kleurenspectrum te tonen, kunnen we dat witte licht door een prisma laten gaan. Een prisma is een driehoekig stuk glas, dat elke kleur onder een specifieke hoek breekt. Bijvoorbeeld, rood licht wordt licht afgebogen, terwijl geel licht meer wordt afgebogen. Door het licht op een papiertje op te vangen, kunnen we alle kleuren van zichtbaar licht zien verschijnen, met rood aan de bovenkant en violet aan de onderkant. Er is ook straling die buiten dit bereik wordt gebroken: infrarood boven rood en ultraviolet onder violet, maar deze zijn niet zichtbaar voor onze ogen.

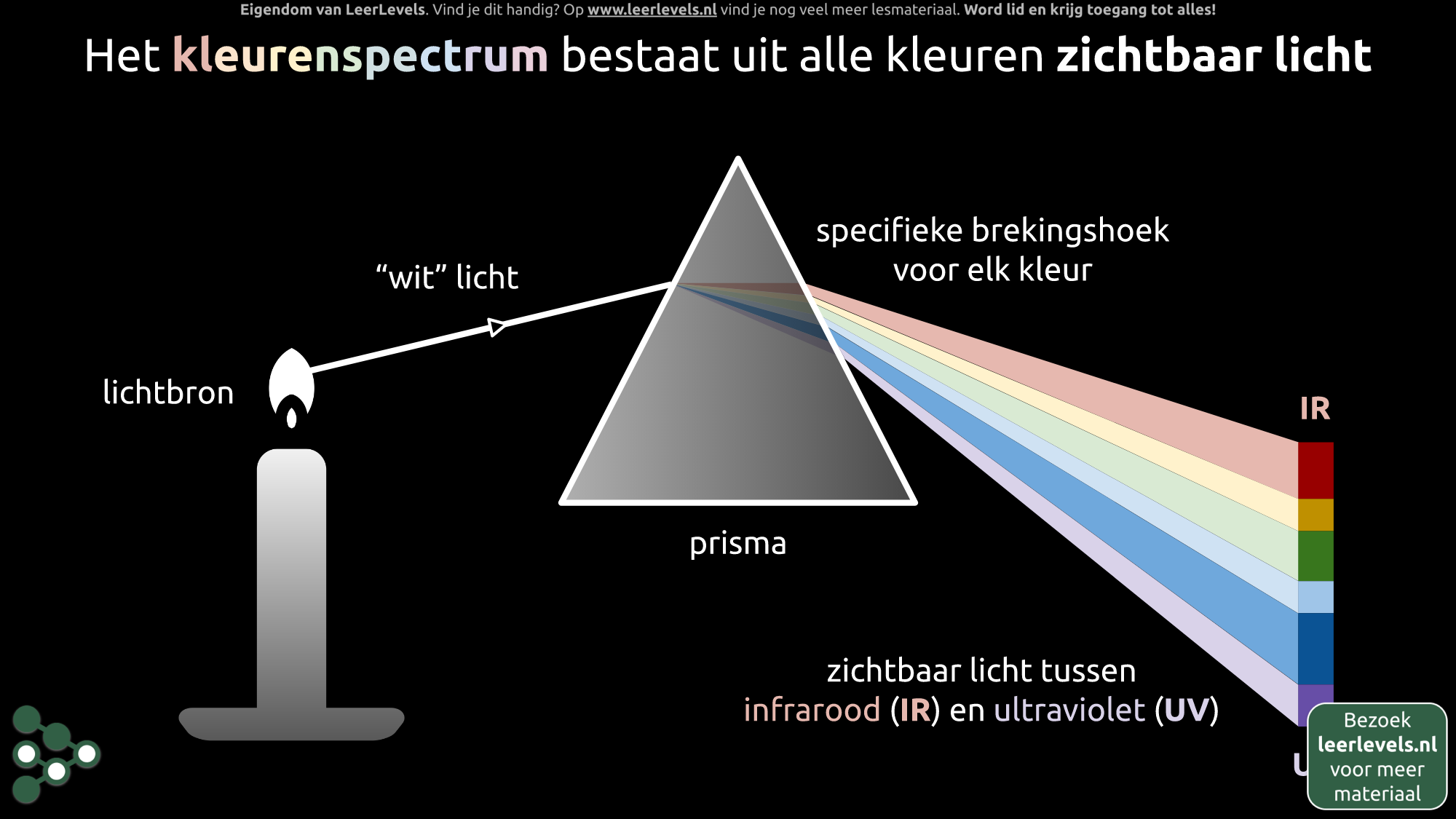
(Afbeelding: Animatie voor Kleurenspectrum)

Terug naar overzicht Meld je aan

Kleurfilter

Een kleurenfilter is een ding dat een specifieke kleur opslorpt en de kleur van het licht dat erdoor gaat verandert. Bijvoorbeeld, als we een magenta filter gebruiken en er rood, groen en blauw licht op schijnen, dan absorbeert het filter groen licht en laat het blauw en rood licht door. Als blauw en rood licht gecombineerd worden, ontstaat magenta. Als je dit in het licht houdt, zie je magenta en geen groen. Er worden geen formules, grootheden of eenheden gebruikt in deze uitleg.

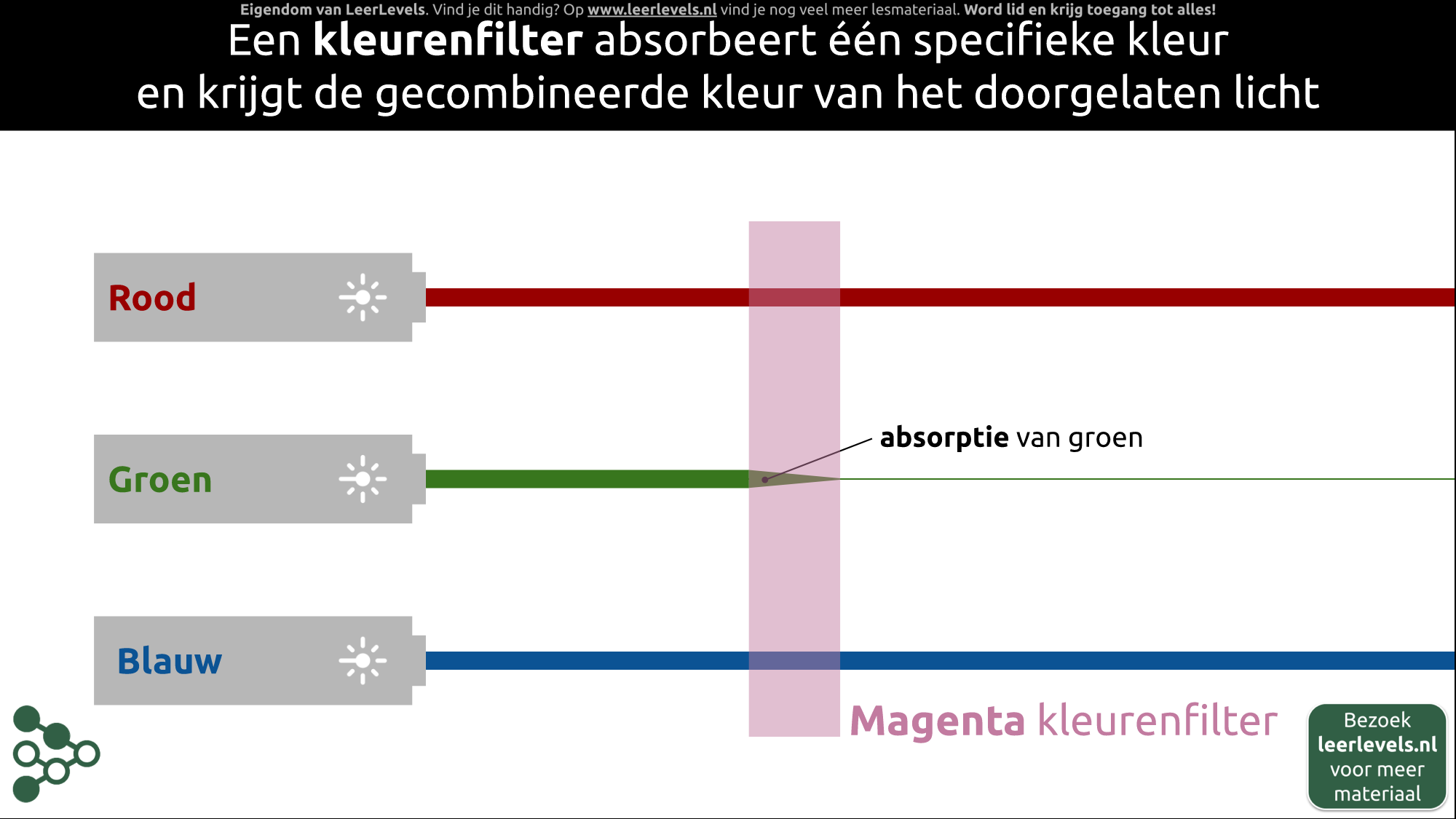
(Afbeelding: Animatie voor Kleurfilter)

Terug naar overzicht Meld je aan

Kortsluiting

Kortsluiting treedt op wanneer de polen van een spanningsbron direct met elkaar worden verbonden zonder enige weerstand. In een goed ontworpen schakeling met weerstand kan de stroom gecontroleerd door een apparaat stromen, waardoor deze wordt begrensd. Als we het circuit echter kortsluiten of bijvoorbeeld een lampje verwijderen, is er niets dat voorkomt dat de spanningsbron een enorme stroom produceert. Dit kan leiden tot een enorme stroomsterkte, wat zeer schadelijk kan zijn voor zowel de spanningsbron als de bekabeling. Bovendien is er een veiligheidsrisico, omdat overbelasting kan resulteren in schade of zelfs elektrocutie bij aanraking van het apparaat. Het is daarom belangrijk om kortsluitingen te vermijden.

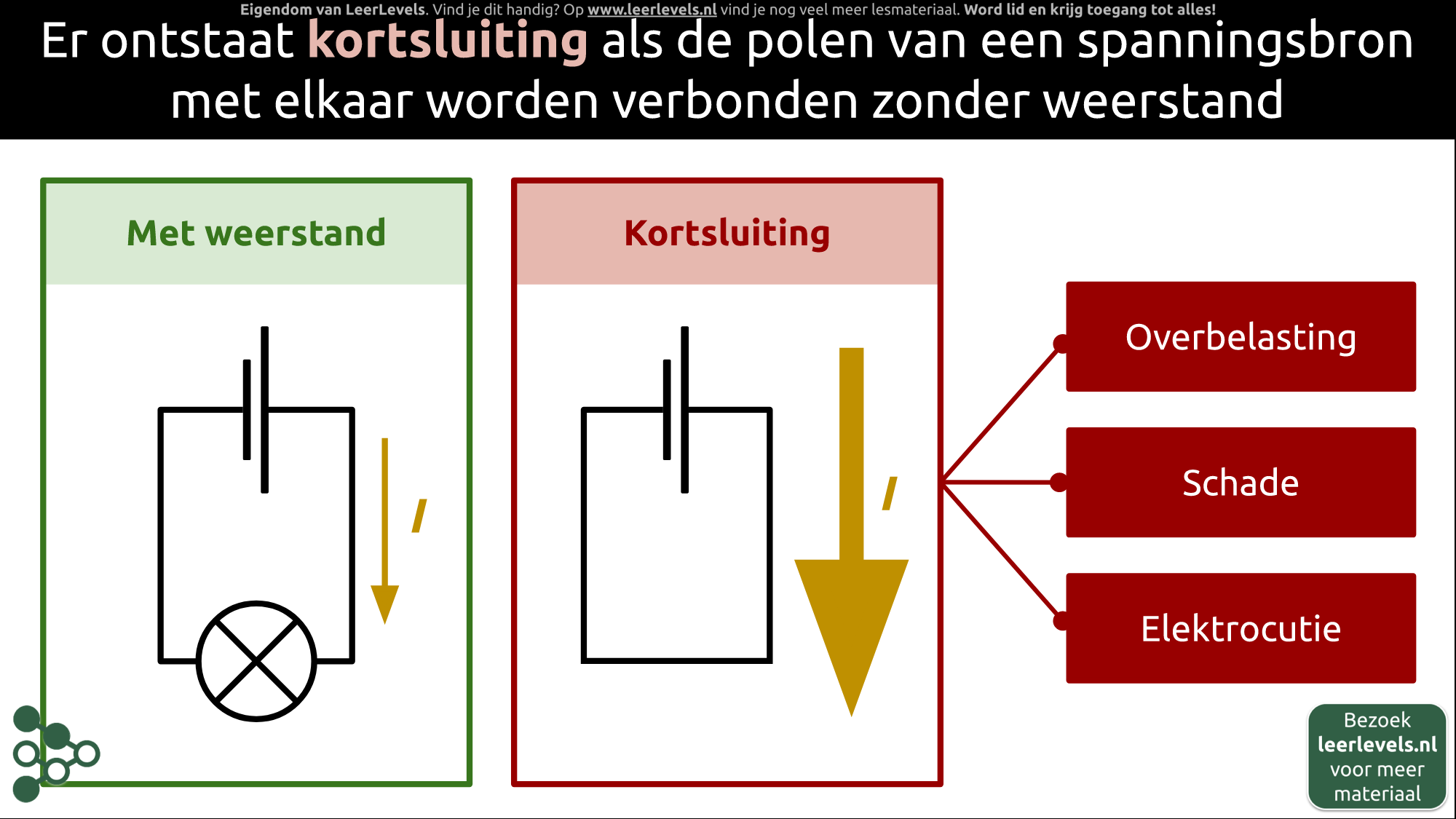
(Afbeelding: Animatie voor Kortsluiting)

Terug naar overzicht Meld je aan

Kracht

Tegenwerkende kracht

Als je een berg beklimt, zijn er krachten die je tegenhouden. In een auto werkt zwaartekracht op de auto en drukt deze naar beneden. Luchtweerstand zorgt ervoor dat je tegenwind krijgt. Er is wrijving en als je remt, wordt de weerstand groter. Bij het beklimmen van een berg zijn er ook tegenwerkende krachten, zoals rolweerstand, die het moeilijk maken om omhoog te gaan. Of je nu loopt of op de fiets zit, deze drie tegenwerkende krachten zijn er altijd. Tegenwerkende krachten vertragen een voorwerp.

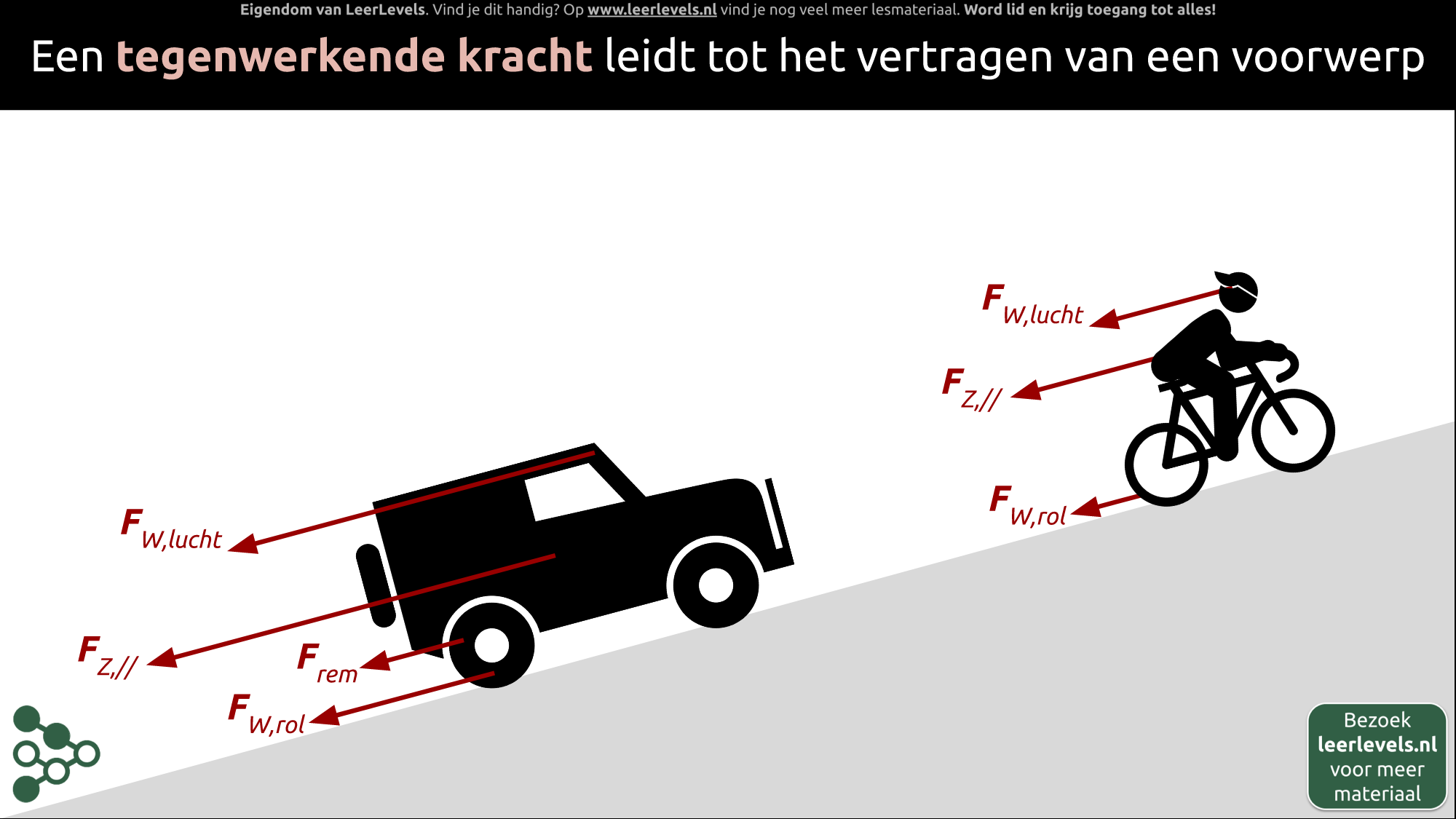
(Afbeelding: Animatie voor Tegenwerkende kracht)

Eenheid Newton

De newton (N) is een maat voor kracht. Het vertelt ons hoeveel kracht er nodig is om een object van 1 kilogram een versnelling van 1 meter per seconde per seconde te geven. Dit kan bijvoorbeeld de kracht zijn die nodig is om een bal te gooien of een deur te duwen.

Eén newton kracht is gelijk aan de kracht waarmee de aarde aan een appel van 100 gram trekt. Als je dus een appel van 100 gram optilt, voel je een kracht van 1 newton.

De zwaartekracht op een literfles water of frisdrank is ongeveer 10 newton. Dit betekent dat als je een fles water optilt, je een kracht van ongeveer 10 newton voelt. Dit geldt ook voor andere voorwerpen met een massa van ongeveer 1 kilogram.

De zwaartekracht op een kind van 50 kilogram is ongeveer 500 newton. Dit is de kracht waarmee de aarde het kind naar beneden trekt. Als het kind bijvoorbeeld op de grond staat, voelt het een kracht van ongeveer 500 newton.

(Afbeelding: Animatie voor Eenheid Newton)

Kracht

Wanneer een kracht op een voorwerp wordt uitgeoefend, kan dit leiden tot veranderingen in snelheid of vorm.

Een voorbeeld van het veranderen van de snelheid is wanneer je stilstaat en jezelf afzet tegen de grond. In dit geval versnel je en krijg je een snelheid. Een ander voorbeeld, waarbij de grootte van de snelheid constant blijft maar de richting verandert, is wanneer een auto een bocht neemt. Het veranderen van de richting van de snelheid vereist ook kracht, zelfs als de grootte van de snelheid hetzelfde blijft.

Een kracht kan ook een object vervormen, zoals bij het gebruik van een oefenapparaat met je handen. Deze vervorming is dus ook het gevolg van een uitgeoefende kracht.

Het is belangrijk op te merken dat we hier over kracht spreken, maar eigenlijk het effect van kracht bedoelen. Als de krachten op een voorwerp elkaar volledig opheffen, verandert er niets. Echter, als er een onbalans is in de krachten die op het voorwerp werken, kan dit leiden tot veranderingen in snelheid of vorm.

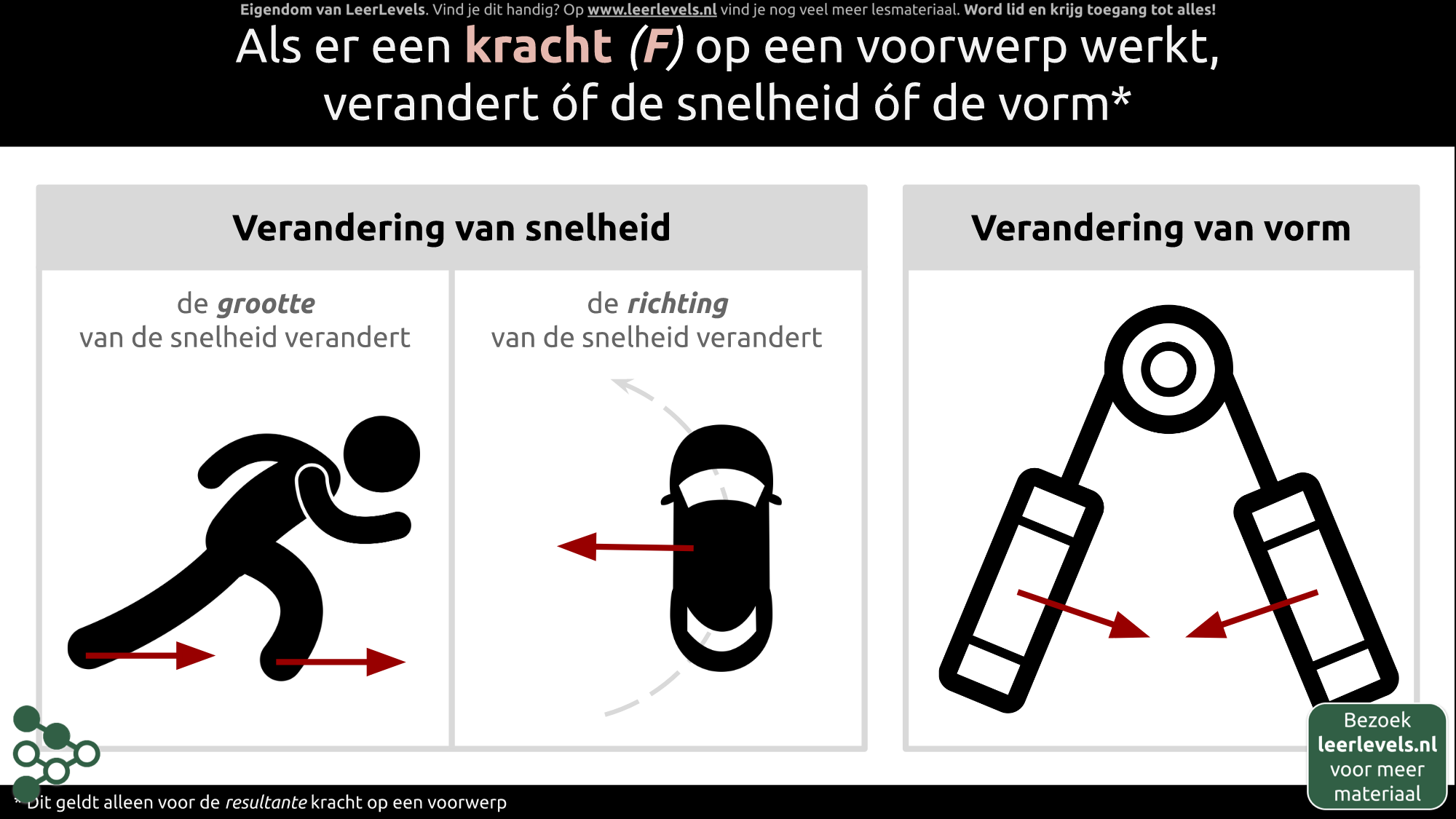
(Afbeelding: Animatie voor Kracht)

Werklijn

De werklijn is de rechte, denkbeeldige lijn die in het verlengde van een kracht ligt. Deze lijn is relevant wanneer je bijvoorbeeld een kracht uitoefent op een sleutel of een veer indrukt. Kortom, de werklijn is eenvoudigweg het verlengde van de kracht en loopt oneindig door in beide richtingen.

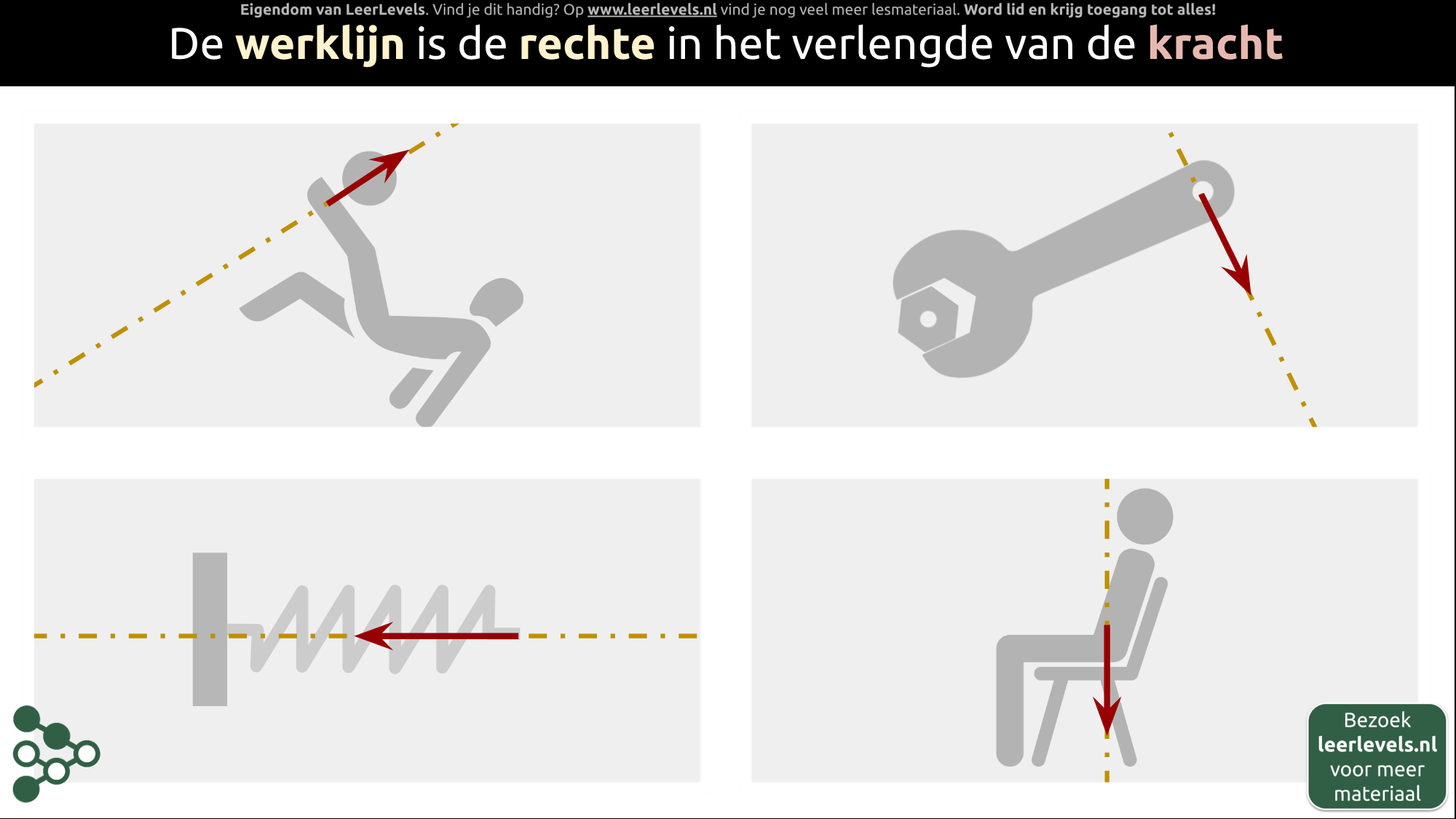
(Afbeelding: Animatie voor Werklijn)

Terug naar overzicht Meld je aan

Krachten

Krachten door contact

Er zijn negen bekende voorbeelden van krachten die direct werken op een voorwerp dat aangeraakt moet worden om de kracht te laten bestaan. De normaalkracht zorgt ervoor dat je niet door een bed heenzakt. De spankracht is de kracht waarmee bijvoorbeeld een touw een kracht doorgeeft aan een ophangpunt. Spierkracht is de kracht die een mens uitoefent met zijn spieren. Kleefkracht zorgt ervoor dat plakband aan een muur blijft zitten en veerkracht ontstaat wanneer een veer wordt ingedrukt of uitgerekt. Op een bootje voel je de opwaartse kracht die ervoor zorgt dat het bootje niet zinkt en als je een voorwerp over een oppervlak beweegt, ervaar je schuifwrijving waardoor het wordt tegengehouden. Rolwrijving treedt op als de banden van een fiets draaien en luchtwrijving treedt op bij beweging door de lucht. Alle negen vormen van kracht komen we dagelijks tegen. Formules, grootheden of eenheden worden niet genoemd.

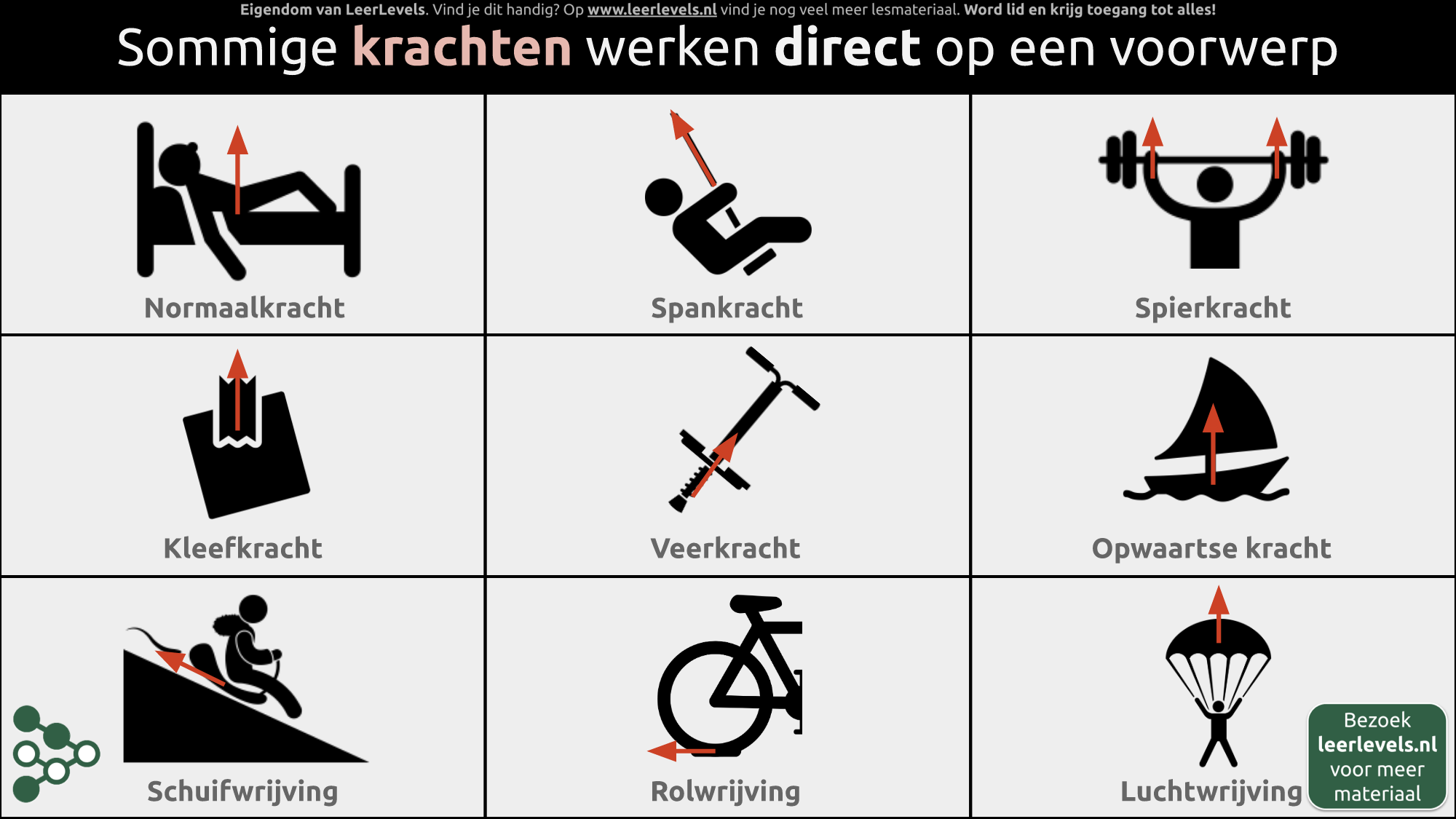
(Afbeelding: Animatie voor Krachten door contact)

Opheffen krachten

Als je niet versnelt in een bepaalde richting, dan heffen alle krachten in die richting elkaar op. Dit betekent bijvoorbeeld dat als je in een hangmat ligt, de zwaartekracht die je naar beneden trekt en de kracht van de hangmat die je omhoog duwt elkaar opheffen. Hetzelfde geldt voor een boot die op het water drijft of zelfs voor een massa die stil hangt aan een veer. Deze wet geldt ook voor horizontale krachten, zoals wrijvingskracht en spierkracht bij het fietsen. Als deze krachten even groot zijn, blijf je op constante snelheid rijden. Kortom: als je niet versnelt, heffen alle krachten in die richting elkaar op.

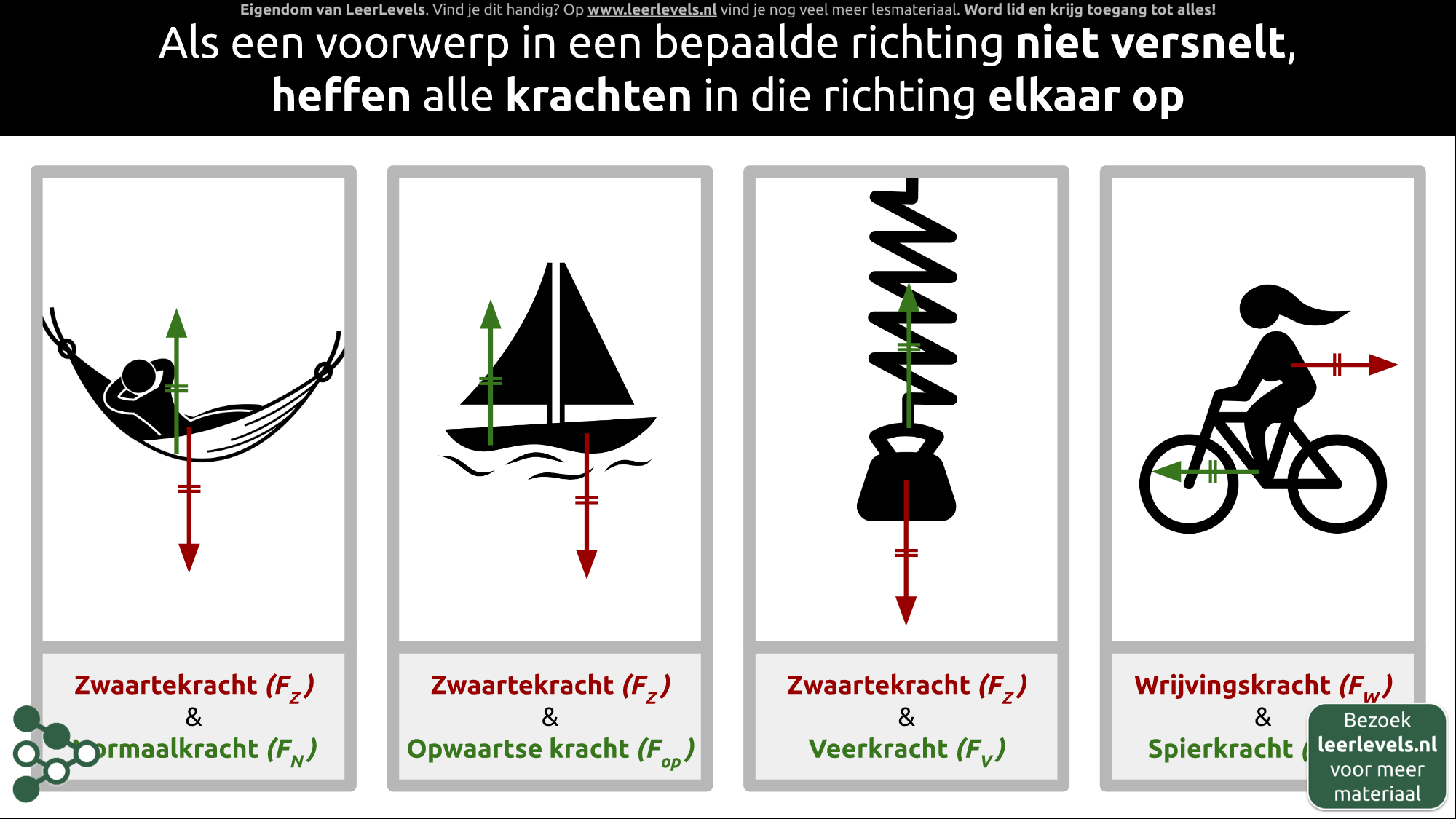
(Afbeelding: Animatie voor Opheffen krachten)

Terug naar overzicht Meld je aan

Krachten ontbinden

Krachten ontbinden scenario's

Als de resultante kracht in een opdracht nul is, kun je vaak een kracht ontbinden in handig gekozen componenten. Bijvoorbeeld bij een blok op een helling moet je de zwaartekracht ontbinden in componenten langs en loodrecht op de helling. De parallelle component is vaak gelijk aan de zwaartekracht en de loodrechte component is vaak gelijk aan de normaalkracht. Bij een slee moet je de spankracht ontbinden in horizontale en verticale componenten. De horizontale component is vaak gelijk aan de wrijvingskracht en de verticale component is nodig om de normaalkracht te berekenen. Bij een slinger moet de verticale component van de spankracht gelijk zijn aan de zwaartekracht en bij een waslijn moet je de som van twee spankrachten ontbinden. Als de resultante kracht nul is, moet je de kracht slim ontbinden.

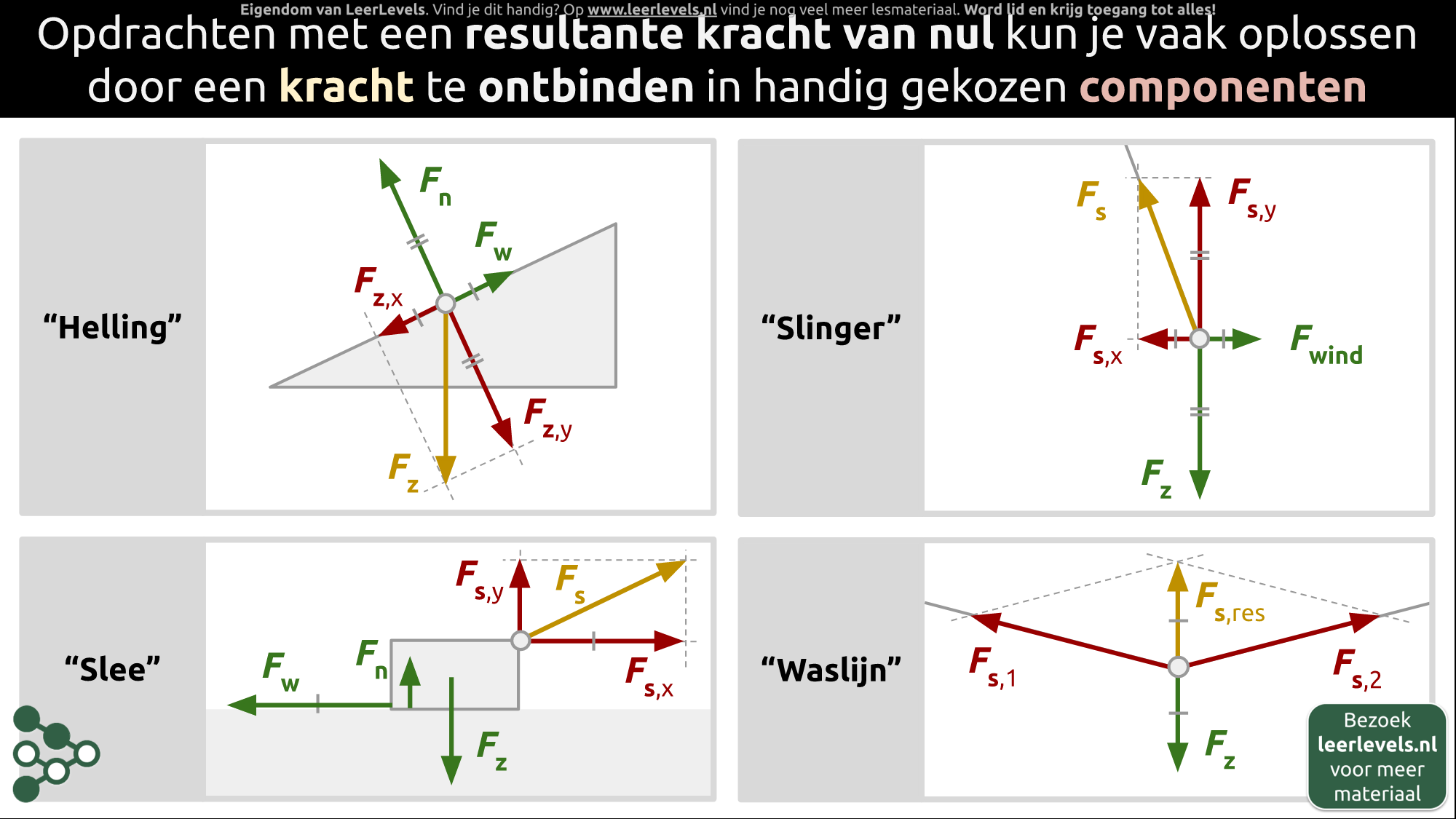
(Afbeelding: Animatie voor Krachten ontbinden scenario's)

Krachten ontbinden in een rechthoekig assenstelsel

Bij krachten die op een object werken, kunnen we de kracht ontbinden in componenten langs de x- en y-as van een rechthoekig assenstelsel om de kracht in elke richting te bepalen. Dit is handig als bijvoorbeeld een boot wordt voortgetrokken door twee sleepboten onder onbekende hoeken. Om dit te doen gebruiken we de krachten F1 en F2 en bepalen we hun x- en y-componenten. Om de x-component van F1 te vinden trekken we een lijn van het beginpunt van F1 parallel aan de y-as en bepalen we waar deze de x-as snijdt. Voor de y-component doen we hetzelfde maar dan parallel aan de x-as. Dit doen we ook voor F2. Om de totale kracht naar voren op de boot te vinden, nemen we de som van F1x en F2x. Het gebruik van een rechthoekig assenstelsel is handig omdat we de componenten afzonderlijk van elkaar kunnen bekijken.

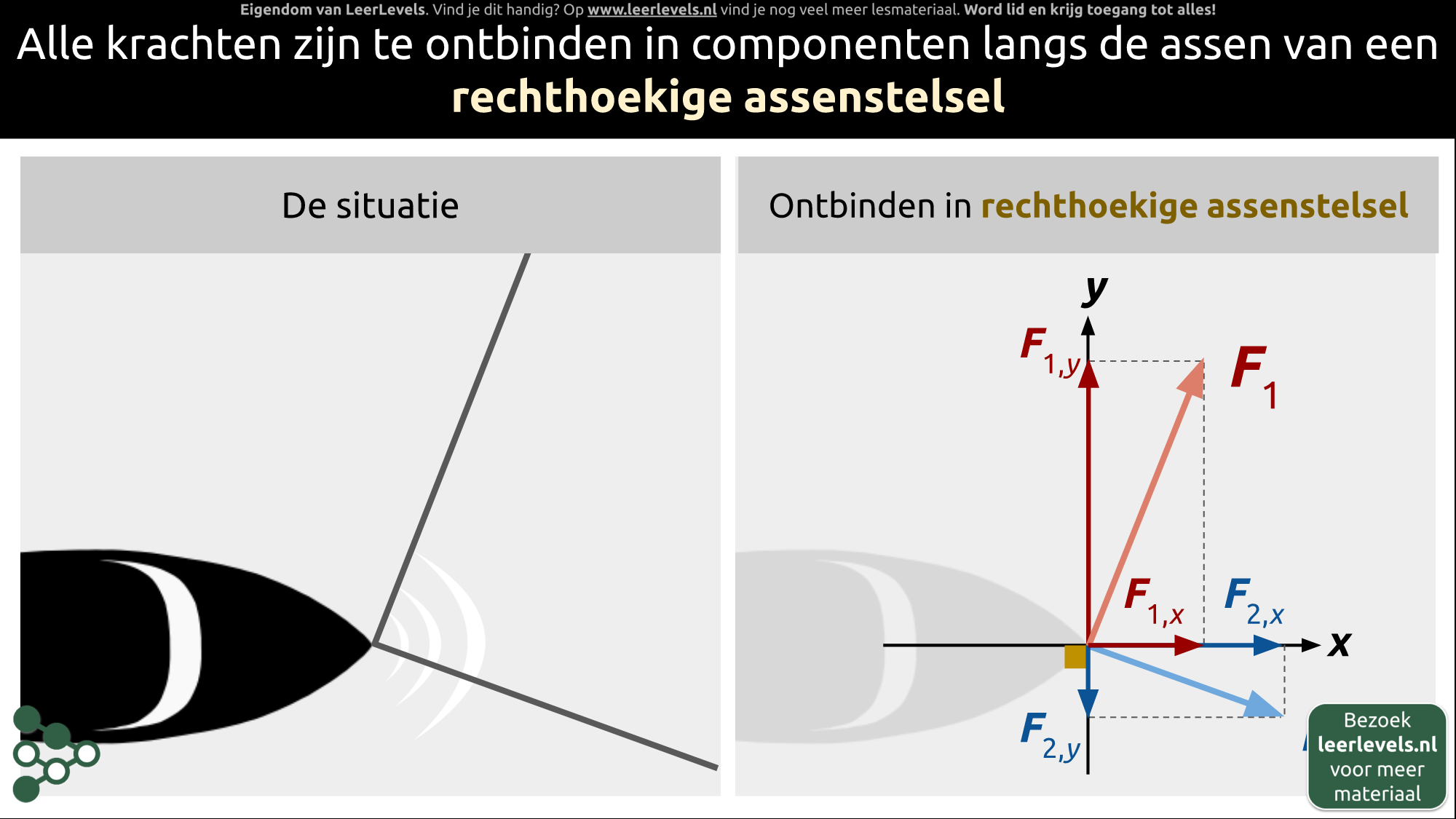
(Afbeelding: Animatie voor Krachten ontbinden in een rechthoekig assenstelsel)

Terug naar overzicht Meld je aan

Krachtenevenwicht

Krachtenevenwicht in sterren

In sterren is er balans tussen twee krachten: de stralingskracht die vanuit de kern naar buiten duwt, en de zwaartekracht die de ster naar binnen probeert te trekken. De ster heeft een mantel met verschillende lagen, en elke laag wordt beïnvloed door deze krachten. De stralingskracht wordt veroorzaakt door fotonen die vanuit de kern uitgestraald worden en tegen de laag botsen, waardoor de laag naar buiten geduwd wordt. Hoewel fotonen geen massa hebben, oefenen ze wel een kleine kracht uit vanwege hun impuls. Doordat er zoveel fotonen zijn, ontstaat er een grote kracht vanuit de kern naar buiten. De zwaartekracht is afhankelijk van de afstand tussen de laag en de kern, en van de dichtheid van de kern. Het vermogen dat uitgestraald wordt, heeft ook invloed op de stralingskracht. Sterren doorlopen een complexe levenscyclus doordat het evenwicht tussen deze krachten continu verandert.

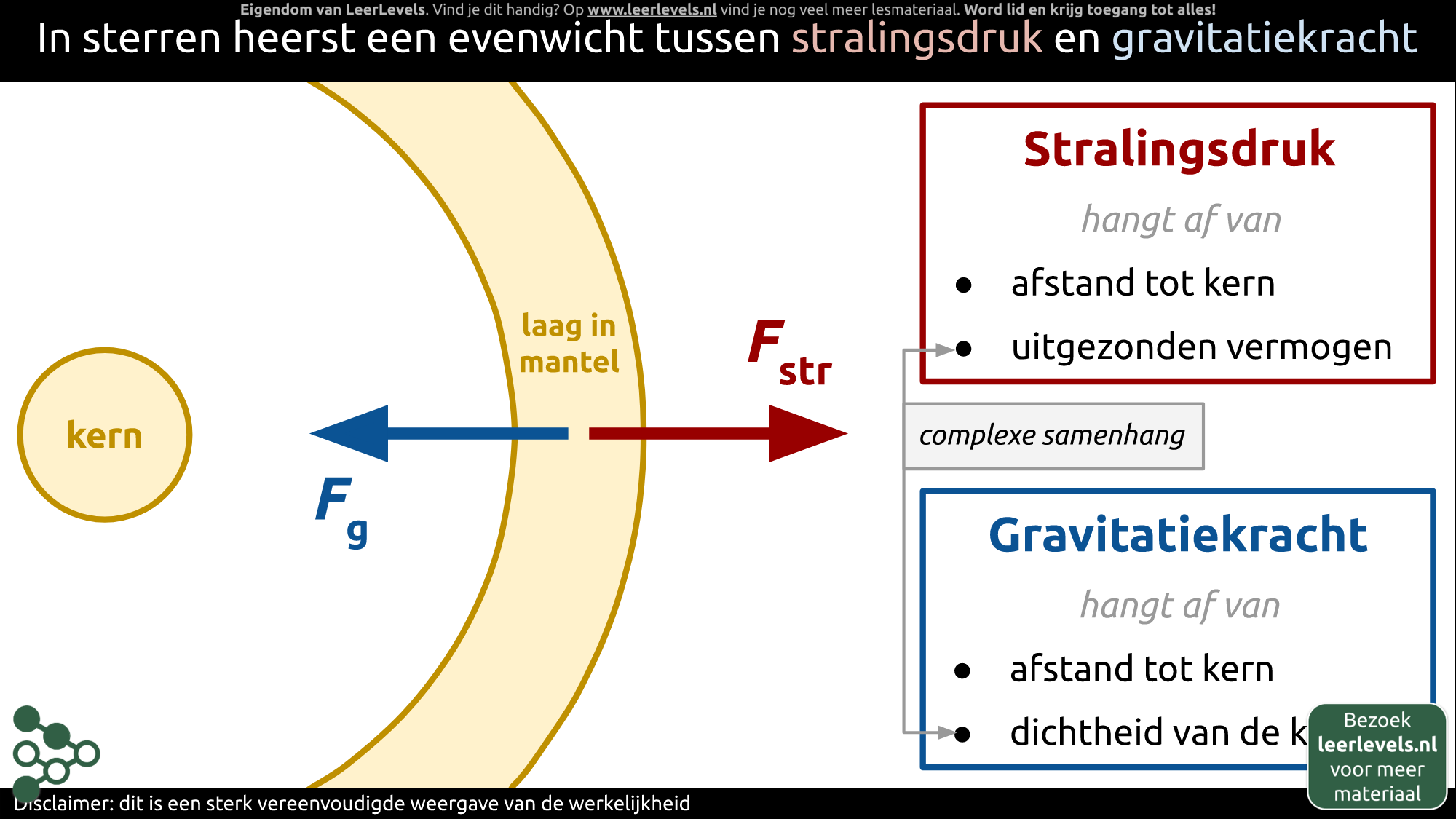
(Afbeelding: Animatie voor Krachtenevenwicht in sterren)

Krachtenevenwicht veer

Een veer in rust heeft evenveel kracht omhoog als omlaag. Als je de veer naar beneden trekt en hij uitrekt, gaat de veerkracht omhoog en wil de veer terug naar rust. Om de veer op zijn plaats te houden, moet de kracht die je gebruikt even groot zijn als de kracht van de veer in rust. Als je de veer verder naar beneden trekt, wordt de veerkracht groter en moet je nog harder trekken om hem op zijn plaats te houden. Als je dan loslaat, gaat de massa trillen tot hij weer in rust is onder invloed van zwaartekracht. Kortom: als een veer niet beweegt, zijn de krachten omhoog en omlaag gelijk.

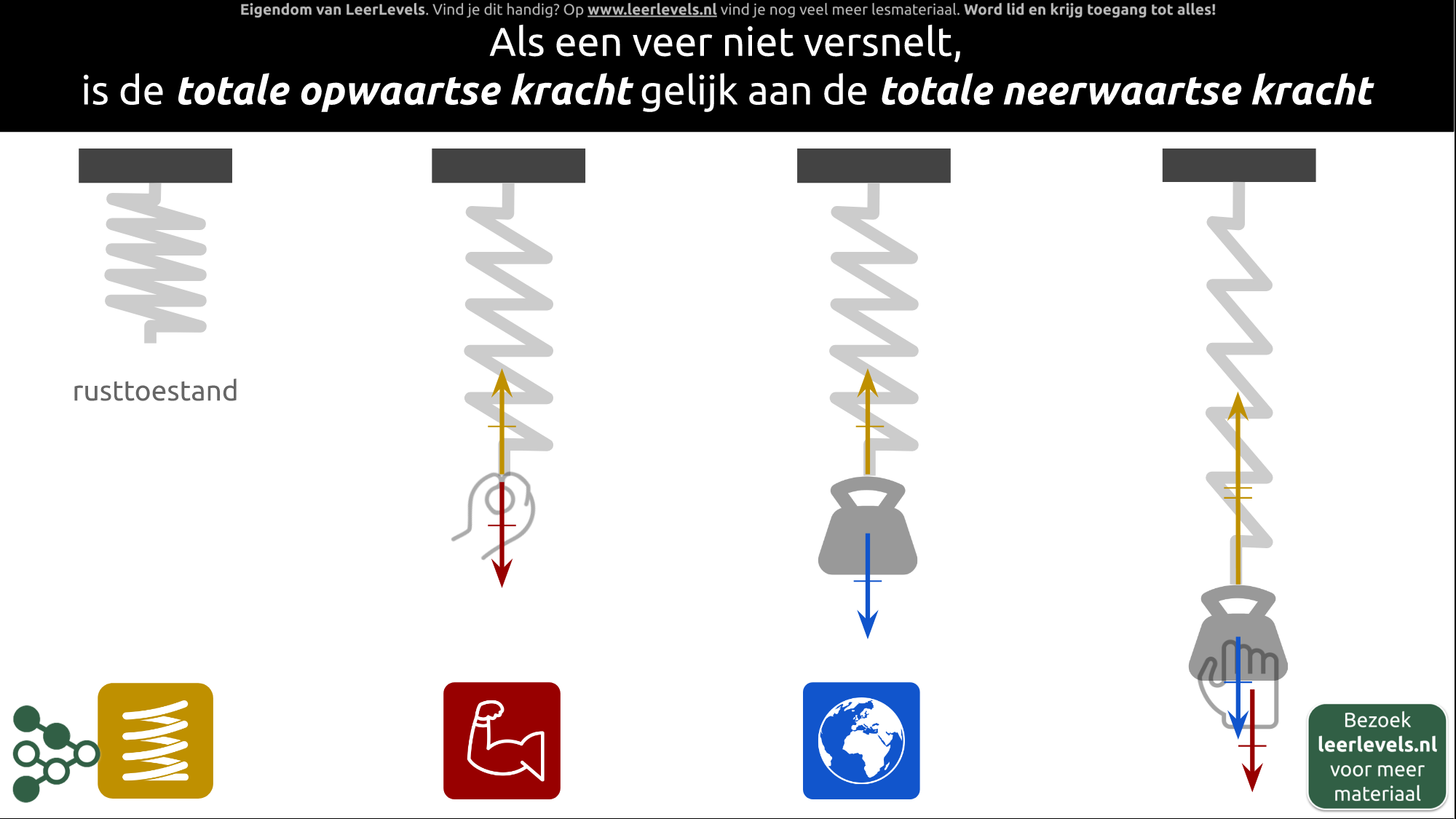
(Afbeelding: Animatie voor Krachtenevenwicht veer)

Krachtenevenwicht

Bij krachtenevenwicht kun je kijken naar horizontale en verticale krachtenevenwicht apart. Bijvoorbeeld bij een slinger die aan twee touwen hangt, waarbij er een kracht naar linksboven, naar rechtsboven en zwaartekracht naar beneden werken. Deze krachten worden ontbonden langs een rechthoekig assenstelsel in bijvoorbeeld F1x en F1y. Door te weten dat er geen versnelling is, kunnen we de horizontale en verticale richting apart behandelen. In horizontale richting geldt: F2x - F1x = 0. Dit betekent dat de twee vectoren even lang zijn, maar in tegengestelde richting wijzen. In de verticale richting wijzen er twee krachten naar boven en één naar beneden. Door dit te berekenen, kun je bepalen wat andere gegevens zijn.

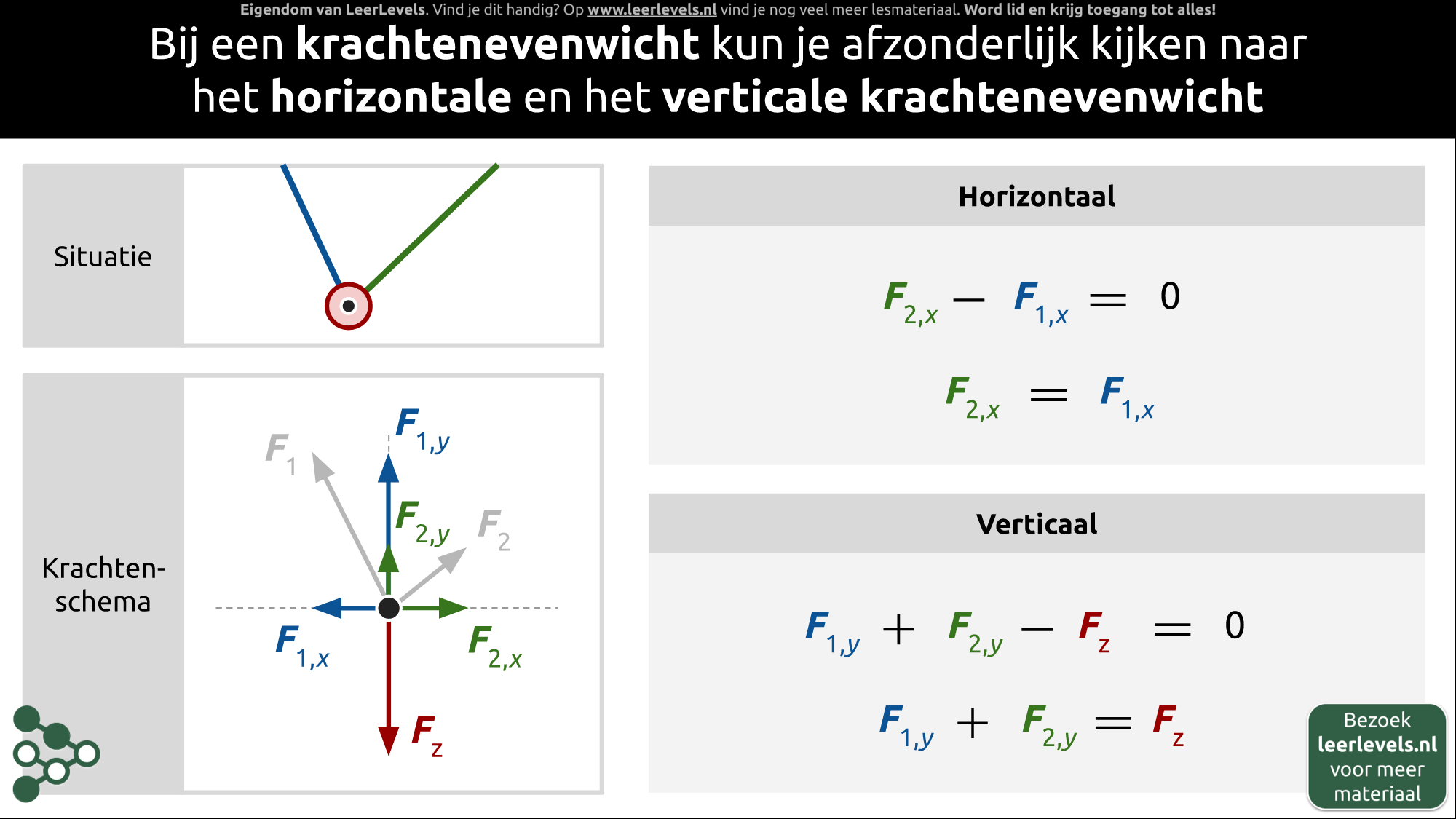
(Afbeelding: Animatie voor Krachtenevenwicht)

Terug naar overzicht Meld je aan

Krachtenschaal

Krachtenschaal concept

Een krachtenschaal bij een krachtendiagram vertaalt de lengte van een vector naar de grootte van de kracht. Dit werkt net als bij een kaart waarbij je een schaal hebt om afstanden te meten. Als een cm op de kaart gelijk is aan bijvoorbeeld 100 km, dan kun je berekenen dat de gemeten afstand op de kaart gelijk is aan 100 keer die afstand in het echt. Bij een krachtendiagram werkt het hetzelfde, maar dan heet het een krachtenschaal. Als je bijvoorbeeld een appel hebt waar een kracht op werkt en de lengte van de vector is 2 cm en elke cm is gelijk aan 1 N, dan is de kracht 2 N. Als je een zwaar voorwerp hebt, bijvoorbeeld 40 N, dan kun je niet dezelfde schaal gebruiken. Je moet dan een andere schaal gebruiken waarbij elke cm bijvoorbeeld gelijk is aan 20 N. Met behulp van een krachtenschaal kun je de verhouding kiezen tussen de getekende vector en de grootte van de bijbehorende kracht die geschikt is voor die situatie.

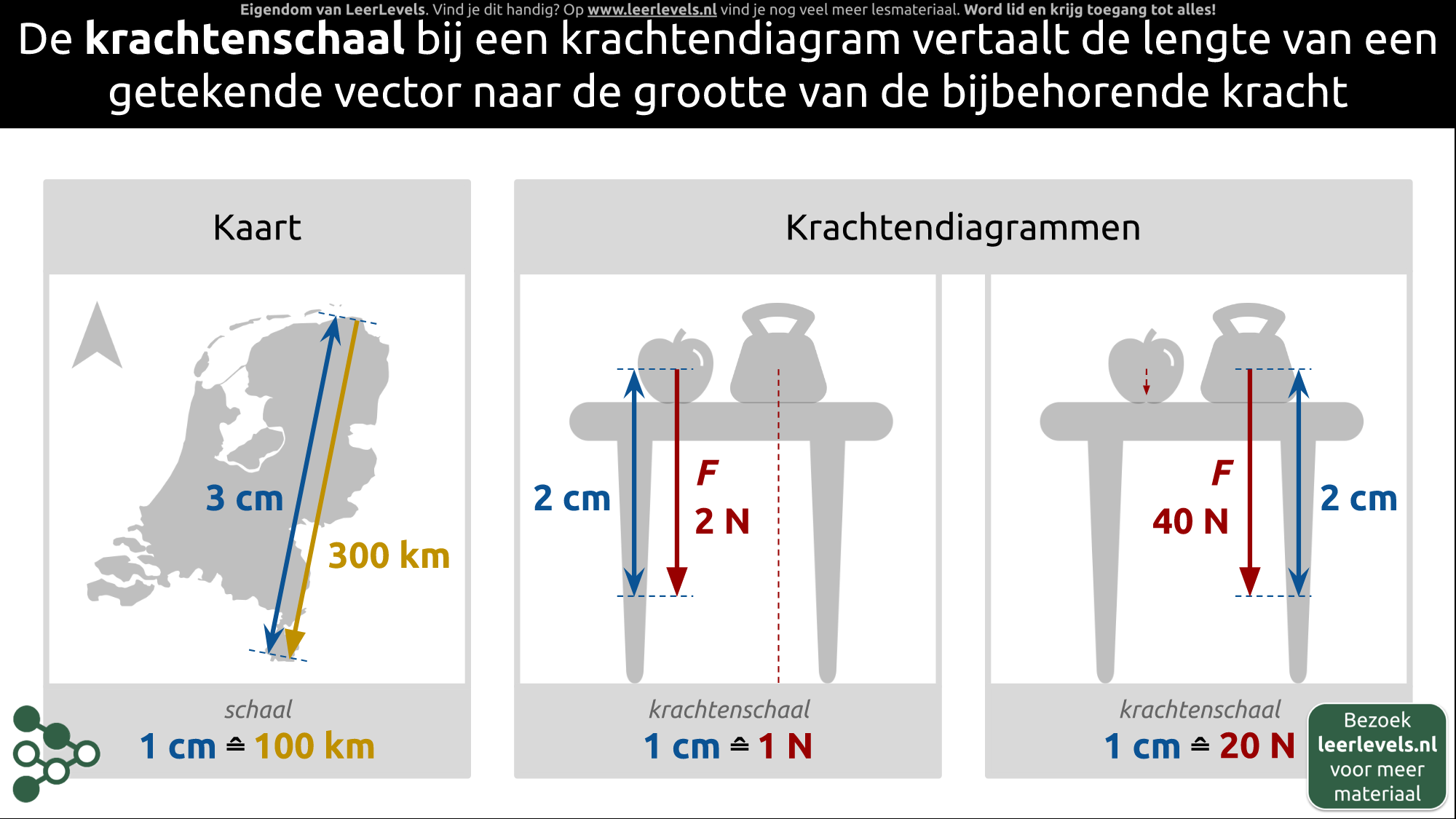
(Afbeelding: Animatie voor Krachtenschaal concept)

Krachtenschaal toepassen

Krachtschalen worden gebruikt om de grootte van de kracht te bepalen. Je hebt hiervoor een liniaal of verhoudingstabel nodig. Stap 1 is om de lengte van de vector te meten met behulp van een getekende kracht, bijvoorbeeld 2 centimeter. De krachtschaal is 100 Newton per centimeter. Als je dit invult in de verhoudingstabel, kun je berekenen dat de bijbehorende kracht 200 N is. Omgekeerd kun je ook de krachtschaal bepalen. Stel dat een vectorpijl van 3 cm overeenkomt met 4500 N. Dan kun je dit invullen en door aan de verhoudingstabel ook 1 cm toe te voegen, kun je berekenen wat de bijbehorende kracht is, in dit geval 1500 N. Notatie: lengte vector = 2 cm, krachtschaal = 100 (N)/(cm), kracht = 200 N; lengte vector = 3 cm, kracht = 4500 N, bijbehorende krachtschaal = 1500 (N)/(cm).

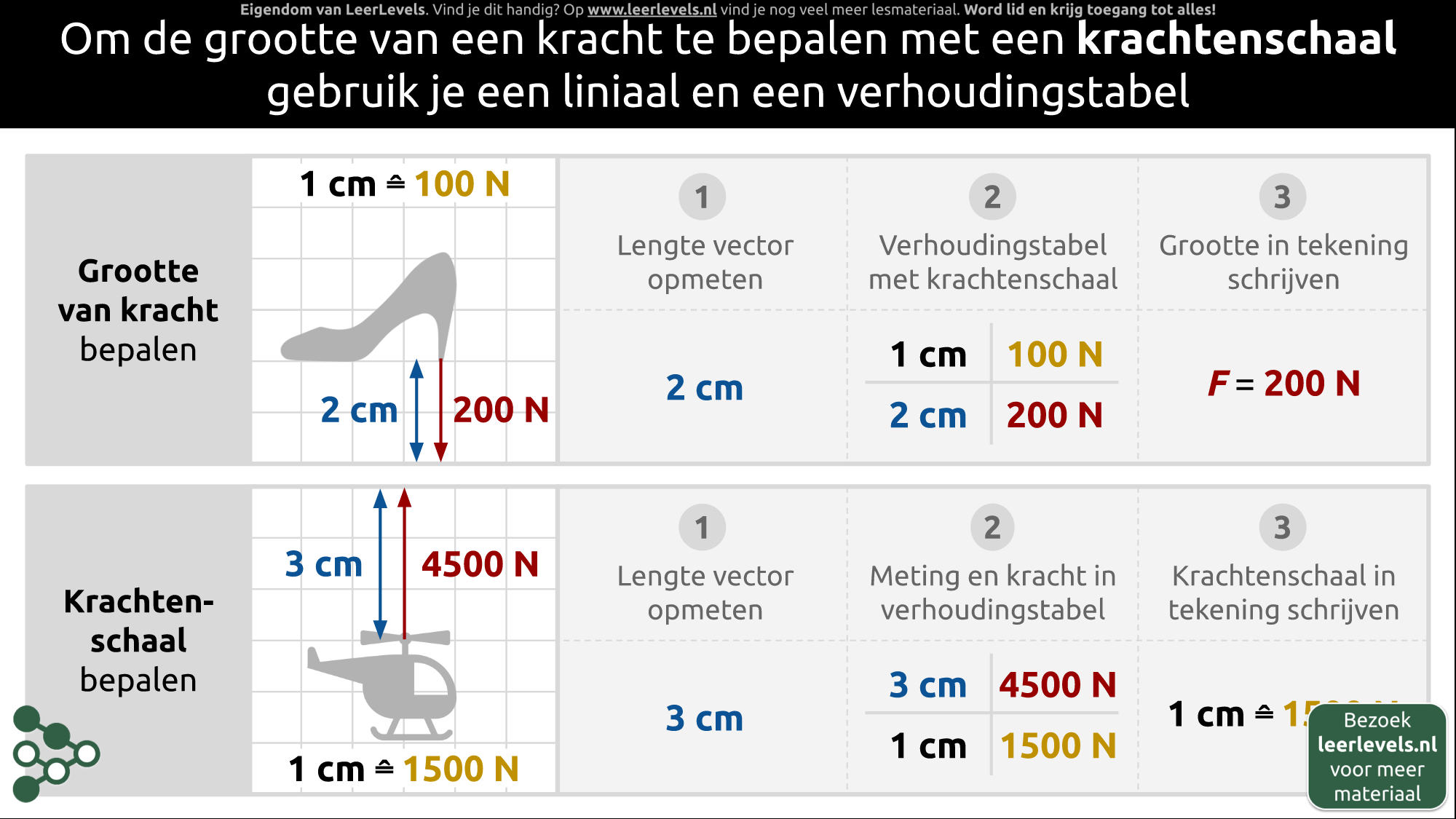
(Afbeelding: Animatie voor Krachtenschaal toepassen)

Terug naar overzicht Meld je aan

Krachtenschema

Een krachtenschema laat alleen de krachten zien die op een voorwerp werken. Als bijvoorbeeld een bal aan een touw onder een ophangpunt hangt, tekenen we een pijl naar boven die de kracht van het touw weergeeft en een pijl naar beneden die de kracht van de zwaartekracht weergeeft. Als er meer dan één touw is, tekenen we alleen het punt waarop de krachten werken met de pijlen die de richting van de krachten aangeven. Dit schema is handig omdat we later makkelijker kunnen berekenen wat de verschillende krachten zijn. Het geeft een eenvoudige weergave van de werkelijkheid.

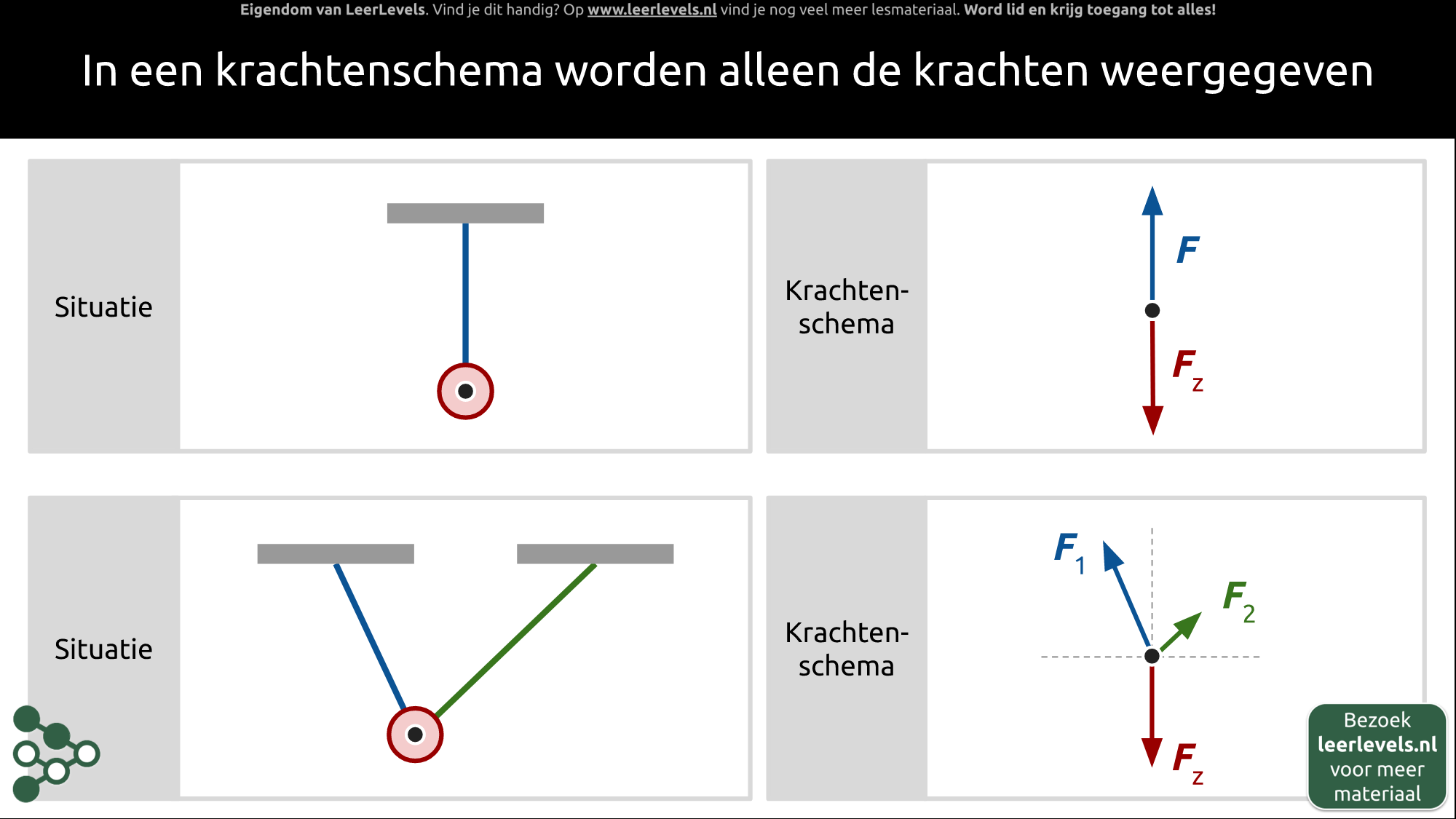
(Afbeelding: Animatie voor Krachtenschema)

Terug naar overzicht Meld je aan

Kringproces

Kring process concept

Bij een kringproces ondergaat een systeem meerdere toestandsveranderingen en keert uiteindelijk terug naar de begintoestand.

Een kringproces begint met een begintoestand waarin de toestandsvariabelen bepaalde waarden hebben. Vervolgens ondergaat het systeem een reeks toestandsveranderingen en bereikt achtereenvolgens. Om van het proces een kringproces te maken, moet het systeem weer terugkeren naar de begintoestand.

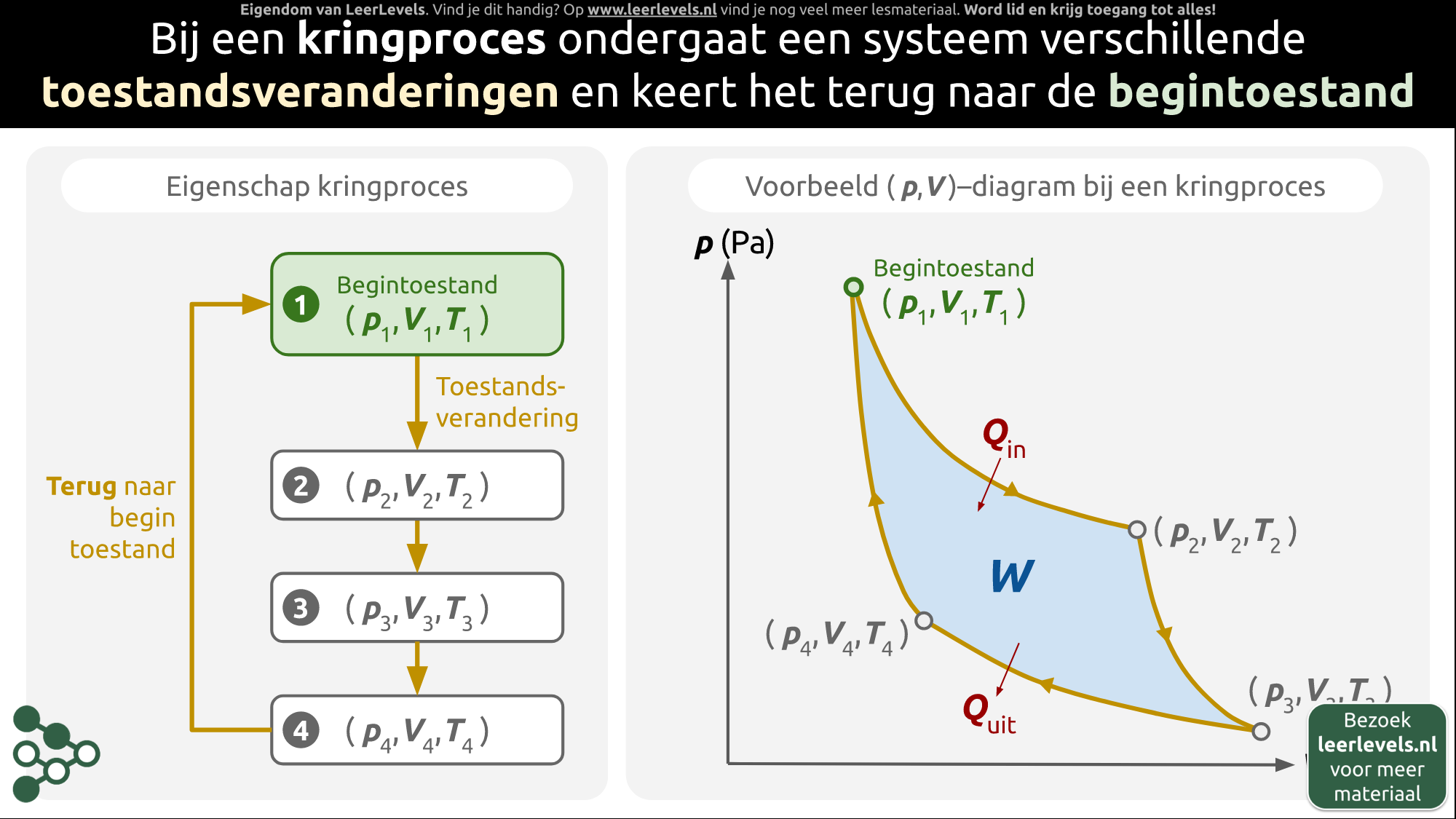
(Afbeelding: Animatie voor Kring process concept)

Terug naar overzicht Meld je aan

Kristalrooster

Kristalrooster concept

In een kristalrooster worden de atomen van een vaste stof geordend volgens een regelmatig patroon. Dit patroon kan verschillende vormen hebben, zoals kubisch (zoals bij keukenzout) of hexagonaal (zoals bij bergkristal). Ook andere vormen, zoals rechthoeken of ongelijke zijden van driehoeken, zijn mogelijk. De rangschikking van de atomen bepaalt de eigenschappen van de stof, zoals de vorm van bergkristal en de manier waarop een kristal het licht weerkaatst.

Kortom, een kristalrooster bestaat altijd uit atomen die regelmatig zijn gerangschikt.

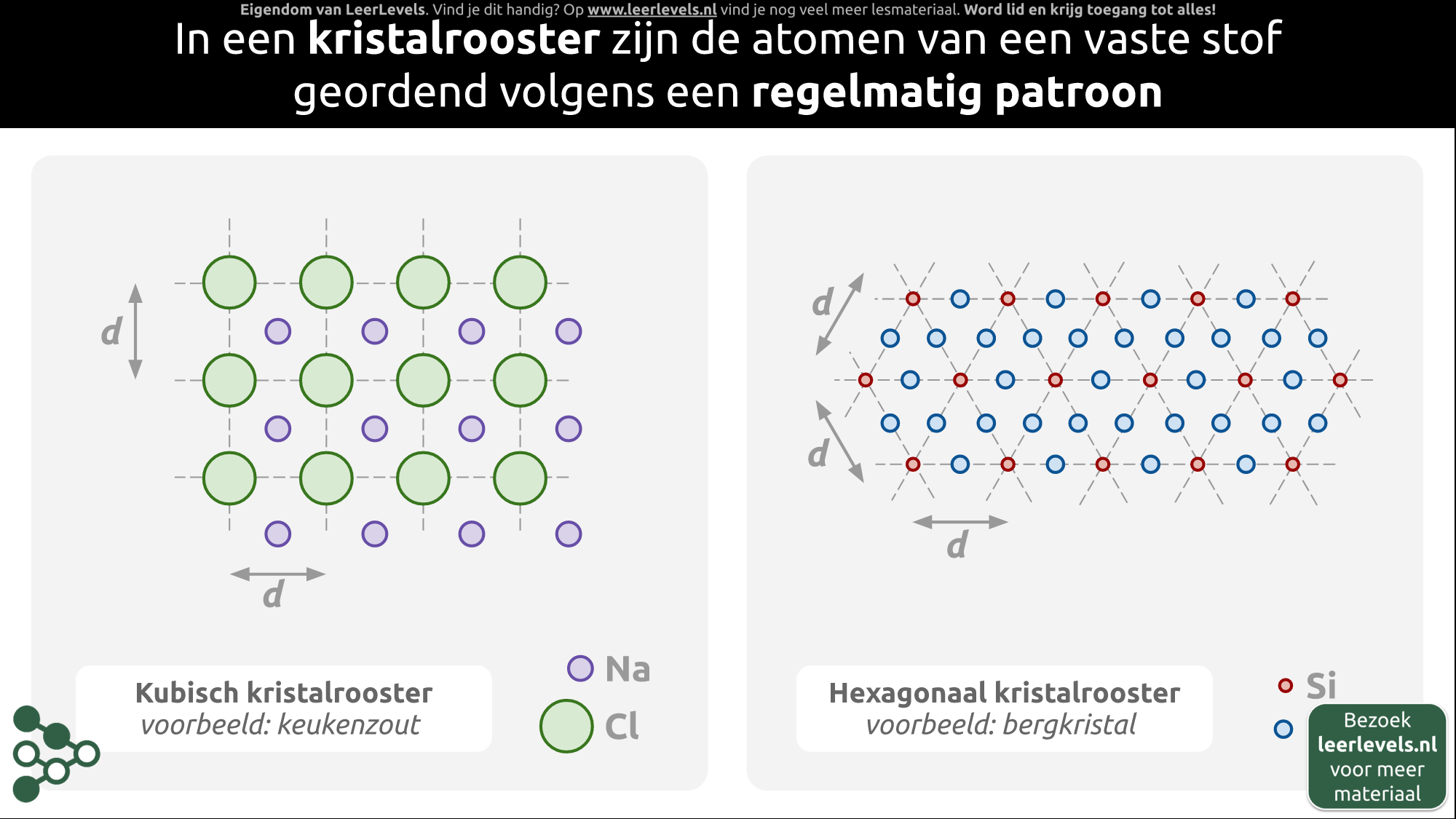
(Afbeelding: Animatie voor Kristalrooster concept)

Kristralrooster diffractie

Met diffractie aan een kristalrooster kun je de afstanden tussen atomen bepalen.

Neem als voorbeeld dit kubische kristalrooster, waarbij de blauwe bolletjes de atomen van een vaste stof voorstellen. Het idee van diffractie is dat je een golf op het kristal afstuurt onder een bepaalde hoek θ. Dit kan licht zijn - vaak worden röntgenstralen gebruikt - maar ook elektronen, aangezien deze ook een golflengte hebben. Wanneer de straal, laten we zeggen dat het licht is, op een atoom valt, wordt deze teruggekaatst, en een parallelle lichtstraal ook. De onderste lichtstraal legt een iets grotere afstand af dan de bovenste, de extra weglengte.

De twee weerkaatste lichtstralen kunnen elkaar versterken of juist uitdoven. Constructieve interferentie treedt op wanneer de twee golven in fase zijn, oftewel wanneer het extra stukje weglengte gelijk is aan n · λ, waarbij λ de gebruikte golflengte is. Deze extra weglengte kun je met behulp van driehoeksmeetkunde bepalen en is gelijk aan 2d sin θ.
Het mooie hiervan is dat je hiermee de afstand tussen atomen kunt bepalen. Je kunt dan de formule opschrijven als d = (n · λ)/(2 sin θ). Als je de golflengte kent waarmee je op een kristal schijnt en je vindt de hoek waarbij versterking wordt waargenomen, kun je d berekenen. Kort samengevat: met diffractie aan een kristalrooster kun je de afstanden tussen atomen bepalen.

$Afbeelding voor Kristralrooster diffractie$

(Afbeelding: Animatie voor Kristralrooster diffractie)

Terug naar overzicht Meld je aan

Kwadratenwet

Kwadratenwet concept

Als een lichtbron verder weg is, wordt de intensiteit van het licht dat het afgeeft minder sterk. Dit komt doordat het licht zich moet verspreiden over een groter oppervlak. De formule om het oppervlak van een bol te berekenen is Abol = 4π r². Ter illustratie, het oppervlak van een bol is vier keer zo groot als het oppervlak van een cirkel met dezelfde straal. Als je de intensiteit van het licht in een bepaalde richting wilt berekenen, kun je de formule I = Pbron / Abol gebruiken. Hierbij is Pbron de kracht van de lichtbron en Abol het oppervlak van de bol waarover het licht wordt verspreid. Dus als je verder weg bent, wordt de intensiteit van het licht minder en zal het oppervlak waarover het licht wordt verspreid groter worden. Dit wordt de kwadratenwet genoemd omdat de intensiteit van het licht kwadratisch afneemt naarmate de afstand groter wordt.

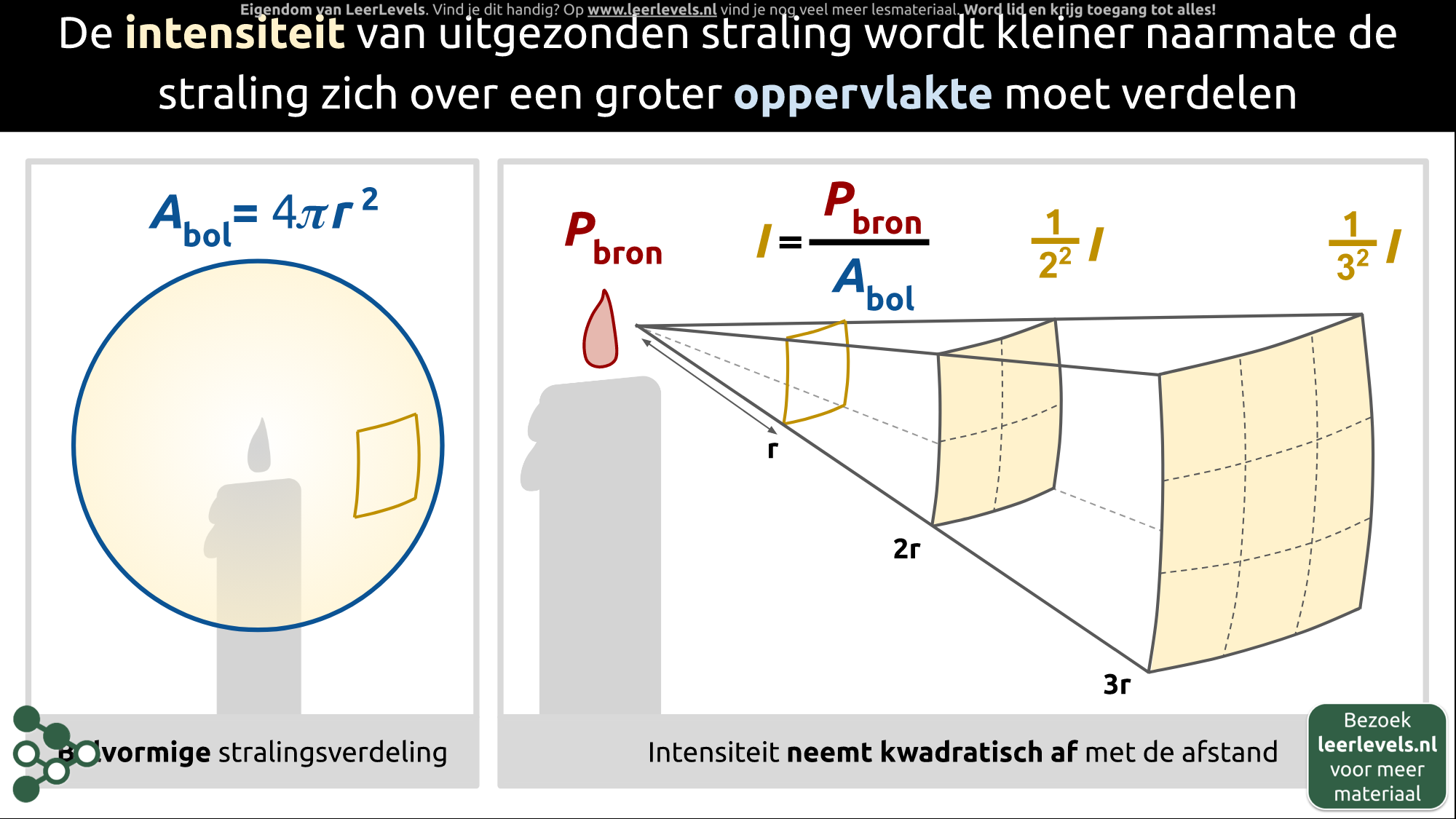
(Afbeelding: Animatie voor Kwadratenwet concept)

Kwadratenwet formule

Volgens de kwadratenwet neemt de intensiteit van straling kwadratisch af met de afstand tot de bron. Dit betekent dat de straling verdeeld wordt over een boloppervlak. De formule hiervoor is:

I = (Pbron)/(4 π r²

waarbij I de gemeten intensiteit is op een afstand r van de bron in W/m², Pbron het vermogen van de bron in W, en r de afstand tot de bron in m.

(Afbeelding: Animatie voor Kwadratenwet formule)

Terug naar overzicht Meld je aan

Lading

Lading concept

Lading is een eigenschap die bepaalt hoe een deeltje wordt beïnvloed door een elektrisch of magnetisch veld. Een soortgelijk verschijnsel treedt op bij een elektroscoop, een apparaat dat je kunt opladen en dat werkt als een bol. Wanneer iemand een neutraal geladen elektroscoop aanraakt, zal deze persoon een negatieve elektrische lading krijgen. Elektronen met een negatieve lading verspreiden zich door het hele lichaam en zorgen ervoor dat het haar overeind gaat staan. Dit is niet gevaarlijk zolang de lading laag blijft.

Wanneer een grote hoeveelheid van dezelfde lading zich ophoopt, stoten deze ladingen elkaar af. Hierdoor kan het haar dezelfde lading krijgen als het hoofd, waardoor het haar zo ver mogelijk van het hoofd weg gaat staan en recht overeind komt te staan. Lading bepaalt dus deze interacties en beïnvloedt hoe een deeltje reageert.

(Afbeelding: Animatie voor Lading concept)

Netto lading

De netto lading van een voorwerp geeft aan hoeveel meer protonen (p⁺ er zijn dan elektronen (e⁻). Laten we eens kijken naar verschillende situaties en de bijbehorende netto lading:

1. Stel dat je vier protonen en geen elektronen hebt. Dan is de netto lading + 4, omdat er vier meer protonen zijn dan elektronen.
2. In een situatie met drie protonen en één elektron is de netto lading + 2, omdat er twee meer protonen zijn dan elektronen.
3. Als er vier protonen en vier elektronen zijn, is de netto lading van het voorwerp 0.
4. Aan de andere kant, als er vier elektronen en één proton zijn, is de netto lading -3.
5. Als we alleen maar vijf elektronen hebben, dan is de lading -5.

Kortom, de netto lading van een voorwerp geeft aan hoeveel meer protonen er zijn dan elektronen.

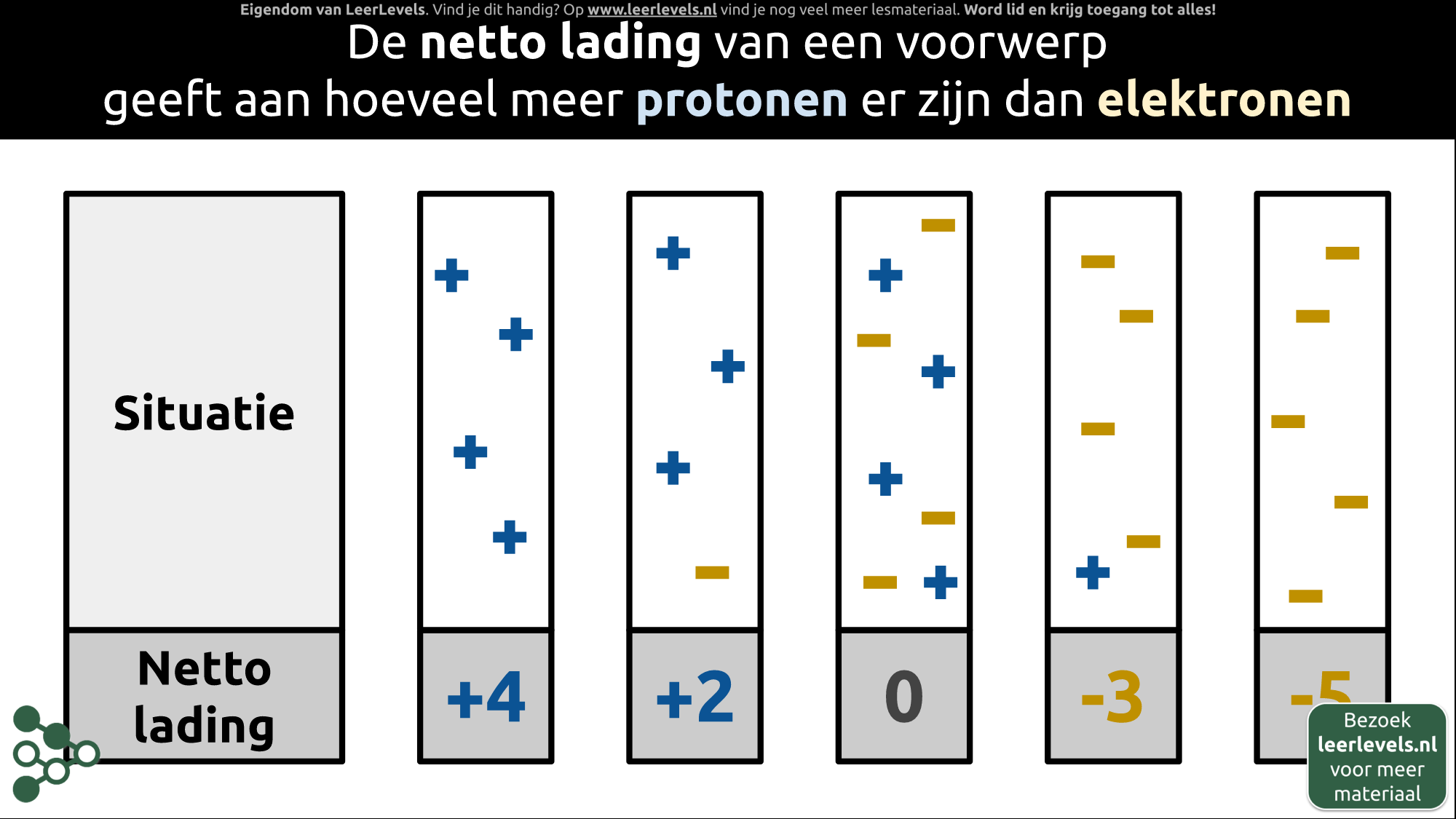
(Afbeelding: Animatie voor Netto lading)

Lading van elementaire deeltjes

Er zijn drie kleine deeltjes in een atoom: protonen, neutronen en elektronen. Protonen hebben een positieve lading, neutronen hebben geen lading en elektronen hebben een kleine negatieve lading. De lading van een proton is + 1, de lading van een neutron is 0 en de lading van een elektron is -1.

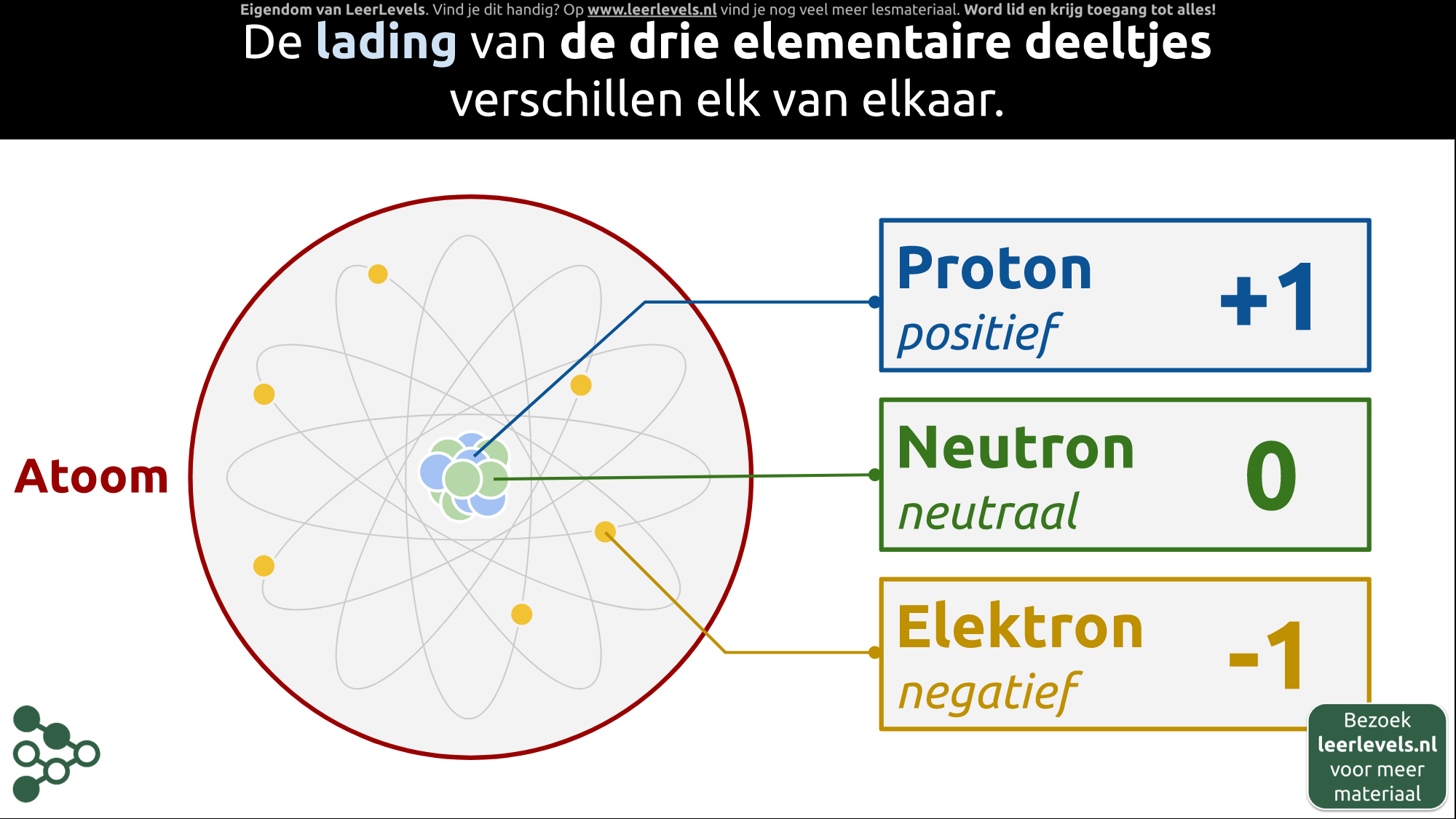
(Afbeelding: Animatie voor Lading van elementaire deeltjes)

Influentie

Een neutraal object kan lokaal geladen worden door influentie. Wanneer je een positief geladen ballon bij een plafond houdt, worden elektronen in het plafond aangetrokken. Hoewel het plafond zelf neutraal is, kunnen de elektronen een beetje dichterbij de ballon komen. De positieve ladingen in het plafond kunnen echter niet bewegen. Hierdoor ontstaan er lokaal negatieve ladingen in het plafond, die de positieve lading van de ballon aantrekken. Als je het goed doet, kun je de ballon tegen het plafond laten hangen. Dit fenomeen, waarbij een neutraal object lokaal geladen wordt, is een resultaat van influentie.

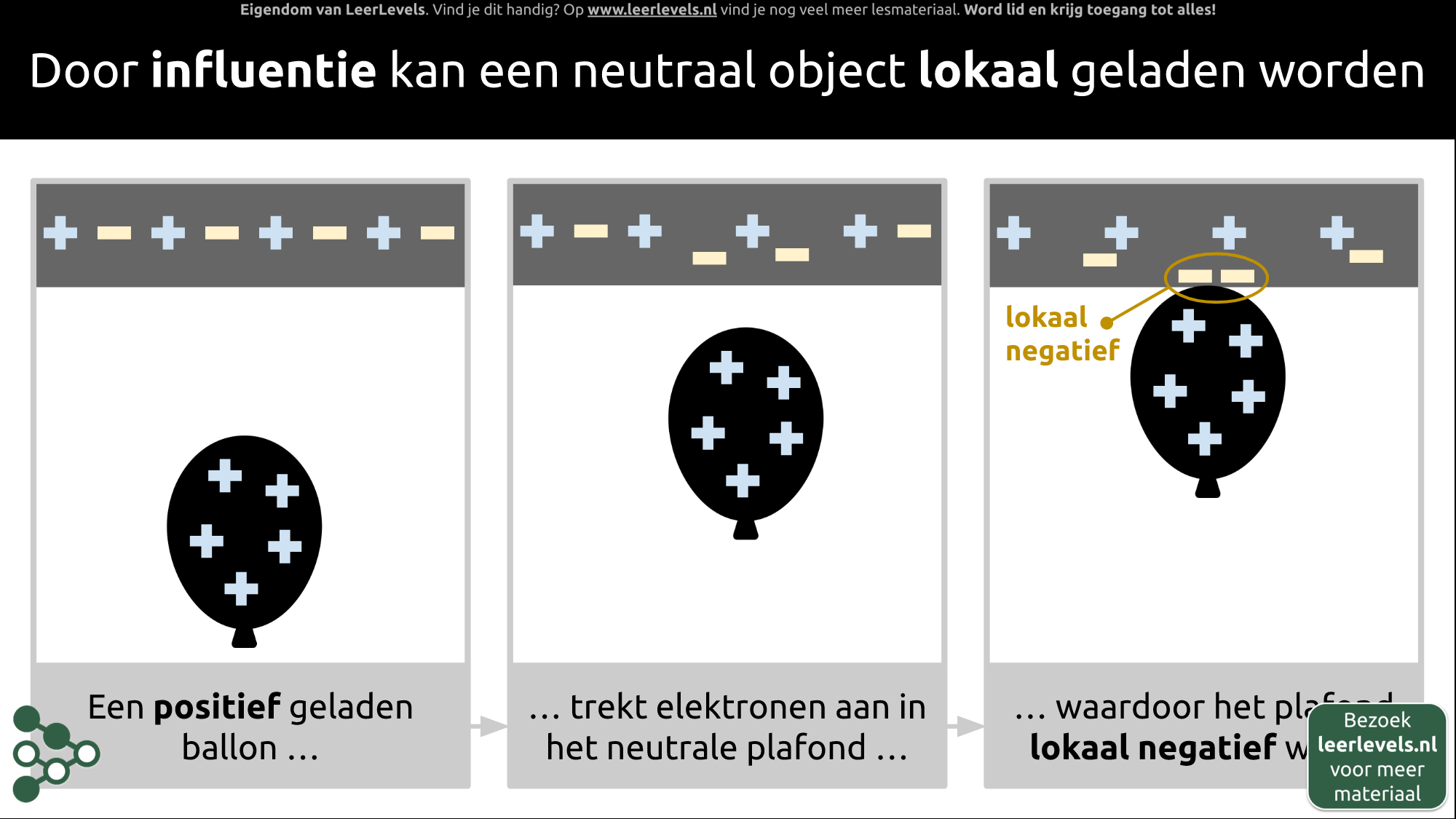
(Afbeelding: Animatie voor Influentie)

Ladingsverschil

Wanneer voorwerpen een verschillend nettolading hebben, spreken we van een ladingsverschil. Stel je hebt twee geïsoleerde bollen: de eerste heeft een lading van -10 en de tweede van + 2. Als we de bollen met elkaar verbinden, zal een stroom ontstaan om het ladingsverschil te neutraliseren, wat betekent dat elektronen gaan bewegen. Als er na deze beweging nog één elektron meer aan de ene kant is, zal de eerste bol een lading van -9 hebben en de tweede een lading van + 1. Uiteindelijk stabiliseert de situatie wanneer er geen ladingsverschil meer is. In dit specifieke geval gebeurt dat wanneer beide bollen een lading van -4 hebben.

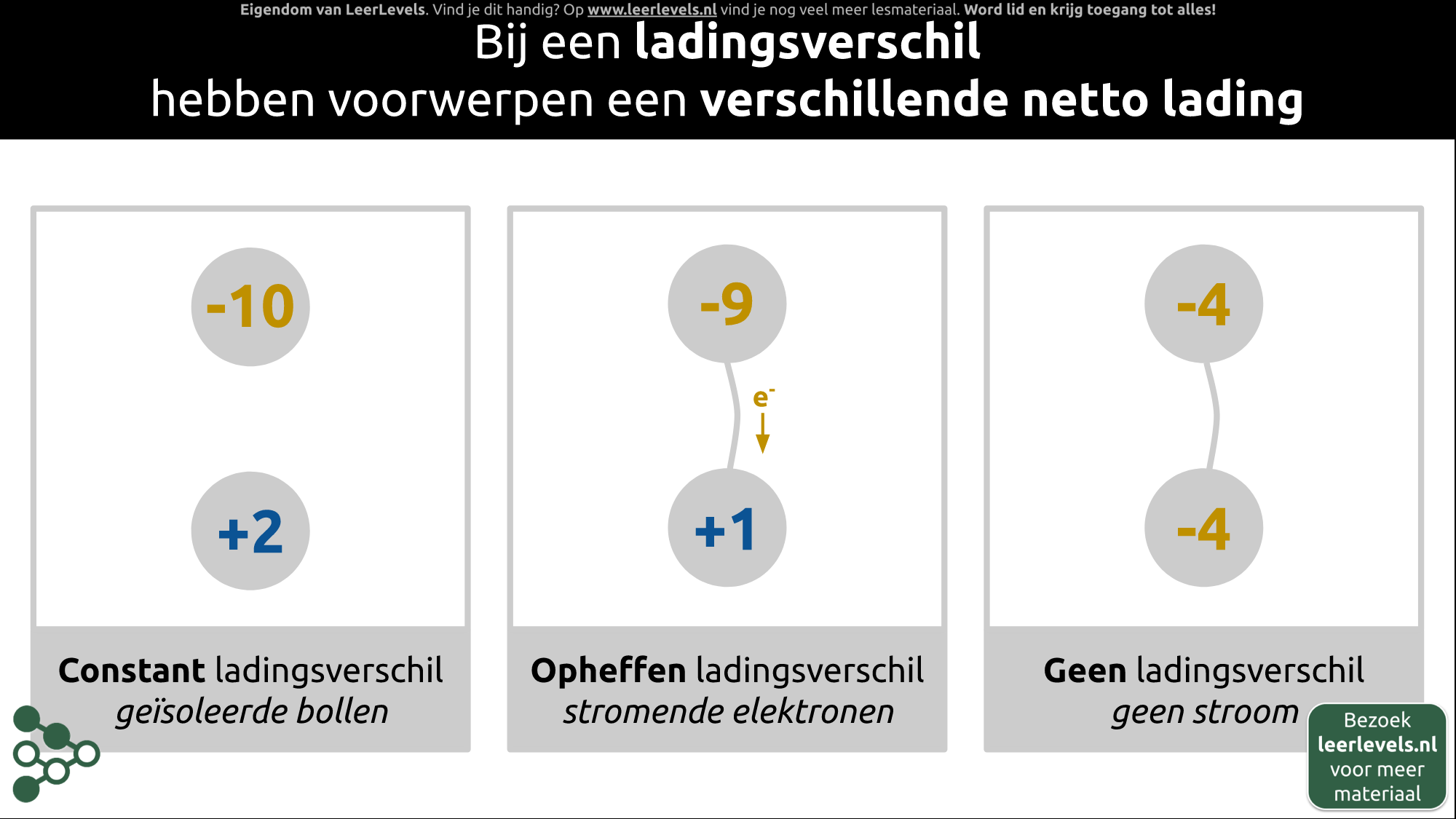
(Afbeelding: Animatie voor Ladingsverschil)

Terug naar overzicht Meld je aan

Lens

Vorm en sterkte van een lens

De sterkte (S) en brandpuntsafstand (f) van een lens worden bepaald door de bolheid van een positieve lens of de holheid van een negatieve lens.

Laten we kijken naar positieve en negatieve lenzen en hoe hun vorm de sterkte (S) en brandpuntsafstand (f) beïnvloedt.

Een positieve lens is bolvormig en convergent. Lichtstralen die evenwijdig aan de optische as op de lens vallen, gaan door het brandpunt op een afstand f van de lens.
Een negatieve lens is hol en divergent. Lichtstralen die op deze lens vallen, divergeren en lijken te komen uit het brandpunt F vóór de lens, op een afstand f.

Als de positieve lens minder bol is, is deze minder sterk en dus minder convergent. Lichtstralen die op de lens vallen, gaan nog steeds door het brandpunt, maar de brandpuntsafstand is nu groter.

Een negatieve lens die minder hol is, is ook minder sterk en dus minder divergent. De brandpuntsafstand is ook langer.

Als de positieve lens meer bol is, is deze sterker en dus meer convergent. De brandpuntsafstand wordt kleiner.

Hetzelfde geldt voor een negatieve lens die meer hol is. De brandpuntsafstand is kleiner.

Dus als een lens normaal bolvormig of holvormig is, zijn de sterkte (S) en brandpuntsafstand (f) normaal. Als de lens minder bol of hol is, is de sterkte (S) kleiner en de brandpuntsafstand (f) groter. Als de lens meer bol of hol is, is de sterkte (S) groter en de brandpuntsafstand (f) kleiner.

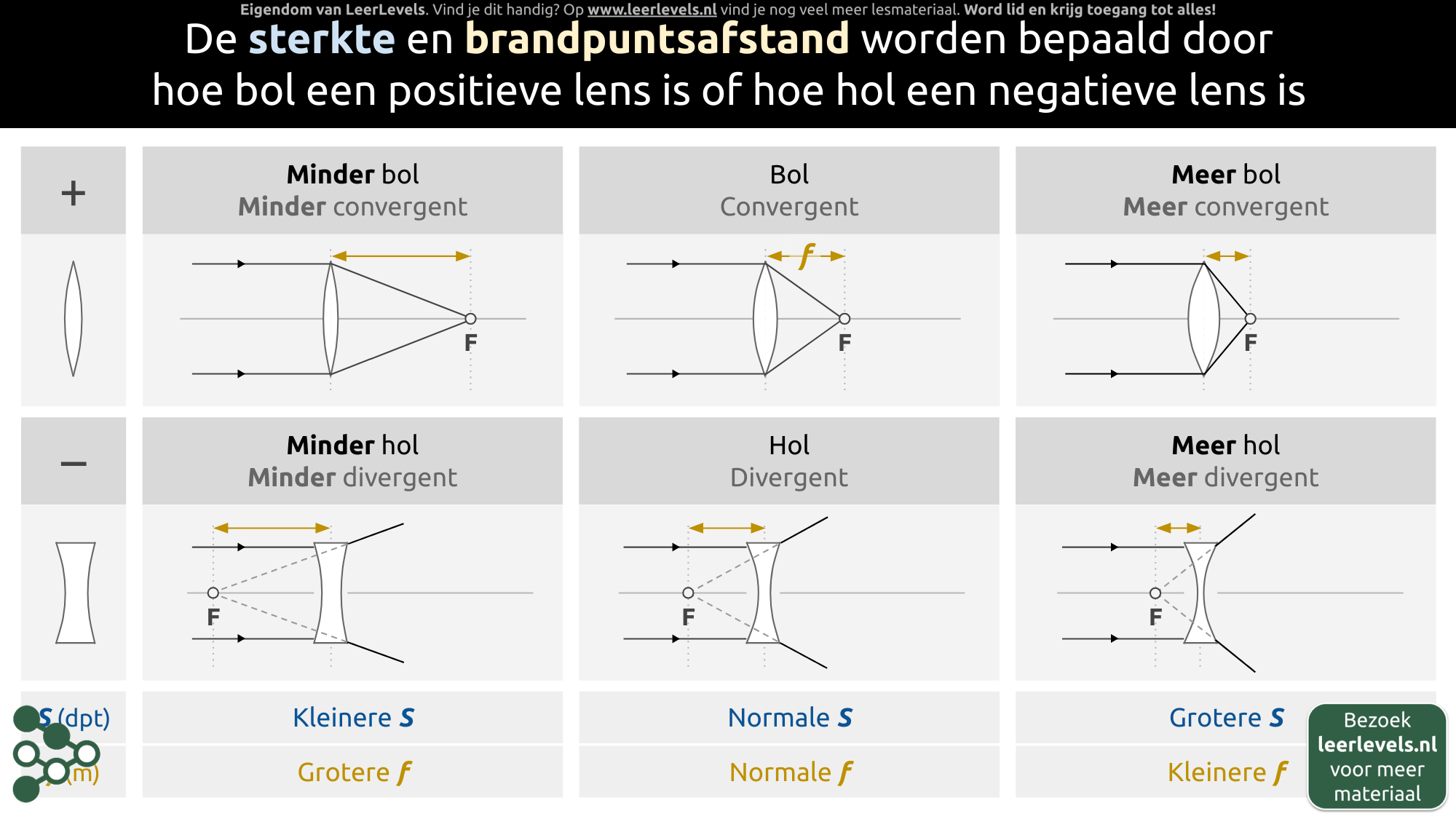
(Afbeelding: Animatie voor Vorm en sterkte van een lens)

Eigenschappen positieve en negatieve lens

Een positieve lens is een convergerende lens, terwijl een negatieve lens divergerend is. Dit houdt in dat een positieve lens bol is en het licht samenbrengt, terwijl een negatieve lens hol is en het licht verspreidt. Een positieve lens buigt lichtstralen naar de optische as toe, terwijl een negatieve lens de lichtstralen juist van de optische as afbuigt. In schema's wordt een positieve lens aangeduid met een plusteken $ + $, en een negatieve lens met een minteken $-$.

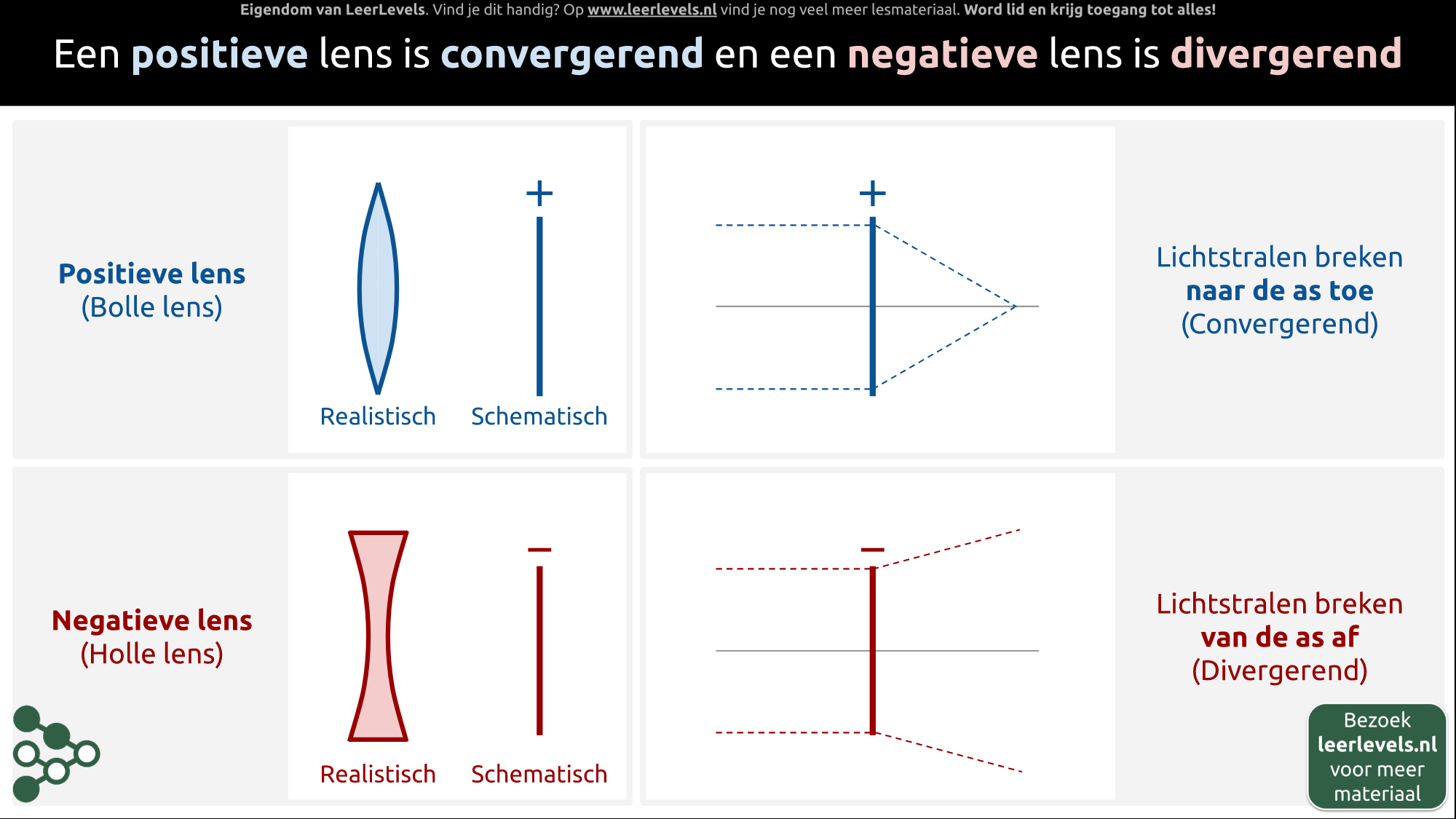
(Afbeelding: Animatie voor Eigenschappen positieve en negatieve lens)

Terug naar overzicht Meld je aan

Lenzenformule

De lenzenformule legt het verband uit tussen de brandpuntsafstand (f), voorwerpafstand (v) en beeldafstand (b).

De lenzenformule kan worden geschreven als:

1/f = 1/v + 1/b

Hierin is f de brandpuntsafstand in meter, v de voorwerpafstand in meter en b de beeldafstand in meter. Met behulp van deze formule kan één van de drie grootheden worden berekend als de andere twee bekend zijn.

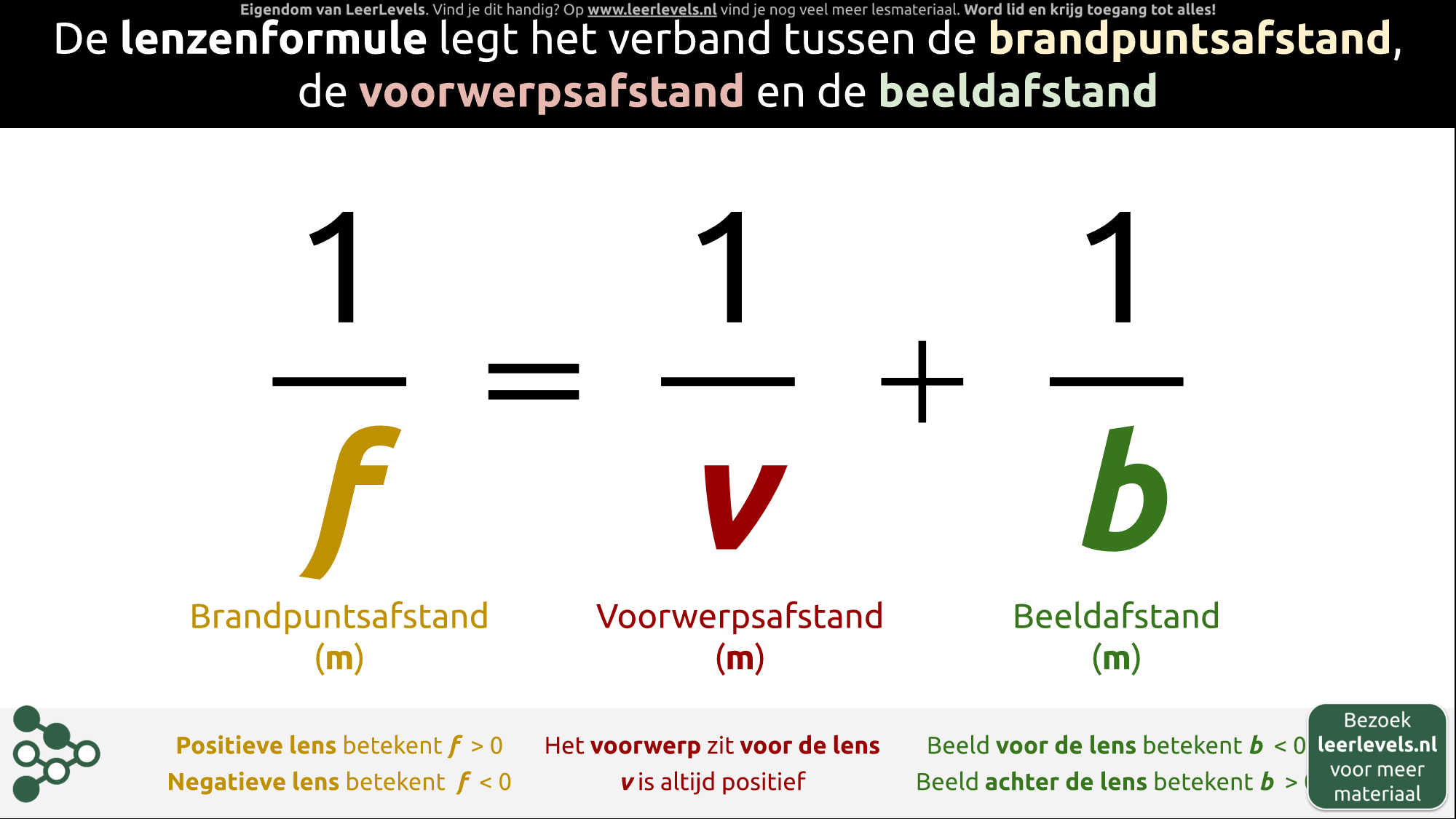
(Afbeelding: Animatie voor Lenzenformule)

Terug naar overzicht Meld je aan

Lenzenmakersformule

De brandpuntsafstand van een lens wordt bepaald door de vorm en het materiaal waar de lens van gemaakt is.

Stel dat we een lens hebben met een bolling aan de ene kant, met een kromtestraal R1, en een bolling aan de andere kant, met een kromtestraal R2. De optische as van de lens gaat door de middelpunten van de cirkels die gevormd worden door de kromtestralen. De lens heeft een dikte d, en buiten de lens heeft het medium een brekingsindex n0. De lens zelf is gemaakt van een materiaal met brekingsindex n.

Wanneer lichtstralen op deze lens vallen, breken ze bij het binnengaan van de lens en breken ze opnieuw bij het verlaten van de lens, om vervolgens samen te komen bij het brandpunt op een afstand f, gemeten vanaf de lijn die de snijpunten van de twee cirkels van de kromtestralen verbindt.

In dit schema wordt R gebruikt om de kromtestraal aan te duiden. Deze is positief als de kromming een bolle lensvlak oplevert, en negatief als de kromming een holle lensvlak oplevert. Verder is d de dikte van de lens in meter, n0 de brekingsindex van het medium buiten de lens, en n de brekingsindex van de lens zelf.

De lenzenmakersformule legt een verband tussen deze grootheden, zoals hieronder weergegeven:

1/f = ((n- n0))/(n0)((1)/(R1) + (1)/(R2)) - ((n-n0)d)/(nR1R2)

Met behulp van deze formule kan worden bepaald hoe de vorm van de lens eruit moet zien wanneer een lens met een bepaald materiaal en een bepaalde sterkte wordt gemaakt.

Dit is een algemene formule, maar in veel gevallen gebruiken we een vereenvoudigde versie waarbij we aannemen dat de lens dun is. Dit betekent dat we de dikte d kunnen verwaarlozen en aannemen dat er lucht buiten de lens zit met n0 = 1. Dit leidt tot de volgende formule:

1/f = (n-1)((1)/(R1) + (1)/(R2))

(Afbeelding: Animatie voor Lenzenmakersformule)

Terug naar overzicht Meld je aan

Licht

Reflectie, absorptie en transmissie

Als er licht op een voorwerp schijnt, kan het op drie manieren reageren: reflectie, absorptie en transmissie. Reflectie gebeurt als het licht op een gebogen spiegel valt en weer terugkaatst naar een centraal punt. Dit kan worden gebruikt om warmte te genereren met behulp van een buis op dat punt. Absorptie gebeurt wanneer het licht wordt omgezet in warmte. Dit kan worden gebruikt als energiebron. Transmissie betekent dat het licht door een materiaal gaat, zoals glas in een plantenkas. Dit proces wordt transmissie genoemd. Kortom, licht kan reflecteren, absorberen of transmissie ondergaan.

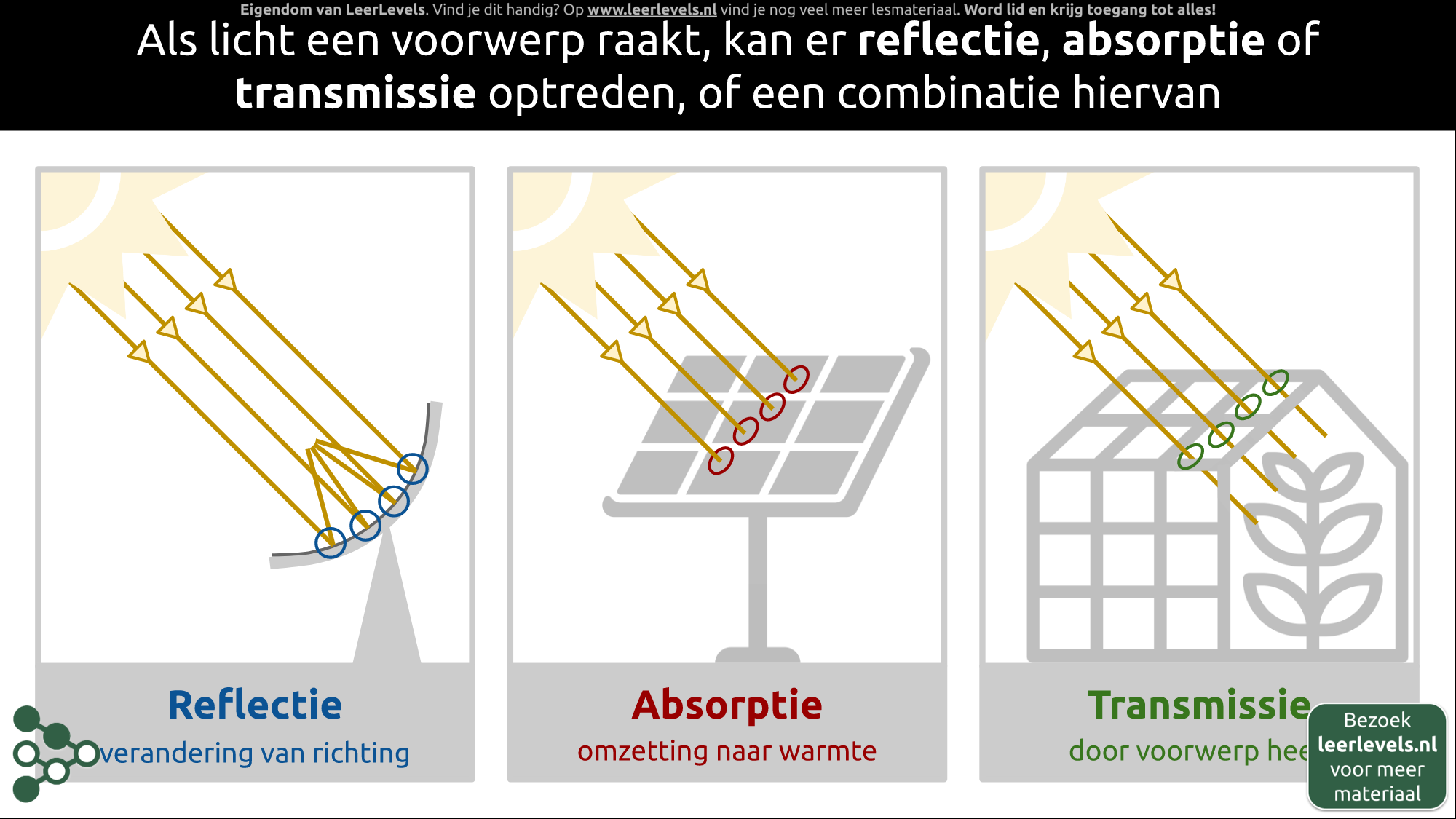
(Afbeelding: Animatie voor Reflectie, absorptie en transmissie)

Terug naar overzicht Meld je aan

Lichtbreking

Lichtbreking concept

Lichtbreking treedt op wanneer het licht van de ene stof naar de andere gaat en er een verschil is in de brekingsindex van beide stoffen. Als het licht van een stof met een lage brekingsindex naar een stof met een hoge brekingsindex gaat, zal de lichtstraal een beetje afbuigen naar de normaal toe. Als het licht van een stof met een hoge brekingsindex naar een stof met een lage brekingsindex gaat, zal de lichtstraal een beetje afbuigen van de normaal af. Het afbuigen van de lichtstraal kan worden vergeleken met een raceauto die de ene stof verlaat en de andere binnengaat. Lichtbreking wordt veroorzaakt door het verschil in snelheid waarmee licht zich verplaatst in de ene of de andere stof.

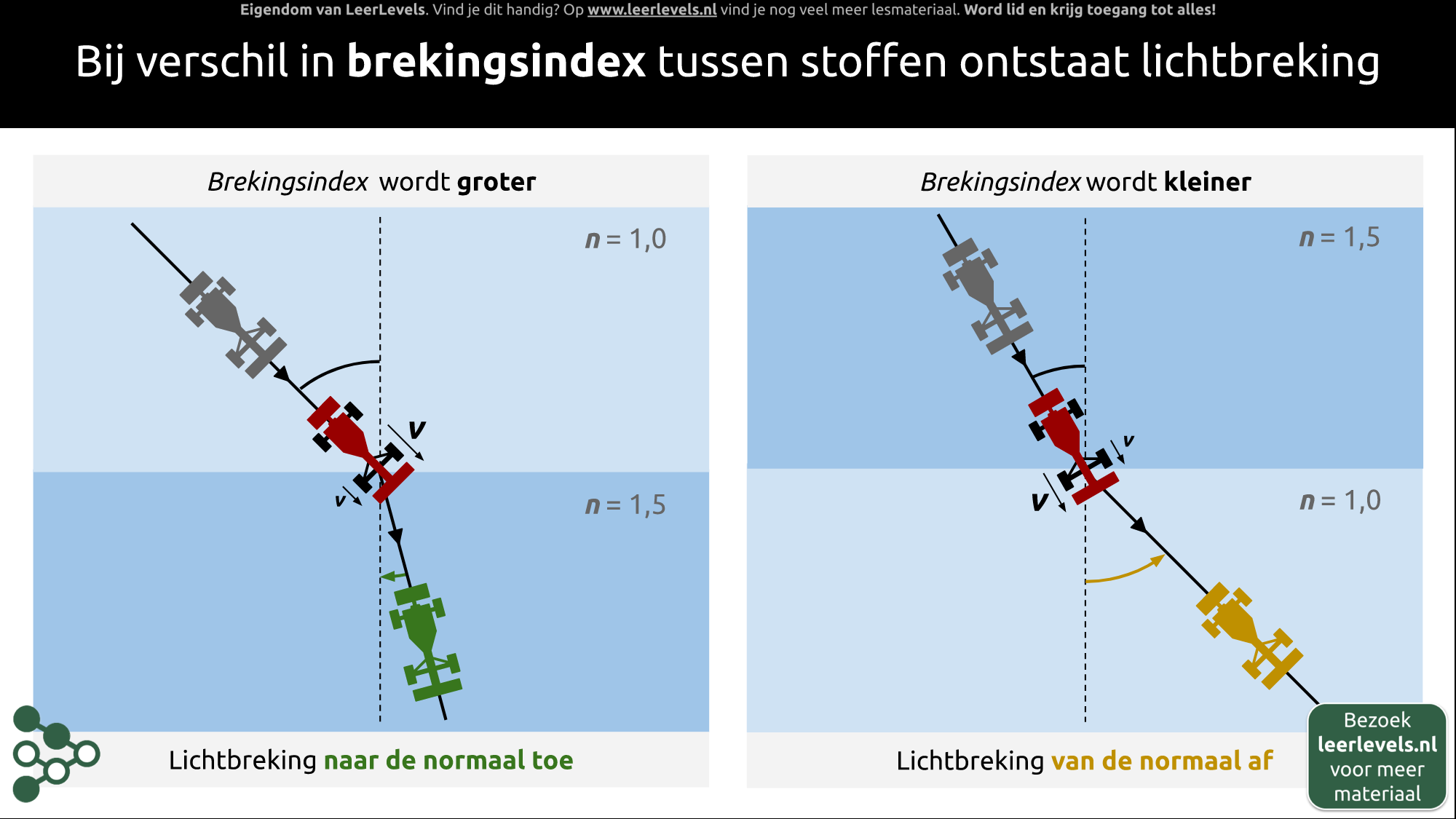
(Afbeelding: Animatie voor Lichtbreking concept)

Terug naar overzicht Meld je aan

Lichtbundels

Soorten lichtbundels

Het verschil tussen divergente, evenwijdige en convergente lichtbundels heeft te maken met hoe het licht beweegt. Als we een lens tussen onszelf en een lichtbron plaatsen, zien we verschillende soorten lichtbundels. Bij een divergente lichtbundel wijzen alle pijltjes van het licht van elkaar weg. Als we deze lichtbundel door een lens laten gaan, kunnen de stralen parallel aan elkaar gaan lopen en krijgen we een evenwijdige lichtbundel. Als we deze bundel weer door een lens laten gaan, worden de stralen naar elkaar toe gebogen en komen dichter bij elkaar. Dit noemen we een convergente bundel en op de plek waar de lichtstralen samenkomen kan het erg warm worden. Het is belangrijk om te onthouden dat deze verschillende soorten lichtbundels ontstaan door de manier waarop de lichtstralen bewegen.

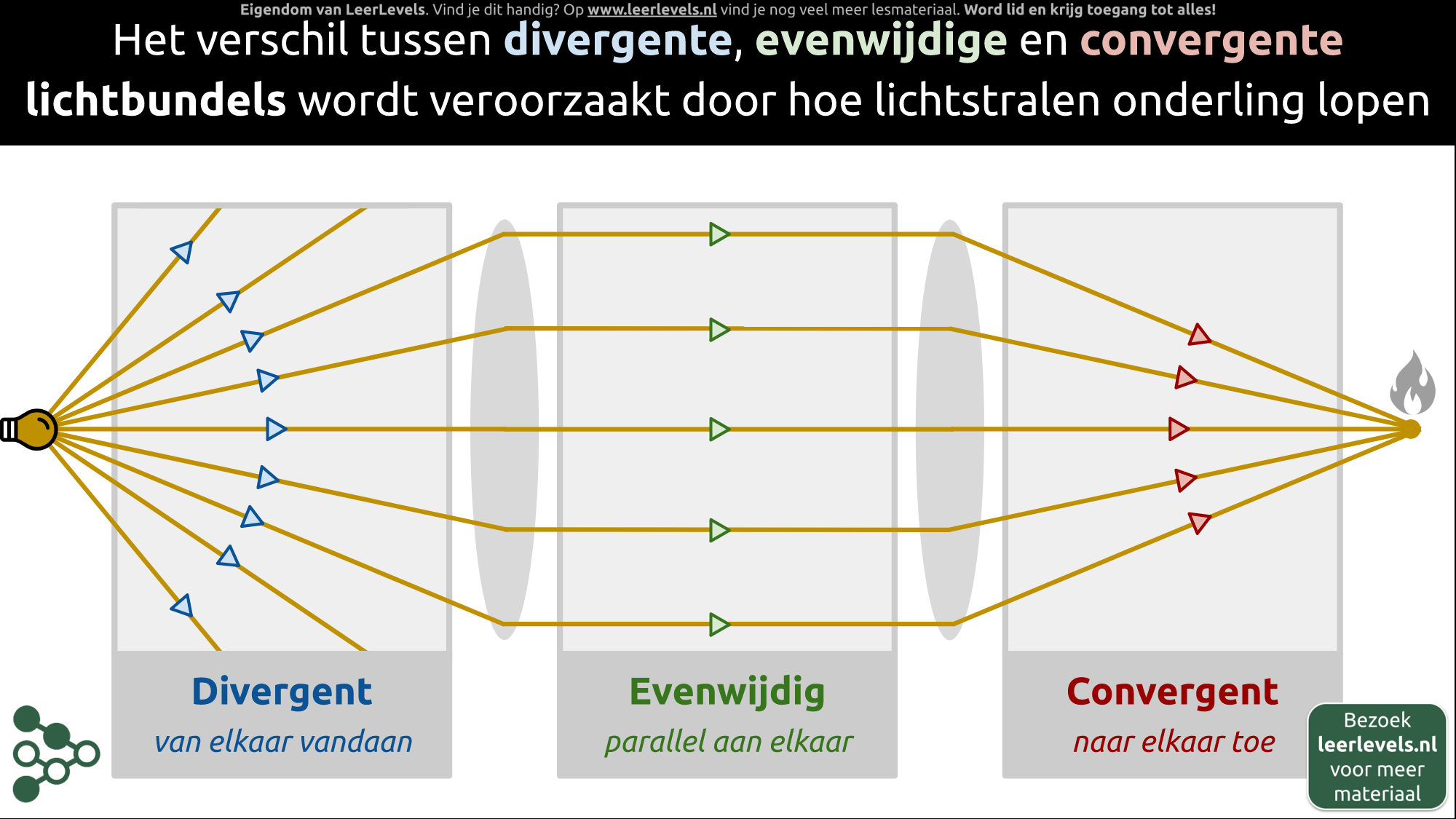
(Afbeelding: Animatie voor Soorten lichtbundels)

Terug naar overzicht Meld je aan

Lichtjaar

Een lichtjaar is de afstand die licht in een jaar aflegt, oftewel een enorme afstand. Om deze afstand te berekenen, gebruiken we de snelheid formule: v = s/t. Hierbij staat v voor snelheid, s voor afstand en t voor tijd. In dit geval is de afstand van een lichtjaar gelijk aan de lichtsnelheid (3 x 10⁸ m/s) keer de tijd van een jaar (ongeveer 31,5 miljoen seconden). Door deze waarden in te vullen in de formule, komen we uit op ongeveer 10¹⁶ meter. Dit betekent dat licht in een jaar tijd een ongelooflijk grote afstand aflegt.

(Afbeelding: Animatie voor Lichtjaar)

Terug naar overzicht Meld je aan

Lichtsnelheid

De lichtsnelheid is de snelste mogelijke snelheid in het heelal. Het is zo snel dat we het kunnen vergelijken met andere snelheden: wandelen = 3,6 km/u, fietsen = 36 km/u, extreme auto's = 100 meter/seconde en een raket = 10,000 meter/seconde. Licht vanuit een lamp gaat met een snelheid van 299,792,458 meter/seconde, wat de lichtsnelheid is en niks kan sneller gaan dan dat. Als je in de buurt van deze snelheid komt, zullen er speciale dingen gebeuren met de tijd volgens de speciale relativiteitstheorie.

(Afbeelding: Animatie voor Lichtsnelheid)

Terug naar overzicht Meld je aan

Lineaire versneller

In een lineaire versneller wordt elektrische energie omgezet in kinetische energie. Een lineaire versneller heeft vaak de volgende opstelling: er zijn twee condensatorplaten. De eerste stap is dat er door een warmtebron bij de linker condensatorplaat een lading vrijkomt. Deze lading heeft op dat moment alleen elektrische energie en beweegt nog niet. Binnen een fractie van een seconde zorgt de elektrische kracht ervoor dat de lading versnelt. De elektrische kracht blijft constant, omdat deze alleen afhankelijk is van de lading en de veldsterkte. De snelheid van de lading neemt toe, en wanneer de lading de rechterkant heeft bereikt, is er alleen nog maar kinetische energie aanwezig. Je kunt de snelheid berekenen door gebruik te maken van het principe van energiebehoud. We weten namelijk dat de totale energie constant blijft, wat betekent dat

Δ Eel + Δ Ek = 0

Aangezien er aan het begin alleen elektrische energie was en aan het eind alleen nog maar kinetische energie is, mogen we dit vereenvoudigen naar:

Eel,begin = Ek,eind

Door formules in te vullen voor de elektrische energie en de kinetische energie krijgen we:

q · U = ½ · m · veind²

Oplossen voor veind geeft:

v = √((2 · q · U)/(m))

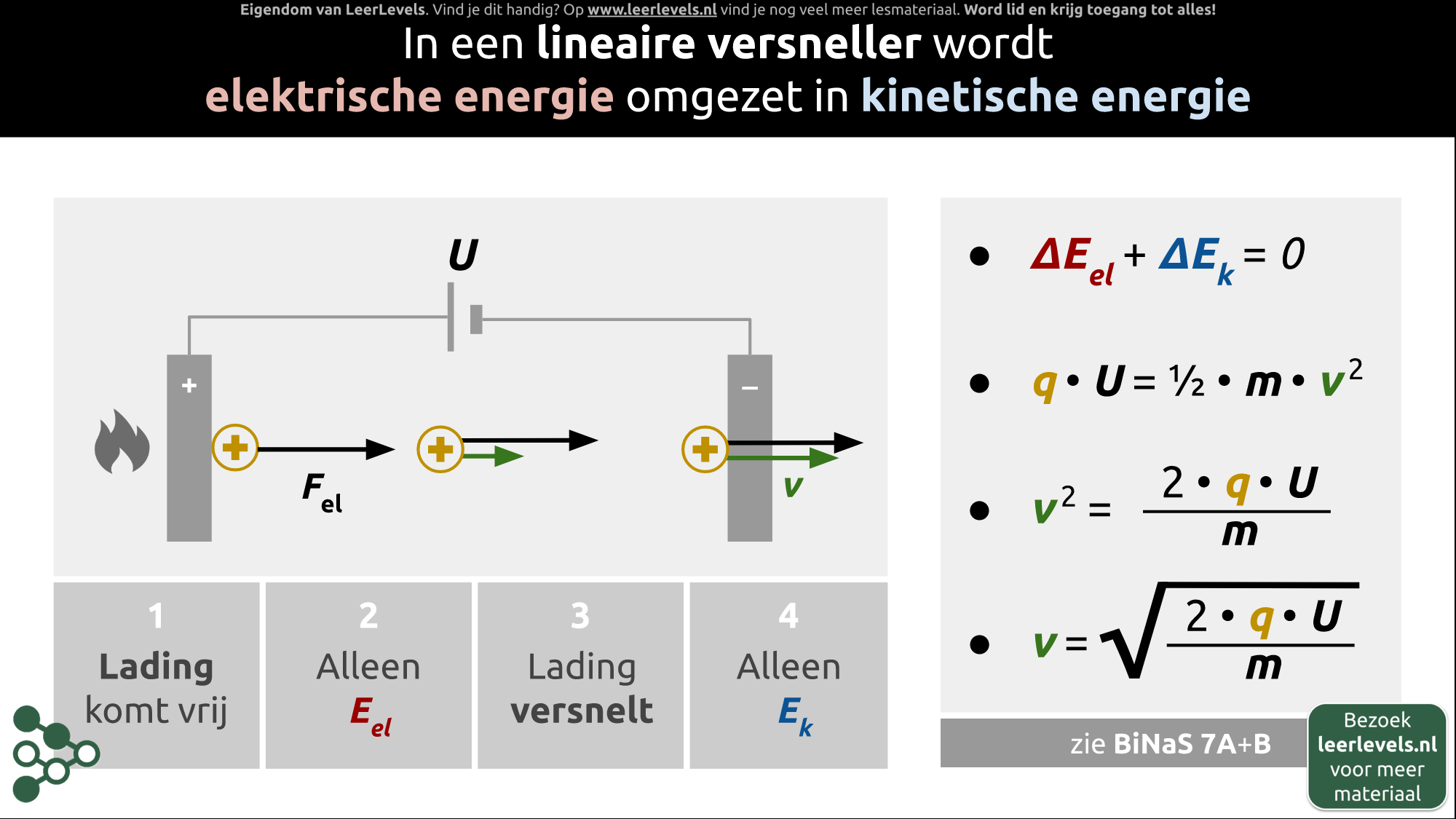
(Afbeelding: Animatie voor Lineaire versneller)

Terug naar overzicht Meld je aan

Logaritme

Logaritme concept

Het logaritme is een rekenfunctie waarmee je snel exponentiële vergelijkingen kunt oplossen. Bijvoorbeeld: als je de vergelijking 10x = 100 hebt, weet je misschien al dat x gelijk is aan 2. Maar je kunt het ook berekenen met het logaritme: x is gelijk aan 10 \log(100), wat ook 2 is. Bij complexere vergelijkingen, zoals 2x = 256, kun je het logaritme gebruiken om de oplossing snel te berekenen. In dit geval is x gelijk aan 2 \log(256), wat gelijk is aan 8. Het logaritme kan worden geschreven als n \log y, wat betekent dat n het getal is dat je moet gebruiken als exponent op een bepaald getal om y te krijgen.

(Afbeelding: Animatie voor Logaritme concept)

Logaritme rekenregels

Om logaritmes toe te passen heb je rekenregels nodig, die je kunt vinden in tabel 36D van BiNaS. Twee van deze regels zijn erg belangrijk. De eerste regel luidt:

\log(ab) = b · \log(a)

Om deze regel te illustreren, kijken we naar een voorbeeld. Stel dat we te maken hebben met een vervalreactie waarbij na een bepaalde tijd nog 30% van de kernen aanwezig is. We beginnen met 100% en na verloop van tijd is er dus nog 30% over. De overeenkomstige vergelijking is als volgt:

30\% = 100\% · 0,5t/t1/2)

Hierbij is t1/2 de halveringstijd.

Om deze vergelijking op te lossen voor t of t1/2, maken we gebruik van de rekenregel. Eerst delen we de vergelijking aan beide zijden door 100%. Dit geeft:

0,3 = 0,5t/t1/2)

Om het exponent vrij te maken, nemen we de logaritme aan beide zijden van de vergelijking. Dit geeft:

\log(0,3) = \log(0,5t/t1/2))

Door de rekenregel toe te passen, kunnen we deze vergelijking schrijven als:

\log(0,3) = (t)/(t1/2) · \log(0,5)

Daaruit volgt:

(t)/(t1/2) = ( \log(0,3))/(\log(0,5))

De tweede rekenregel luidt:

a\log b = (c\log(b))/(c \log(a))

Dit betekent dat je voor een logaritme, zelfs als je geen knopje hebt op je rekenmachine, deze altijd kunt berekenen met behulp van een logaritme die je wel hebt. Stel dat je de vergelijking hebt:

2x = 2048

Om x te berekenen maken we gebruik van logaritmen. Dit geeft:

x = ² \log(2048)

Aangezien de 2-log functie niet op je rekenmachine zit, maken we gebruik van de 10-log functie. Door de rekenregel toe te passen, krijgen we:

x = (¹⁰\log(2048))/(¹⁰ \log(2)) = 11

Beide rekenregels zijn nodig om logaritmen toe te passen bij natuurkunde, vooral bij radioactief verval.

(Afbeelding: Animatie voor Logaritme rekenregels)

Terug naar overzicht Meld je aan

Lorentzkracht

Lorentzkracht draad concept

Als we een elektrische stroom loodrecht op een magneetveld plaatsen, ondervindt deze stroom een kracht, genaamd de Lorentzkracht. Deze kracht staat loodrecht op zowel de stroom als het veld.

Als we naar een hoefijzermagneet kijken, loopt het magneetveld van noord naar zuid. Als we een stroomdraad tussen deze magneten plaatsen, waarbij de stroom naar links loopt, ondervindt deze kracht de Lorentzkracht, die gericht is naar ons toe. Dit komt omdat de stroom loodrecht staat op het magnetisch veld.

Als we dit van bovenaf bekijken, wijst het B-veld naar beneden, terwijl de stroom naar links loopt. In dit geval wijst de Lorentzkracht naar beneden.

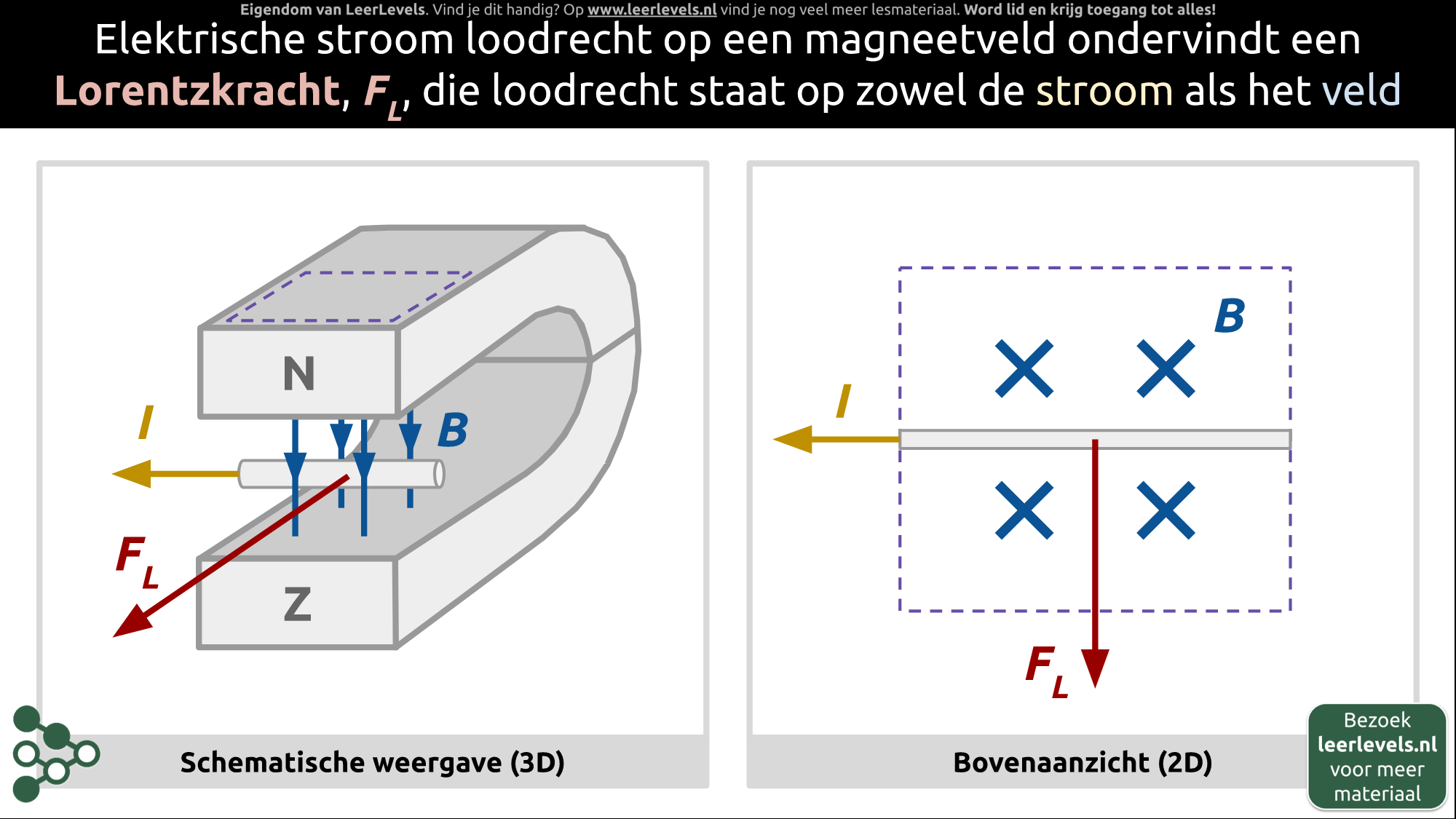
(Afbeelding: Animatie voor Lorentzkracht draad concept)

Lorentzkracht draad formule

De kracht op een draad in een magnetisch veld heet de Lorentzkracht en wordt weergegeven als FL. De grootte van deze kracht hangt af van de magnetische veldsterkte (B), de stroomsterkte (I) en de lengte van de draad in het magnetische veld (l). Deze drie grootheden zijn met elkaar vermenigvuldigd: FL = BIL. Let op: alleen de lengte van de draad die zich in het magnetische veld bevindt, telt mee voor de berekening van de kracht.

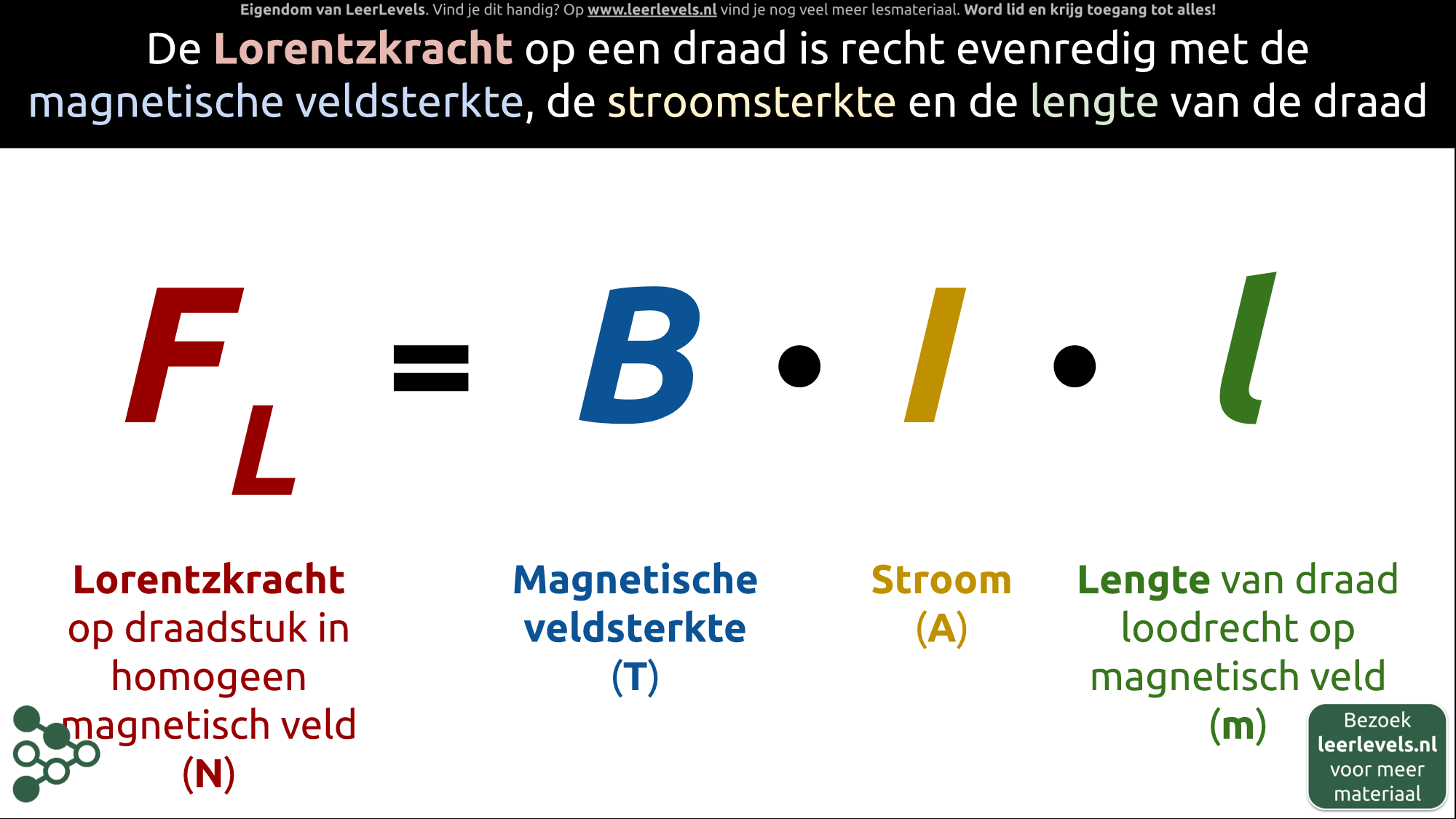
(Afbeelding: Animatie voor Lorentzkracht draad formule)

Lorentzkracht lading concept

Als iets met een lading beweegt en loodrecht op een magnetisch veld, dan ondervindt het een kracht die loodrecht staat op de bewegingsrichting en het veld. Stel je een hoefijzermagneet voor met een magnetisch veld dat overal hetzelfde is. In het midden van dat veld beweegt een lading met een positieve lading en gaat naar links. Dan wijst de kracht die erop werkt naar beneden. Als je er van bovenaf naar kijkt, dan gaat het magnetisch veld het papier in (gemarkeerd met kruisjes), gaat de lading naar links en wijst de kracht naar beneden.

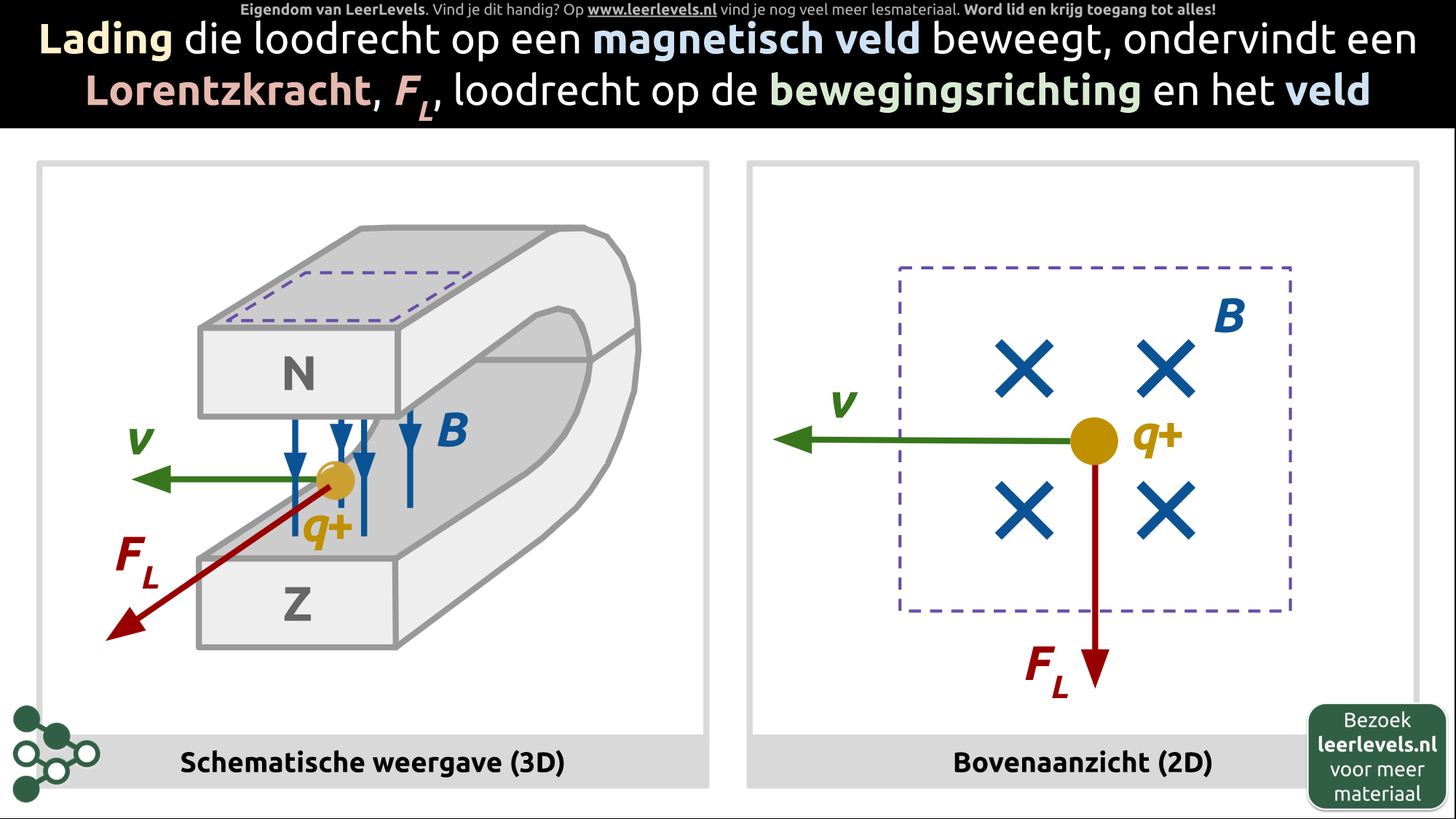
(Afbeelding: Animatie voor Lorentzkracht lading concept)

Lorentzkracht lading formule

Als een lading door een magnetisch veld beweegt, ondervindt het een kracht die de Lorentzkracht wordt genoemd. Deze kracht hangt af van de sterkte van het magnetisch veld (B), de grootte van de lading (q) en de snelheid van de lading (v). Als er geen magnetisch veld aanwezig is, is er geen Lorentzkracht. In een egaal magnetisch veld wordt de Lorentzkracht berekend met de formule FL = B · q · v. Hierbij is B uitgedrukt in Tesla, q in Coulomb en v in meter per seconde. Deze formule is alleen van toepassing op deeltjes in het magnetische veld. Dit is de Lorentzkracht op een lading.

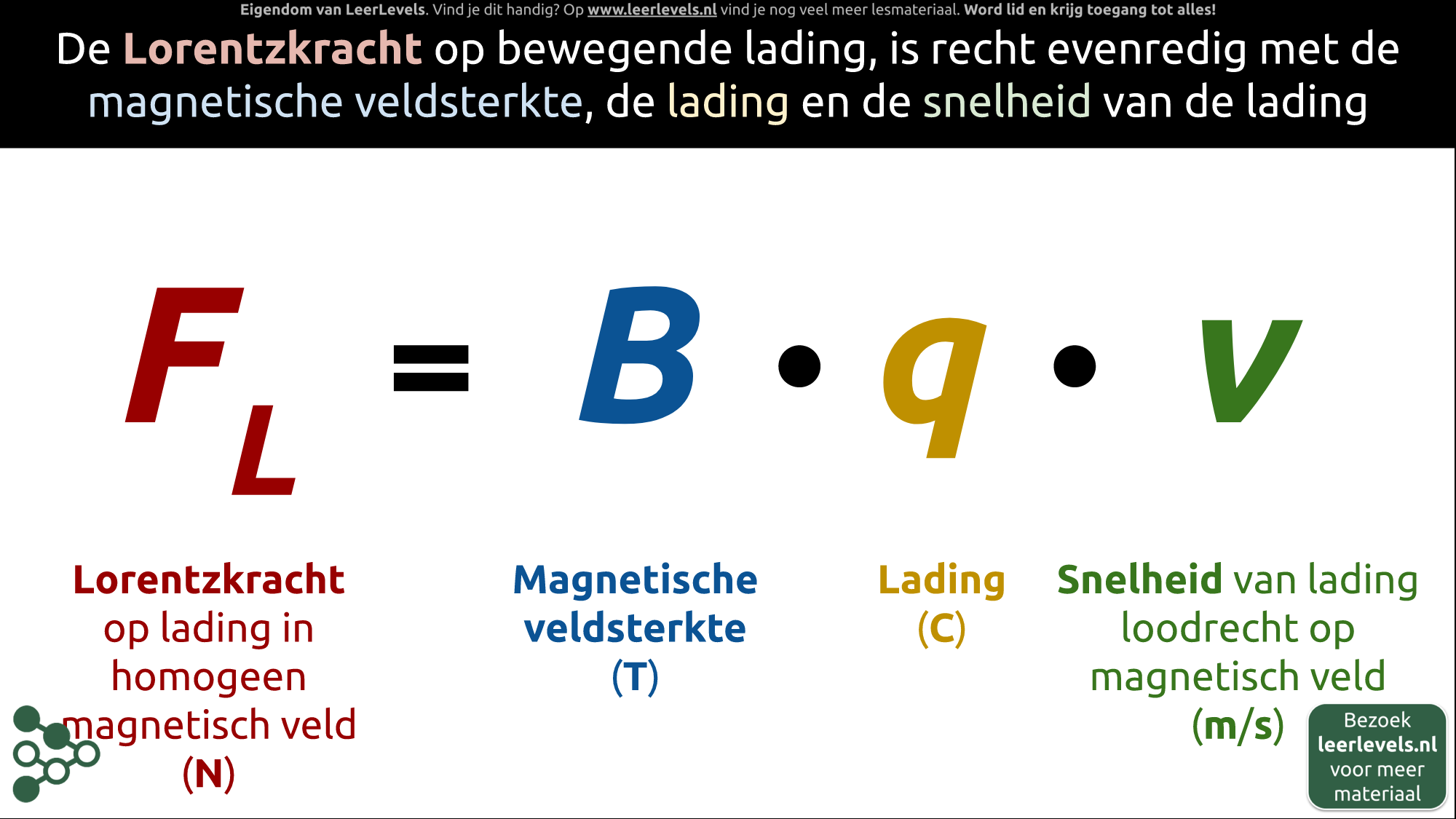
(Afbeelding: Animatie voor Lorentzkracht lading formule)

Linkerhandregel Lorentzkracht

Om de richting te onthouden van de Lorentzkracht (FL), het magnetische veld (B) en de stroom (I), kun je met je linkerhand een pistool na doen. Je duim geeft de richting van de kracht aan omdat dit je sterkste vinger is. Daarnaast geeft je wijsvinger de richting van B aan en je middelvinger de richting van I. Deze drie vingers moeten loodrecht op elkaar staan. Het is ook mogelijk om in plaats van stroomsterkte de richting van positieve ladingen te gebruiken. Als je te maken hebt met negatieve ladingen, kun je het beste doen alsof het positieve ladingen zijn die de andere kant op bewegen. Onthoud dat de volgorde waarin je de vingers gebruikt samen staat voor FBI, zoals bij een pistool.

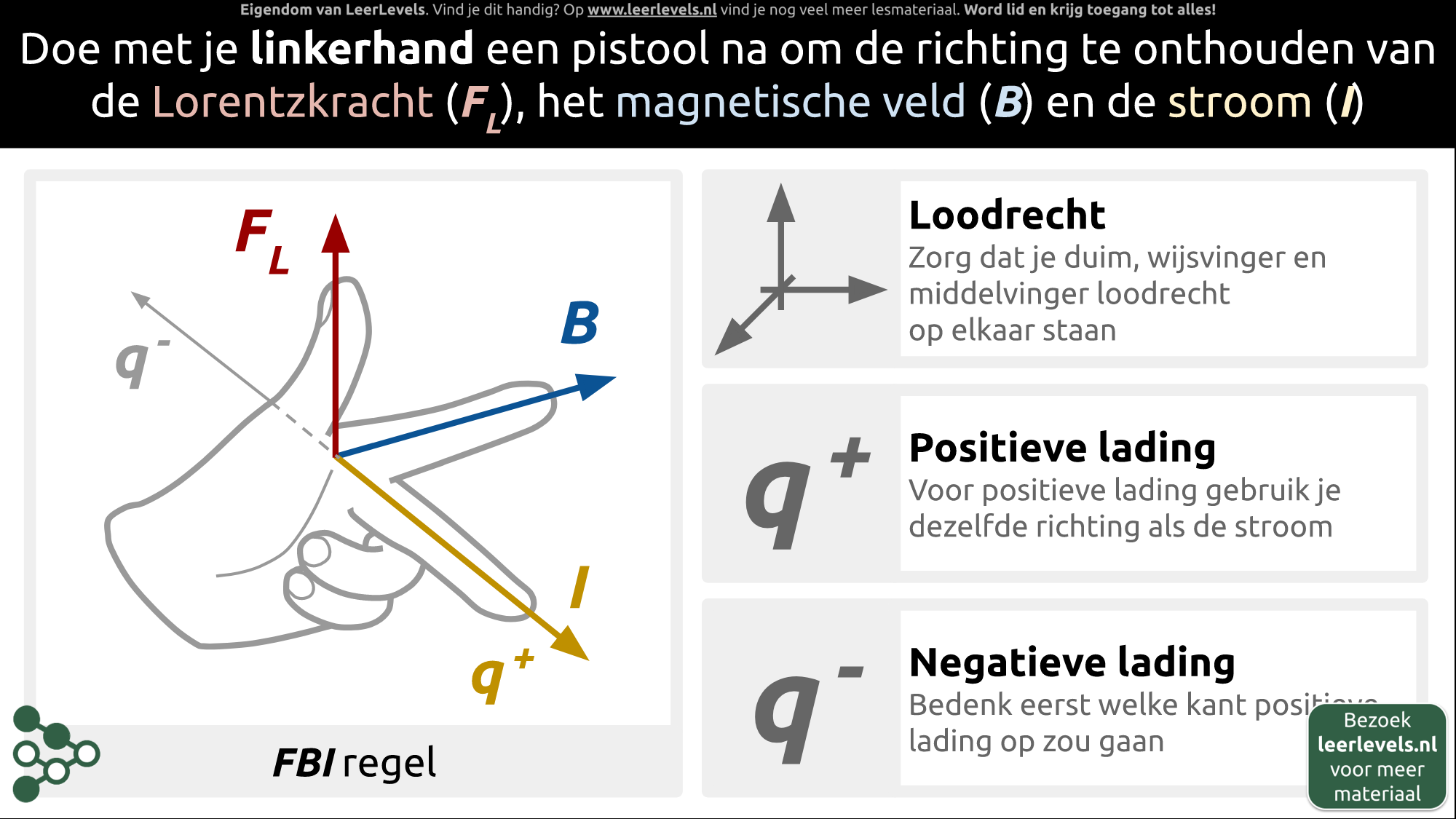
(Afbeelding: Animatie voor Linkerhandregel Lorentzkracht)

Lorentzkracht op winding

Een elektrische winding kan bewegen door de Lorentzkracht, die ontstaat wanneer er stroom door de winding loopt in een magnetisch veld. Stel je voor dat je tegen een getekende winding aankijkt die zich bevindt in een homogeen magnetisch veld. Als er stroom doorheen loopt in de aangegeven richting, ontstaat er een kracht die de winding doet draaien. Dit komt doordat de FBI-regel bepaalt dat de kracht bovenin naar rechts wijst en onderin naar links. Door het moment dat hierdoor ontstaat, draait de winding totdat de kracht niet meer voor een moment zorgt. Op dat moment is er evenwicht en zou de winding tot stilstand komen. Wanneer je op het juiste moment de stroomrichting verandert, kun je een elektromotor maken.

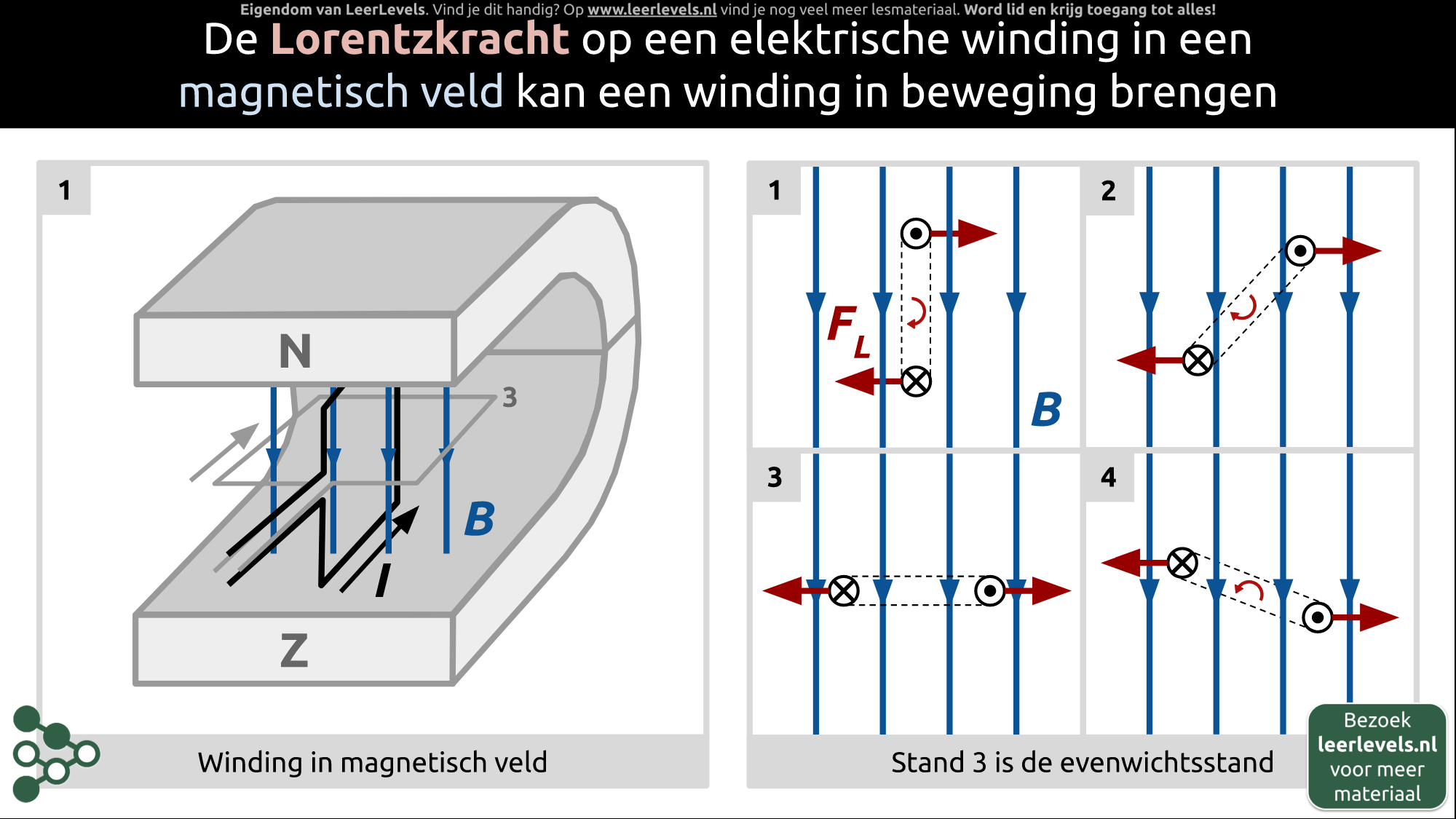
(Afbeelding: Animatie voor Lorentzkracht op winding)

Lorentzkracht als middelpuntzoekende kracht

Als een geladen deeltje door een magnetisch veld vliegt, beweegt het in een cirkel. Dit komt doordat de lorentzkracht het deeltje naar het midden trekt. Als het deeltje een positieve lading heeft en in het veld vliegt, is de richting van de lorentzkracht naar beneden gericht. Hierdoor verandert de bewegingsrichting van het deeltje en ontstaat er een cirkelbeweging. De straal van deze cirkelbeweging kan berekend worden met de formule r = (mv)/(Bq), waarbij m de massa van het deeltje is, v de snelheid, B de veldsterkte en q de lading van het deeltje. Als de lading groter is, zal de cirkel kleiner zijn. Bij een neutraal deeltje is er geen cirkelbeweging omdat de lading nul is. Een lichter deeltje zal ook makkelijker van richting veranderen dan een zwaarder deeltje. De snelheid van het deeltje heeft ook invloed op de grootte van de cirkelbeweging. Een hogere snelheid betekent een grotere cirkel. Hoe kleiner de snelheid, hoe scherper de bocht. Dit komt doordat iets met een lagere snelheid makkelijker van richting verandert.

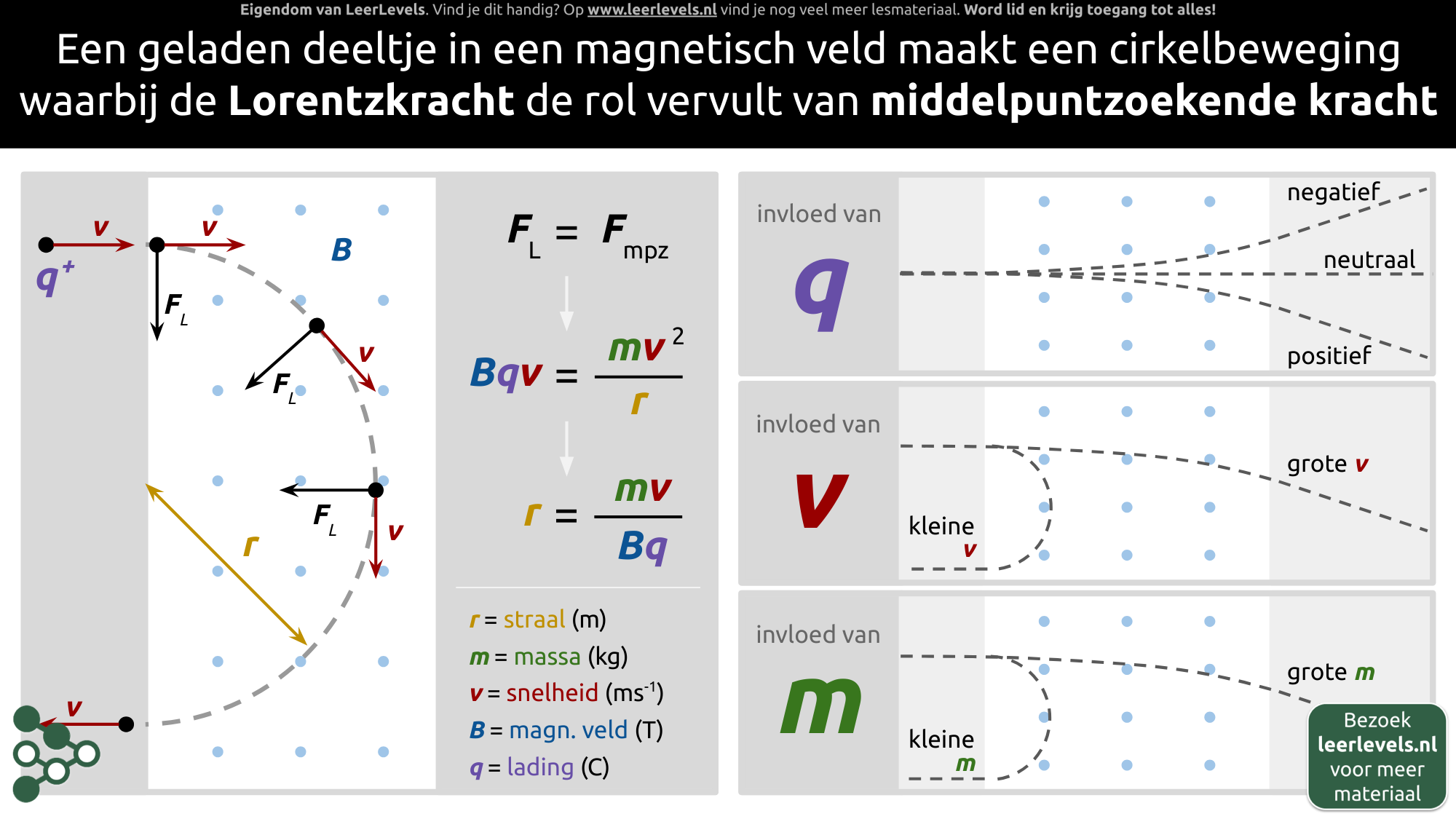
(Afbeelding: Animatie voor Lorentzkracht als middelpuntzoekende kracht)

Terug naar overzicht Meld je aan

Luchtwrijving

Luchtwrijving concept

Luchtwrijving ontstaat als iets door de lucht beweegt en de lucht opzij duwt. Dit zorgt voor weerstand. Het maakt uit welke vorm het bewegende voorwerp heeft. Een hoekig voorwerp, zoals een auto, zorgt voor meer weerstand dan een gestroomlijnde auto, zoals een Tesla.

Dit geldt ook voor vliegtuigen, waarbij de vorm van het vliegtuig van invloed is op de weerstand die het heeft in de lucht. Als de lucht makkelijk om het voorwerp heen kan bewegen, zal de weerstand kleiner zijn.

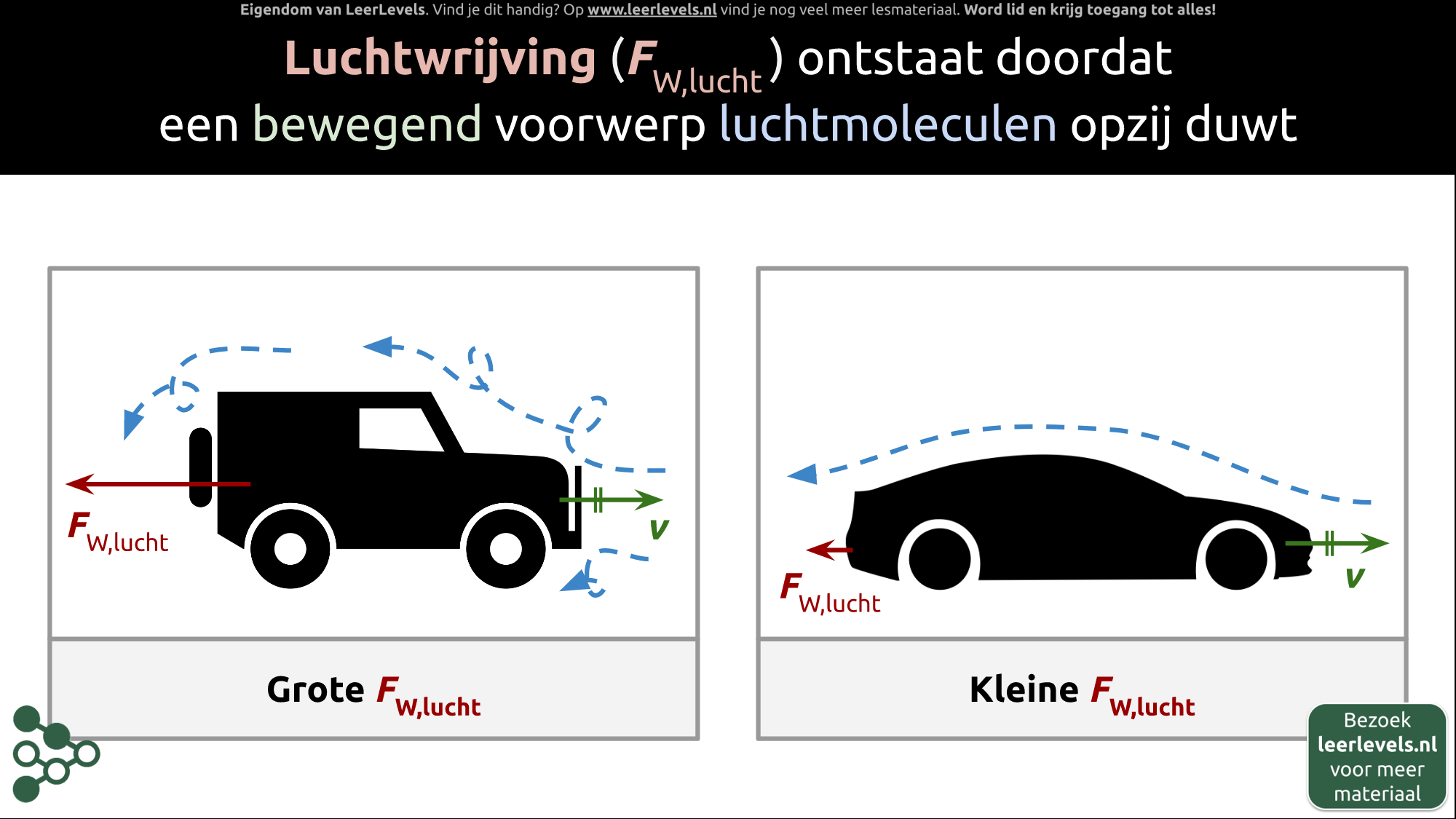
(Afbeelding: Animatie voor Luchtwrijving concept)

Luchtwrijving formule

De luchtwrijving hangt af van verschillende dingen. We gebruiken een formule met letters en cijfers om dit te berekenen. De luchtwrijving hangt af van hoe dicht de lucht is (ρ), de vorm van het voorwerp (Cw en A) en hoe snel het voorwerp gaat (v). De lucht is meestal ongeveer één kilogram per kubieke meter, maar dit kan soms veranderen als er veel druk is. De vorm van het voorwerp speelt ook een rol in de luchtwrijving. Een kubus heeft bijvoorbeeld meer luchtwrijving dan een bol omdat de vorm anders is. Het frontale oppervlak (A) is waar de wind tegenaan botst als het voorwerp door de lucht gaat. Bijvoorbeeld, een kubus heeft een vierkant frontaal oppervlak en een bol heeft een cirkelvormig frontaal oppervlak. Als we de snelheid (v) kennen, moeten we die vermenigvuldigen met zichzelf (kwadrateren) in de formule. De luchtwrijving is altijd in de tegenovergestelde richting van de snelheid.

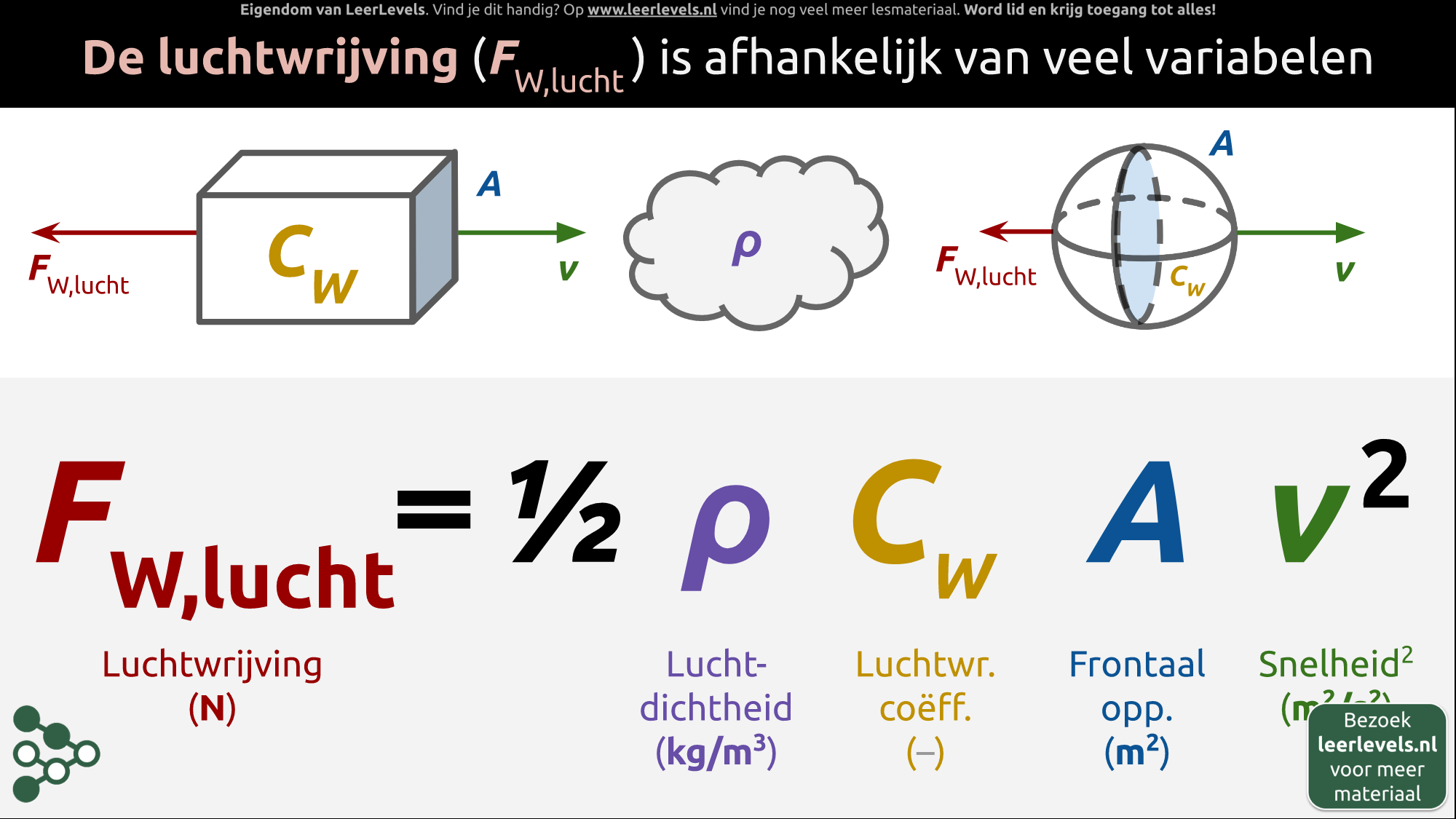
(Afbeelding: Animatie voor Luchtwrijving formule)

Luchtwrijvingscoëfficiënt

De luchtwrijvingscoëfficiënt is een getal dat vertelt hoe lastig het is voor lucht om rond een voorwerp te gaan. Dit heeft vooral te maken met de vorm van het voorwerp. Als je bijvoorbeeld een paraplu achter je aan trekt en dezelfde paraplu voor je uit duwt, gaat de tweede situatie makkelijker, omdat de vorm van de paraplu ervoor zorgt dat lucht er beter omheen kan gaan. Ronde vormen zijn beter dan hoekige of vierkante vormen. De luchtwrijvingscoëfficiënt wordt uitgedrukt met symbolen zoals CD.

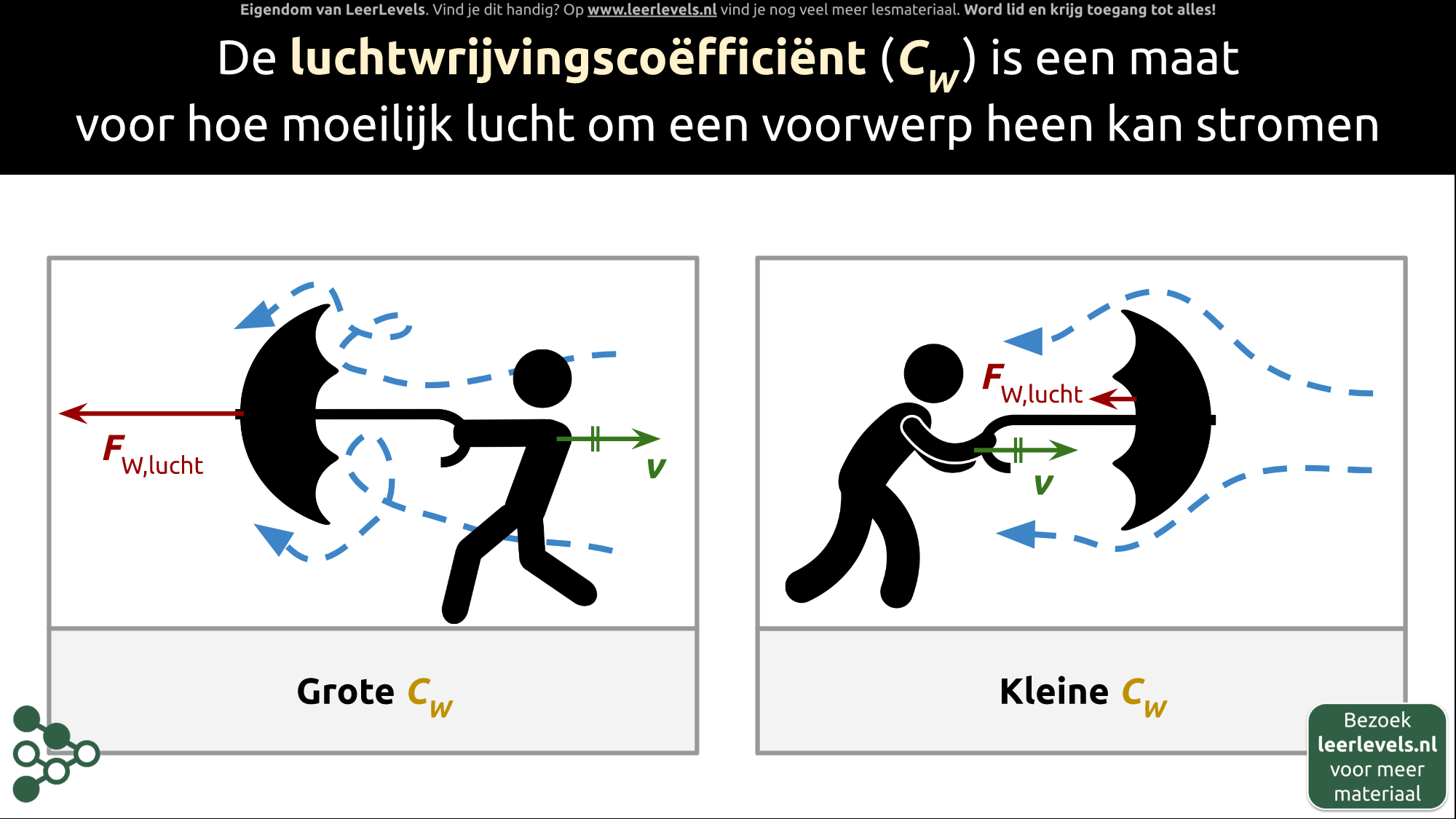
(Afbeelding: Animatie voor Luchtwrijvingscoëfficiënt)

Terug naar overzicht Meld je aan

Magneten

Typen magneten

Verschillende objecten hebben verschillende magnetische eigenschappen. Dit komt door kleine gebiedjes binnen het materiaal, genaamd Weissgebiedjes, die ontstaan door iets dat spin wordt genoemd. Spin heeft invloed op de magnetische eigenschappen van het materiaal. Niet-magnetische materialen hebben geen Weissgebiedjes en kunnen niet gemagnetiseerd worden, zoals een stuk papier of een vaas. Magnetiseerbare materialen hebben magnetische gebiedjes die zich richten naar een externe magneet en elkaar aantrekken. Als de magnetische gebiedjes gelijkgericht zijn, hebben we een echte magneet, bijvoorbeeld een staafmagneet. Het type magnetisme wordt bepaald door de aanwezigheid en het type van Weissgebiedjes. Deze magnetische gebiedjes kunnen veranderen als het materiaal verhit wordt of er een grote impact plaatsvindt.

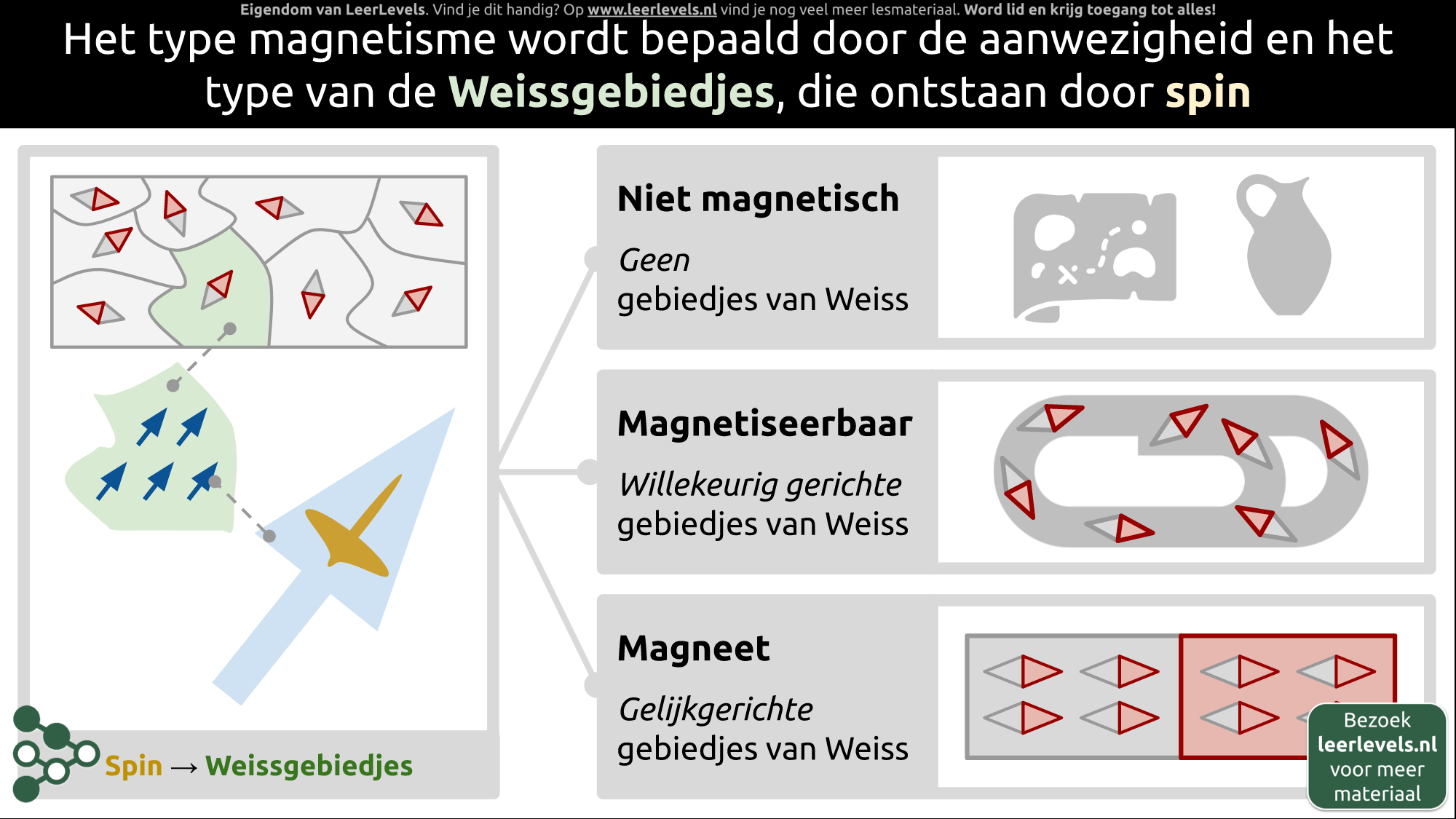
(Afbeelding: Animatie voor Typen magneten)

Terug naar overzicht Meld je aan

Magnetisch veld

Magnetisch veld concept

Een magnetisch veld geeft aan welke kant de noordpool van een magneet wijst. Bij een staafmagneet wordt het magnetisch veld rondom de magneet gecreëerd. Door een kleine magneet, zoals een naaldmagneet, boven de staafmagneet te houden, wijst de naald naar de zuidpool van de staafmagneet. Hieruit kan je de richting van het magnetisch veld bepalen. Dit wordt een magnetische veldlijn genoemd en geldt op elke plaats in de ruimte. Door het experiment op verschillende plaatsen te herhalen, kan je de veldlijnen op die locaties bepalen. Het magnetisch veld is spiegelbeeldig en blijft in dezelfde richting wijzen. De magnetische veldlijnen geven aan waar de noordpool van een naaldmagneet naartoe wijst.

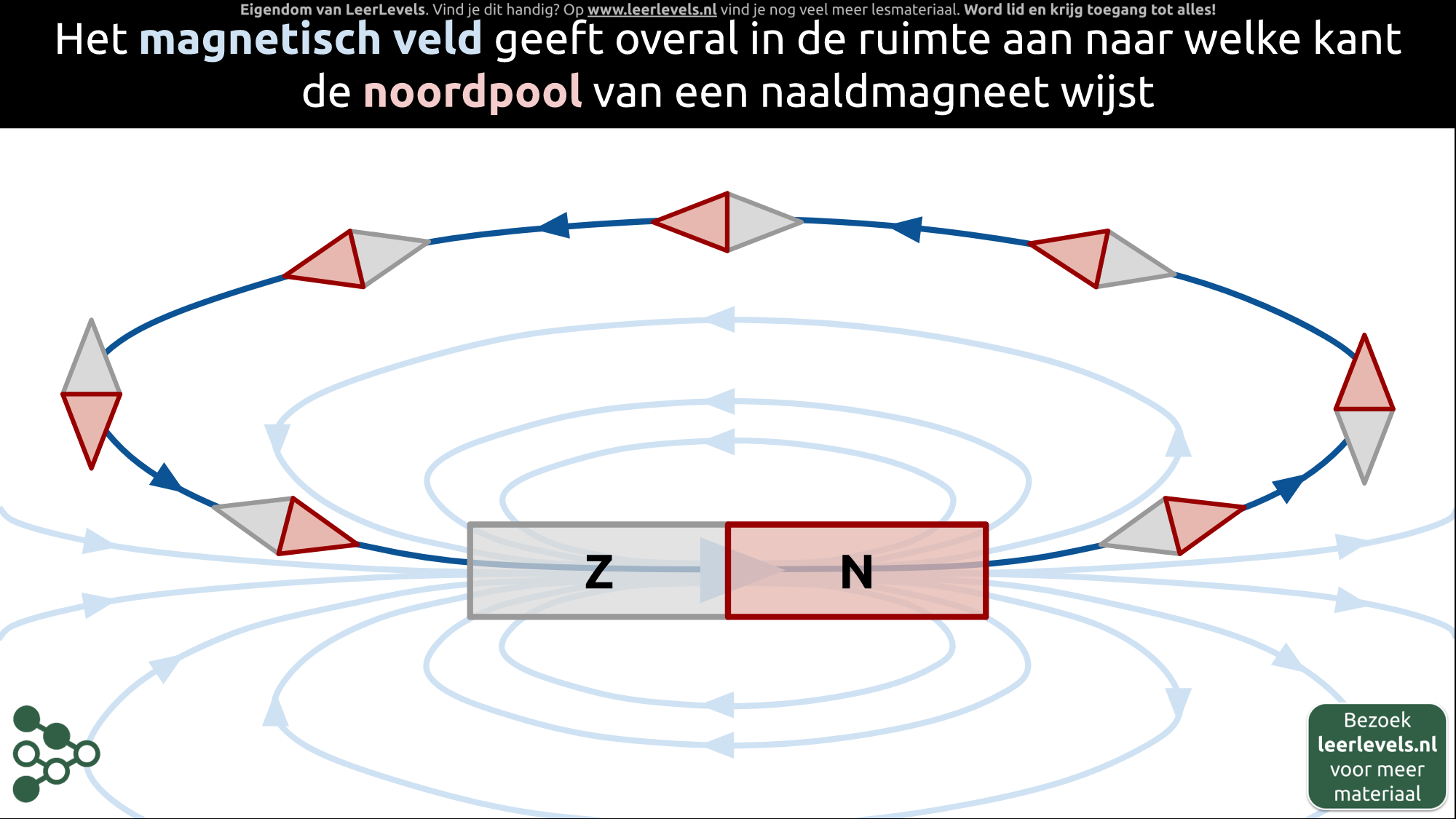
(Afbeelding: Animatie voor Magnetisch veld concept)

Magnetisch veld eigenschappen

Een magnetisch veld heeft eigenschappen die bepalen hoe de magnetische veldlijnen lopen. Buiten een magneet lopen de veldlijnen van noord naar zuid, maar binnen de magneet lopen ze precies andersom, van zuid naar noord en vormen ze een gesloten kring. Hoe dichter bij de magneet, hoe sterker het magnetisch veld is. Dit is te zien aan de veldlijnen die dichter bij elkaar liggen in de buurt van de magneet. Een magneet heeft altijd een noord- en zuidpool. Als je de magneet in tweeën breekt, ontstaan er twee nieuwe magneten met elk een noord- en zuidpool.

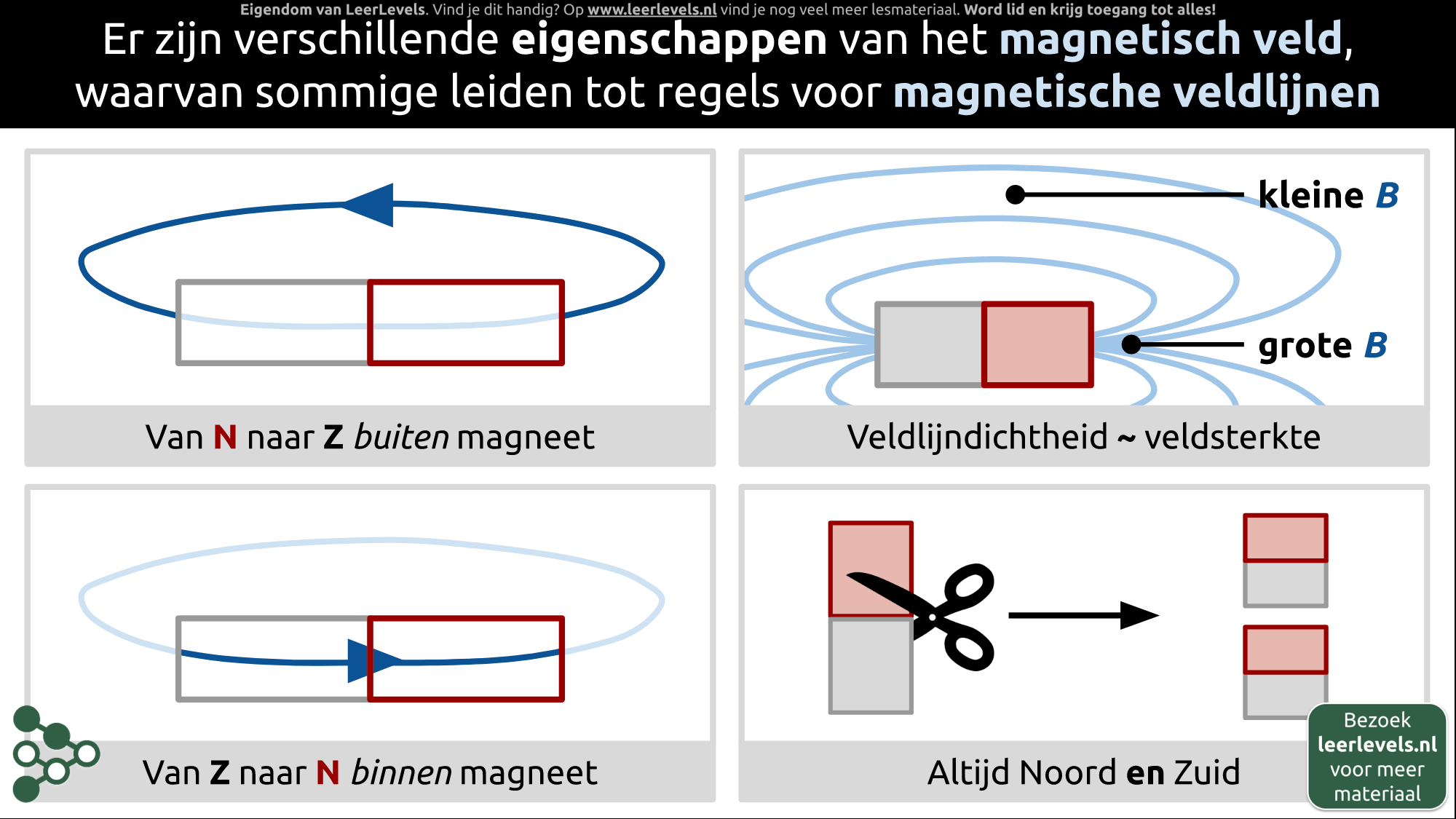
(Afbeelding: Animatie voor Magnetisch veld eigenschappen)

Magnetisch veld draad

Wanneer er stroom door een draad stroomt, ontstaat er een magnetisch veld rondom de draad. Dit kun je zichtbaar maken door magneten neer te leggen die zich richten naar de locatie van het magnetisch veld. De sterkte van het magnetisch veld is recht evenredig met de stroomsterkte en omgekeerd evenredig met de afstand tot de draad. Dit betekent dat hoe groter de stroomsterkte is, hoe sterker het magnetisch veld wordt en hoe dichterbij de draad, hoe sterker het magnetisch veld is. Het magnetisch veld heeft invloed op de lading die door de draad stroomt.

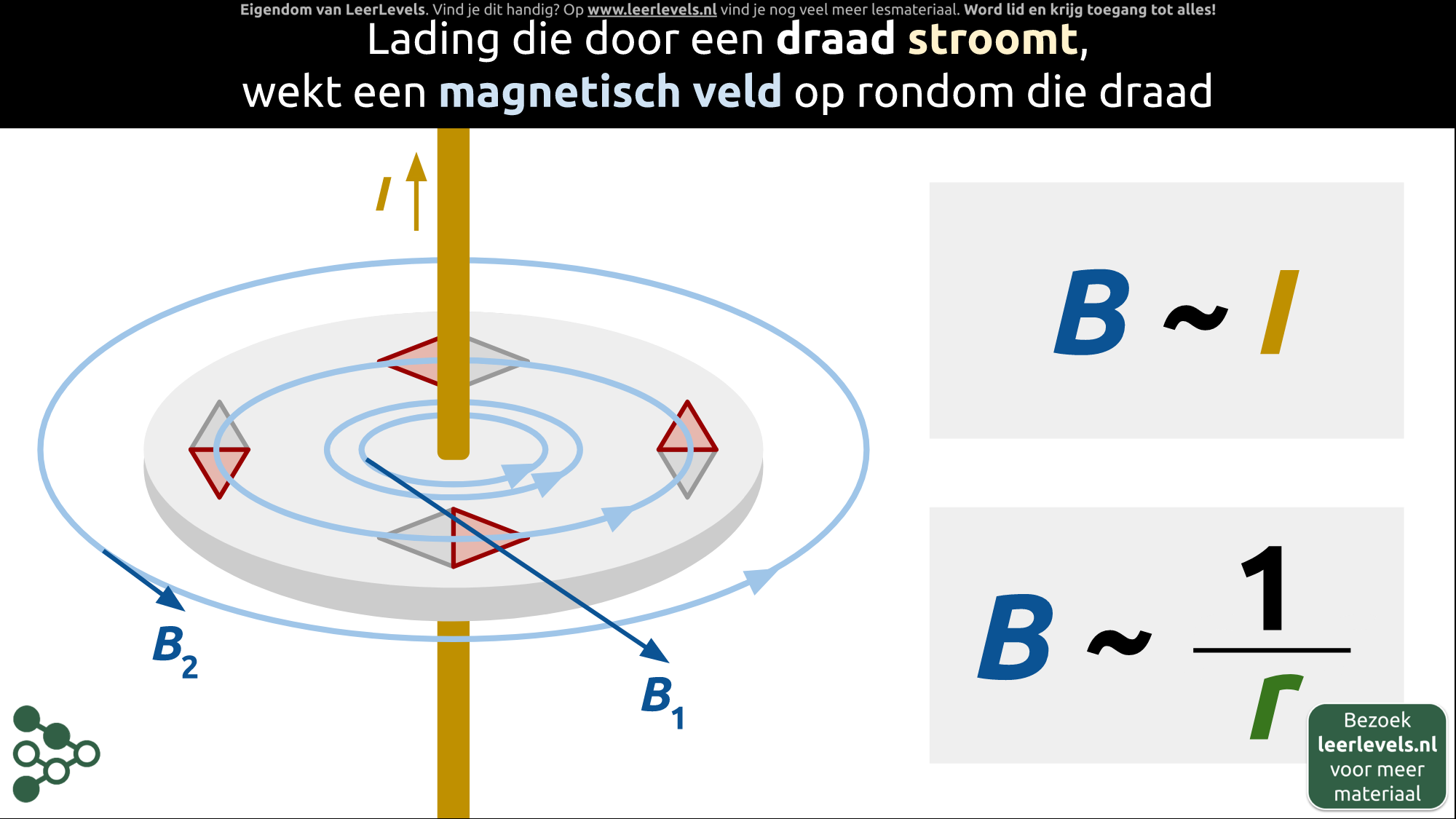
(Afbeelding: Animatie voor Magnetisch veld draad)

Magnetisch veld spoel

Wanneer er stroom door een spoel loopt, wordt er een magnetisch veld binnen de spoel opgewekt. Dit veld is binnen de spoel ongeveer homogeen. Er zijn twee zaken die je moet weten over het magnetisch veld dat in de spoel ontstaat.

Ten eerste is de veldsterkte recht evenredig met de stroomsterkte. Als je dus een grotere stroom door de spoel laat lopen, is de veldsterkte ook groter.

Ten tweede beïnvloedt het aantal windingen van de spoel de sterkte van het veld. Bijvoorbeeld, als je dezelfde stroom door een spoel met twee keer zoveel windingen stuurt, is het magnetische veld ook twee keer zo sterk. Zowel de stroomsterkte I als het aantal windingen N hebben invloed op de magnetische veldsterkte B.

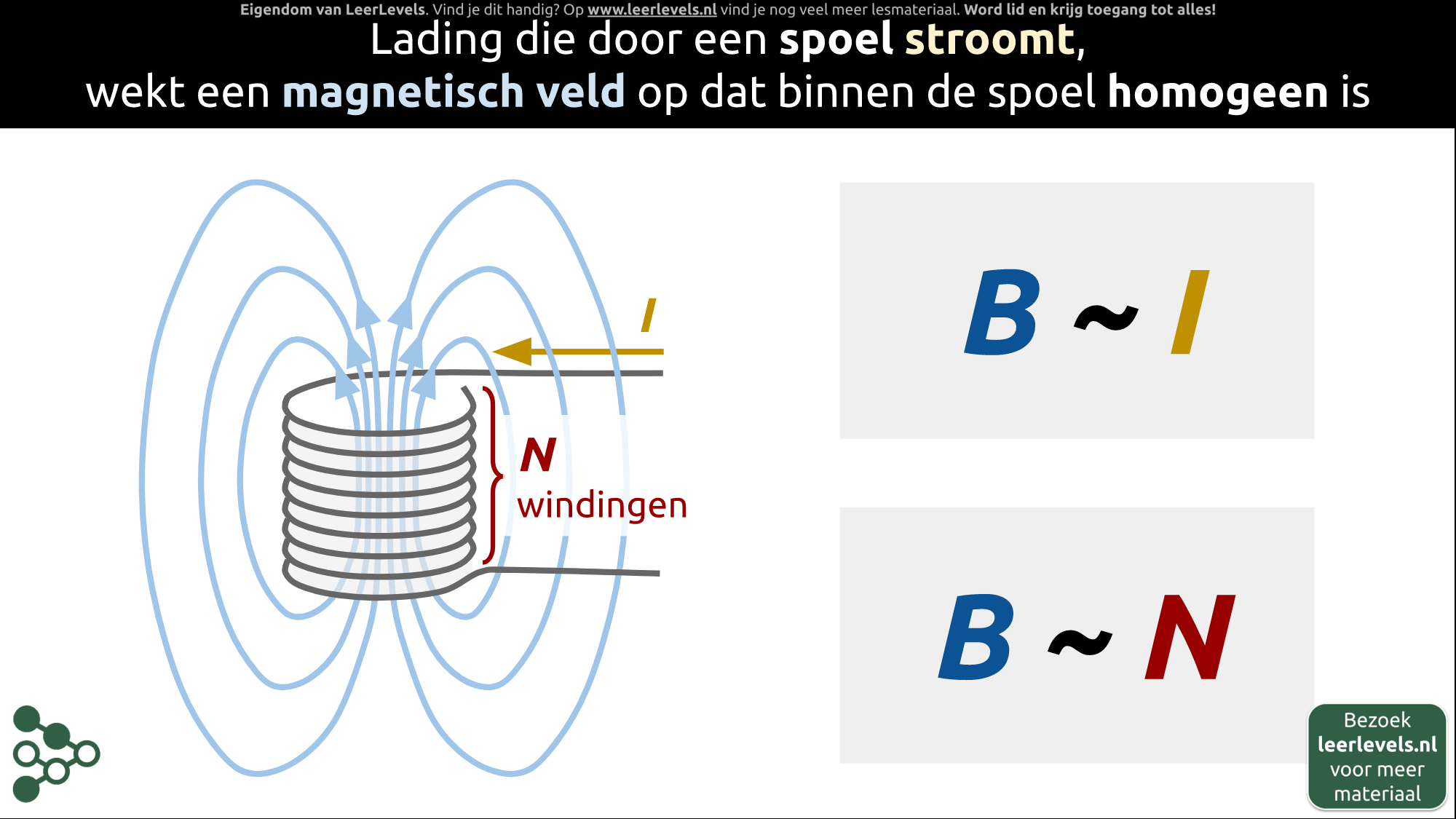
(Afbeelding: Animatie voor Magnetisch veld spoel)

Terug naar overzicht Meld je aan

Magnetische flux

Magnetische flux concept

Magnetische flux meet hoeveel magnetische veldlijnen door een oppervlak gaan. Bij een spoel waar de veldlijnen parallel lopen, is de flux nul. Als de spoel schuin staat of de veldlijnen slechts deels erdoorheen gaan, is de flux klein. Als de winding loodrecht op de veldlijnen staat en alle veldlijnen erdoorheen gaan, is de flux groot. Dit is te vergelijken met het vullen van een emmer. De magnetische flux wordt uitgedrukt in de eenheid Weber (Wb) en is gelijk aan het oppervlak waar de veldlijnen doorheen gaan vermenigvuldigd met de magnetische inductie (B) loodrecht op dat oppervlak.

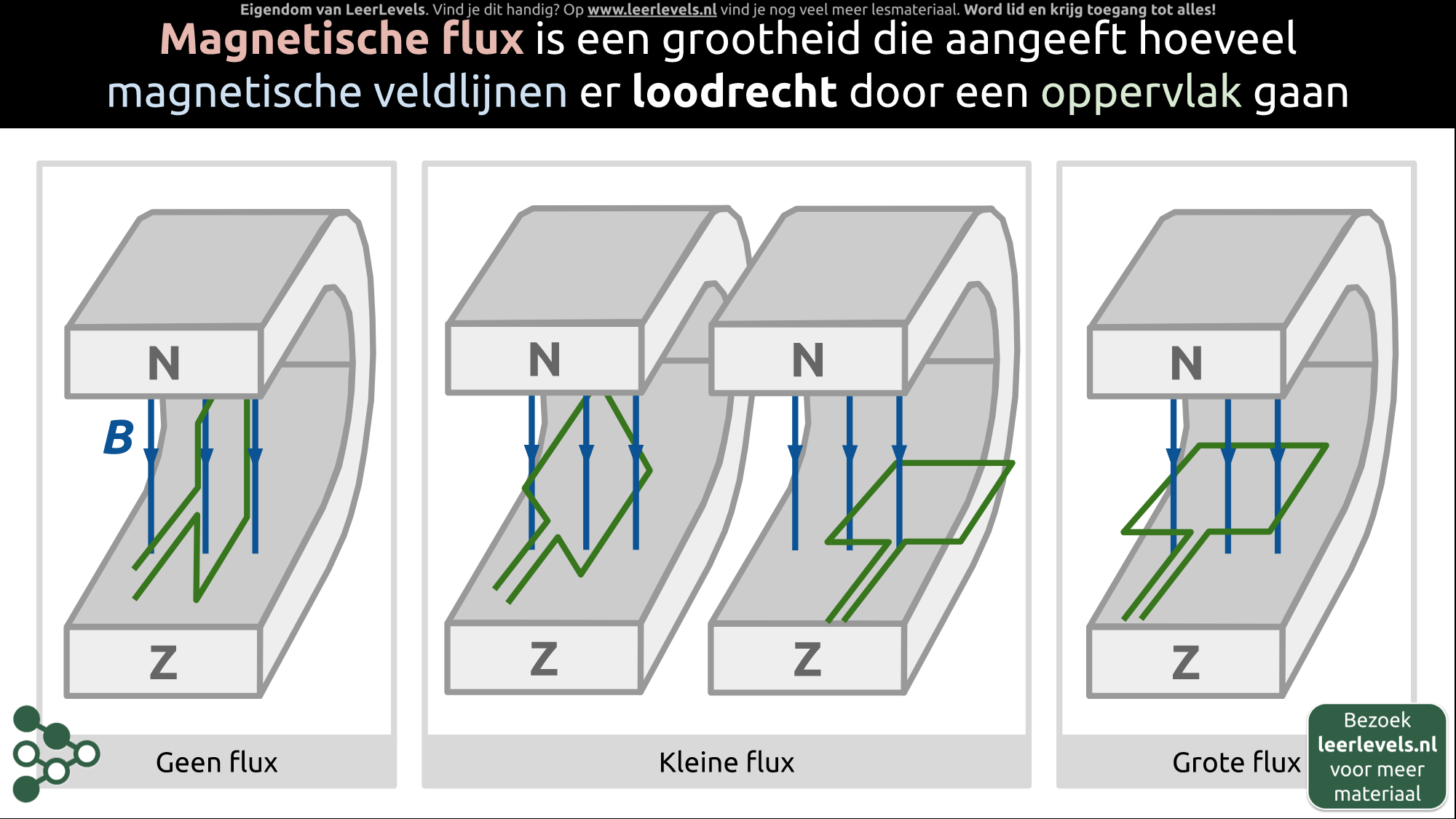
(Afbeelding: Animatie voor Magnetische flux concept)

Magnetische flux formule

De magnetische flux door een spoel is afhankelijk van de grootte van de spoel en de sterkte van het magnetisch veld dat er loodrecht op staat. Dit wordt aangeduid met het symbool φ en wordt gemeten in weber. De formule is φ = B · A, waarbij B de sterkte van het loodrechtstaande magnetische veld in tesla is en A het oppervlak van de spoel in vierkante meter is. Als het magnetisch veld niet loodrecht staat, moet de hoek α tussen het veld en de normaal op het oppervlak worden berekend en moet B worden berekend als B⟂ = B · cos(α).

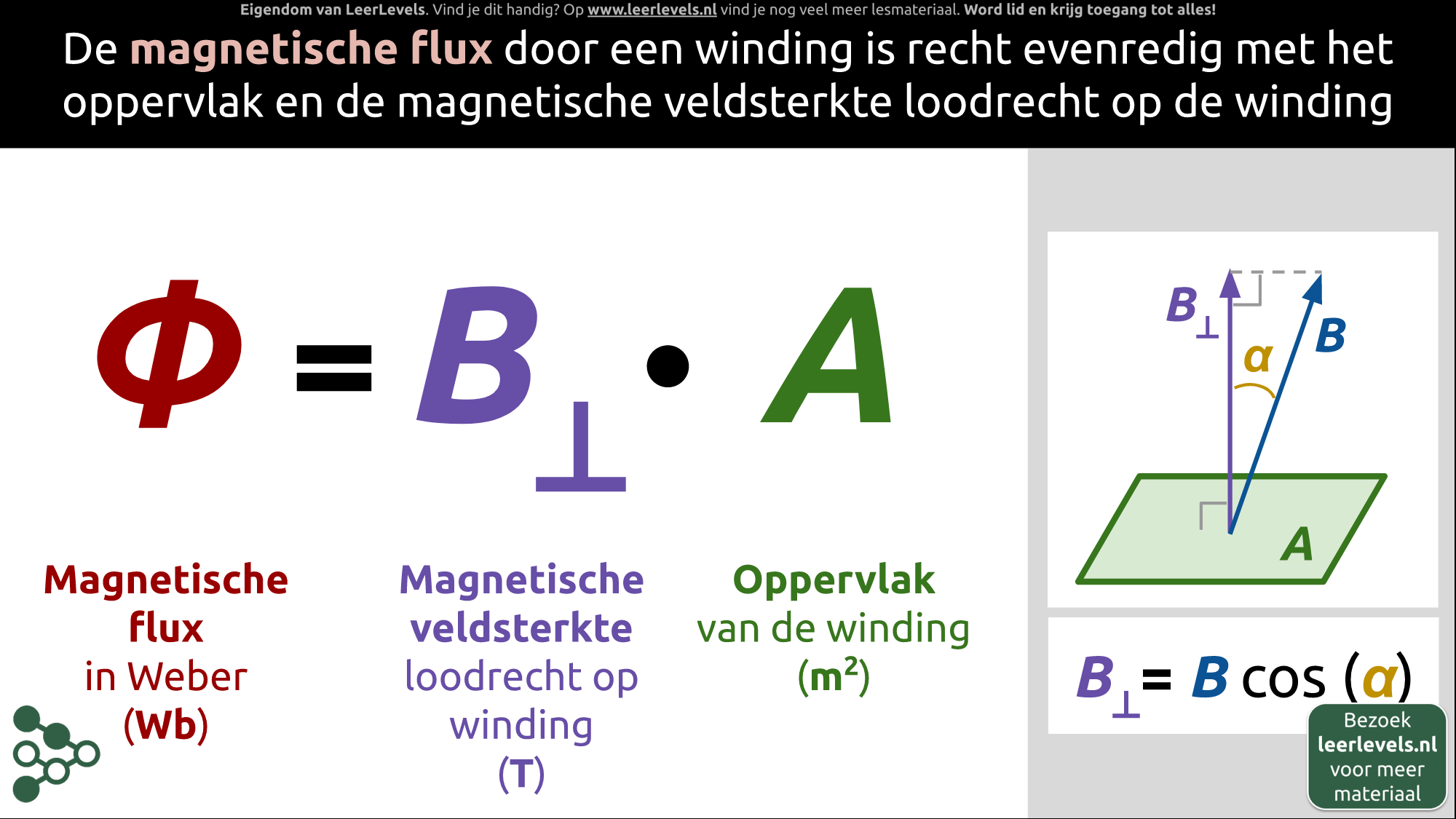
(Afbeelding: Animatie voor Magnetische flux formule)

Terug naar overzicht Meld je aan

Magnetisme

Magneten hebben een noordpool en een zuidpool. Een magneet kan niet alleen een noordpool of een zuidpool hebben; beide polen moeten aanwezig zijn. Als je deze magneten bij elkaar houdt, zul je merken dat ze elkaar aantrekken wanneer de polen verschillend zijn, oftewel de noordpool trekt de zuidpool aan en vice versa. Maar als je dezelfde polen bij elkaar houdt, zullen ze elkaar juist afstoten.

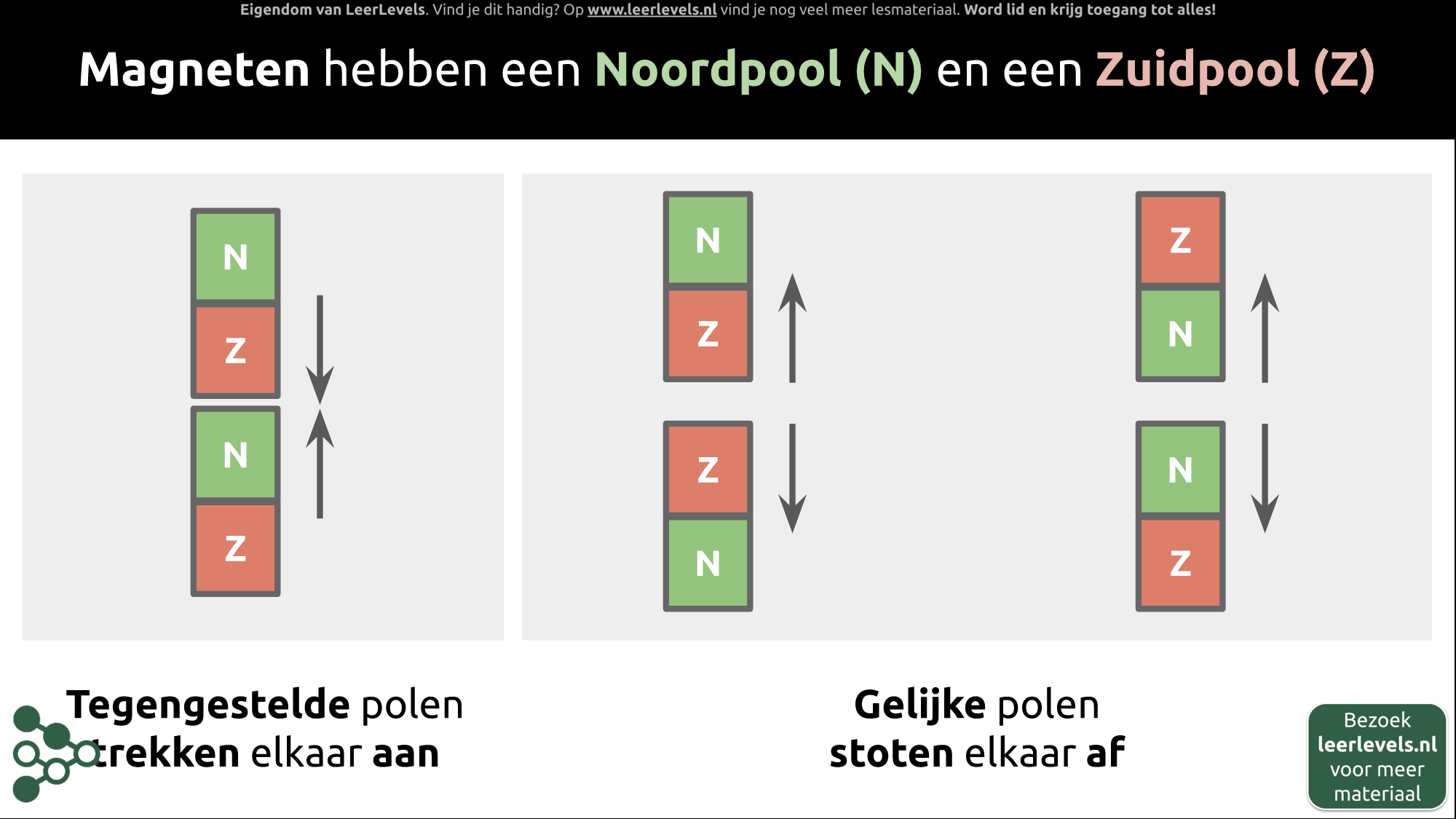
(Afbeelding: Animatie voor Magnetisme)

Magnetisme concept

Magnetisme is het verschijnsel waarbij magneten of gemagnetiseerde voorwerpen kracht op elkaar uitoefenen. Elke magneet heeft altijd een noordpool en een zuidpool en kan in verschillende vormen voorkomen, zoals een staafmagneet, naaldmagneet of hoefijzermagneet. De kleuren op de magneet geven aan welke kant de noord- en zuidpool is, waarbij rood bijna altijd de noordpool aanduidt. Wanneer je twee magneten bij elkaar brengt, oefenen ze kracht op elkaar uit. Dit leidt tot aantrekking bij tegengestelde polen en tot afstoting bij gelijke polen.

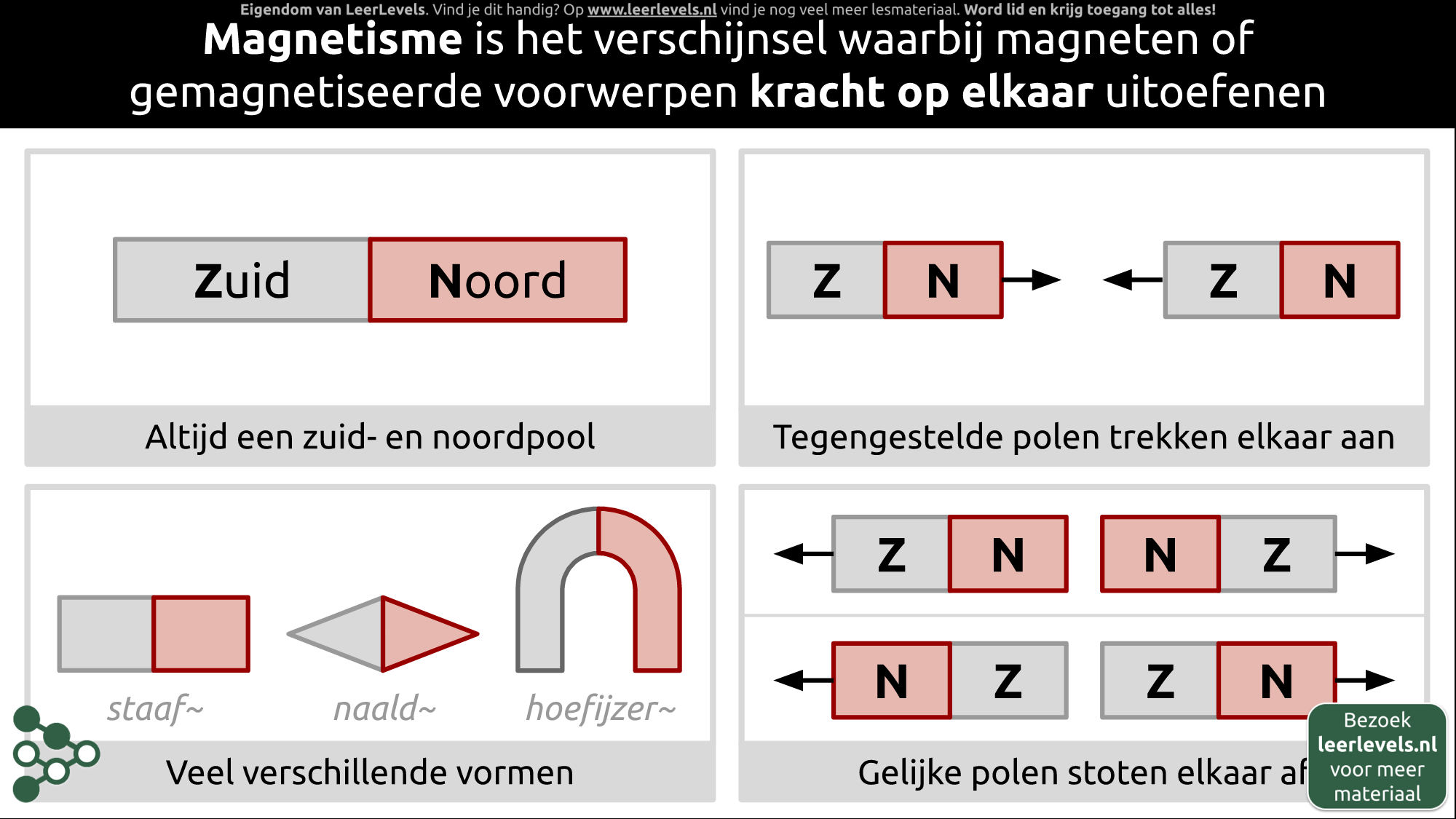
(Afbeelding: Animatie voor Magnetisme concept)

Terug naar overzicht Meld je aan

Massa

Kilogram

Een kilogram is de SI-eenheid voor massa en komt ongeveer overeen met de massa van een liter water. We kunnen bijvoorbeeld zeggen dat een volwassen persoon ongeveer 80 kilogram weegt. De kilogram wordt gebruikt om de massa van allerlei voorwerpen aan te geven. Soms gebruiken we gram, wat gelijk is aan (1)/(1000) kilogram. Hoewel we soms andere voorvoegsels gebruiken, zoals milligram, is de kilogram de standaardeenheid van massa.

(Afbeelding: Animatie voor Kilogram)

Massa

De massa van een voorwerp is belangrijk, want het bepaalt hoeveel kracht er nodig is om het voorwerp te bewegen. Kleine voorwerpen, zoals golfballen, hebben weinig massa en hebben daarom weinig kracht nodig om te bewegen. Grote voorwerpen, zoals bowlingballen of schepen, hebben meer massa en hebben daarom meer kracht nodig om te bewegen. Dit heeft niets te maken met zwaartekracht of andere krachten. Zelfs in de ruimte zou je meer kracht nodig hebben om een zwaar voorwerp te bewegen dan een lichter voorwerp. De massa van een voorwerp wordt weergegeven met de m-grootheid en de eenheid kilogram.

(Afbeelding: Animatie voor Massa)

Massa, gewicht en zwaartekracht

Massa, zwaartekracht en gewicht zijn drie verschillende dingen die vaak door elkaar gehaald worden. Massa is de eigenschap van een voorwerp die het altijd heeft, ongeacht of het stil staat of beweegt. Zwaartekracht is de kracht waarmee de aarde of andere hemellichamen voorwerpen aantrekken en wordt berekend als massa maal de versnelling van de zwaartekracht ($Fg = m · g$). Gewicht is de kracht waarmee een voorwerp op de ondergrond of ophanging drukt en wordt berekend als zwaartekracht. Als het voorwerp stil staat, is het gewicht gelijk aan de zwaartekracht. Als het voorwerp versnelt, heeft het meer kracht nodig om te versnellen en wordt het gewicht groter. Het is belangrijk om te onthouden dat de eenheid van gewicht niet kilogram is, maar newton ($1 kg \equiv 9,81 N$).

(Afbeelding: Animatie voor Massa, gewicht en zwaartekracht)

Terug naar overzicht Meld je aan

Massadefect

Massadefect concept

Het massadeffect verwijst naar de massa die verdwijnt tijdens een vervalreactie, waarbij deze massa wordt omgezet in energie. Neem bijvoorbeeld uranium (element nummer 92, afgekort als U). Dit element ondergaat alfaverval en verandert hierdoor in thorium-231 en helium-4. Opmerkelijk genoeg blijkt dat de massa van de ontstane producten kleiner is dan die van het oorspronkelijke uranium. Dit verschil in massa wordt het massadeffect genoemd. De ontbrekende massa is omgezet in energie, die verschillende vormen kan aannemen: het kan kinetische energie zijn van de vrijgekomen deeltjes, straling zoals gammastraling, of warmte die kan worden opgevangen.

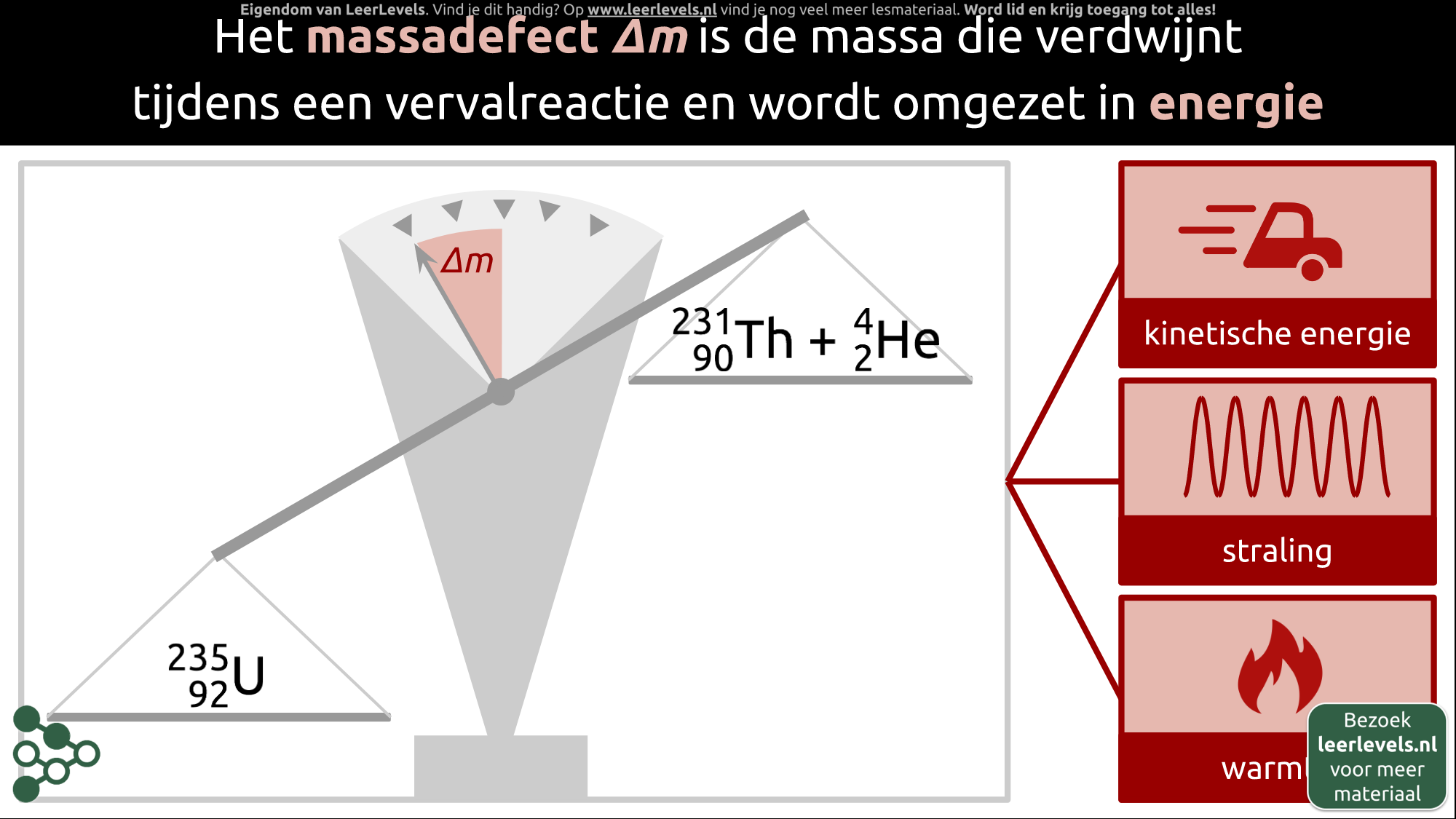
(Afbeelding: Animatie voor Massadefect concept)

Massadefect formule

De energie die vrijkomt bij een kernreactie wordt bepaald door het massadefect en de lichtsnelheid. Deze energie is gelijk aan het massadefect in kilogram vermenigvuldigd met het kwadraat van de lichtsnelheid:

Δ E = Δ m · c²

De lichtsnelheid c heeft in SI-eenheden al een aanzienlijke waarde, namelijk 3 × 10⁸ m/s. Het kwadraat hiervan is nog veel groter, namelijk 9 × 10¹⁶, wat bijna 10¹⁷ is. Dit houdt in dat voor elke kilogram die verdwijnt, er 10¹⁷ Joule vrijkomt, wat zeer veel is. Dit proces wordt onder andere gebruikt om kerncentrales te laten functioneren.

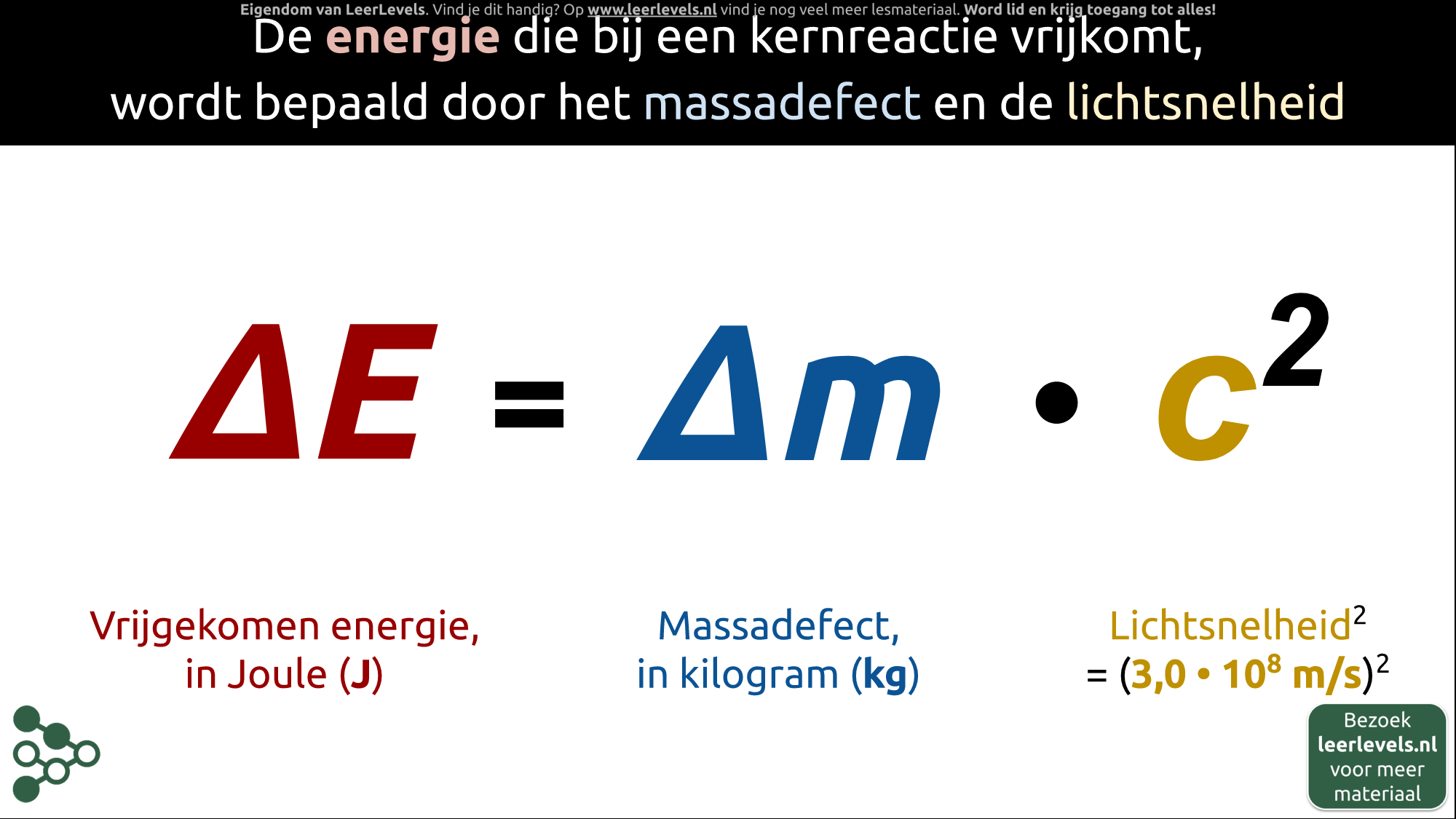
(Afbeelding: Animatie voor Massadefect formule)

Terug naar overzicht Meld je aan

Materiaaleigenschappen

Elk materiaal heeft eigenschappen, die we stofeigenschappen noemen. Deze eigenschappen kunnen we in drie categorieën verdelen: chemisch, fysisch en mechanisch. Chemische eigenschappen zijn dingen als kleur, geur, smaak, giftigheid en brandbaarheid. Deze eigenschappen kun je al met een paar moleculen zien. Fysische eigenschappen zijn bijvoorbeeld dichtheid, fase, soortelijke warmte, smeltpunt en elektrische weerstand en krijgen we pas goed te zien als we meerdere moleculen hebben. We kunnen deze eigenschappen wel op molecuulniveau bepalen. Mechanische eigenschappen zeggen iets over elasticiteit, buigsterkte, treksterkte, duwsterkte en brosheid. We kunnen deze eigenschappen minder goed op moleculeniveau bepalen, omdat ze meer over het hele materiaal gaan. Toch weten we ook bij enkele moleculen al iets over deze eigenschappen. Kortom, elk materiaal heeft verschillende stofeigenschappen.

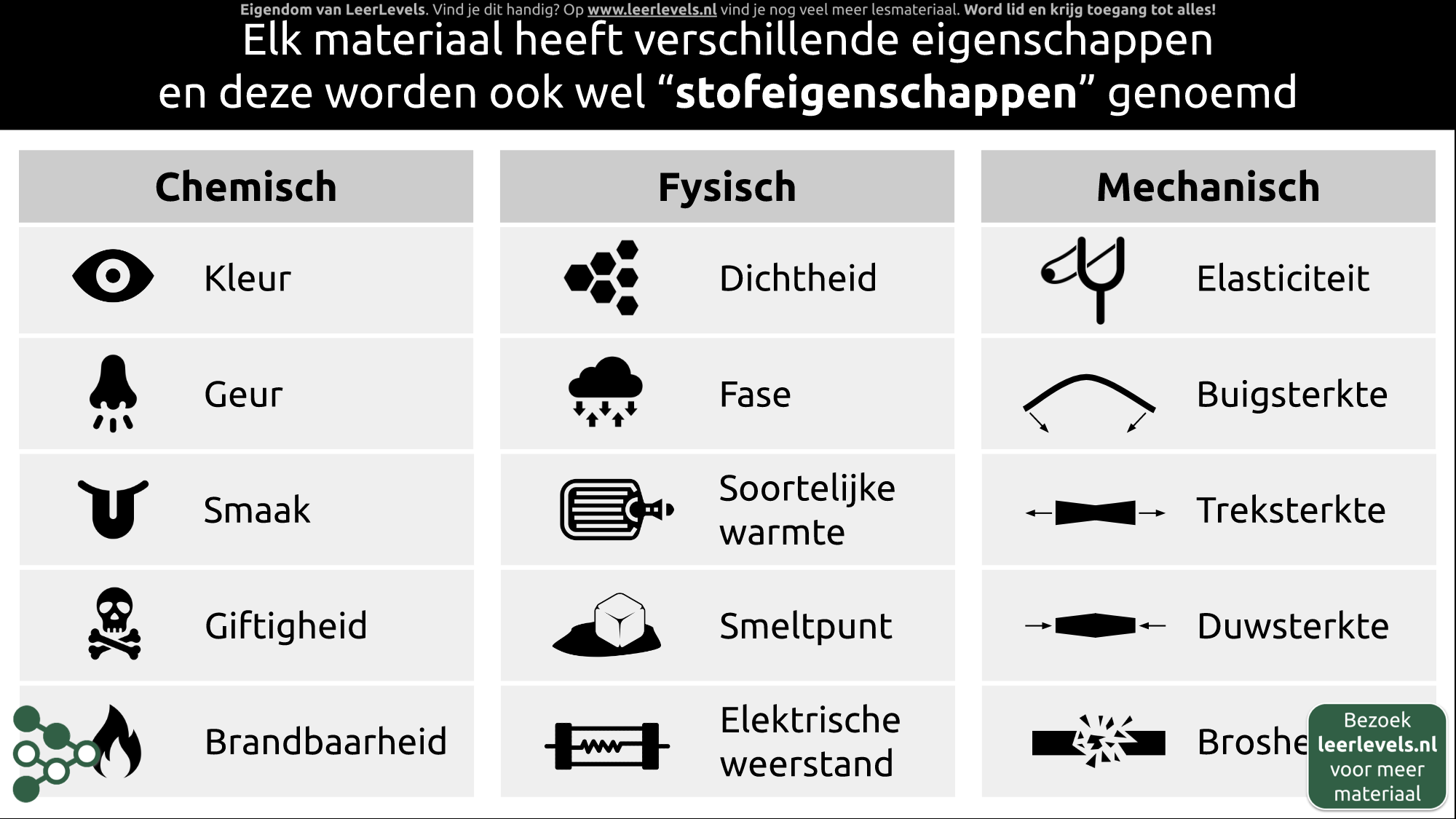
(Afbeelding: Animatie voor Materiaaleigenschappen)

Terug naar overzicht Meld je aan

Mechanische energie

Mechanische en overige energie

De totale energie in een systeem, die bestaat uit kinetische en potentiële energie, wordt mechanische energie genoemd. Als er geen externe krachten arbeid uitoefenen op het systeem, blijft de mechanische energie constant. Met deze energie kan arbeid worden verricht. Mechanische energie is onder te verdelen in twee categorieën: kinetische energie en potentiële energie.

Potentiële energie heeft verschillende vormen: veerenergie en gravitatie-energie zijn hier voorbeelden van. Zwaarte-energie is een specifieke vorm van gravitatie-energie die van toepassing is op aarde.

Behalve mechanische energie zijn er ook andere energievormen, zoals warmte (op microscopisch niveau vergelijkbaar met kinetische energie), elektrische energie en chemische energie (op microscopisch niveau vormen vergelijkbaar met potentiële energie).

Verder is er nog EM-straling – waarvan het zichtbare deel ook wel "licht" wordt genoemd – wat bestaat uit elektromagnetische velden. Tot slot is er kernenergie. Elektromagnetische straling en kernenergie zijn niet gerelateerd aan potentiële energie.

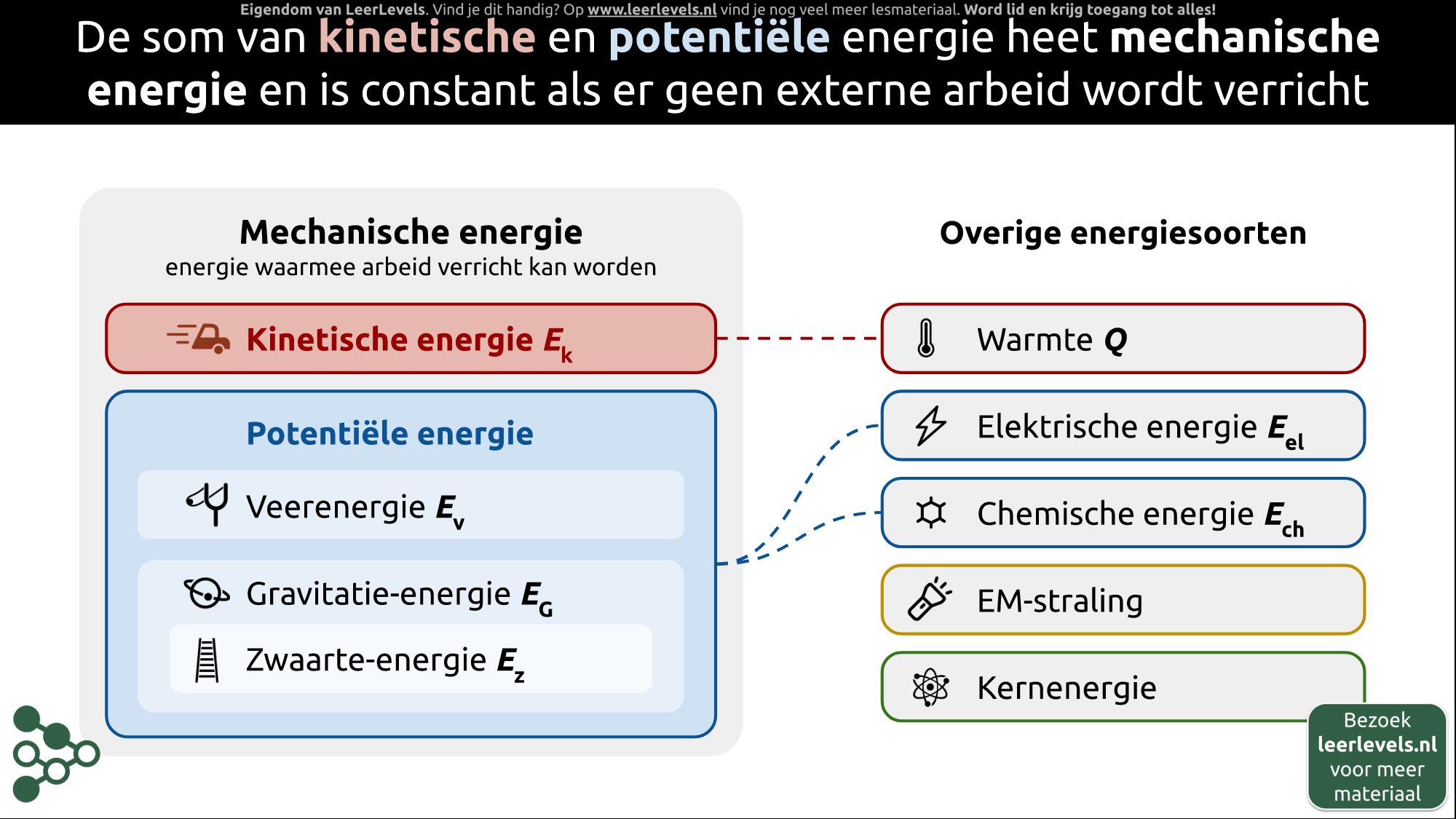
(Afbeelding: Animatie voor Mechanische en overige energie)

Terug naar overzicht Meld je aan

Mechanische spanning

Mechanische spanning concept

Mechanische spanning betekent hoeveel trekkracht er op een draad wordt uitgeoefend per oppervlakte. Je kunt dit vergelijken met een gewicht dat aan een draad hangt. De oppervlakte van de draad en de zwaartekracht van het gewicht bepalen de trekkracht op de draad. Als de oppervlakte groot is en het gewicht zwaar, dan is de spanning normaal. Als het gewicht kleiner wordt, neemt de spanning af. Maar als de draad dunner wordt, blijft de spanning gelijk. Als je een groot gewicht aan een dunne draad hangt, is er een grote spanning omdat er veel kracht op een klein oppervlak moet worden verdeeld. Je drukt de mechanische spanning uit met de formule stress = (force)/(area).

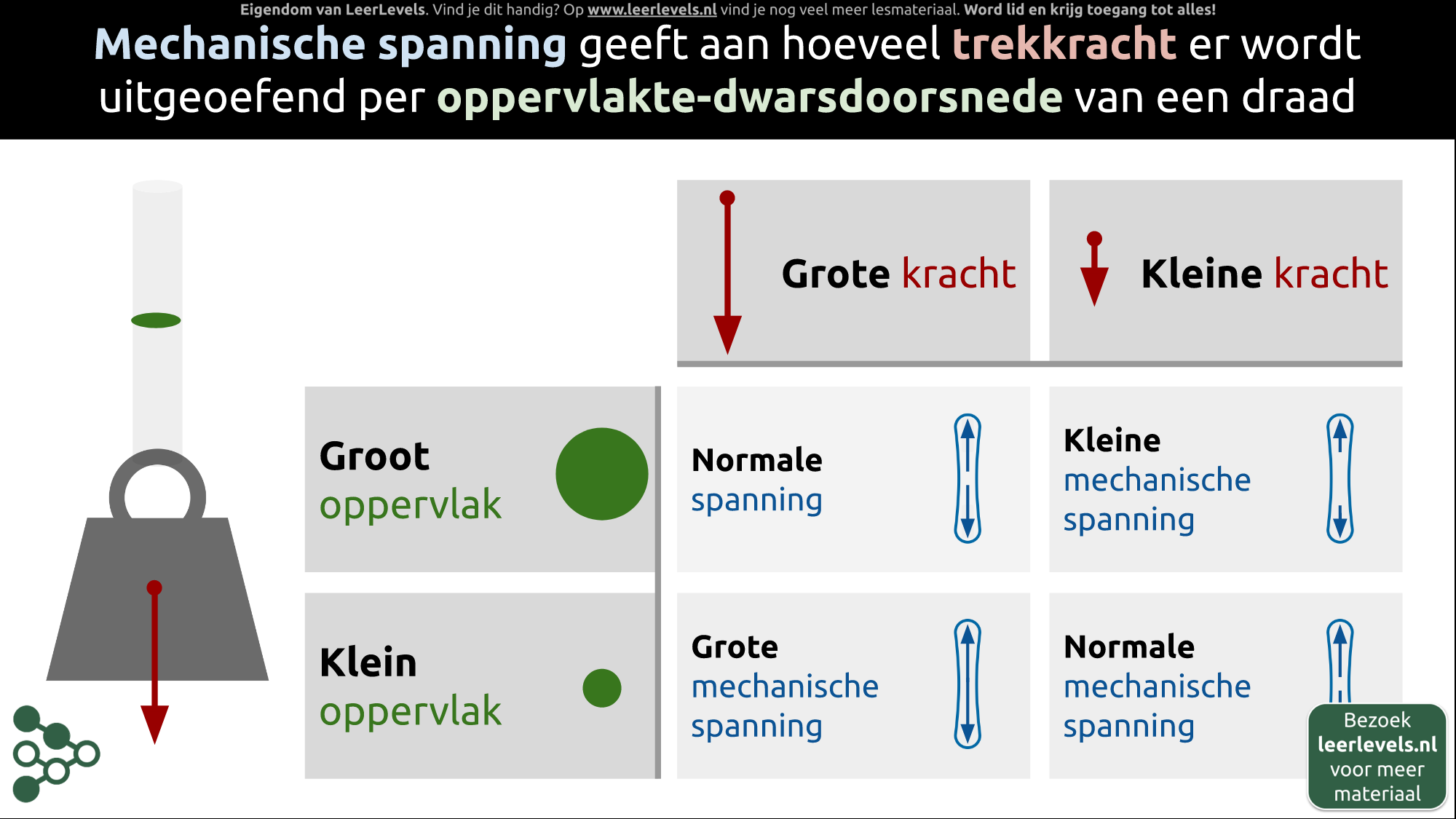
(Afbeelding: Animatie voor Mechanische spanning concept)

Mechanische spanning formule

De mechanische spanning van een draad hangt af van hoe hard er aan getrokken wordt en van de dikte van de draad. Hoe harder er aan getrokken wordt en hoe dunner de draad, hoe hoger de spanning wordt. Dit wordt uitgedrukt in pascal (Pa) en kan berekend worden door de trekkracht op de draad in newton (N) te delen door de dwarsdoorsnede van de draad in vierkante meter (m²). Met andere woorden, als er veel spanning op een draad staat betekent dat er veel kracht op een hele dunne oppervlakte wordt uitgeoefend.

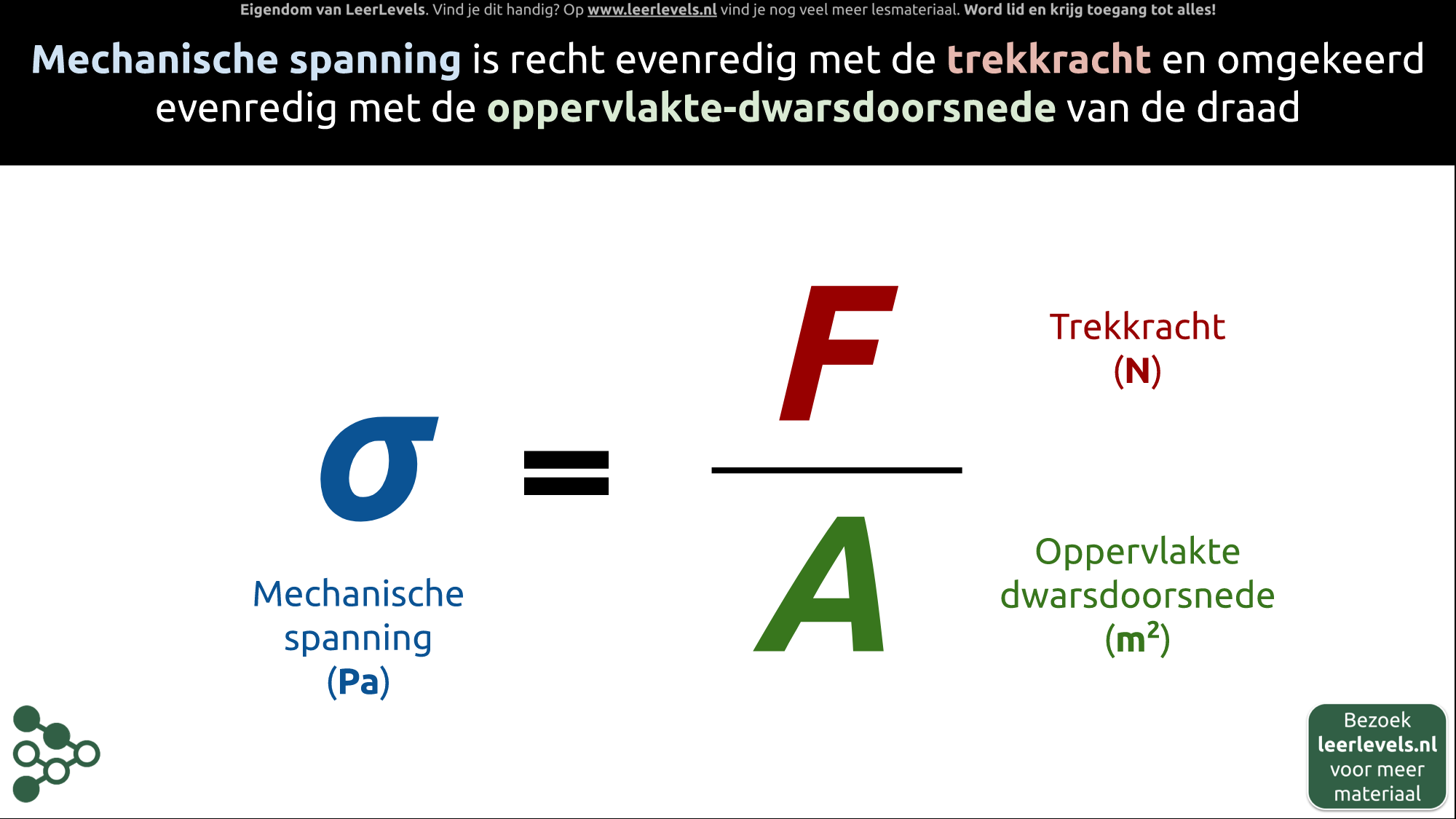
(Afbeelding: Animatie voor Mechanische spanning formule)

Terug naar overzicht Meld je aan

Meetbereik

Meetbereik concept

Een meetbereik is het gebied van waardes dat je kan meten met een bepaald meetinstrument. Bijvoorbeeld, een geodriehoek kan waardes meten van min 8 centimeter tot plus 8 centimeter. Een liniaal kan waardes meten van 0 tot 30 centimeter. Een rolmaat kan waardes meten van 0 tot 5 meter. Hetzelfde principe geldt voor temperatuur. Bijvoorbeeld, een thermometer kan temperaturen meten tussen 35 en 42 graden Celsius. Temperaturen onder 35 of boven 42 graden vallen buiten het meetbereik en kunnen niet worden afgelezen. Voor massa kan een weegschaal worden gebruikt die een meetbereik heeft van 0 tot 5 kilogram.

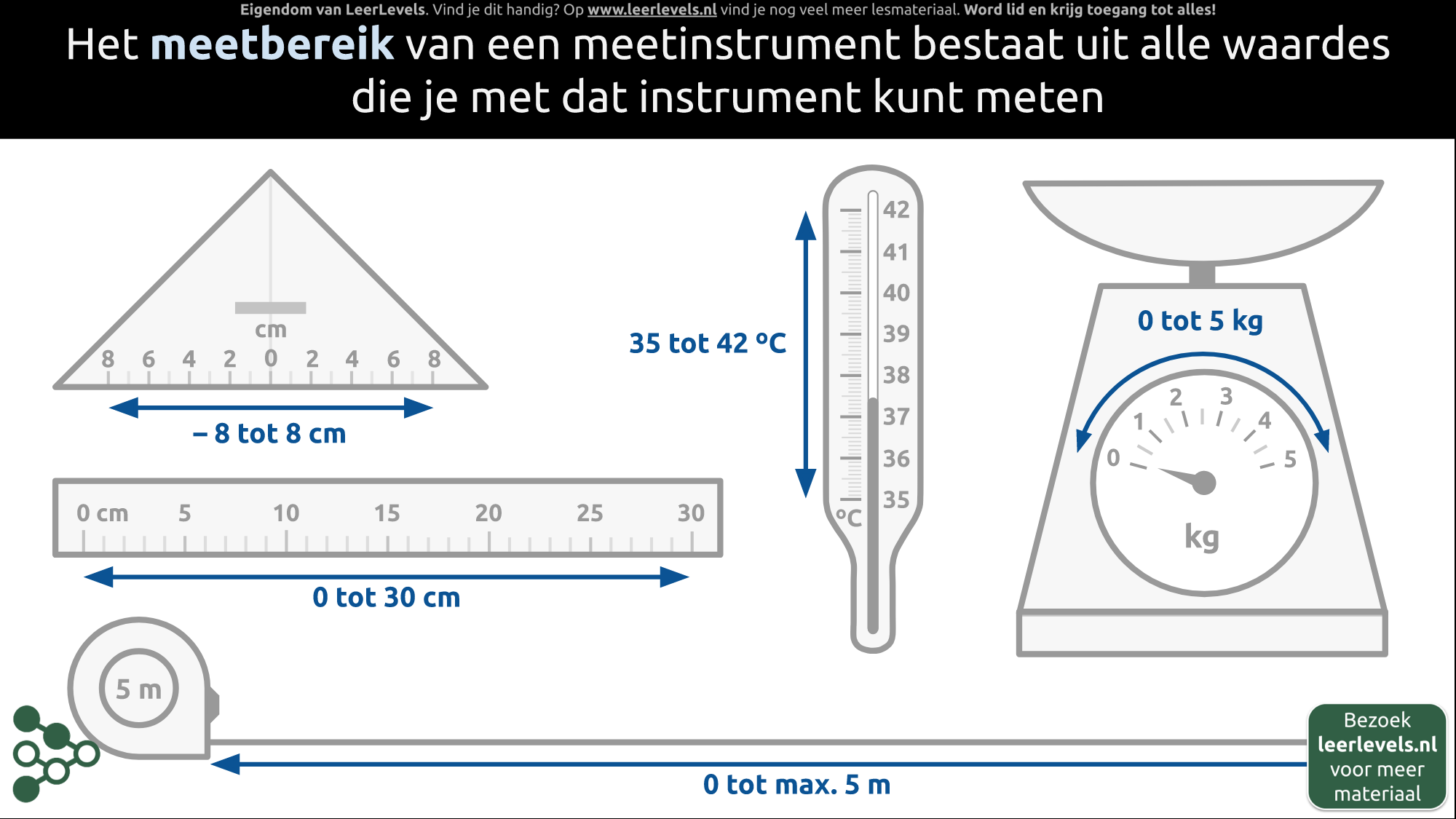
(Afbeelding: Animatie voor Meetbereik concept)

Terug naar overzicht Meld je aan

Meetfout

De totale meetfout wordt veroorzaakt door drie typen fouten: de structurele meetfout, de toevallige meetfout en de afleesfout.

De structurele fout is systematisch van aard. Een voorbeeld hiervan is een digitaal horloge dat op de verkeerde tijdzone staat. Dit resulteert in een structurele fout van bijvoorbeeld één uur, waardoor het horloge altijd een uur achterloopt. In dit geval is de toevallige fout verwaarloosbaar klein en is er geen sprake van een afleesfout. Toch is de totale meetfout aanzienlijk, namelijk één uur.

Bij een analoge klok met alleen een kleine wijzer kan er sprake zijn van een kleine structurele fout, maar geen toevallige fouten. Doordat er alleen een kleine wijzer is, kan de afleesfout aanzienlijk zijn, mogelijk tot wel vijftien minuten afwijking.

Een derde voorbeeld is een zandloper die normaliter vijf minuten loopt. Als de zandkorrels net iets te groot of te klein zijn, kan de duur gemiddeld iets afwijken, wat een kleine structurele fout veroorzaakt. Ook kan er een toevallige fout van ongeveer 30 seconden optreden, bijvoorbeeld door zandkorrels die verkeerd vallen of een blokkade. Het aflezen gaat over het algemeen goed, maar soms is de precieze seconde waarop het laatste zandkorrelje valt, moeilijk te bepalen.

Bij al deze voorbeelden moet je de totale meetfout bepalen door de som van deze drie fouten te nemen. Meestal is er één fout die dominant is en extra aandacht vereist. Om een nauwkeurige meting te doen, dien je de structurele meetfout, de toevallige meetfout en de afleesfout zorgvuldig in overweging te nemen.

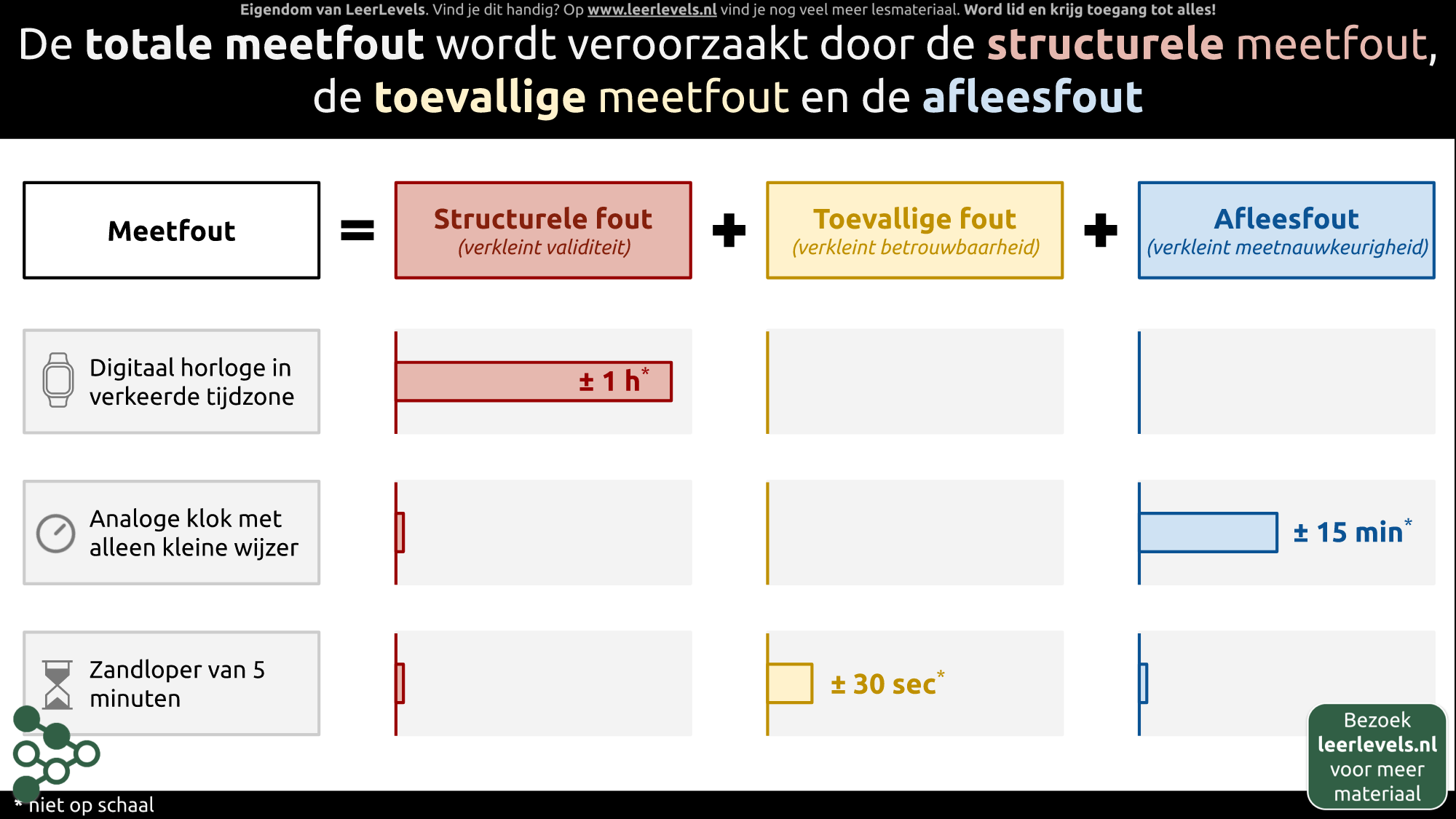
(Afbeelding: Animatie voor Meetfout)

Terug naar overzicht Meld je aan

Meetinstrumenten

Voltmeter en ampèremeter

Om de stroom door een element te meten of de spanning over een element te meten, moet je de meter correct aansluiten. Voor het meten van de stroom moet je de ampèremeter in serie aansluiten. Voor het meten van de spanning moet je de voltmeter parallel aansluiten.

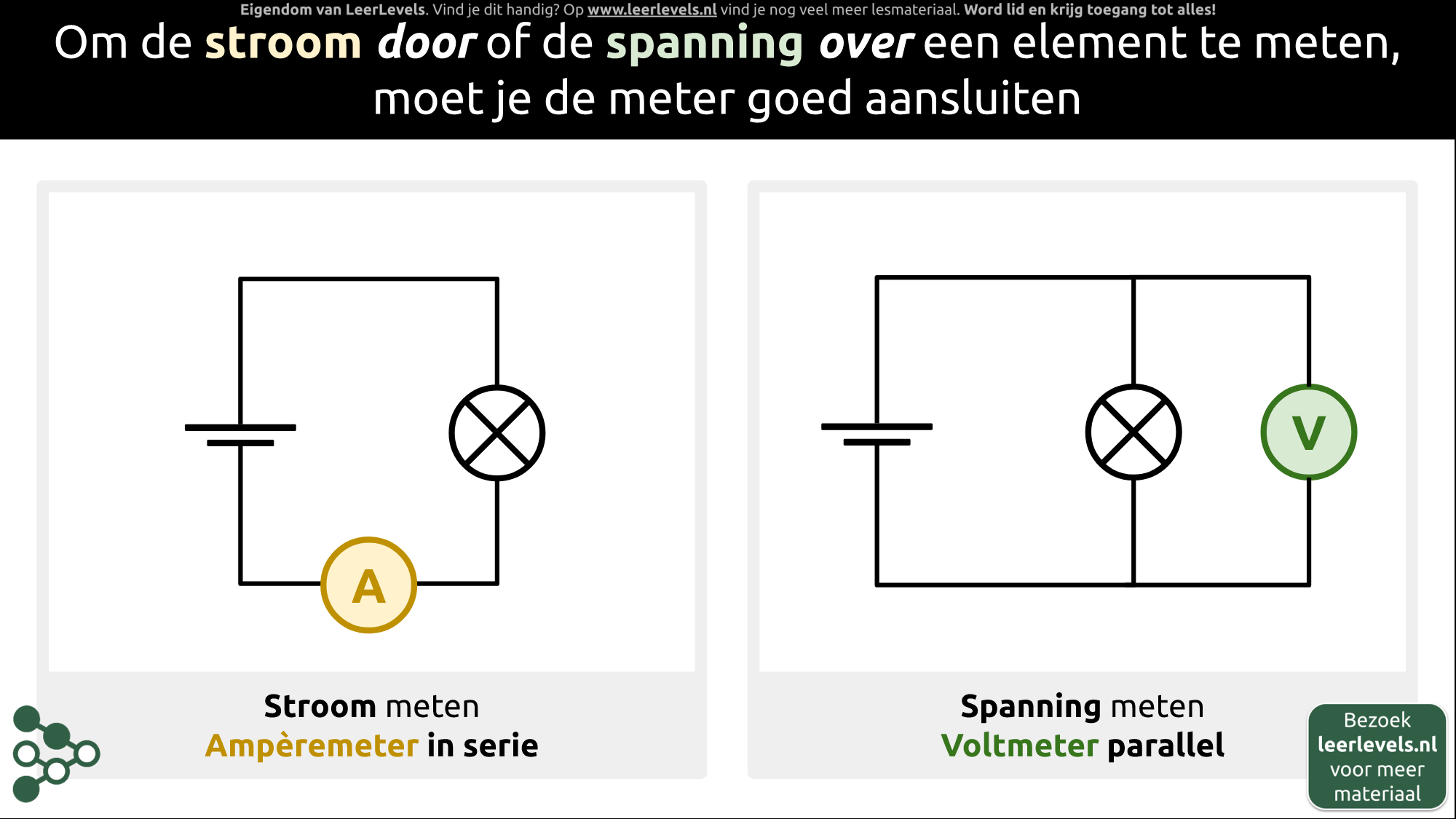
(Afbeelding: Animatie voor Voltmeter en ampèremeter)

Terug naar overzicht Meld je aan

Meetnauwkeurigheid

De meetnauwkeurigheid geeft aan hoe precies je een meting kunt doen. Voor de meeste instrumenten is deze nauwkeurigheid 10% van het kleinste streepje op de schaal. Als voorbeeld gebruiken we een maatbeker met een schaal van tien centiliter. Omdat er geen streepjes tussen zitten, is het kleinste streepje tien centiliter en is de meetnauwkeurigheid dus één centiliter. Dit betekent dat als je denkt dat je zeven centiliter hebt gemeten, je werkelijke meting binnen een marge van één centiliter kan vallen.

In een ander voorbeeld hebben we een maatbeker met streepjes van één centiliter. De meetnauwkeurigheid is dan 0,1 centiliter. Als je denkt dat je 6,6 centiliter hebt gemeten, kan je werkelijke meting binnen een marge van 0,1 centiliter vallen. Hierdoor is deze meting nauwkeuriger dan de vorige meting.

Er zijn situaties waarbij het lastiger is om nauwkeurig te meten, bijvoorbeeld als de streepjes moeilijk te zien zijn of als de grens tussen de vloeistof en het schaaldeel onduidelijk is. In deze gevallen kan de meetnauwkeurigheid lager zijn en kan je beste schatting plus of min 50% van het kleinste streepje zijn.

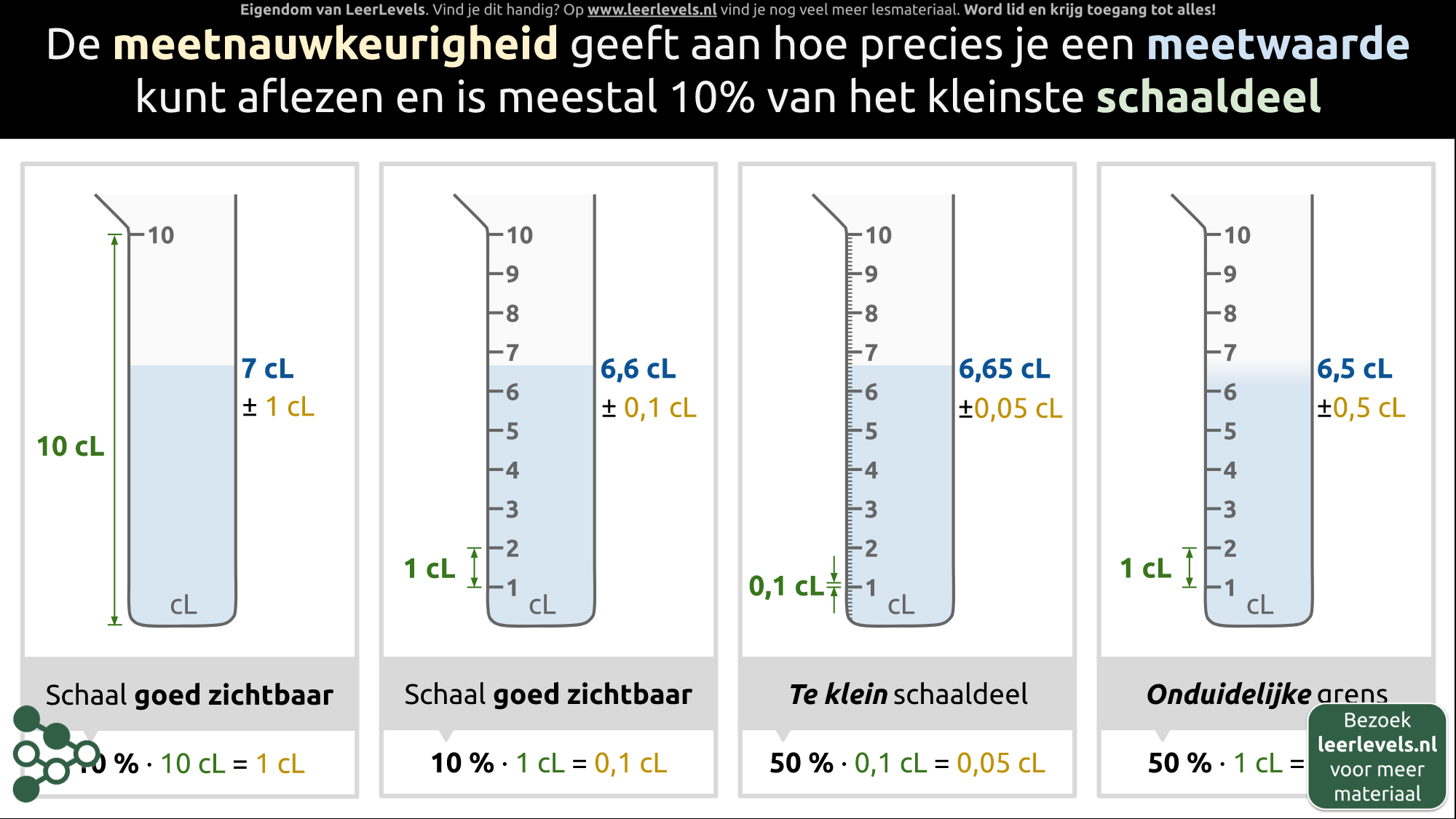
(Afbeelding: Animatie voor Meetnauwkeurigheid)

Terug naar overzicht Meld je aan

Mengsel

Eindtemperatuur mengsel

De formule om de eindtemperatuur van een mengsel te bepalen is de formule van warmteoverdracht en soortelijke warmte. Om deze formule toe te passen, heb je de begintemperatuur van het mengsel, de massa en soortelijke warmte van elk materiaal nodig. In dit voorbeeld hebben we 200 gram water (mw) en 50 gram koper (mk). De soortelijke warmte van water (cw) is 4,2 Jg⁻¹K⁻¹ en van koper (ck) is het 0,46 Jg⁻¹K⁻¹. De begintemperatuur van het water (T1,w) is 10 oC en die van het koper (T1,k) is 100 oC. De eindtemperatuur van het mengsel (T2) willen we berekenen.

De formule voor warmteoverdracht en soortelijke warmte is: Q = m.c.ΔT, waarbij Q de hoeveelheid toegevoerde warmte is, m de massa van het materiaal, c de soortelijke warmte en ΔT de verandering in temperatuur. Om de eindtemperatuur van het mengsel te bepalen, moeten we Qop (toegevoerde warmte aan het koper) en Qaf (afgegeven warmte door het water) berekenen en gelijkstellen aan elkaar.

We weten dat Qaf gelijk is aan Qop, dus we kunnen deze formule gebruiken:

mw.cw.ΔTw = mk.ck.ΔTk

In deze formule is ΔTw de verandering in temperatuur van het water en ΔTk de verandering in temperatuur van het koper. We weten dat ΔT = T2 - T1.

Als we de gegeven waarden invullen in deze formule en oplossen voor T2, dan vinden we dat de eindtemperatuur van het mengsel 12,17 oC is. Dit betekent dat de temperatuur van het mengsel met 0,17 oC gestegen is.

(Afbeelding: Animatie voor Eindtemperatuur mengsel)

Terug naar overzicht Meld je aan

Mengsels

Soorten mengsels

Sommige stoffen kunnen niet goed met elkaar mengen. Maar er zijn drie manieren waarop het toch kan gebeuren.

De eerste is een "oplossing". Dit is een perfect gemengd mengsel waarin je de verschillende stoffen niet meer kunt zien. Bijvoorbeeld als je suiker en thee in water doet, mengen ze goed en krijg je een lekkere zoete drank.

De tweede is een "emulsie". Dit is een mengsel van vloeistoffen die normaal niet mengen. Bijvoorbeeld, olie en azijn of water mengen niet goed, maar als je eigeel toevoegt, krijg je mayonaise.

De derde is een "suspensie". Dit is wanneer hele kleine stukjes van een stof in een vloeistof blijven hangen. Bijvoorbeeld als je pigment in water mengt, krijg je verf. Na het drogen blijft alleen het pigment over, en dat is waarom verf kleur heeft.

Dit zijn de drie manieren waarop verschillende stoffen elkaar toch kunnen mengen: oplossing, emulsie en suspensie.

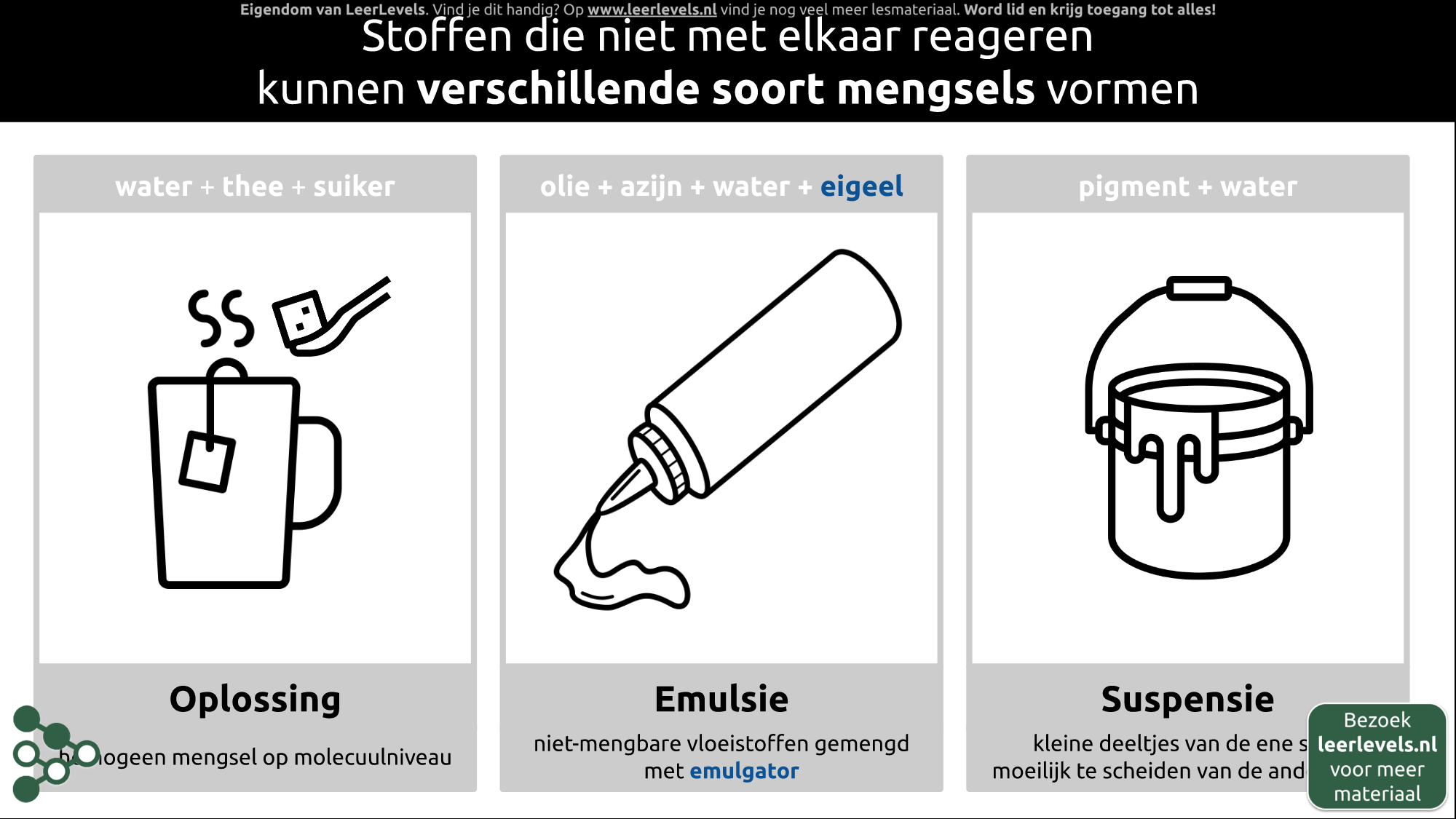
(Afbeelding: Animatie voor Soorten mengsels)

Terug naar overzicht Meld je aan

Metingen

Meetbereik en meetnauwkeurigheid

Als je een meting doet met een apparaat, zoals een voltmeter, moet je kiezen hoe groot de range van de meting moet zijn. Als je een grotere range kiest, zoals 0 tot 30 volt, dan wordt de nauwkeurigheid kleiner. Dit komt doordat de schaalverdeling kleiner wordt, waardoor het moeilijker is om precies af te lezen waar de wijzer staat. Als je een kleinere range kiest, zoals 0 tot 3 volt, dan wordt de nauwkeurigheid groter. In dit geval is het makkelijker om de waarde preciezer af te lezen. Met deze informatie kun je bepalen hoe precies jouw meting is.

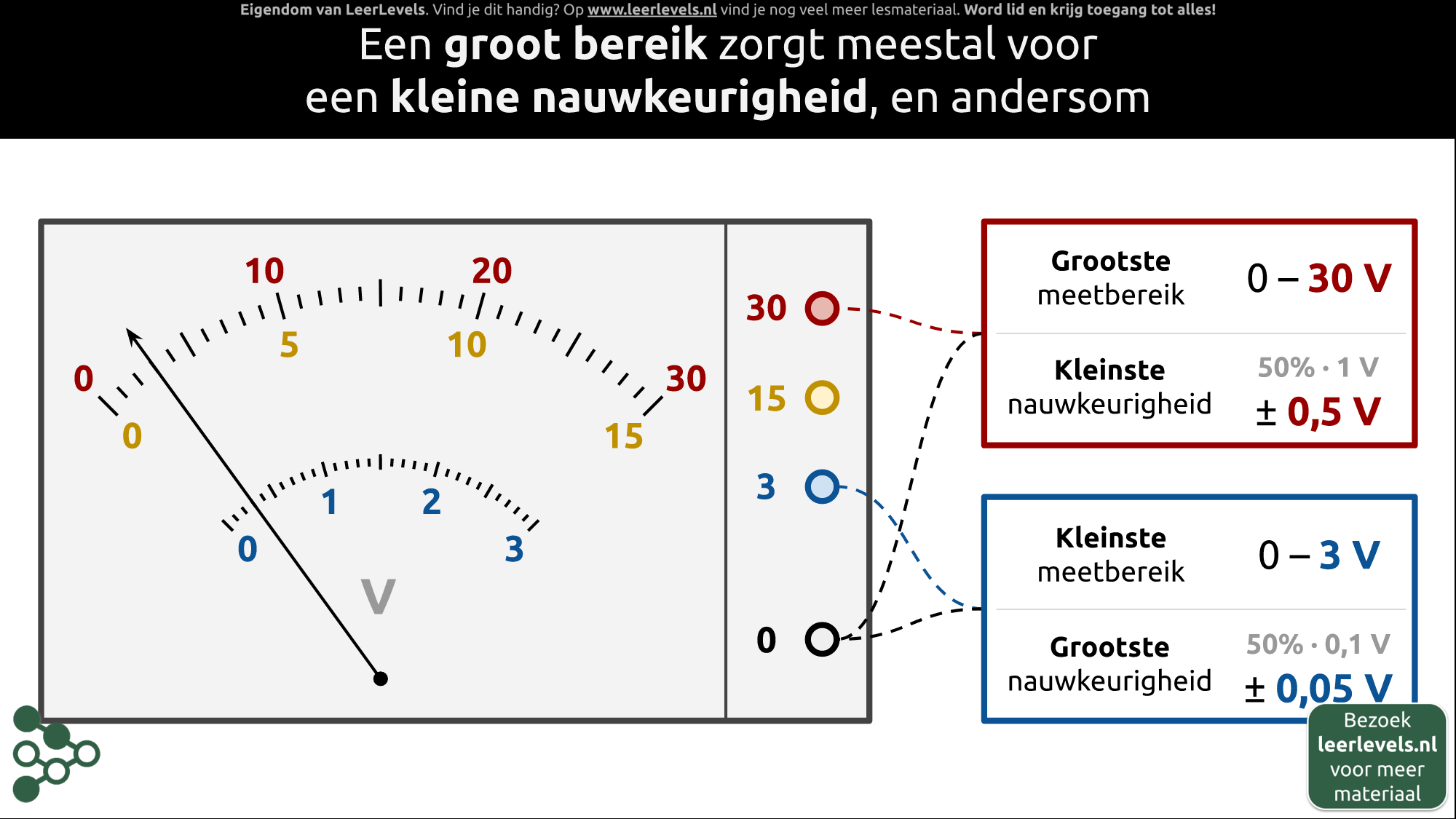
(Afbeelding: Animatie voor Meetbereik en meetnauwkeurigheid)

Terug naar overzicht Meld je aan

Microscopie

Microscopie resolutie

De maximale resolutie die je met microscopie kunt bereiken, wordt bepaald door de golflengte van de gebruikte straling. Bij een lichtmicroscoop, die werkt met een lichtbron die fotonen uitzendt, gaan deze fotonen door het object en worden ze door lenzen gefocust, waardoor je het object kunt bekijken. De mate van detail die je kunt zien, hangt af van de golflengte van het licht. Als de golflengte vergelijkbaar is met de grootte van het object, treedt er interferentie op en kun je meer details zien. Lichtmicroscopen gebruiken zichtbaar licht met een golflengte van ongeveer 400 tot 700 nanometer. Blauw licht heeft een golflengte van ongeveer 400 nanometer, terwijl rood licht een golflengte van ongeveer 700 nanometer heeft. De beste resolutie die je met een lichtmicroscoop kunt bereiken, is dus ongeveer 400 nanometer.

In vergelijking daarmee biedt een elektronenmicroscoop een veel hogere resolutie, omdat elektronen een kortere golflengte hebben dan licht. Elektronen worden op het monster afgevuurd en met magnetische lenzen op een sensor geprojecteerd. De sensor meet dit en zet het om naar een beeld. De golflengte van elektronen wordt bepaald door hun energie. Vaak wordt er een spanning van ongeveer 100 kV gebruikt. Voor elektronen betekent dit een energie van 100 keV = 1,6 × 10⁻¹⁴ Joule. De De Broglie-golflengte komt dan uit op ongeveer 0,004 nanometer. De maximale resolutie van een elektronenmicroscoop is dus ongeveer 10⁵ keer beter dan die van een lichtmicroscoop.

Kortom, als je een elektronenmicroscoop kunt gebruiken (hoewel niet geschikt voor alle samples), kun je veel nauwkeurigere beelden maken. De maximale resolutie die je met microscopie kunt bereiken, is altijd vergelijkbaar met de golflengte van de gebruikte straling.

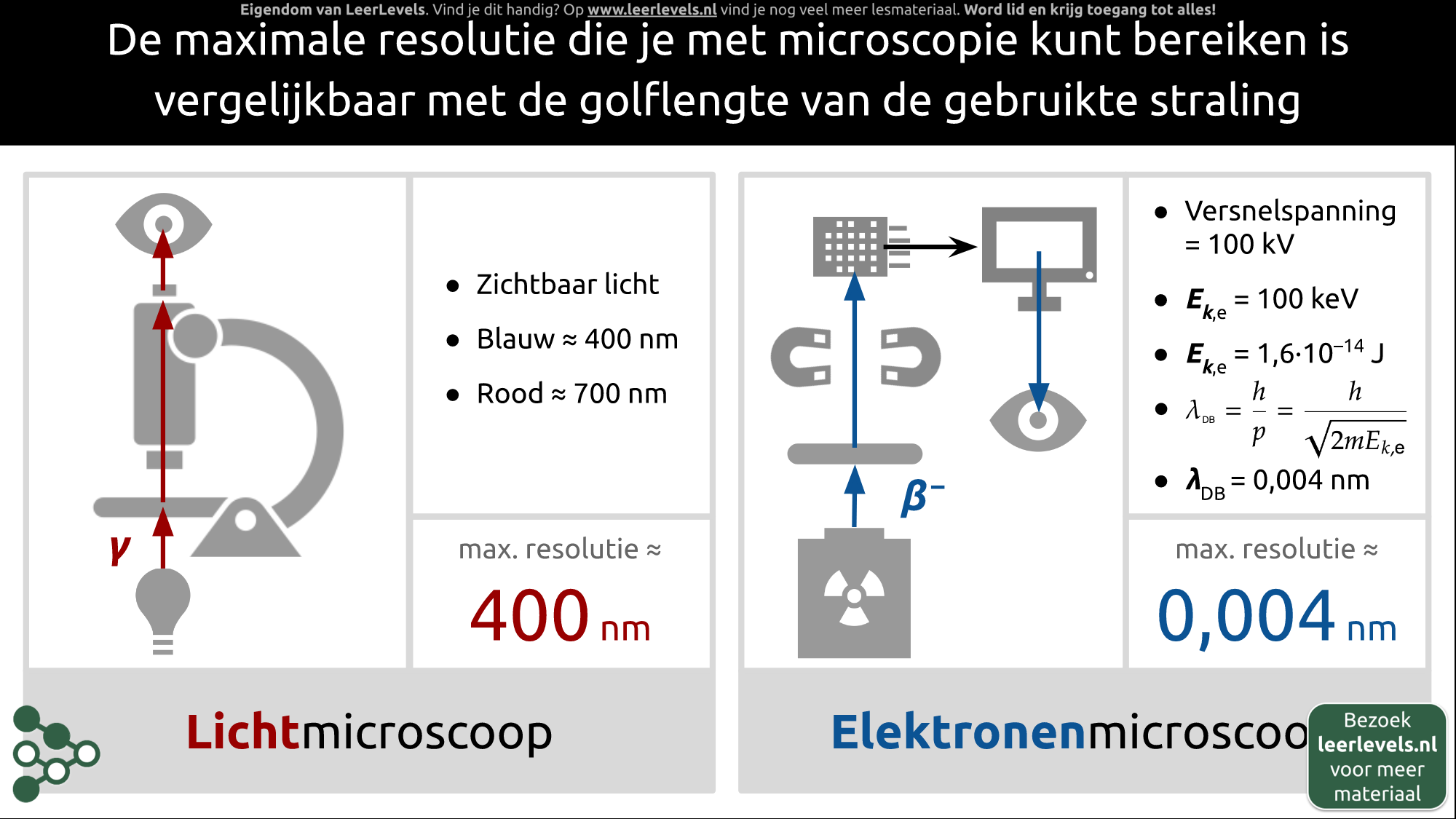
(Afbeelding: Animatie voor Microscopie resolutie)

Terug naar overzicht Meld je aan

Middelpuntzoekende kracht

Middelpuntzoekende kracht concept

De middelpuntzoekende kracht is de kracht die ervoor zorgt dat je in een looping of bocht blijft. Het is de som van alle krachten die samen zorgen voor de middelpuntzoekende versnelling. Bijvoorbeeld, als je in een looping bent, werkt de zwaartekracht naar beneden en de normaalkracht naar boven. De middelpuntzoekende kracht wordt gevormd door de som van deze krachten. Het is dus geen nieuwe kracht, maar een combinatie van de bestaande krachten. In een looping is de middelpuntzoekende kracht altijd even groot, omdat de snelheid constant blijft en er dus een constante middelpuntzoekende versnelling en kracht nodig is.

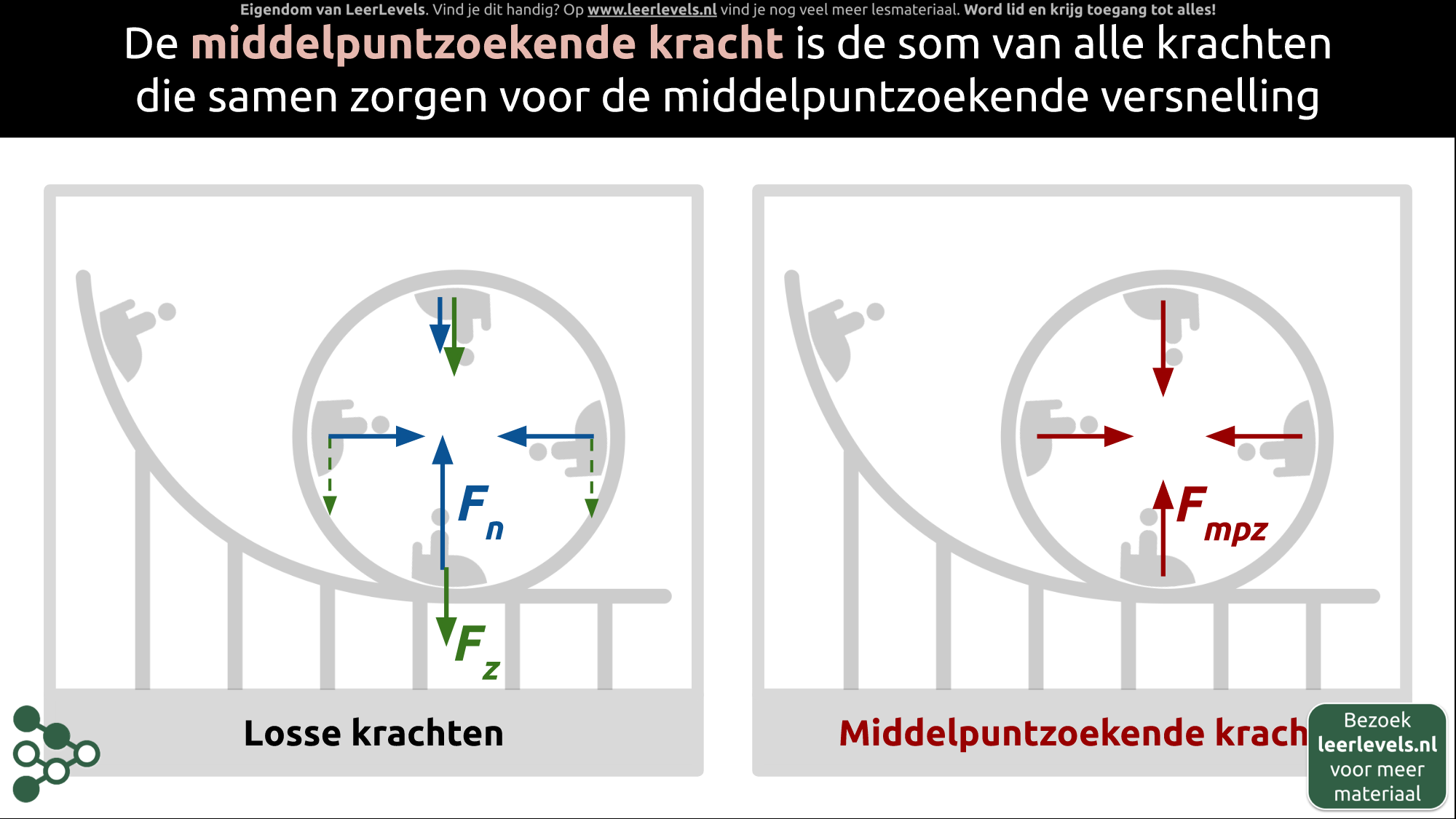
(Afbeelding: Animatie voor Middelpuntzoekende kracht concept)

Middelpuntzoekende kracht formule

De kracht die ervoor zorgt dat een object in een cirkel blijft bewegen, noemen we de middelpuntzoekende kracht. Deze kracht hangt af van de massa van het object en de versnelling richting het middelpunt van de cirkel. We kunnen dit als volgt noteren: Fmpz = m · ampz.

De eenheid van middelpuntzoekende kracht is de Newton, de massa wordt uitgedrukt in kilogram en de middelpuntsversnelling in meter per seconde kwadraat.

Als het gaat om een cirkelbeweging met een bepaalde baansnelheid v in meter per seconde en baanstraal r in meter, kunnen we de formule ook opschrijven als Fmpz = (m · v²)/(r).

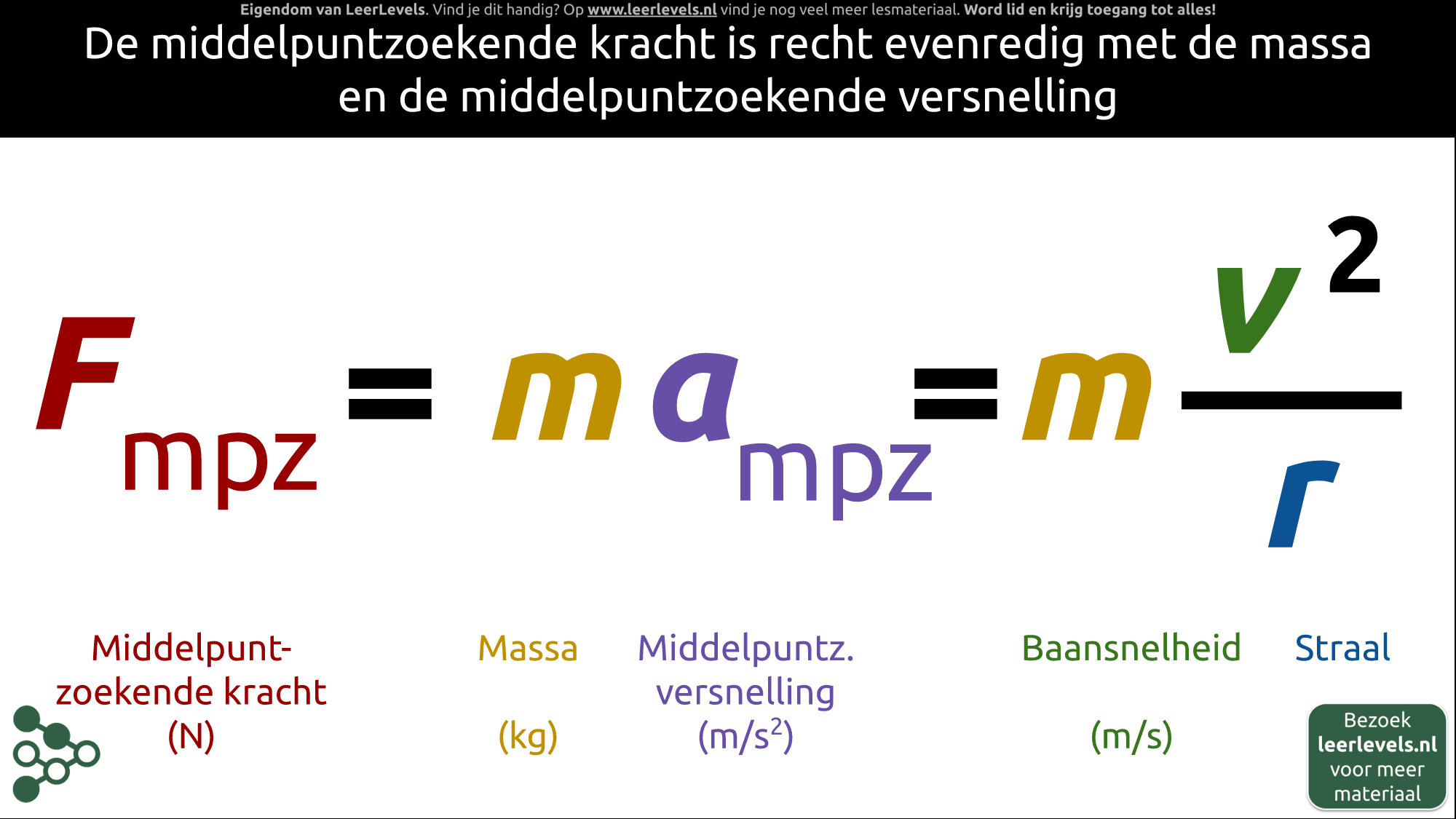
(Afbeelding: Animatie voor Middelpuntzoekende kracht formule)

Terug naar overzicht Meld je aan

Middelpuntzoekende versnelling

Middelpuntzoekende versnelling afleiding

Met vectorsommen bereken je de middelpuntzoekende versnelling. Stel dat je met de auto een rondje maakt, dan is de totale snelheidsverandering de som van alle kleine paarse vectoren (dv) die samen de rode Delta v vormen. De totale snelheidsverandering is 2piv omdat het een cirkel is. De baan van de cirkel is r en de afstand is 2pir. De tijd die je erover doet, Delta t, is gelijk aan 2pir/v. De formule voor de middelpuntzoekende versnelling is ampz = delta v / delta t. Als we alles invullen, wordt dat ampz = (2piv)/(2pir / v) = v²/r. Dit geeft aan hoe de formule voor ampz wordt afgeleid.

(Afbeelding: Animatie voor Middelpuntzoekende versnelling afleiding)

Middelpuntzoekende versnelling concept

De middelpuntzoekende versnelling (ampz) zorgt ervoor dat de snelheid van een object van richting verandert en er een cirkelbaan ontstaat, zoals bij een tennisbal aan een touw. De grootte van de snelheid blijft constant, alleen de richting verandert. De grootte van de versnelling hangt af van de snelheid (v) en de straal (r) van de baan en is constant. Hoe groter de snelheid en hoe scherper de bocht, hoe groter de ampz-versnelling. Dit effect van de snelheid is groter dan het effect van de baanstraal en wordt weergegeven door de formule ampz = (v²)/(r).

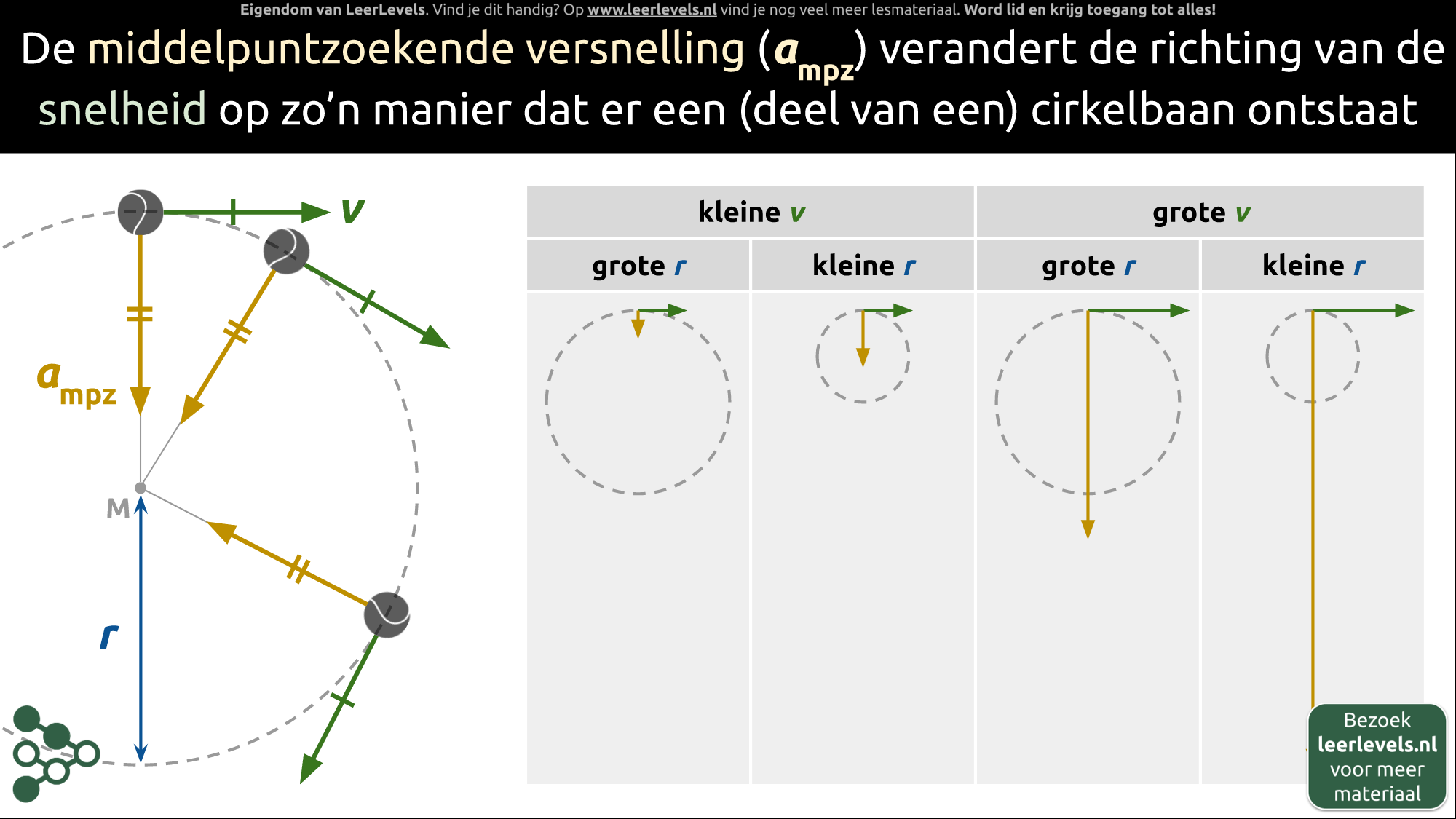
(Afbeelding: Animatie voor Middelpuntzoekende versnelling concept)

Middelpuntzoekende versnelling formule

De middelpuntzoekende versnelling kan worden berekend met behulp van een formule die aangeeft dat de versnelling kwadratisch evenredig is met de snelheid en omgekeerd evenredig met de straal. Deze formule luidt:

a = (v²)/(r)

waarbij a de versnelling is in m/s², v de snelheid in m/s, en r de straal in m

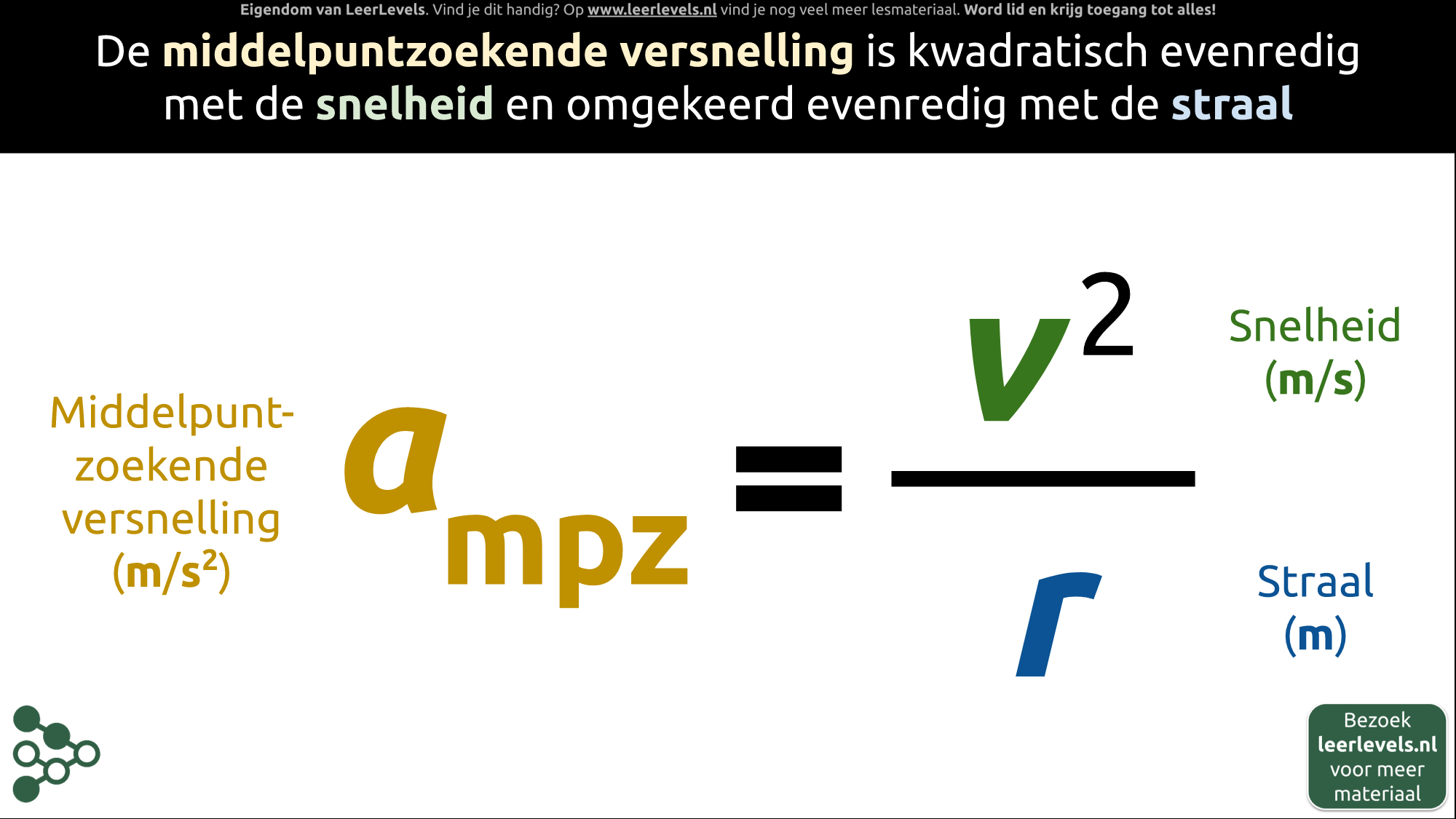
(Afbeelding: Animatie voor Middelpuntzoekende versnelling formule)

Terug naar overzicht Meld je aan

Model

Tijdstapjes bij model

In een model is de grootte van de tijdstap dt belangrijk. Dit beïnvloedt de nauwkeurigheid en benodigde rekentijd van het model. Je kunt het vergelijken met een bal die recht omhoog wordt gegooid en steeds sneller naar beneden valt. Het model hiervan heeft regels voor snelheid en hoogte die afhankelijk zijn van de tijdstap dt. Een grote tijdstap zorgt voor onnauwkeurigheid, terwijl een kleine tijdstap zorgt voor een betere benadering van de werkelijkheid. Het nadeel van een kleine tijdstap is dat het model veel langzamer wordt. Het is daarom belangrijk om bij de keuze van de tijdstap te kijken naar de snelheid van het proces dat wordt gemodelleerd. Bij snelle processen is een kleine tijdstap nodig voor nauwkeurigheid, terwijl bij langzamere processen een grotere tijdstap kan worden gebruikt.

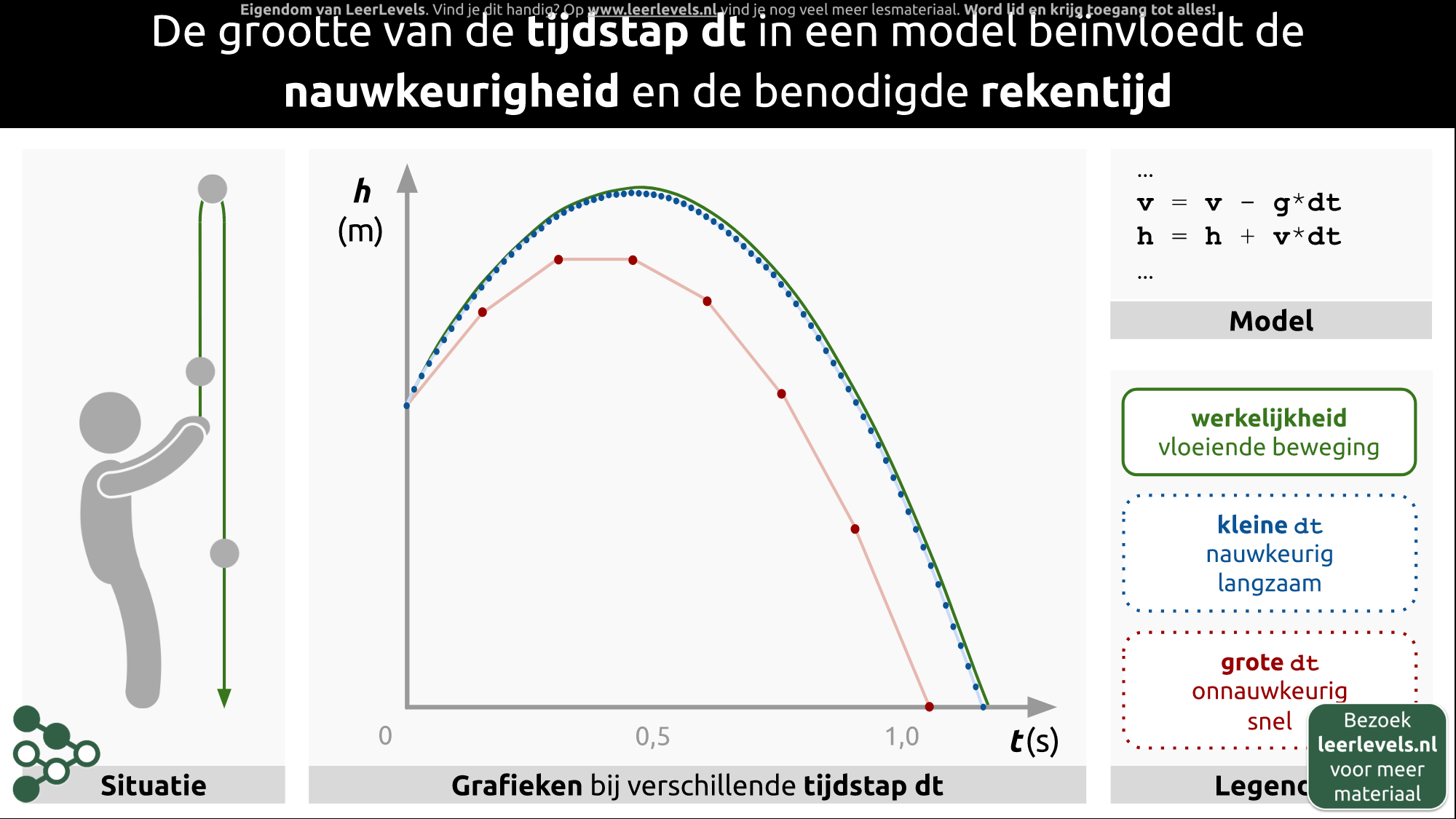
(Afbeelding: Animatie voor Tijdstapjes bij model)

Model eenparig versnelde beweging

Een eenparig versnelde beweging is een beweging waarbij zowel de snelheid als de afstand steeds meer toenemen. Dit model wordt geïllustreerd door een atleet die continu versnelt. Een topatleet kan bijvoorbeeld een versnelling van 4 m/s² behalen, die als startwaarde wordt gebruikt bij het model. De startwaarden voor snelheid en afstand zijn respectievelijk 0 en 0. De starttijd is t = 0 s en het tijdstapje dt is gelijk aan 0,1 s.

Er worden drie modelregels gebruikt om deze beweging te simuleren. De nieuwe afstand is gelijk aan de oude afstand plus de snelheid keer het tijdstapje dt. Daarnaast is de nieuwe tijd gelijk aan de oude tijd plus dt. De snelheid neemt ook toe, en wel met de versnelling vermenigvuldigd met dt. Dit leidt tot een nieuwe snelheid die berekend wordt door de oude snelheid op te tellen bij de product van a en dt.

Het model kan worden gevisualiseerd met grafieken van de versnelling, snelheid en afstand. De versnelling blijft constant, dus ligt de bijbehorende grafiek constant op een horizontale lijn. De snelheid en afstand stijgen echter elk tijdstapje evenveel.

Kortom, bij een eenparig versnelde beweging nemen de snelheid en afstand steeds toe.

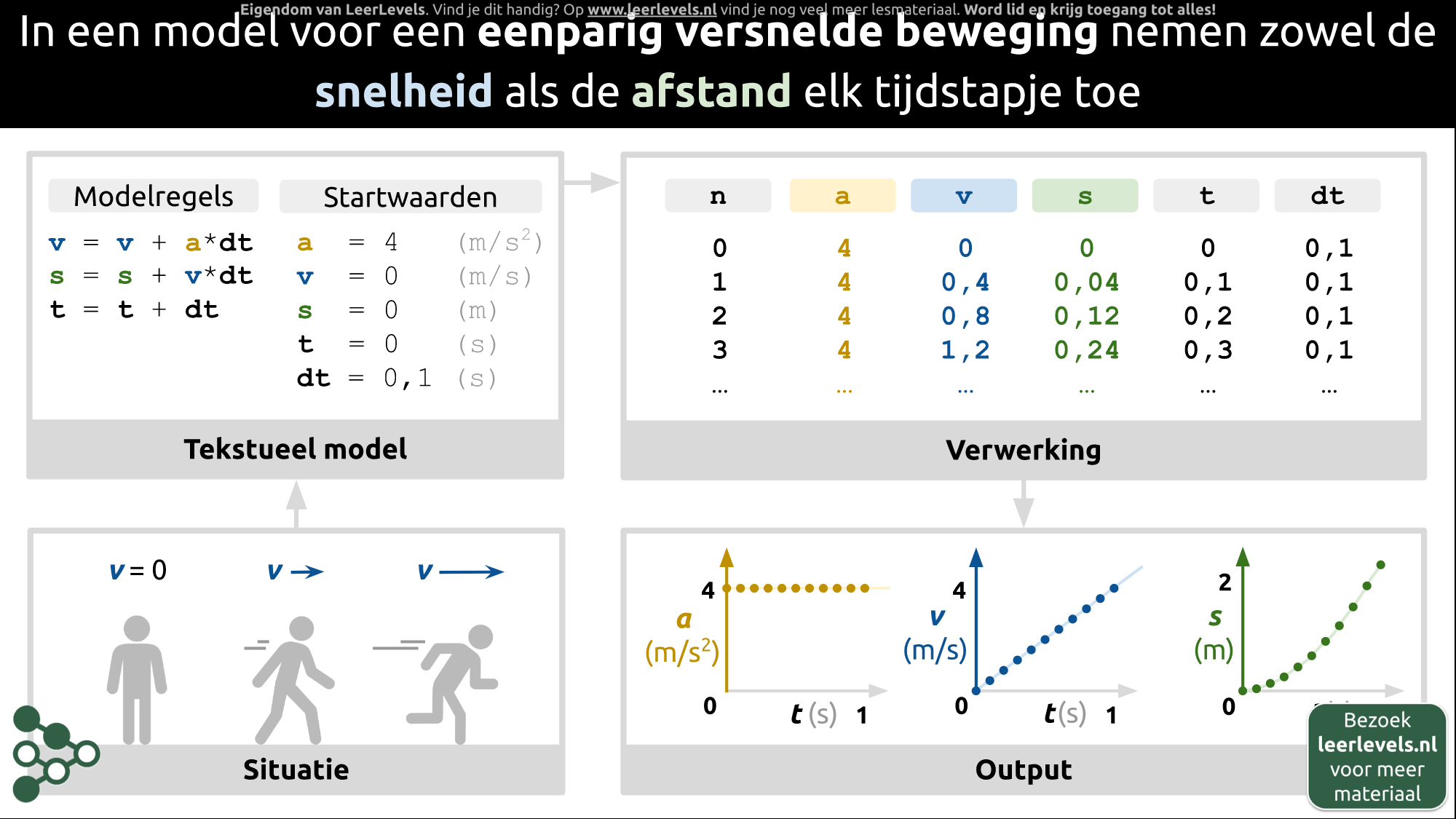
(Afbeelding: Animatie voor Model eenparig versnelde beweging)

Als-dan-voorwaarde in een model

Een als-dan-voorwaarde legt uit wat er gebeurt bij bepaalde omstandigheden in een model. Bijvoorbeeld, als je op het gaspedaal trapt van een auto, dan gaat de auto steeds sneller. Maar als je na 5 seconden constant wil rijden, moet de kracht nul worden. In het model typ je 'als t>5' en dan 'dan Fres = 0' om de kracht te veranderen. Het model laat zien dat de snelheid lineair toeneemt tot t = 5 s en daarna constant blijft. Dit betekent dat de auto geen kracht meer heeft en op constante snelheid rijdt.

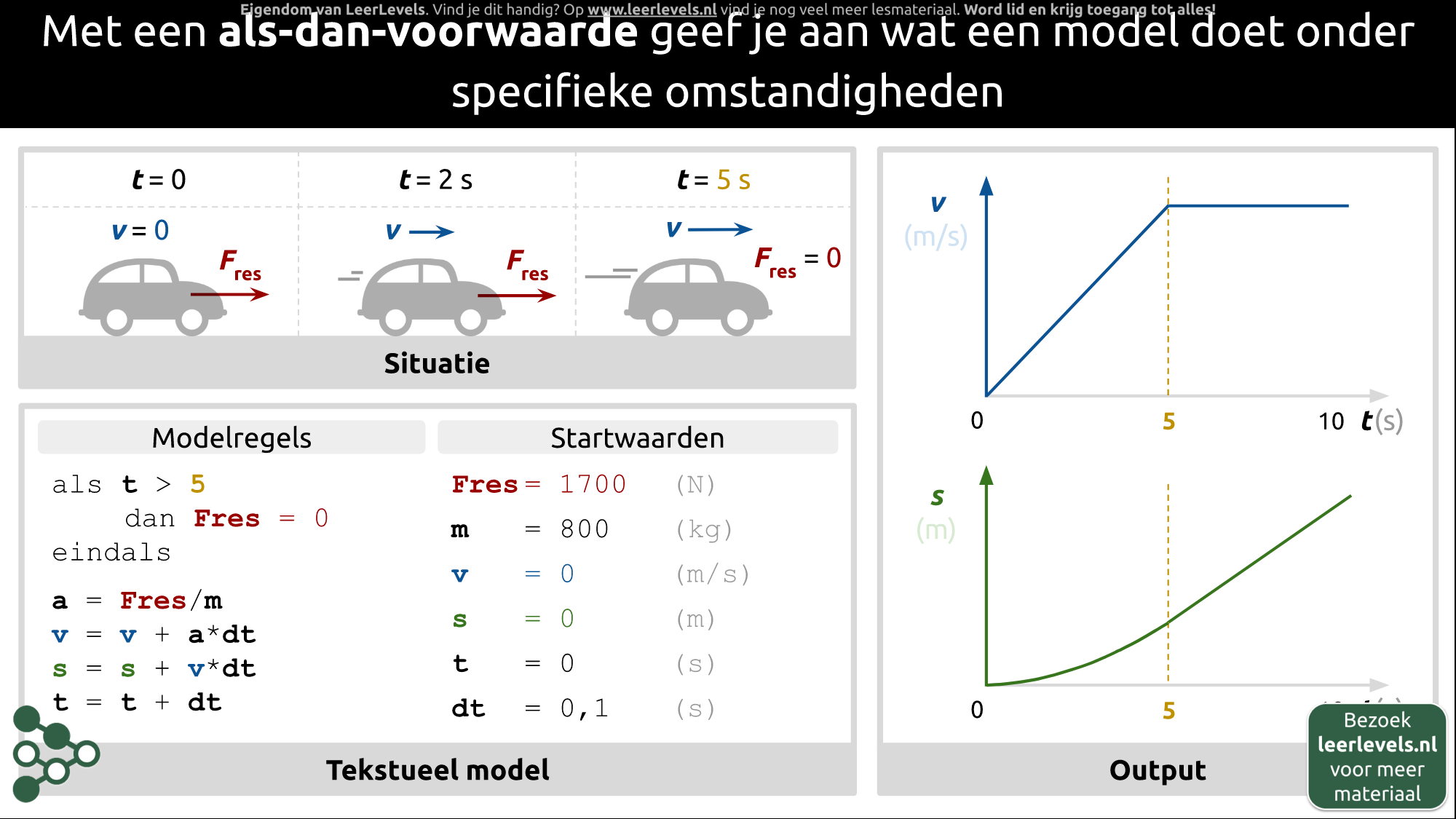
(Afbeelding: Animatie voor Als-dan-voorwaarde in een model)

Stopvoorwaarde in een model

De stopvoorwaarde bepaalt wanneer een model stopt met uitvoeren. Om te zien hoe dit werkt, bekijken we een vrije val zonder luchtweerstand. De zwaartekracht zorgt ervoor dat de bal een versnelling naar beneden heeft en steeds sneller valt. In het model zie je daarom een a van -9,81 m/s²; dit is de valversnelling op aarde. Het minteken geeft aan dat de richting naar beneden is. De bal begint met een snelheid van 0, een hoogte van 1,5 m, op tijdstip 0, en er worden tijdstapjes van 0,05 s genomen. De modelregels volgen die van een eenparig versnelde beweging.

Met dit model maken we een grafiek van de hoogte als functie van de tijd. Wanneer de hoogte 0 bereikt, oftewel de grond, gebeurt er iets vreemds: de bal blijft door de grond vallen. Vanuit het model gezien is dit logisch, omdat er niet is aangegeven dat er een grond is, dus het model rekent verder. Een model begrijpt niet automatisch onlogische situaties. Voor jou zijn de berekeningen onder de grond echter niet nuttig; daarom is het handig als het model stopt zodra de bal de grond raakt. Dit doe je met een stopvoorwaarde. Je typt 'als h kleiner is dan 0', dus een negatieve hoogte (onder de grond), 'dan stop' zodat het model stopt met uitvoeren, zelfs als het aantal opgegeven iteraties nog niet is bereikt. 'Eindals' is nodig om de voorwaarde af te sluiten. Merk op dat als je had getypt 'als h = 0 dan stop eindals', het niet zou werken. In de grafiek is er geen enkel punt waar h precies gelijk is aan 0. Met deze voorwaarde stopt het model wanneer de bal de grond raakt. Het eerste punt waar h negatief is, wordt niet meer weergegeven.

(Afbeelding: Animatie voor Stopvoorwaarde in een model)

Toepassing: model voor een gedempte trilling

Bij een gedempte trilling beweegt iets op en neer doordat het aan een veer hangt en losgelaten wordt. Er werkt hierbij een wrijvingskracht die de beweging afremt. Dit kan bijvoorbeeld de wrijving in lucht of in een vloeistof zoals water zijn. Bij het maken van een model voor deze trilling moet je rekening houden met de richting van de krachten die hierbij meespelen, zoals de veerkracht, de zwaartekracht en de wrijvingskracht. We gebruiken hiervoor positieve en negatieve richtingen.

In het model moeten we gebruikmaken van de mintekens in de formules. Zo is bijvoorbeeld de veerkracht positef als het object omhoog gaat en negatief als het omlaag gaat. De zwaartekracht werkt altijd naar beneden en de wrijvingskracht werkt juist tegen de bewegingsrichting in. Door deze krachten met elkaar op te tellen, krijgen we de Fres, daarmee kunnen we de versnelling berekenen. Hiermee kunnen we de snelheid, de uitwijking en de tijd bepalen.

In het model hebben we startwaarden nodig, bijvoorbeeld dat de uitwijking omlaag is omdat het object aan de veer werd neergehangen. De demping van de trilling zorgt ervoor dat het object elke trilling minder ver uitwijkt dan de vorige keer. Het model kan ook zonder demping gemaakt worden, maar dan blijft het object oneindig doortrillen.

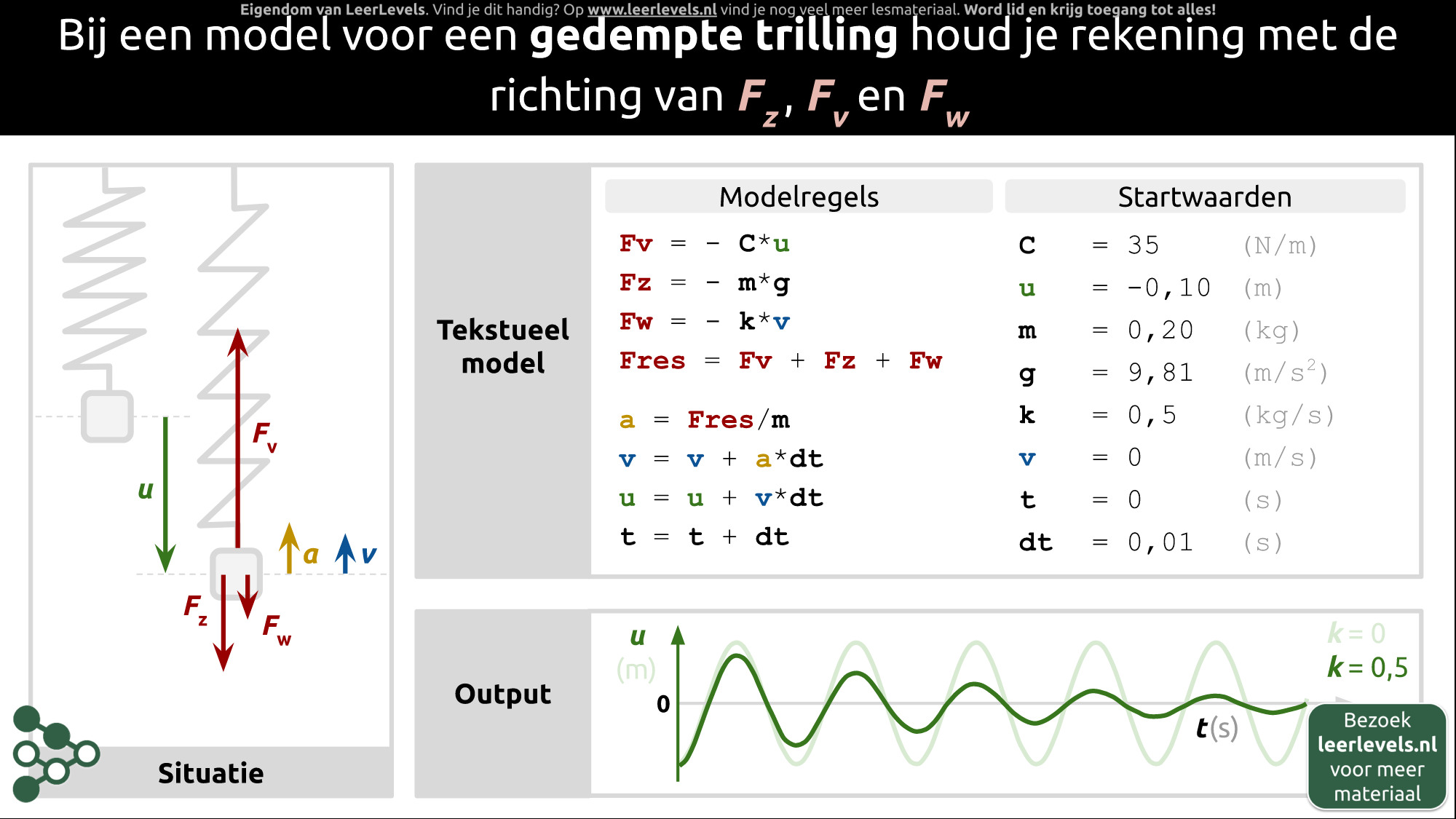
(Afbeelding: Animatie voor Toepassing: model voor een gedempte trilling)

Toepassing: model voor radioactief verval

Radioactief jodium-131 is een stof die in ziekenhuizen wordt gebruikt om patiënten te behandelen. Deze stof vervalt in de tijd naar xenon-131 en maakt daarbij bèta- en gammastraling vrij. Om te weten hoeveel jodium en xenon er na een bepaalde tijd over zijn, kunnen we gebruikmaken van een model voor radioactief verval.

Dit model begint met de activiteit van jodium, wat de snelheid is waarmee kernen vervallen per seconde. De activiteit is afhankelijk van het aantal aanwezige kernen, dus als er meer jodium is, zal er meer activiteit zijn. De constante c kan worden berekend door de halveringstijd van de stof te kennen.

Als er een tijdstap voorbijgaat, zal er een deel van de jodiumkernen vervallen en xenonkernen worden. Het aantal vervallen kernen is gelijk aan de activiteit vermenigvuldigd met de tijdstap. Het nieuwe aantal jodiumkernen is het oude aantal minus het aantal vervallen kernen en het nieuwe aantal xenonkernen is het oude aantal plus het aantal vervallen kernen.

Bij dit model horen een aantal startwaarden. De constante c voor jodium-131 is 10⁻⁶. We beginnen met 1000 jodiumkernen en een tijdstap van 1000 seconden. Omdat de halveringstijd van jodium-131 8 dagen is, hoeven we niet elke seconde een nieuwe berekening te doen.

De grafiek van jodium laat zien dat de lijn sneller daalt aan het begin, als er nog veel jodiumkernen zijn. Na verloop van tijd neemt de activiteit en daarmee de snelheid van vervallen af. Hierdoor zal het aantal xenonkernen aan het begin snel stijgen en aan het einde minder snel. De activiteit hangt dus af van het aantal aanwezige kernen.

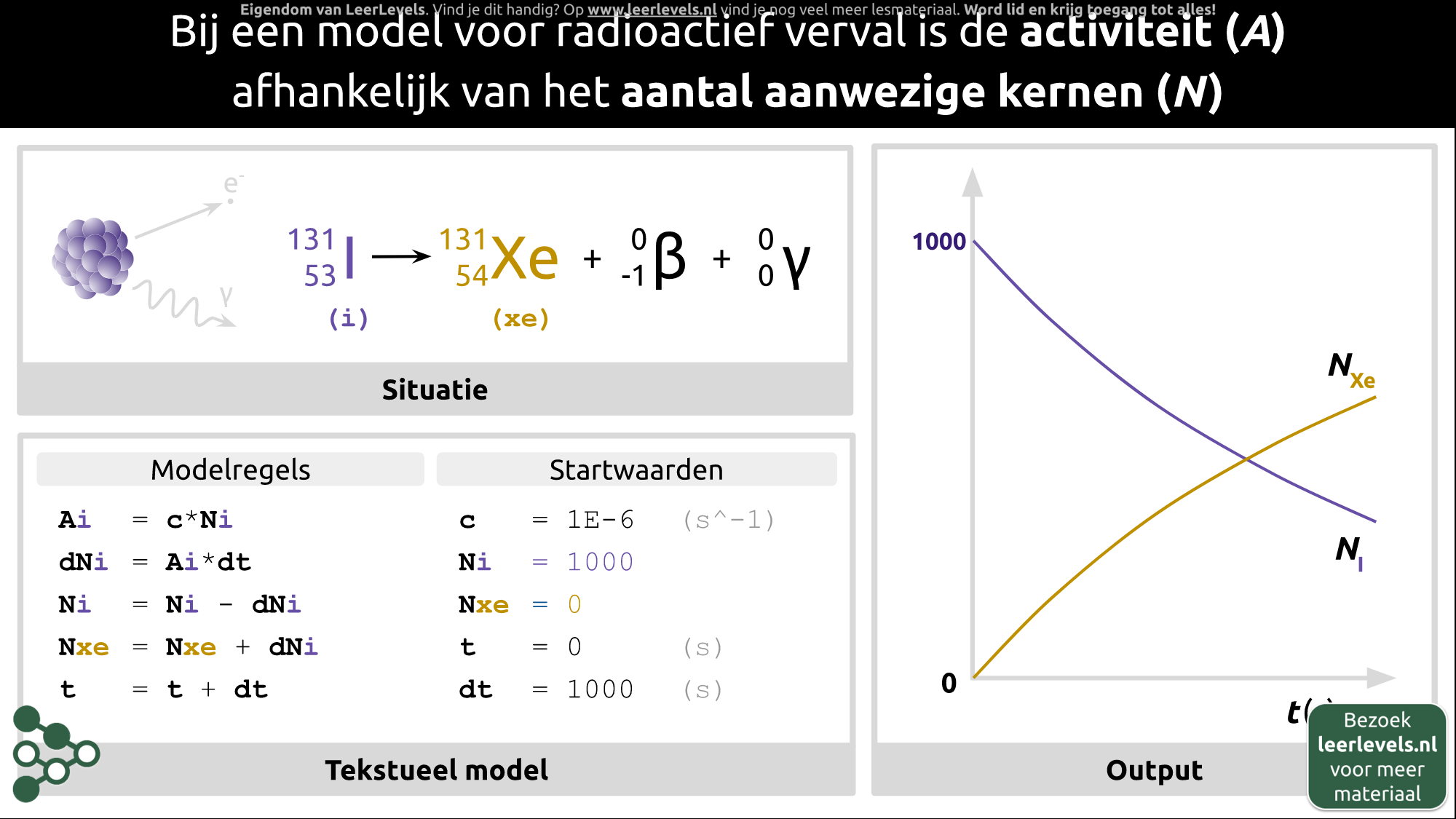
(Afbeelding: Animatie voor Toepassing: model voor radioactief verval)

Terug naar overzicht Meld je aan

Modelleren

Modelleren input en output

Een model is een manier om de werkelijkheid te beschrijven met formules. Als we bijvoorbeeld een appel laten vallen, zijn factoren zoals de hoogte en beginversnelling belangrijk om te weten waar de appel zal landen. Bij ingewikkelder situaties maken we een lijst van welke factoren een rol spelen. Door deze factoren om te zetten in een grafisch model wordt het overzichtelijk. Bijvoorbeeld, als we de hoogte van een appel willen zien, maken we een grafiek van de snelheid en verandering van hoogte over de tijd. Het maken van een goede formule kan echter moeilijk zijn, vooral als er ingewikkelde patronen zijn. Toch kunnen we door te modelleren voorspellingen doen over verschillende situaties en objecten. Het model gebruikt formules als input en produceert vaak een grafische output.

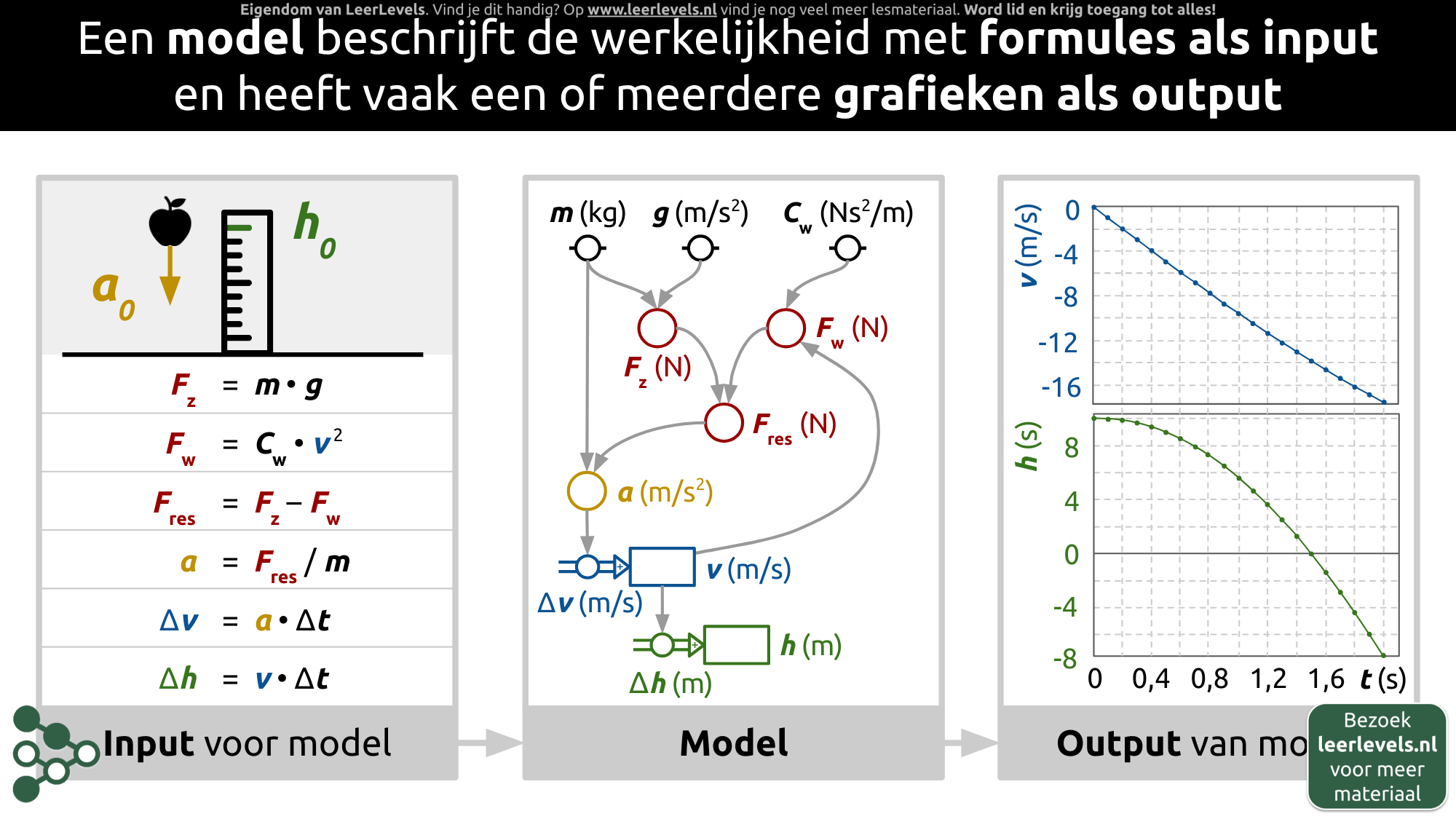
(Afbeelding: Animatie voor Modelleren input en output)

Modelleren concept

Bij modelleren wordt de werkelijkheid vereenvoudigd tot een aantal dingen die belangrijk zijn en hoe ze met elkaar te maken hebben. Bijvoorbeeld, stel je voor dat je een kraan hebt die een emmer met water vult. Om hier een model van te maken, moet je kijken welke dingen belangrijk zijn. In dit geval is het belangrijkste ding hoeveel water er in de emmer zit, dit kan worden gemeten in volume. Dit heet de toestandsvariabele.

Op dit moment gebeuren er niet veel dingen. Het enige wat er gebeurt is dat er water in de emmer stroomt met een bepaalde snelheid, uitgedrukt in liters per seconde. Dit wordt een stroom genoemd, omdat het aangeeft hoeveel water er per seconde de emmer ingaat.

Wat bepaalt nu hoeveel water er per seconde in de emmer gaat? Dit wordt beïnvloed door de stand van de kraan, die kan worden veranderd. De stand van de kraan wordt een hulpvariabele genoemd.

Als er nu ook water uit de emmer lekt, moet het model worden aangepast. Er is nu niet alleen een instroomsnelheid, maar ook een uitstroomsnelheid. Dit wordt een nieuwe stroom genoemd. Op deze manier wordt elke seconde een klein beetje water uit de emmer gehaald. De grootte van het uitstroomgat en het volume van het water beïnvloeden hoeveel water eruit gaat.

Om het model te laten werken, is er ook een formule nodig. Met deze formules en hoe de verschillende grootheden samenhangen, kun je voorspellen wanneer de emmer vol is of hoe ver je de kraan moet openen om de instroomsnelheid gelijk te maken aan de uitstroomsnelheid. Dit is een simpel voorbeeld van modelleren: een situatie waarbij we de werkelijkheid vereenvoudigen tot een aantal grootheden en hoe ze met elkaar te maken hebben.

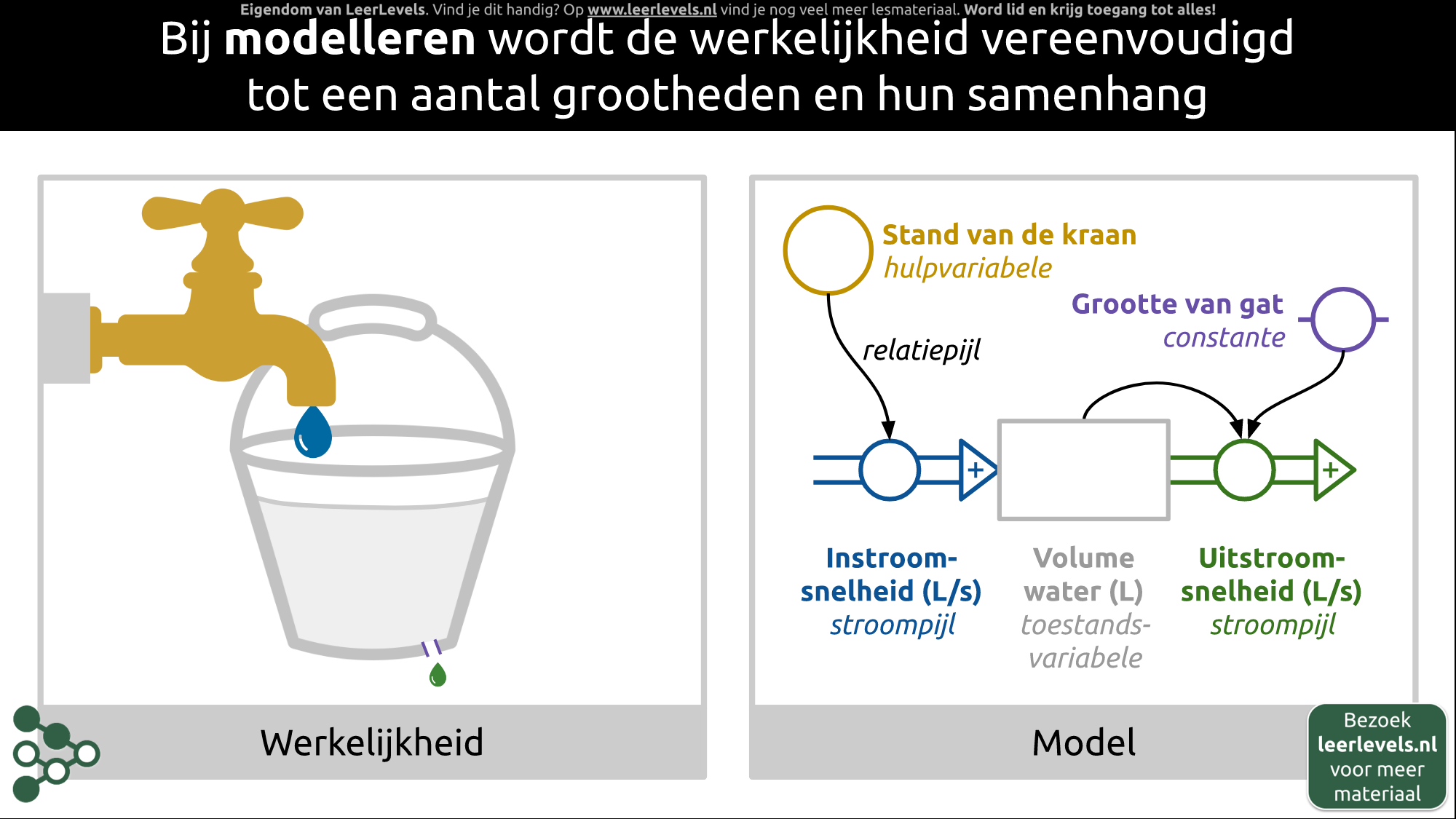
(Afbeelding: Animatie voor Modelleren concept)

Terug naar overzicht Meld je aan

Molecuul

Een molecuul is het kleinste deel van een stof dat de chemische eigenschappen van die stof behoudt. Het is opgebouwd uit atomen.

Een voorbeeld van een atoom is het koolstofatoom. Alle atomen worden ook wel elementen genoemd. Koolstof is een veelvoorkomend element. Zodra je atomen samenvoegt, vormen ze moleculen. Bijvoorbeeld, water bestaat uit één zuurstofatoom en twee waterstofatomen.

Moleculen kunnen ook groot zijn. Een voorbeeld hiervan is het glucosemolecuul, C6H12O6. Dit molecuul bestaat uit zes koolstofatomen, twaalf waterstofatomen en zes zuurstofatomen.

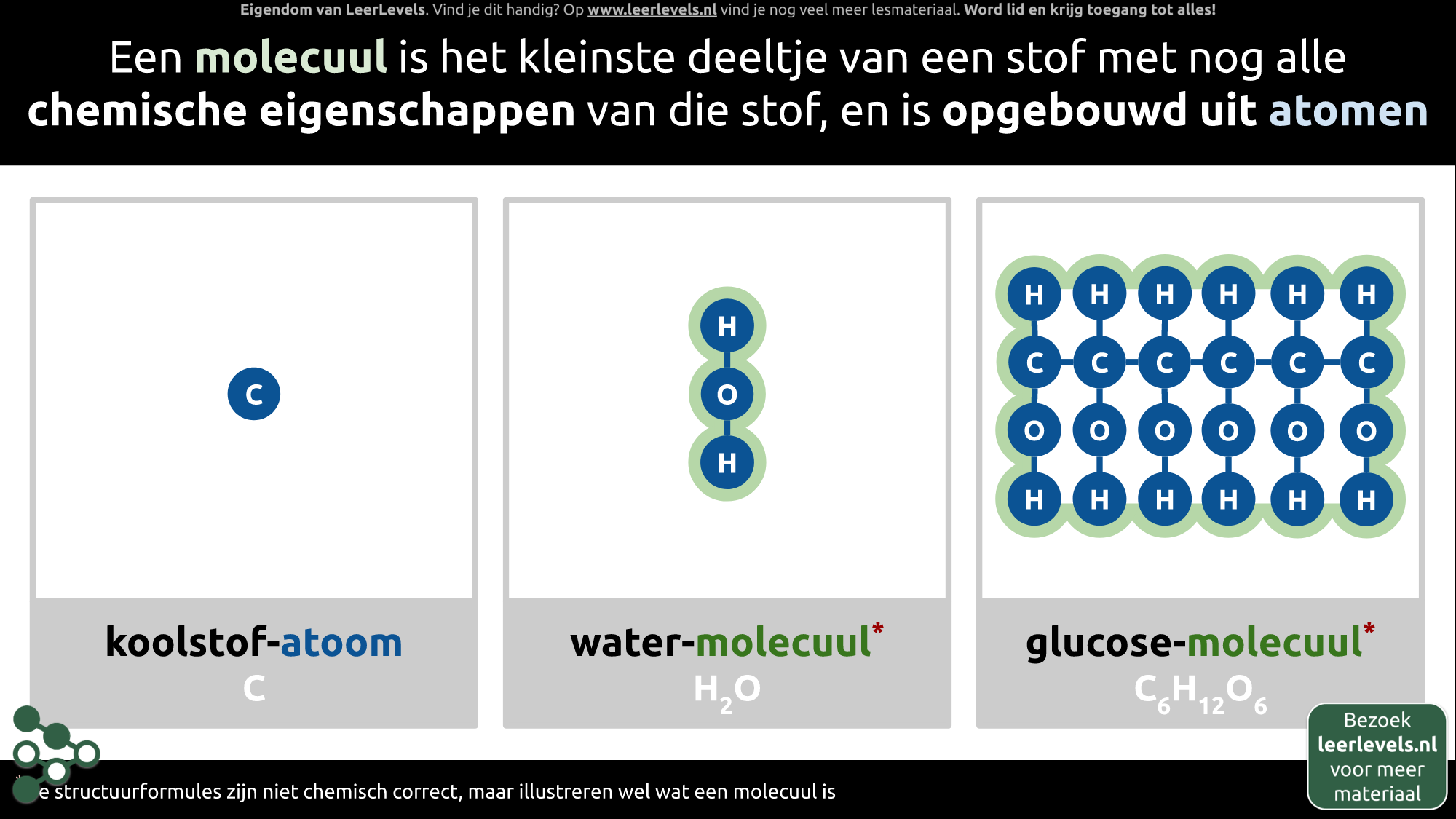
(Afbeelding: Animatie voor Molecuul)

Molecuulmodel

Het molecuulmodel bestaat uit drie regels die veel natuurkundige processen kunnen voorspellen. De eerste regel zegt dat moleculen niet veranderen als ze van fase veranderen. Dit betekent dat een molecuul hetzelfde blijft in de vaste, vloeibare en gasfase. Regel twee zegt dat hogere temperaturen ervoor zorgen dat moleculen sneller bewegen. Moleculen in de gasfase bewegen over het algemeen sneller dan moleculen in de vaste fase. De derde regel is dat als moleculen verder uit elkaar staan, hun onderlinge aantrekkingskracht afneemt. Deze kracht wordt de Van der Waals-kracht genoemd. Samengevat vormen deze drie regels het molecuulmodel en kunnen ze gebruikt worden om verschillende natuurkundige processen te voorspellen.

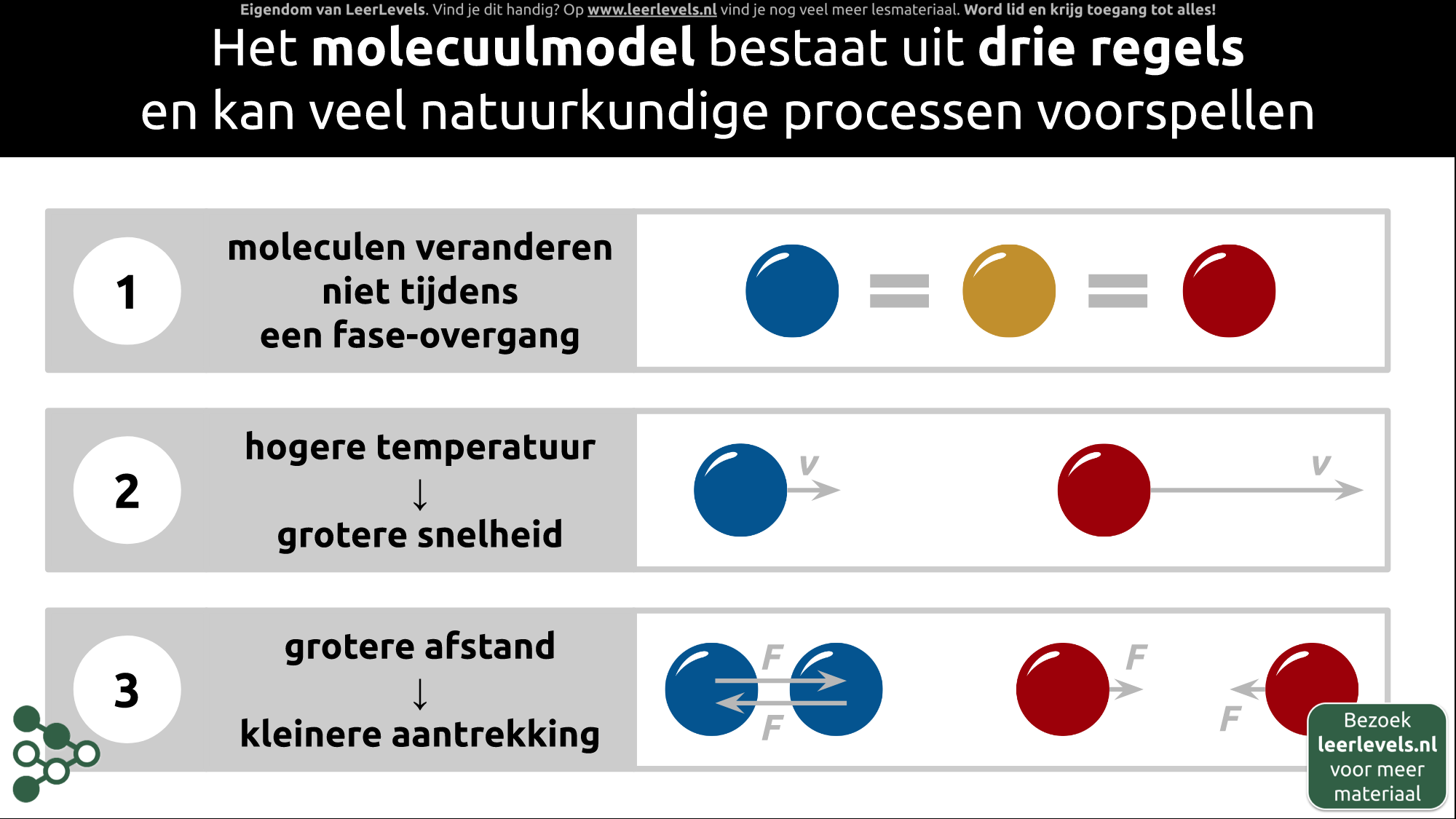
(Afbeelding: Animatie voor Molecuulmodel)

Terug naar overzicht Meld je aan

Moment

Arm

De arm van een kracht is de afstand van het draaipunt naar de werklijn van de kracht. Als je een weegschaal hebt en de zwaartekracht erop inwerkt, teken je eerst de werklijn en dan de kortste afstand naar het draaipunt. Dit heet de arm en staat loodrecht op de werklijn. Bij krachten onder een andere hoek moet je de werklijn tekenen om de juiste afstand te vinden. Als de kracht loodrecht op de arm staat, hoeft de werklijn niet getekend te worden. In de rechter situatie is de arm korter dan in de linker situatie, waardoor het losmaken van de moer moeilijker kan zijn. De arm wordt uitgedrukt in meters.

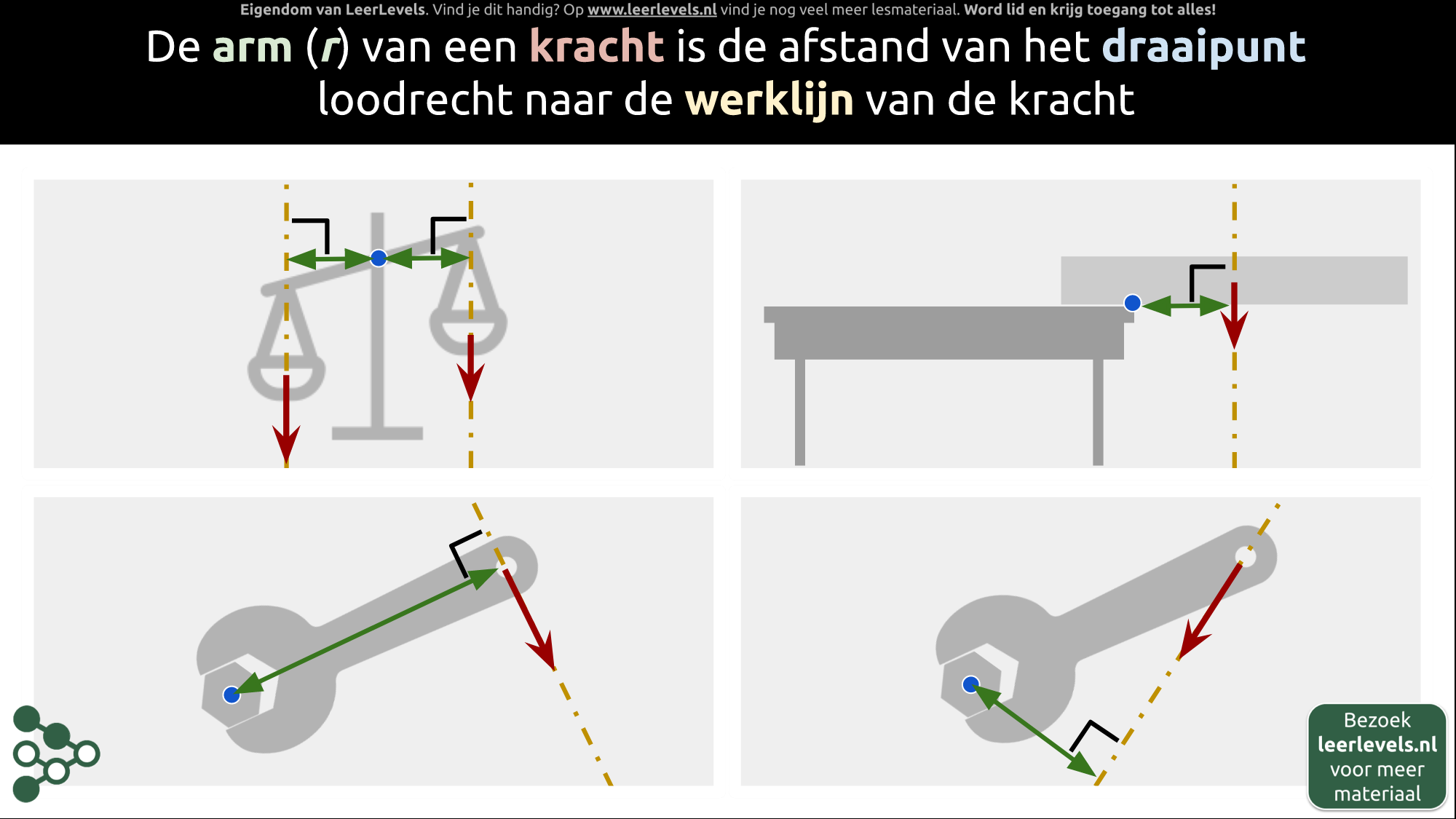
(Afbeelding: Animatie voor Arm)

Moment toepassen

Het moment berekenen is niet moeilijk als we weten hoe groot de kracht is en hoe ver deze op een arm zit. Een voorbeeld is het losdraaien van een moer met een kracht van 1000 N op een arm van 0,1 m. Het moment berekenen we met de formule moment = kracht × arm. Het moment is dan 25 Nm. Als we de kracht verdubbelen naar 2000 N, wordt het moment ook verdubbeld naar 50 Nm. Als we de arm ook verdubbelen naar 0,2 m, wordt het moment versterkt met een factor 4 en wordt het 100 Nm. Het is belangrijk om een schets te maken om de kracht en arm nauwkeurig te meten en het moment te berekenen.

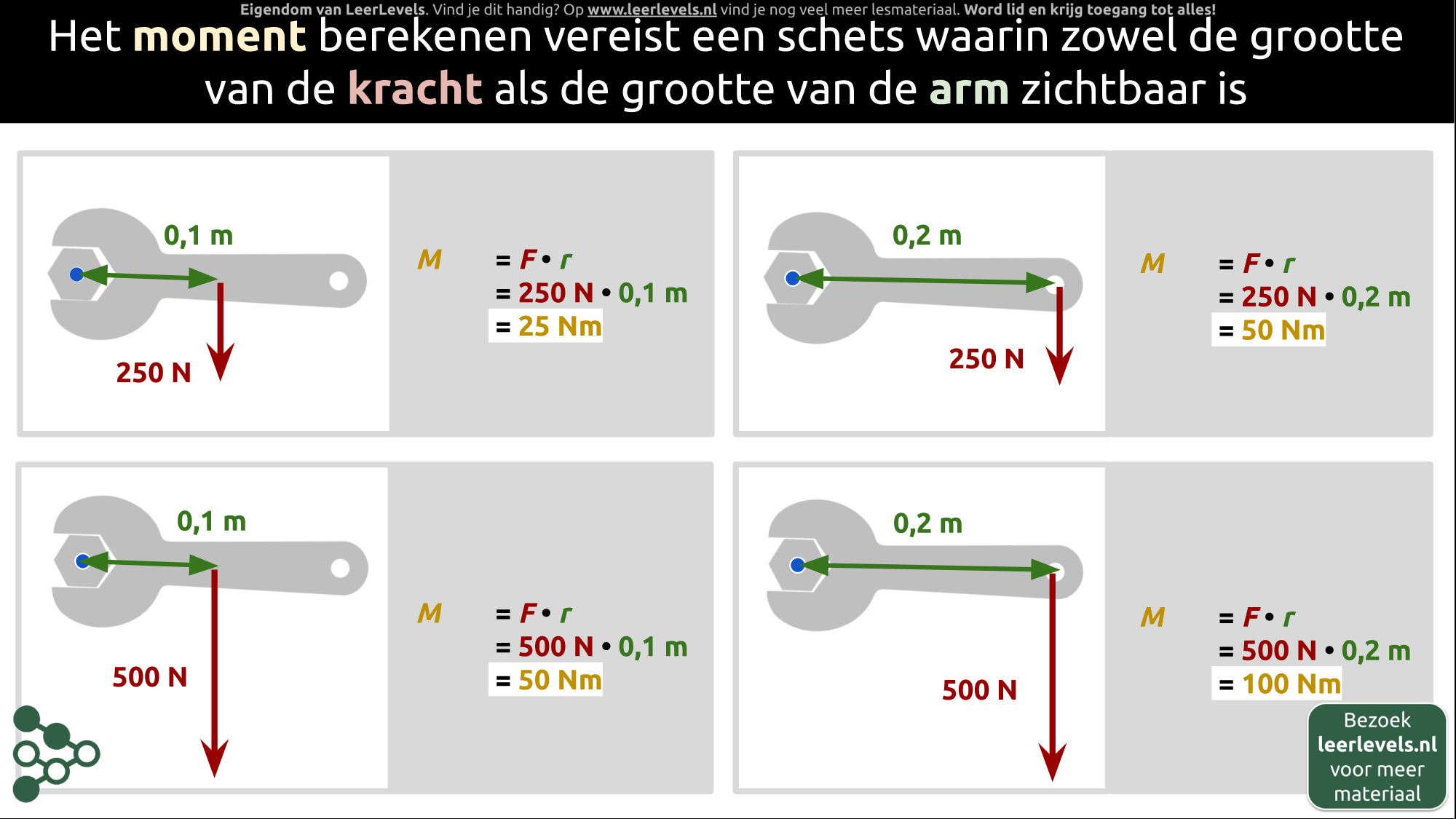
(Afbeelding: Animatie voor Moment toepassen)

Moment concept

Het moment is hoe goed een kracht iets kan laten draaien. Als je een klein gewichtje dichtbij het draaipunt hangt, is het moeilijk om iets te draaien. Dit noemen we een "klein" moment. Hang je het gewichtje verder weg, dan wordt het makkelijker om iets te draaien. Dit noemen we een "normaal" moment. Hoe groter het gewicht, hoe makkelijker het is om iets te draaien. Als het gewicht ver weg is van het draaipunt, is dat het makkelijkst, dit noemen we een "groot" moment. Het moment hangt af van de grootte van de kracht en de afstand tot het draaipunt.

(Afbeelding: Animatie voor Moment concept)

Moment formule

Het moment is recht evenredig met de kracht en de bijbehorende arm. In formulevorm ziet dit er als volgt uit:

M = F · r

waarbij M staat voor het moment in newtonmeter (Nm), F voor de kracht in Newton (N)en r voor de arm in meter (m). Merk op dat het moment in Newton keer meter wordt uitgedrukt, en dus niet in newton per meter.

(Afbeelding: Animatie voor Moment formule)

Terug naar overzicht Meld je aan

Momentenevenwicht

Momentenevenwicht concept

Als iets draait en niet beweegt, heet dat momentenevenwicht. Dat kan op verschillende manieren komen. Bijvoorbeeld met een evenwichtsbalk waar een poppetje links staat en een gewicht rechts met dezelfde massa en dezelfde afstand tot het draaipunt. Dan is het systeem in balans. Als je meer massa toevoegt, moet je het dichterbij het draaipunt zetten om het in balans te houden. Als de helft van je massa op de balk staat, moet je het twee keer zo ver van het draaipunt zetten om balans te houden. Als er momentenevenwicht is, is er balans in het draaiend systeem. Dit kan op verschillende manieren gebeuren.

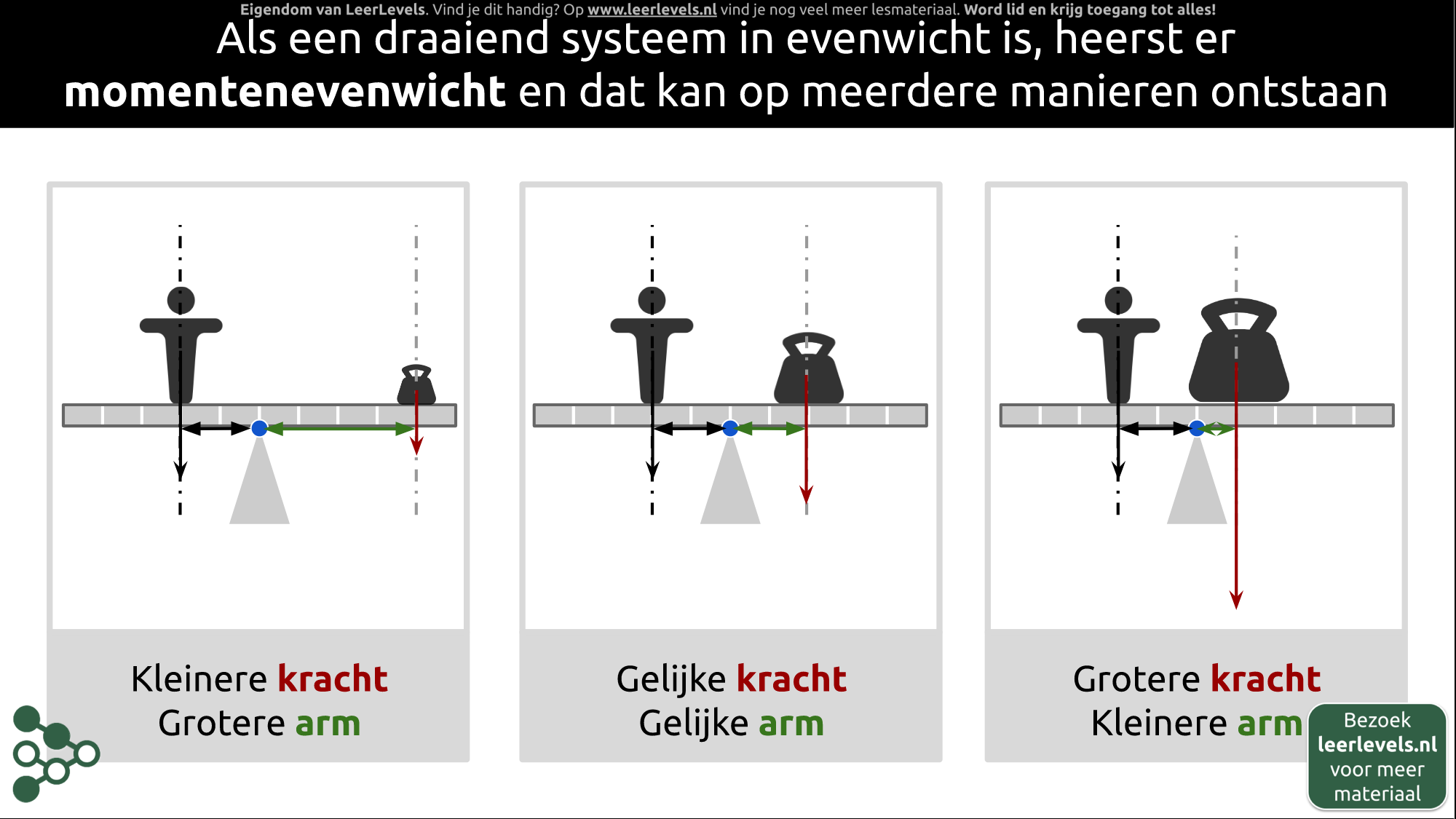
(Afbeelding: Animatie voor Momentenevenwicht concept)

Momentenevenwicht voorbeeldsom

Als we willen berekenen welke massa het contragewicht van een hijskraan moet hebben, kunnen we daarbij het best een schets gebruiken. In de schets moeten we de relevante informatie toevoegen, zoals de massa van de persoon die wordt opgetild, de massa van het contragewicht, de zwaartekracht en het draaipunt. Om te kunnen rekenen, moeten we ook weten wat de armen zijn. Als we alle informatie hebben, kunnen we de massa van het contragewicht berekenen met behulp van de formule voor momentenevenwicht: kracht links keer arm links is gelijk aan kracht rechts keer arm rechts. Door enkele simpele stappen uit te voeren, kunnen we dit omzetten naar de formule mL = mR× rR/RL, waarbij mL de massa aan de linker kant is, mR de massa aan de rechter kant, en rL en rR de lengtes van respectievelijk de linker en de rechter arm. Als we de waardes invullen in de formule, krijgen we als antwoord de massa van het contragewicht. Het is ook mogelijk om eerst de waardes in te vullen en dan de formule te gebruiken om de massa van het contragewicht te berekenen als de oorspronkelijke waardes veranderen.

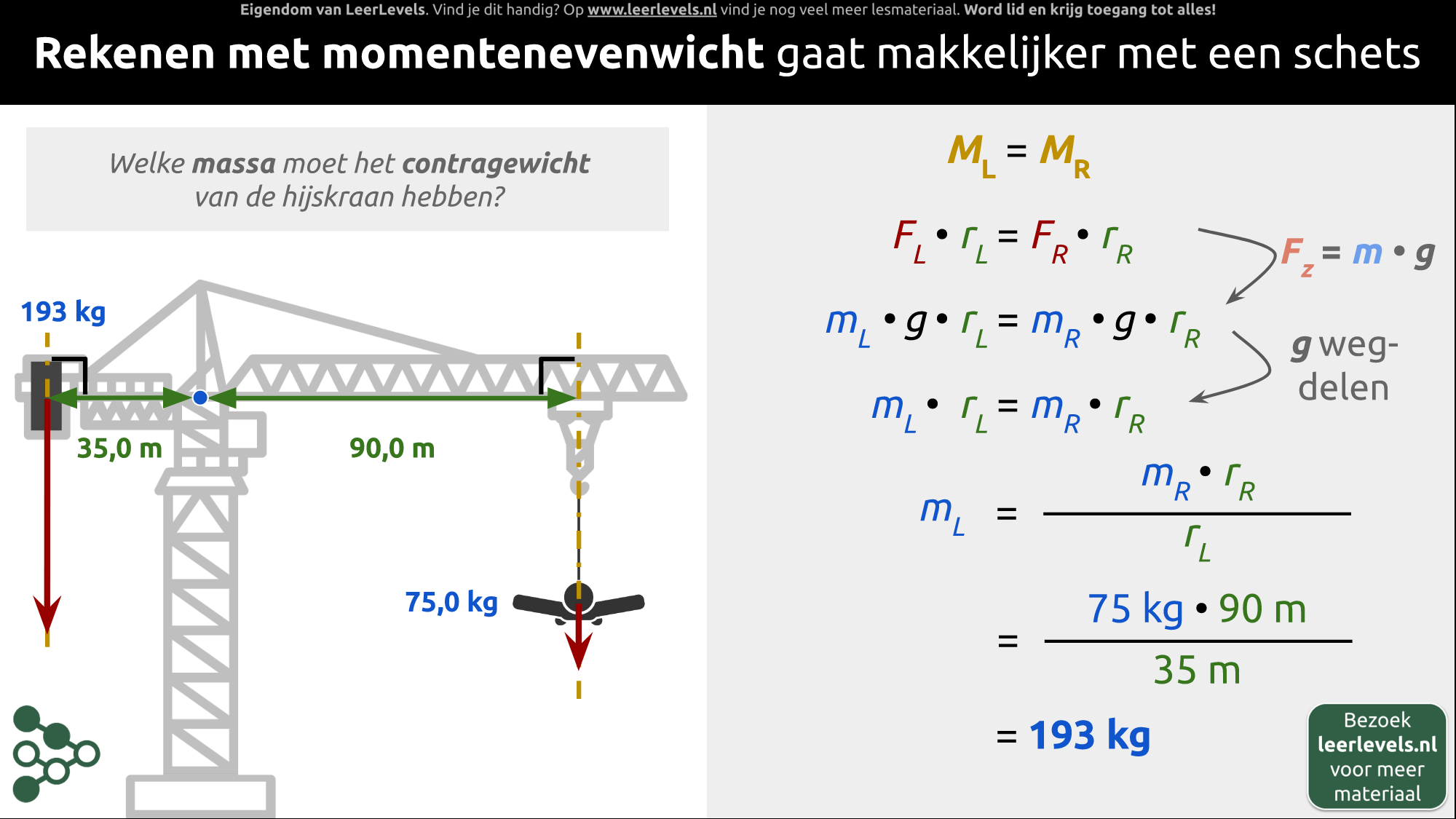
(Afbeelding: Animatie voor Momentenevenwicht voorbeeldsom)

Momentenevenwicht formule

Bij momentevenwicht is het moment dat linksom werkt gelijk aan het moment dat rechtsom werkt. Dit kan worden weergegeven met de formule:

∑ Mlinks = ∑ Mrechts

Als er aan beide kanten van een voorwerp één kracht aanwezig is, kun je dit beschrijven in termen van kracht en arm. Bijvoorbeeld:

Flinks · rlinks = Frechts · rrechts

Deze formule is alleen van toepassing wanneer er aan beide zijden slechts één kracht is die voor het moment zorgt.

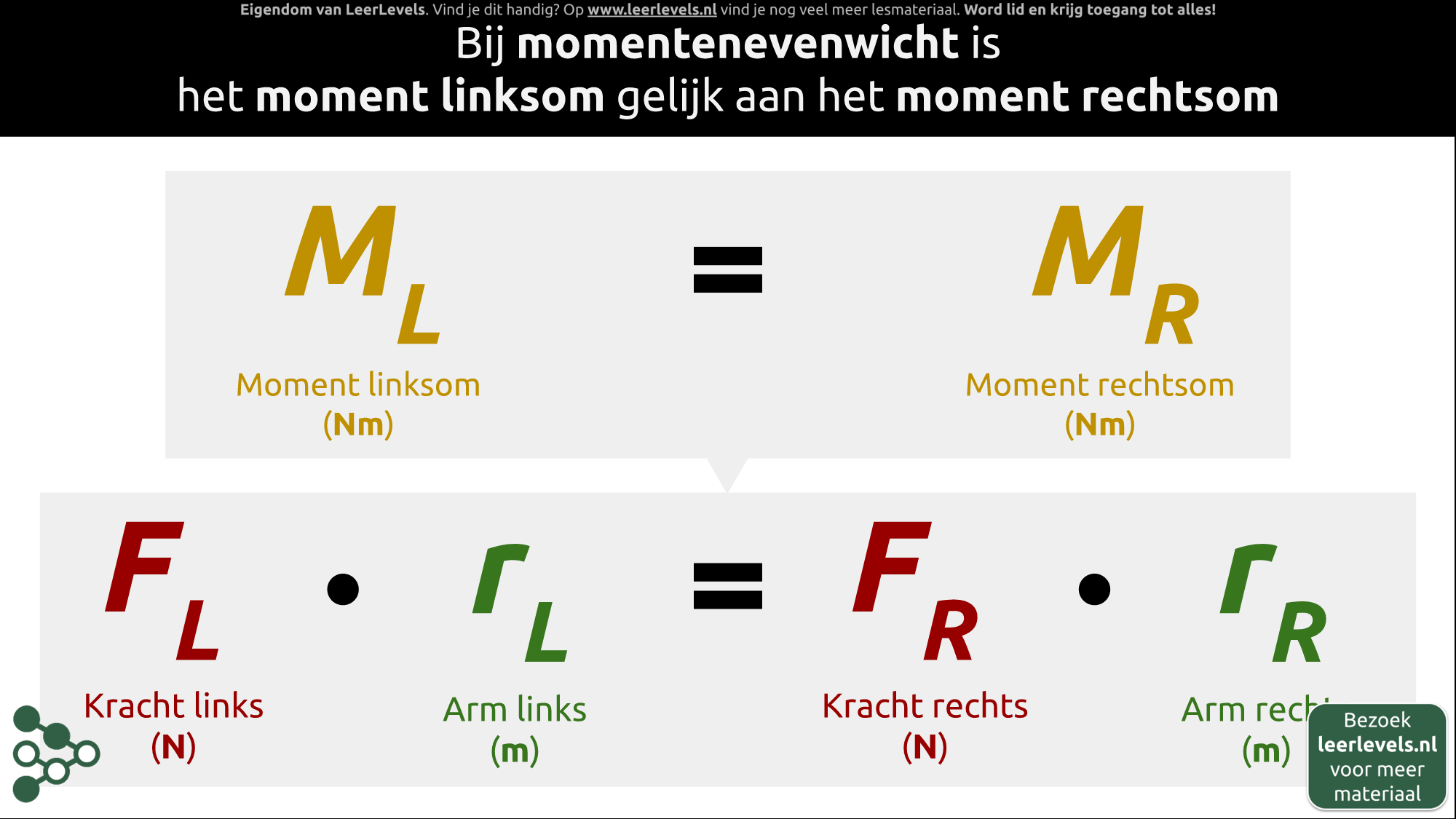
(Afbeelding: Animatie voor Momentenevenwicht formule)

Terug naar overzicht Meld je aan

Multimeter

Een multimeter is een apparaat waarmee je elektrische dingen kunt meten. Het heeft een draaiknop met verschillende symbolen erop en je kunt hem zo instellen dat hij spanning en stroom kan meten. Er zijn vier categorieën waarop je kunt meten: wisselspanning, gelijkspanning, wisselstroom en gelijkstroom. Als je bijvoorbeeld het symbool voor wisselspanning instelt en de multimeter aansluit op netspanning, dan zou je ongeveer 230 volt moeten meten. Je kunt ook weerstand en temperatuur meten door speciale elementen op de multimeter aan te sluiten. Het belangrijkste is dat de multimeter verschillende standen heeft waarmee hij verschillende dingen kan meten.

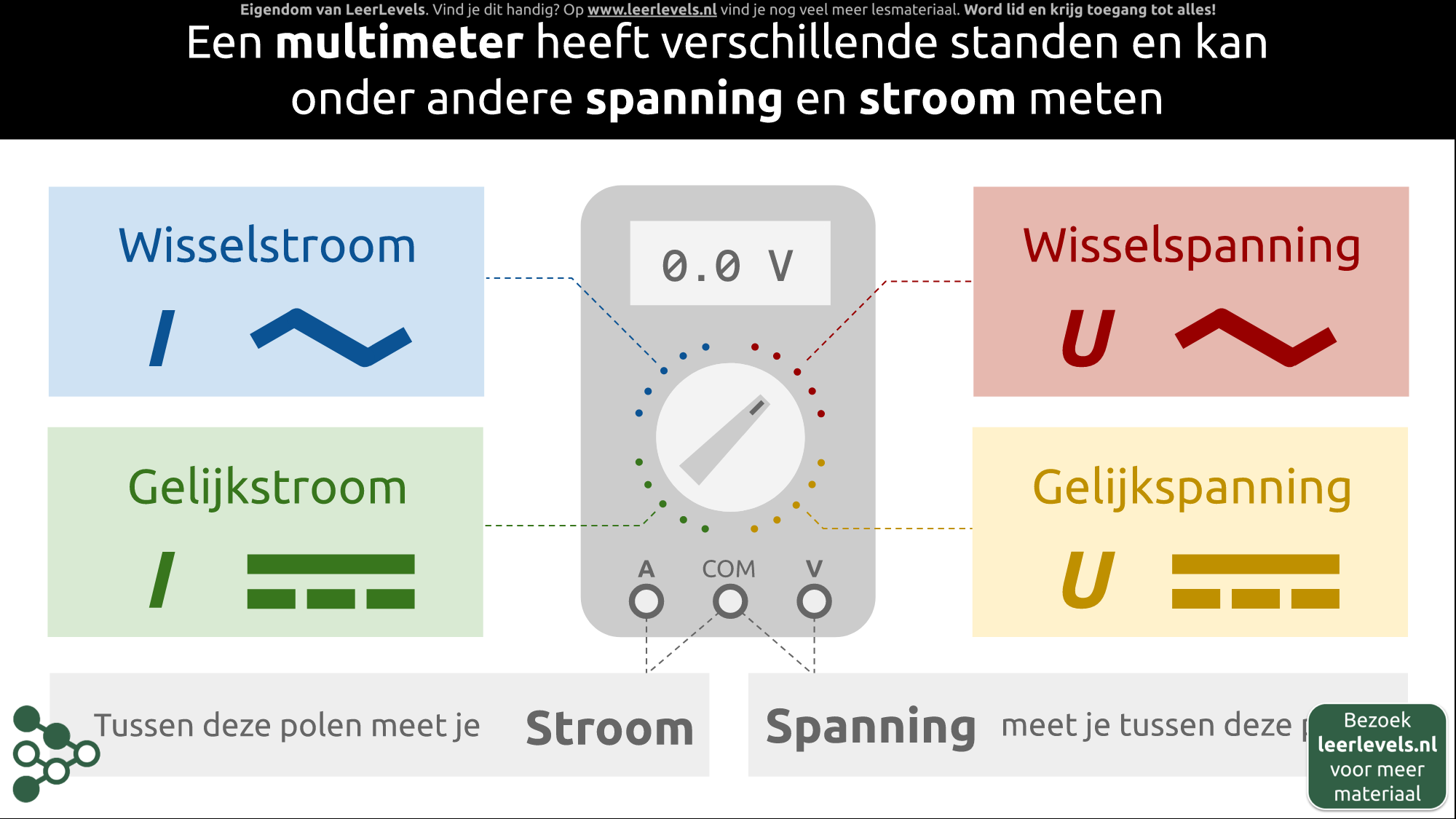
(Afbeelding: Animatie voor Multimeter)

Terug naar overzicht Meld je aan

Natuurkunde

Natuurkunde tips

Hier zijn drie tips voor leerlingen die natuurkunde leren:

1. Probeer altijd negens te halen in plaats van zesjes. Dit maakt het leren en onthouden van de stof veel makkelijker.

2. Zorg voor een goede basis door de grootheden (F, m, a, etc.) en eenheden (N, kg, m/s², etc.) uit je hoofd te leren. Ook het memoriseren van formules helpt hierbij.

3. Maak veel opdrachten om routine te ontwikkelen bij het maken van proefwerken. Alleen op deze manier krijg je inzicht in de stof en het vakgebied.

Succes!

(Afbeelding: Animatie voor Natuurkunde tips)

Doel van natuurkunde

Het doel van de natuurkunde is om de eigenschappen van energie, materie en straling te beschrijven. Hiervoor maken we gebruik van verschillende gereedschappen: meetbare grootheden, eenheden om deze grootheden uit te drukken, en formules die de relaties tussen de grootheden bepalen.

Een voorbeeld van een grootheid is massa, die wordt uitgedrukt in kilogram (kg), en het bijbehorende volume, uitgedrukt in kubieke meter (m³). De relatie tussen deze twee grootheden noemen we dichtheid en deze wordt uitgedrukt in kilogram per kubieke meter (kg/m³).

In de natuurkunde zijn er veel grootheden. Om deze informatie effectief te kunnen toepassen, is het essentieel te begrijpen wat deze grootheden precies betekenen. Het uiteindelijke doel van de natuurkunde is dan ook om deze grootheden zodanig te beschrijven dat we de eigenschappen van energie, materie en straling kunnen koppelen en voorspellen hoe deze zich zullen gedragen.

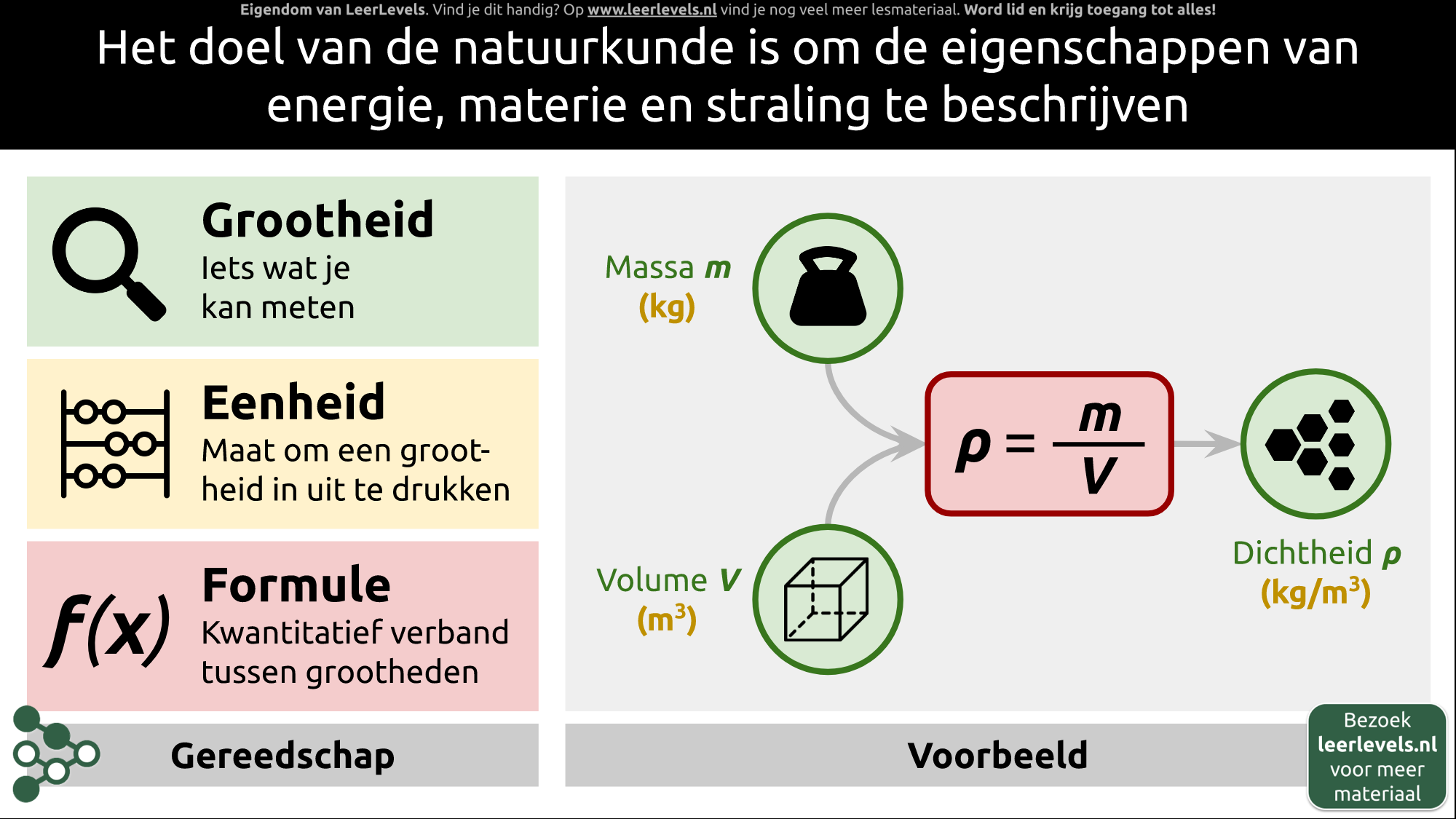
(Afbeelding: Animatie voor Doel van natuurkunde)

Terug naar overzicht Meld je aan

Netspanning

Het stopcontact levert wisselspanning van 230 volt en een frequentie van 50 hertz; dit wordt ook wel netspanning genoemd. Als je een multimeter aansluit op een stopcontact, lees je een netspanning af van 230 V en een frequentie van 50 Hz. De plus- en minpool wisselen vijftig keer per seconde van plaats in de wisselspanning. Het symbool voor wisselspanning is een gekantelde S. Dit komt doordat energiecentrales energie opwekken met een dynamo die een wisselspanning oplevert.

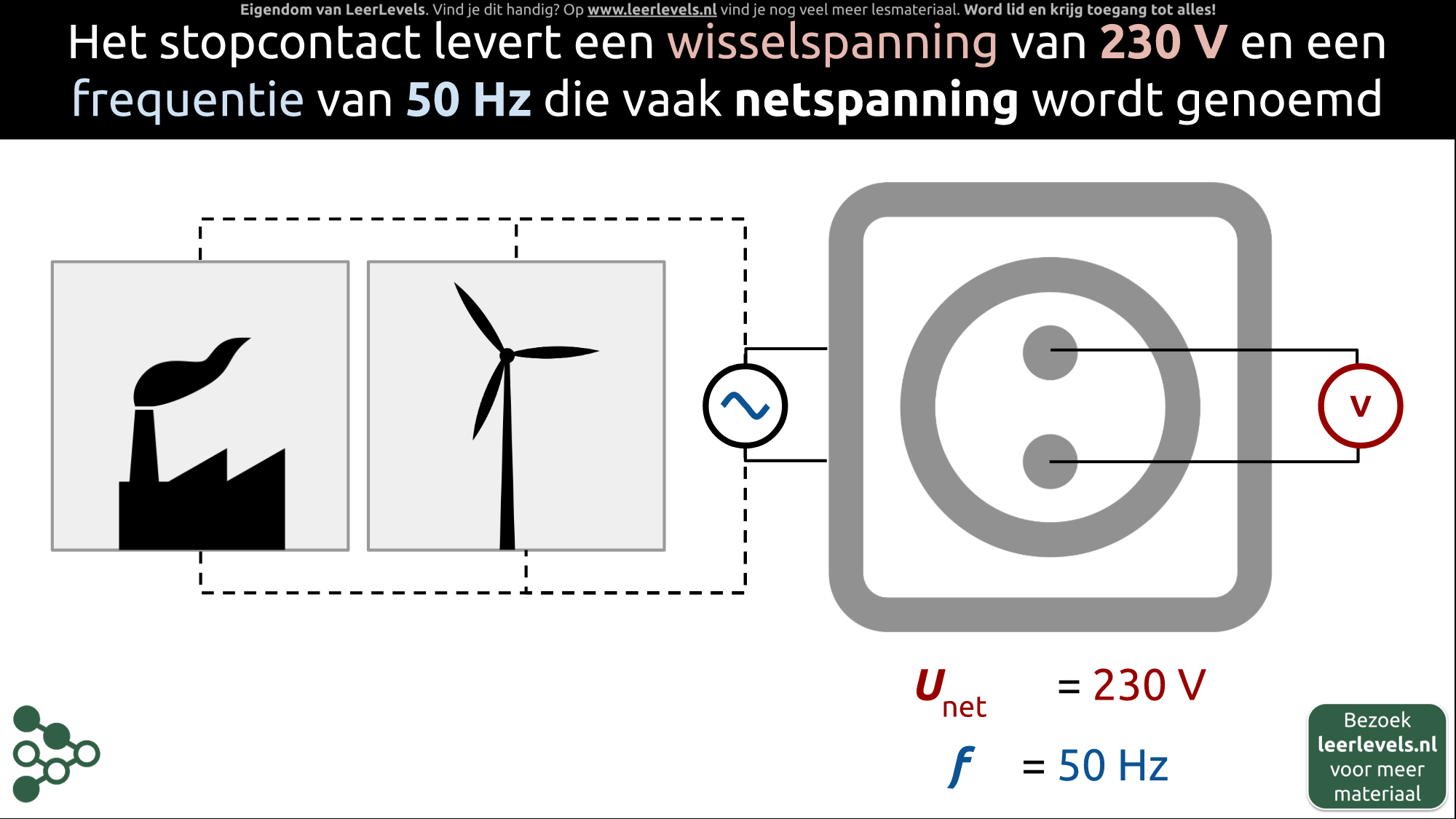
(Afbeelding: Animatie voor Netspanning)

Terug naar overzicht Meld je aan

Normaalkracht

De normaalkracht zorgt ervoor dat voorwerpen niet door elkaar heen kunnen gaan. Als een bal op een tafel ligt, staat de normaalkracht loodrecht op het oppervlak van de tafel. Dit komt doordat de zwaartekracht van de aarde de bal naar beneden trekt, waardoor de bal tegen de tafel botst en een kracht op de tafel uitoefent. De tafel duwt dan terug op de bal, wat de normaalkracht is. Op microscopisch niveau worden elektronen afgestoten, wat resulteert in een normaalkracht die omhoog op de bal en omlaag op de tafel werkt wanneer twee oppervlakken elkaar raken. De afstoting van elektronen creëert de normaalkracht.

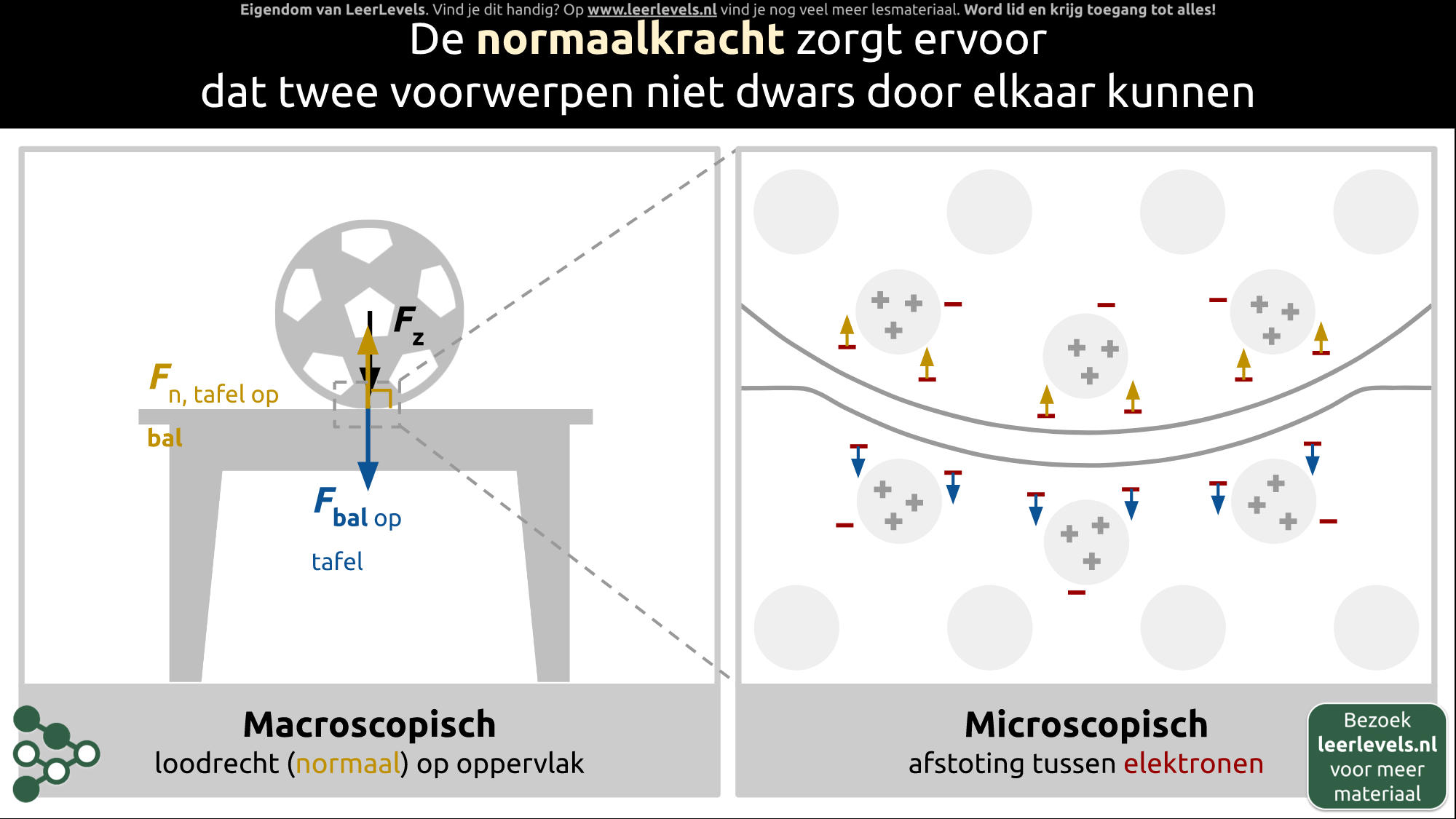
(Afbeelding: Animatie voor Normaalkracht)

Terug naar overzicht Meld je aan

Onbepaaldheidsrelatie

Onbepaaldheidsrelatie Heisenberg concept

Volgens de onbepaaldheidsrelatie van Heisenberg kun je niet tegelijkertijd weten waar een deeltje zich bevindt en hoeveel snelheid het heeft. Als het deeltje eruit ziet als een klassieke golf, weten we wel de snelheid, maar niet de exacte locatie. Als het deeltje heel precies op één plaats is, weten we niet precies hoe snel het gaat. Er zijn ook situaties waarin we een redelijk goed idee hebben van zowel de locatie als de snelheid. In het algemeen is het onmogelijk om beide grootheden precies te kennen. Dat is de onbepaaldheidsrelatie van Heisenberg.

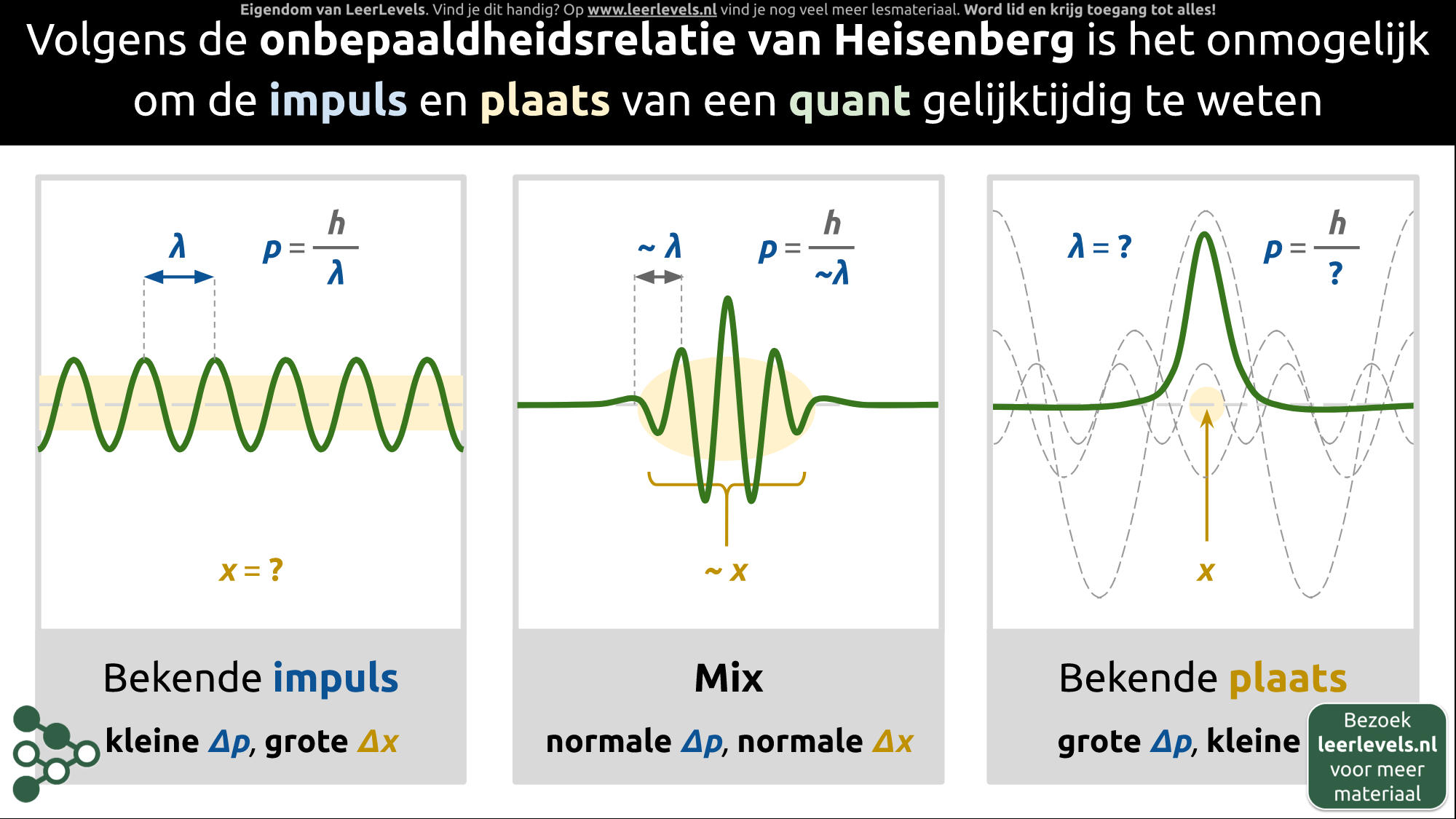
(Afbeelding: Animatie voor Onbepaaldheidsrelatie Heisenberg concept)

Onbepaaldheidsrelatie Heisenberg formule

De onbepaaldheidsrelatie van Heisenberg betekent dat de plaats en de impuls van een kwantumdeeltje niet precies kunnen worden bepaald. Hoe nauwkeuriger de plaats van het deeltje wordt bepaald, hoe minder precies de impuls kan worden bepaald. De constante van Planck speelt hierbij een rol. Dit betekent dat het product van de onbepaaldheid in de plaats (Δ x) en de onbepaaldheid in de impuls (Δ p) groter moet zijn dan een bepaalde waarde. Als de onbepaaldheid in de plaats bekend is, kan de minimale onbepaaldheid in de impuls worden berekend. Deze relatie wordt de onbepaaldheidsrelatie van Heisenberg genoemd.

(Afbeelding: Animatie voor Onbepaaldheidsrelatie Heisenberg formule)

Terug naar overzicht Meld je aan

Ontsnappingssnelheid

Ontsnappingssnelheid concept

Een voorwerp met de ontsnappingssnelheid vo kan zich uiteindelijk oneindig ver van een hemellichaam verwijderen en zal op die afstand geen snelheid meer hebben. We kunnen drie situaties onderscheiden

Snelheid is kleiner dan ontspanningssnelheid (v1 < v0)

Stel dat je een raket vanaf de aarde lanceert met als doel het oneindige te bereiken, weergegeven als r = \infty. Als je lanceert met een snelheid v1 die kleiner is dan de ontsnappingssnelheid, stijgt de raket omhoog, maar verliest hij al snel al zijn snelheid. Vervolgens valt hij weer terug naar de aarde.

Snelheid is gelijk dan ontspanningssnelheid (v1 = v0)
Als je een raket precies met de ontsnappingssnelheid lanceert, bereikt de raket theoretisch het oneindige. Op deze afstand wordt de raket niet meer door de zwaartekracht van de aarde beïnvloed. Alle energie van de raket is gebruikt om aan de zwaartekracht van de aarde te ontsnappen. De raket heeft dan geen snelheid meer.

Snelheid is gelijk dan ontspanningssnelheid (v1 > v0)
Wanneer je een raket lanceert met een snelheid groter dan de ontsnappingssnelheid, kan de raket theoretisch het oneindige bereiken en behoudt het daar zelfs nog een snelheid. Dit is essentieel om in een redelijke tijd naar een andere planeet te reizen.

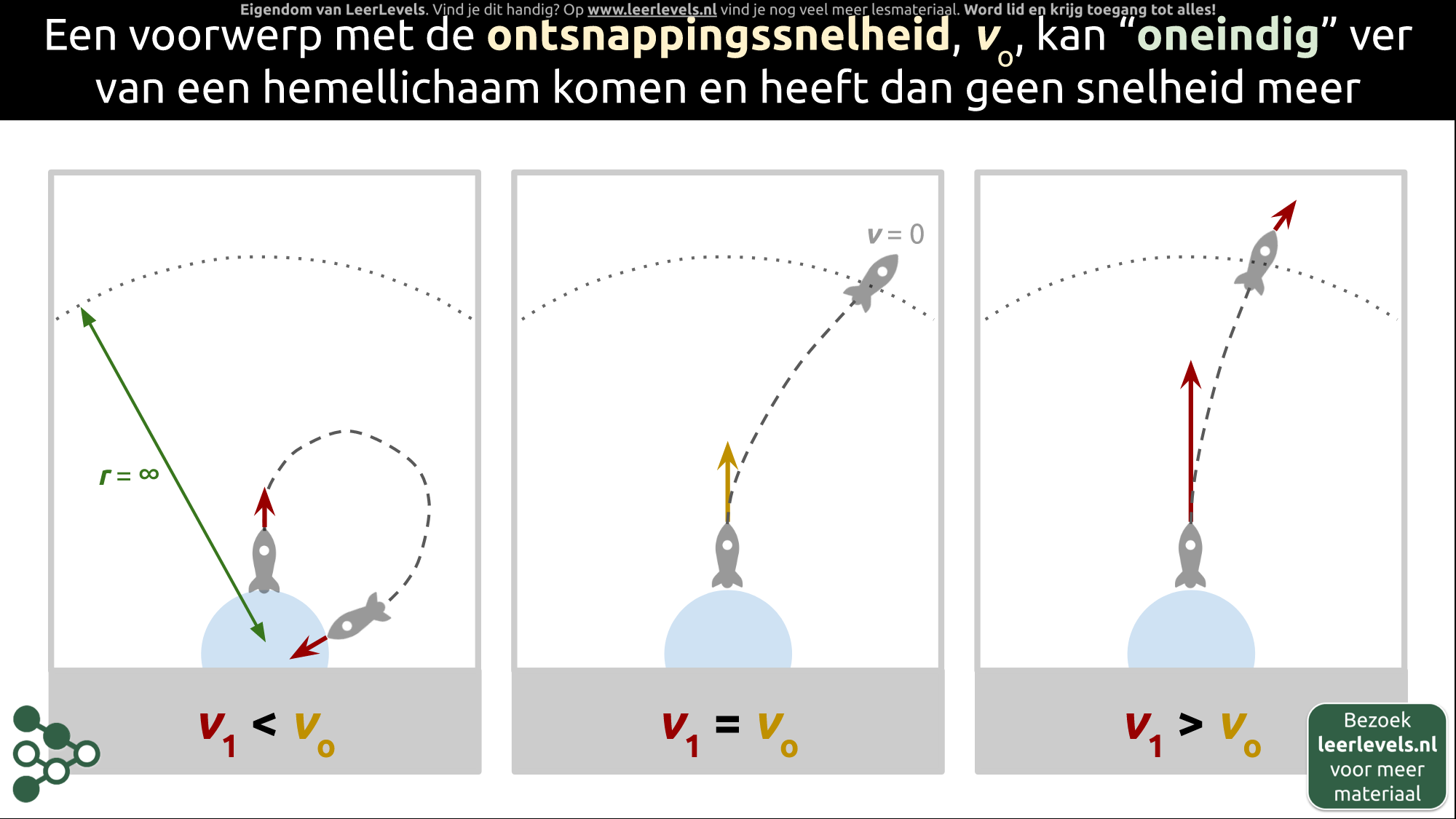
(Afbeelding: Animatie voor Ontsnappingssnelheid concept)

Ontsnappingssnelheid formule

De snelheid waarmee je moet bewegen om te ontsnappen van een hemellichaam hangt af van de massa en de afstand. Deze snelheid wordt berekend met de formule vo = √(2 · G · M/r), waarbij vo de ontsnappingssnelheid in meter per seconde is, G de gravitatieconstante in m³/kg · s² is, M de massa van het hemellichaam waar je vanaf wilt ontsnappen in kg is en r de afstand tussen de zwaartepunten in meters is. Let op dat je de juiste waarde invult voor r. Als je wilt weten wat de ontsnappingssnelheid is vanaf het oppervlak van de aarde, vul dan de straal van de aarde in. Als je wilt weten welke snelheid een satelliet nodig heeft, vul dan de baanstraal in.

(Afbeelding: Animatie voor Ontsnappingssnelheid formule)

Terug naar overzicht Meld je aan

Oppervlakte

Oppervlakte benaderen met hokjes

Het oppervlakte onder een grafiek kan worden berekend door het aantal hokjes te vermenigvuldigen met de oppervlakte van een hokje. Het aantal hoekjes komt ongeveer overeen met het oppervlak onder de grafiek. Om het oppervlak te berekenen, moet je het aantal hoekjes tellen en het oppervlak van een hoekje vinden. Dit kan worden afgeleid van de assen in het grafiekje. Je moet de eenheden omrekenen voordat je deze met elkaar vermenigvuldigt om het oppervlak te krijgen. Bijvoorbeeld, oppervlak van een hokje = 30 seconden · 2 meter per seconde = 60 meter. Als er 22 hokjes onder de lijn zijn geteld, dan is het totale oppervlak van deze hoek gelijk aan 1,3 km, dat is oppervlakte van een hoekje · aantal hoekjes, in dit geval 60 meter · 22.

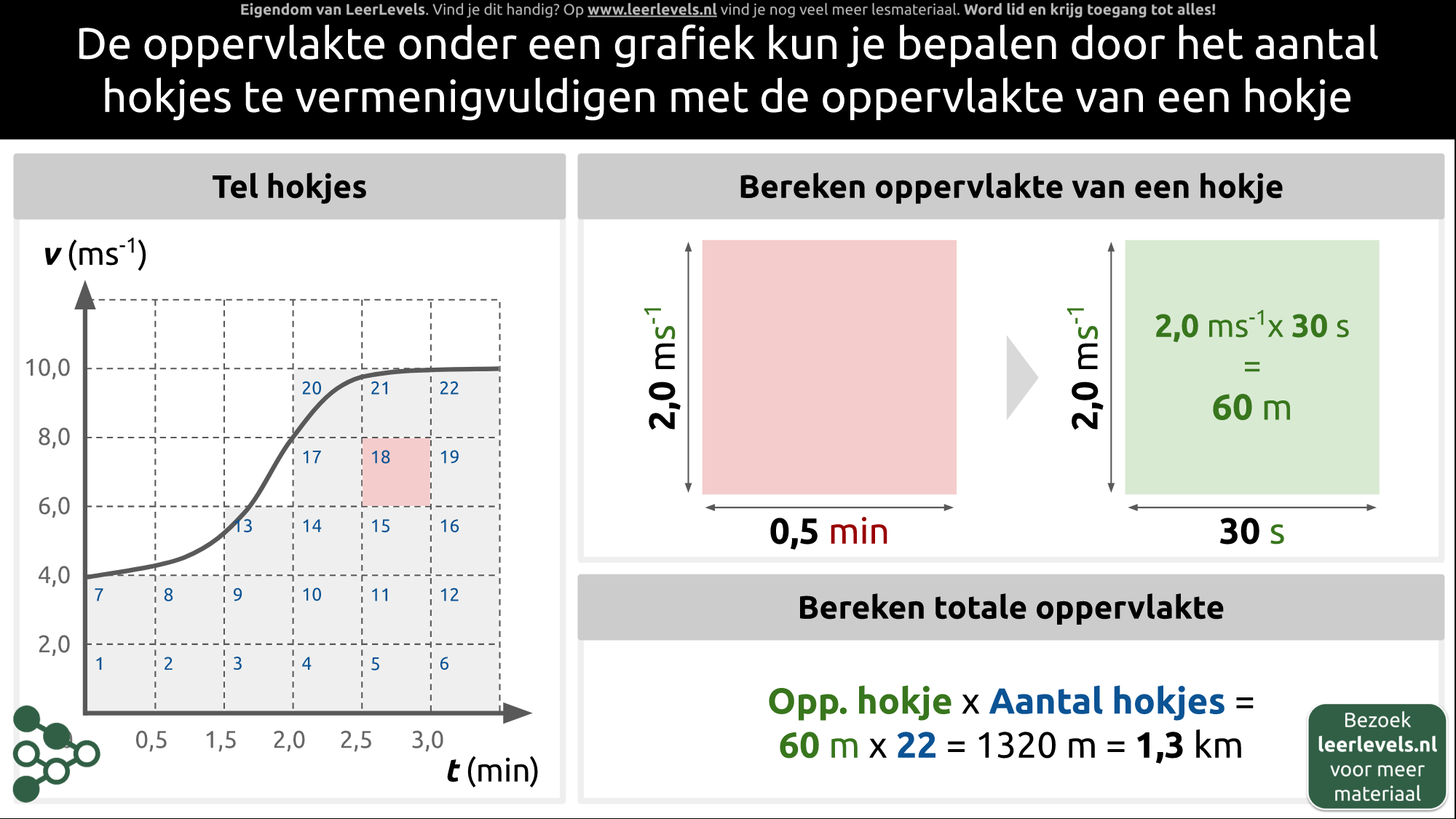
(Afbeelding: Animatie voor Oppervlakte benaderen met hokjes)

Oppervlakte formules 2D

Om het oppervlakte van basisvormen te berekenen, kan je gebruik maken van formules. In Binas tabel 36b kan je een overzicht hiervan vinden. De oppervlakte van een rechthoek kan berekend worden door de breedte (b) te vermenigvuldigen met de hoogte (h). Voor een driehoek kan de oppervlakte berekend worden door de helft van de bijbehorende rechthoek te nemen (½ b h), waarbij de breedte (b) en hoogte (h) van de driehoek gebruikt worden. Bij het berekenen van de oppervlakte van een cirkel is het belangrijk om de formule te weten: π r², waarbij π ongeveer 3,14 is en r de straal van de cirkel is. Al deze formules zijn terug te vinden in Binas. Het is handig om deze basisvormen (rechthoek, driehoek, cirkel) te kennen, maar het uit het hoofd leren van de formules is niet verplicht.

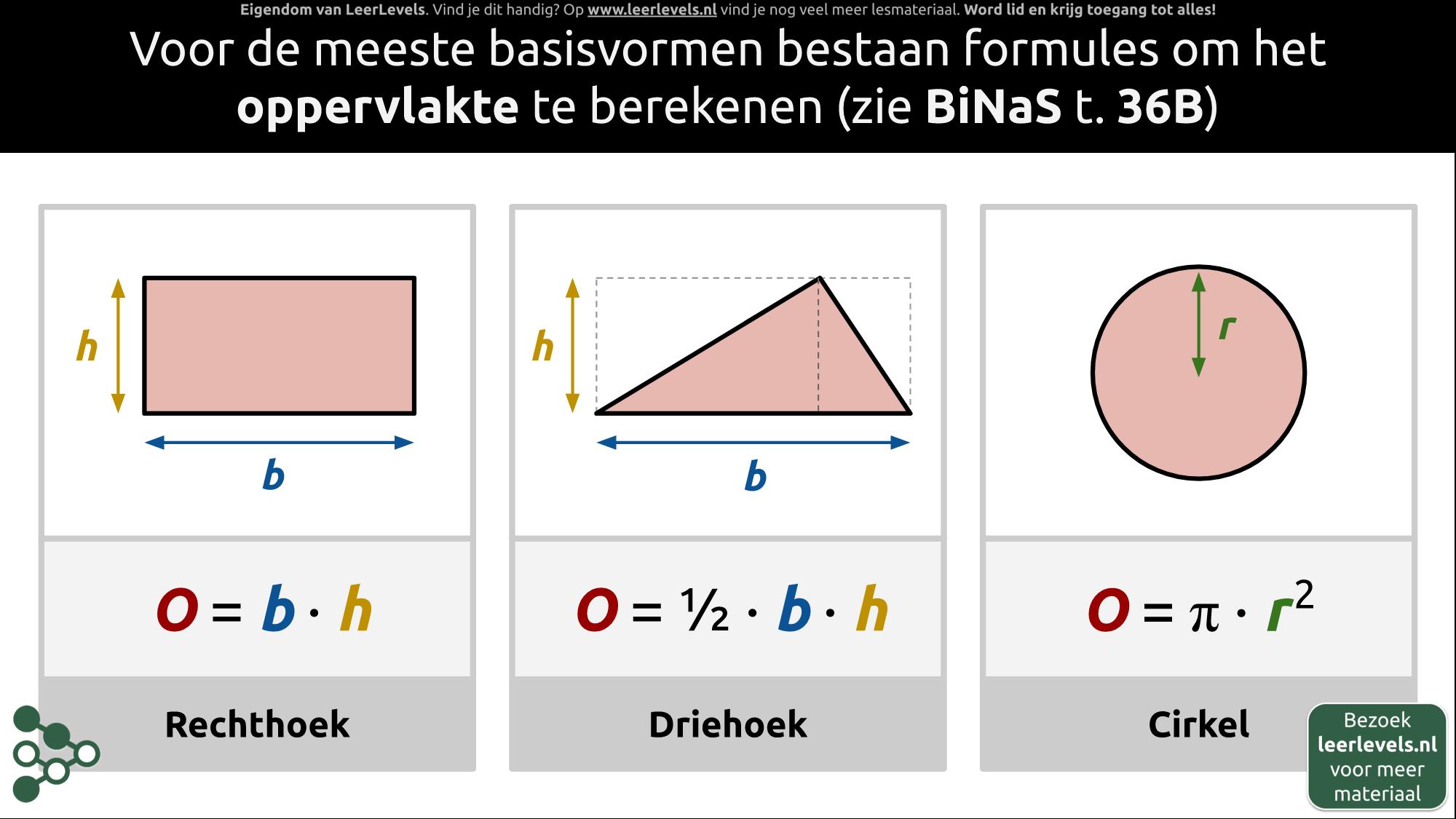
(Afbeelding: Animatie voor Oppervlakte formules 2D)

Terug naar overzicht Meld je aan

Oppervlaktemethode

Eenheden bij oppervlaktemethode

Bij een grafiek in de natuurkunde kan je soms de oppervlakte onder de grafiek gebruiken. Om deze oppervlakte te berekenen, vermenigvuldig je de lengte met de breedte. De eenheid van de oppervlakte is de eenheid van de y-as vermenigvuldigd met de eenheid van de x-as. Bijvoorbeeld Jouler per seconde vermenigvuldigd met seconde is Joule. Het oppervlak kan in sommige grafieken gemakkelijk worden berekend, maar in andere gevallen kan dit moeilijker zijn. Het is echter altijd even simpel om de eenheid van de oppervlakte te bepalen door de productregel te gebruiken. Bijvoorbeeld watt per vierkante meter per nanometer vermenigvuldigd met nanometer is gelijk aan watt per vierkante meter. In het algemeen is de eenheid van de oppervlakte het product van de eenheden van de assen.

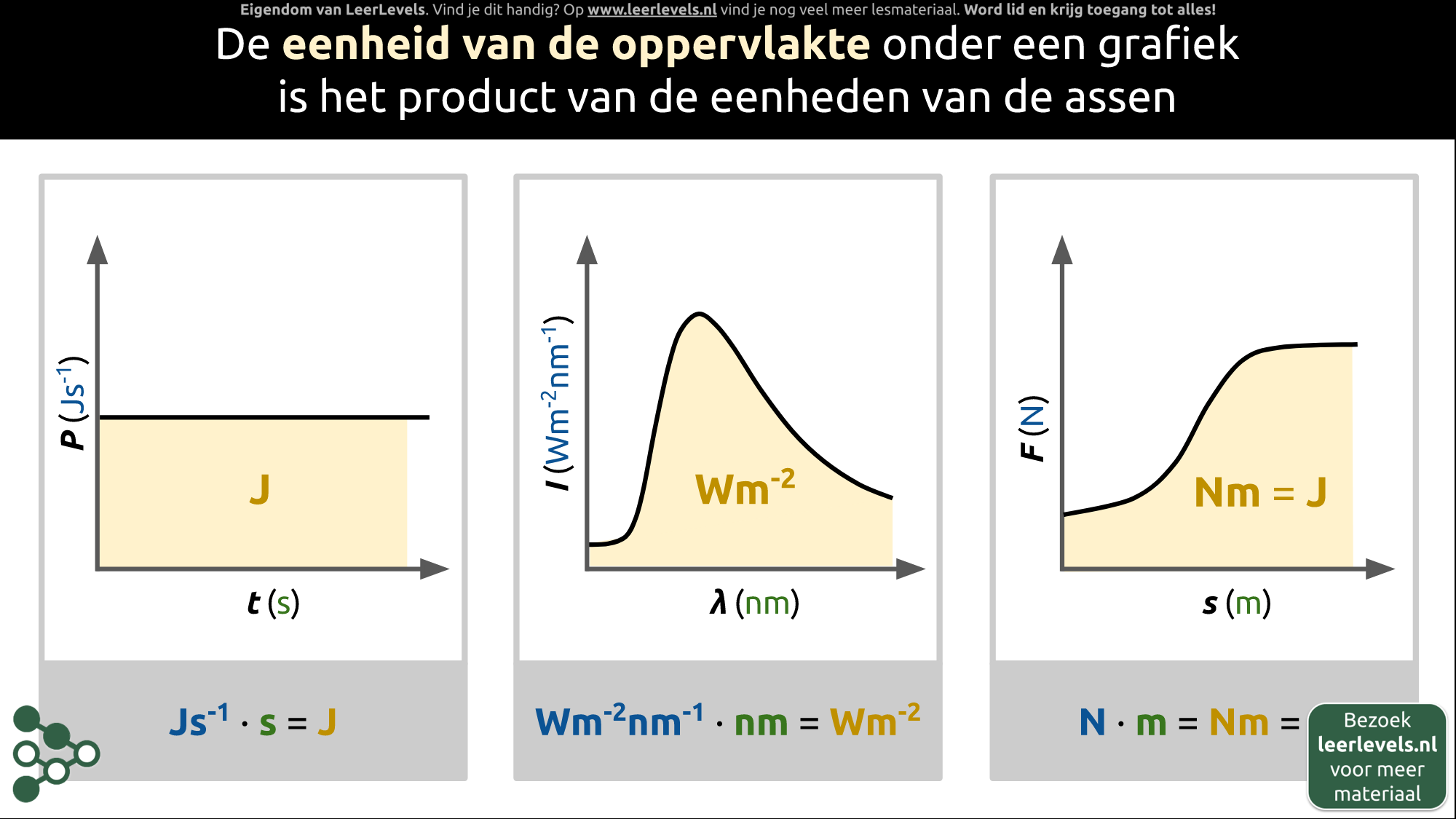
(Afbeelding: Animatie voor Eenheden bij oppervlaktemethode)

Oppervlaktemethode concept

De oppervlaktemethode is een manier om het oppervlak onder een grafiek te berekenen. Voor rechte lijnen kun je vijf stappen volgen:

1. Kies de punten.
2. Voeg hulplijnen toe (verticaal naar beneden).
3. Bepaal het oppervlak per deel.
4. Tel deze delen bij elkaar op.
5. Tel alle stukjes bij elkaar op.

In een grafiek kun je aflezen wat de waardes van x1, x2, y1 en y2 zijn. Zo kun je met de oppervlaktemethode het oppervlak onder de grafiek berekenen.

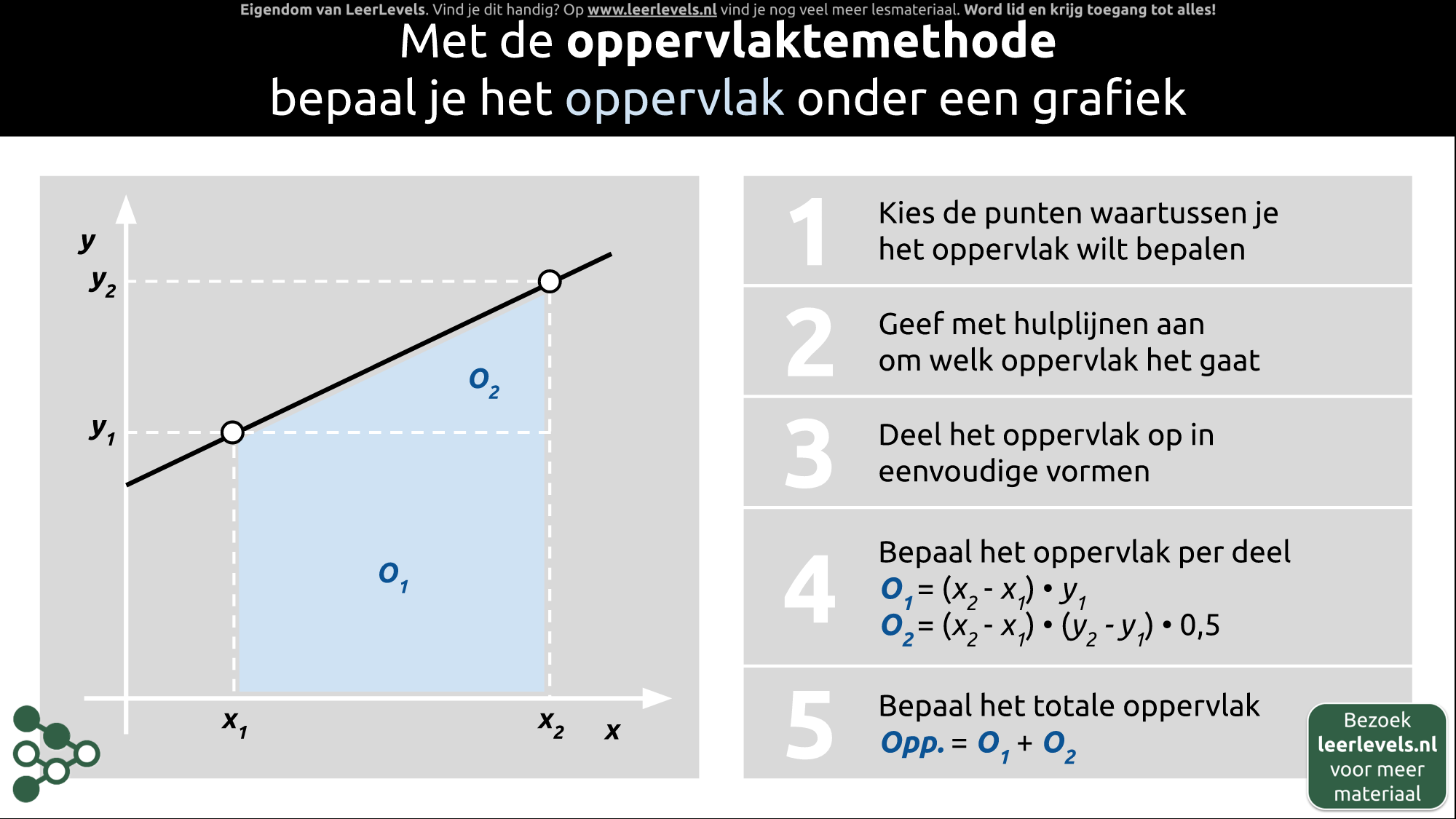
(Afbeelding: Animatie voor Oppervlaktemethode concept)

Oppervlaktemethode onder de x-as

De oppervlaktemethode laat zien hoe ver iets beweegt. Bij een grafiek waarbij de lijn onder de x-as loopt, is het gebied negatief. Als we kijken naar een diagram van snelheid tegen tijd en een diagram van afstand tegen tijd, kunnen we het verband tussen de twee zien. Als de snelheid constant is, is de grafiek in een rechte lijn. Maar als de snelheid verandert, wordt het lastiger. We kunnen de oppervlaktemethode gebruiken om te zien hoe ver iemand heeft gereisd. Als we bijvoorbeeld naar een specifieke periode van de reis kijken, kunnen we zien hoe ver iemand heeft gereisd in die tijd. Als de snelheid negatief is, betekent dit dat de persoon achteruit gaat. Een voorbeeld van dit soort analyse is bijvoorbeeld dat iemand in de eerste 8 seconden 40 meter heeft afgelegd, waarna hij nog 10 meter aflegt tussen 4 en 8 seconden en uiteindelijk terugkomt waar hij is begonnen. Als je goed kijkt naar de grafieken, kun je zelfs berekenen hoe ver iemand in een bepaalde periode is gereisd.

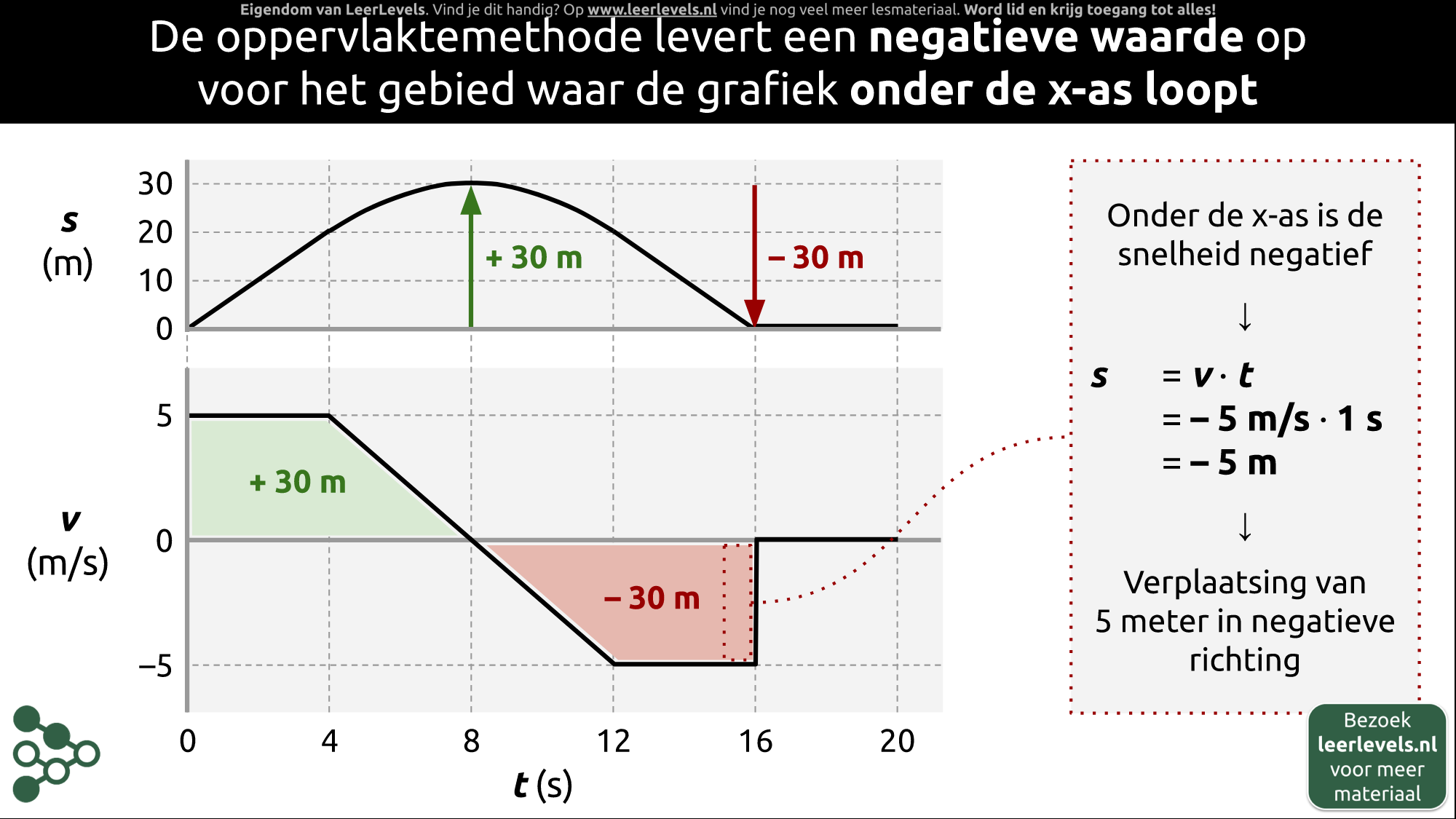
(Afbeelding: Animatie voor Oppervlaktemethode onder de x-as)

Terug naar overzicht Meld je aan

Opwaartse kracht

Als iets in een stof zit, duwt die stof omhoog tegen het object, wat we opwaartse kracht noemen. Deze kracht is gelijk aan de zwaartekracht op de stof die is verplaatst door het object. Bij het blazen van bellen is de opwaartse kracht klein omdat de bel klein is en weinig lucht verplaatst. Bij een ballon die meer massa verplaatst, is de opwaartse kracht groter. Een heliumballon kan zelfs een grotere opwaartse kracht hebben dan het gewicht van de ballon zelf. Een bal die in water drijft, verplaatst een beetje water en heeft een redelijke opwaartse kracht. Grote schepen die veel water verplaatsen, hebben een grote opwaartse kracht. Als iets in water drijft, is de zwaartekracht precies gelijk aan de opwaartse kracht. Daarom is de resulterende kracht nul.

(Afbeelding: Animatie voor Opwaartse kracht)

Terug naar overzicht Meld je aan

Oscilloscope

Oscilloscoop en oscillogram

Een oscilloscoop is een apparaat dat trillingen meet in elektrische signalen en weergeeft met behulp van een oscillogram. Je sluit elektrische snoeren aan op het apparaat die een elektrisch signaal produceren, bijvoorbeeld door het aan te sluiten op een microfoon. Hierdoor verschijnt er een golfpatroon op het scherm. De trilling die weergegeven wordt in de tijd noemen we het oscillogram, deze wordt rechts vergroot weergegeven. Om het oscillogram in te stellen kan je twee dingen aanpassen: delta T en delta U. Delta T geeft aan hoeveel seconden er in een vakje (div) passen, bijvoorbeeld 2 milliseconden per div. Delta U geeft aan hoeveel volt per div wordt getekend, bijvoorbeeld 1 V/div. Vaak moet je wat finetunen om de trilling mooi in beeld te krijgen. Als je eenmaal een goede afstemming hebt gevonden, kan je informatie aflezen over de trillingstijd en amplitude. De oscilloscoop meet trillingen in elektrische signalen en geeft deze weer met behulp van een oscillogram.

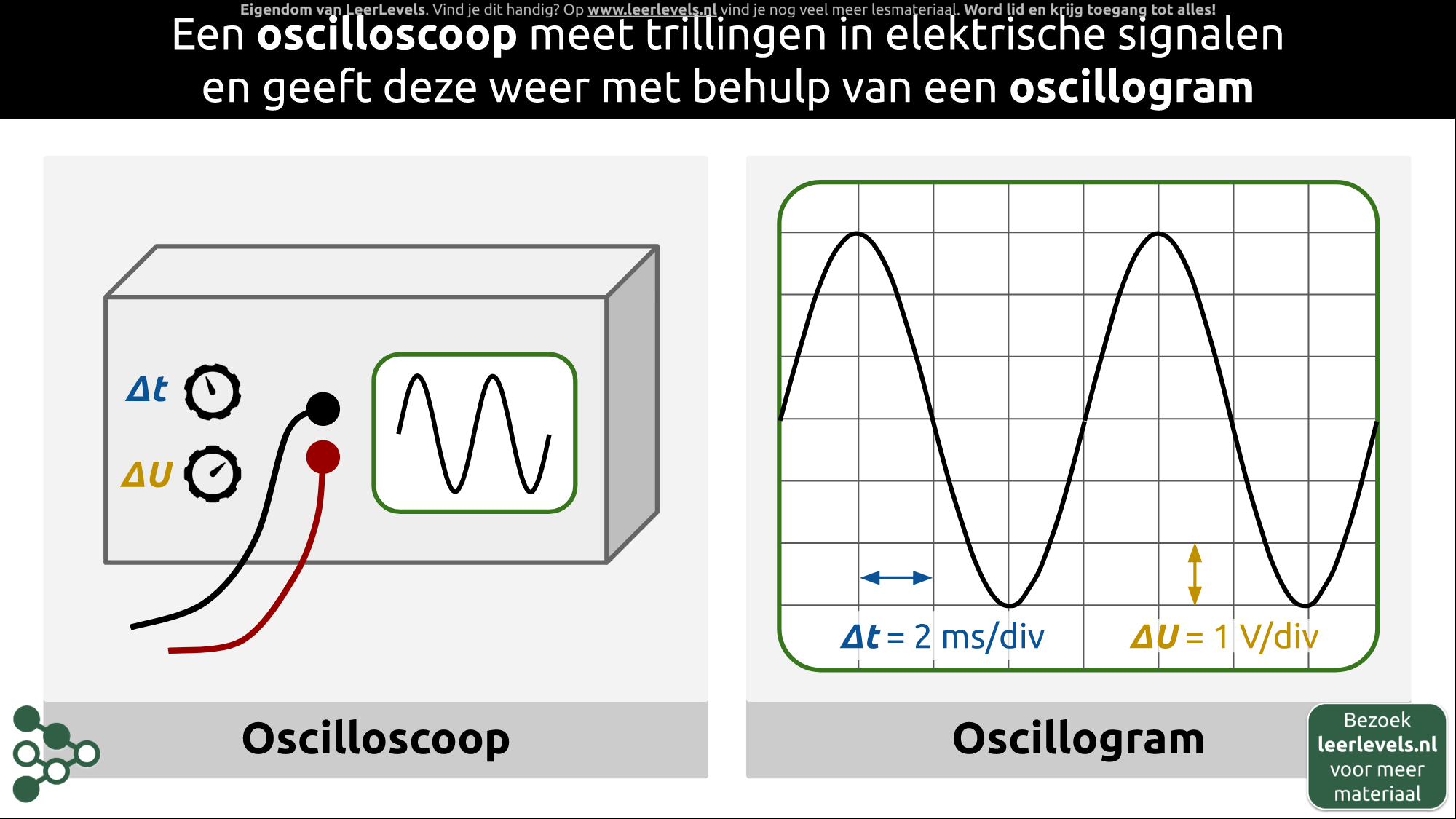
(Afbeelding: Animatie voor Oscilloscoop en oscillogram)

Terug naar overzicht Meld je aan

Overbelasting

Overbelasting treedt op wanneer er een te hoge elektrische stroom door een schakeling loopt, waardoor deze defect kan raken. Stel dat een lampje is aangesloten op een spanning van 6V en zonder problemen brandt. Verhogen we echter de spanning naar 15V, dan neemt ook de stroomsterkte toe. Als het lampje op deze verhoogde spanning wordt aangesloten, zal het onmiddellijk doorbranden. Hierdoor breekt de gloeidraad en stopt de stroomvoorziening, waardoor het lampje uitgaat. Dit illustreert het fenomeen van overbelasting.

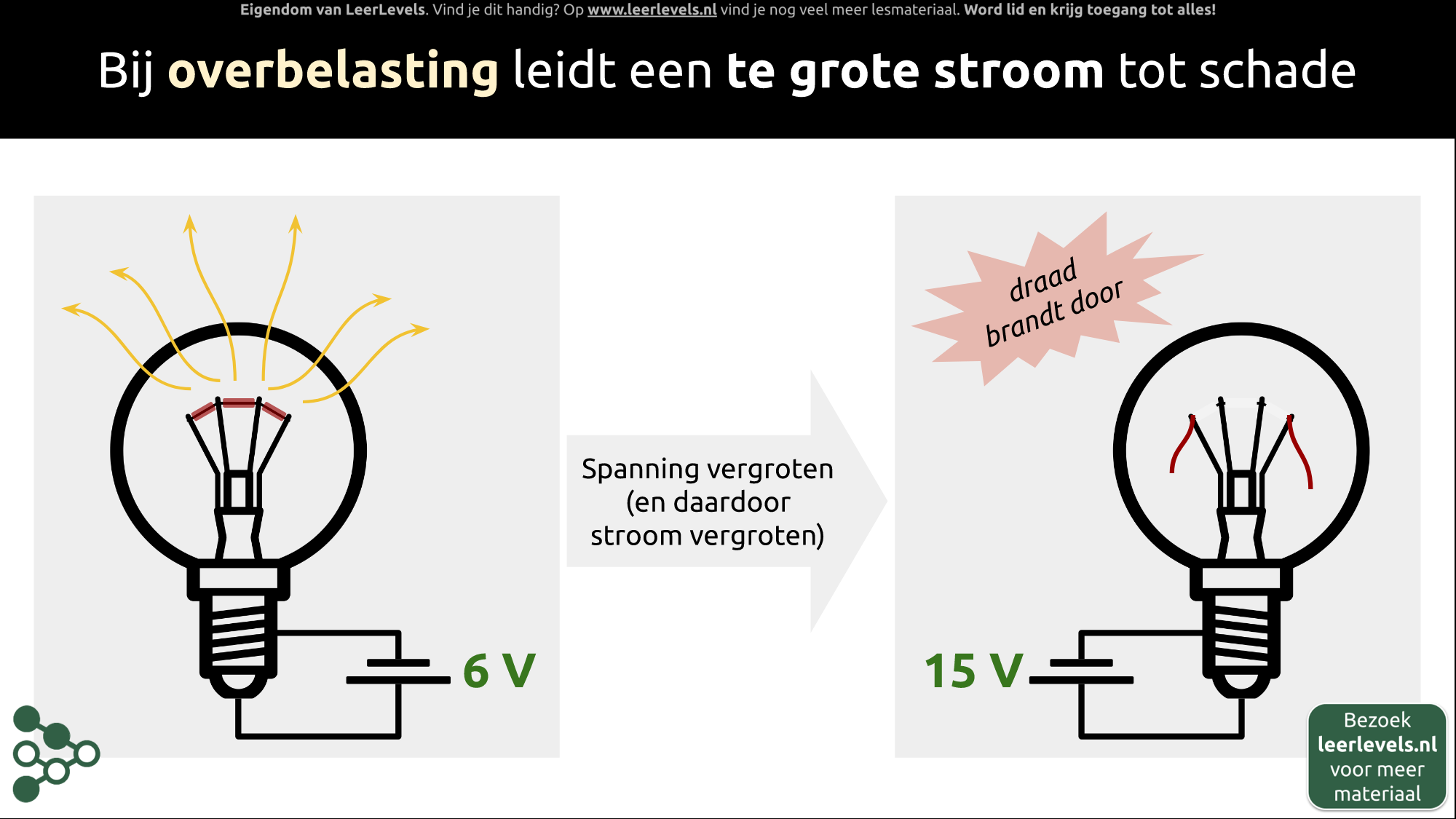
(Afbeelding: Animatie voor Overbelasting)

Terug naar overzicht Meld je aan

PET-scan

Een PET-scan is een onderzoek waarbij een injectie wordt gegeven met radioactief materiaal genaamd tracer. Dit materiaal zendt beta + straling uit en als het in de hersenen belandt, zal het voornamelijk daar vervallen. Tijdens dit vervalproces ontstaan er twee fotonen die worden gedetecteerd door een scanner waar de patiënt in ligt. Zo kan de exacte locatie van het verval berekend worden en kunnen er 3D-beelden worden gemaakt van de plekken waar de tracer zich bevindt. PET staat voor Positron Emission Tomography.

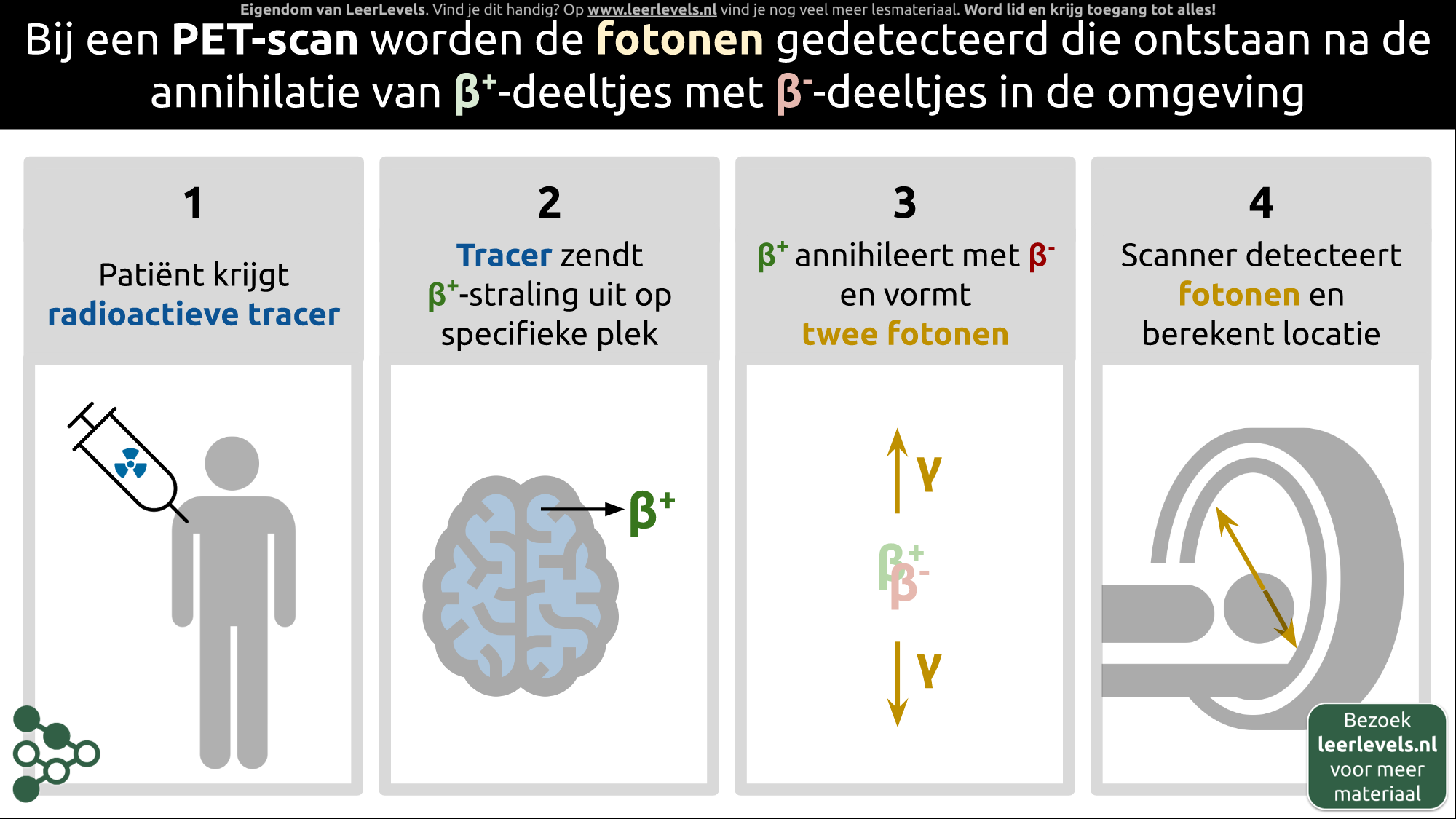
(Afbeelding: Animatie voor PET-scan)

Terug naar overzicht Meld je aan

Parallax

Parallax concept

Bij een parallaxmeting gebruik je een hoek om te bepalen hoe ver iets weg is. Dit doen we eigenlijk altijd al, want als we iets dichtbij kijken, kijken we onder een andere hoek dan wanneer we iets verder weg bekijken. Onze hersenen weten ongeveer wat de afstand is tussen onze ogen en gebruiken de kijkhoek om te berekenen hoe ver iets is. Bij een echte parallaxmeting wordt gebruik gemaakt van het feit dat de aarde in de zomer op een andere plek staat dan in de winter. Als je in de zomer en winter naar dezelfde ster kijkt, kun je berekenen hoe ver die ster weg is. De afstand w is twee keer de baanstraal van de aarde (w = 2 AE) en de hoek p kun je meten. Met deze gegevens kun je de afstand d bepalen.

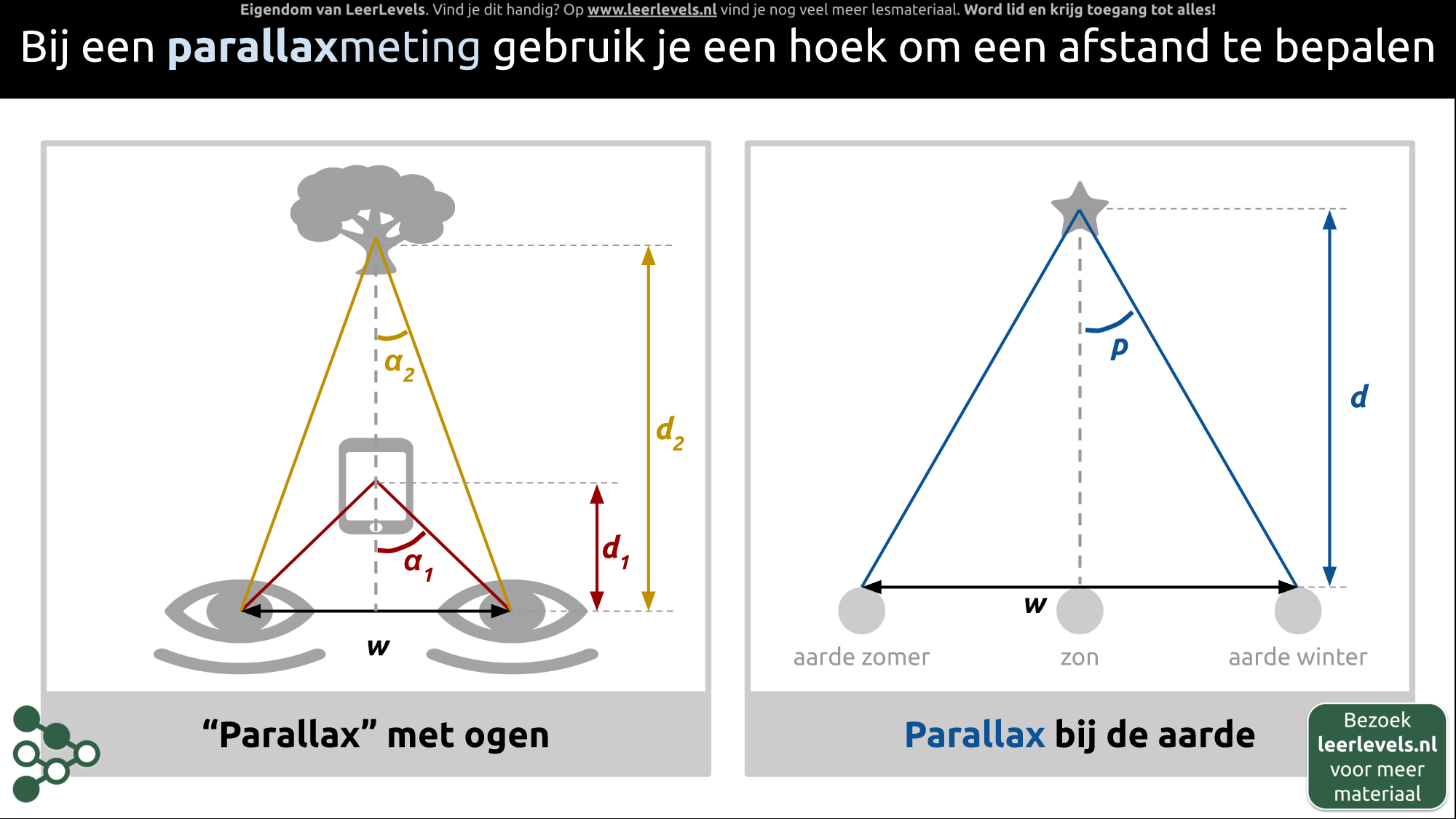
(Afbeelding: Animatie voor Parallax concept)

Parallax afleiding

Met parallax kun je de afstand tussen een ster en de aarde berekenen. Om de afstand te vinden meet je de hoek waaronder je de ster ziet met een half jaar tussenpauze. Deze hoek wordt parallax genoemd en wordt aangeduid met de letter p. De afstand d tot de ster is dan d = h/tan(p), waarbij h de afstand van de aarde tot aan de zon is (precies 1 AE). Voor kleine hoeken zoals bij een parallax van 1 boogminuut (1/60°) is tan(p) ongeveer gelijk aan p. Een boogminuut komt overeen met π/(180 · 60) radialen. Invullen in de formule geeft d = 0,05 lichtjaar. Dit betekent dat bij elke boogminuut parallax de afstand tot de ster 0,05 lichtjaar is. Let op: dit geldt alleen voor kleine hoeken.

(Afbeelding: Animatie voor Parallax afleiding)

Parallax formule

De afstand van een ster is omgekeerd evenredig met de parallax. In formulevorm betekent dit:

d = (1 AE)/(p)

waarbij AE staat voor de astronomische eenheid en p de parallax is in radialen. We kunnen ook zeggen dat de afstand 3,26 lichtjaar bedraagt voor een parallax van één boogseconde. Als je een parallax van 5 boogseconden meet, deel je de 3,26 lichtjaar door 5, wat resulteert in een afstand van ongeveer 0,65 lichtjaar.

(Afbeelding: Animatie voor Parallax formule)

Terug naar overzicht Meld je aan

Parallelschakeling

Stroomverdeling parallelschakeling

Een parallelschakeling is een soort elektrisch circuit waarbij de stroom door elke weerstand evenredig is aan de geleidbaarheid van die weerstand. Stel je hebt een spanning van 4 volt en 3 weerstanden met geleidbaarheid 1, 2 en 3 Siemens. Als de stroom in totaal 24 ampère is, zal de meeste stroom door de weerstand met de grootste geleidbaarheid stromen. Dit komt doordat het gemakkelijker is om door een weerstand met een hogere geleidbaarheid te stromen. De stromen door de drie weerstanden zullen respectievelijk 4, 8 en 12 ampère zijn. Dit kan worden berekend met de formule I = U / G, waarbij I de stroom, U de spanning en G de geleidbaarheid is. In een parallelschakeling is de spanning over elke weerstand gelijk en dus geldt de formule I1/G1 = I2/G2 = I3/G3. Dit bewijst dat in een parallelschakeling de stroom door elke weerstand recht evenredig is met de geleidbaarheid van die weerstand.

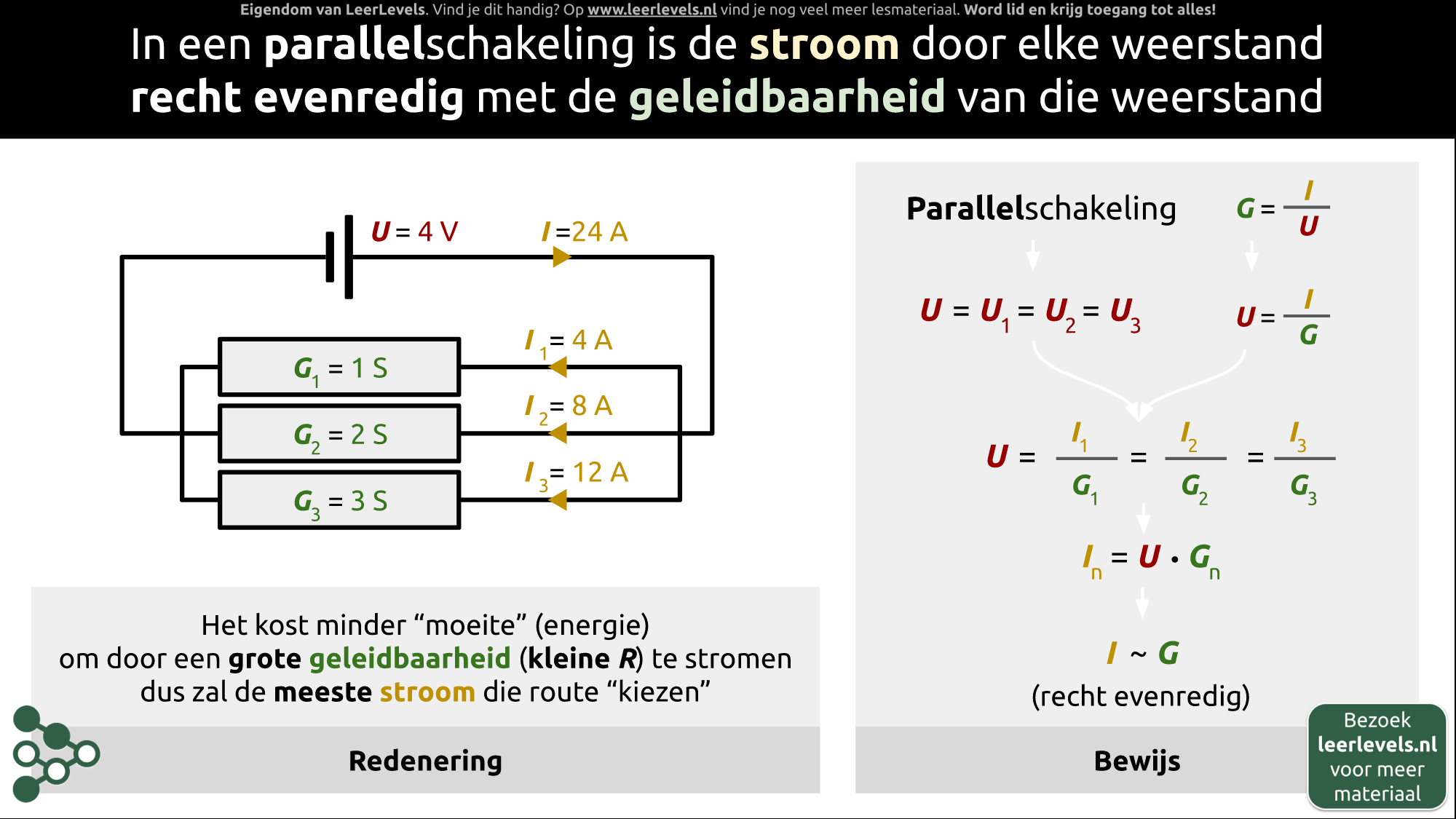
(Afbeelding: Animatie voor Stroomverdeling parallelschakeling)

Terug naar overzicht Meld je aan

Pauliprincipe

Pauliprincipe elektronen

Het principe van Pauli bepaalt dat meerdere elektronen in een energieput niet dezelfde quantumtoestand kunnen hebben.

Een kleurstofmolecuul fungeert als een energieput met lengte L en heeft een barrière aan de zijkanten, waardoor een elektron niet gemakkelijk kan ontsnappen. Het bijzondere aan deze energieput is dat er meerdere elektronen aanwezig zijn. De koolstofketen bestaat uit meer dan 20 koolstofatomen, waarvan elk één elektron levert dat vrij door de keten kan bewegen.

De energieput van het molecuul, met lengte L, kan worden weergegeven en men kan de energieniveaus berekenen van de grondtoestand, eerste aangeslagen toestand, enzovoort. Het uitsluitingsprincipe van Pauli stelt dat elektronen niet dezelfde quantumtoestand mogen hebben. Ze kunnen daarom niet allemaal in de grondtoestand aanwezig zijn. Wat gebeurt er dan wel? Elk energieniveau kan twee elektronen bevatten: één met spin omhoog en één met spin omlaag. Om het voorbeeld eenvoudig te houden, kijken we naar zes elektronen in de put, waarvan er dus twee in de eerste aangeslagen toestand zitten en twee in de tweede aangeslagen toestand. In totaal zijn er zes, dus de derde aangeslagen toestand is leeg.

De sprong naar de eerste lege plaats bepaalt welk licht het molecuul kan absorberen. De frequentie hiervan kan worden berekend met behulp van de formule E = h · f. Licht dat niet wordt geabsorbeerd, wordt gereflecteerd en kan in het oog terechtkomen, waardoor de kleur van het molecuul wordt bepaald. Als bijvoorbeeld paars en blauw licht worden geabsorbeerd, reflecteren groen, geel en rood, waardoor de kleurstof als geel of oranje wordt waargenomen. Dit alles wordt veroorzaakt doordat meerdere elektronen in een energieput volgens het uitsluitingsprincipe van Pauli niet dezelfde quantumtoestand mogen hebben.

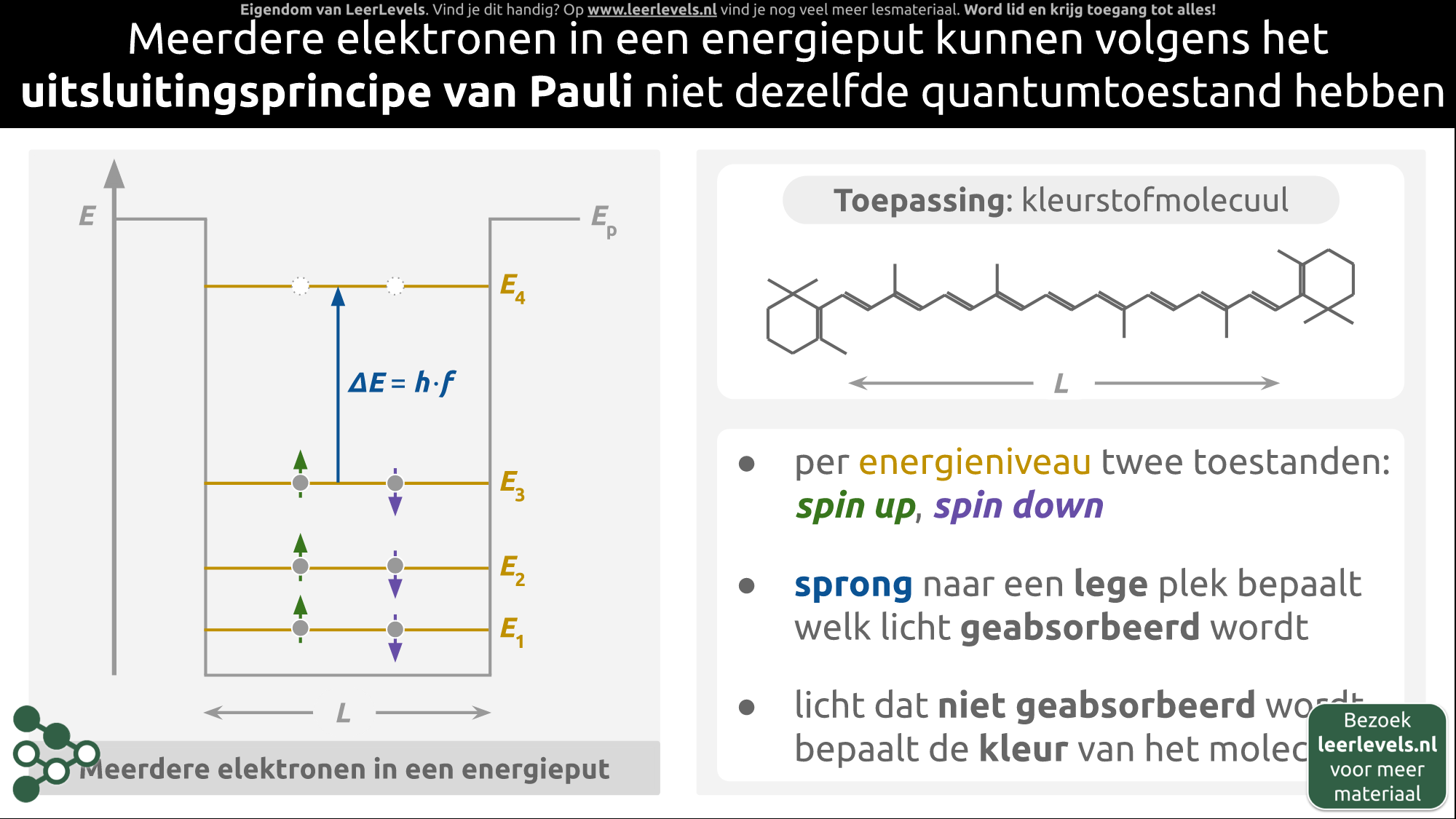
(Afbeelding: Animatie voor Pauliprincipe elektronen)

Terug naar overzicht Meld je aan

Planckkromme

Planckkromme concept

Een Planck-kromme is een manier om te zien welk licht een warm object uitstraalt. Als we bijvoorbeeld kijken naar een object dat heel heet is - laten we zeggen 5000 graden Celsius - dan kunnen we het licht dat daarvan afkomt onderzoeken met spectroscopie. Het spectrum dat we dan zien, heeft een vorm die lijkt op een kromme met een piek rond de 600 nanometer, iets geelachtigs. Op de verticale as van de kromme staat de intensiteit van het licht, vaak in Watt per vierkante meter per nanometer. Dat betekent hoeveel vermogen er per vierkante meter wordt uitgezonden voor elke mogelijke golflengte. Stel dat we kijken naar het punt op de kromme waar de golflengte 500 nanometer is en de intensiteit 3,5 · 10⁴ Watt per vierkante meter per nanometer is. Dit betekent dat binnen een bereik van 1 nanometer rondom de golflengte van 500 nanometer, het object een vermogen uitzendt van 3,5 · 10⁴ Watt per vierkante meter. Het oppervlak onder de kromme geeft aan hoeveel totaal vermogen het object uitzendt per vierkante meter.

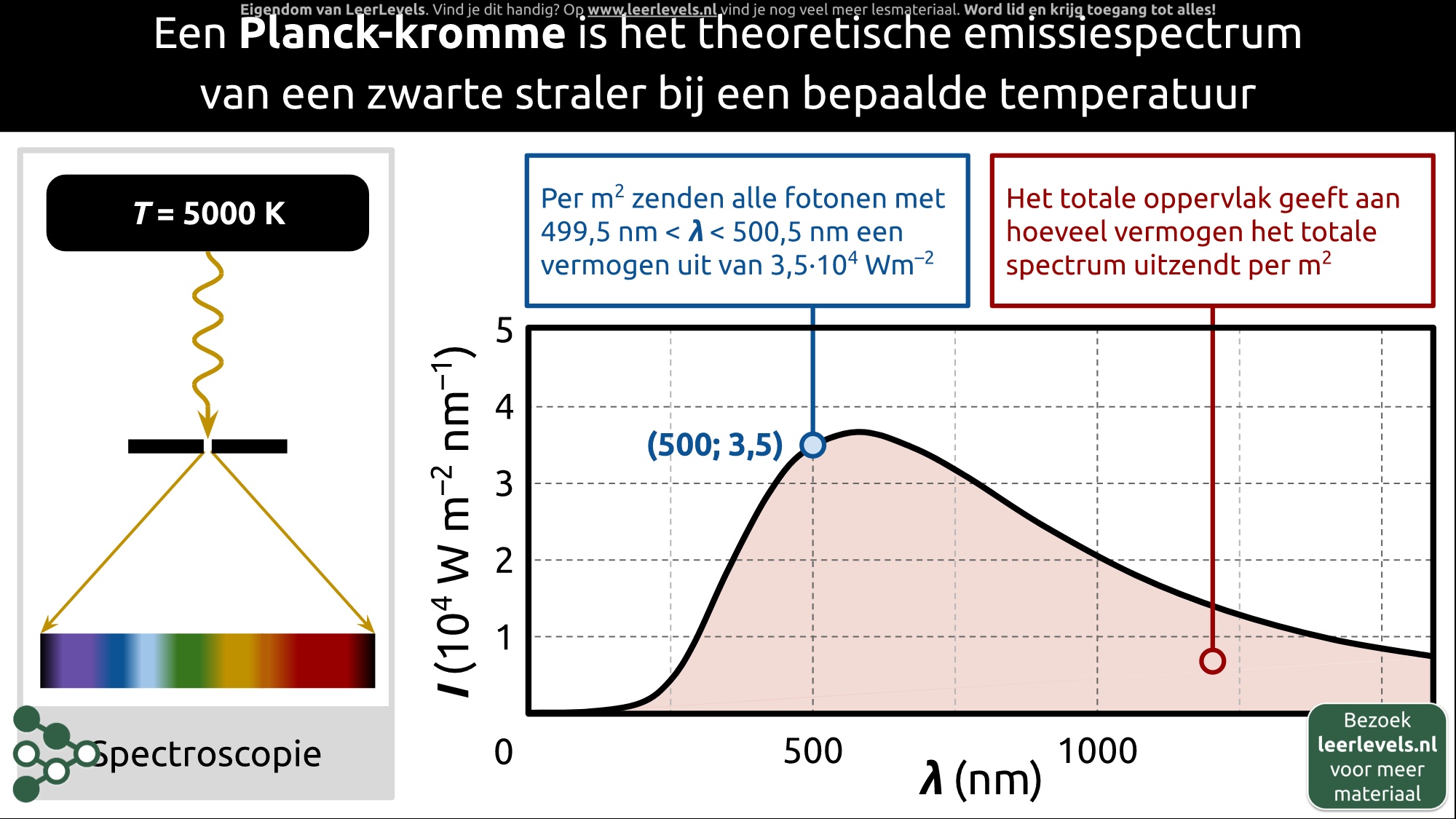
(Afbeelding: Animatie voor Planckkromme concept)

Terug naar overzicht Meld je aan

Planeetbaan

Een planeetbaan kan ellipsvormig zijn, maar vaak wordt het simpeler voorgesteld als een cirkelvormige baan. De aarde bijvoorbeeld draait in een ellipsbaan om de zon, waarbij de zon zich bevindt in een van de twee brandpunten van de ellips. De andere belangrijke punten van deze baan zijn het aphelium (het punt waar de aarde het verst van de zon verwijderd is en de snelheid het laagst is) en het perihelium (het punt waar de aarde het dichtst bij de zon is en de snelheid het hoogst is). Gewoonlijk wordt een cirkelvormige baan gebruikt om de planeetbanen te vereenvoudigen. In zo'n versimpelde baan blijven de straal en de baansnelheid constant.

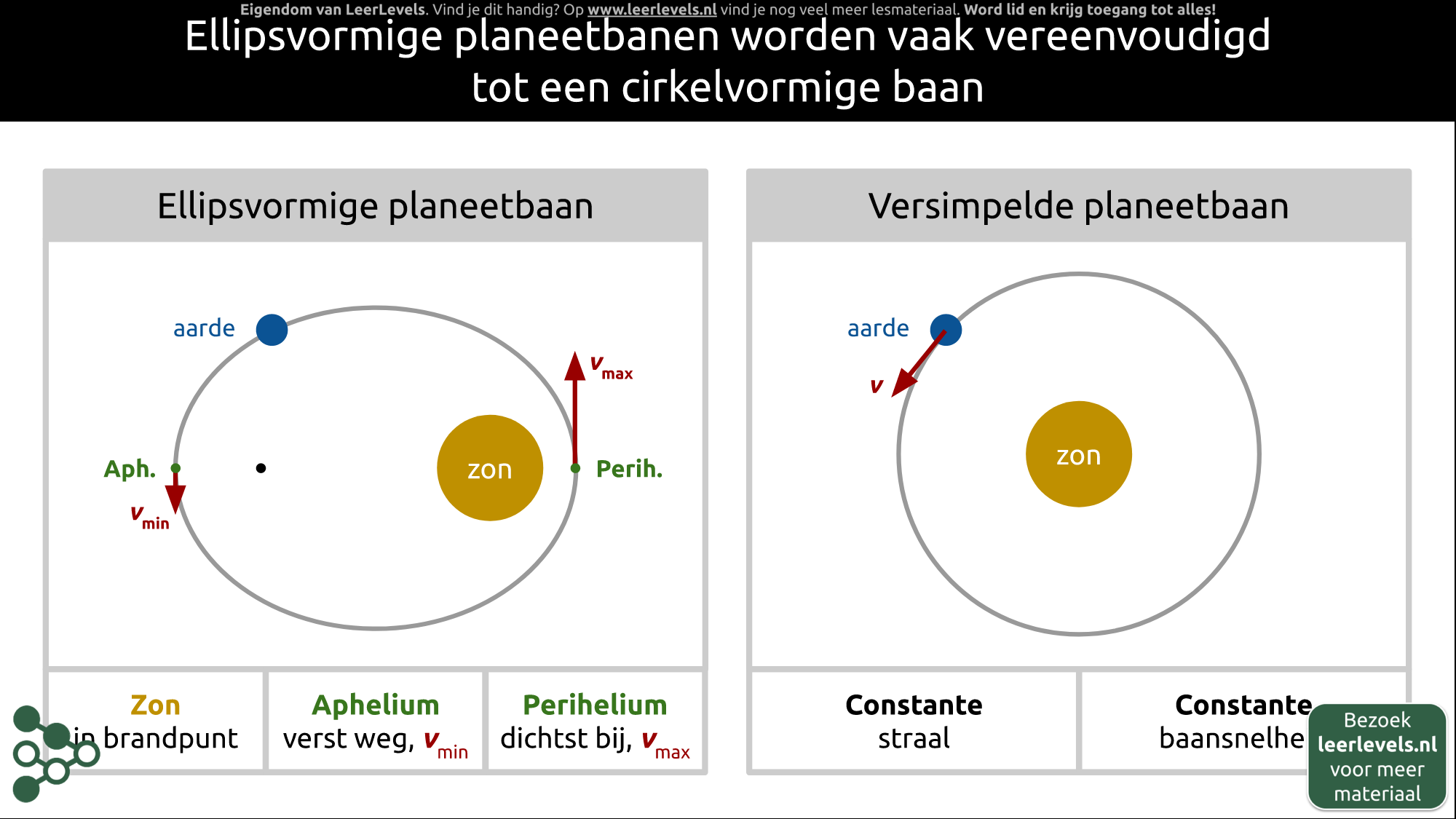
(Afbeelding: Animatie voor Planeetbaan)

Terug naar overzicht Meld je aan

Planeetbanen

Open en gesloten planeetbanen

Voorwerpen kunnen langs of rondom een hemellichaam bewegen. Als ze een open baan hebben, bewegen ze langs het hemellichaam en zijn ze niet gebonden. Een voorbeeld hiervan is een komeet die langs de zon scheert. Als de totale energie groter of gelijk is aan nul, heeft de komeet voldoende snelheid om weg te bewegen van de zon. Als een voorwerp een gesloten baan heeft, beweegt het om het hemellichaam heen en is het gebonden. Een voorbeeld hiervan is de aarde die om de zon heen draait. Als de totale energie kleiner is dan nul, is het voorwerp gebonden. Dit wordt weergegeven met de formule: E = K + U < 0, waarbij E de totale energie voorstelt, K de kinetische energie en U de gravitatie-energie.

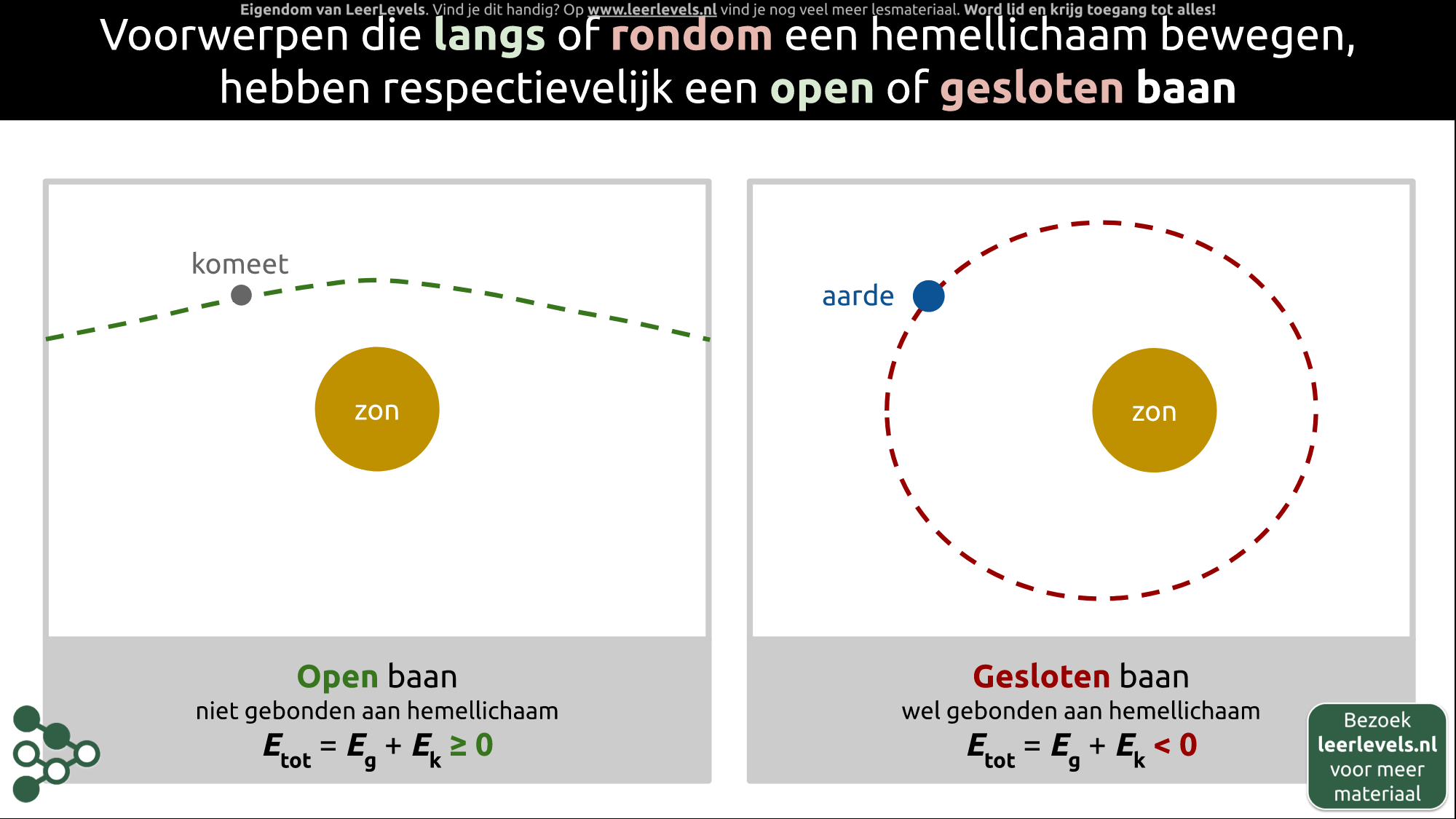
(Afbeelding: Animatie voor Open en gesloten planeetbanen)

Terug naar overzicht Meld je aan

Potentiaalput

Oneindige potentiaalput golffuncties

Als je een deeltje opsluit in een oneindig diepe potentiaalput, is de golffuntie een staande golf die precies in de put past. Deze put heeft verschillende energieniveaus die elk overeenkomen met een specifieke golffunctie. Voor de grondtoestand (n = 1) hebben we de eerste golffunctie, voor n = 2 de tweede, etc. Hogere waarden van n komen overeen met hogere energie. Dit betekent dat de energie discrete waarden aanneemt. Er is geen energie tussen n = 1 en n = 2, omdat bij n = 1 precies een halve golflengte past binnen de breedte van de put, en bij n = 2 een hele golflengte. Aangezien de golffunctie aan de randen van de put nul moet zijn, door de oneindig hoge wanden, passen golflengtes daartussen niet in de put. Daarom bestaan de bijbehorende energieniveaus niet. Omdat alleen bepaalde energieën mogelijk zijn, noemen we dit 'gequantiseerde energie'.

De waarschijnlijkheid om een deeltje op een bepaalde locatie in de put te vinden, krijg je door het kwadraat van de golffunctie te nemen. De x-coördinaten lopen van x = 0 tot x = L, waarbij L de breedte van de put is. De kans om het deeltje bij x = 0 of x = L te vinden is 0, omdat de golffunctie op die punten altijd nul is. In de grondtoestand (n = 1) ligt de grootste waarschijnlijkheid precies halverwege de put, waar de amplitude van de golffunctie maximaal is, dus ook het kwadraat. Voor n = 2 is de waarschijnlijkheid halverwege juist nul, omdat de golffunctie daar een knoop heeft en de amplitude nul is.

Een opvallend aspect is de nulpuntsenergie, die hoort bij de grondtoestand. Hierbij past een halve golflengte in de put, dus is de golflengte tweemaal de breedte van de put. Met deze golflengte kan de energie worden berekend, die groter is dan 0. Zelfs in de grondtoestand heeft een deeltje energie. Dit verschilt van het klassieke idee dat deeltjes bij de laagste energie stilstaan zonder kinetische energie (en dus zonder snelheid).

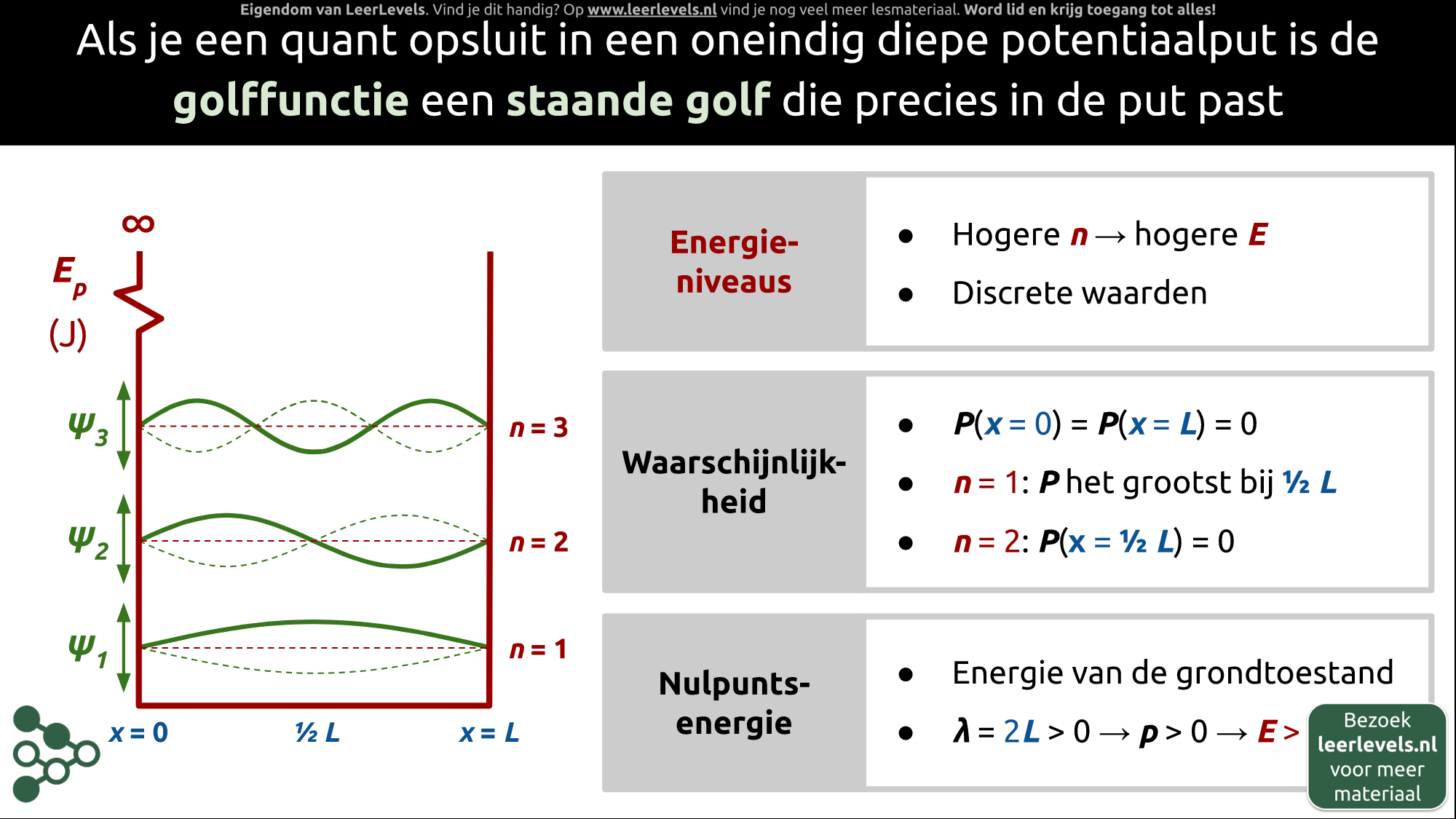
(Afbeelding: Animatie voor Oneindige potentiaalput golffuncties)

Oneindige potentiaalput energie formule

De totale energie van een kwantumdeeltje in een oneindig diepe potentiaalput hangt onder andere af van de aangeslagen toestand waarin het zich bevindt:

En = (n²h²) / (8 · m · L²)

Hierin geldt:

· En = de energie van het deeltje in de n_e toestand (in J)
· n = de 'teller' van de aangeslagen toestand, met de grondtoestand (n = 1), eerste aangeslagen toestand (n = 2), etc.
· h = de constante van Planck (6,62607 · 10⁻³⁴ Js)
· m = de massa van het kwantumdeeltje (in kg)
· L = de lengte van de potentiaalput (in m).

Het belangrijkste punt is dat de energie kwadratisch evenredig is met de aangeslagen toestand. Bij de overgang van de grondtoestand naar de eerste aangeslagen toestand wordt de energie dus vier keer zo groot.

(Afbeelding: Animatie voor Oneindige potentiaalput energie formule)

Oneindige potentiaalput concept

De theoretische oneindig diepe potentiaalput is een eendimensionale gevangenis waaruit elektronen niet kunnen ontsnappen. Stel je voor dat je een draad hebt met aan beide uiteinden zeer grote negatieve ladingen. Daartussen plaats je een elektron. Het elektron kan vrij bewegen, maar wil niet te dicht bij de negatieve ladingen komen omdat het daardoor wordt afgestoten.

In een diagram kun je dit weergeven door naar de potentiële energie te kijken. Je zult zien dat naarmate het elektron dichter bij een van de negatieve ladingen komt, de potentiële energie sterk toeneemt. Dit gebeurt omdat de ladingen het elektron steeds sterker zullen afstoten naarmate het dichterbij komt. Als je dit visueel zou weergeven, zou het er als volgt uitzien: het model van de oneindig diepe potentiaalput wordt gereduceerd tot een systeem met oneindig hoge muren.

Als je veronderstelt dat de ladingen zeer dicht bij de draad zitten en de afstand nul wordt, zou de potentiële energie naar oneindig stijgen. We beschouwen dit als een put met een bepaalde breedte. Aan de linkerkant stellen we x = 0 en aan de rechterkant x = L. Dit vormt een eendimensionale put met lengte L. Het elektron beweegt heen en weer tussen de muren van de put.

(Afbeelding: Animatie voor Oneindige potentiaalput concept)

Oneindige potentiaalput toestanden

De verschillende toestanden van een oneindig diepe potentiaalput hebben elk hun eigen golffunctie. Voor de grondtoestand is de golffunctie de eenvoudigste sinusfunctie. Gestippeld is deze golffunctie een halve periode verder weergegeven. Als we het kwadraat van de golffunctie nemen, krijgen we de kansverdeling die aangeeft waar we het kwantumdeeltje waarschijnlijk zullen vinden. Als we metingen uitvoeren langs de eendimensionale put, kunnen we bijvoorbeeld een elektron op een bepaalde plek aantreffen. Voor de grondtoestand is deze kansdichtheid het grootst in het midden van de put. Op dezelfde manier kunnen we dit proces toepassen op de eerste en tweede aangeslagen toestanden. Voor deze toestanden zien de golffuncties er anders uit; bij de eerste aangeslagen toestand is de golffunctie gelijk aan een hele golflengte van de sinus, terwijl het bij de tweede aangeslagen toestand anderhalve golflengte van de sinus is. De gele gebieden geven opnieuw aan waar de kans het grootst is om bij een meting een kwantumdeeltje te detecteren.

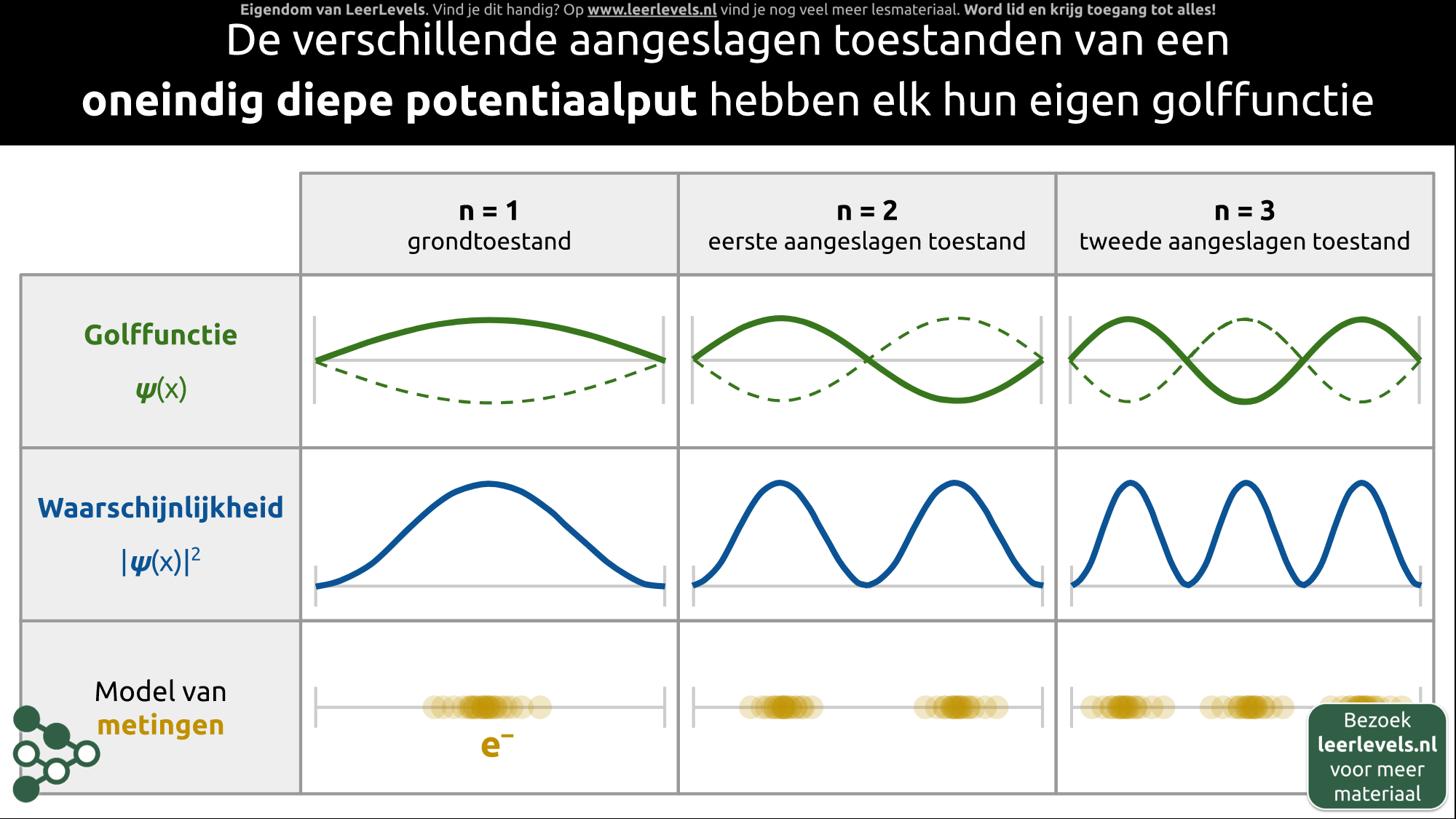
(Afbeelding: Animatie voor Oneindige potentiaalput toestanden)

Oneindige potentiaalput 3D

In het kwantummechanische atoommodel bevinden elektronen zich in een driedimensionale potentiaalput, vergelijkbaar met een "deeltje in een doosje". In een eendimensionaal model heb je een put met een breedte L en oneindig hoge muren. Het deeltje kan zich hier slechts in één richting bewegen. Bij meerdere waarnemingen wordt het deeltje meestal in het midden aangetroffen.

In de realiteit is de situatie vrijwel altijd driedimensionaal, met een x-, y- en z-as. Het meer realistische atoommodel beschrijft daarom niet een put, maar een doosje waarin de potentiële energie buiten de doos oneindig groot is en binnen de doos nul. Toepassing van de Schrödingervergelijking laat zien dat het deeltje in de grondtoestand met de grootste waarschijnlijkheid in het midden van de doos aanwezig is. Hoewel het deeltje in principe overal in de doos kan worden aangetroffen, is de grootste kans in het midden.

Dit verschilt aanzienlijk van het schillenmodel, waarbij een elektron zich alleen in een specifieke schil kan bevinden. In het kwantummechanische atoommodel kun je enkel over een kansverdeling spreken.

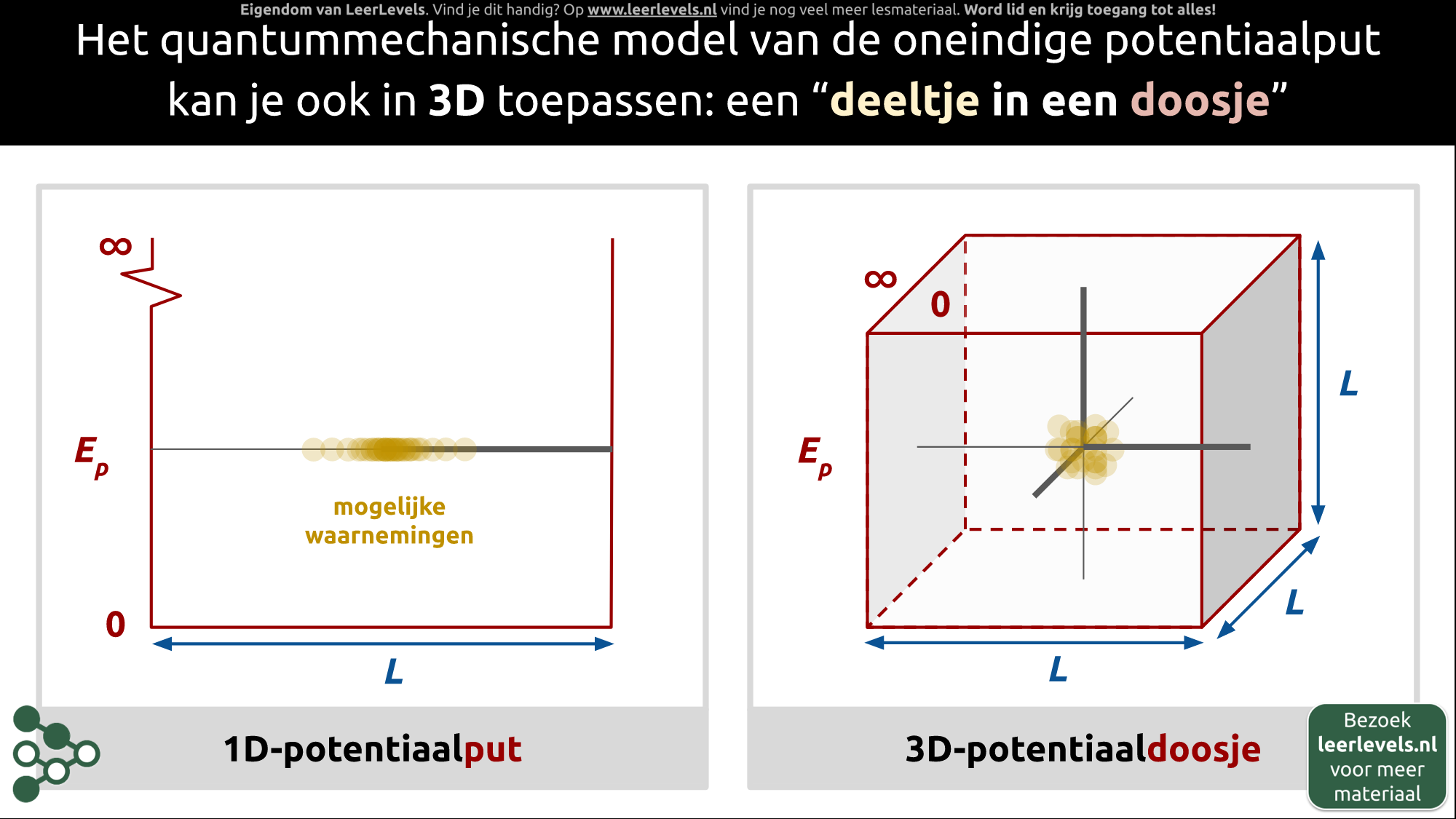
(Afbeelding: Animatie voor Oneindige potentiaalput 3D)

Eindige potentiaalput concept

De eindig diepe potentiaalput is vergelijkbaar met een eendimensionale gevangenis waar elektronen kunnen ontsnappen als ze voldoende energie hebben. Stel je een draad voor met aan weerszijden twee grote negatieve ladingen en ertussenin een elektron. Dit elektron wil niet te dichtbij de negatieve ladingen komen vanwege de afstotende krachten. Dit effect kan worden weergegeven met de potentiële energie: in de buurt van de grote negatieve ladingen neemt de potentiële energie toe, waardoor het elektron zich tussen deze ladingen bevindt.

In een vereenvoudigde weergave worden de wanden van de put getekend als een stapfunctie. Binnen de muren is de potentiële energie nul, terwijl buiten de muren de potentiële energie groter is, maar niet oneindig. Dit betekent dat er een kans is dat het elektron buiten de muren terechtkomt. De put loopt van x = 0 tot x = L.

Het belangrijkste punt is dat de potentiële energie buiten de put niet naar oneindig stijgt, waardoor het elektron ook links van x = 0 en rechts van x = L kan komen.

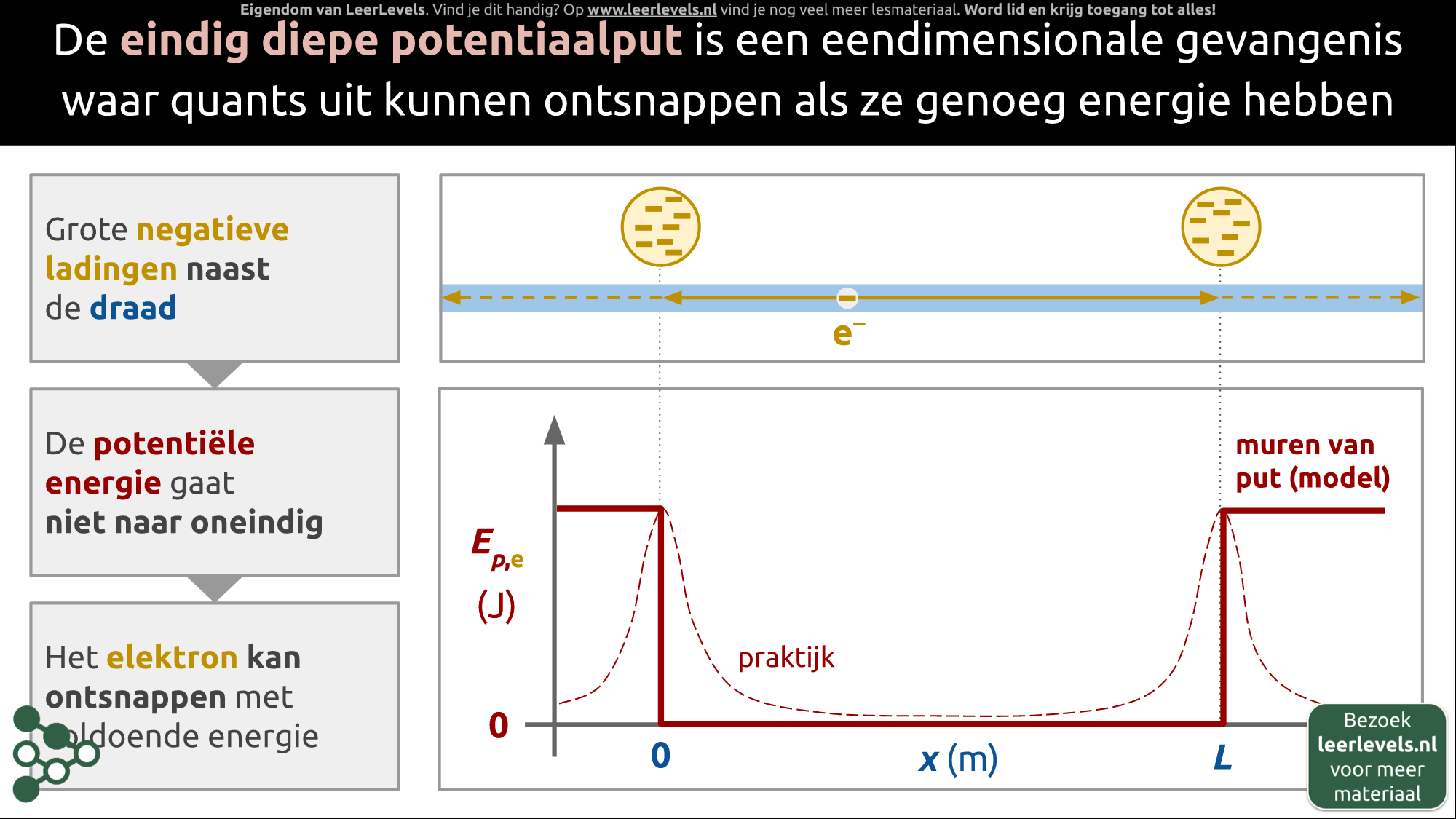
(Afbeelding: Animatie voor Eindige potentiaalput concept)

Eindige en oneindige potentiaalput

In een oneindig diepe potentiaalput kan een quantumdeeltje nooit buiten de muren worden aangetroffen, maar in een eindig diepe put is dit wel mogelijk. De vereenvoudigde Schrödingervergelijking ziet er als volgt uit: de tweede afgeleide naar de plaats van de golffunctie ((∂² φ)/(∂ x² is evenredig aan de golffunctie keer het verschil tussen potentiële en kinetische energie ((Ep-Ek)/(C) · φ):

(∂²φ)/(∂x²) = ((Ep - Ek)/C) · φ

Oneindig diepe put

In een oneindig diepe put geldt dat Ep binnen de put nul. Als je ervan uitgaat dat Ek niet afhankelijk is van de plaats, kun je bovenstaande vergelijking verder vereenvoudigen naar: (∂² φ)/(∂ x²=⁻k · φ, waarin k een nieuwe constante is (k = (-Ek)/(C)). Als je deze differentiaalvergelijking oplost, volgt dat de golffunctie een sinusoïde moet zijn.

Buiten de oneindig diepe put is de Ep oneindig. Dit kan alleen als de golffunctie nul is (φ = 0). Vanwege continuïteit moet de golffunctie bij de randen van de put ook nul zijn. Visueel ziet dat er zo uit: de grondtoestand bevat één halve golflengte van een sinusoïde, de eerste aangeslagen toestand twee halve golflengtes, enzovoort.

Eindig diepe put

Bij een eindig diepe put veranderen er echter enkele zaken. Binnen de put is de situatie hetzelfde, met een sinusoïde als de oplossing voor de golffunctie. Maar buiten de put is de potentiële energie niet langer oneindig. Wanneer je de oplossing voor de golffunctie zoekt, blijkt deze buiten de put geen nul te zijn, maar een exponentieel dalende functie. In een tekening zie je dat de golffunctie buiten de muren niet abrupt naar nul gaat, maar een dalende exponentiële vorm aanneemt. De functie daalt dus vrij snel naar nul, maar niet onmiddellijk. Dit is ook zichtbaar in de eerste aangeslagen toestand.

Dit heeft de bijzondere consequentie dat de waarschijnlijkheid, het kwadraat van de golffunctie, buiten de put niet nul is. In het geel gearceerde gebied is de waarschijnlijkheid niet nul, zelfs als het elektron niet voldoende energie heeft om volgens de klassieke mechanica buiten de put te komen. Dit maakt tunneling mogelijk: het proces waarbij een deeltje ergens doorheen kan gaan, zelfs als het klassiek gezien niet genoeg energie heeft. Dit fenomeen is het gevolg van het golfgedrag van deeltjes.

(Afbeelding: Animatie voor Eindige en oneindige potentiaalput)

Terug naar overzicht Meld je aan

Potentiële energie

De potentiële energie van een object hangt af van de positie ten opzichte van andere objecten. Neem bijvoorbeeld zwaarte-energie: je hebt weinig zwaarte-energie wanneer je onderaan een trap staat, en relatief veel als je bovenaan de trap staat. Bij gravitatie-energie geldt dat je weinig energie hebt als je dicht bij een planeet bent, terwijl je veel energie hebt als je verder weg bent. Voor veerenergie heb je weinig energie als de veer niet is uitgerekt, maar veel energie wanneer de veer flink is uitgerekt. In alle gevallen is de hoeveelheid energie afhankelijk van de plaats ten opzichte van respectievelijk de grond, de aarde en de rusttoestand van de veer.

De potentiële energie van een voorwerp heeft alleen betekenis ten opzicht van een bepaald ander object of voorwerp. Dat maakt het lastig om van één object iets te zeggen over de potentiële energie. Als iemand op een trap staat, is er niet één duidelijke hoogte. Meet je ten opzichte van de onderkant van de trap? Of ten opzichte van zeeniveau? Of misschien ten opzichte van het middelpunt van de aarde? In de praktijk wordt de potentiële energie daarom vooral gebruikt om de energie van twee verschillende locaties met elkaar te vergelijken.

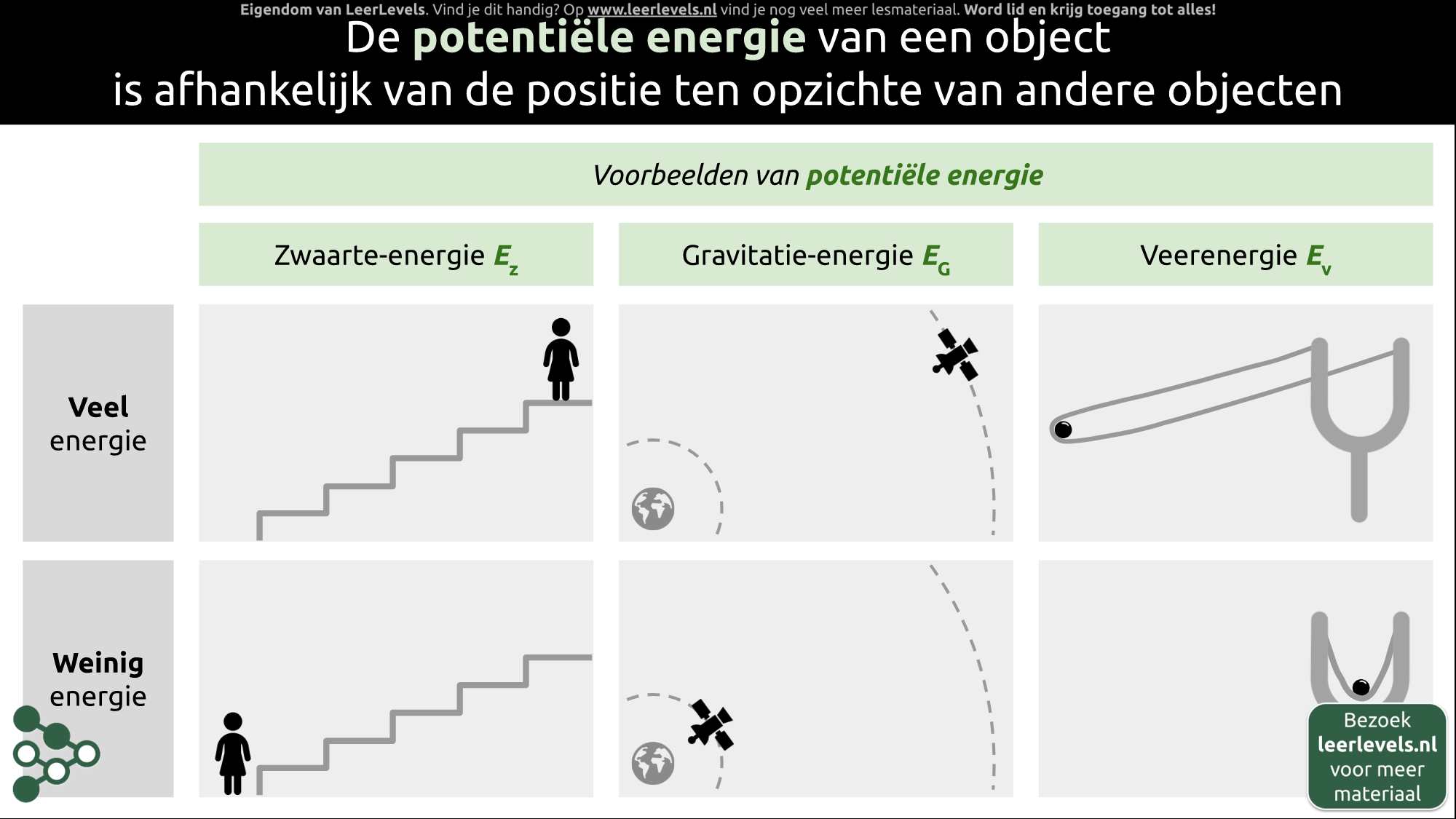
(Afbeelding: Animatie voor Potentiële energie)

Terug naar overzicht Meld je aan

Probleemoplossing

Oplossingsstrategie

Bij natuurkunde hebben we een oplossingsstrategie van vijf stappen. Stap 1: bepaal wat er gevraagd wordt en welke gegevens je nodig hebt. Bijvoorbeeld: hoeveel liter past er in een aquarium van 20 cm x 10 cm x 10 cm. Stap 2: kijk naar de gegevens die je al hebt. Bijvoorbeeld: de lengte en hoogte van het aquarium. Stap 3: vind de formule of vergelijking die je nodig hebt. Bijvoorbeeld: V = l · b · h (volume is gelijk aan lengte keer breedte keer hoogte). Stap 4: voer de berekening uit en vind het antwoord. Bijvoorbeeld: 20 liter. Stap 5: controleer het antwoord en corrigeer eventuele fouten. Bijvoorbeeld: controleer de significantie van de cijfers en gebruik juiste eenheden. Zo kun je succesvol de oplossingsstrategie voor natuurkunde toepassen. V = l · b · h en 1 liter = 1 dm³.

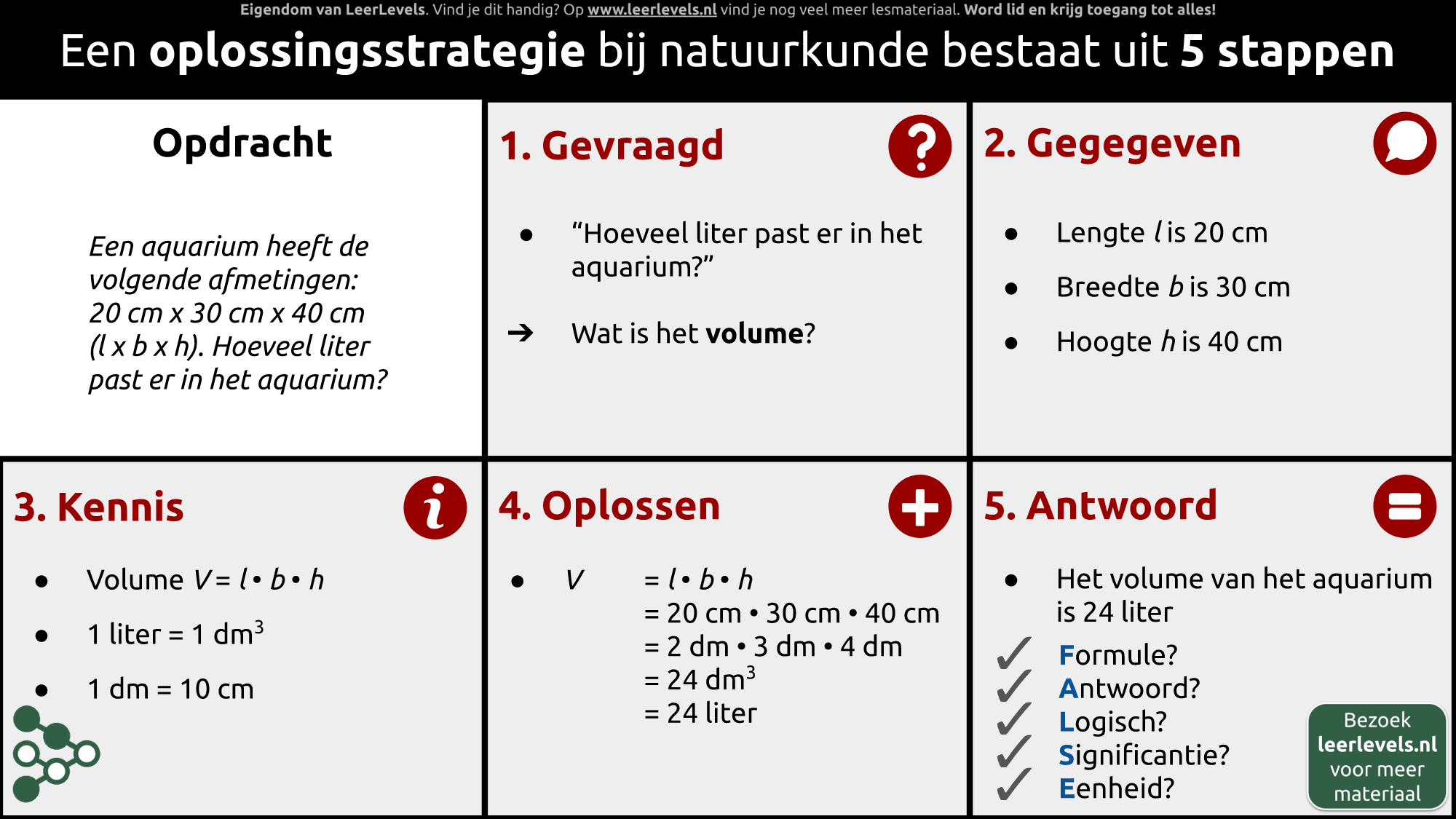
(Afbeelding: Animatie voor Oplossingsstrategie)

Informatie uit vraag gebruiken

Bij opdrachten krijg je op verschillende manieren informatie.

1. Een wet - dit is een nieuw stukje natuurkunde dat je moet gebruiken om de vraag te beantwoorden. Bijvoorbeeld: sterren vanaf 2 zonmassa's kunnen een zwart gat worden.

2. Een formule - dit is een wiskundig verband tussen grootheden en de betekenis van de variabelen wordt uitgelegd. Bijvoorbeeld: E = CV², om de energie van een object te berekenen.

3. Directe informatie - bijvoorbeeld: Usain legt 10 meter af in 2 seconden. Zo kan je direct de snelheid berekenen.

4. Indirecte informatie - dit is informatie die nog verwerkt moet worden voordat het bruikbaar is. Bijvoorbeeld: een gouden staaf heeft een afmeting van 30×10×5 cm, waaruit je de massa kan berekenen in combinatie met de dichtheid.

5. Een tabel - hieruit moet je belangrijke informatie aflezen. Bijvoorbeeld: wat is de gemiddelde luchtdruk op een bepaalde hoogte?

6. Een figuur - dit is een grafische weergave die je zelf moet kunnen interpreteren. Bijvoorbeeld: een kaartje van Nederland met een schaalverdeling om afstanden af te lezen.

Er zijn dus verschillende vormen van informatie die je moet kunnen begrijpen om een antwoord op de vraag te kunnen geven.

(Afbeelding: Animatie voor Informatie uit vraag gebruiken)

Terug naar overzicht Meld je aan

Procenten

Rekenen met procenten

Bij rekenen met procenten is het belangrijk om goed te kijken naar de woorden 'toename', 'keer' en 'afname'. Als je bijvoorbeeld een toename van 20% hebt, betekent dit dat je 20% van de oorspronkelijke waarde bij de waarde optelt. Dit resulteert in een waarde van 1,2 keer de oorspronkelijke waarde. Als er gesproken wordt over een toename van 200%, dan betekent dit dat je twee keer de oorspronkelijke waarde bij de waarde optelt. Dit resulteert in een waarde van 3 keer de oorspronkelijke waarde. Een afname van 50% betekent dat je 50% van de oorspronkelijke waarde van de waarde afhaalt. Dit resulteert in een waarde van 0,5 keer de oorspronkelijke waarde. Keer 50% betekent hetzelfde als een afname van 50%. Een afname van 100% resulteert in een waarde van nul. Let dus goed op de precieze formulering van procentenformules, omdat dit de uitkomst bepaalt.

(Afbeelding: Animatie voor Rekenen met procenten)

Terug naar overzicht Meld je aan

Projectielbeweging

Projectielbeweging concept

Een projectielbeweging is wanneer iets met een beginnelijk snelheid onder een hoek wordt afgeschoten en daarna door zwaartekracht en eventuele wrijving wordt beïnvloed. Als we het projectiel in het begin met een hoogte van 0 bekijken, dan splitsen we de beginsnelheid in een horizontale en verticale snelheid. Er werkt zwaartekracht op het projectiel, die de verticale snelheid vermindert. Als er geen wrijving is, blijft de horizontale snelheid constant. Na verloop van tijd wordt de verticale snelheid nul en beweegt het projectiel alleen horizontaal. Vanwege de zwaartekracht accelereert het projectiel naar beneden en raakt uiteindelijk de grond. Als er geen wrijving is, is de snelheid waarmee het projectiel de grond raakt gelijk aan de beginsnelheid. Dit volgt uit vergelijkingen voor de snelheid en energiebehoud. Tijdens de landing is er een grote opwaartse normaalkracht om de snelheid te verminderen.

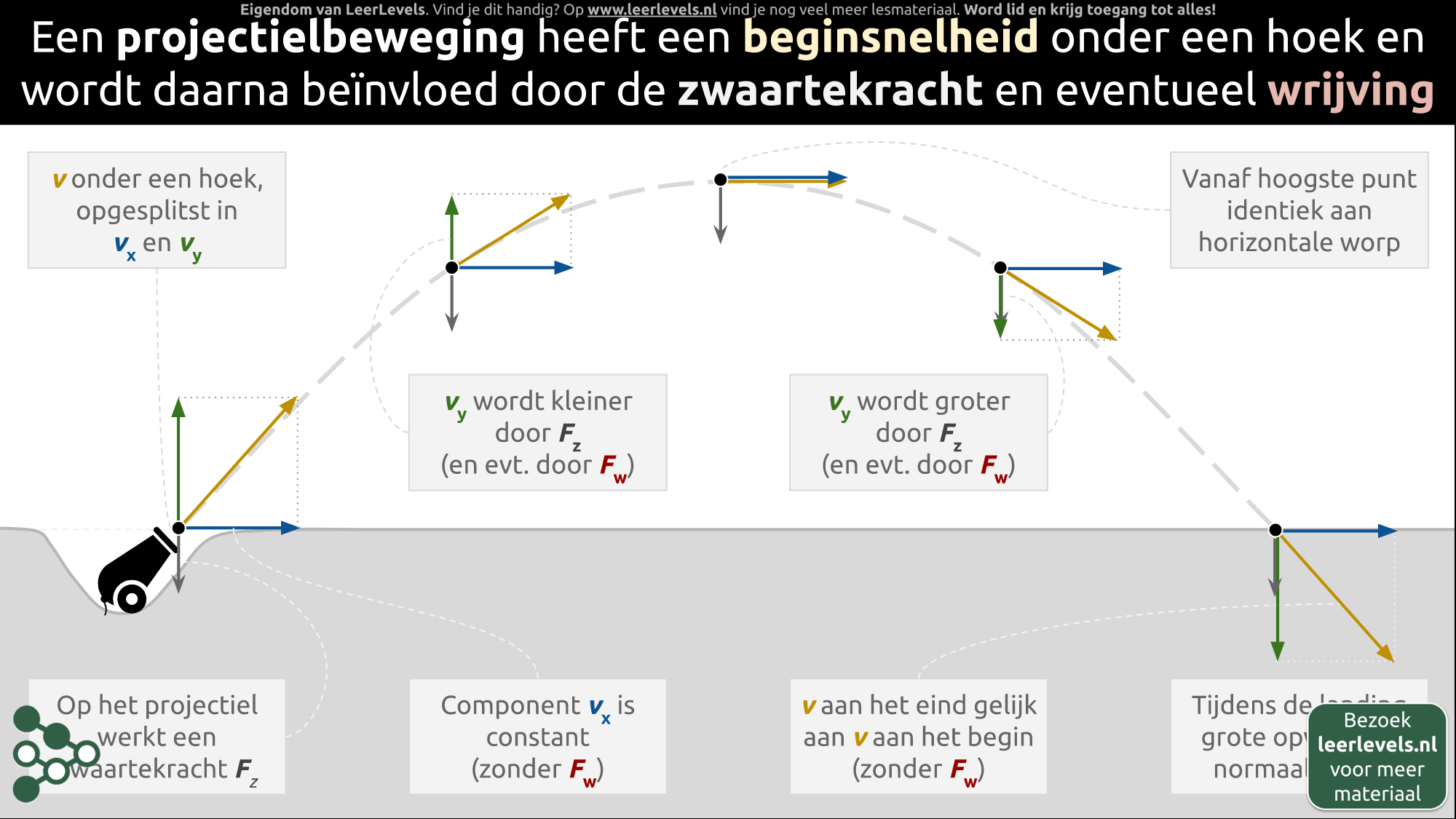
(Afbeelding: Animatie voor Projectielbeweging concept)

Terug naar overzicht Meld je aan

Quant

Quant concept

Een quant is een verschijnsel met zowel golf- als deeltjeseigenschappen. Wanneer we naar een deeltje kijken, zien we het vaak als een bolletje op een specifieke plek. Bij een golf kennen we eigenschappen zoals golflengte, maar we kunnen niet exact aangeven op welke plek de golf is. Een quant is een combinatie hiervan, een gelokaliseerde golf, ook wel een golfpakket genoemd. Of we het als golf of als deeltje moeten beschouwen, hangt af van de omstandigheden. Soms vertoont het deeltjesgedrag, zoals botsingen. Dit kan plaatsvinden tussen gelijke of verschillende quanta. Een foton kan bijvoorbeeld botsen met een elektron. Een botsing is onvermijdelijk als de golflengte van het quant veel kleiner is dan het object waartegen het botst. Als we mensen als quanta beschouwen, hebben we een extreem kleine golflengte door onze grote impuls. Hierdoor voldoen we snel aan de voorwaarde dat onze golflengte kleiner is dan de afmetingen van het object waar we tegen botsen. Daarom kunnen mensen niet door een bakstenen muur bewegen.

Daarnaast is er golfgedrag, zoals interferentie. Interferentie treedt op bij gelijksoortige quanta, zoals twee fotonen of twee elektronen, en er moeten minstens twee bundels zijn. Een belangrijke uitzondering is dat elektronen in het dubbelspleetexperiment met zichzelf kunnen interfereren, omdat de dubbele spleet als twee bundels kan worden gezien. Een andere vorm van golfgedrag is buiging. Buiging treedt op wanneer de golflengte veel groter is dan de opening waar het doorheen gaat. Wanneer een mens door een deur loopt, is zijn De Broglie golflengte veel kleiner dan de afmeting van de deur, dus zal hij niet afbuigen. Voor een watergolf die door een kleine opening gaat kan de golflengte groter zijn dan de opening, waardoor de golf zich buiten de opening in alle richtingen verspreidt. Een andere voorwaarde voor buiging is dat het object waardoor buiging plaatsvindt stevig bevestigd moet zijn.

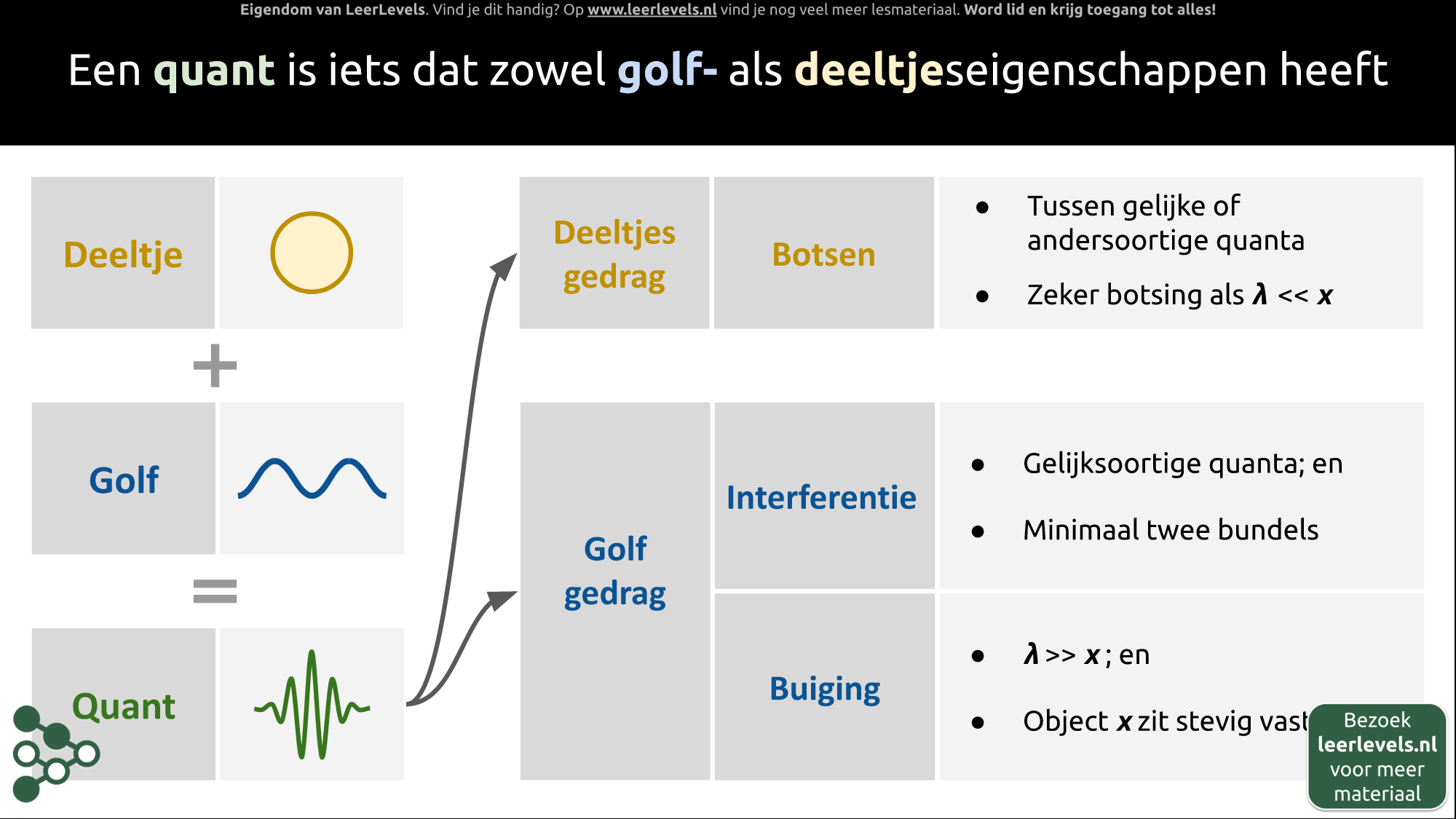
(Afbeelding: Animatie voor Quant concept)

Quant golffunctie

De golffunctie waarmee een quantumdeeltje wordt beschreven, geeft de waarschijnlijkheid aan om het deeltje op een bepaalde locatie te meten. Deze golffunctie, aangeduid met het symbool Ψ, is afhankelijk van de plaats x. In een één-dimensionale weergave kan Ψ er bijvoorbeeld uitzien als een gelokaliseerde sinusoïde met grote amplitude rondom een bepaald punt en een kleiner wordende amplitude aan weerszijden van dit punt. Deze golffunctie is een theoretische golf die wordt gebruikt om interferentie te berekenen. Hoewel de golf het deeltje beschrijft, heeft het zelf geen fysieke betekenis. Het is dus niet zo dat als de golf omlaag gaat, het deeltje ook omlaag gaat; er is geen directe relatie. De golffunctie Ψ heeft een vreemde eenheid. Dit wordt duidelijk wanneer we het kwadraat ervan nemen, omdat dit kwadraat plotseling de betekenis krijgt van de waarschijnlijkheid dat je een deeltje ergens waarneemt. Wanneer je dit grafisch afbeeldt, ontstaat er een patroon dat de kansverdeling toont om het deeltje op een bepaalde plaats te vinden. Hoe groter de amplitude, hoe groter de kans om het deeltje op die plek aan te treffen. Waar de golffunctie nul is, is de kans ook nul, en daar zul je het deeltje nooit meten. Het kwadraat van de golffunctie is dus een praktische kansverdeling die voorspelt waar je een quantumdeeltje kunt meten.

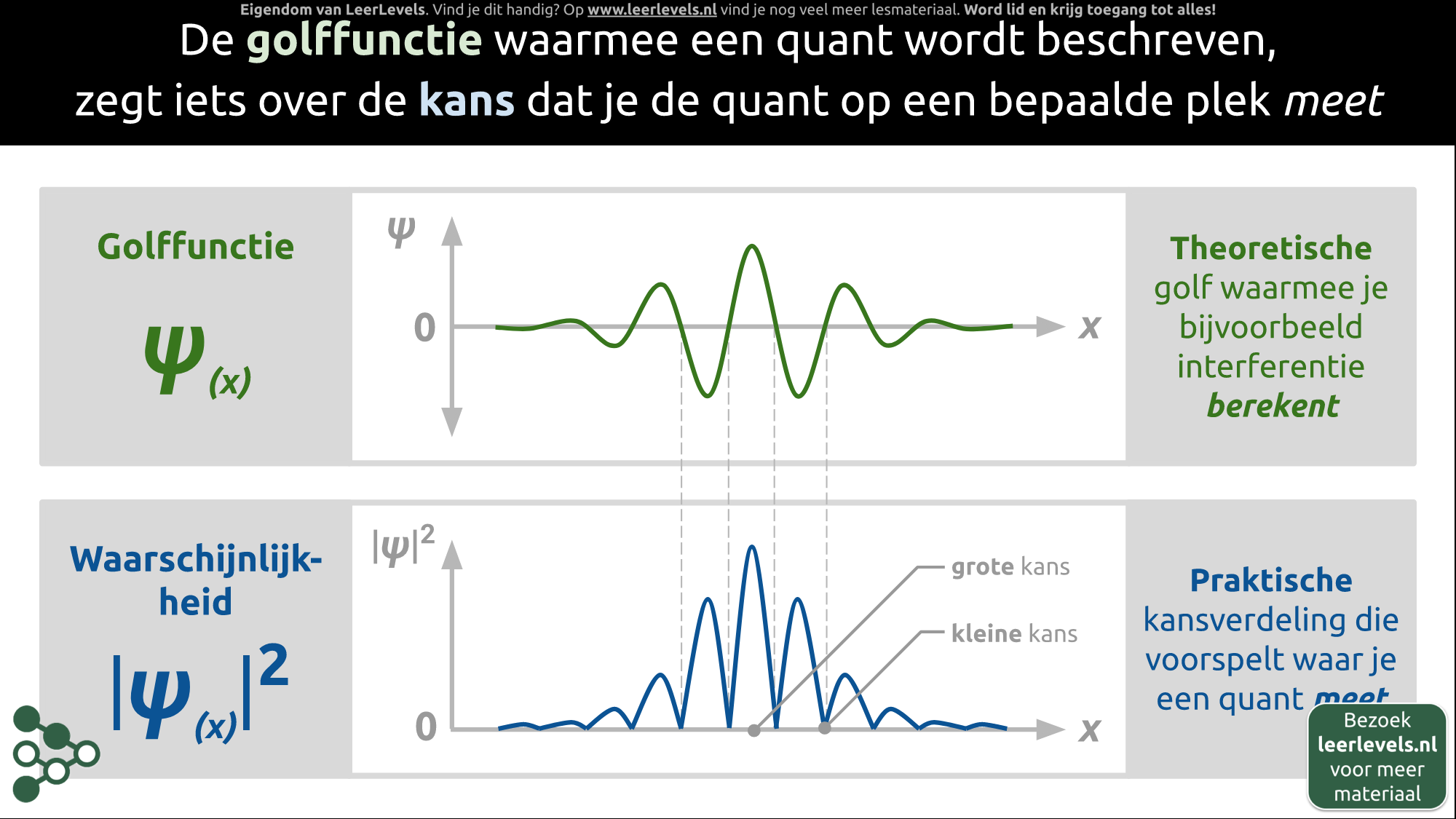
(Afbeelding: Animatie voor Quant golffunctie)

Terug naar overzicht Meld je aan

Raaklijnmethode

Om de helling van een grafiek te bepalen, gebruiken we de raaklijnmethode.
Hierbij nemen we drie stappen:

1. We kiezen het punt waar we de helling willen berekenen, dit noemen we punt P.
2. We tekenen een raaklijn door punt P met dezelfde helling als de grafiek op dit punt. Dit doen we door te kijken waar de lijn evenwijdig loopt aan de grafiek.
3. We berekenen de helling met de formule Δ y / Δ x tussen twee punten op de raaklijn die ver uit elkaar liggen.

Op deze manier kunnen we op een makkelijke manier de helling van een grafiek in een bepaald punt bepalen.

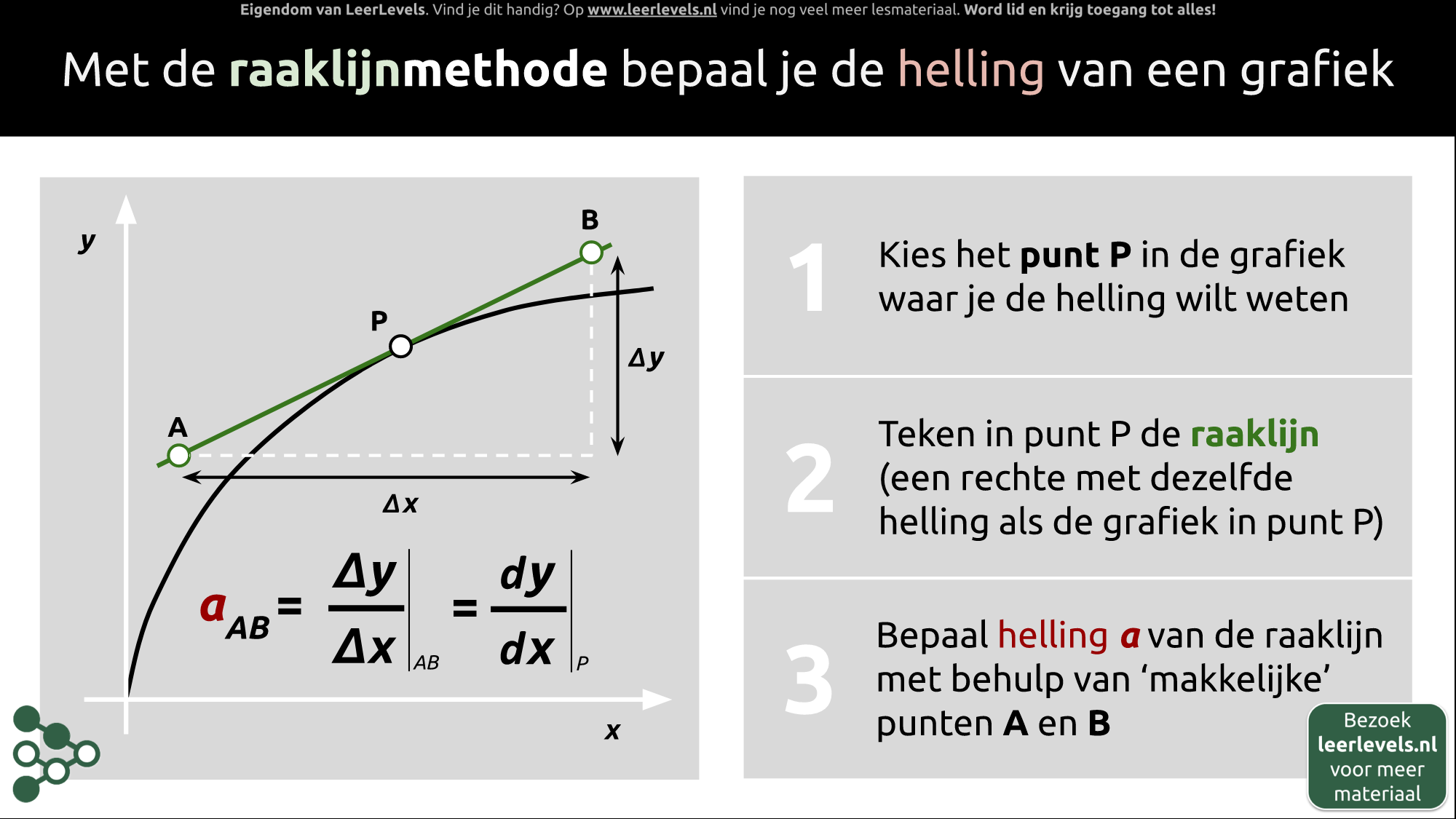
(Afbeelding: Animatie voor Raaklijnmethode)

Terug naar overzicht Meld je aan

Radioactieve straling

Alfa-, bèta- en gammastraling

Als radioactief materiaal vervalt, geeft het straling vrij. Er zijn drie soorten straling: alfa (α), beta (β) en gamma (γ). Alfastraling bestaat uit deeltjes met een heliumkern en heeft veel massa, terwijl betastraling bestaat uit elektronen of positronen en weinig massa heeft. Gammastraling is een soort elektromagnetische straling met verschillende frequenties. Radioactieve materialen kunnen één of meer van deze soorten straling uitzenden, elk met hun eigen eigenschappen. Sommige soorten straling dringen dieper door in materialen en hebben grotere effecten op de gezondheid dan andere. Dus bij radioactief verval komt alfa-, beta- of gammastraling vrij, elk met hun eigen unieke eigenschappen.

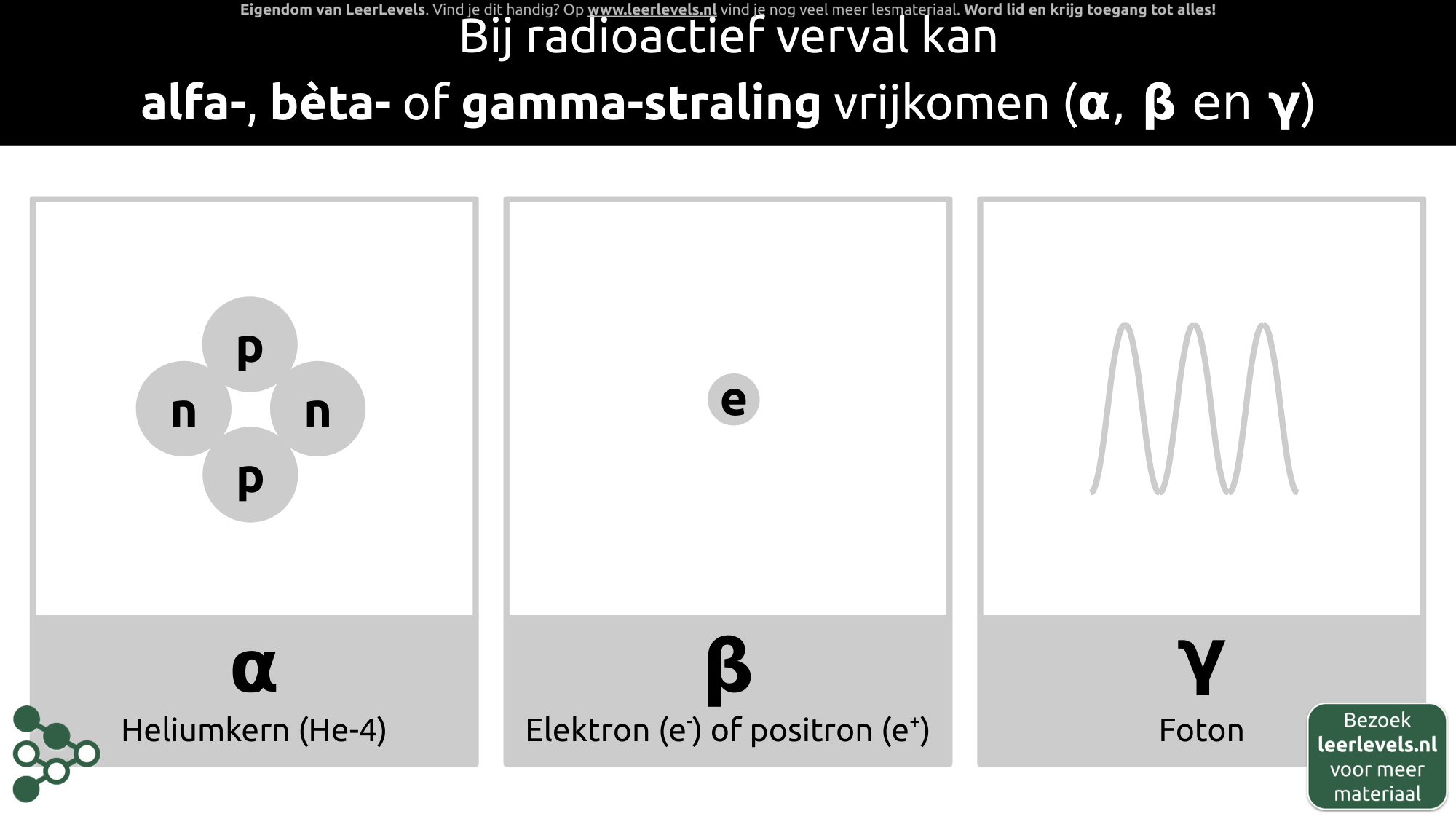
(Afbeelding: Animatie voor Alfa-, bèta- en gammastraling)

Terug naar overzicht Meld je aan

Radioactiviteit

Radioactief verval

Radioactief verval is het proces waarbij een atoom spontaan verandert in een ander atoom door het uitzenden of opnemen van een deeltje. Laten we beginnen met het voorbeeld van uranium-235. Voor het verval heeft het atoom een kern met 235 kerndeeltjes, waarvan 92 protonen. Soms kan een groepje van 2 protonen en 2 neutronen zich spontaan afscheiden van de rest van de kern. Zo'n groepje is gelijk aan een heliumkern en staat bekend als een alfadeeltje (α-deeltje). Wanneer dit verval plaatsvindt, blijft er een atoom over met 2 protonen en 2 neutronen minder dan uranium-235. De resulterende dochterkern is thorium-231. Dit is een voorbeeld van een vervalreactie.

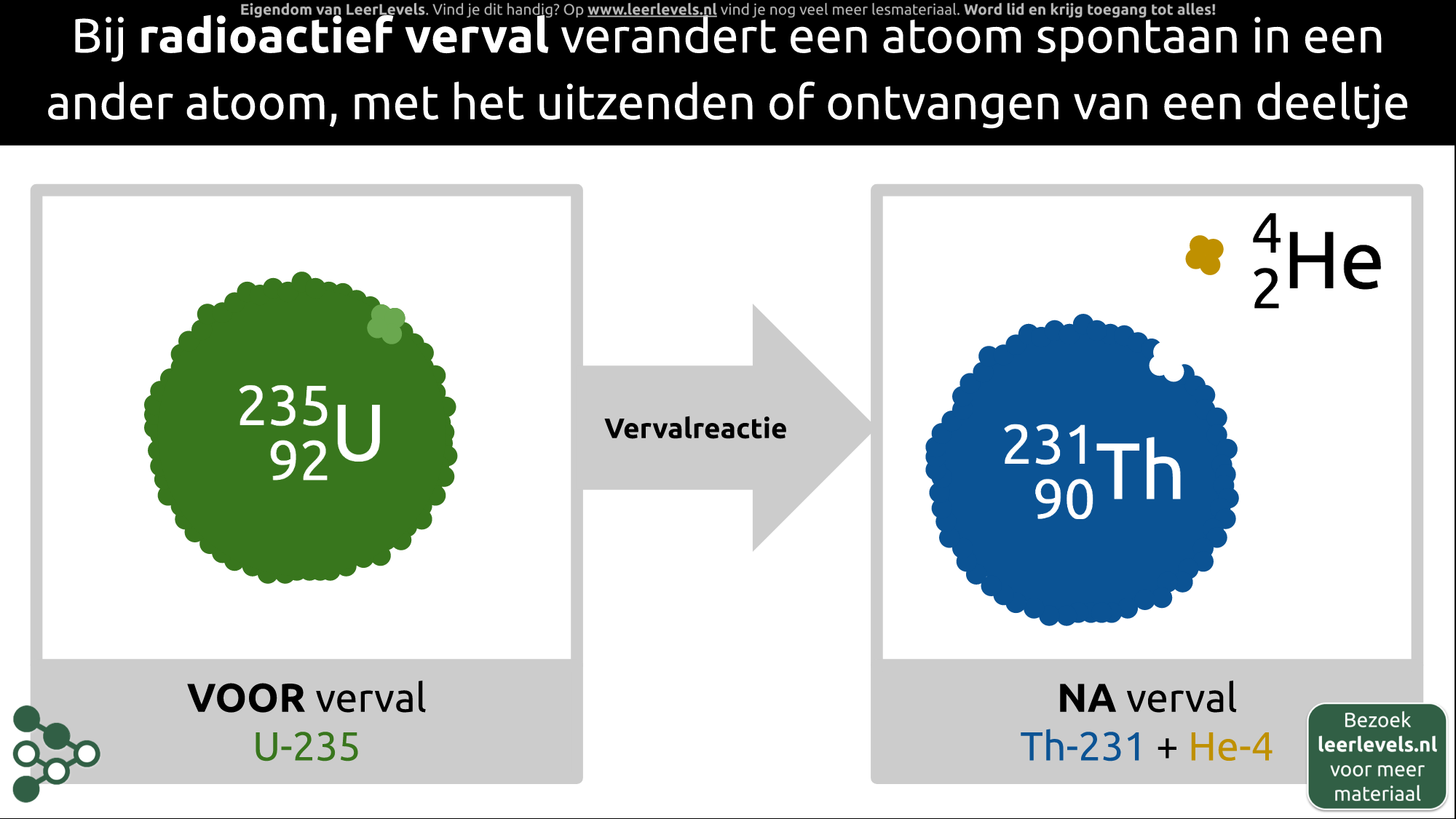
(Afbeelding: Animatie voor Radioactief verval)

Terug naar overzicht Meld je aan

Reacties

Exotherm en endothem

Een proces kan exotherm of endotherm zijn. Bij een exotherm proces komt er energie vrij. Bijvoorbeeld, bij de verbranding van hout komt warmte vrij. Een endotherm proces daarentegen vereist energie, zoals het smelten van ijs. Dit smelten gebeurt alleen wanneer er energie aan het ijs wordt toegevoegd, waardoor de temperatuur stijgt en het ijs smelt. Of een proces exotherm of endotherm is, hangt af van de vraag of er energie vrijkomt of juist nodig is.

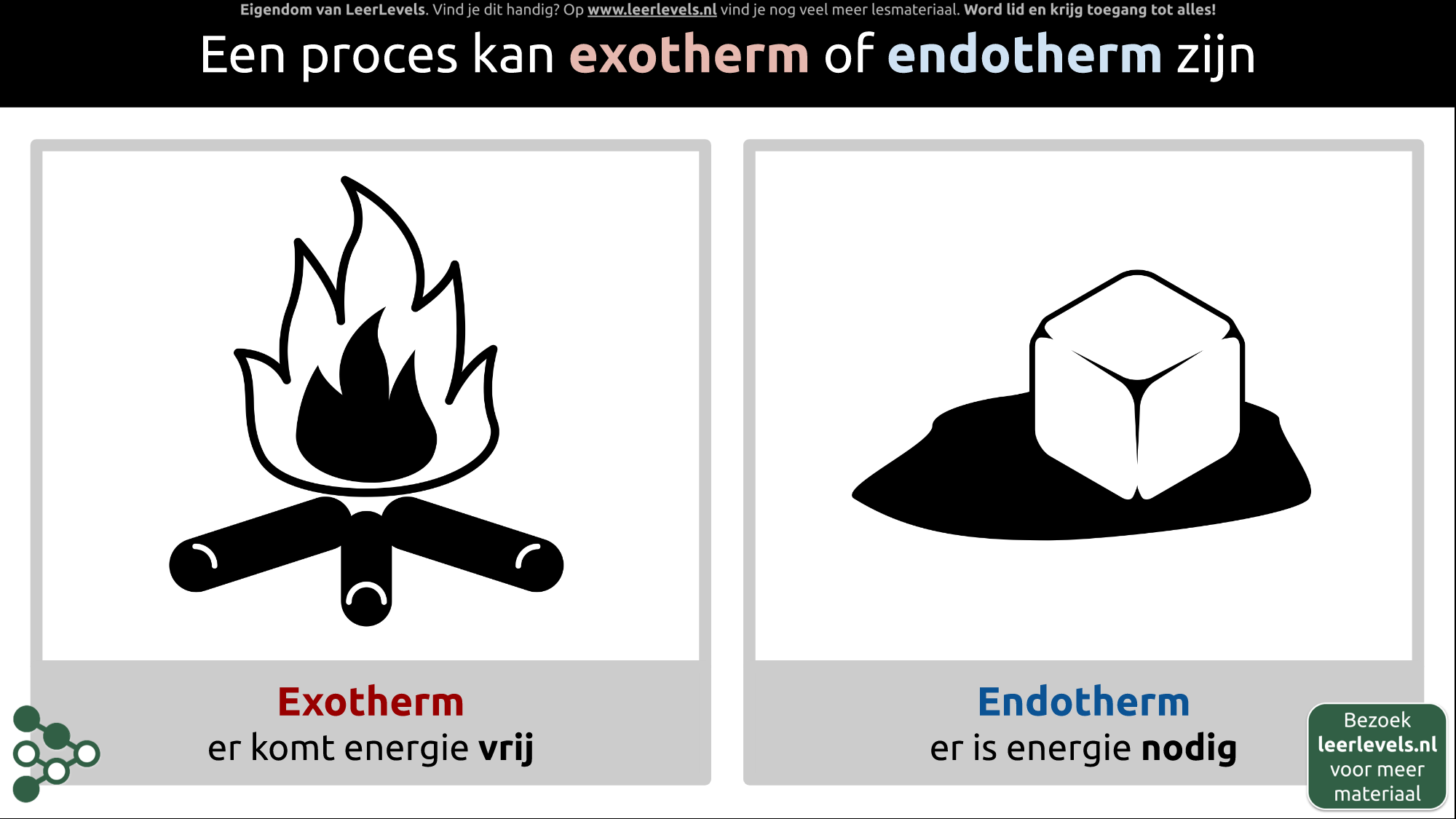
(Afbeelding: Animatie voor Exotherm en endothem)

Terug naar overzicht Meld je aan

Rechterhandregels

Als er een stroom door een draad of spoel loopt, ontstaat er een magnetisch veld. Er zijn twee regels om de richting van dit magnetische veld te bepalen. Voor een draad, steek je duim omhoog in de richting van de stroom en wijzen je vingers naar de richting van het magnetische veld om de draad heen. Bij een spoel is het andersom. Gebruik je vingers om de richting van de stroom in de spoel aan te geven en je duim wijst dan naar de richting van het magnetisch veld binnen in de spoel. Onthoud dat je de rechterhandregel gebruikt voor zowel de draad als de spoel, maar dat je in elk geval de stroom of het magnetisch veld op een andere manier bepaalt. Bij de draad heeft één draad cirkelvormige velden eromheen, en bij de spoel zijn er vaak meerdere windingen tussen de richting van de stroom. Er zijn geen formules of grootheden in deze uitleg.

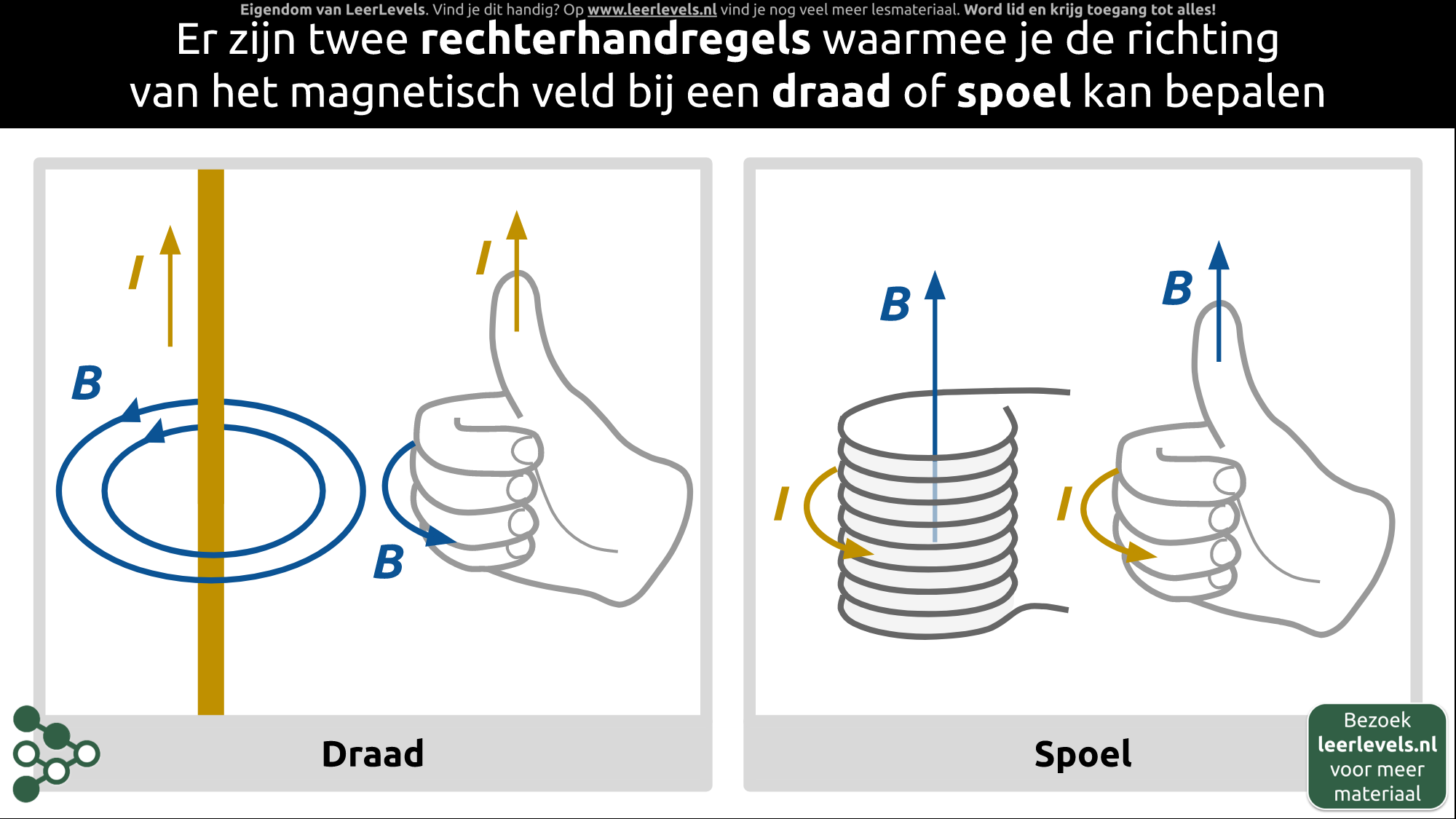
(Afbeelding: Animatie voor Rechterhandregels)

Terug naar overzicht Meld je aan

Recyclen

Recyclen betekent dat je grondstoffen opnieuw gebruikt, bijvoorbeeld door papier te maken van hout en dat papier weer in te zamelen om er nieuw papier van te maken. Er zijn twee soorten recyclen: upcyclen en downcycling. Bij upcyclen is het eindproduct beter dan wat je ervoor had, bijvoorbeeld door kostbare metalen uit oude telefoons te halen en er juwelen van te maken. Bij downcycling is het eindproduct minder zuiver, bijvoorbeeld als papier wordt gerecycled tot wc-papier. Het is belangrijk om te recyclen zodat grondstoffen opnieuw gebruikt kunnen worden en er minder afval is.

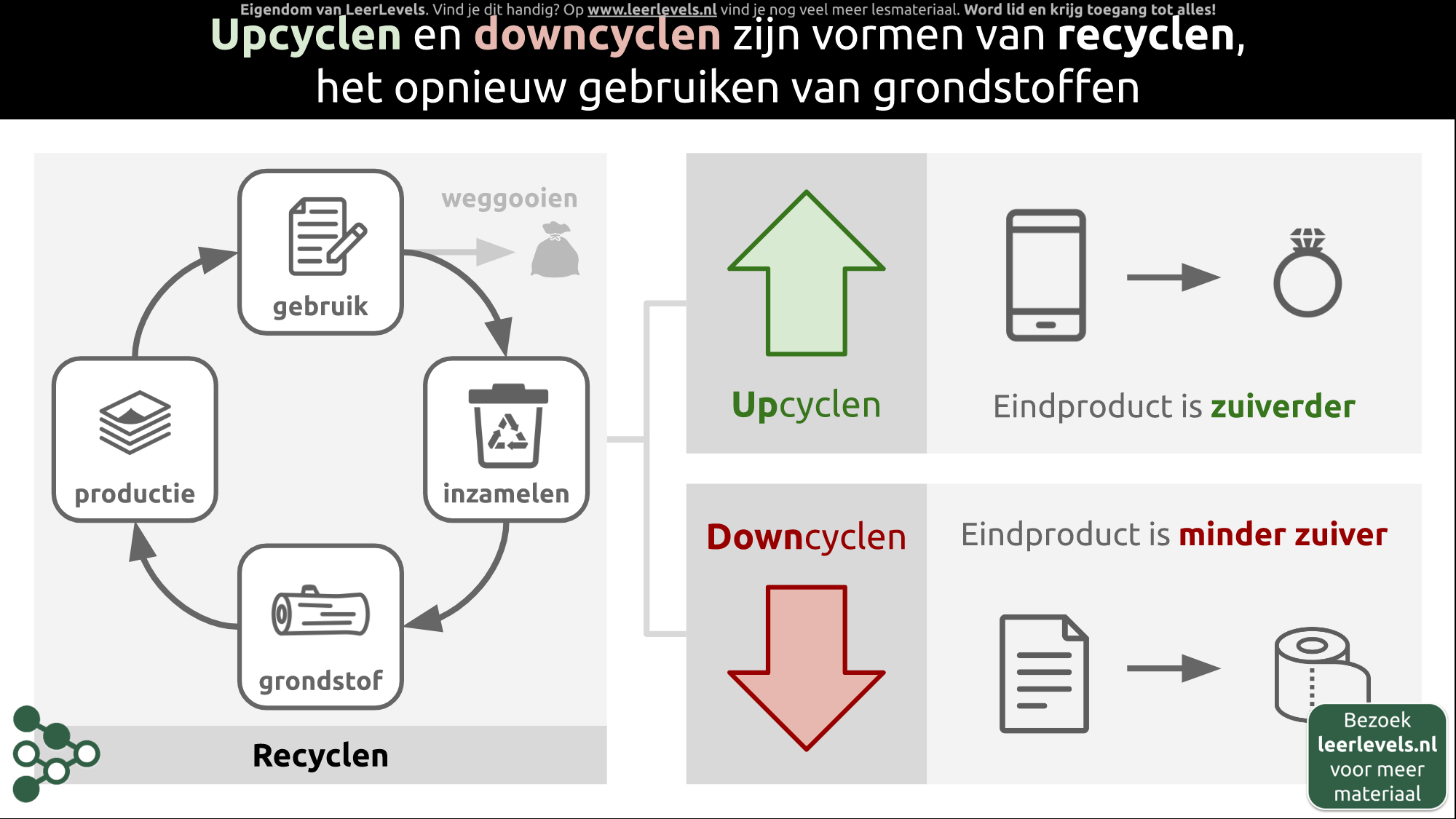
(Afbeelding: Animatie voor Recyclen)

Terug naar overzicht Meld je aan

Reflectie

Diffuuse en spiegelende reflectie

Reflectie van licht kan diffuus of spiegelend zijn. Bij diffuse reflectie worden lichtstralen in willekeurige richtingen verspreid. Dit gebeurt omdat de stralen in alle richtingen verstrooid worden. Wanneer lichtstralen op een handspiegel vallen, treedt een andere vorm van reflectie op. Hierbij worden alle lichtstralen op een voorspelbare manier weerkaatst, wat spiegelende reflectie wordt genoemd. Deze voorspelbaarheid maakt het mogelijk om met behulp van een spiegel precies te bepalen waar de lichtstralen zich verder zullen verplaatsen. Kortom, reflectie kan diffuus of spiegelend zijn, afhankelijk van het oppervlak.

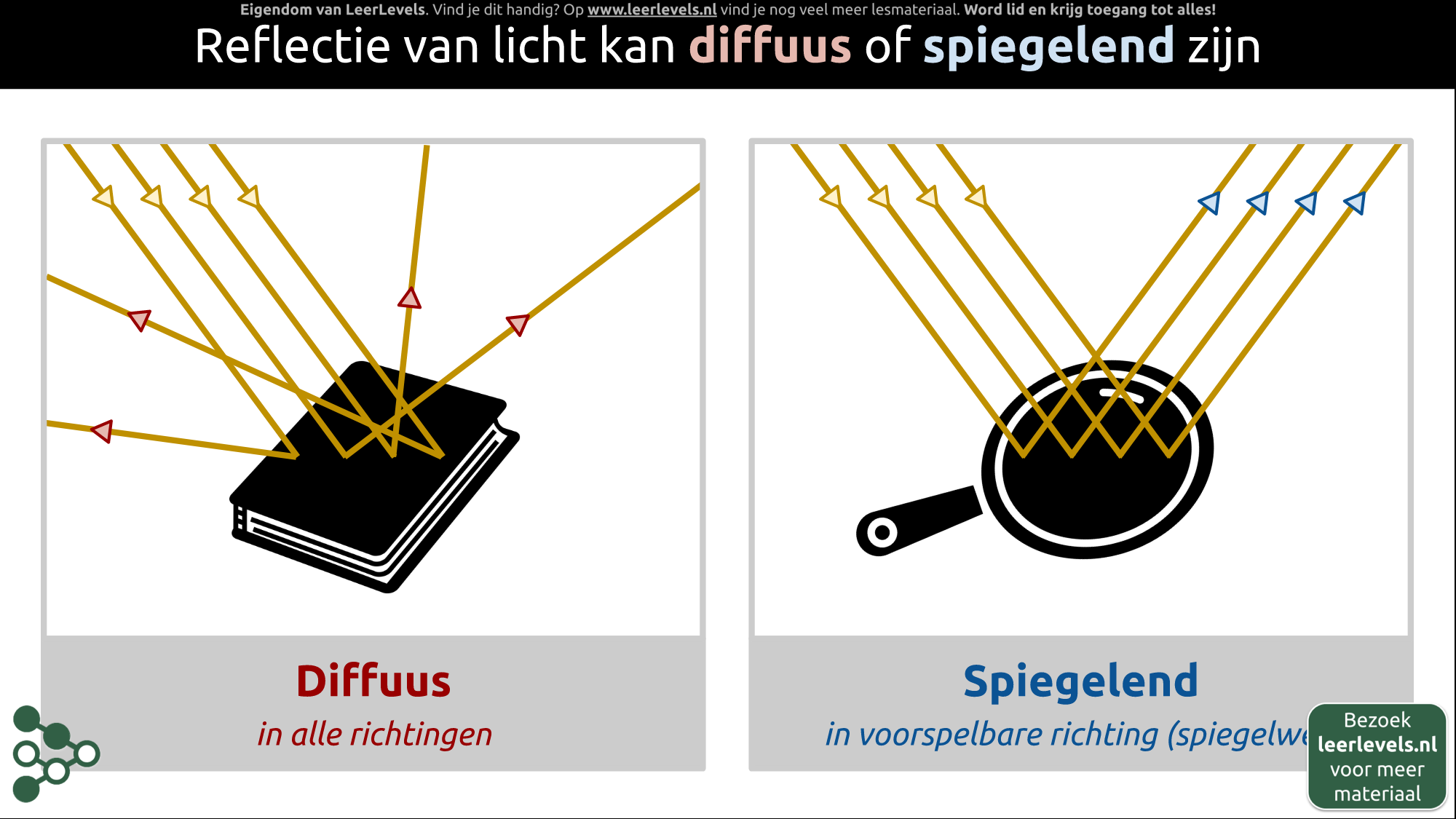
(Afbeelding: Animatie voor Diffuuse en spiegelende reflectie)

Reflecterende lichtstraal tekenen

Stel je voor dat iemand voor een spiegel staat en je wilt achterhalen hoe de lichtstraal van zijn schoenen naar zijn ogen beweegt. Volg hiervoor de onderstaande stappen:

- Stap 1: Kies de punten waar je de lichtstralen wilt tekenen, zoals tussen de schoenen en het oog.
- Stap 2: Teken het spiegelbeeld van de persoon en plaats de gekozen punten eveneens in het spiegelbeeld.
- Stap 3: Teken hulplijnen tussen de punten. Als je bijvoorbeeld wilt bepalen hoe de lichtstraal van de schoenen naar het oog gaat, teken dan de lijn van de schoenen in het spiegelbeeld naar het oog van de persoon.
- Stap 4: Teken de reflecterende lichtstralen. Teken de lichtstraal vanuit de schoen, via de spiegel, naar het oog van de persoon. Vanaf de spiegel naar het oog volgt de lichtstraal de hulplijn die je in de vorige stap hebt getekend.

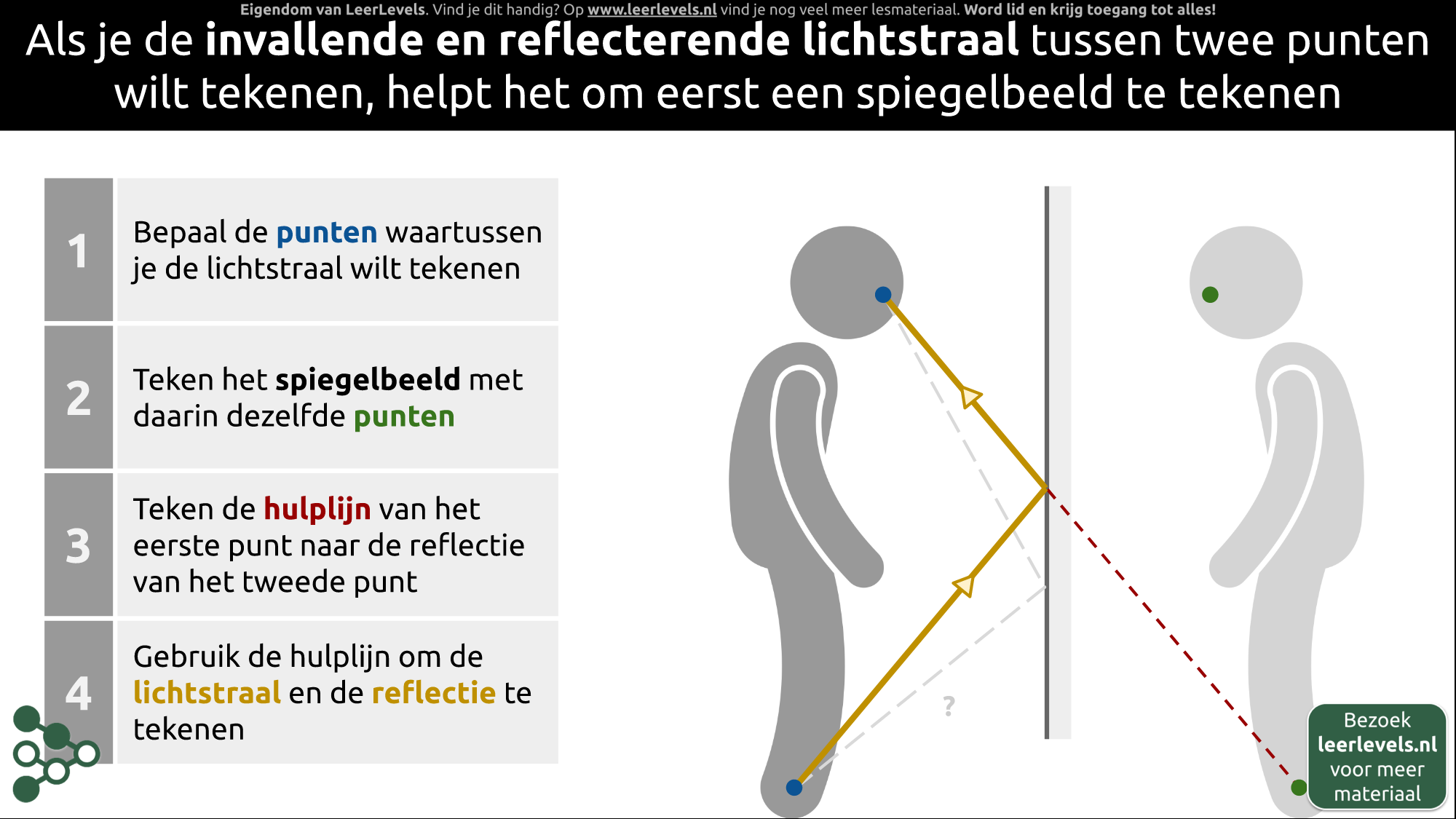
(Afbeelding: Animatie voor Reflecterende lichtstraal tekenen)

Terug naar overzicht Meld je aan

Rek

Relatieve uitzetting en rek concept

Relatieve uitzetting betekent de toename van lengte of volume, meestal uitgedrukt in procenten. Als een draad wordt uitgerekt, wordt het 'rek' genoemd en geeft het de lengtetoename per meter aan. Bijvoorbeeld, als een draad met een kwart van zijn lengte wordt uitgerekt, is de rek 0,25 of 25%. Bij een volume is de relatieve uitzetting de toename van het volume per kubieke meter. Als bijvoorbeeld een kubus twee keer zo groot wordt gemaakt in lengte, breedte en hoogte, ontstaan er zeven nieuwe kubussen van hetzelfde volume. De relatieve uitzetting is dan 7 of 700%. Om het uit te drukken gebruiken we meestal procenten.

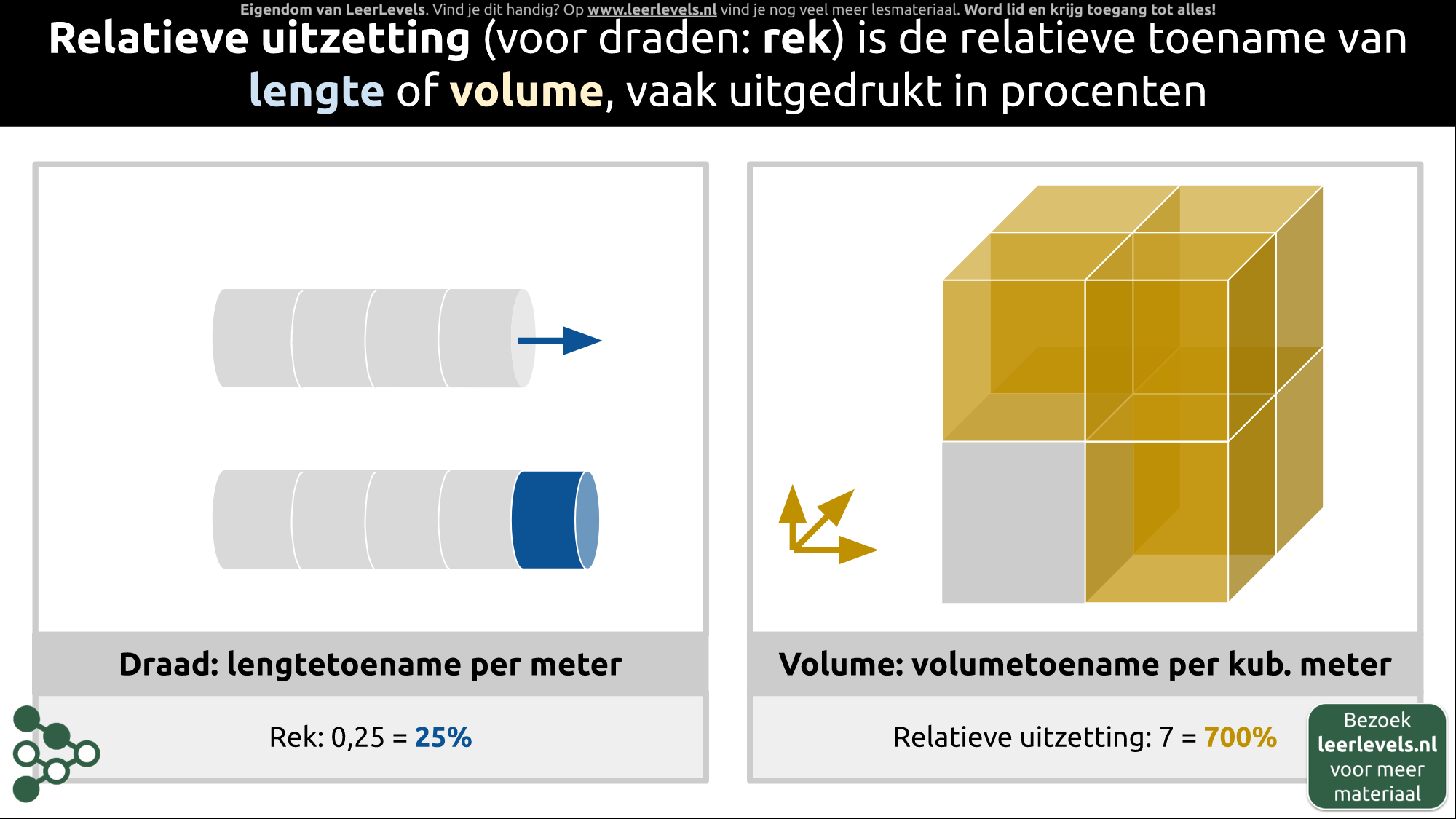
(Afbeelding: Animatie voor Relatieve uitzetting en rek concept)

Rek formule

Wanneer een draad warmer wordt, zet hij uit. De mate waarin dit gebeurt, heet de rek en wordt gemeten in procenten. Dit is een verhouding tussen de lengte toename en de begin lengte van de draad. Elke stof heeft zijn eigen constante die bepaalt hoeveel een draad uitzet per graden Celsius. Deze constante wordt de lineaire uitzettingscoëfficiënt genoemd en staat vaak in een tabel. Om de rek te berekenen, vermenigvuldig je de lineaire uitzettingscoëfficiënt met de temperatuurstijging in Kelvin.

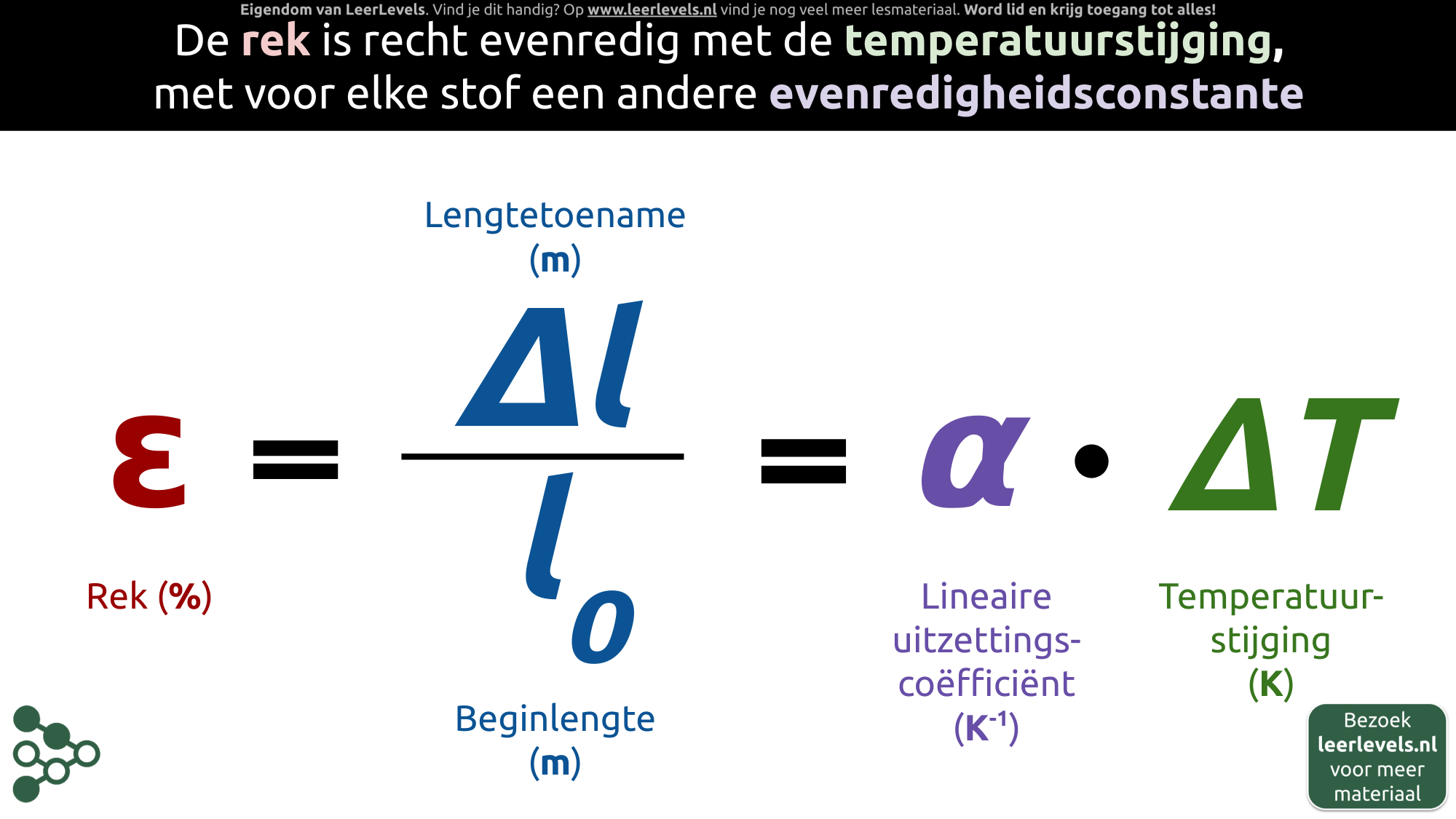
(Afbeelding: Animatie voor Rek formule)

Terug naar overzicht Meld je aan

Rekenen

Rekenen voor natuurkunde

Rekenen voor natuurkunde betekent dat je een lege plek in een formule invult met de juiste getallen en eenheden. Dit noemen we ook wel het vrijmaken van een variabele. Als voorbeeld gaan we berekenen hoe lang een sprinter doet over een rondje. We weten dat de snelheid van de sprinter 25 km/u is en dat de afstand van het rondje 400 meter is. We kunnen dan de formule v = s / t gebruiken, waarbij v de snelheid is, s de afstand en t de tijd. We willen de tijd weten, dus we moeten de formule omschrijven naar t = s / v. We vullen dan de gegevens in: t = 400 m / 25 km/u. Let op: de eenheden van snelheid en afstand moeten hetzelfde zijn. We rekenen de km/u om naar m/s: 25 km/u = 25,000 m/u = 6,94 m/s (1 km = 1,000 m en 1 u = 3,600 s). Nu kunnen we de formule invullen: t = 400 m / 6,94 m/s = 57,74 s. Dit ronden we af naar 58 s.

(Afbeelding: Animatie voor Rekenen voor natuurkunde)

Terug naar overzicht Meld je aan

Rekenmachine

Rekenmachine volgorde

Een grafische rekenmachine voert berekeningen uit in een vaste volgorde: eerst haakjes, dan machten en wortels, dan keer en delen, en ten slotte plus en min. Binnen elke categorie gaat hij van links naar rechts. Als er bijvoorbeeld 4 + 6/2 staat, begint hij met delen en komt hij uit op 4 + 3 = 7. Bij 2⁸⁻²³ begint hij met de haakjes en binnen de haakjes met het keer-teken, dus komt hij uit op 2⁸⁻⁶=²² = 4. Als de formule verandert, verandert de uitkomst. Bijvoorbeeld, in 4 · 6/3 komt hij uit op 24/3 = 8, terwijl bij 3/6 · 4 hij begint met delen en op 0,5 · 4 = 2 uitkomt. Maar als er haakjes geplaatst worden, heeft het grote invloed. Bij 3/(64) begint hij met de haakjes en komt hij uit op 3/24 = 0,125. Kijk dus goed naar de formule als je de rekenmachine gebruikt.

(Afbeelding: Animatie voor Rekenmachine volgorde)

Rekenmachine breuken

Als je een breuk wilt berekenen met een grafische rekenmachine, zorg er dan voor dat je haakjes om de noemer zet. Anders krijg je mogelijk een verkeerd antwoord. Bijvoorbeeld, als je 3 gedeeld door 6 keer 4 wilt berekenen, moet je het schrijven als 3 / (64), anders krijg je het verkeerde antwoord. Hetzelfde geldt als je 2,000 gedeeld door 2 keer de vierde macht wilt berekenen. Je moet het schrijven als 2,000 / (2(10⁴ om het juiste antwoord te krijgen. Als je een breuk binnen een breuk hebt, moet je ook haakjes gebruiken. Als je 2/1/3 + 6 berekent, krijg je het verkeerde antwoord, maar als je 2/(1/(3 + 6)) gebruikt, krijg je het juiste antwoord. Dus onthoud: zet altijd haakjes om de noemer als je een breuk berekent met een grafische rekenmachine.

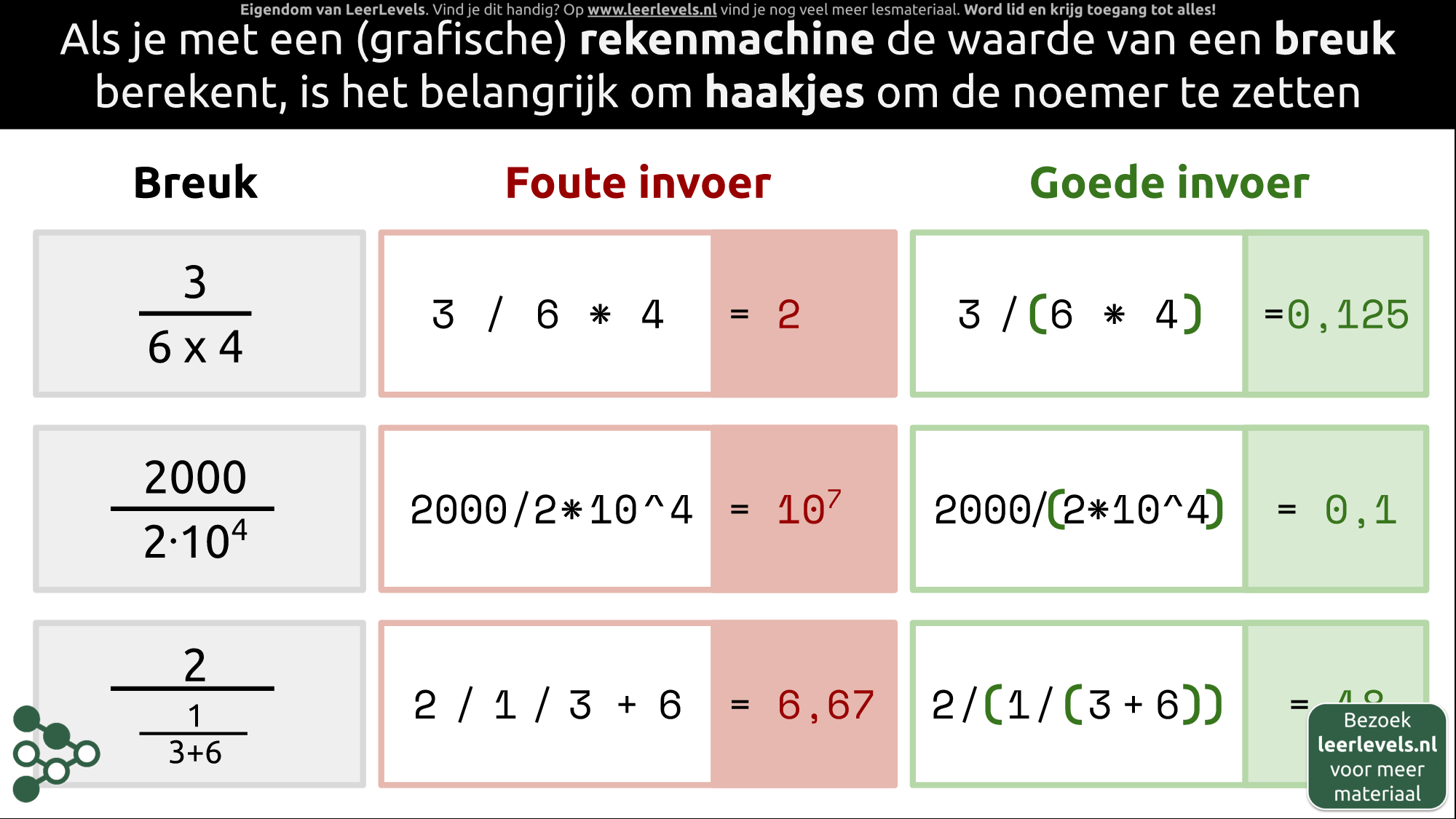
(Afbeelding: Animatie voor Rekenmachine breuken)

Terug naar overzicht Meld je aan

Rendement

Rendement concept

Het rendement van een energieomzetting geeft aan welk percentage van de ingevoerde energie nuttig kan worden gebruikt. Bij een gloeilamp is het rendement laag, omdat een groot deel van de energie wordt omgezet in warmte in plaats van licht. Warmte is in dit geval niet nuttig, dus het rendement is laag. Bij een spaarlamp, of nog beter, een LED-lamp, wordt een veel groter deel van de energie omgezet in nuttig licht, met slechts een klein beetje warmte. Dit betekent dat het rendement hoog is. Hoe meer nuttige energie er uit een systeem komt, des te hoger het rendement.

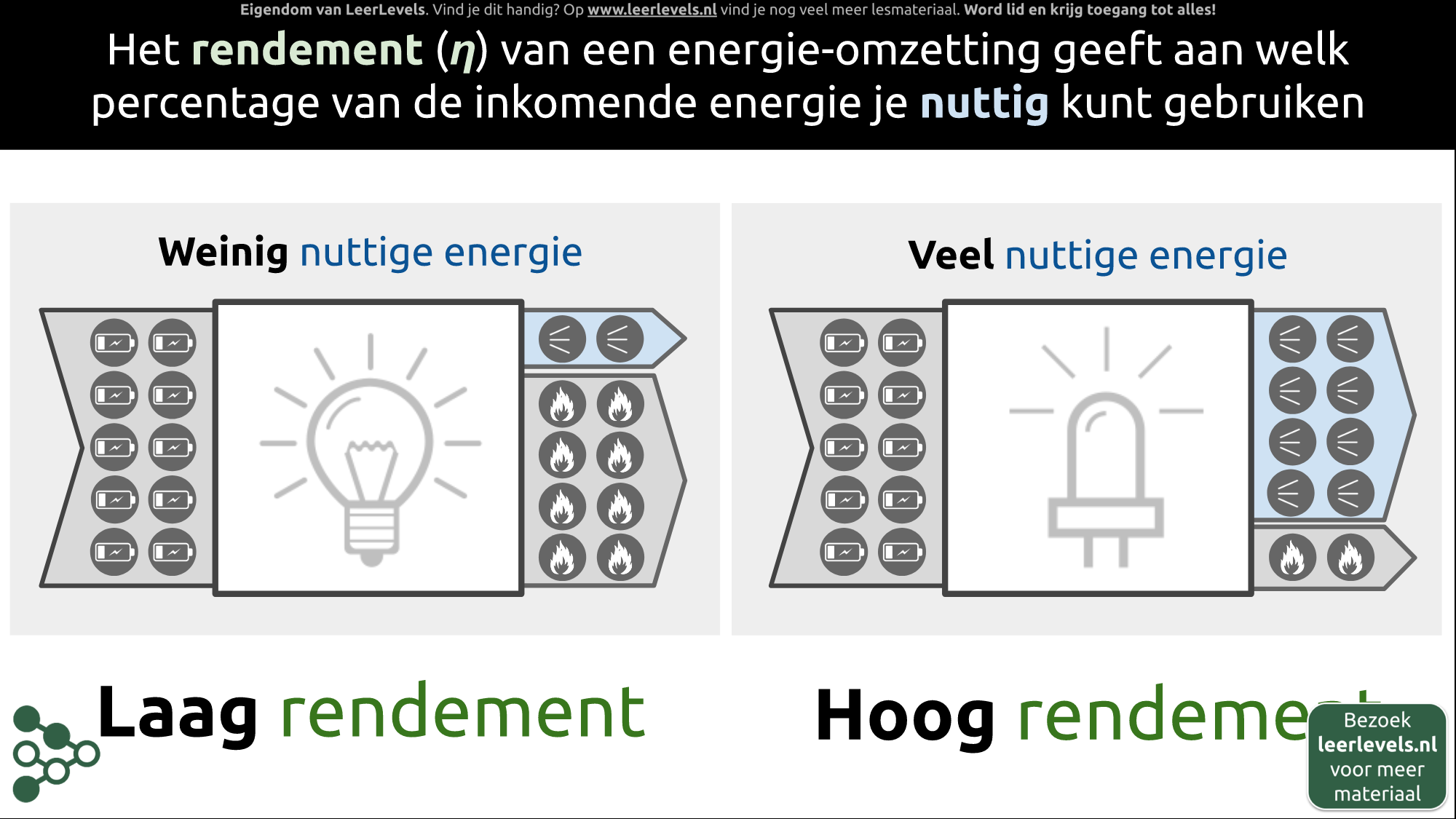
(Afbeelding: Animatie voor Rendement concept)

Rendement formule

Je kunt het rendement (η ) van energieomzetting berekenen met behulp van zowel de omgezette energie als het gebruikte vermogen. Rendement is de verhouding tussen de nuttige energie en de totale energie:

η = (Enuttig)/(Etotaal)

Het is belangrijk dat zowel de nuttige als de totale energie in dezelfde eenheid worden uitgedrukt, bijvoorbeeld in Joules. De uitkomst van deze formule is een factor. Vaak wordt rendement als percentages gegeven. Een rendement van 90 \% betekent een factor van 0,9.

Een andere manier om het rendement te berekenen is via vermogens. Hierbij is het rendement de verhouding tussen het nuttige vermogen en het totale vermogen:

η = (Pnuttig)/(Ptotaal)

Ook hier is het belangrijk dat zowel het nuttige als het totale vermogen in dezelfde eenheid worden uitgedrukt.

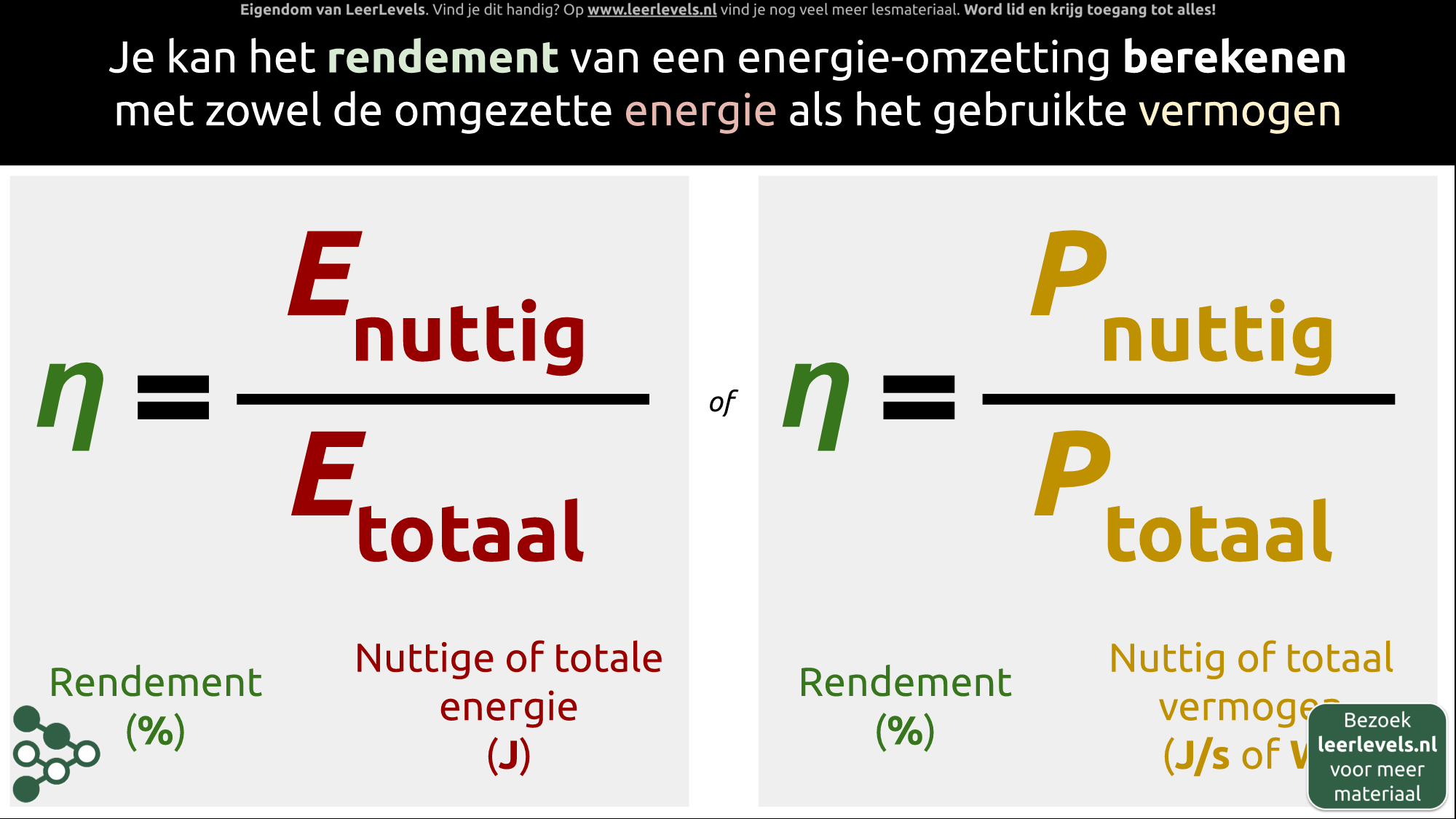
(Afbeelding: Animatie voor Rendement formule)

Terug naar overzicht Meld je aan

Resonantie

Resonantie en demping

Als iets trilt, kan de amplitude (de grootte van de beweging) veranderen. Bij resonantie wordt de amplitude groter als er kracht wordt uitgeoefend in dezelfde richting als de snelheid. Dit gebeurt bijvoorbeeld als je op een schommel duwt terwijl deze al beweegt. Bij demping wordt de amplitude juist kleiner omdat de kracht die op het voorwerp werkt tegengesteld is aan de snelheid. Dit gebeurt bijvoorbeeld door luchtwrijving op een schommel. In beide gevallen blijft de trillingstijd (de tijd die een trilling nodig heeft om een compleet cyclus te doorlopen) constant. In het u-t diagram, waarin de uitwijking (verticaal) tegen de tijd (horizontaal) is uitgezet, blijft de afstand tussen de pieken steeds hetzelfde bij resonantie en wordt de uitwijking juist steeds kleiner bij demping.

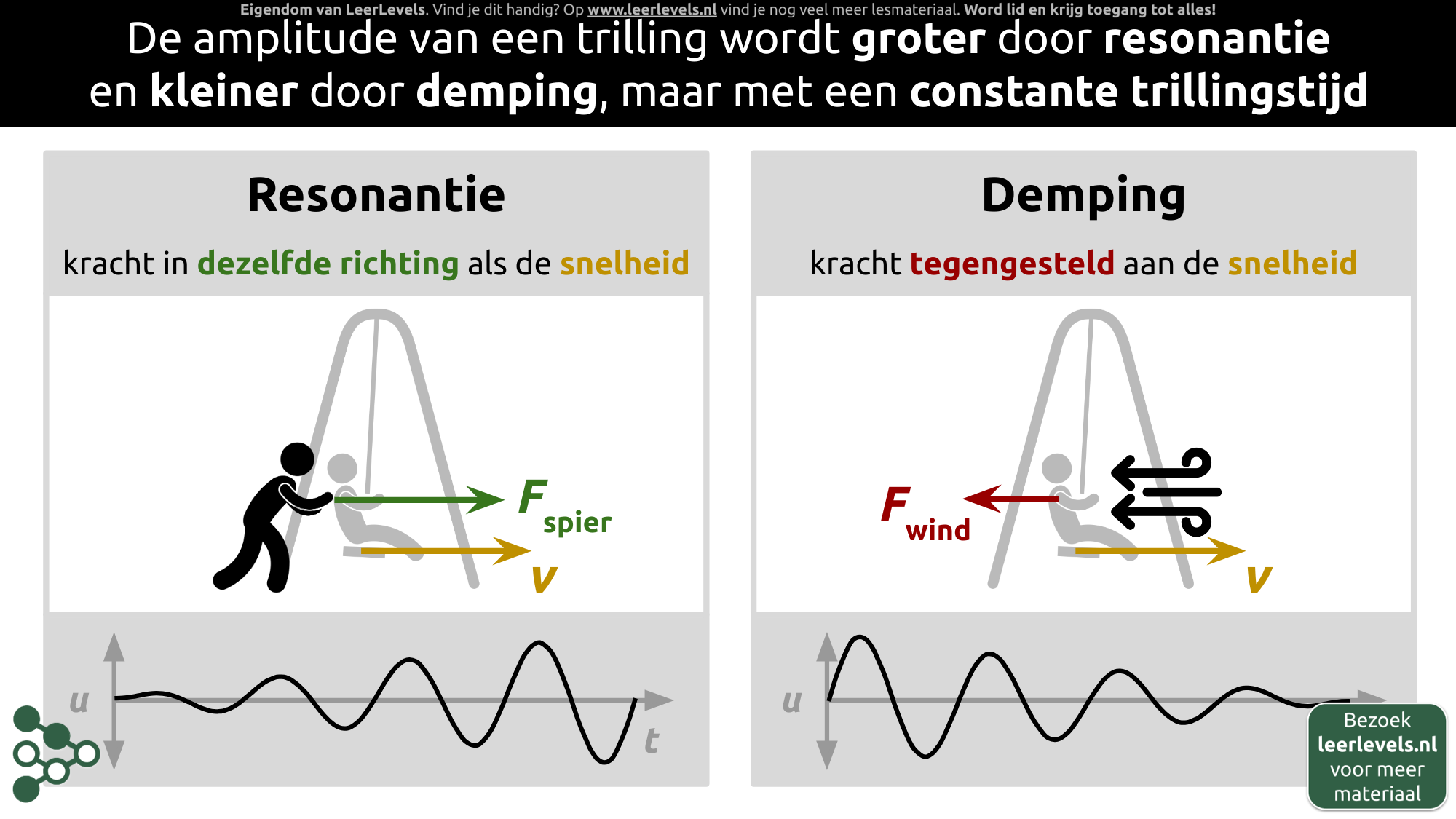
(Afbeelding: Animatie voor Resonantie en demping)

Terug naar overzicht Meld je aan

Resultante

Resultante kracht

De resultante kracht, ook wel netto kracht genoemd, is de som van alle krachten die op een voorwerp werken. In één dimensie geldt dat de resultante kracht gelijk is aan de voortstuwende kracht min de tegenwerkende kracht:

Fres = Fvoorts. - Ftegenw.

Hierbij is Fvoorts. de som van alle voortstuwende krachten en Ftegenw. de som van alle tegenwerkende krachten. Stel dat we een voortstuwende kracht hebben van 400N, geleverd door spierkracht, en er zijn tegenwerkende krachten zoals wrijvingskracht en luchtweerstand met een gezamenlijke waarde van 300N. Dan berekenen we de resultante kracht door 400N - 300N te doen. Dit resulteert in een netto kracht van 100N.

In meerdere dimensies werkt dit echter anders. Als je bijvoorbeeld een basketbal door de lucht gooit, werken er verschillende krachten op de bal, zoals de zwaartekracht die naar beneden werkt en de wrijvingskracht die naar achteren werkt omdat de bal door de lucht vliegt. Om de resultante kracht in dit geval te berekenen, moeten we alle vectorpijlen optellen, bijvoorbeeld met behulp van de kop-staart methode. Hoe meer vectoren erbij betrokken zijn, hoe ingewikkelder het wordt. Maar de kracht blijft altijd gelijk aan de som van alle krachten die op het voorwerp werken, zowel in twee als in drie dimensies.

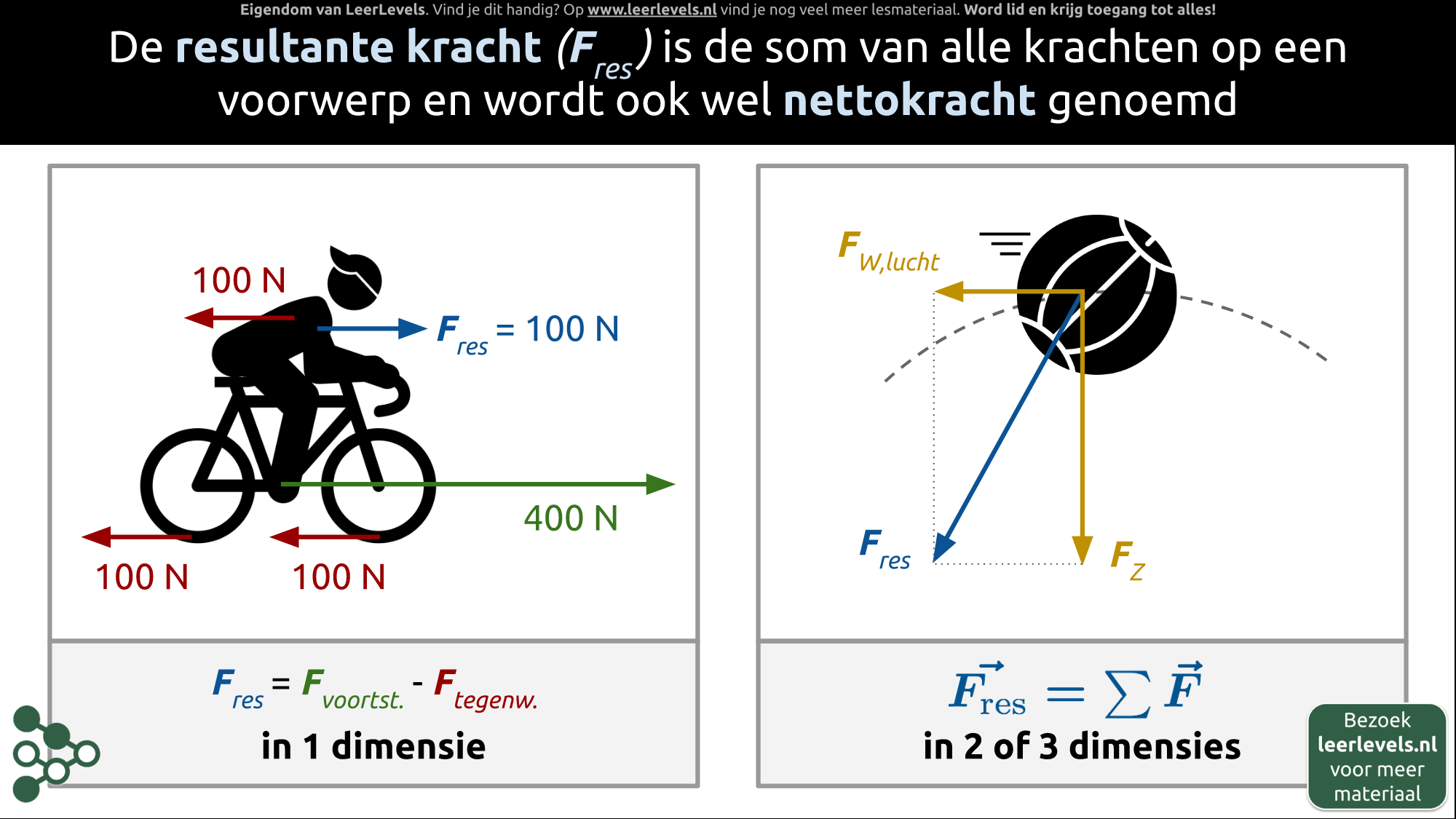
(Afbeelding: Animatie voor Resultante kracht)

Resultante kracht en resultant vermogen

De resulterende kracht op een voorwerp is recht evenredig met het vermogen waarmee de arbeid wordt verricht. Laten we dit uitleggen aan de hand van een voorbeeld met een auto. Eerst bekijken we de resulterende kracht: wanneer een auto met een bepaalde snelheid v rijdt, werken er doorgaans een aantal krachten op in: een motorkracht naar voren, wrijvingskrachten naar achteren en luchtweerstand die het voertuig tegenwerkt.

De resulterende kracht is gelijk aan de motorkracht naar voren, verminderd met de luchtweerstand en de rolweerstand. Wat betekent dit? Als de resulterende kracht gelijk is aan 0, verandert de snelheid niet: er is geen versnelling of vertraging. Is de resulterende kracht groter dan 0, dan neemt de snelheid toe. Is de resulterende kracht kleiner dan 0, dan neemt de snelheid af. Dit hangt direct samen met het verrichte vermogen.

Het vermogen laat ons zien hoeveel energie per tijdseenheid nodig is om een bepaalde snelheid te bereiken. Er gaat echter ook vermogen verloren aan lucht- en rolweerstand; deze krachten verrichten negatieve arbeid en onttrekken energie aan de auto. Het resulterende vermogen kan worden berekend met de vergelijking:

Pres = Pmotor - Pluchtwrijving - Prolwrijving

Het resulterende vermogen is gelijk aan

Pres = Fres · v

Hieruit kunnen we concluderen dat als de snelheid constant blijft, verandert de kinetische energie niet en is het resulterende vermogen nul. Versnelt de auto, dan is het resulterende vermogen positief. Vertraagt de auto, dan is het resulterende vermogen negatief.

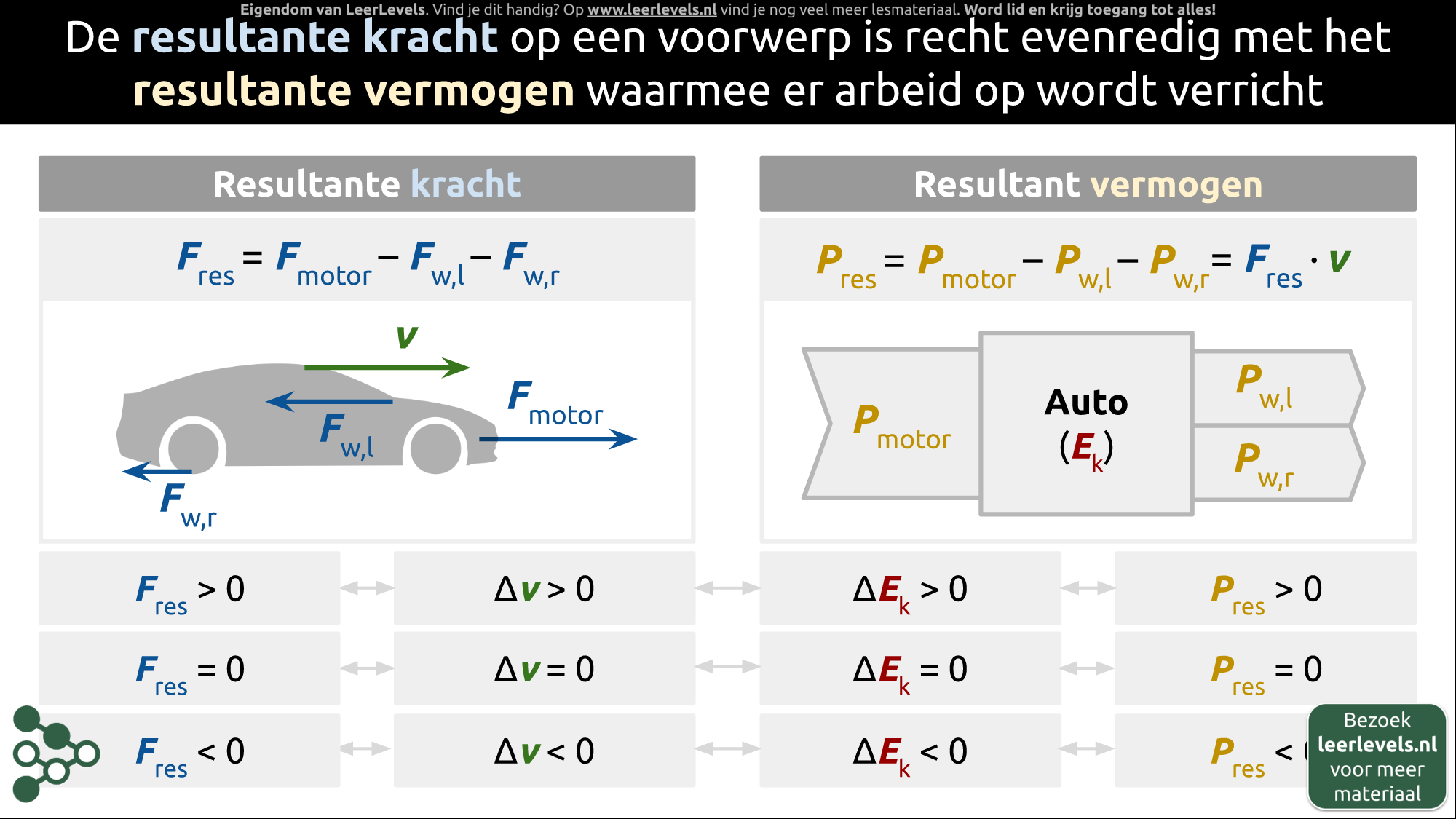
(Afbeelding: Animatie voor Resultante kracht en resultant vermogen)

Terug naar overzicht Meld je aan

Roodverschuiving

Roodverschuiving en blauwverschuiving

Het Doppler-effect zorgt ervoor dat licht van een bewegende bron van kleur verandert. Als de bron niet beweegt, zien we de kleur zoals deze is. Maar als de bron naar ons toebeweegt, wordt de kleur meer blauw en als de bron van ons af beweegt, wordt de kleur meer rood. Dit komt doordat de frequentie van het licht verandert als de afstand van de bron verandert. Een hogere frequentie betekent meer energie en blauwer licht, een lagere frequentie betekent minder energie en roder licht.

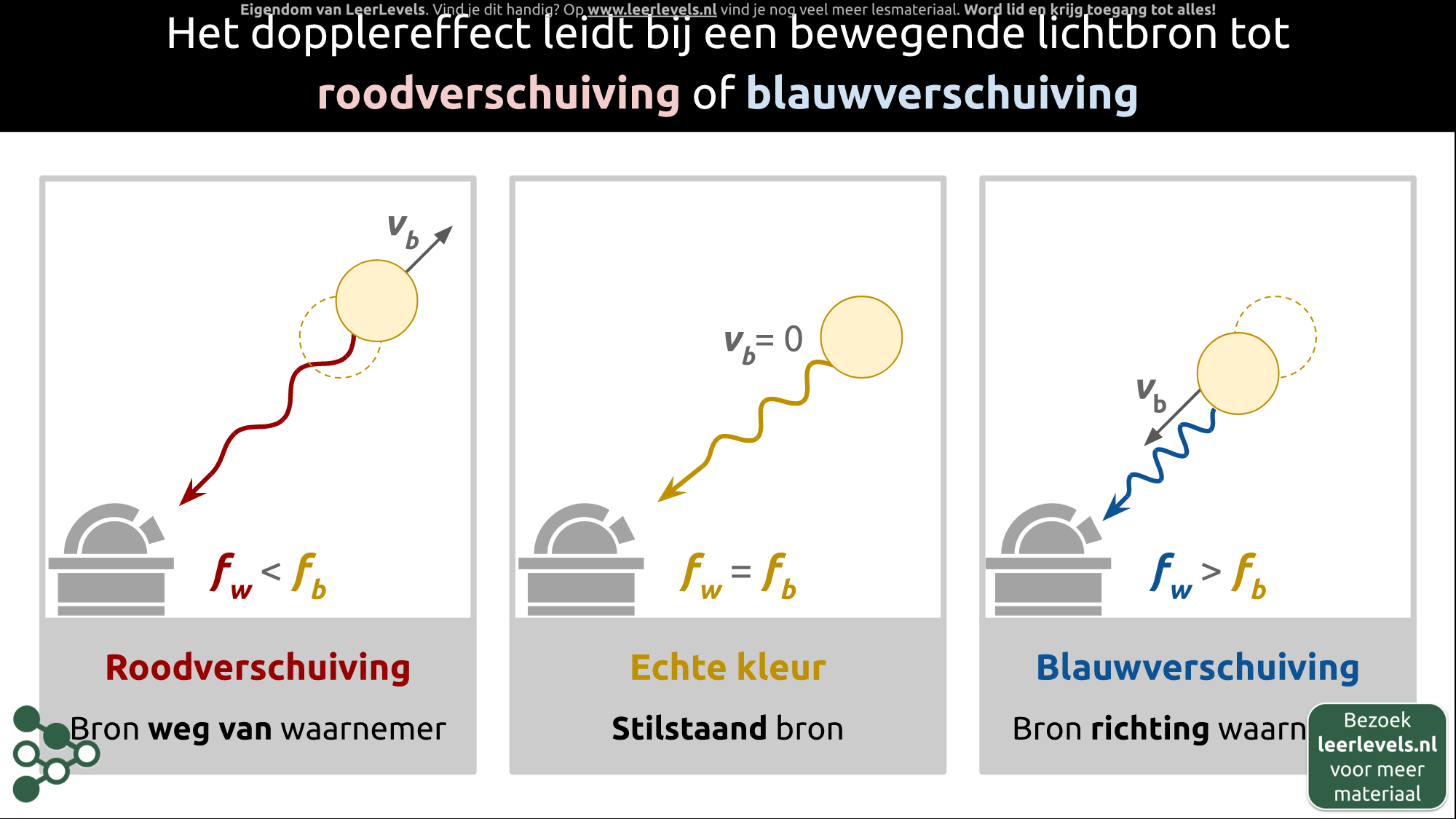
(Afbeelding: Animatie voor Roodverschuiving en blauwverschuiving)

Terug naar overzicht Meld je aan

Ruimtelijke eenheden

Ruimtelijke eenheden omrekenen conceptueel

Om eenheden om te rekenen, moet je kijken hoe vaak ze in elkaar passen. Hierbij kunnen we kijken naar lengtes, oppervlaktes en inhoud.

Als we bijvoorbeeld kijken naar meters en decimeters, dan weten we dat er 10 decimeters passen in een meter. Dus 1 meter is gelijk aan 10 decimeters. Als we dit toepassen op oppervlaktes, weten we dat 1 vierkante meter gelijk is aan 100 vierkante decimeter omdat er 10 decimeters passen in elke dimensie.

Als we nog een dimensie toevoegen, hoogte bijvoorbeeld, kunnen we kijken naar kubieke meters en kubieke decimeters. Bijvoorbeeld, als we een blokje hebben van 1 meter bij 1 meter bij 1 meter, weten we dat er 1000 kubieke decimeters passen omdat er 10 decimeters passen in elke dimensie, dus 1 m³ = 1000 dm³.

Kortom, om eenheden om te rekenen, moet je kijken naar hoe vaak ze in elkaar passen in de verschillende dimensies.

(Afbeelding: Animatie voor Ruimtelijke eenheden omrekenen conceptueel)

Ruimtelijke eenheden omrekenen wiskundig

Als we een afstand of oppervlakte in verschillende dimensies willen omrekenen, moeten we rekening houden met de grootte van de omrekenstap. In één dimensie (1D) is 1 meter gelijk aan 10 decimeter (dm), wat we kunnen schrijven als m = 10¹dm. In twee dimensies (2D), kunnen we uitrekenen hoeveel blokjes van 1 dm x 1 dm er passen in een blok van 1 m x 1 m. Met wiskunde vinden we dat m² = (10¹dm)² = 10²dm² = 100 dm². In drie dimensies (3D) werkt dit hetzelfde: m³ = (10¹dm)³ = 10³dm³ = 1000 dm³. Als we bijvoorbeeld kilometers (km) willen omrekenen naar vierkante kilometers (km²), gebruiken we de formule 1 km = 10³m, dus 1 km² = (10³m)² = 10⁶m². Het is belangrijk om de rekenregels te volgen om de juiste uitkomst te krijgen.

(Afbeelding: Animatie voor Ruimtelijke eenheden omrekenen wiskundig)

Terug naar overzicht Meld je aan

Röntgenfoto

Een röntgenfoto werkt doordat röntgenstraling gemakkelijker door zacht weefsel gaat dan door hard weefsel, zoals botten. Het proces verloopt als volgt: er is een bron die röntgenstraling produceert. Hoe dit precies gebeurt, is hier niet belangrijk. Wanneer je deze röntgenstraling op bijvoorbeeld een hand richt, zal het zachte weefsel de straling doorlaten. Vervolgens bereikt de straling een gevoelige plaat. Harde weefsels, zoals botten, laten de röntgenstraling niet door, waardoor er een schaduw op de gevoelige plaat ontstaat. Bij het ontwikkelen van de röntgenfoto wordt een negatief gemaakt van de belichting, waardoor de harde weefsels juist wit worden. Dit maakt het eenvoudig om bijvoorbeeld botbreuken te herkennen. Kortom, een röntgenfoto maakt gebruik van het feit dat röntgenstraling wel door zachte weefsels kan passeren, maar niet door botten.

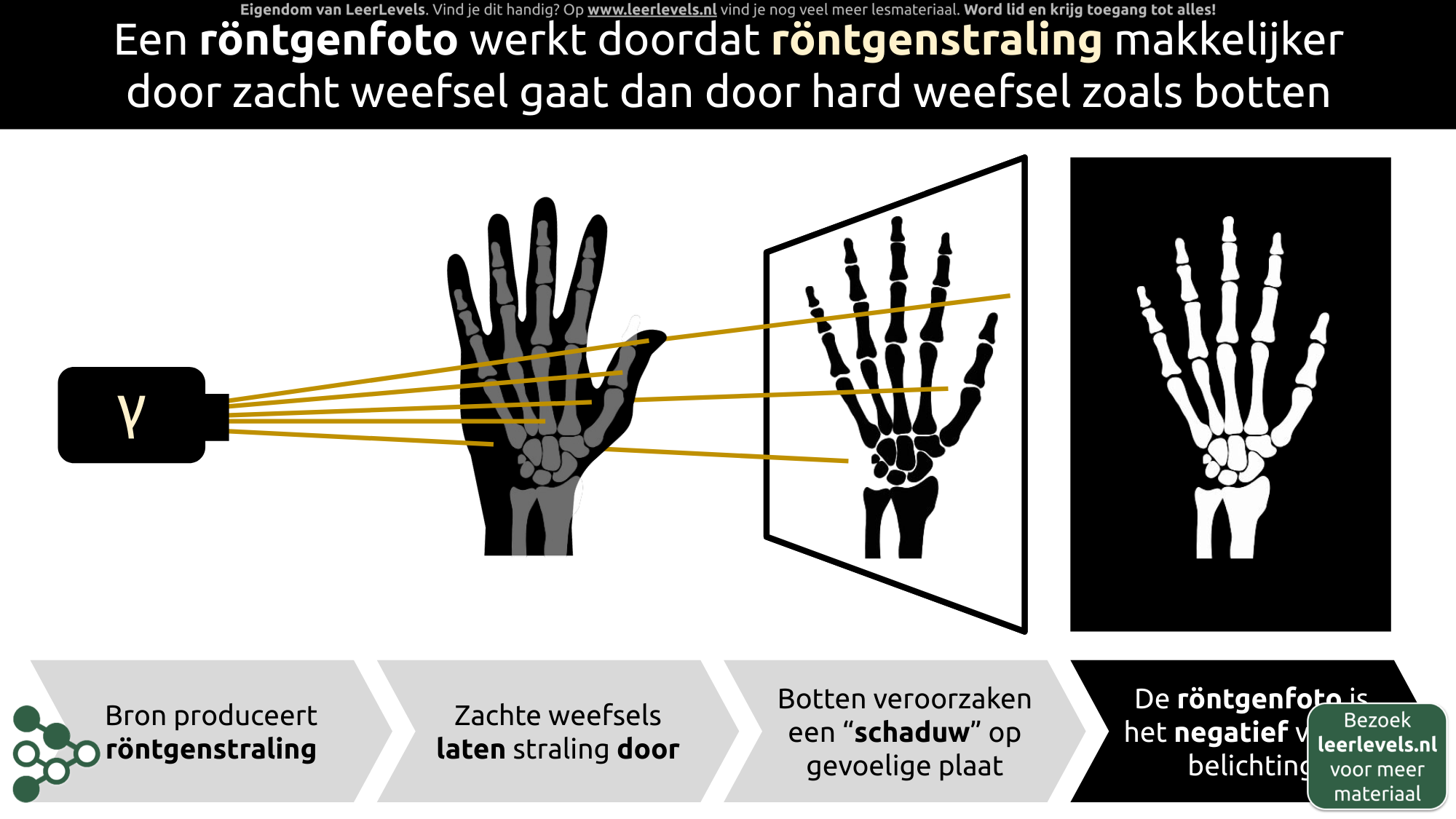
(Afbeelding: Animatie voor Röntgenfoto)

Terug naar overzicht Meld je aan

SOSCASTOA

SOSCASTOA concept

Een rechthoekige driehoek is een driehoek met één rechte hoek. De langste zijde heet de schuine zijde en staat tegenover de rechte hoek. De andere twee zijden zijn de aanliggende en overstaande zijde. Bij een kleine hoek is de verhouding tussen de overstaande en schuine zijde bijna nul, de verhouding tussen de aanliggende en schuine zijde is bijna 1 en de verhouding tussen de overstaande en aanliggende zijde is bijna nul. Bij een grote hoek zijn de verhoudingen andersom: de verhouding tussen overstaande en schuine zijde is bijna 1, de verhouding tussen aanliggende en schuine zijde is bijna 0 en de verhouding tussen overstaande en aanliggende zijde gaat naar oneindig. Er zijn formules, goniometrische functies genaamd, die precies de waarden van deze verhoudingen geven.

(Afbeelding: Animatie voor SOSCASTOA concept)

SOSCASTOA formules

SOSCASTOA is een handig trucje bij goniometrie voor rechthoekige driehoeken. Stel je voor dat je een rechthoekige driehoek hebt, met een hoek van 90 graden rechtsonder. Vanuit deze hoek (laten we hem alfa noemen) heb je drie zijden: de schuine zijde (s), de aanliggende zijde (a) en de overstaande zijde (o). Er zijn drie formules die je kunt gebruiken:

- Sinus: sin(α) = o/s
- Cosinus: cos(α) = a/s
- Tangens: tan(α) = o/a

Als je deze formules wilt onthouden, is er een handig ezelsbruggetje: SOSCASTOA. Dit staat voor Sinus is Overstaand gedeeld door Schuin, Cosinus is Aanliggend gedeeld door Schuin en Tangens is Overstaand gedeeld door Aanliggend. Door SOSCASTOA te onthouden, weet je altijd welke formule je moet gebruiken voor welke zijden van de rechthoekige driehoek.

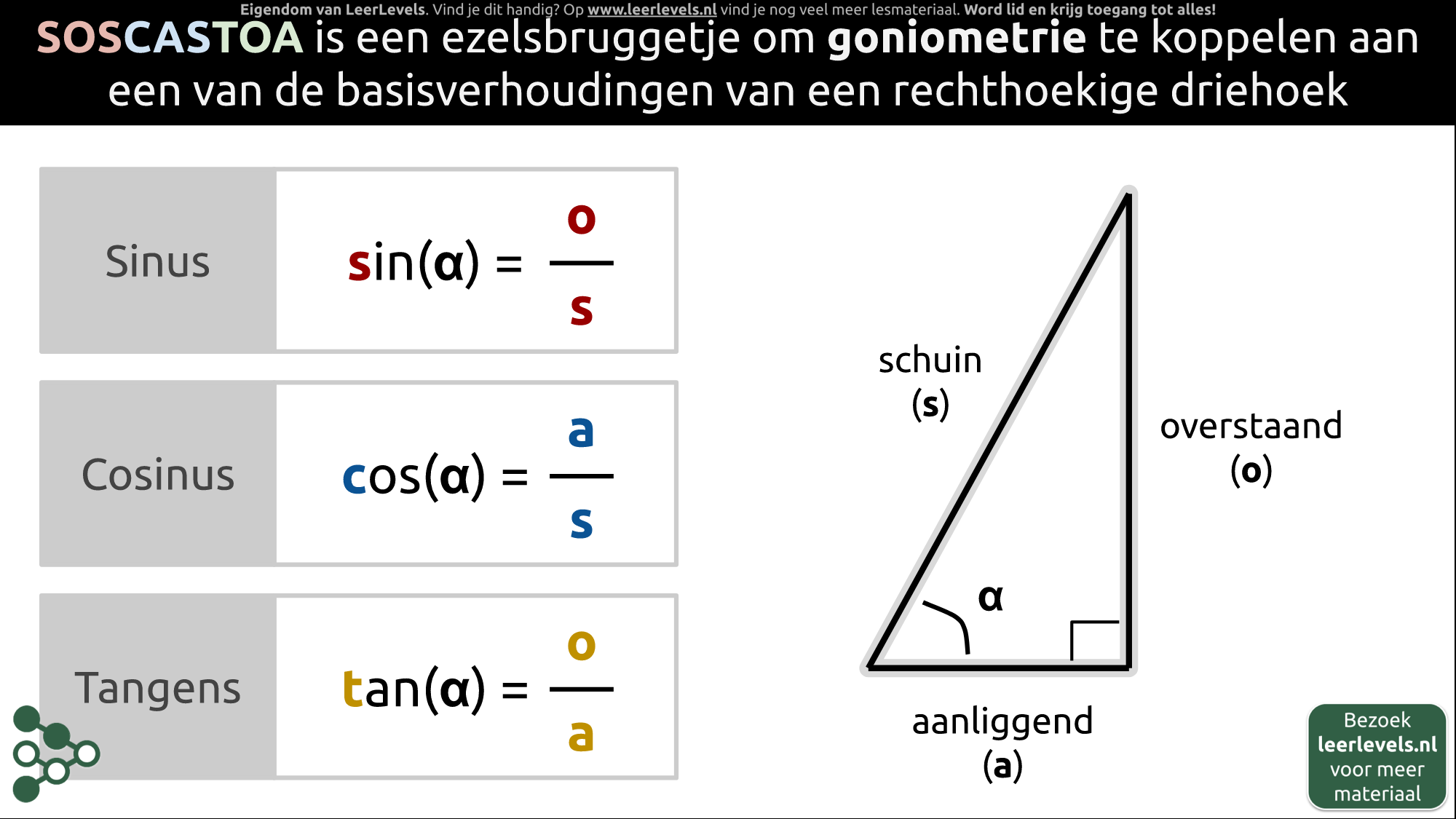
(Afbeelding: Animatie voor SOSCASTOA formules)

SOSCASTOA hoek berekenen

Met inverse goniometrische functies kun je een hoek berekenen in een rechthoekige driehoek als je de lengte van twee zijden kent. Als je bijvoorbeeld de overstaande en schuine zijde kent en de hoek alfa wilt berekenen, gebruik je de sinus functie: sin(α) = overstaande / schuine zijde. Maar om vervolgens de hoek alfa te krijgen, gebruik je de inverse sinus functie: sin⁻¹ (overstaande / schuine zijde).

Als je de cosinus functie gebruikt voor de overstaande en schuine zijde van een andere driehoek, dan gebruik je de inverse cosinus functie om de hoek te berekenen. Als je de tangens functie gebruikt voor de overstaande en aanliggende zijde van een driehoek, dan gebruik je de inverse tangens functie om de hoek te berekenen.

Belangrijk is dat je de zijden in dezelfde eenheid meet en rekening houdt met de modus van je rekenmachine (graden of radialen). De inverse sinus, cosinus en tangens functies helpen je om een hoek te berekenen in een rechthoekige driehoek als je de lengte van twee zijden kent.

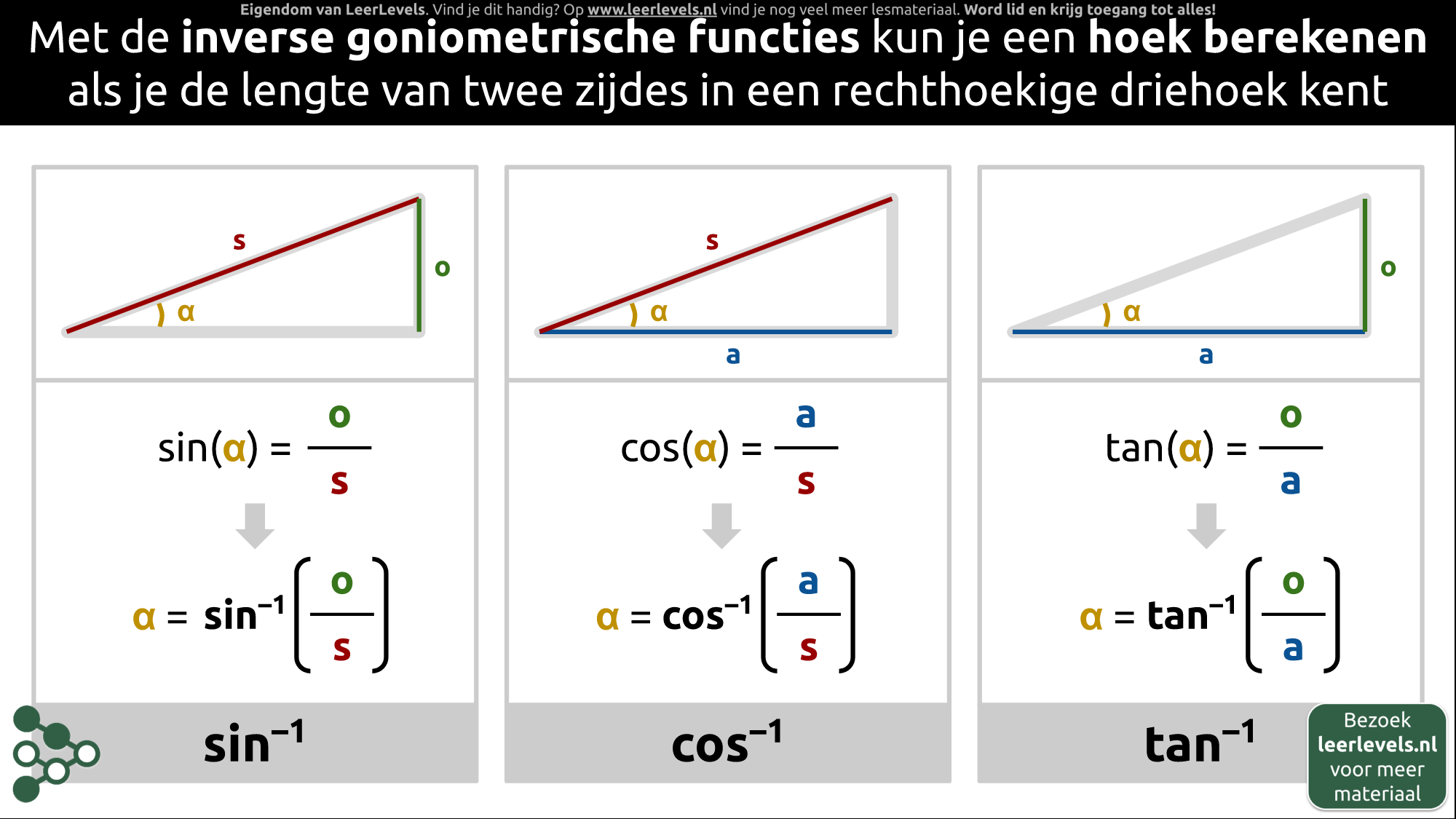
(Afbeelding: Animatie voor SOSCASTOA hoek berekenen)

Terug naar overzicht Meld je aan

Satelliet

Satelliet toepassingen

De toepassing van een satelliet bepaalt welk type baan het meest geschikt is. Er zijn verschillende toepassingen mogelijk, zoals telecommunicatie, weersvoorspellingen, wetenschappelijk onderzoek en militaire doeleinden. Voor communicatie en weersvoorspellingen is het wenselijk dat een satelliet op een vaste plek blijft. Hiervoor gebruikt men een geostationaire baan. Voor onderzoek of militaire doeleinden wil je echter dat de satelliet verschillende locaties boven de aarde kan bereiken. In dat geval kies je eerder voor een polaire baan.

(Afbeelding: Animatie voor Satelliet toepassingen)

Terug naar overzicht Meld je aan

Satellietbanen

Satellieten in een geostationaire baan blijven op één plek boven de evenaar en draaien daar altijd. Om dit mogelijk te maken, moet de tijd die de satelliet nodig heeft om rond de aarde te draaien gelijk zijn aan de tijd die de aarde nodig heeft om om haar eigen as te draaien, ongeveer 24 uur. Satellieten kunnen ook in polaire banen geplaatst worden, waarbij ze steeds een ander deel van de aarde zien doordat ze om de aarde heen bewegen. Satellieten worden gebruikt voor diverse doeleinden en er zijn verschillende opties wat betreft baan en duur, afhankelijk van het doel. Geostationaire banen worden weergegeven met de formule: T = 24 uur.

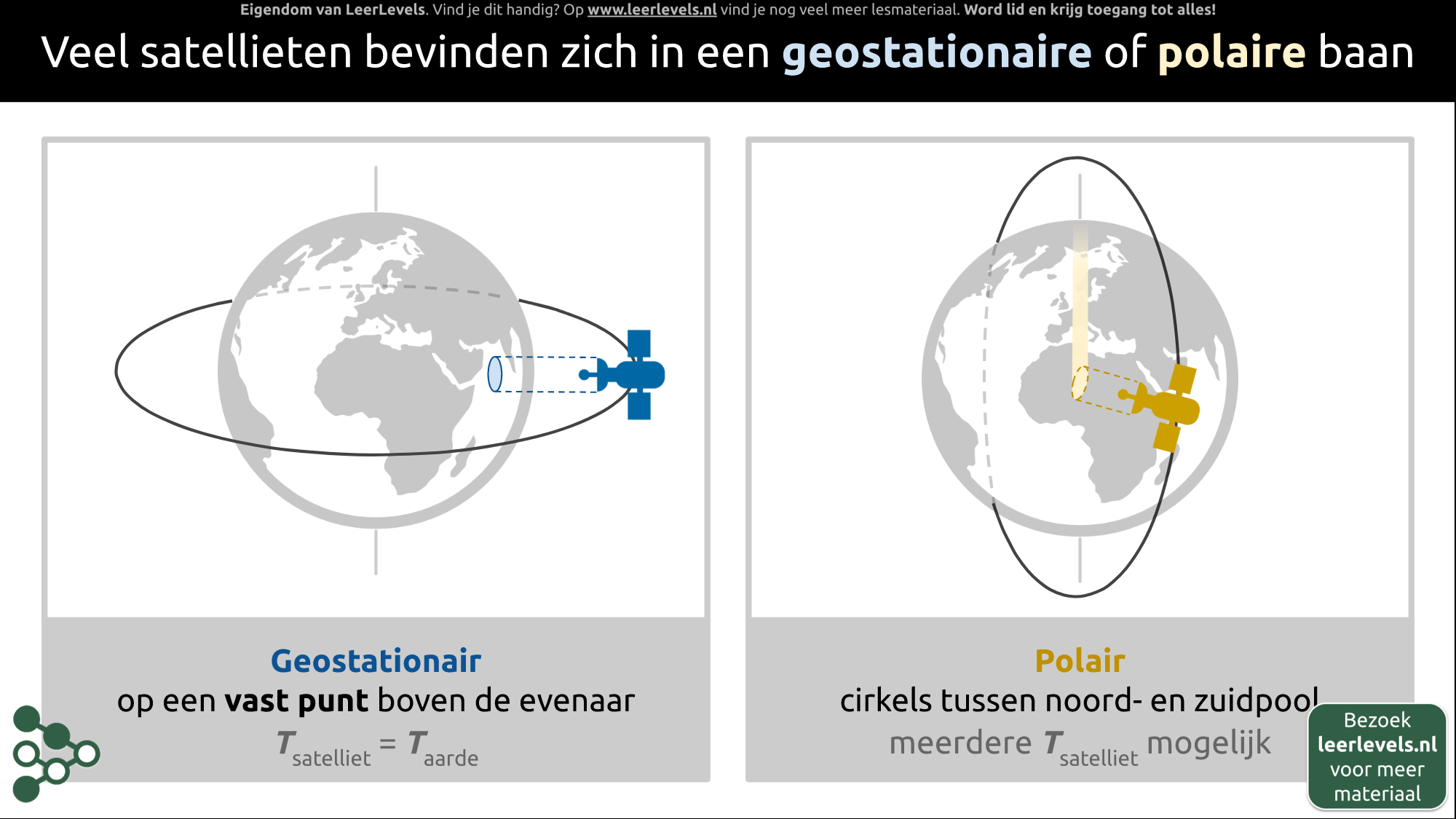
(Afbeelding: Animatie voor Satellietbanen)

Terug naar overzicht Meld je aan

Schaduw

Schaduw en halfschaduw

Schaduw ontstaat wanneer licht wordt geblokkeerd door een object. Het type schaduw dat ontstaat hangt af van het aantal lichtbronnen en de locatie van eventuele blokkades. Een blokkade kan er bijvoorbeeld voor zorgen dat sommige lichtstralen niet doorheen kunnen en dat er daardoor schaduw ontstaat. Bij één lichtbron zijn er plekken waar licht is en plekken waar schaduw is. Wanneer er meerdere lichtbronnen zijn, ontstaat er kernschaduw in het gebied waar geen enkele lamp licht naartoe schijnt en halfschaduw in het gebied waar slechts één van de twee lampen licht naartoe kan schijnen. Het ontstaan van schaduw en het type schaduw hangt dus af van het aantal lichtbronnen en locatie van blokkades.

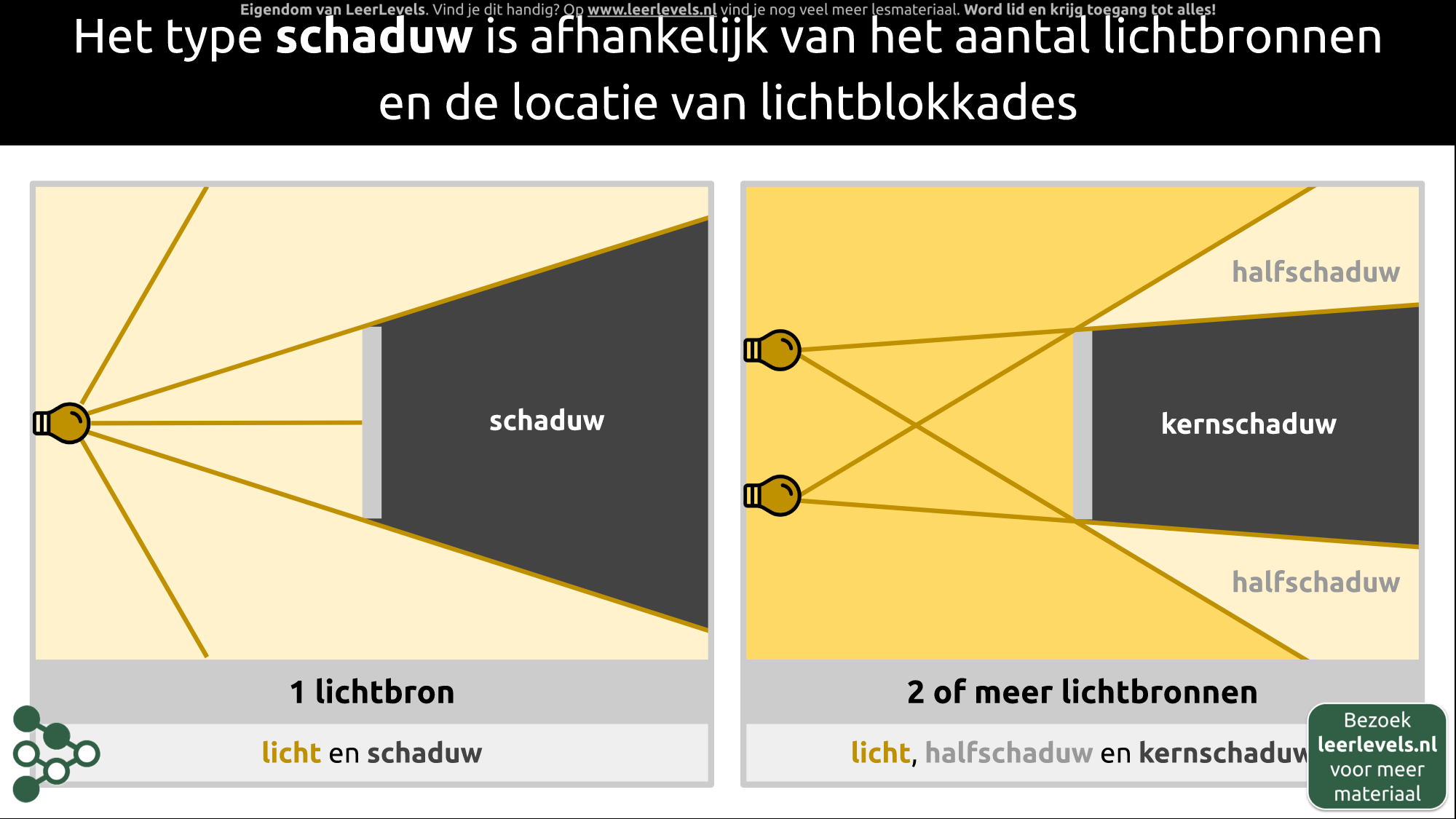
(Afbeelding: Animatie voor Schaduw en halfschaduw)

Terug naar overzicht Meld je aan

Schakeling

Serie- en parallelschakeling concept

Er zijn twee manieren om schakelingen te maken: serie en parallel.

Bij een serieschakeling loopt de stroom door alle onderdelen heen en is de stroom gelijk bij alle onderdelen. Dit betekent dat de stroom door de eerste lamp gelijk is aan de stroom door de tweede lamp.

Bij een parallelschakeling worden de stromen juist over verschillende onderdelen verdeeld. Dit betekent dat de totale stroom zich moet splitsen in de verschillende onderdelen. De totale stroom is dan gelijk aan de optelsom van beide stromen op het punt waar ze samenkomen.

Als de stroom door alle apparaten gelijk blijft, wordt dit een serieschakeling genoemd. Als de stroom verdeeld wordt over de apparaten, spreek je van een parallelschakeling.

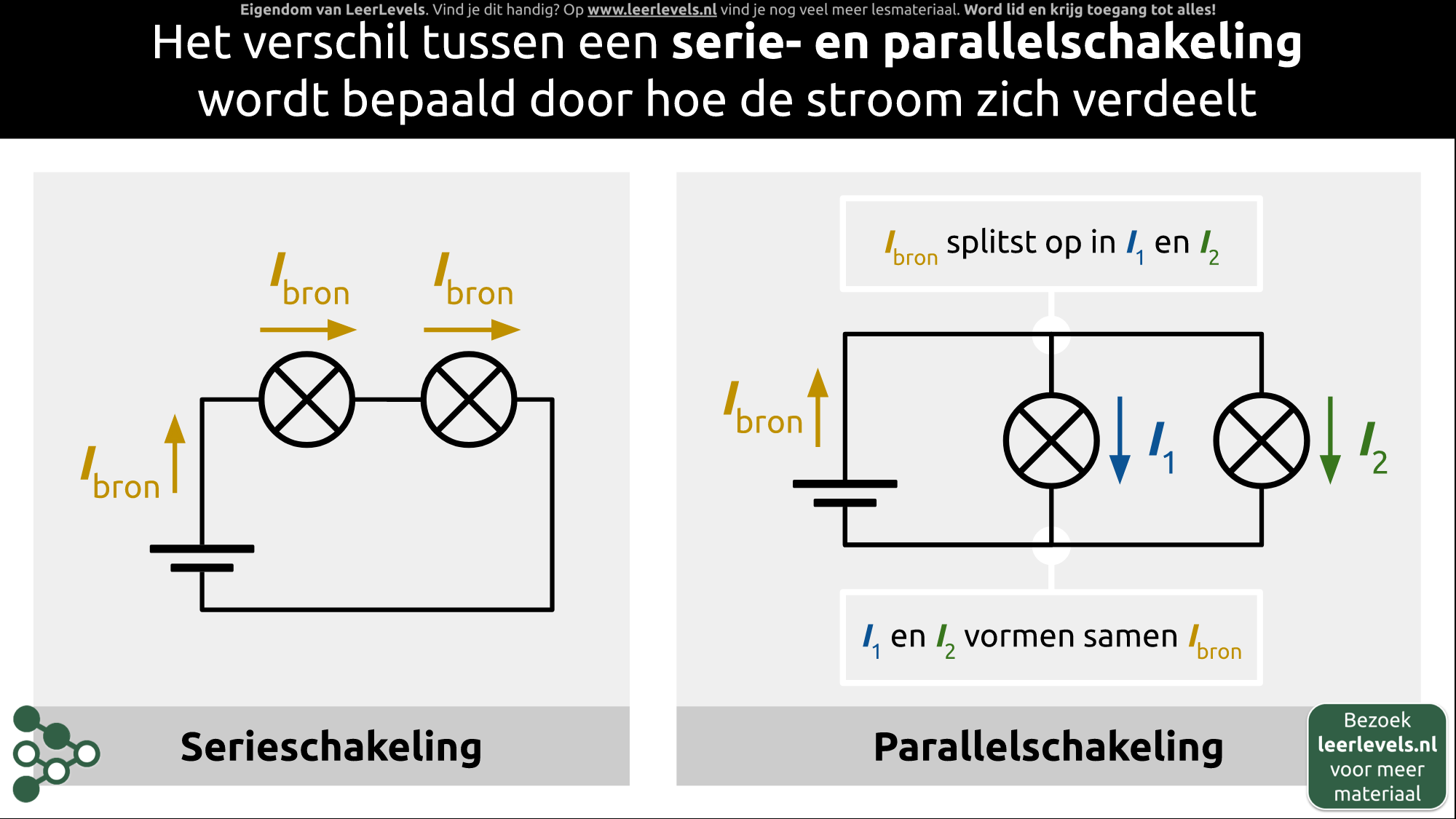
(Afbeelding: Animatie voor Serie- en parallelschakeling concept)

Serie- en parallelschakeling eigenschappen

Er zijn twee manieren om elektrische componenten met elkaar te verbinden. Dit noemen we een "serieschakeling" en een "parallelschakeling". Een serieschakeling betekent dat de stroom door alle componenten hetzelfde is, terwijl de spanning verdeeld wordt over de verschillende componenten. Bij een parallelschakeling is de spanning overal gelijk, maar wordt de stroom verdeeld bij elke splitsing. Hierbij kan de stroom slechts één pad kiezen, terwijl de spanning hetzelfde blijft over alle componenten. De bronspanning is dan gelijk aan elk van de individuele spanningen en de bronstroom is juist gelijk aan de som van alle individuele stromen.

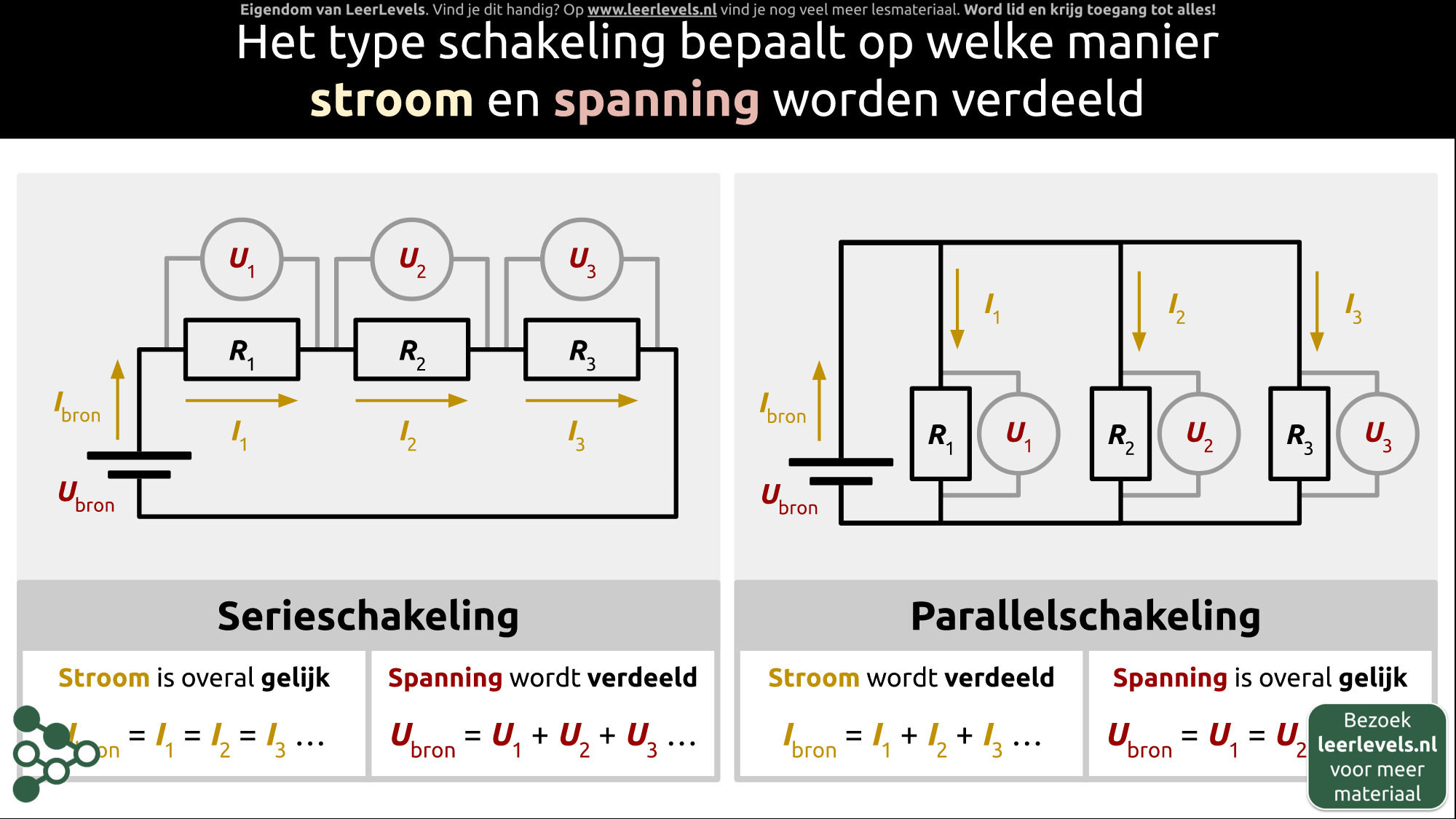
(Afbeelding: Animatie voor Serie- en parallelschakeling eigenschappen)

Terug naar overzicht Meld je aan

Schatten

Je kunt bij het schatten van grootheden gebruik maken van gemiddelde waardes en algemene kennis. Bijvoorbeeld: als je gevraagd wordt om een afstand te schatten, dan kun je ervan uitgaan dat een verdieping ongeveer 3 meter hoog is, een mens tussen 1,5 en 2 meter lang is en de afstand tussen de topjes van je pink en duim ongeveer 20 centimeter is. Bij snelheden kun je bijvoorbeeld zeggen dat een auto ongeveer 100 km/h rijdt, een fietser tussen de 15 en 20 km/h en een wandelaar ongeveer 5 km/h. Voor massa kun je bijvoorbeeld zeggen dat een mens tussen de 50 en 100 kg weegt, een pak melk 1 kg weegt en een suikerklontje een paar gram. Het is belangrijk om de ordegrootte goed te krijgen, dus maak een mens niet 10 meter lang en een suikerklontje niet microgrammen zwaar. Vertrouw op je algemene kennis en gebruik gemiddelde waardes.

(Afbeelding: Animatie voor Schatten)

Terug naar overzicht Meld je aan

Scheidingsmethodes

Er zijn drie manieren om mengsels te scheiden. De eerste manier is indampen. Hierbij verwarm je het mengsel totdat de vloeistof verdampt en er residu overblijft. Deze methode is geschikt voor oplossingen, zoals water met zout. Door het water te laten verdampen, blijft het zout achter. De tweede manier is bezinken. Het mengsel wordt dan een tijdje stilgehouden, waardoor de zwaardere stoffen naar de bodem zakken. Dit werkt alleen voor emulsies en suspensies, niet voor oplossingen. Als het bezinksel dik genoeg is, kan het worden afgescheiden. De derde manier is filtreren. Het mengsel wordt gefilterd op basis van de grootte van de deeltjes. Het filtraat gaat door de filter heen, terwijl het residu achterblijft. Deze methode werkt vooral voor suspensies, zoals koffie met koffiepoeder. Door het mengsel te filteren, blijft het koffiepoeder achter en blijft de opgeloste koffiesmaak in het water over. Elke methode is geschikt voor andere soorten mengsels.

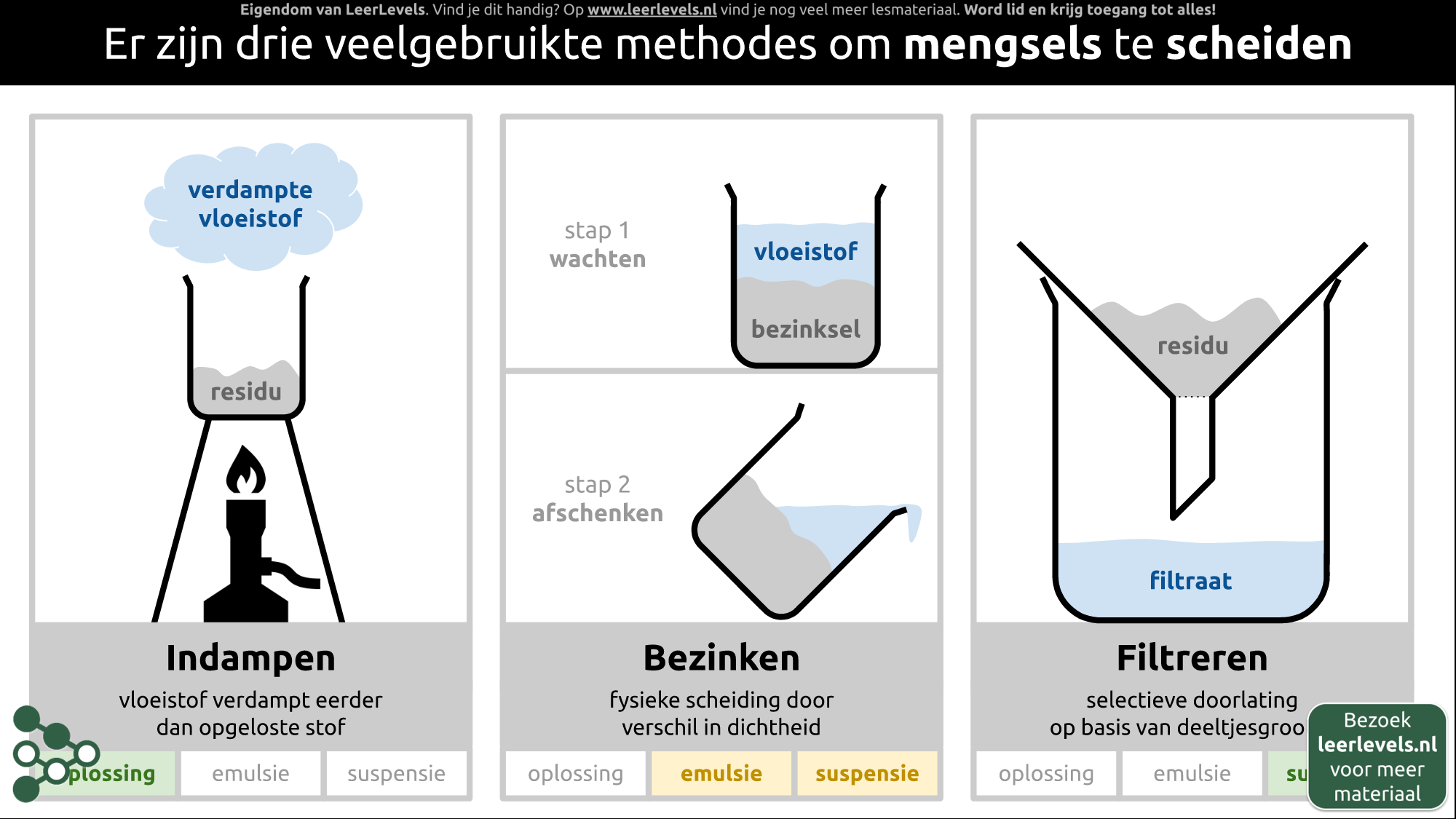
(Afbeelding: Animatie voor Scheidingsmethodes)

Terug naar overzicht Meld je aan

SchrÃ¶dingervergelijking

Schrödingervergelijking formule

De golffunctie van een deeltje dat heel klein is, wordt berekend met een moeilijke formule: de Schrödingervergelijking. Deze vergelijking heeft te maken met hoe snel de golffunctie verandert op verschillende plekken. Er zijn een paar getallen die gebruikt worden in de formule om de golffunctie te berekenen, zoals de massa van het deeltje en de Planckconstante (ℏ). Maar het belangrijkste om te onthouden is dat de golffunctie moet voldoen aan de Schrödingervergelijking, anders werkt de formule niet goed. De formule geeft geen directe waarde voor de golffunctie, maar beschrijft wel hoe de golffunctie eruit moet zien.

(Afbeelding: Animatie voor Schrödingervergelijking formule)

Schrödingervergelijking oplossen

De Schrödingervergelijking helpt ons voorspellen hoe de golffunctie eruitziet in een diepe put waar de potentiële energie oneindig groot wordt aan de randen. Binnen de put is de potentiële energie gelijk aan nul en buiten de put oneindig. Door de vergelijking op te lossen, vinden we dat de golffunctie in het groene gebied een sinusfunctie is met een bepaalde amplitude en dat de golffunctie bij de randen nul moet zijn. De simpelste sinus die we kunnen tekenen is die met één halve golflengte. Buiten de put moet de golffunctie nul zijn om geen plotselinge sprongen te maken. De eerste mogelijkheid daarvoor is een volledige periode van een sinus met nul aan de randen. Formules en symbolen die voorkomen zijn de Schrödingervergelijking (Ψ), de potentiële energie (V), de tweede afgeleide ((∂²)/(∂ x² en de amplitude (A).

(Afbeelding: Animatie voor Schrödingervergelijking oplossen)

Terug naar overzicht Meld je aan

Schuifweerstand

Een schuifweerstand is een onderdeel waarmee je de totale weerstand in tweeën kunt delen. Dit werkt door middel van een schuifje dat je kunt verplaatsen. Je kunt bijvoorbeeld een lampje aansluiten op dit onderdeel. Als je het schuifje verplaatst, verandert de weerstand. Als de totale weerstand bijvoorbeeld 100 Ohm is, en het linkerdeel van de schuifweerstand 80 Ohm is, dan moet het rechterdeel 20 Ohm zijn om het totaal 100 Ohm te houden. Als je het schuifje op een andere plek zet, verandert de weerstandsverdeling weer.

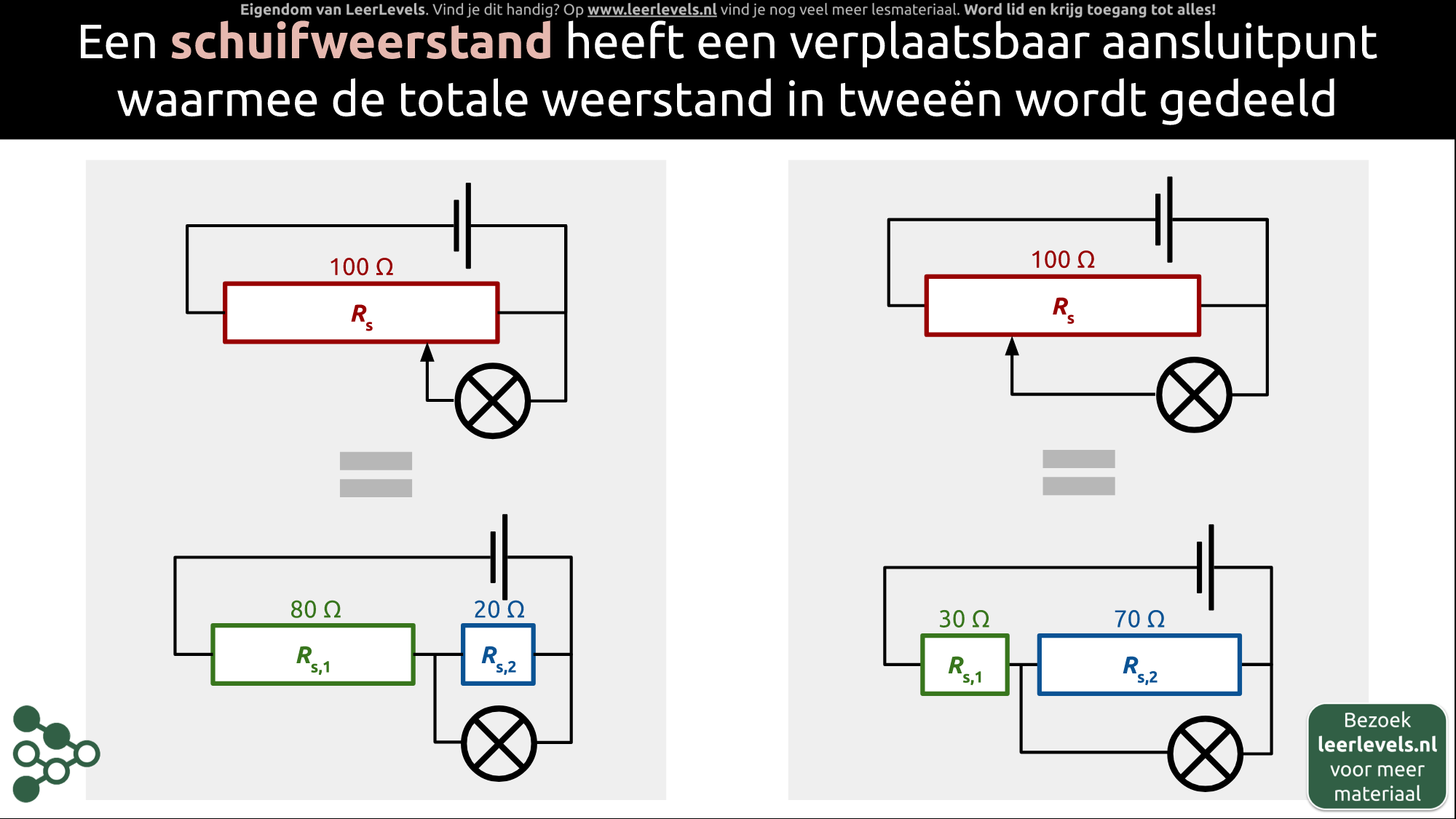
(Afbeelding: Animatie voor Schuifweerstand)

Terug naar overzicht Meld je aan

Serieschakeling

Spanningsverdeling serieschakeling

Een serieschakeling is een verbinding van componenten waarbij de stroom door alle componenten hetzelfde is. Bij een serieschakeling is de spanning over elke component recht evenredig met de grootte van die component. Bijvoorbeeld, als er een bron van 12 volt is en er zijn drie weerstanden van 1, 2 en 3 ohm, zal de grootste spanning over de grootste weerstand staan, wat betekent dat er 2 volt over de eerste weerstand staat, 4 volt over de tweede weerstand en 6 volt over de derde weerstand. Dit kan bewezen worden met behulp van de wet van Ohm: U = I × R. Bij een serieschakeling is de stroom overal gelijk, dus U1/R1 = U2/R2 = U3/R3. Dit betekent dat een willekeurige spanning gelijk moet zijn aan de stroom keer de bijbehorende weerstand. Dit betekent dat U en R recht evenredig zijn bij een bepaalde stroom.

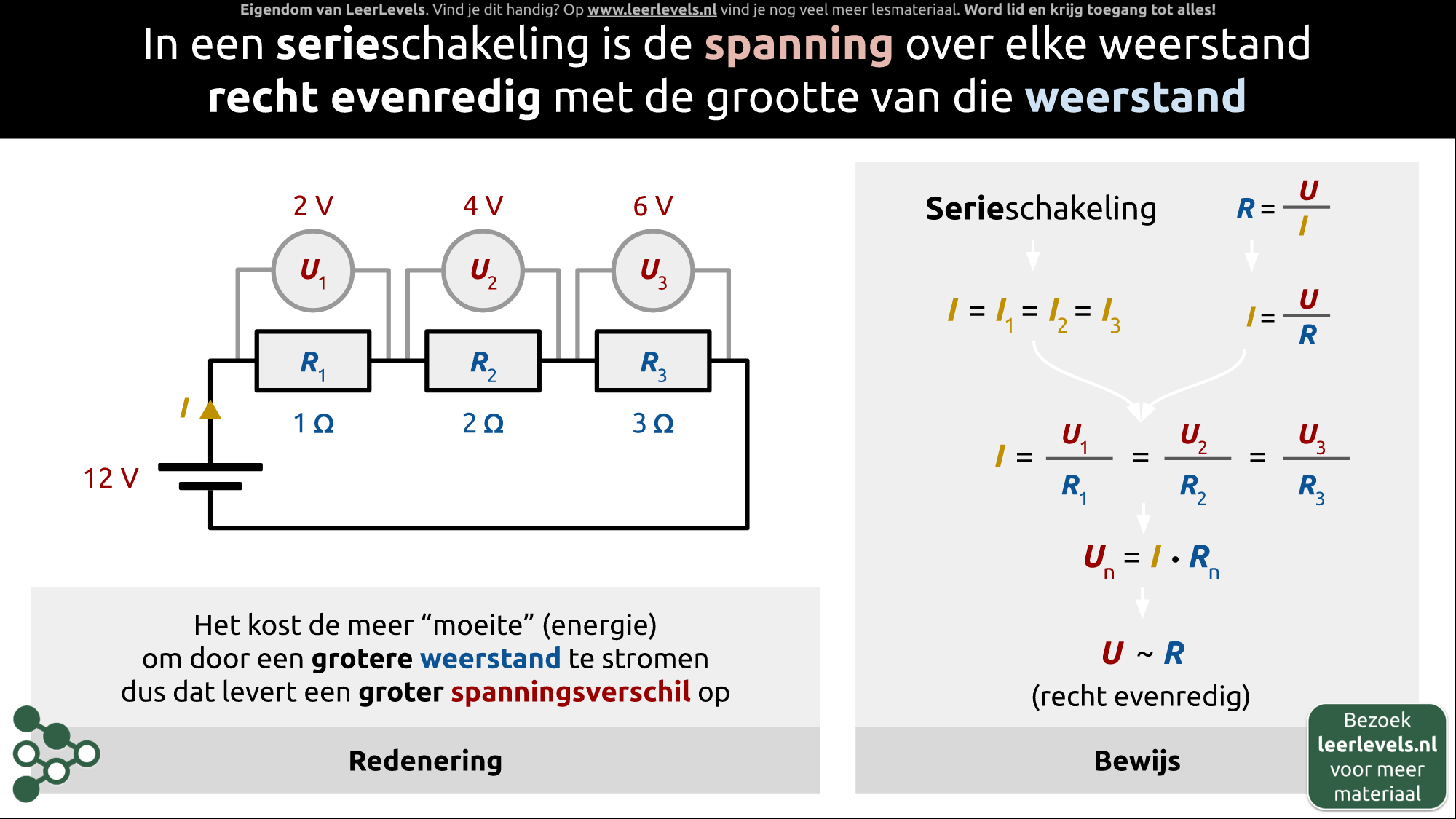
(Afbeelding: Animatie voor Spanningsverdeling serieschakeling)

Terug naar overzicht Meld je aan

Significante cijfers

Significante cijfers concept

Het aantal significante cijfers in een getal geeft aan hoe nauwkeurig het is. Als een waarde wordt afgerond tot één cijfer, is de nauwkeurigheid relatief laag, bijvoorbeeld bij het beschrijven van de grootte van een dobbelsteen. Als een waarde wordt afgerond tot twee cijfers, is de nauwkeurigheid hoger, geschikt bijvoorbeeld voor het beschrijven van de lengte van een spijker. Een nog hogere nauwkeurigheid wordt bereikt door de waarde af te ronden tot drie cijfers, zoals bij het beschrijven van de diepte van sleutelgroeven. In het algemeen geldt: hoe meer significante cijfers, hoe groter de nauwkeurigheid.

(Afbeelding: Animatie voor Significante cijfers concept)

Significante cijfers definitie

Cijfers zijn belangrijk als ze voldoen aan bepaalde voorwaarden. Meestal zijn alle cijfers belangrijk, bijvoorbeeld in 12,30 zijn er 4 belangrijke cijfers. Er zijn echter drie uitzonderingen. De eerste uitzondering zijn de beginnende nullen, deze tellen niet mee. Bijvoorbeeld, in 0,01 is er slechts één belangrijk cijfer. De tweede uitzondering geldt voor wetenschappelijke notatie, machten van 10 tellen niet mee. Bijvoorbeeld, in 1,2 × 10³ zijn er slechts 2 belangrijke cijfers. De derde uitzondering geldt voor SI-voorvoegsels. Bijvoorbeeld, in 123 km telt "kilo" niet mee. Samengevat, cijfers zijn belangrijk tenzij er uitzonderingen gelden.

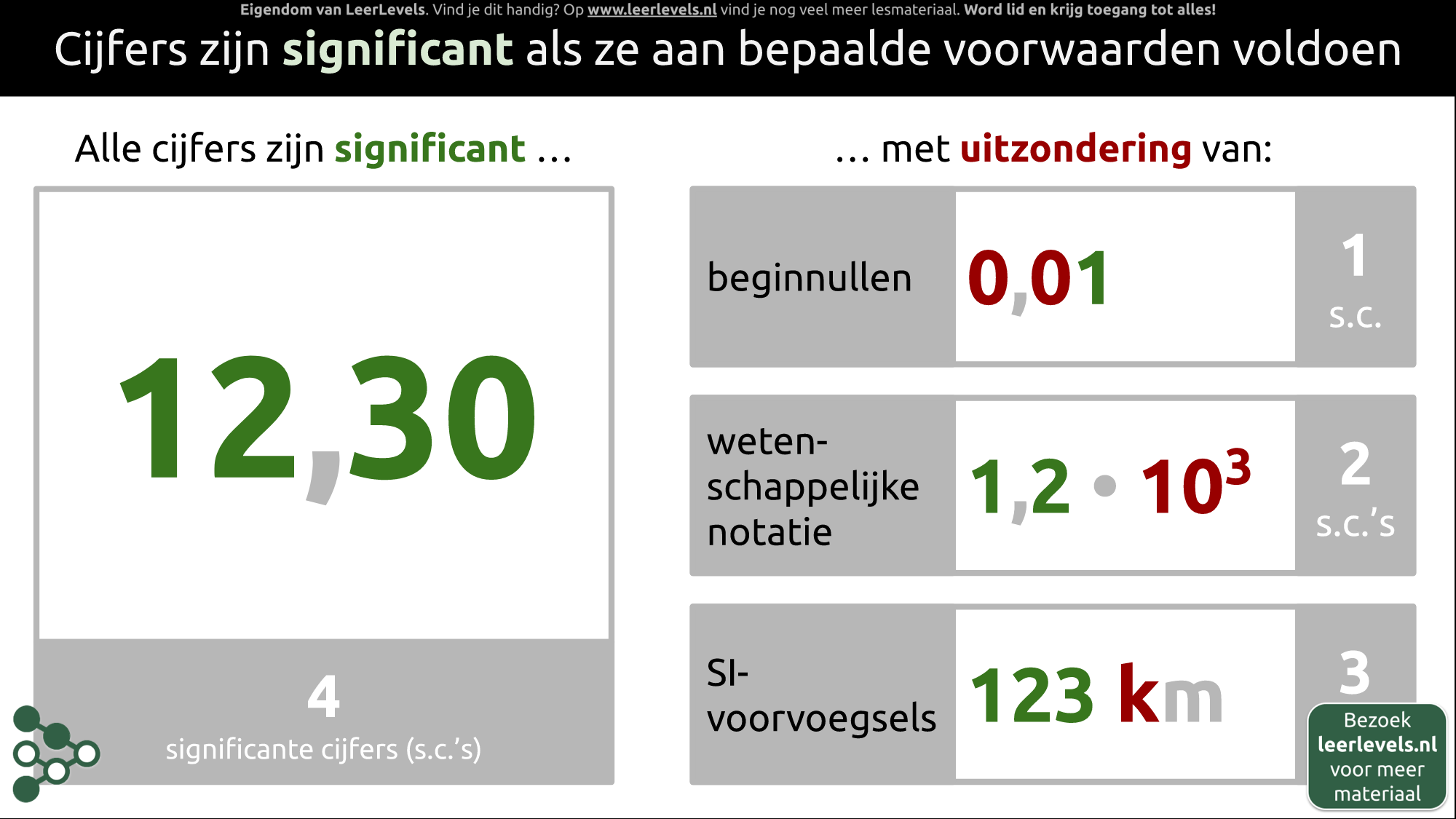
(Afbeelding: Animatie voor Significante cijfers definitie)

Significante cijfers toepassen

Om significante cijfers toe te passen bij berekeningen, doorloop je vijf stappen. Als voorbeeld nemen we de berekening van de snelheid waarbij de afstand 10 km was en de tijd 53,1 seconden was. Eerst voeren we de berekening uit, v = 10,000 m / 53,1 s, wat neerkomt op 188,323918 m/s. Daarna bepalen we het aantal significante cijfers, wat het kleinste aantal van de meetwaarden is, dus twee in dit geval. Vervolgens ronden we af op het derde getal, wat resulteert in 190,000000 m/s. We laten alleen de significante cijfers staan (190) en passen de wetenschappelijke notatie toe, wat resulteert in 19 x 10¹ m/s of 1,9 x 10² m/s. Dit zijn beide twee significante cijfers en de waarde is hetzelfde.

(Afbeelding: Animatie voor Significante cijfers toepassen)

Terug naar overzicht Meld je aan

Sinusoïde

Een sinusoïde is een golfvormige grafiek die hoort bij de goniometrische functies sinus en cosinus. De standaard sinusgolf begint omhoog, gaat weer naar beneden en komt terug op nul. Deze golf is op het domein van 0 tot 2π (x tussen 0 en 2π) met een bereik van -1 tot + 1. Er zijn variaties mogelijk op deze sinusgolf. De functie 0,5 · sin(x) lijkt op de standaard sinusgolf, maar met de uitwijking over de helft van de golf, zoals in de groene grafiek. De functie sin(2x) is de standaard sinusgolf, maar samengedrukt. Deze gaat twee keer zo snel op en neer, en bij x = π ben je al terug bij het begin. De functie -sin(0,5x) is juist uitgerekt en geklapt om de x-as. Dit ziet eruit als de blauwe grafiek. De cosinus-functie heeft dezelfde golfvorm als de sinus, maar begint niet bij 0 in de positieve richting, maar bij 1 in de negatieve richting. Dit is te zien in de gele grafiek.

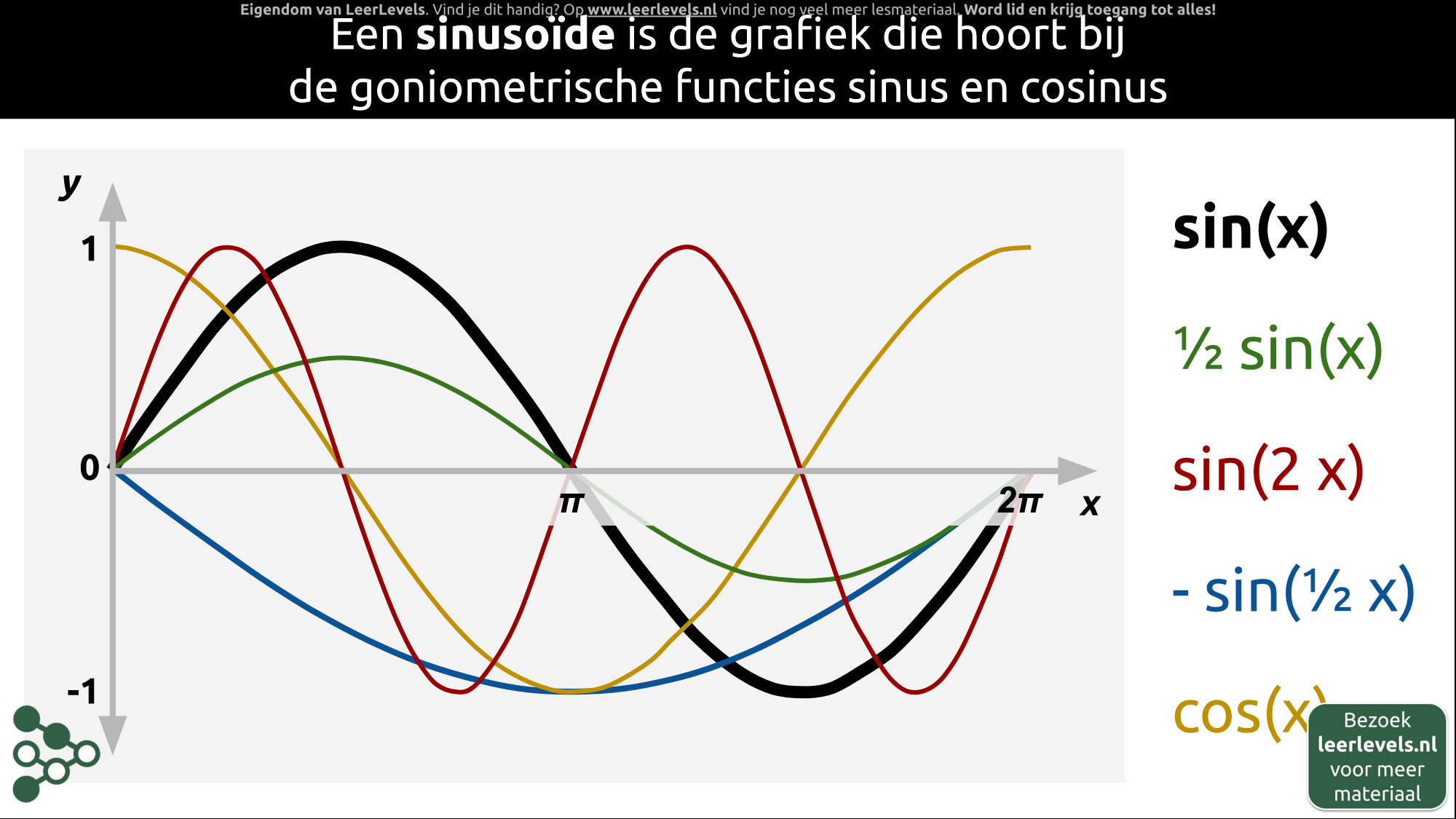
(Afbeelding: Animatie voor Sinusoïde)

Terug naar overzicht Meld je aan

Snelheid

Snelheid concept

De snelheid van een voorwerp, aangeduid met v, geeft aan hoeveel afstand er in een bepaalde tijd wordt afgelegd. Stel dat we kijken naar tijdstip nul en iemand zien ontspannen op een stoel. Er vliegt een vliegtuig voorbij en iemand laat zijn hond uit.

Als we één seconde later opnieuw kijken, zien we dat de persoon op de stoel niet bewogen heeft. Zijn snelheid is dus nul. De persoon die de hond uitlaat, heeft zich een beetje verplaatst en heeft dus een kleine snelheid. De persoon in het vliegtuig heeft in die ene seconde een grote afstand afgelegd en heeft dus een grote snelheid.

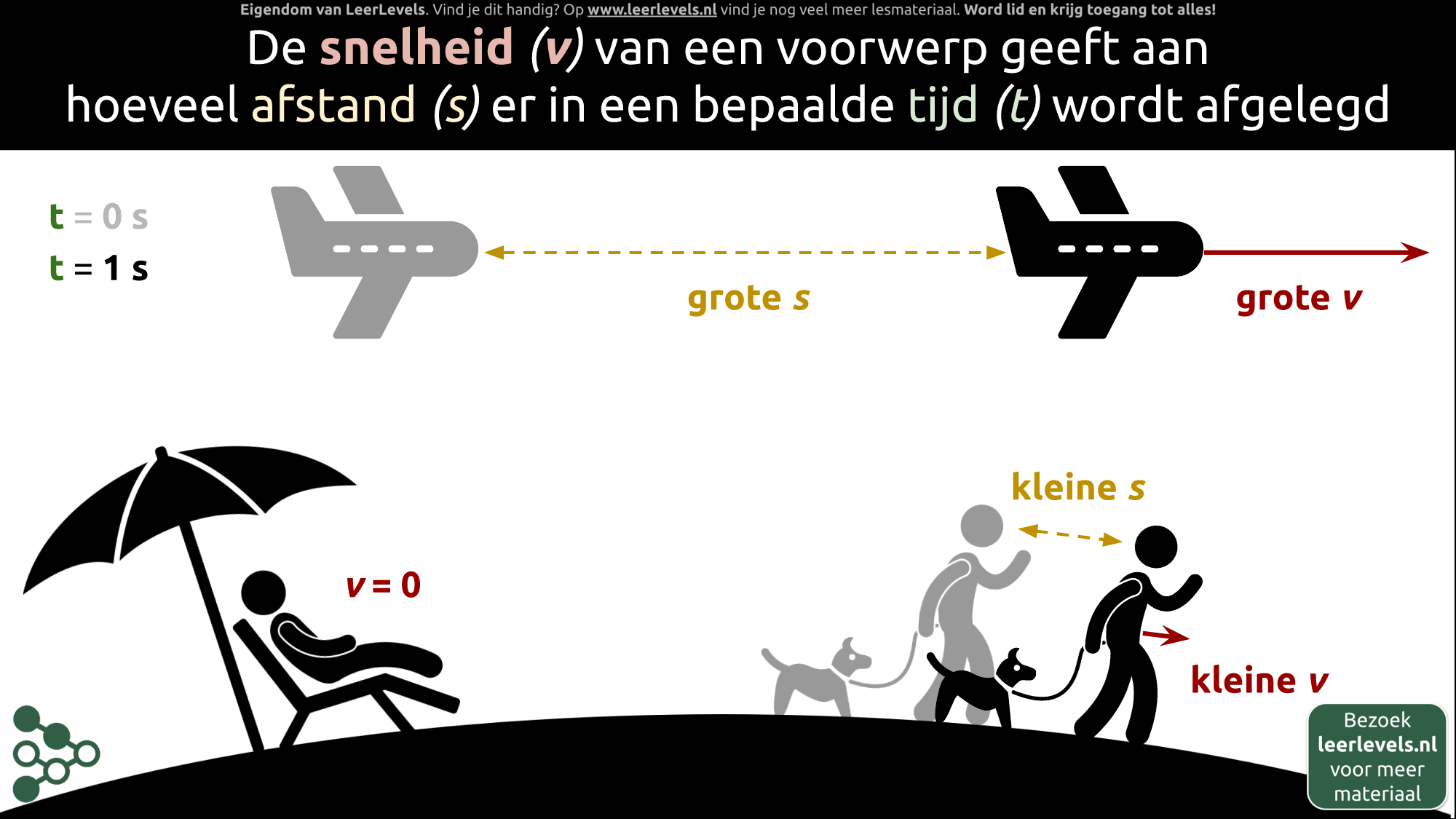
(Afbeelding: Animatie voor Snelheid concept)

Snelheid formule

Snelheid (v) hangt af van de afstand (s) en de tijd (t). Als je de snelheid in meters per seconde uitdrukt, gaat het over hoeveel meter er in 1 seconde wordt afgelegd. Je kunt snelheid ook definiëren als Δ x gedeeld door Δ t, waarbij Δ x het verschil in plaats is (een soort van afstand) en Δ t het verschil in tijd. Bijvoorbeeld, als je om 1 uur 's middags op een bepaalde plaats bent en om 2 uur 's middags op een andere plaats, dan is Δ t = 1 uur (omgerekend naar seconden is dat Δ t = 3600 seconden). De formule die je moet gebruiken hangt af van de opdracht.

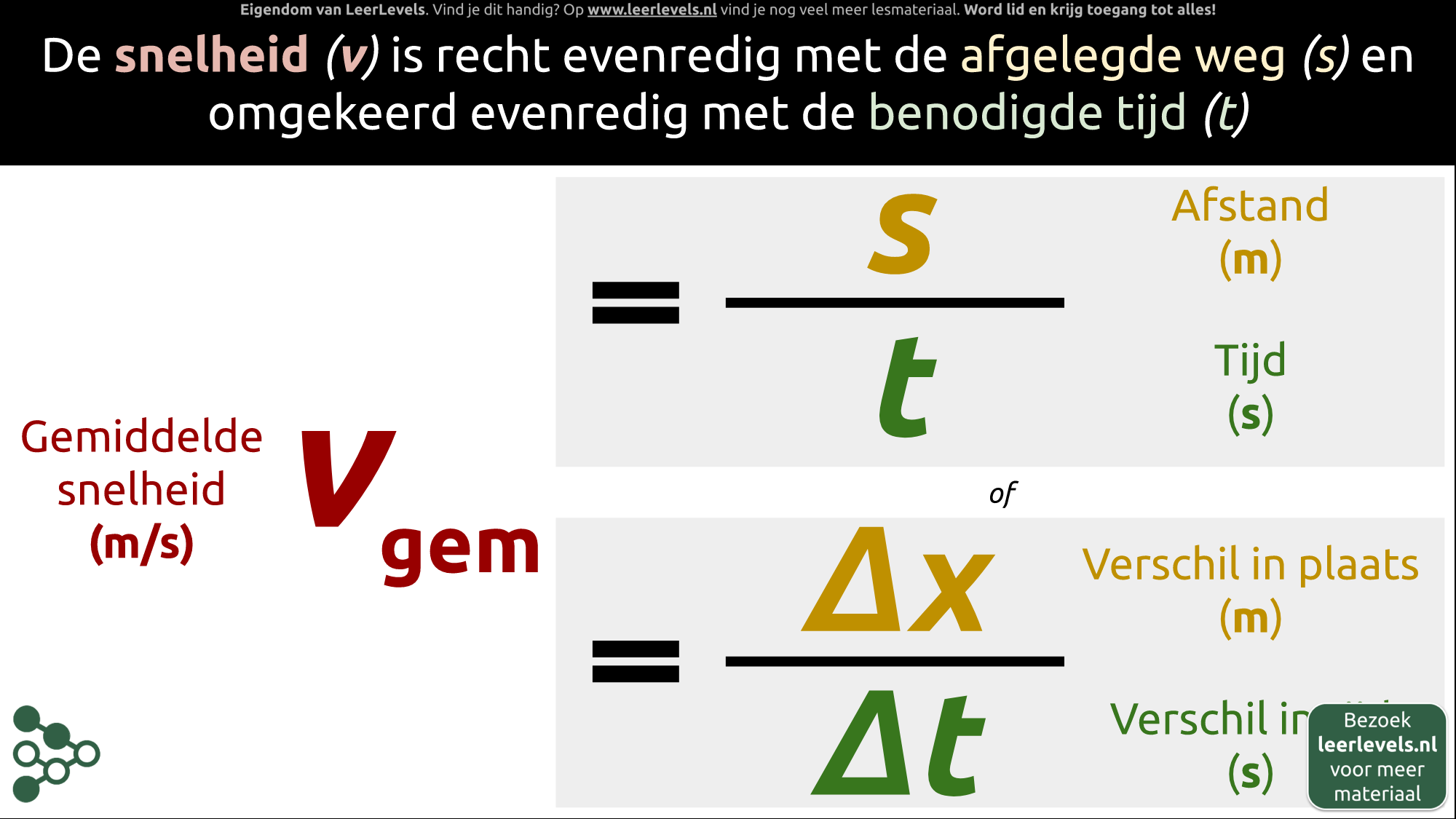
(Afbeelding: Animatie voor Snelheid formule)

Snelheid omrekenen

Snelheid wordt vaak uitgedrukt in km/h of in m/s. Voor bepaalde berekeningen moet je deze eenheden soms omzetten. Om van m/s naar km/h om te zetten, moeten we het volgende in gedachten houden:

- 1 kilometer is gelijk aan 1000 meter.
- 1 uur is gelijk aan 3600 seconden.

Hieruit volgt dat:

1 m/s = (1000 m)/(1 km) × (3600 s)/(1 h) = 3,6 km/h

Dus, om een snelheid van m/s om te zetten naar km/h, moeten we vermenigvuldigen met 3,6. Om een snelheid van km/h om te zetten naar m/s, moeten we delen door 3,6.

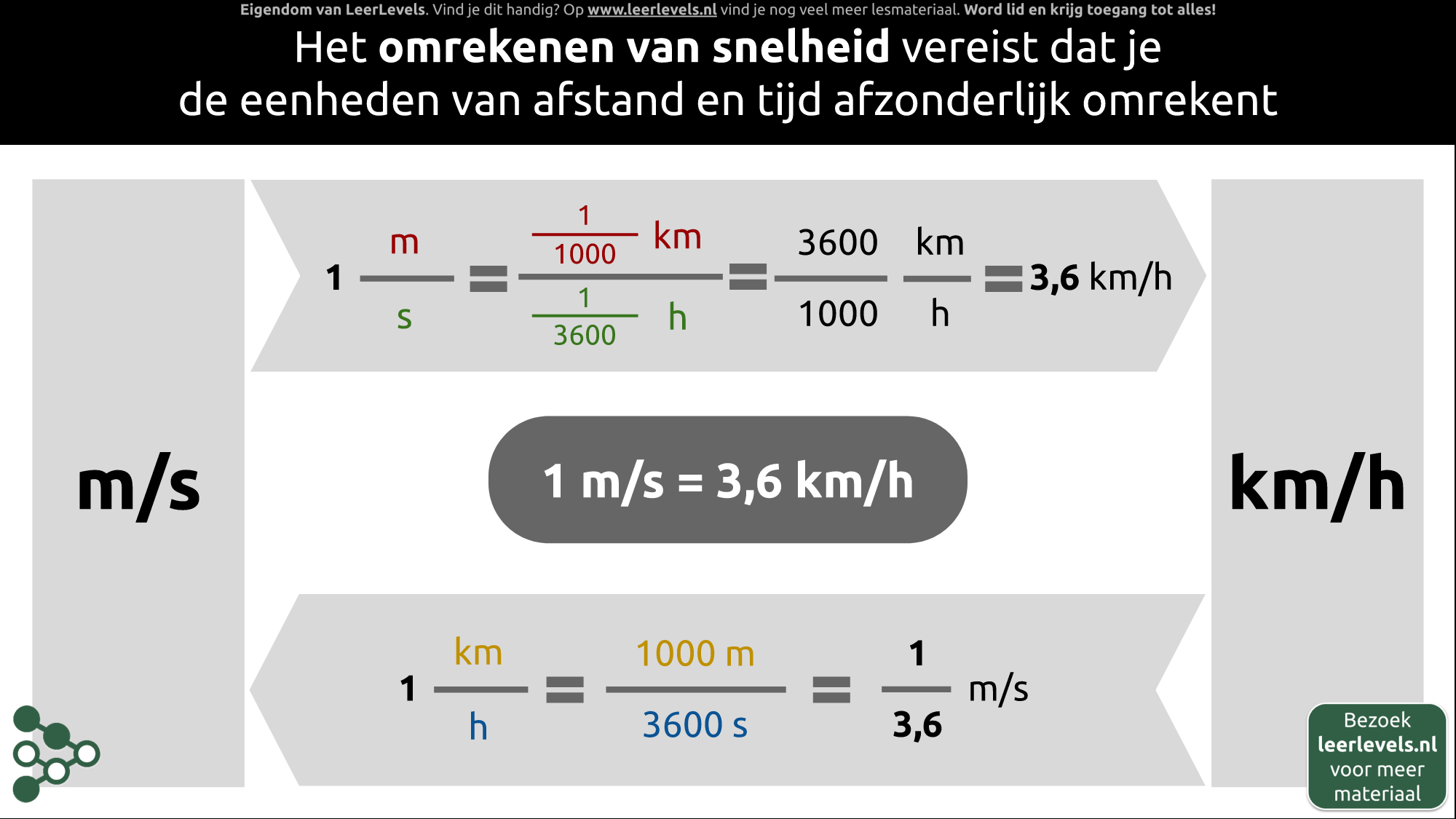
(Afbeelding: Animatie voor Snelheid omrekenen)

Gemiddelde en momentane snelheid

Bij snelheid kunnen we kijken naar gemiddelde snelheid en momentane snelheid. Gemiddelde snelheid noemen we v met een streep erboven en geeft de snelheid over een bepaalde tijd. Als we de gemiddelde snelheid tussen punt A en punt B willen berekenen, nemen we het verschil in afstand gedeeld door het verschil in tijd. Momentane snelheid is de snelheid op een specifiek tijdstip, bijvoorbeeld op punt C. Om de momentane snelheid te berekenen hebben we een raaklijn nodig. We zoomen in op de grafiek en nemen de helling van de grafiek op dat punt. We pakken twee punten en nemen het kleine verschil in afstand gedeeld door het kleine verschil in tijd. Beide methoden kunnen gebruikt worden om snelheid te meten, maar het hangt af van de situatie welke methode het meest geschikt is.

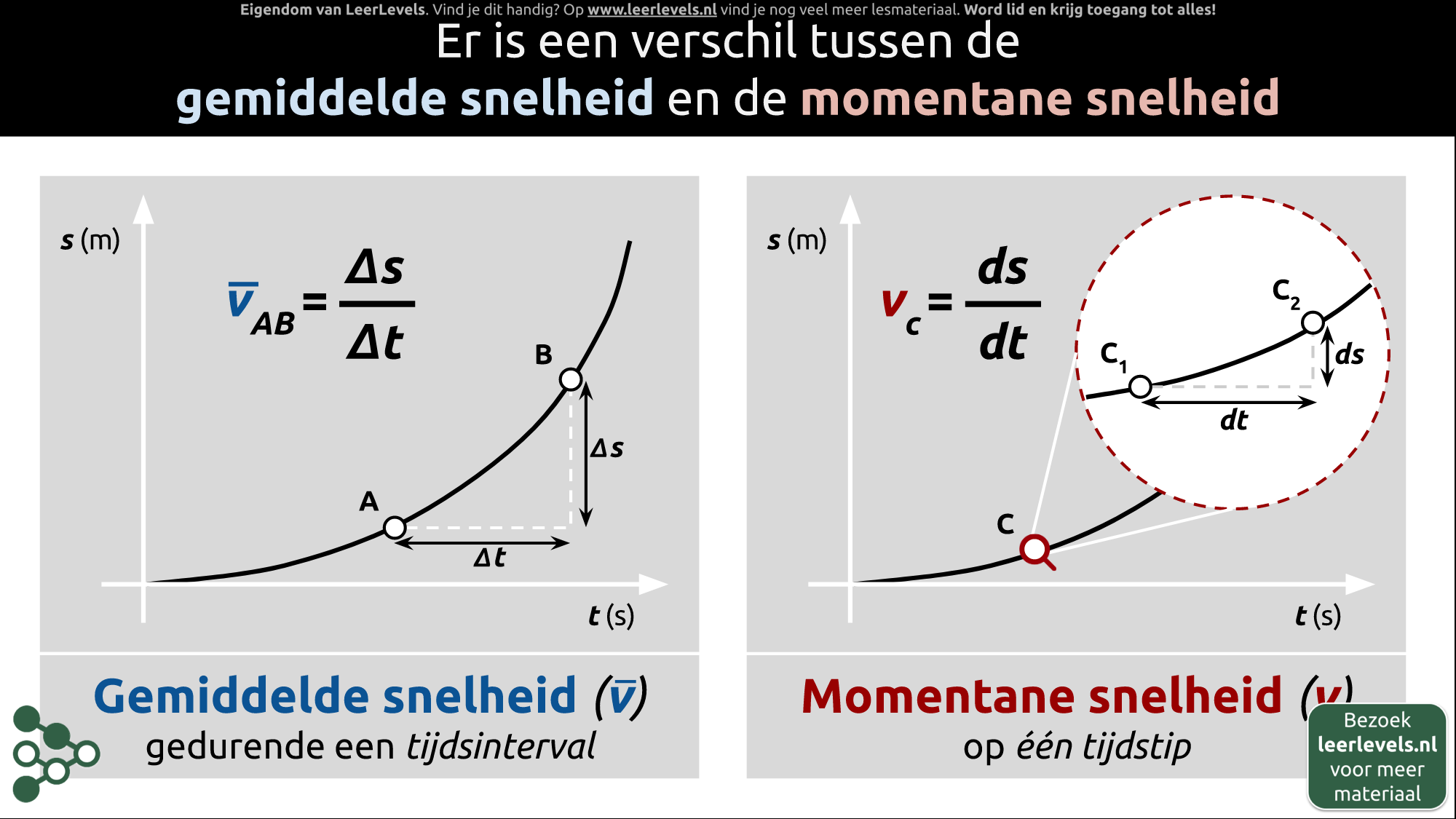
(Afbeelding: Animatie voor Gemiddelde en momentane snelheid)

Snelheidsbepaling van sterren formules

Als we willen weten hoe snel een ster beweegt, kunnen we kijken naar de twee soorten snelheden die een ster heeft: tangentiële snelheid en radiële snelheid. Om de tangentiële snelheid te berekenen, moeten we de hoeksnelheid van de ster meten en de afstand tot de ster bepalen met een parallaxmeting. Dan kunnen we de formule vtan = ω · r gebruiken. Om de radiële snelheid te berekenen, maken we gebruik van de dopplerverschuiving van het licht van de ster. We weten welke frequenties bij welke absorptielijnen horen. Als we de dopplerverschuiving meten, kunnen we de formule vrad = (Δ λ)/(λ) · c gebruiken om de snelheid te berekenen. Hierbij is vrad de radiële snelheid in meters per seconde, Δ λ de dopplerverschuiving in bijvoorbeeld nanometer, λ de oorspronkelijke golflengte in dezelfde eenheid als de verschuiving en c de lichtsnelheid in meters per seconde. Als we beide soorten snelheden hebben berekend, kunnen we de stelling van Pythagoras gebruiken om de totale snelheid te vinden. We kunnen Tabel 32B uit BiNaS gebruiken om ons hierbij te helpen.

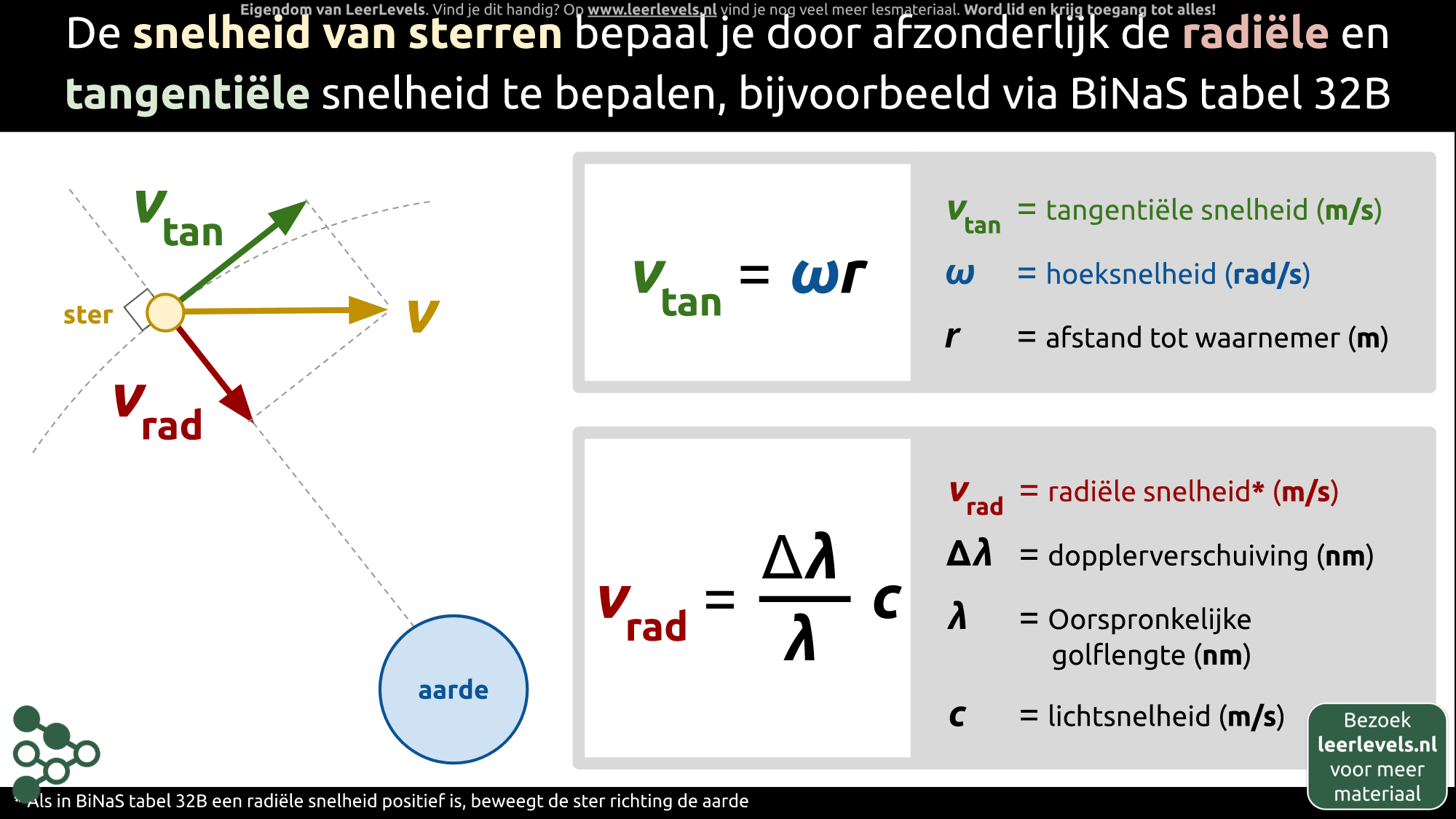
(Afbeelding: Animatie voor Snelheidsbepaling van sterren formules)

Terug naar overzicht Meld je aan

Soortelijke warmte

Soortelijke warmte concept

De soortelijke warmte van een materiaal geeft aan hoeveel energie nodig is om het op te warmen. Water heeft bijvoorbeeld een grote soortelijke warmte, dus er is veel energie nodig om water op te warmen. Voor een temperatuurstijging van 25 graden is er ongeveer 100J nodig en voor een temperatuurstijging van 15 graden is er ongeveer 67J nodig. Maar koper heeft een kleine soortelijke warmte, dus er is minder energie nodig om dezelfde hoeveelheid op te warmen. Voor een gram koper is er maar 10J nodig om hetzelfde aantal graden op te warmen. De hoeveelheid energie die nodig is om een materiaal op te warmen wordt ook wel soortelijke warmte genoemd en verschilt per materiaal.

(Afbeelding: Animatie voor Soortelijke warmte concept)

Soortelijke warmte formule

Om te berekenen hoeveel warmte nodig is om een bepaalde hoeveelheid materiaal een bepaald temperatuurverschil te geven, kun je de formule Q = m · c · Δ T gebruiken. Hierbij staat Q voor de hoeveelheid energie die nodig is, m voor de massa van het materiaal, c voor de soortelijke warmte van het materiaal (uitgedrukt in J/kg/K of J/kg/°C) en Δ T voor het temperatuurverschil (uitgedrukt in kelvin of graden Celsius).

(Afbeelding: Animatie voor Soortelijke warmte formule)

Terug naar overzicht Meld je aan

Soortelijke weerstand

Soortelijke weerstand concept

Soortelijke weerstand is hoe moeilijk een materiaal stroom geleidt. Koper geleidt stroom goed omdat het een kleine soortelijke weerstand heeft. Goud en zilver hebben ook goede geleiding, maar plastic heeft een grote soortelijke weerstand en geleidt daardoor slecht. Als een materiaal een grote soortelijke weerstand heeft, betekent dit dat het een slechte geleiding heeft en dus grote weerstanden zal hebben. Verschillende materialen hebben verschillende soortelijke weerstanden en het is belangrijk om hier rekening mee te houden bij het ontwerpen van elektrische circuits.

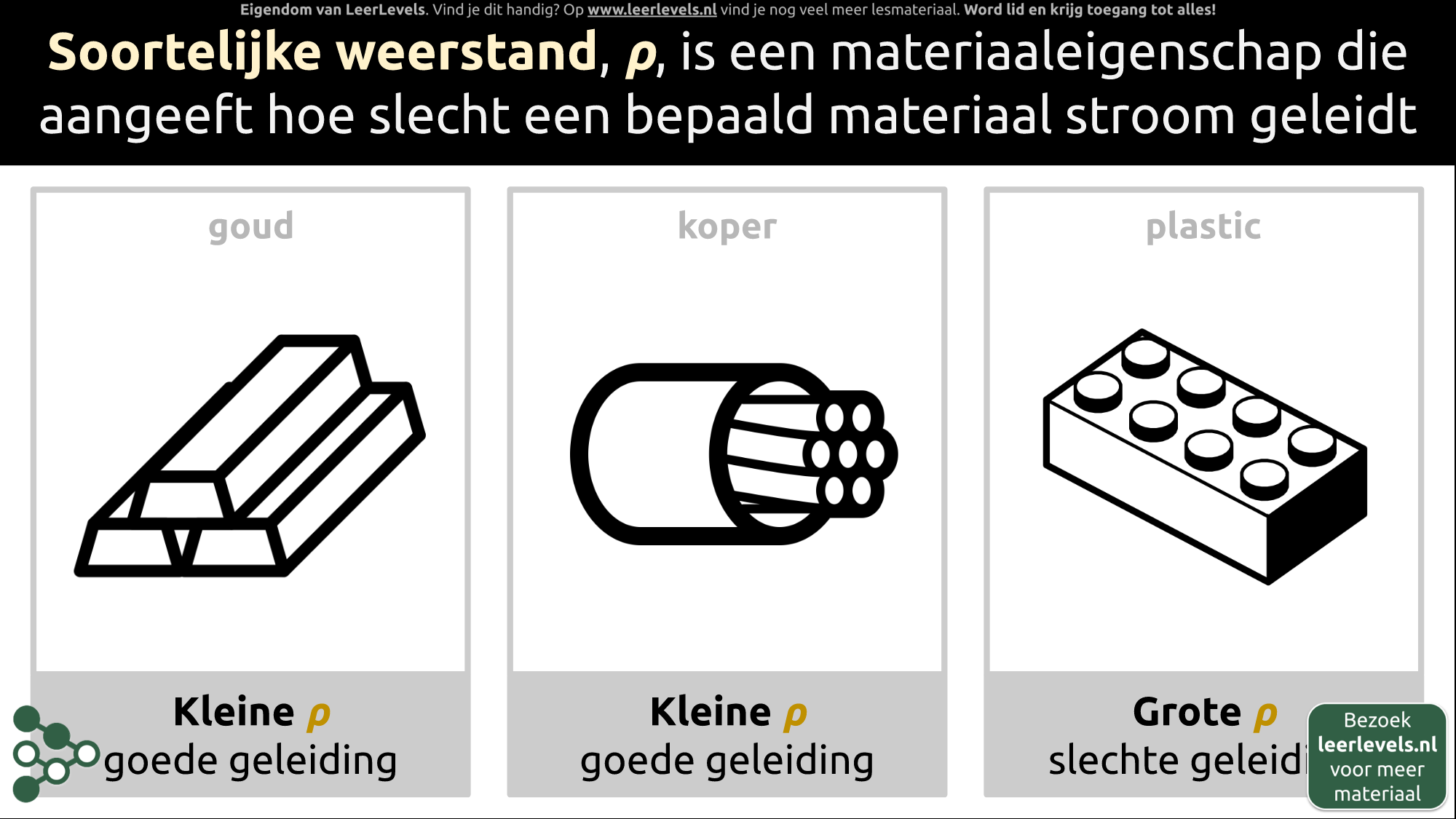
(Afbeelding: Animatie voor Soortelijke weerstand concept)

Soortelijke weerstand formule

Weerstand is recht evenredig met de soortelijke weerstand en de lengte, en omgekeerd evenredig met het oppervlak. Stel dat je een draad hebt met lengte l en soortelijke weerstand ρ, en je wilt de weerstand van die draad berekenen, dan heb je verschillende parameters nodig. Om te beginnen heb je de lengte van de draad nodig, aangezien de weerstand groter wordt als de lengte van de draad groter is. De formule voor het oppervlak van de draad staat bovenaan. Als je het oppervlak van de draad vergroot, maak je een dikkere draad en heb je meer ruimte waar stroom doorheen kan. Hierdoor wordt de weerstand lager. Als de soortelijke weerstand groot is, betekent dit dat het moeilijker is om er stroom doorheen te laten lopen en zal de totale weerstand groter zijn. De formule voor de weerstand kan worden omschreven als

R = (l · ρ)/(A)

waarbij R de weerstand is, l de lengte, ρ de soortelijke weerstand en A het oppervlak. Hiermee kun je ook de grotere weerstand berekenen als je een andere parameter hebt.

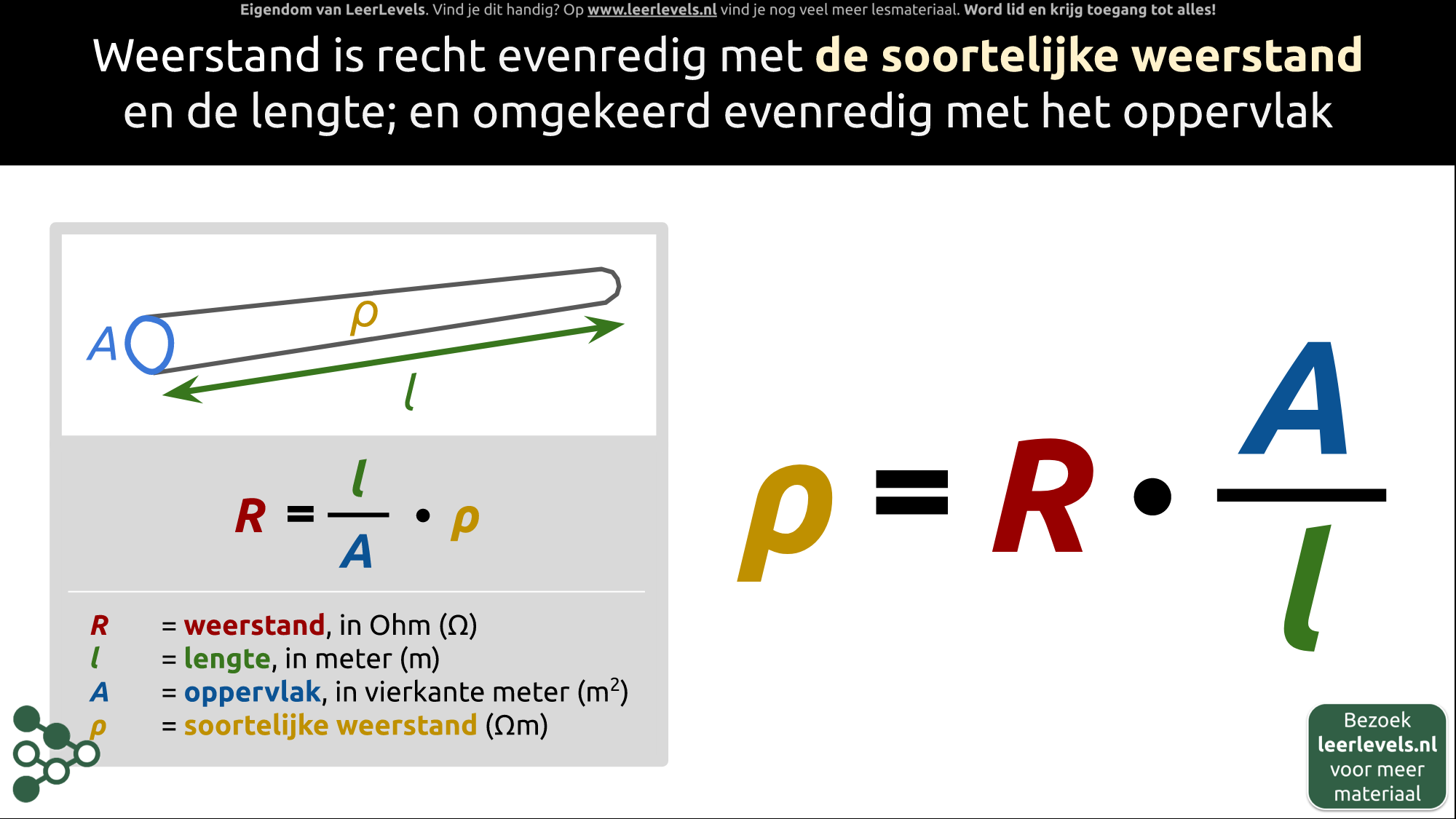
(Afbeelding: Animatie voor Soortelijke weerstand formule)

Toepassen soortelijke weerstand

Bij het berekenen van de weerstand van een koperdraad moet rekening worden gehouden met de soortelijke weerstand. Om dit te berekenen zijn meerdere stappen nodig.
Als eerste begin je met de formule voor de soortelijke weerstand:

R = (ρ · l)/(A)

waarbij R de weerstand is, ρ de soortelijke weerstand, l de lengte, en A het oppervlak.

Voor deze formule hebben we de lengte en het oppervlak van de koperdraad nodig. In dit geval is de lengte gegeven als 1 kilometer (1 km) met een diameter van 5 mm. Het oppervlak van de doorsnede van de draad bereken je als volgt:

A = π ( d/2 )²

waarbij d de diameter is.

De soortelijke weerstand van koper kan worden opgezocht en bedraagt 1,7 × 10⁻⁸ Ω · m. Vervolgens kun je de formule invullen en de verschillende machten van 10 in de eenheden bij elkaar zetten. Na vereenvoudiging krijg je als resultaat dat de weerstand van de koperdraad 5,4 Ω is. Het is dus belangrijk om deze stappen te volgen om de weerstand van een draad te kunnen berekenen.

(Afbeelding: Animatie voor Toepassen soortelijke weerstand)

Terug naar overzicht Meld je aan

Spanning

Gelijkspanning en wisselspanning

Bij wisselspanning verandert de richting van de spanningsbron, en daarmee de stroom, voortdurend. Laten we gelijkspanning eens vergelijken met wisselspanning. Bij gelijkspanning, aangeduid met een symbool dat lijkt op het reguliere plus- en min-teken, stroomt de stroom altijd in dezelfde richting, namelijk van plus naar min.

Bij wisselspanning daarentegen, aangeduid met een ander symbool, kan de polariteit van de pluskant continu veranderen. Hierdoor kan de stroom afwisselend in beide richtingen lopen. Het is ook mogelijk dat de pluskant aan de andere kant wordt geplaatst, waardoor de stroom precies de andere kant op loopt.

Bij wisselspanning wisselt de polariteit dus voortdurend, waarbij de pluspool steeds aan de andere kant komt te zitten. In een normaal stopcontact verandert de polariteit ongeveer 50 keer per seconde. Dit wordt de frequentie genoemd. Een standaard stopcontact heeft een frequentie van 50 Hz, wat betekent dat de polariteit 50 keer per seconde wisselt.

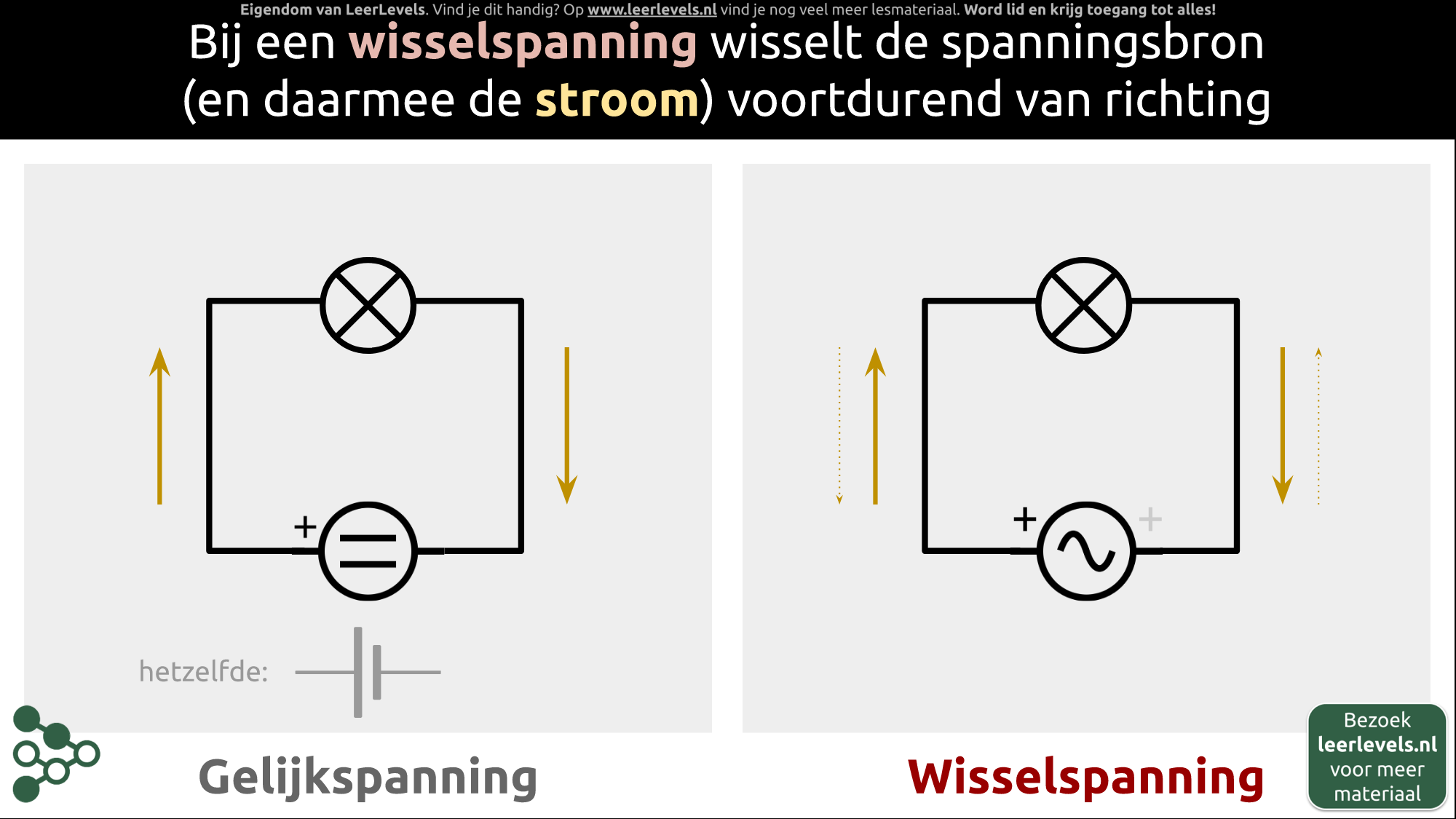
(Afbeelding: Animatie voor Gelijkspanning en wisselspanning)

Spanning concept

Elektrische spanning (U) geeft aan hoeveel energie er per lading wordt afgegeven in een gesloten stroomkring. Een kleine spanning betekent weinig energie per lading en een grote spanning betekent juist veel energie per lading. Dit kan je vergelijken met een vrachtwagen die energie vervoert en afgeeft bijvoorbeeld aan een lampje. Bij een grote spanning kan de vrachtwagen meer energie vervoeren en zal het lampje feller branden. De lading verdwijnt niet, maar wanneer de vrachtwagen terug bij de bron is, wordt er weer energie ingeladen en start het proces opnieuw. Dus bij elektrische spanning gaat het om de hoeveelheid energie die per lading wordt afgegeven in een gesloten stroomkring.

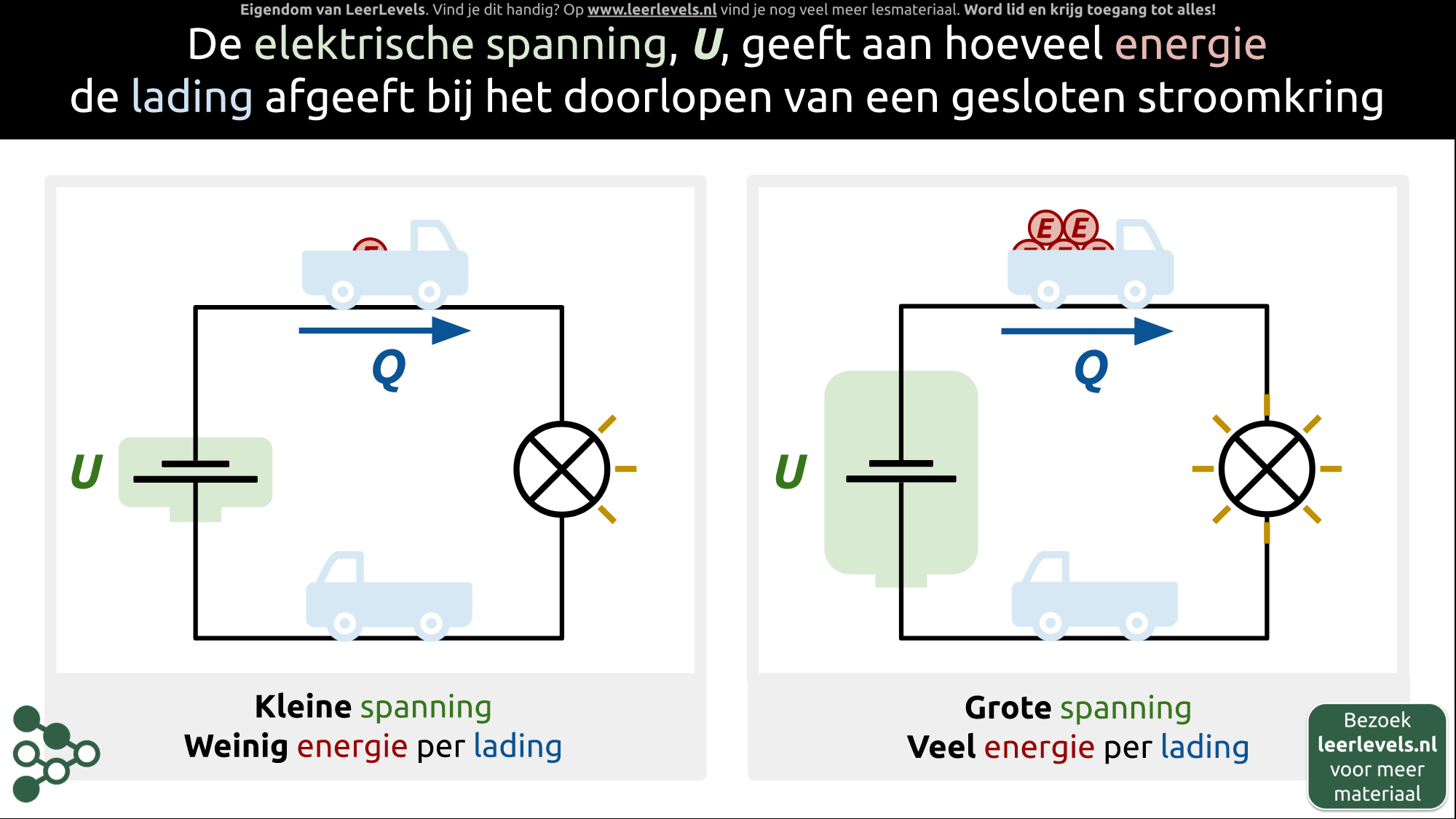
(Afbeelding: Animatie voor Spanning concept)

Spanningsbronnen combineren

Met meerdere batterijen kun je een hogere spanning of stroom krijgen. Bijvoorbeeld: als we twee batterijen van 9 volt achter elkaar zetten en ze aansluiten op een lampje, zal het lampje een spanning van 18 volt krijgen. Dit komt doordat elke batterij de elektronen omhoog tilt. Dus als twee batterijen van 9 volt worden gebruikt, worden de elektronen 18 volt omhoog getild. Bij parallel schakelen blijft de spanning gelijk, maar kan de stroom worden verdubbeld. Als batterijen parallel worden geschakeld, blijft de spanning hetzelfde.

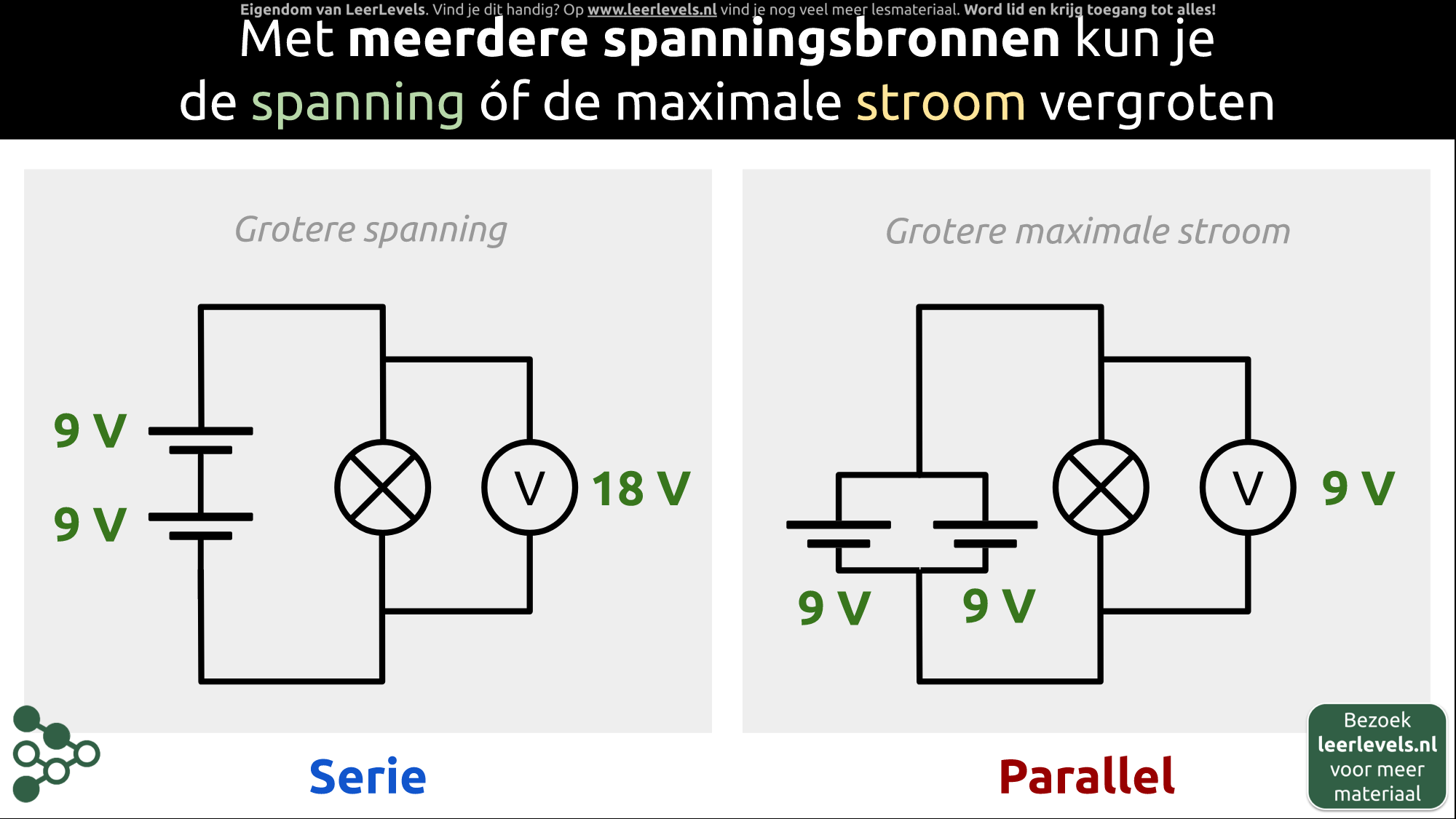
(Afbeelding: Animatie voor Spanningsbronnen combineren)

Spanning formule

De spanning is recht evenredig met de energie en omgekeerd evenredig met de lading die de energie vervoert. Dit houdt in dat de spanning U kan worden uitgedrukt als de energie E gedeeld door de lading Q, oftewel:

U = E/Q

Hierbij is U de spanning in volt, E de energie in joule, en Q de lading in coulomb. Uit de eenheden blijkt dat volt gelijk moet zijn aan joule per coulomb.

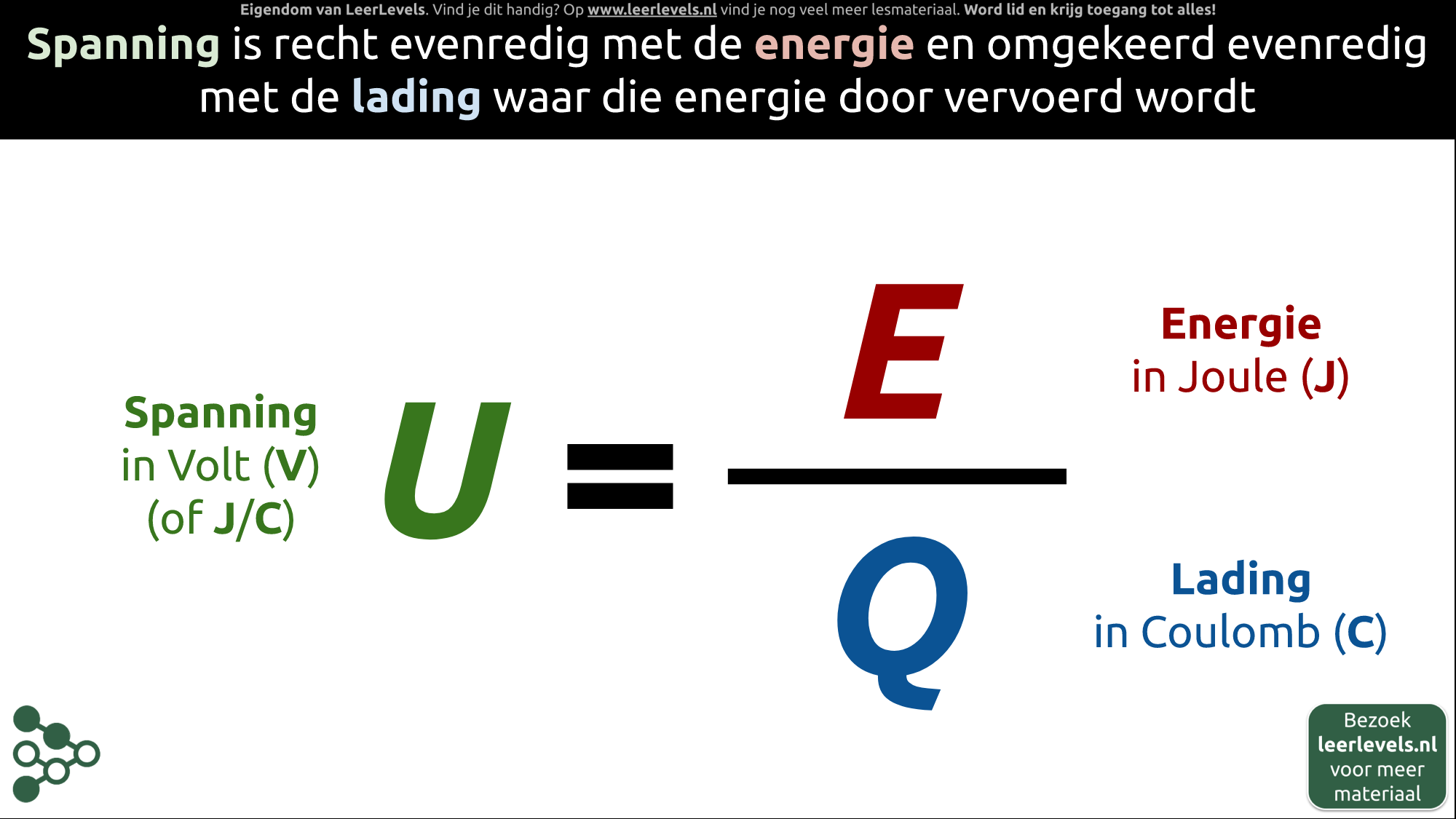
(Afbeelding: Animatie voor Spanning formule)

Versnelspanning en remspanning

Als je een spanningsbron toevoegt aan het foto-elektrische experiment kun je meten hoeveel elektronen vrijkomen of stoppen met stromen. Door een extra spanningsbron toe te voegen, kun je elektronen makkelijker van de kathode naar de anode laten gaan en daarmee de stroom vergroten. Bij kleinere fotonenergie zal de stroom altijd nul zijn omdat er niet genoeg energie is om elektronen vrij te maken. Bij hogere fotonenergie kunnen sommige elektronen zo snel bewegen dat je een hogere spanningsbron nodig hebt om ze bij de anode te laten aankomen. Met remspanning kun je zien welk effect het heeft als je de spanningsbron omdraait. Bij een grotere remspanning zal de stroom uiteindelijk nul worden omdat alle elektronen worden afgestoten. Deze experimenten laten zien dat fotonen alleen elektronen vrij kunnen maken als ze een frequentie hebben van minstens de grensfrequentie.

Formules, grootheden of eenheden:

- Fotonenergie (Ef)
- Spanningsbron (V)
- Elektrische stroom (I)
- Grensfrequentie

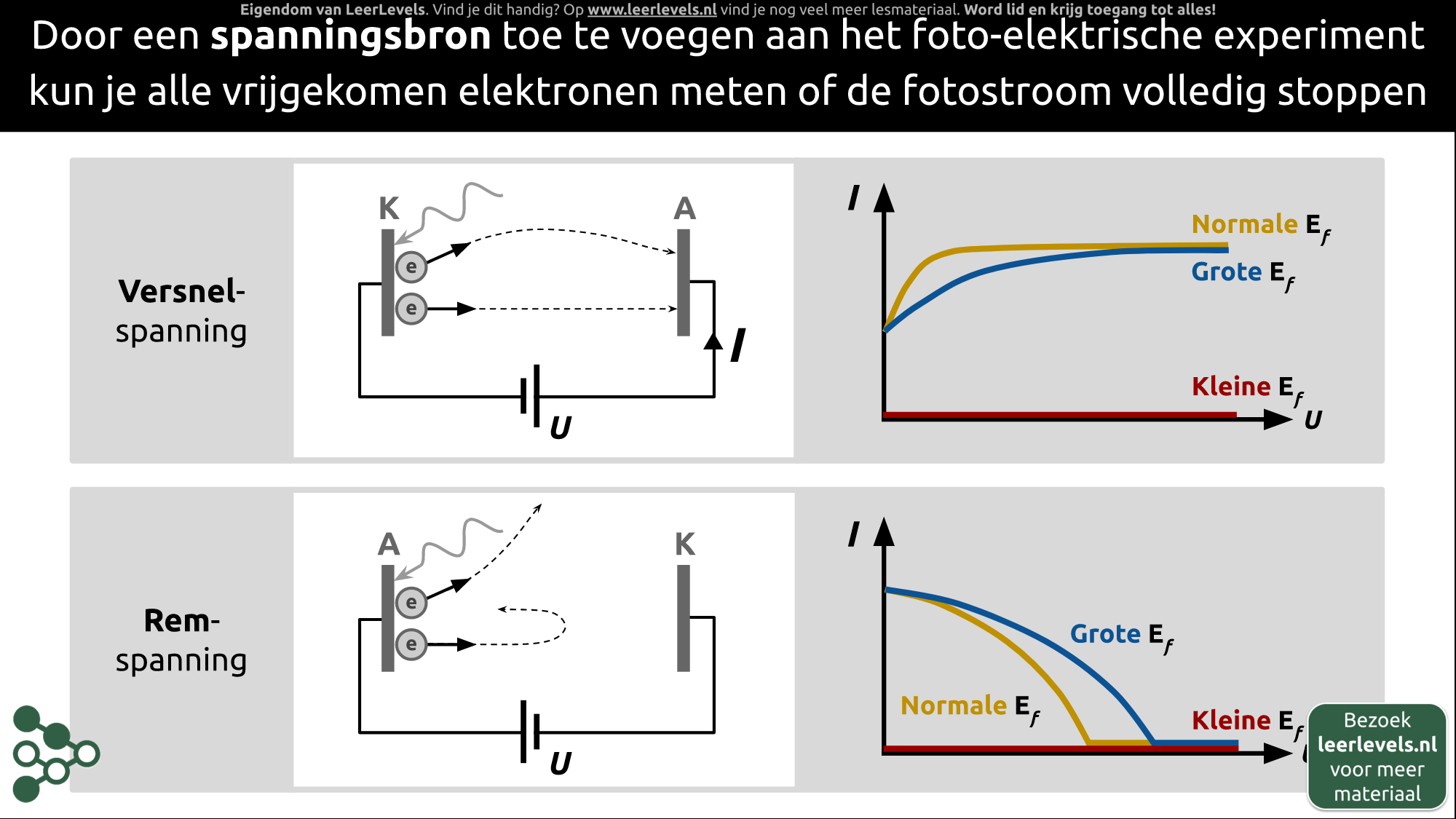
(Afbeelding: Animatie voor Versnelspanning en remspanning)

Draden en gelijke spanning

Een getekende elektrische schakeling heeft lijnen die geen weerstand hebben. Hierdoor hebben punten die met dezelfde lijn zijn verbonden dezelfde spanningswaarde. Bij een parallelschakeling hebben alle punten aan de linkerkant van de spanningsbron een spanningswaarde van 0V en de punten aan de rechterkant een spanningswaarde van 9V. Bij een serieschakeling is het ingewikkelder, omdat de spanningswaarde afhankelijk is van de weerstanden. Bij een combinatie geldt nog steeds dat punten die met elkaar verbonden zijn dezelfde spanningswaarde hebben. Als alle punten verbonden zijn, is er sprake van kortsluiting en kan er een directe verbinding zijn tussen de plus- en minpool. In het kort betekent dit dat getekende lijnen in een schakeling geen weerstand hebben en dat alle punten op dezelfde lijn dezelfde spanningswaarde hebben.

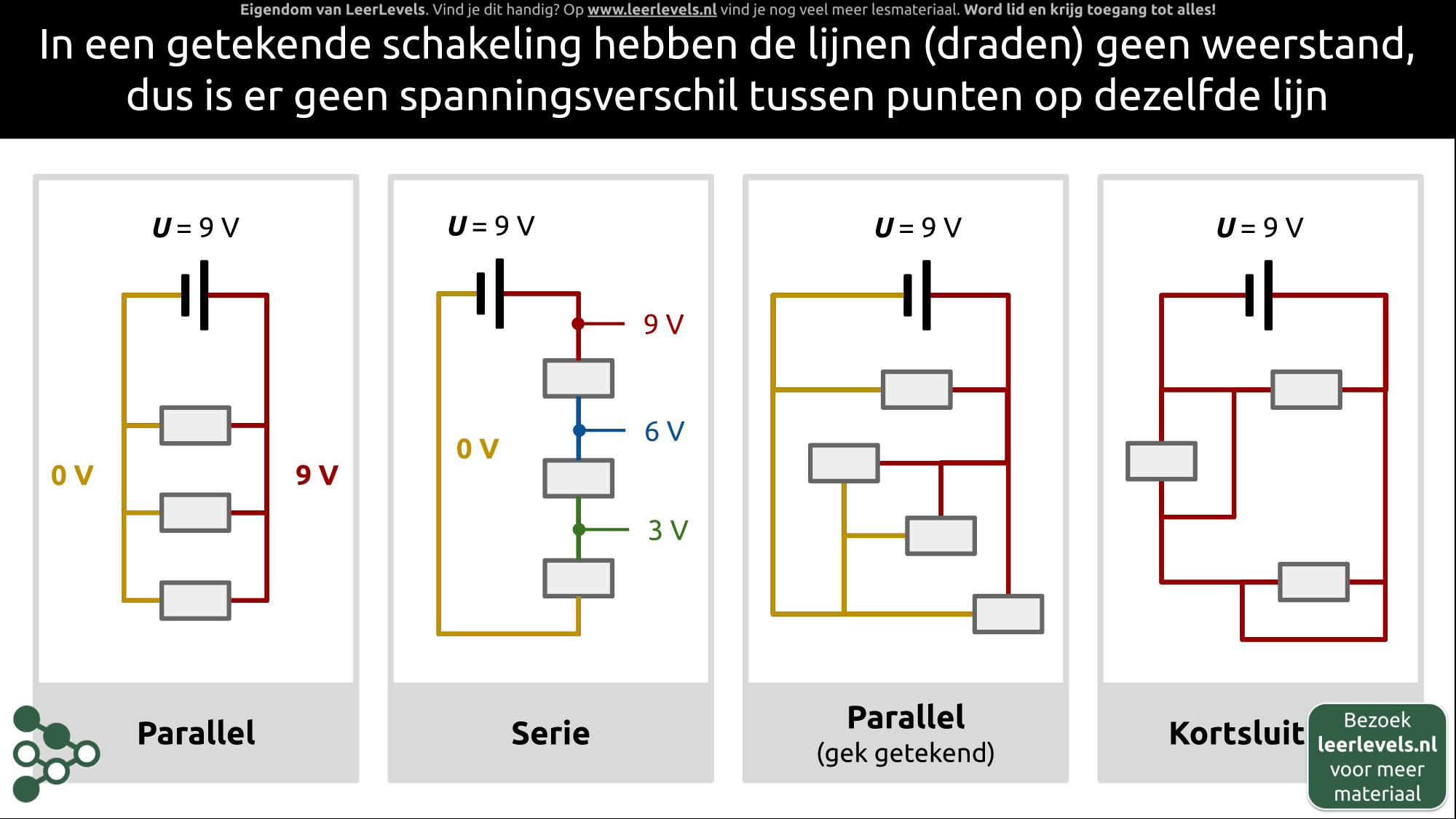
(Afbeelding: Animatie voor Draden en gelijke spanning)

Spanningsbron concept

Een spanningsbron zorgt ervoor dat elektrische energie door een schakeling kan stromen. Als we alleen een spanningsbron en een lampje hebben, weten we dat er stroom gaat lopen. Als we inzoomen op de spanningsbron en er een schema van maken, zien we dat er eerst lading aankomt die nog geen energie heeft. Pas wanneer deze lading bij de spanningsbron aankomt, wordt deze gevuld met energie in de vorm van elektriciteit. De elektriciteit wordt vervolgens aan de lading gegeven, waardoor deze door de schakeling kan stromen en bijvoorbeeld het lampje kan doen branden. In het kort: een spanningsbron geeft elektrische energie aan de lading waardoor deze door de schakeling kan stromen.

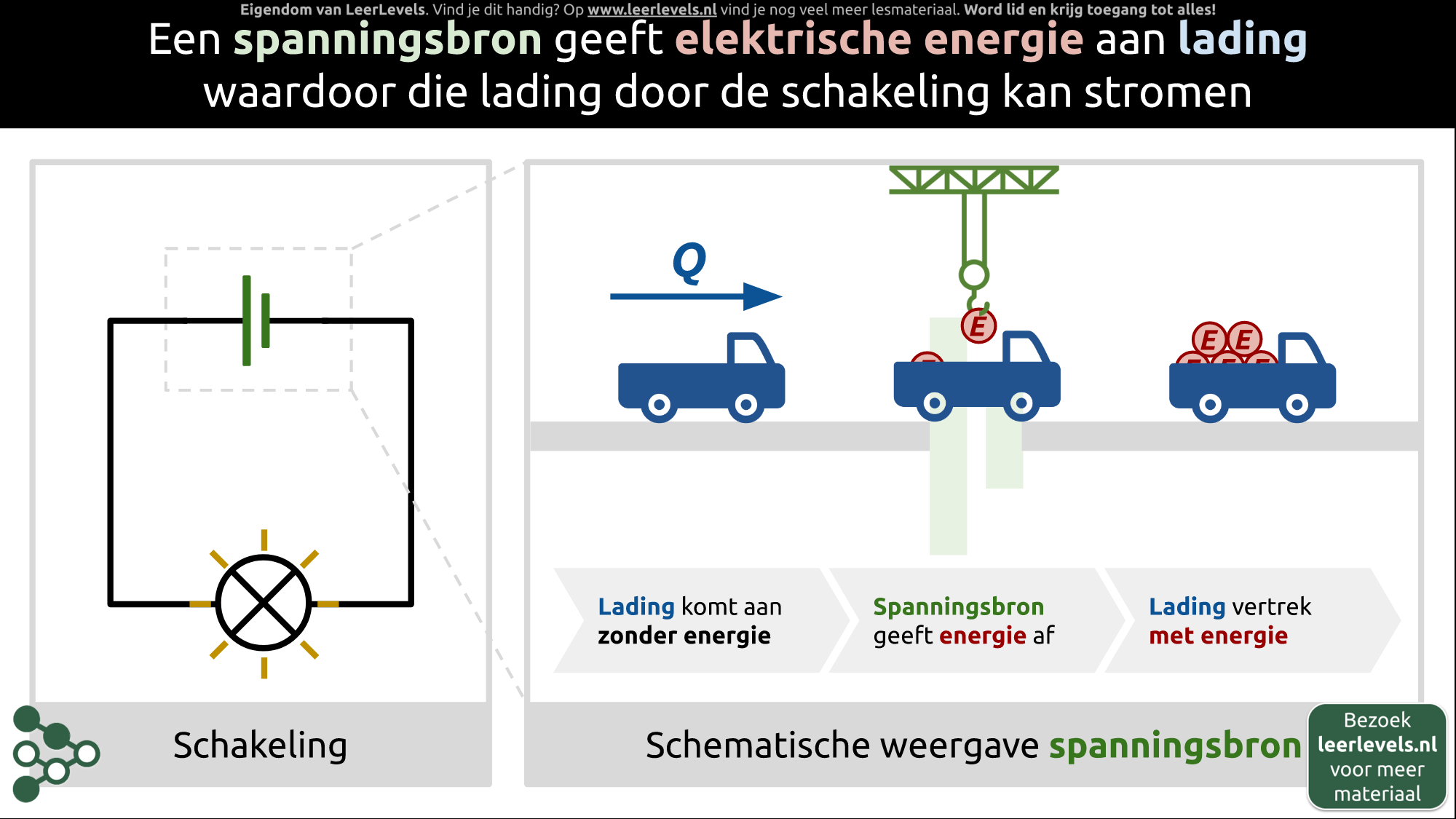
(Afbeelding: Animatie voor Spanningsbron concept)

Terug naar overzicht Meld je aan

Spannings-rekdiagram

(Spanning, rek)-diagram

Een (spanning,rek)-diagram laat zien hoe een materiaal vervormt onder druk. Dit wordt getest door een trekproef uit te voeren, waarbij een materiaal wordt uitgerekt en de spanning wordt gemeten. Het diagram toont de spanning op de verticale as en de rek op de horizontale as. De spanning wordt vaak uitgedrukt in Pascal en de rek in procenten.

Bij lage spanningen treedt elastische vervorming op en bij hogere spanningen treedt plastische vervorming op. Plastische vervorming kan zich manifesteren als vloeien, waarbij het materiaal permanent langer wordt. De spanning waarbij vloeien optreedt staat bekend als de vloeispanning. Boven de vloeispanning lijkt het materiaal minder spanning nodig te hebben om dezelfde mate van rek te bereiken.

Het breekpunt van het materiaal is waar de spanning en rek voorbij het maximale punt gaan en het materiaal breekt. Dit wordt de treksterkte genoemd. Maar als er na het breekpunt nog meer rek plaatsvindt dan zal het materiaal breken.

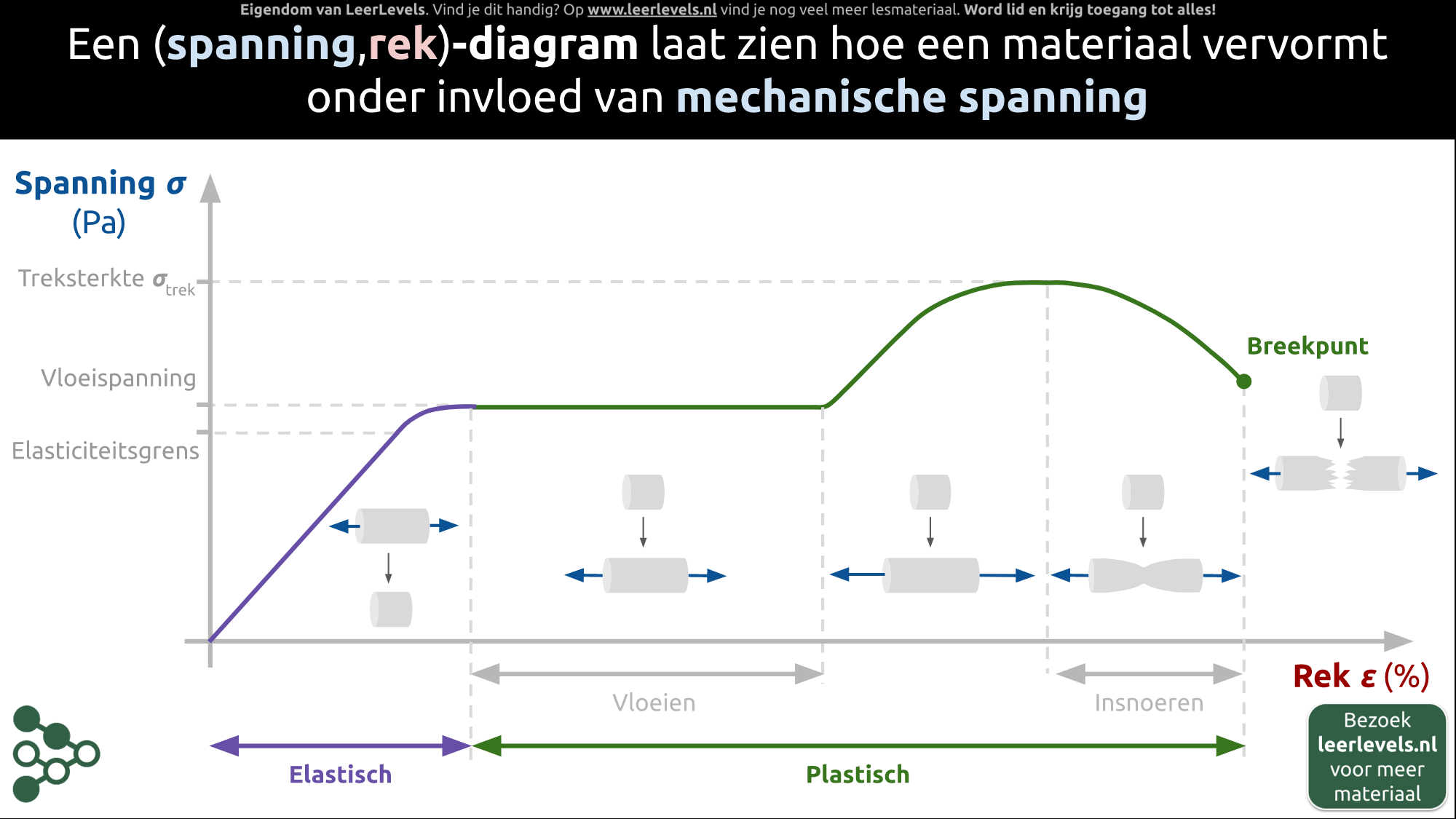
(Afbeelding: Animatie voor (Spanning, rek)-diagram)

Terug naar overzicht Meld je aan

Spectroscopie

Spectroscopie concept

Spectroscopie is een techniek om te onderzoeken welke kleuren er in het licht van een lichtbron aanwezig zijn. Dit wordt gedaan door het licht van bijvoorbeeld een kaars te bekijken met een prisma, waardoor het licht wordt gescheiden in afzonderlijke kleuren. Elke kleur breekt net op een andere manier door het prisma. Hierdoor kunnen de verschillende kleuren geanalyseerd worden met behulp van een spectroscopisch instrument. Dit instrument kijkt naar de exacte kleur en intensiteit van elk segment van het kleurenspectrum. Zo kan bijvoorbeeld worden vastgesteld dat het gele licht bij een kaars oververtegenwoordigd is, waardoor we die als geel ervaren.

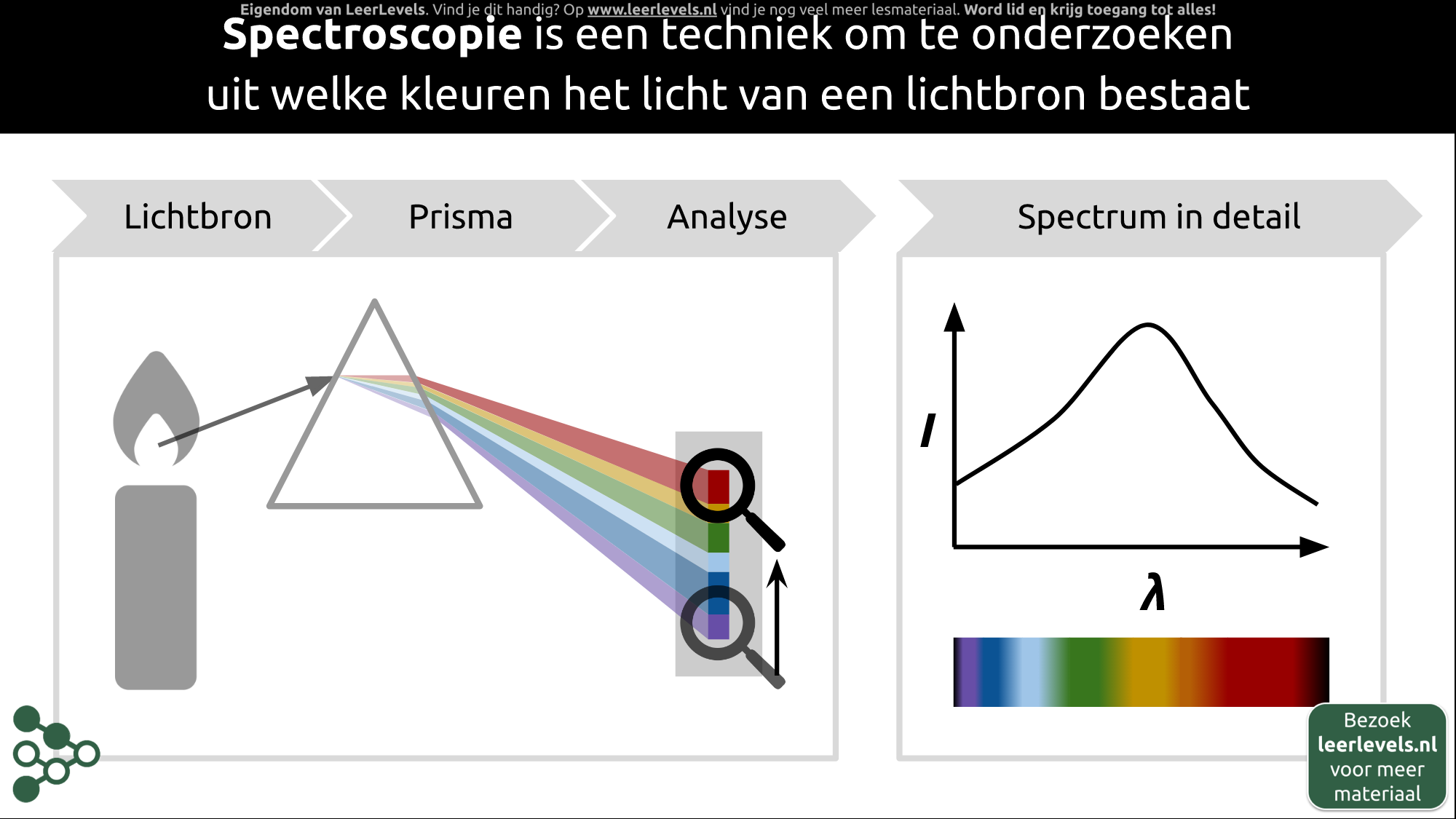
(Afbeelding: Animatie voor Spectroscopie concept)

Terug naar overzicht Meld je aan

Spectrum

Continu en discreet spectrum

In een continu spectrum zijn alle kleuren aanwezig, terwijl een discreet spectrum slechts enkele specifieke kleuren bevat. Kijk je naar een gloeilamp, dan zie je een continu spectrum. Dit betekent dat als je de lichtstraal zou opsplitsen met prisma's of zeer dunne spleten, je alle kleuren van de regenboog zou waarnemen.

In een discreet spectrum, zoals dat van een witte LED-lamp, zie je daarentegen slechts enkele kleuren. Bij een witte LED zie je een blauwe lijn, een groene lijn en een rode lijn. Onze ogen zien deze drie kleuren samen als wit licht. Echter, tussenliggende kleuren, zoals geel of paars, zijn niet aanwezig in het LED-licht.

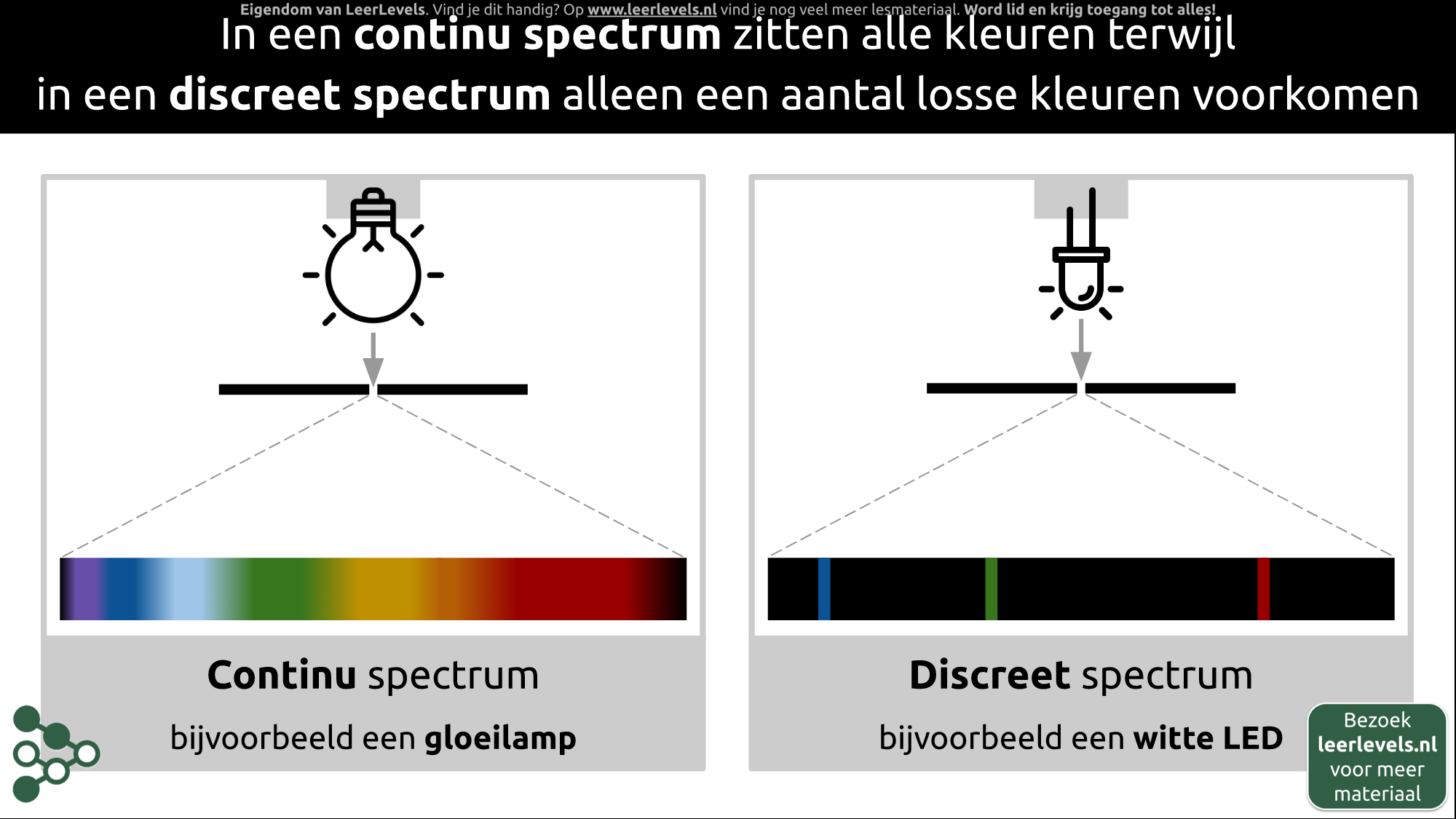
(Afbeelding: Animatie voor Continu en discreet spectrum)

Terug naar overzicht Meld je aan

Spiegelbeeld

Spiegelbeeld tekenen

Het tekenen van een spiegelbeeld doe je in zeven stappen en gebruik je het best een geodriehoek. Hier zijn de stappen:

1. Bepaal het punt dat je wilt spiegelen, zoals bijvoorbeeld de hoekpunten van een driehoek: A, B en C.
2. Zet een potlood op het eerste punt voor gebruikersgemak.
3. Schuif de geodriehoek tegen het potlood aan, zodat de middellijn parallel loopt met de spiegel.
4. Bepaal de afstand tot de middenlijn, dit heet de voorwerpafstand v.
5. Teken aan de andere kant van de spiegel een punt op precies dezelfde afstand. Dit noemen we de beeldafstand en bij een spiegel is de beeldafstand gelijk aan de voorwerpafstand. Dus, dit punt noemen we A', het spiegelbeeld van A.
6. Herhaal dit proces voor alle andere punten om B' en C' te krijgen.
7. Verbindt tot slot de hoekpunten om het spiegelpunt te tekenen.

Belangrijk om te weten: formules, grootheden en eenheden worden niet gebruikt in deze stappen.

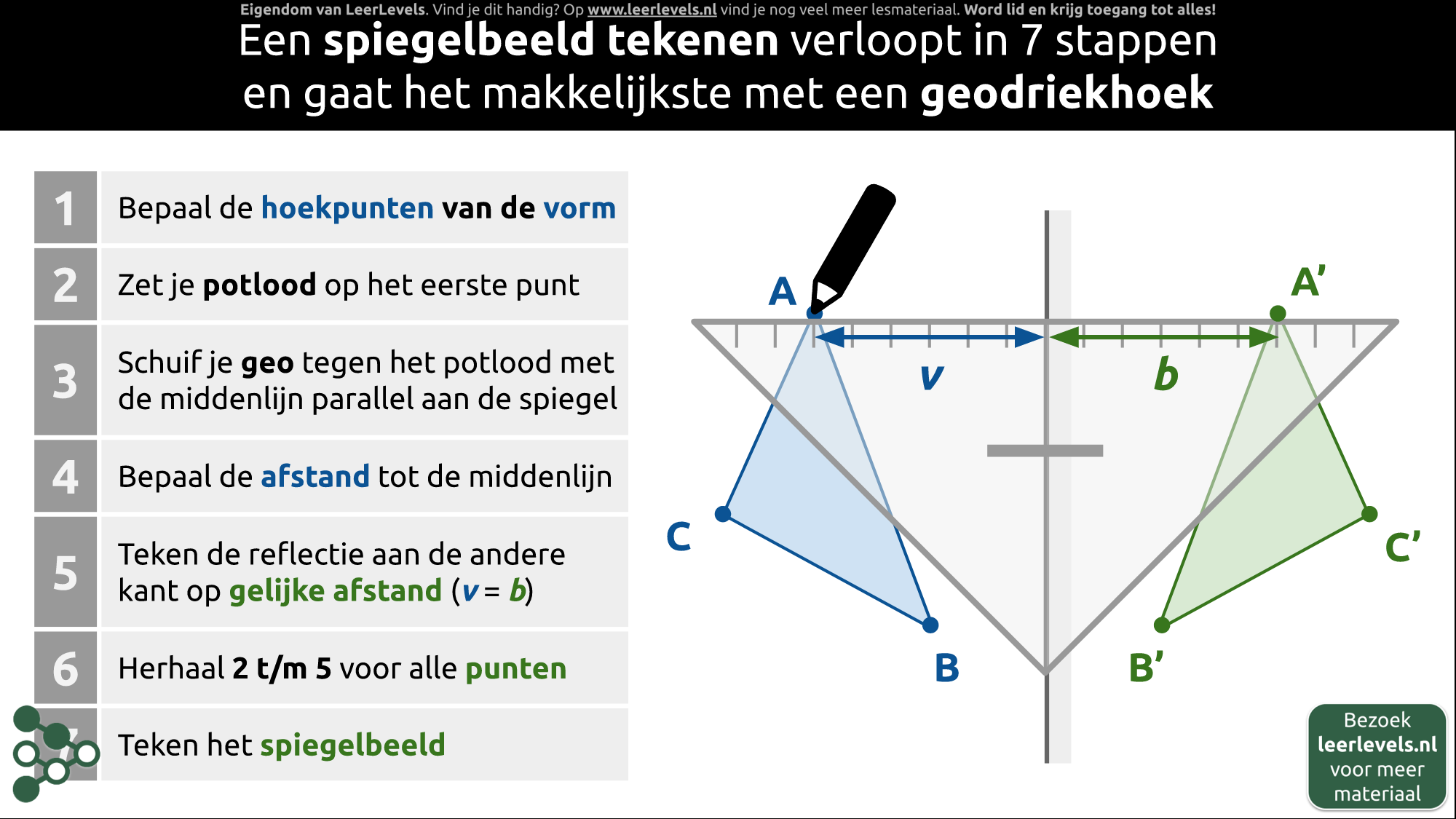
(Afbeelding: Animatie voor Spiegelbeeld tekenen)

Terug naar overzicht Meld je aan

Spiegelwet

De spiegelwet zegt dat als licht op een spiegel valt, de hoek waaronder het licht de spiegel raakt hetzelfde is als de hoek waaronder het licht wordt gereflecteerd. Om deze hoek te meten, meten we de hoek tussen het licht en een lijn die loodrecht op de spiegel staat, de 'normaal'. De hoek tussen de normaal en de lichtstraal noemen we de hoek van inval. De hoek van reflectie is gelijk aan de hoek van inval. Deze hoeken worden gemeten in graden. Dit betekent in formulevorm dat θinval = θreflectie.

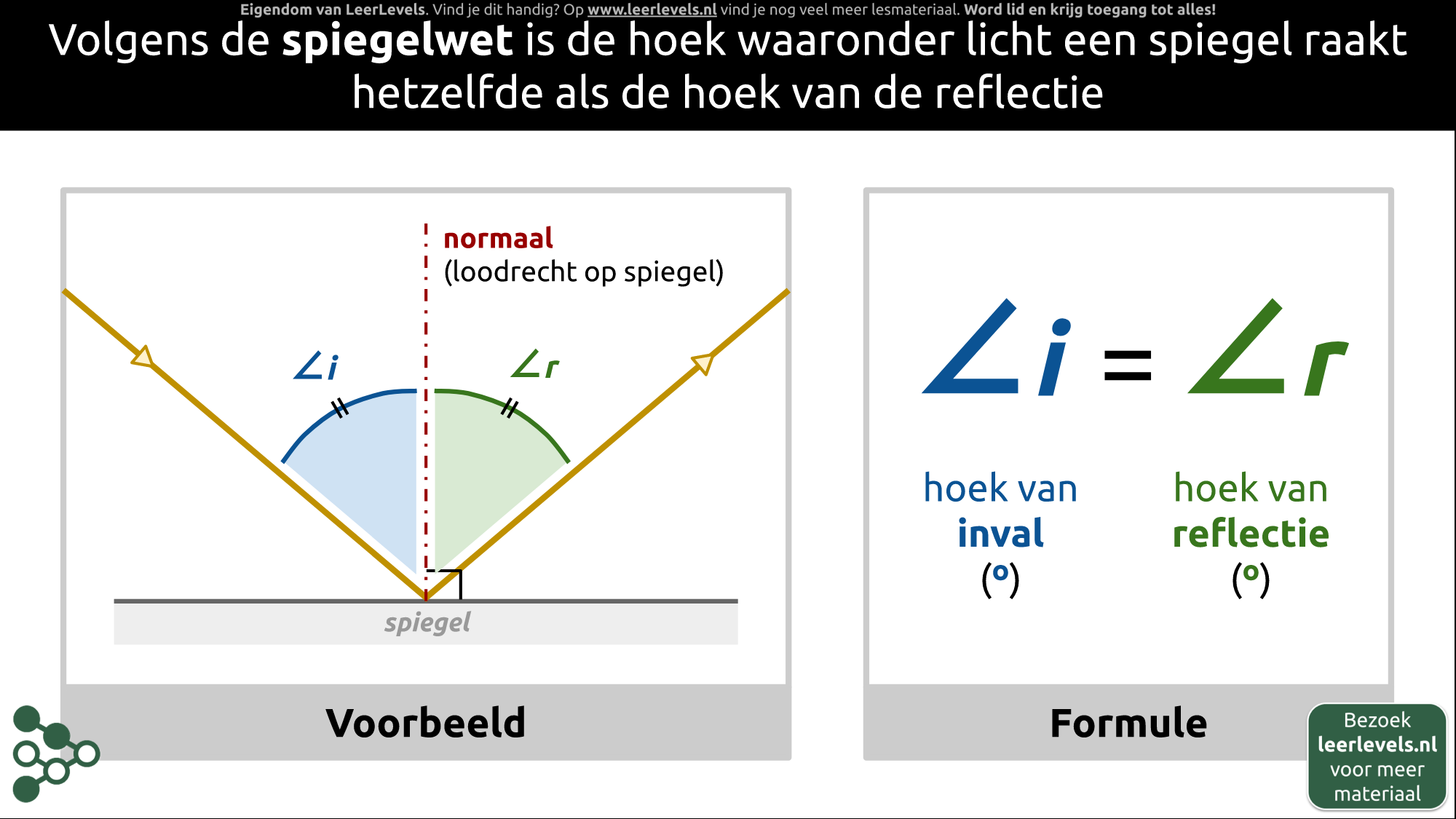
(Afbeelding: Animatie voor Spiegelwet)

Spiegelwet toepassen

De spiegelweg heeft 6 stappen. Bij een vlakke spiegel is de eerste stap het tekenen van de lichtstraal tot aan de spiegel. Als de invalshoek niet gegeven is, meet dan de hoek van inval. Teken een normaal op de plek waar de lichtstraal de spiegel raakt en teken de reflectiehoek met behulp van de spiegelwet (hoek van inval = hoek van reflectie). Trek een lijn van de spiegel naar de reflectiehoek. Bij een bolle spiegel teken je de normaal vanuit het middelpunt naar de plek waar de lichtstraal de spiegel raakt. Een holle spiegel werkt op dezelfde manier als een bolle spiegel.

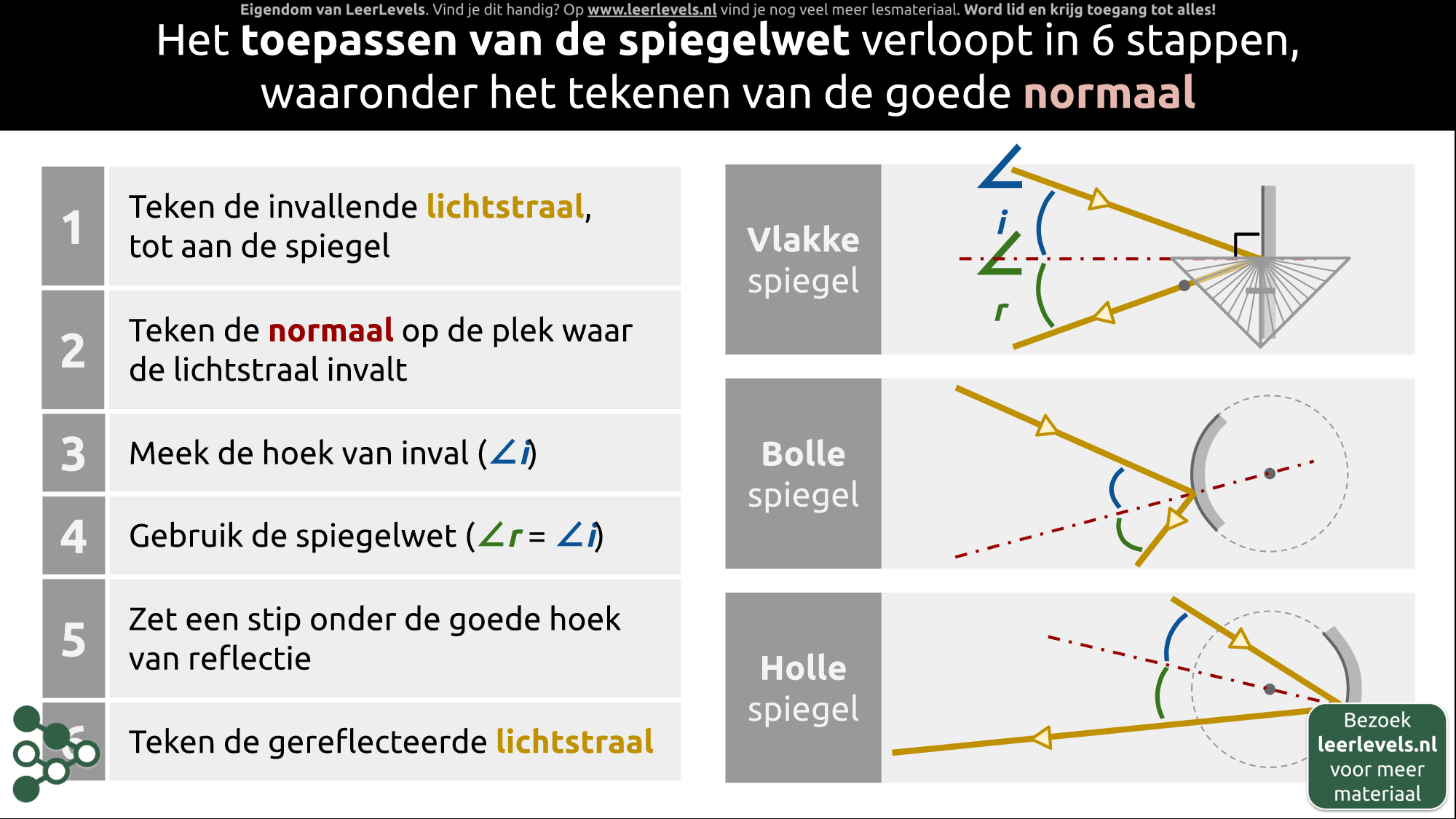
(Afbeelding: Animatie voor Spiegelwet toepassen)

Terug naar overzicht Meld je aan

Spierkracht

Spierkracht en werkkracht

Veel gereedschap maakt gebruik van de hefboom met een draaipunt om een kleine kracht om te zetten in een grotere kracht. Dit kan bijvoorbeeld een rechte balk zijn of twee stokken die aan het uiteinde verbonden zijn. Door een kleine kracht uit te oefenen aan de ene kant van het draaipunt, ontstaat een grotere werkkracht halverwege. Hierdoor wordt het gemakkelijker om bijvoorbeeld een zware balk te tillen of een spijker te verwijderen met een nijptang. Andere voorbeelden van gereedschap dat gebruik maakt van de hefboom zijn de koevoet, hamer, schaar en notenkraker.

Formules, grootheden of eenheden komen niet voor in deze uitleg.

(Afbeelding: Animatie voor Spierkracht en werkkracht)

Terug naar overzicht Meld je aan

Staande golf

Ontstaan staande golf

Staande golven ontstaan als twee golven tegen elkaar in bewegen en elkaar overlappen. Dit noemen we interferentie. De overlapping zorgt voor een hogere amplitude op sommige plekken en een lagere amplitude op andere plekken. Naarmate de twee golven dichter bij elkaar komen, wordt het overlappende gebied groter en ontstaat er een patroon van pieken en dalen die niet meer van plek verschuiven. Dit noemen we een staande golf. De pieken blijven op dezelfde plek, terwijl de dalen ertussen steeds dieper worden. Staande golven worden vaak gebruikt in muziekinstrumenten en bij geluidsinstallaties. De amplitude van de staande golf kan worden berekend met de formule A = 2A0cos(kx)sin(ω t), waarbij A0 de amplitude is van de oorspronkelijke golven, k de golfgetal en ω de hoeksnelheid.

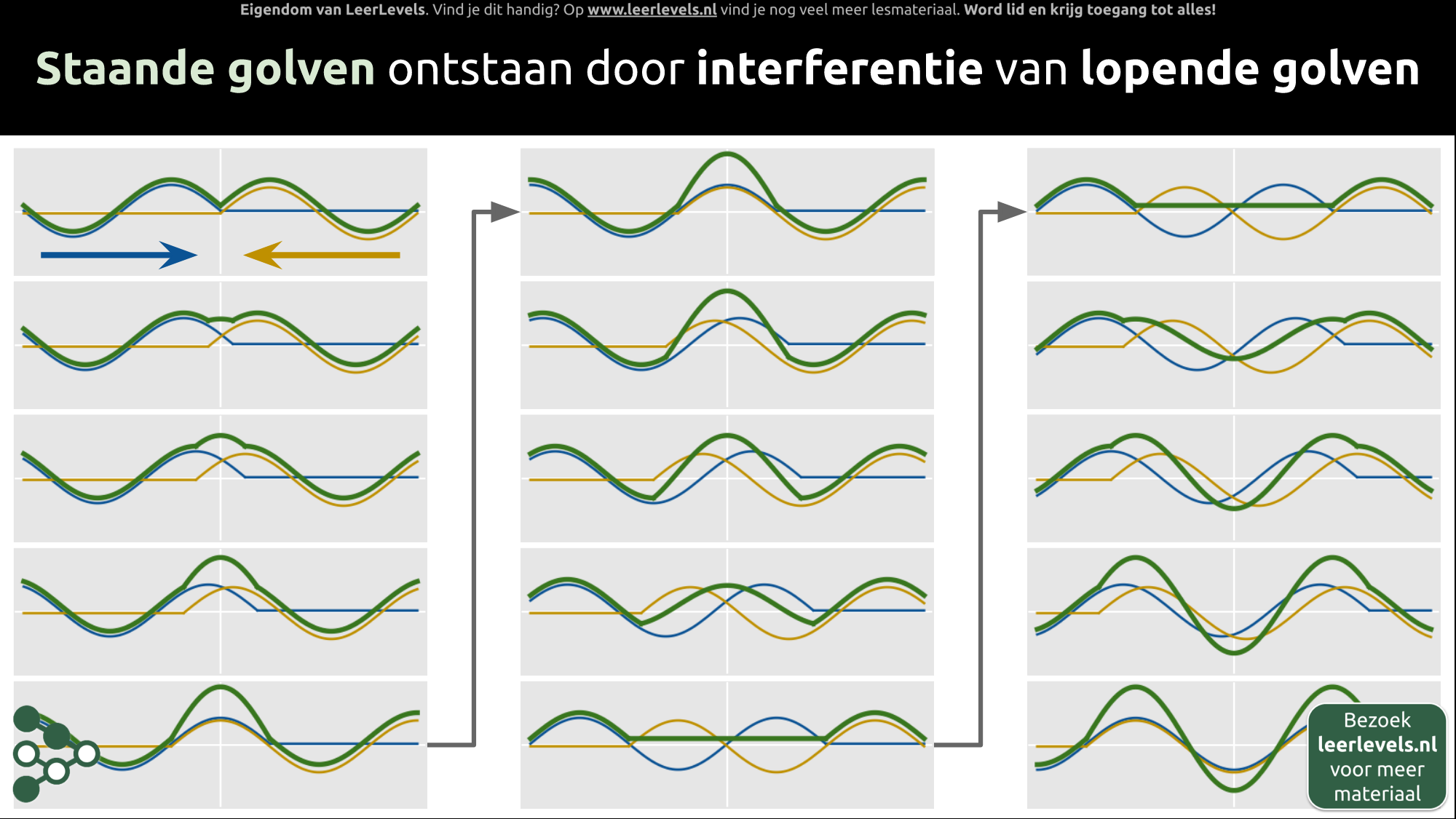
(Afbeelding: Animatie voor Ontstaan staande golf)

Knopen en buiken

Staande golven zijn golven die op één plek blijven, in plaats van te bewegen. Bij staande golven zijn er stukken waar de golf niet beweegt, deze noemen we knopen en ze worden aangeduid met de letter K. Er zijn ook stukken waar de uitwijking afwisselend positief en negatief is, deze noemen we buiken en ze worden aangeduid met de letter B.

Als je naar een echte snaar kijkt, zie je dat er knopen zijn aan de uiteindes, waar de uitwijking altijd 0 is. Daartussenin zijn er buiken, waar de uitwijking maximaal is. Als je naar hogere tonen gaat, komen er meer knopen en buiken bij.

Als de snaar aan beide kanten is ingeklemd, zijn er patronen met knopen en buiken. Als de snaar aan één kant is ingeklemd, is er een knoop aan de ingeklemde kant en een buik aan de andere kant. Bij hogere tonen komen er meer knopen en buiken bij.

Het is belangrijk om te weten dat bij staande golven knopen of buiken kunnen ontstaan. Bij knopen is er geen uitwijking, terwijl bij buiken de uitwijking afwisselend positief en negatief is.

Er worden geen formules, grootheden of eenheden gebruikt in deze uitleg.

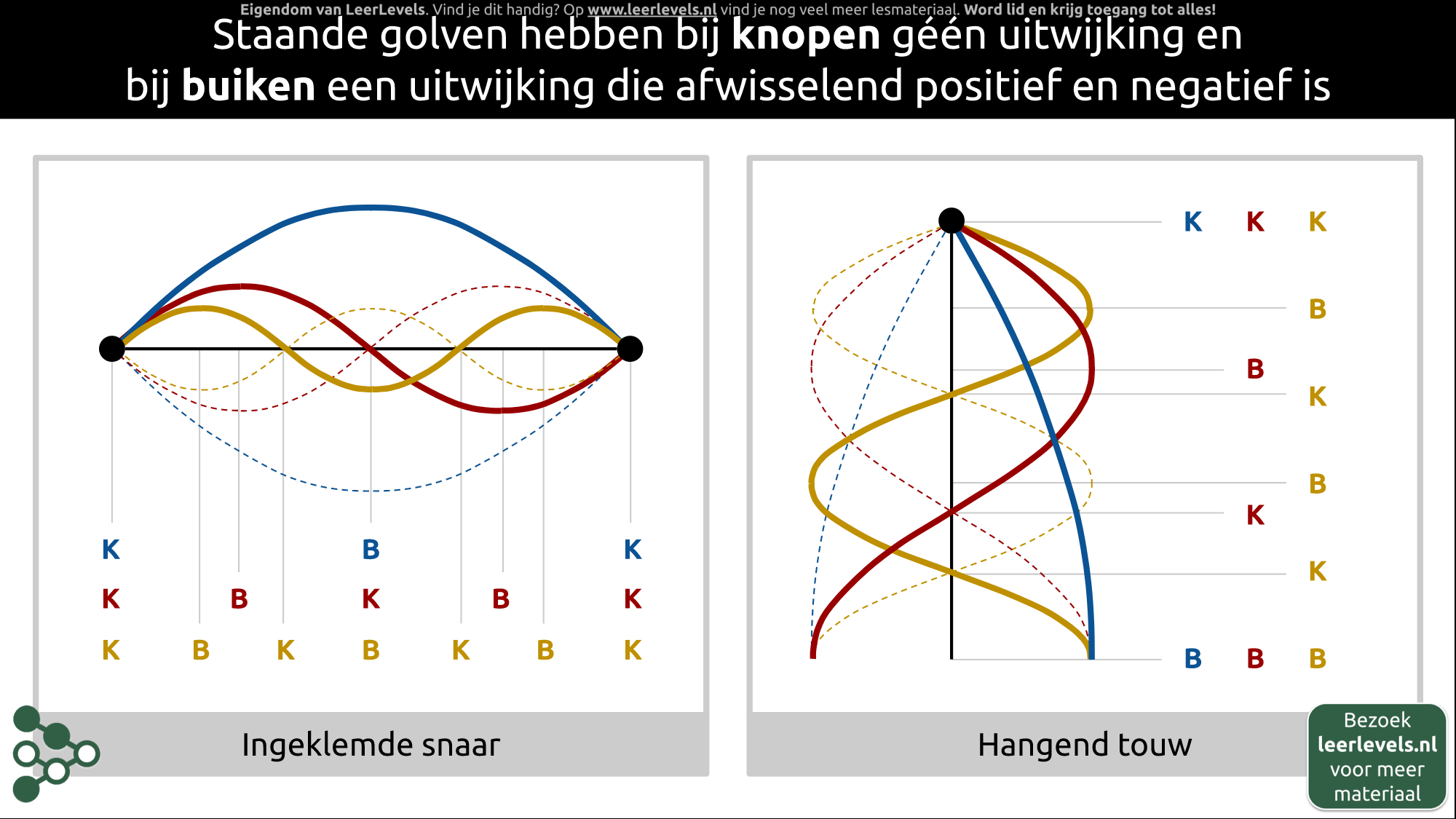
(Afbeelding: Animatie voor Knopen en buiken)

Terug naar overzicht Meld je aan

Stappenplan

Uitleg stappenplan

Soms moet je uitleggen waarom iets gebeurt. Bijvoorbeeld, wat gebeurt er met de trillingstijd van een blokje dat aan een veer hangt als je er nog een blokje onder hangt? Om dit uit te leggen, zijn er vier stappen:

1. Zeg iets slims, zoals een formule. Voor trillingstijd is de formule: t = 2π√( m/C ).

2. Zeg wat hetzelfde blijft. Als je er een tweede blokje ophangt, verandert de veer niet, dus blijft de constante C hetzelfde.

3. Zeg wat er anders is. Als je het tweede blokje ophangt, wordt de massa van het systeem twee keer zo groot.

4. Trek een logische conclusie. Als de massa in de formule twee keer zo groot wordt, dan wordt de trillingstijd wortel 2 keer zo groot. Dit betekent dat de trilling langzamer gaat.

Als je deze stappen volgt bij het beantwoorden van vragen, dan kom je meestal tot het goede antwoord.

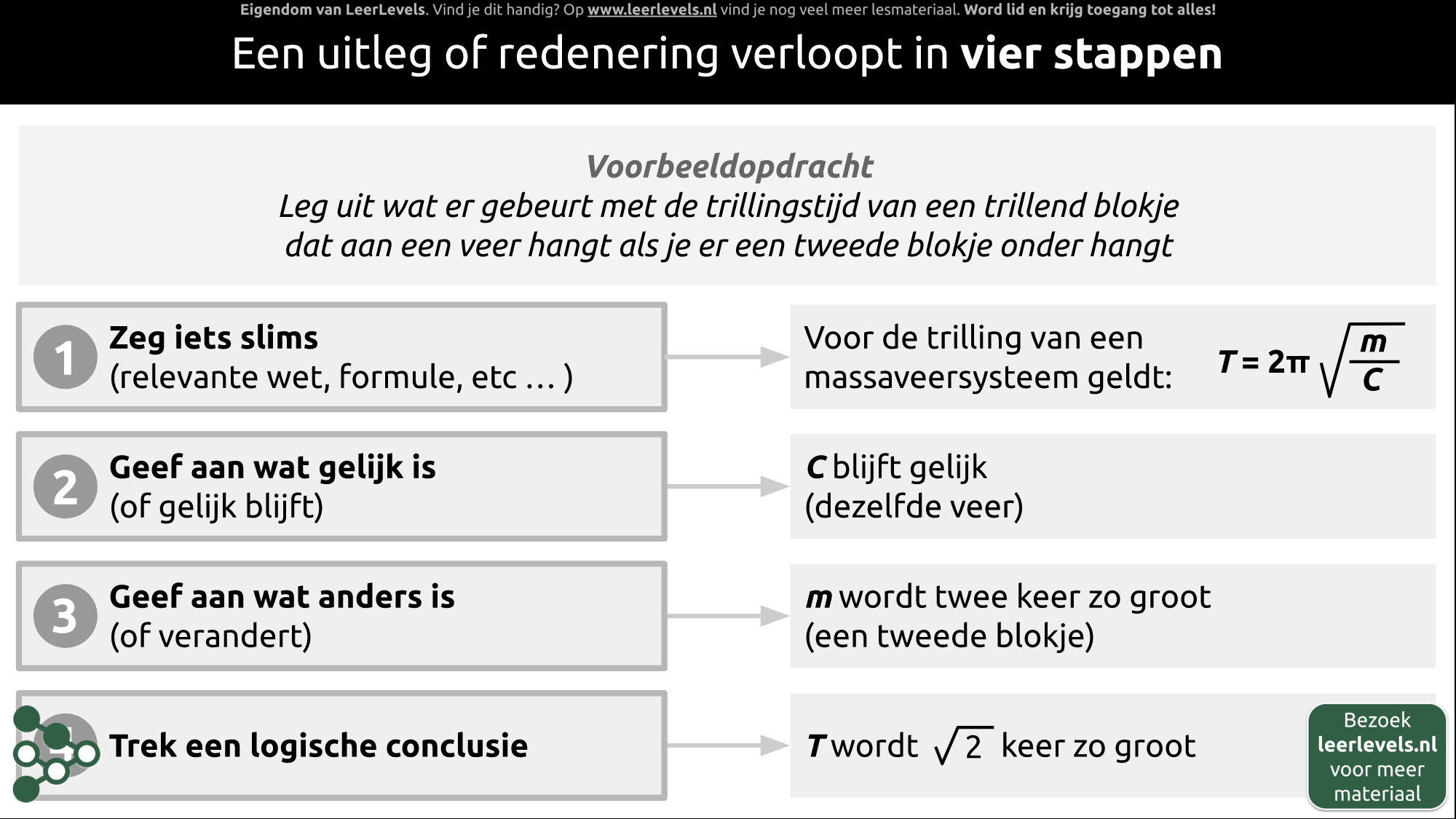
(Afbeelding: Animatie voor Uitleg stappenplan)

Afleiding stappenplan

Bij het afleiden van een formule volgen we meestal vier stappen. Een voorbeeld is de formule P = U²/R, die we moeten afleiden met formules uit het BiNaS boekje. Stap 1 is om relevante formules op te zoeken in BiNaS. Stap 2 is om de grootheid vrij te maken die we willen vervangen. In dit geval willen we de grootheid I vervangen door U en R. Stap 3 is het vervangen van deze grootheid. We vervangen I door U/R. Stap 4 is om de formule te vereenvoudigen. Uiteindelijk krijgen we de afgeleide formule P = U²/R.

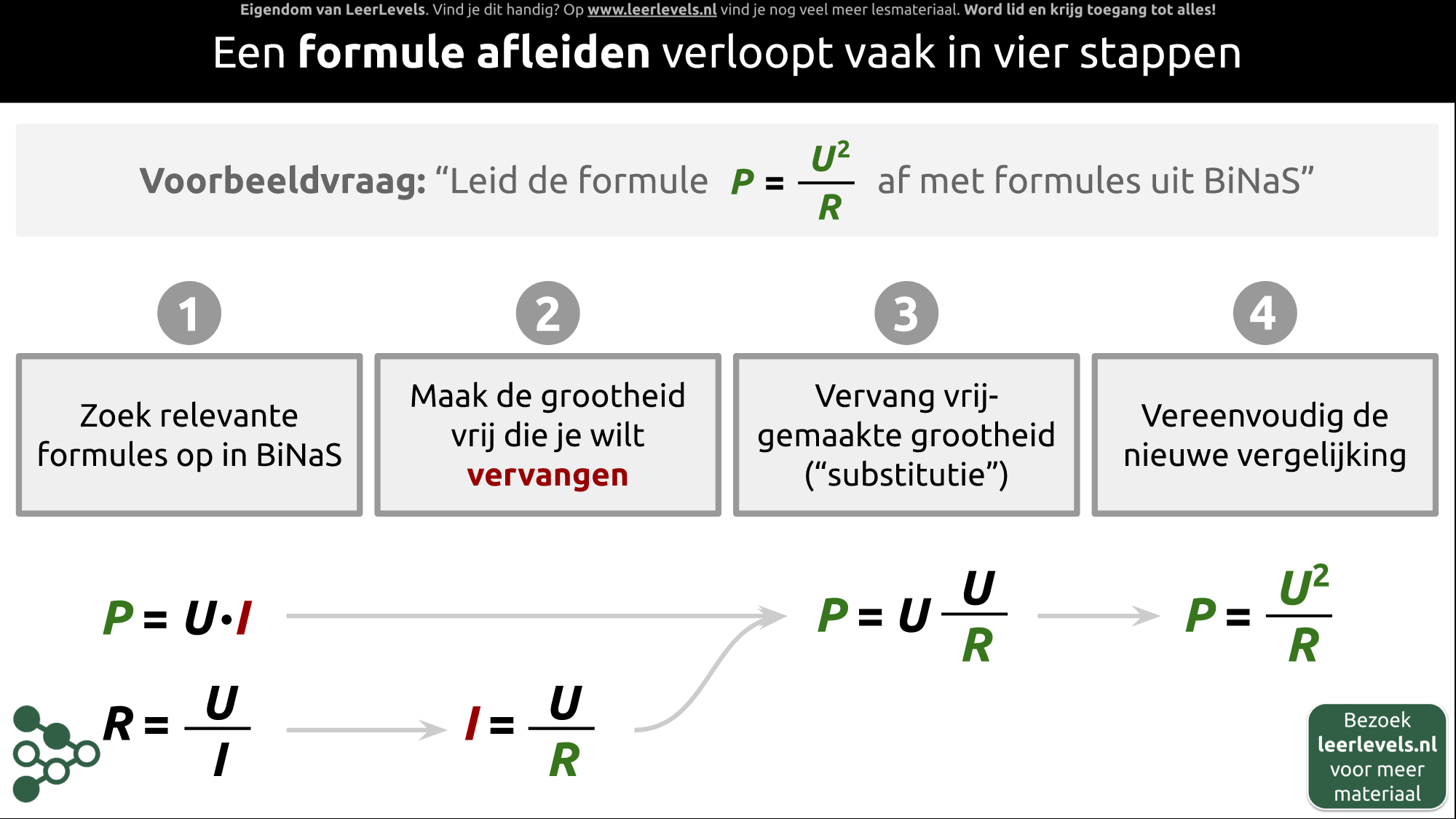
(Afbeelding: Animatie voor Afleiding stappenplan)

Terug naar overzicht Meld je aan

Stelling van Pythagoras

Stelling van Pythagoras formule

De stelling van Pythagoras gaat over rechthoekige driehoeken. Dit zijn driehoeken met een hoek van 90 graden. In zo'n driehoek kun je de lengte van een zijde berekenen met de formule: A² + B² = C². Hierin zijn A en B de lengtes van de rechte zijden en C de lengte van de schuine zijde. Je kunt de stelling van Pythagoras begrijpen door te denken aan de oppervlaktes van vierkanten. Bij een driehoek met zijden van lengte 3, 4 en 5 klopt de stelling van Pythagoras: 3² + 4² = 5². Dit geldt voor elke rechthoekige driehoek. Met deze stelling kun je ook een ontbrekende zijde berekenen als je de andere twee zijden weet. Bijvoorbeeld, als je B en C weet, kun je A berekenen.

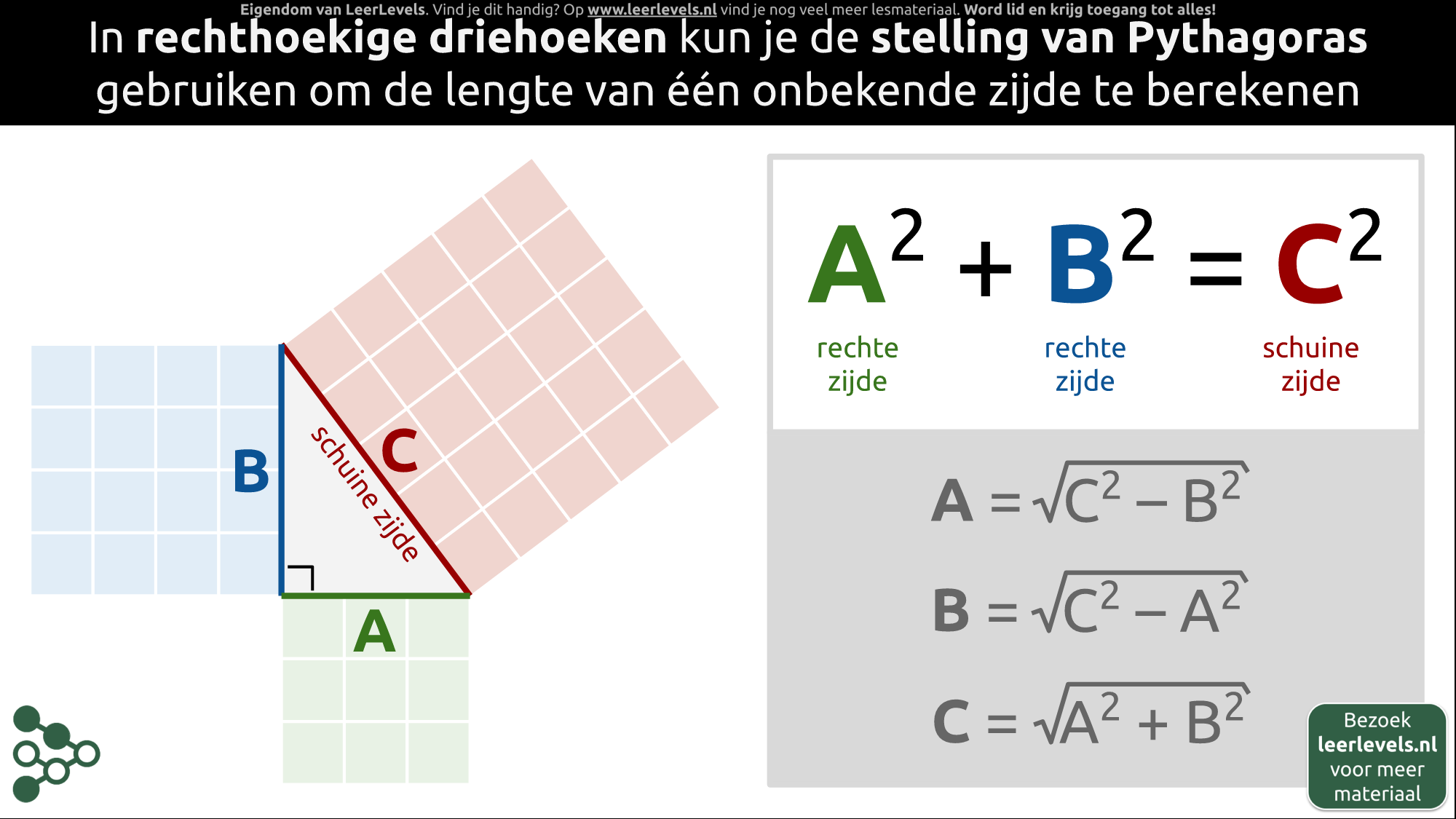
(Afbeelding: Animatie voor Stelling van Pythagoras formule)

Terug naar overzicht Meld je aan

Stern-Gerlach-experiment

Het Stern-Gerlach-experiment dat in 1922 werd uitgevoerd, toonde aan dat deeltjes een gekwantiseerde magnetische eigenschap hebben.

Het idee was om deeltjes, zoals een bundel zilveratomen in dit geval, te beschouwen als kleine magneetjes met een veronderstelde willekeurige oriëntatie. Door deze bundel af te schieten in een niet-homogeen magnetisch veld, kan de magnetische eigenschap worden onderzocht. Volgens de klassieke mechanica wordt verwacht dat de deeltjes worden afgebogen door de magneet, wat resulteert in een brede verdeling op het scherm. De mate van afbuiging hangt af van de invalshoek van het magneetje op het veld.

Echter, het interessante is dat het experiment iets totaal anders onthulde! De bundel splitste in tweeën en er werden twee stippen op het scherm waargenomen in plaats van een brede verdeling. Blijkbaar heeft deze magnetische eigenschap slechts twee waarden; het is gekwantiseerd. Later is dit experiment herhaald met verschillende soorten deeltjes waarbij soms meerdere stippen zichtbaar werden, maar nooit de klassieke brede verdeling.

Dus, het Stern-Gerlach-experiment toont aan dat deeltjes een gekwantiseerde magnetische eigenschap hebben.

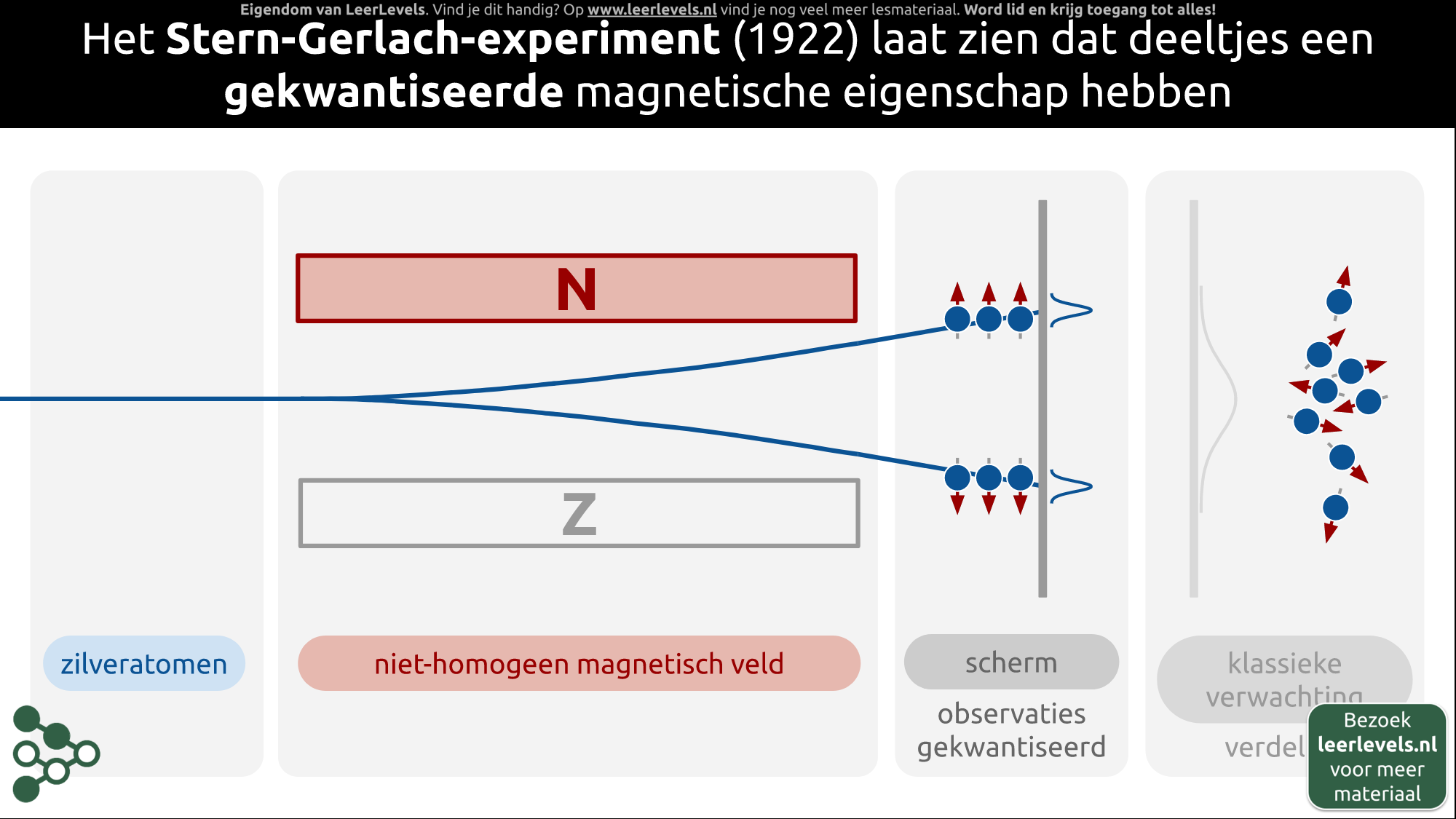
(Afbeelding: Animatie voor Stern-Gerlach-experiment)

Terug naar overzicht Meld je aan

Sterren

Eigenschappen van sterren

Sterrenkundigen gebruiken drie dingen om sterren te categoriseren: de grootte van de ster, de temperatuur en hoeveel licht het uitstraalt. Meestal nemen zij de zon als voorbeeld voor deze drie eigenschappen. Er zijn symbolen bedacht om deze eigenschappen op te schrijven, omdat sterrenkundigen het vaak nodig hebben om ze op te schrijven. Bijvoorbeeld, de grootte van de zon wordt aangeduid met 'R' en een rondje met een stip erin. Deze symbolen worden ook gebruikt voor de temperatuur en hoeveelheid licht om aan te geven dat het om de zon gaat. Als we deze eigenschappen vergelijken met andere sterren zoals Sirius B of Betelgeuse, dan zien we dat deze per ster verschillen. Sirius B heeft bijvoorbeeld een hogere temperatuur dan de zon, ongeveer vier keer zo hoog. Betelgeuse heeft een veel grotere grootte dan de zon, waardoor het 80,000 keer meer licht uitstraalt. Deze eigenschappen helpen sterrenkundigen om sterren te categoriseren.

(Afbeelding: Animatie voor Eigenschappen van sterren)

Terug naar overzicht Meld je aan

Steunvlak

Het steunvlak is het gebied tussen de verst uiteenliggende steunpunten van een voorwerp. Bijvoorbeeld, een stoel rust op vier steunpunten (de poten), en het gebied tussen deze poten is het steunvlak. Hetzelfde geldt voor een camera statief met drie of vier poten. Bij schoenen is het steunvlak het gebied tussen de voorvoet en de hak. Bij een skiër is het steunvlak tussen beide ski's en bij een driewieler heeft de achterkant twee steunpunten en de voorkant één. Het gebied tussen deze punten is het steunvlak. Bij een fiets is het steunvlak niet zozeer een gebied, maar eerder een steunlijn onder de twee wielen.

(Afbeelding: Animatie voor Steunvlak)

Terug naar overzicht Meld je aan

Stopafstand

Stopafstand concept

De stopafstand (sstop) is de afstand die je aflegt als je moet remmen voordat je helemaal stilstaat. Stel dat je aan het fietsen bent en het stoplicht wordt rood. Je blijft nog even doorrijden voordat je begint te remmen. De totale stopafstand is de afstand vanaf het moment dat je het rode licht zag totdat je helemaal stilstaat. De remweg (srem) is alleen de afstand die je aflegt terwijl je werkelijk aan het remmen bent.

Aan het begin van het remmen heb je een constante snelheid. Tijdens de periode dat je het rode licht ziet en nog niet aan het remmen bent, verandert je snelheid niet. Tijdens het remmen vertraag je met een bepaalde negatieve versnelling, maar je snelheid blijft nog steeds positief. Pas als je helemaal stilstaat, zijn zowel de versnelling als de snelheid nul.

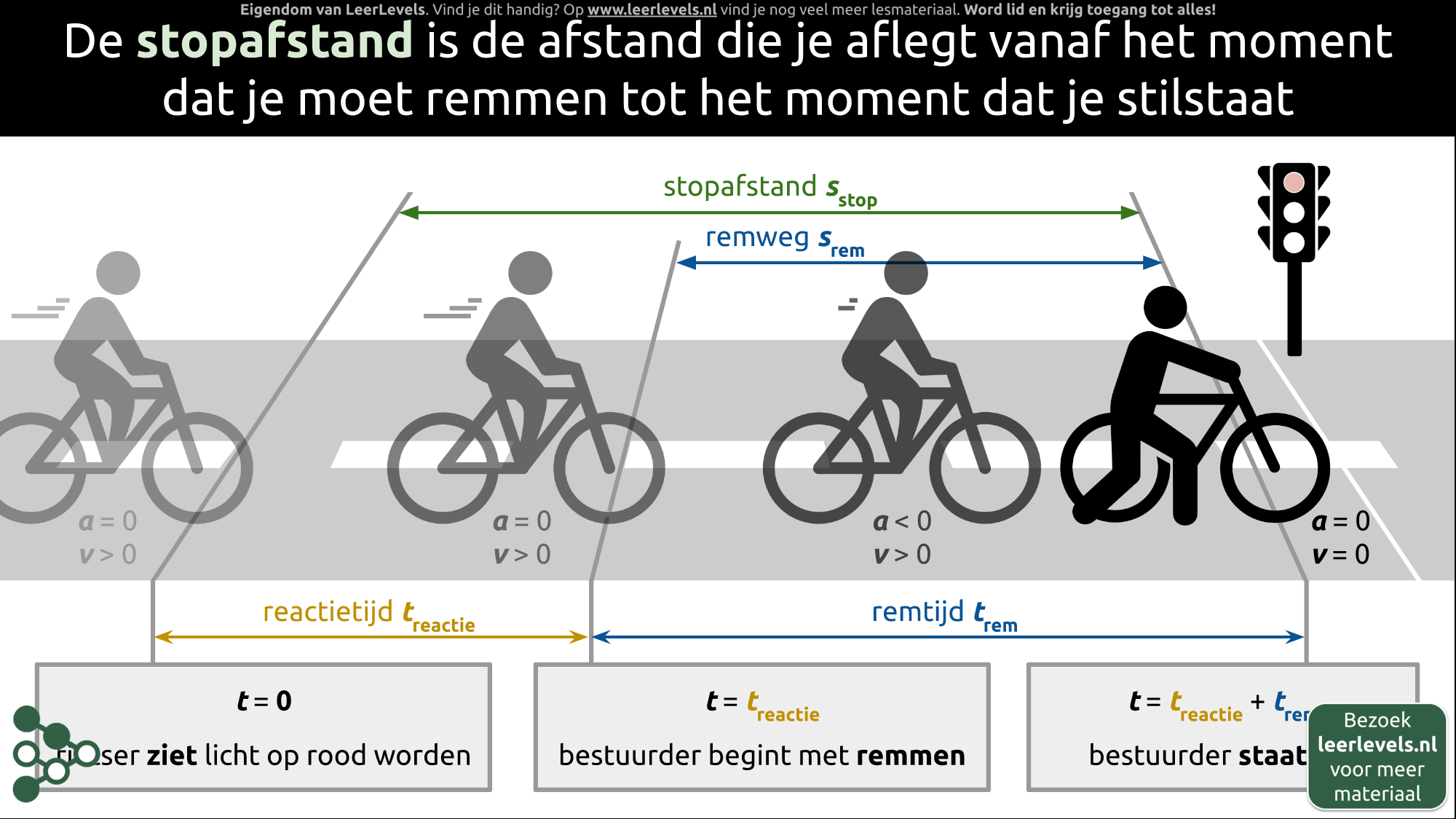
(Afbeelding: Animatie voor Stopafstand concept)

Stopafstand berekenen

Om de stopafstand te berekenen, heb je de beginsnelheid (v0), reactietijd (tr) en de vertraging tijdens het remmen (a) nodig.

Stel dat je met een constante snelheid aankomt bij een stoplicht dat rood wordt, en je dus moet stoppen.
Vervolgens zul je nog een tijdje met dezelfde snelheid doorrijden, namelijk de reactietijd van bijvoorbeeld anderhalve seconde.

Vanaf dat moment hebben we een vertraging van -2,5 m/s². Dit betekent dat de snelheid zal afnemen tot we uiteindelijk stil staan.
Om de remweg te berekenen, kijken we naar het snelheidsverschil gedeeld door de versnelling. In dit geval is dat

(-10)/(-2,5) = 4 s

dus het remmen duurt 4 seconden. Dus na 5,5 s staan we stil.

Als we nu de stopafstand willen berekenen, dan hebben we het oppervlakte onder de grafiek nodig.
Dit kunnen we makkelijk berekenen door eerst naar het rechthoekige oppervlakte te kijken.
Deze oppervlakte heeft een lengte van anderhalve seconde en een hoogte van 10 m/s,
dus komt er een oppervlakte van 15 m uit.
Het oppervlak onder deze driehoek is gelijk aan een half keer 4 seconden keer 10 m/s, dus 20 meter.
Als we willen weten wat de totale stopafstand is, kijken we naar de som van deze oppervlakten.
Dit komt uit op 35 meter.

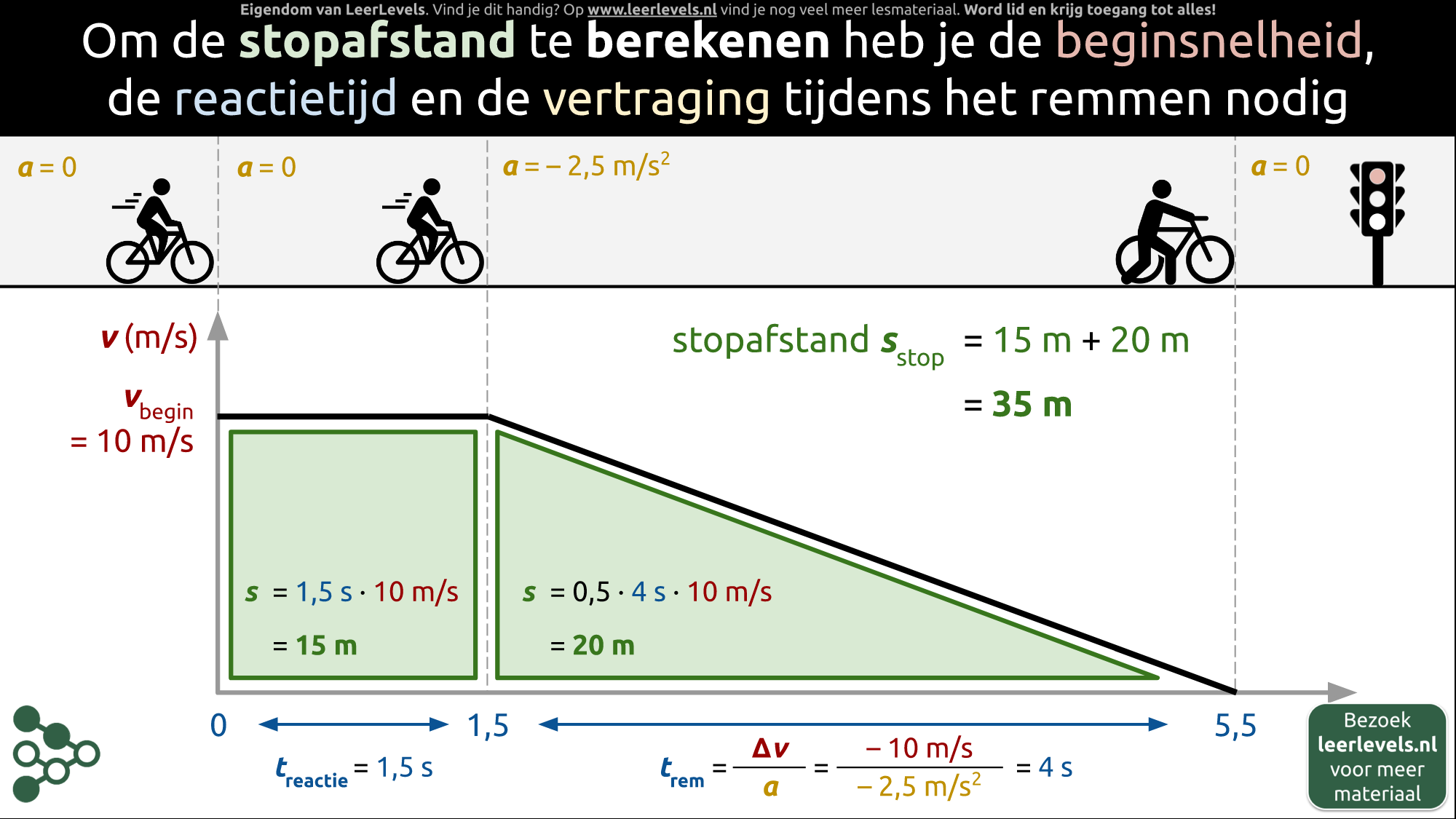
(Afbeelding: Animatie voor Stopafstand berekenen)

Terug naar overzicht Meld je aan

Stralingsenergie

Stralingsenergie komt vrij bij een vervalreactie. Dit kan kinetische energie (alfa en beta) of foton-energie (gamma) zijn. Alfa-deeltjes zijn relatief zwaar en hebben veel energie, zelfs als ze niet snel gaan. Beta-deeltjes zijn veel lichter en bewegen veel sneller. Daarom is de gemiddelde stralingsenergie ongeveer 10 keer kleiner dan bij alfa-deeltjes. Gamma-fotonen hebben geen massa en bewegen met de lichtsnelheid. De hoeveelheid energie hangt af van de frequentie en is gemiddeld zo'n 0,1 MeV bij een vervalreactie.

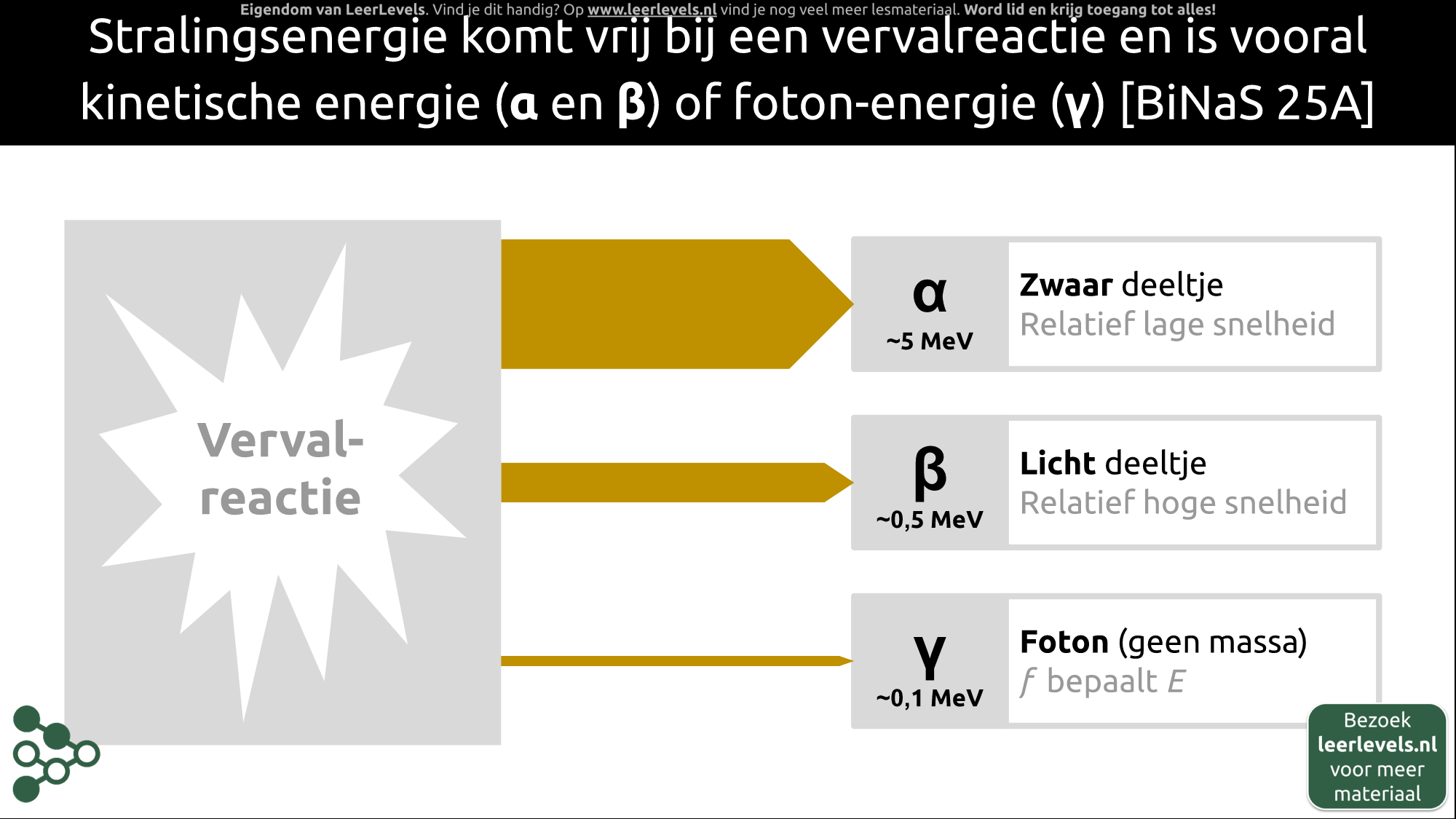
(Afbeelding: Animatie voor Stralingsenergie)

Stralingsenergie formule

Stralingsenergie hangt af van drie dingen: hoeveel energie per deeltje er is, hoeveel deeltjes er vrijkomen per seconde, en hoe lang het proces duurt. De totale stralingsenergie kun je berekenen met de formule: Estr = Edeeltje · A · t. Hierbij druk je de energie uit in Joule, maar soms ook in kleinere eenheden zoals MeV. De activiteit van het proces geef je aan in Bequerel (Bq) en de tijd in seconden (s). Om de stralingsenergie te kunnen berekenen heb je dus deze drie waarden nodig. Dit is eigenlijk best logisch: hoeveel energie wordt er per seconde vrijgegeven en hoelang duurt het proces bij elkaar.

(Afbeelding: Animatie voor Stralingsenergie formule)

Terug naar overzicht Meld je aan

Stralingsevenwicht

Als twee voorwerpen in een afgesloten ruimte dezelfde temperatuur hebben, zenden ze evenveel warmte uit. Als een voorwerp een hogere temperatuur heeft, straalt het meer warmte uit. Dit betekent dat het warmere voorwerp afkoelt terwijl het koelere voorwerp opwarmt door de warmte die het absorbeert. Na verloop van tijd bereiken beide voorwerpen dezelfde temperatuur en stralen ze evenveel warmte uit.

Formules:
- Thermische emissie: P = σ · A · T⁴
- Vermogen: P in Watt
- Stralingsconstante: σ = 5,67 · 10⁻⁸ (W)/(m²K⁴
- Oppervlakte: A in m²
- Temperatuur: T in Kelvin

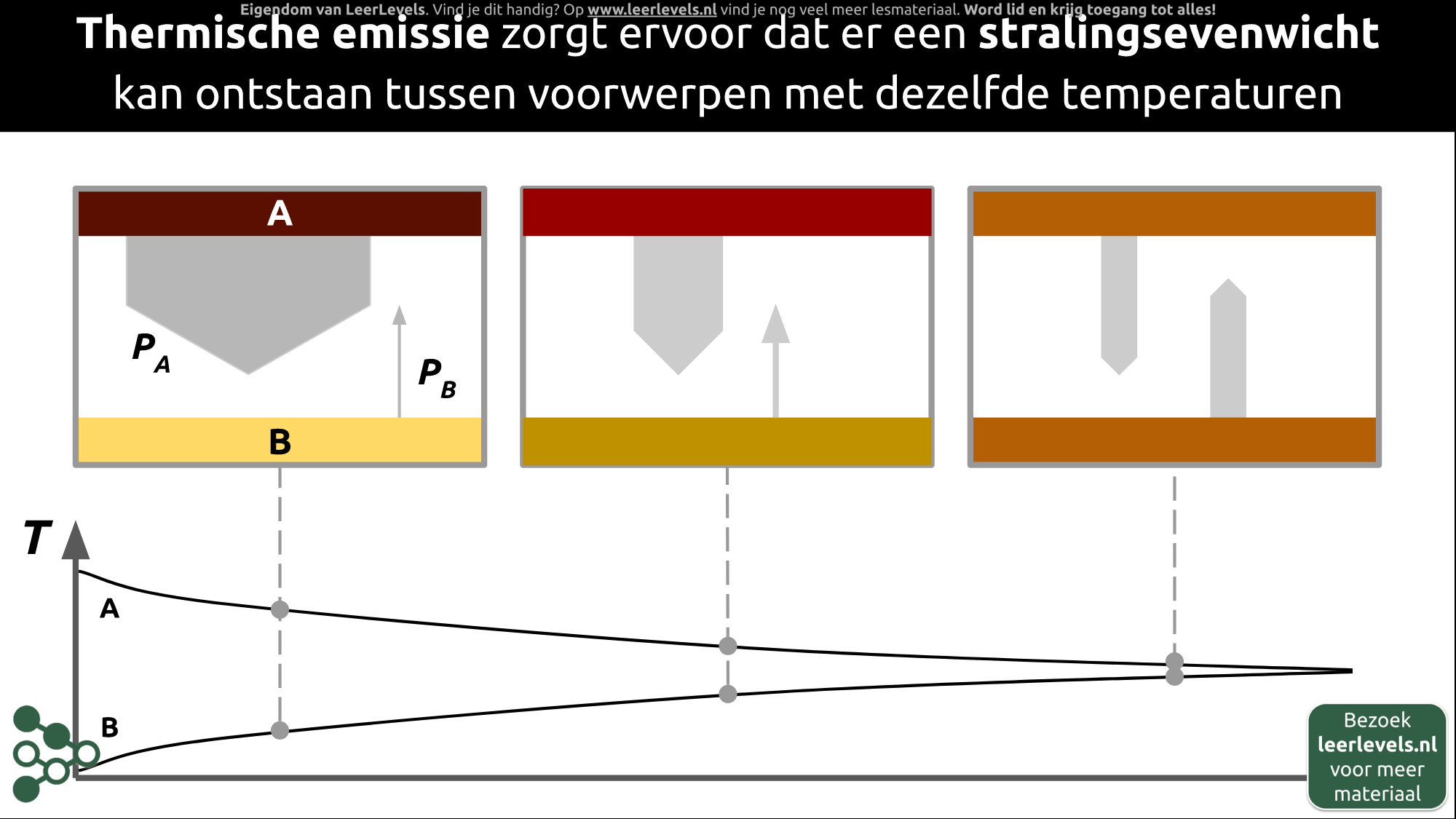
(Afbeelding: Animatie voor Stralingsevenwicht)

Terug naar overzicht Meld je aan

Stroom

Stroom concept

Stroom is een grootheid die aangeeft hoeveel lading er door een schakeling beweegt. Er zijn drie mogelijke toestanden voor de lading. In de eerste toestand blijft de lading op een vaste plek, waardoor er geen stroom is. Wanneer de lading een beetje beweegt, ontstaat er een kleine stroom. Als er veel lading beweegt, is er sprake van een grote stroom. In de praktijk zijn het elektronen die bewegen, maar ze bewegen in de tegenovergestelde richting van de stroomrichting die wij hanteren. Het belangrijkste is dat stroom een grootheid is die aangeeft hoeveel lading er door een schakeling beweegt.

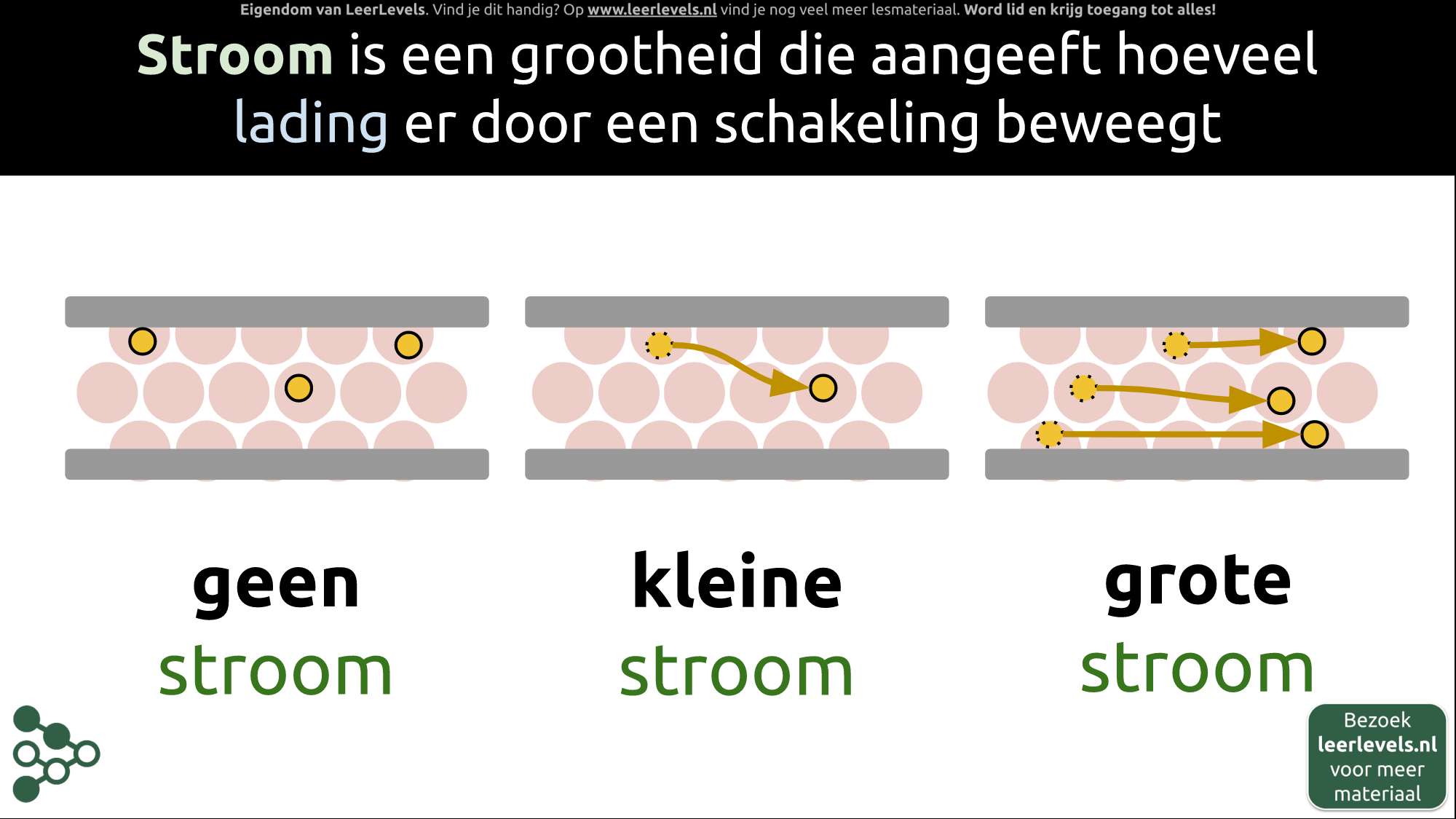
(Afbeelding: Animatie voor Stroom concept)

Stroomkring

De eenvoudigste manier om stroom effectief te laten lopen, bestaat uit drie essentiële onderdelen. Ten eerste is er een spanningsbron nodig die energie levert. Ten tweede zijn er lampjes of andere apparaten die deze energie omzetten. Ten derde is er een gesloten stroomkring nodig. Alleen als de stroomkring gesloten is, kan de stroom daadwerkelijk lopen. Dit betekent dat er een stabiele verbinding tussen alle onderdelen noodzakelijk is om de stroom efficiënt te laten lopen.

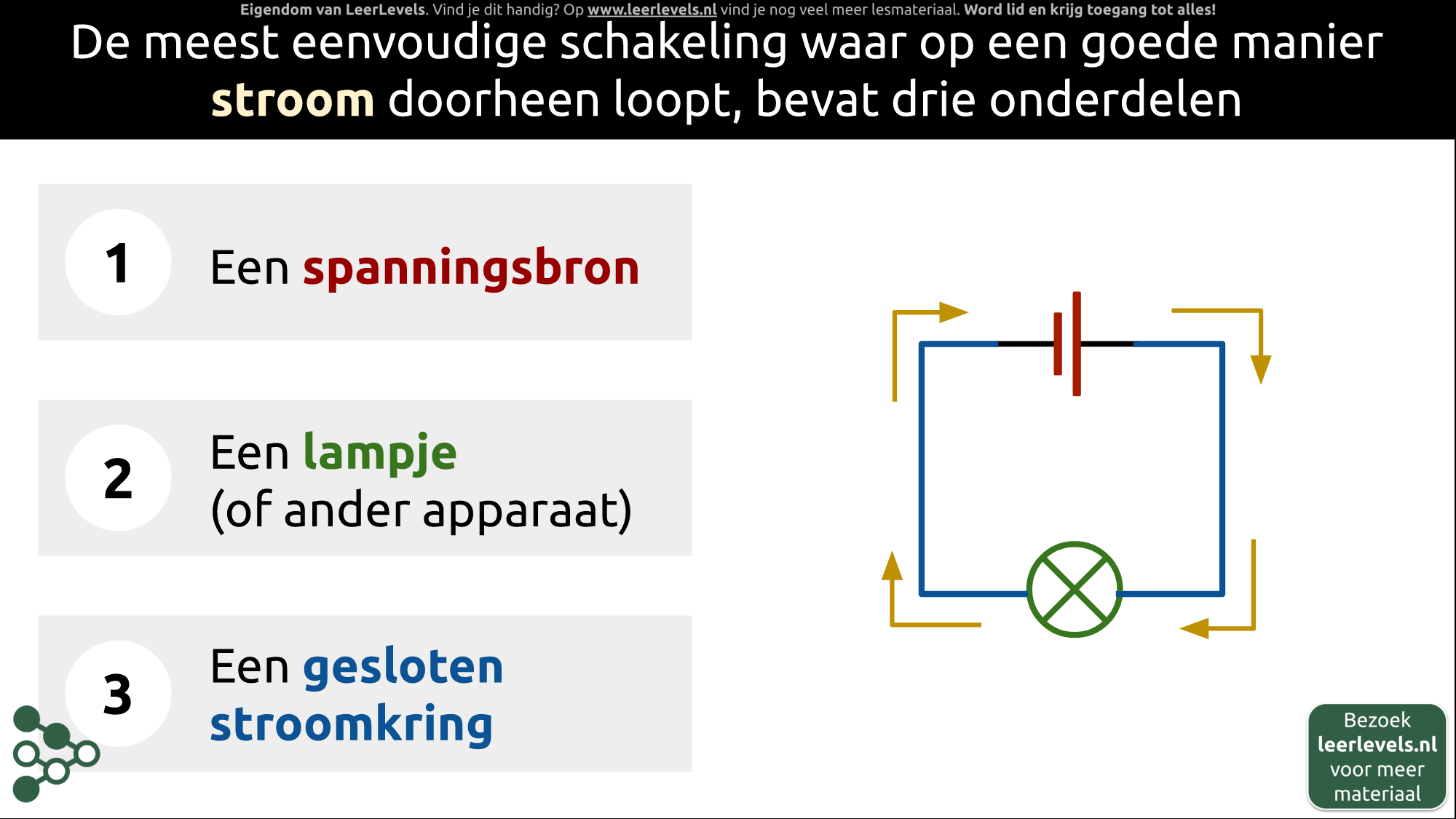
(Afbeelding: Animatie voor Stroomkring)

Terug naar overzicht Meld je aan

Stroomsterkte

Stroomsterkte formule

De elektrische stroomsterkte geeft aan hoeveel elektrische lading er per seconde door een draad of materiaal beweegt. De stroomsterkte wordt gemeten in Ampère (A). De stroomsterkte (I) is afhankelijk van de hoeveelheid lading (Q) en de tijd (t) die nodig is om deze lading te passeren. Dit wordt uitgedrukt met de volgende formule:

I = Q/t

Dus als er meer lading door een punt beweegt of als dit in een kortere tijd gebeurt, zal de stroomsterkte hoger zijn. De lading wordt gemeten in Coulomb (C) en de tijd in seconden (s).

(Afbeelding: Animatie voor Stroomsterkte formule)

Terug naar overzicht Meld je aan

Tandwieloverbrenging

Tandwieloverbrenging concept

Een tandwieloverbrenging is een manier om beweging over te brengen zonder slip en om de snelheid te veranderen door tanden te tellen. Als er bijvoorbeeld een tandwiel met 10 tanden is en het draait 4 rondjes per seconde, dan passeren er 40 tanden op een gegeven punt. Als je een tweede tandwiel aansluit, met ook 10 tanden, zal het ook 4 rondjes per seconde draaien. Maar als het tweede tandwiel slechts 5 tanden heeft, dan moet het sneller bewegen om dezelfde hoeveelheid tandjes in dezelfde tijdseenheid te passeren. Dan draait het tweede tandwiel 8 rondjes per seconde. Door een groter tandwiel aan te sluiten, kan je de snelheid verlagen. Tandwielen kunnen ook worden verbonden met een ketting in plaats van rechtstreeks, maar het resultaat is hetzelfde. Let op dat de tandwielen tegen elkaar in draaien.

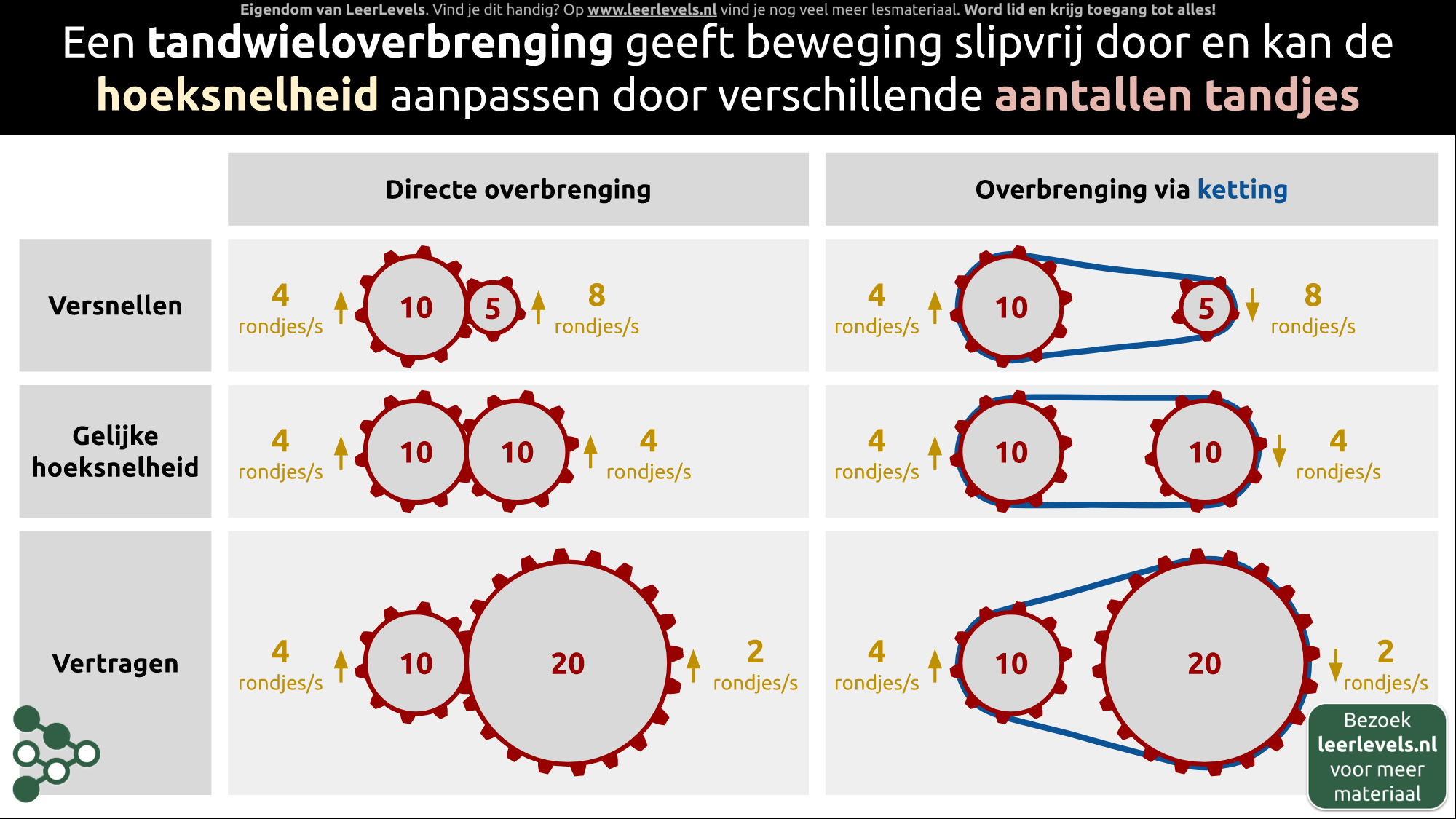
(Afbeelding: Animatie voor Tandwieloverbrenging concept)

Terug naar overzicht Meld je aan

Tekenen

Tekenen bij natuurkunde

Schetsen, tekenen en construeren zijn verschillende manieren om iets weer te geven. Schetsen is een ruwe tekening waarbij niet alle details noodzakelijk zijn, als het maar duidelijk is wat bedoeld wordt. Tekenen doe je nauwkeuriger, zoals bij het maken van een grafiek waarbij de juiste grootheden en eenheden op de assen staan. Bij construeren gebruiken we hulpmiddelen zoals een geodriehoek om loodrechte hoeken te maken en parallelle lijnen te trekken. De formules en grootheden zijn belangrijk, bijvoorbeeld bij het berekenen van de veerkracht door de uitrekking van de veer te meten. Hulplijnen kunnen helpen bij het construeren van de spankracht van een touw. Als je iets moet schetsen, hoef je alleen de basis weer te geven. Bij tekenen moet je nauwkeuriger zijn en bij construeren gebruik je hulpmiddelen om preciezer te werken.

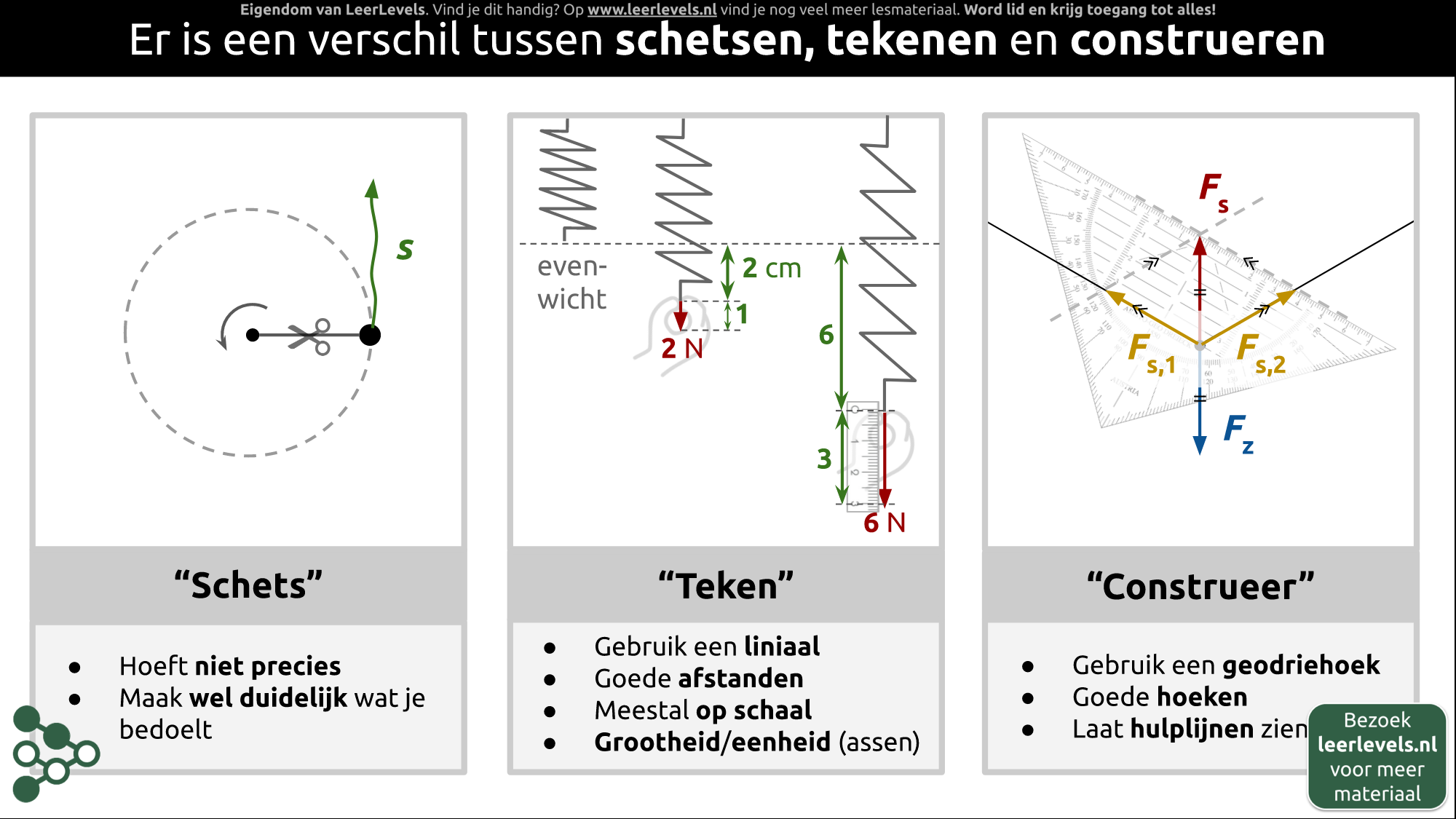
(Afbeelding: Animatie voor Tekenen bij natuurkunde)

Terug naar overzicht Meld je aan

Temperatuur

Temperatuurschalen

Temperatuur heeft te maken met hoe snel moleculen zich bewegen. Meestal zeggen we 'warm' of 'te koud' als we het over de temperatuur hebben. We meten temperatuur in graden Celsius, waarbij 0 graden Celsius het punt is waarop water bevriest en 100 graden Celsius het punt is waarop het kookt. 20 graden Celsius is normaal voor kamertemperatuur. Als water afkoelt, bewegen de moleculen steeds langzamer en kan het van vloeibaar naar vast veranderen. Bij de absolute nulstand stopt alle beweging van deeltjes. Deze temperatuur is gemeten op -273 graden Celsius, maar we noemen dit gewoon 0 graden Celsius. In de natuurkunde gebruiken we Kelvin als standaardeenheid, waarbij 0 Kelvin gelijk is aan de absolute nulstand. Het temperatuurverschil tussen kamertemperatuur en het kookpunt van water is 80 graden in zowel graden Celsius als Kelvin. Dit verschil noemen we delta T. Om graden Celsius in Kelvin te veranderen, voegen we 273 toe aan de temperatuur.

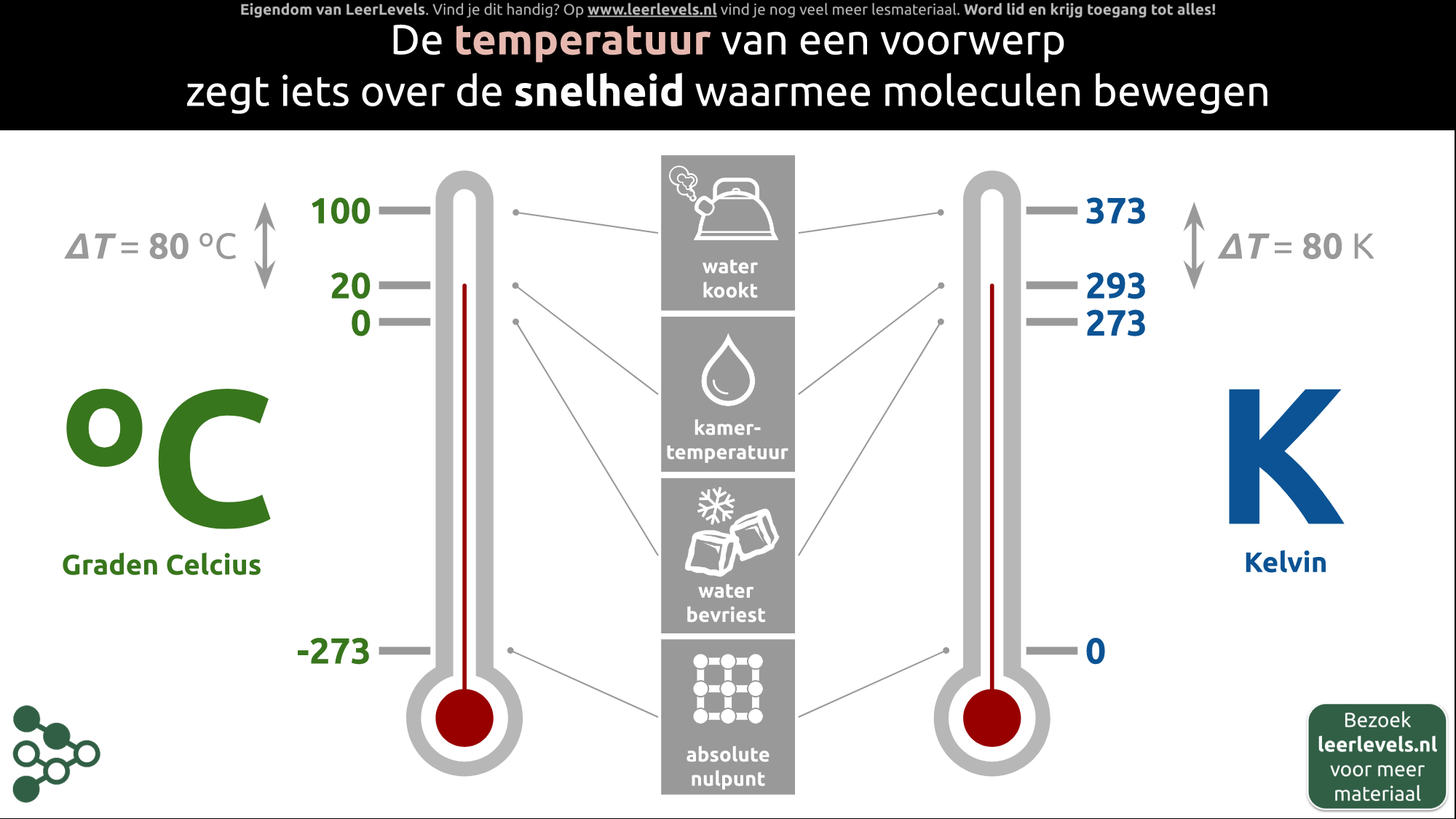
(Afbeelding: Animatie voor Temperatuurschalen)

Terug naar overzicht Meld je aan

Tijd

Tijd concept

Tijd is iets wat ervoor zorgt dat gebeurtenissen na elkaar plaatsvinden. Het is eigenlijk de vierde dimensie, naast lengte, breedte en hoogte. Door tijd kunnen we terugkijken naar het ontstaan van ons heelal zo'n 14 miljard jaar geleden. De aarde ontstond daarvan weer ongeveer 4,5 miljard jaar geleden en de homo sapien bestaat al zo'n 200,000 jaar. De boekdrukkunst is pas zo'n 600 jaar geleden uitgevonden, en maar een klein deel van de mensheid heeft hier gebruik van kunnen maken. Het internet bestaat nu ongeveer 50 jaar, maar pas in 1991 werd het wereldwijde web gelanceerd. Dit alles gebeurde na elkaar, omdat tijd ervoor zorgt dat gebeurtenissen niet allemaal op hetzelfde moment gebeuren.

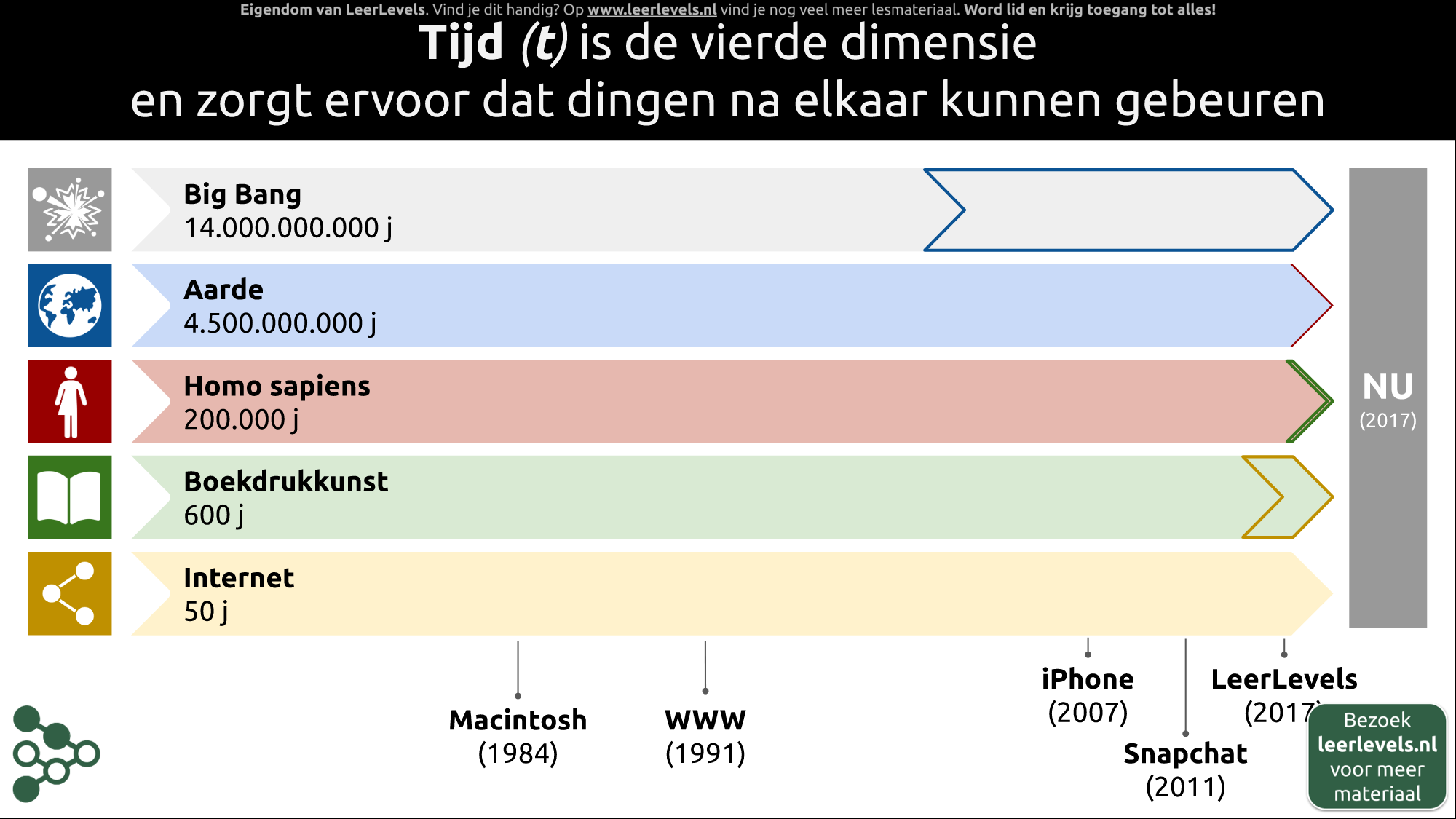
(Afbeelding: Animatie voor Tijd concept)

Eenheid seconde

Een 'seconde' (s) is een term die we gebruiken om tijd te meten. Vroeger was een seconde gebaseerd op de zonnedag, wat de tijd was tussen zonsopkomst en de volgende zonsopgang. Een dag was verdeeld in 24 uur, elk uur in 60 minuten en elke minuut in 60 seconden, wat resulteerde in 86,400 seconden per dag. Maar het bleek dat dagen soms langer of korter duren, waardoor het moeilijk was om een exacte definitie van een seconde te geven. Nu is een seconde gebaseerd op de trillingen van een atoom van cesium-133. Deze trillingen creëren golven en de periode tussen twee opeenvolgende golven is gedefinieerd als de trillingstijd van cesium-133. Een seconde is gedefinieerd als de tijd die nodig is voor 9,192,631,770 trillingen van cesium-133.

(Afbeelding: Animatie voor Eenheid seconde)

Terug naar overzicht Meld je aan

Tralie

Tralie concept

Bij een tralie kunnen golven constructief en destructief interfereren.

Een tralie bestaat uit een reeks parallelle spleten met een tussenafstand van d. Wanneer je er met een laser op schijnt, treedt buiging op bij elke spleet. Elke spleet kan worden beschouwd als een puntbron waarbij de golven elkaar beïnvloeden. Dit fenomeen is vergelijkbaar met dat van een dubbelspleet, maar dan met meerdere puntbronnen.

De dikte van de laserbundel zal meestal ongeveer 1 mm zijn, terwijl de tussenafstand d veel kleiner is, vaak in micrometers, dus 1000 keer zo klein. De golflengte van het licht moet klein zijn ten opzichte van d, meestal is dit enkele honderden nanometers. Het scherm bevindt zich meestal op een afstand van minstens één meter.

Bij dit experiment zie je een stip in het midden van het scherm, ook wel het 0e orde maximum genoemd. Dit komt doordat de golven van alle puntbronnen hier in fase aankomen en elkaar versterken, wat resulteert in constructieve interferentie. Iets boven en onder het midden zijn nog meer versterkingen te zien, dit zijn de 1e orde maxima. Verder naar buiten bevindt zich het 2e orde maximum. Tussen de maxima zie je donkere plekken op het scherm, dit zijn de minima. Hier treedt destructieve interferentie op en doven de golven elkaar uit.

Bij een tralie kunnen golven dus zowel constructief als destructief interfereren.

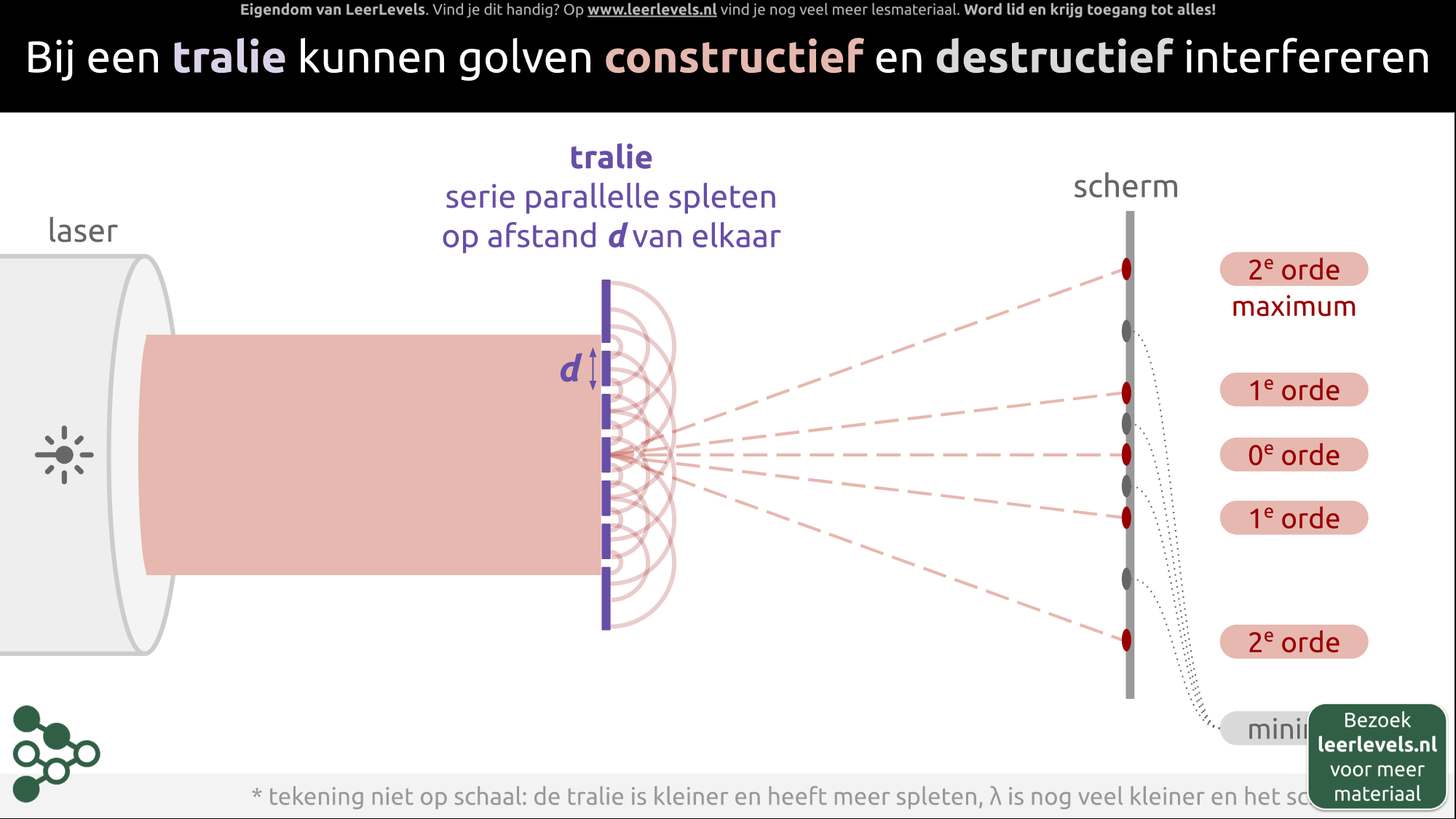
(Afbeelding: Animatie voor Tralie concept)

Tralie formule afleiding

Als licht door twee spleten schijnt, kan er een patroon ontstaan van lichte en donkere strepen. Dit komt door de manier waarop de lichtgolven elkaar beïnvloeden. Als de afstand tussen de spleten en de afstand die het licht aflegt verschillen met een veelvoud van de golflengte van het licht, dan ontstaat er een heldere plek. Dit noemen we constructieve interferentie.

Om te bepalen of er constructieve interferentie plaatsvindt onder een bepaalde hoek, moeten we kijken of de lichtgolven op dezelfde plek pieken en dalen hebben. Als dat zo is, is er constructieve interferentie. De afstand tussen de spleten noemen we Δ x.

Voor twee golven die in fase lopen geldt Δ x = n · λ, waarin n een geheel getal is en λ de golflengte van het licht. Als we de afstand tussen twee spleten d noemen en de hoek waaronder interferentie optreedt α, dan volgt uit goniometrie:

sin(α) = (n · λ)/(d)

Onder elke hoek α die voldoet aan deze formule, is er constructieve interferentie.

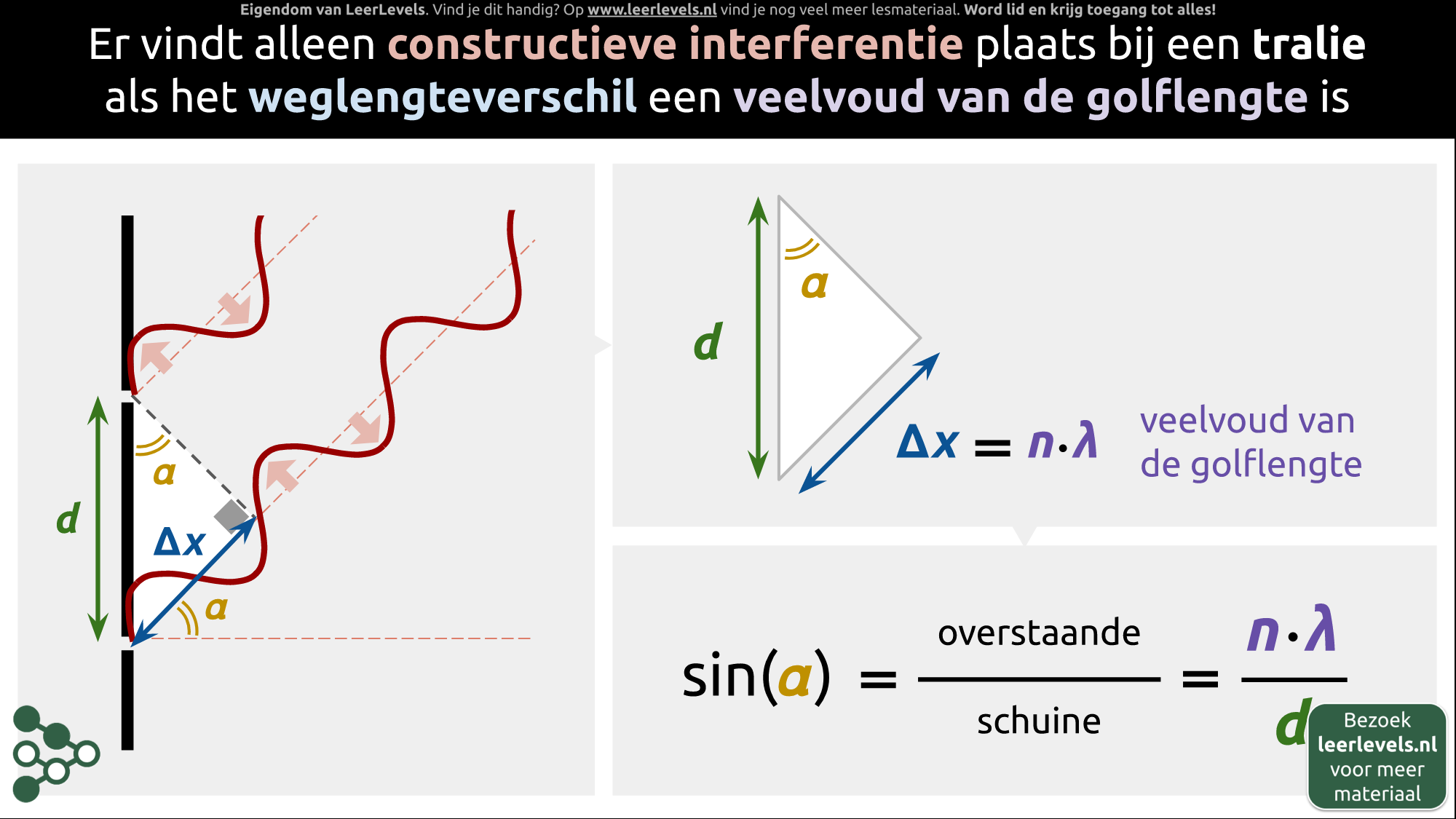
(Afbeelding: Animatie voor Tralie formule afleiding)

Tralie formule

De hoeken waarbij constructieve interferentie optreedt, zijn afhankelijk van de golflengte en de tralieconstante.

In formulevorm:

sin(αn) = (n · λ)/(d)

Hierbij is αn de hoek in graden waaronder het n-de maximum zichtbaar is. De parameter n is de index van het maximum: 0, 1, 2, enzovoort. De grootheid λ staat voor de golflengte in meter en d is de tralieconstante, eveneens in meter. De tralieconstante verwijst naar de afstand tussen de spleten in een tralie, wat een zeer klein getal kan zijn, variërend van enkele micrometers tot zelfs kleiner.

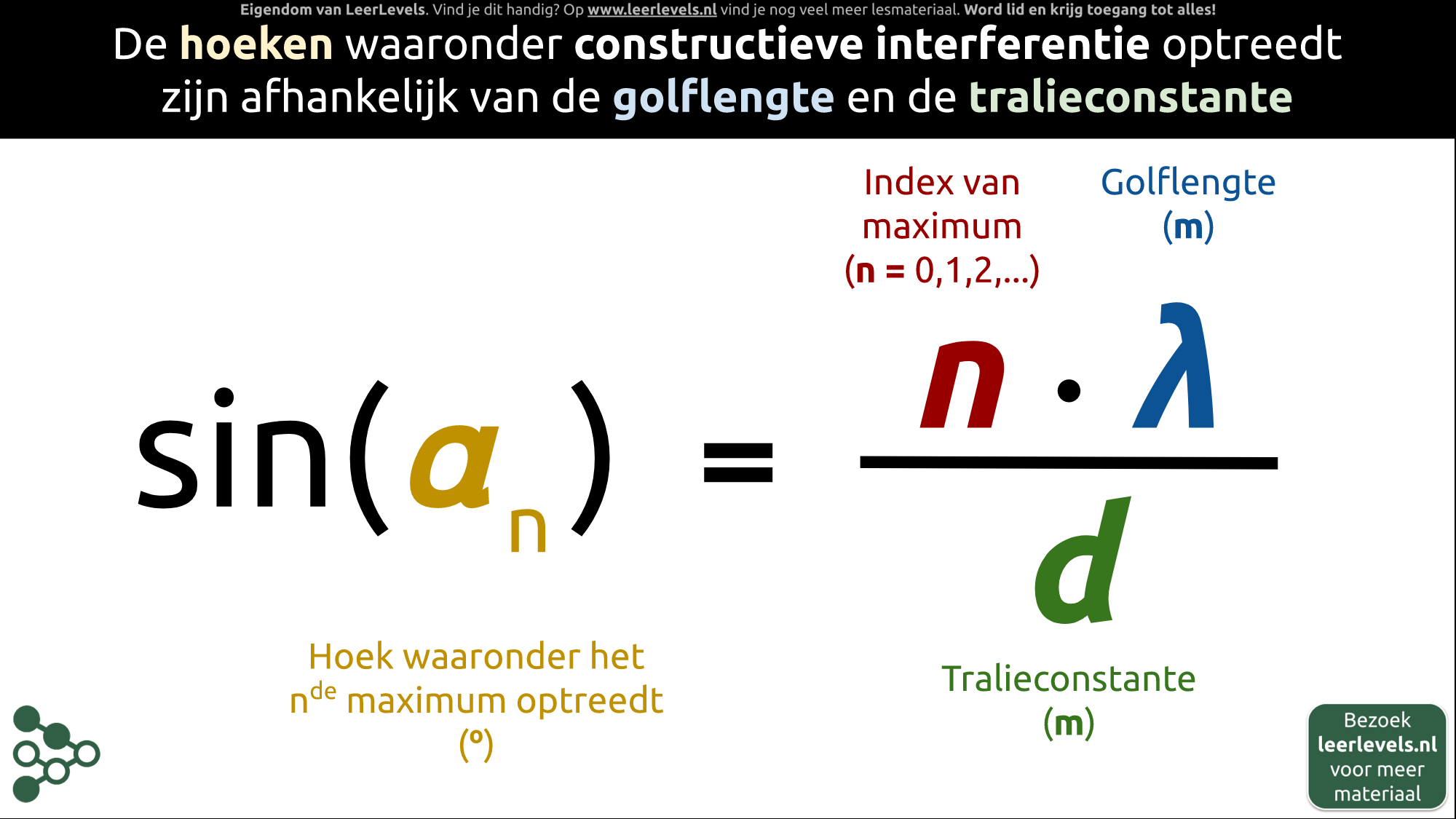
(Afbeelding: Animatie voor Tralie formule)

Terug naar overzicht Meld je aan

Transferbaan

Een transfer baan, ook wel Hohmann baan genoemd, is een handige manier om een satelliet hoger in de ruimte te brengen. Dit doen we in 5 stappen. Eerst lanceren we de satelliet vanaf de aarde naar een parkeerbaan dicht bij de aarde. Daarna geven we de satelliet een extra zetje in snelheid en plaatsing, zodat hij in een grotere ellipsvormige baan terechtkomt. Dit stuk noemen we de transfer baan. Op de juiste afstand van de aarde geven we de satelliet nog een extra zetje in snelheid, zodat hij in een stabiele baan blijft. Dit kan een geostationaire baan zijn, of een andere hogere baan. Door deze twee extra zetjes komt de satelliet hoger in de ruimte.

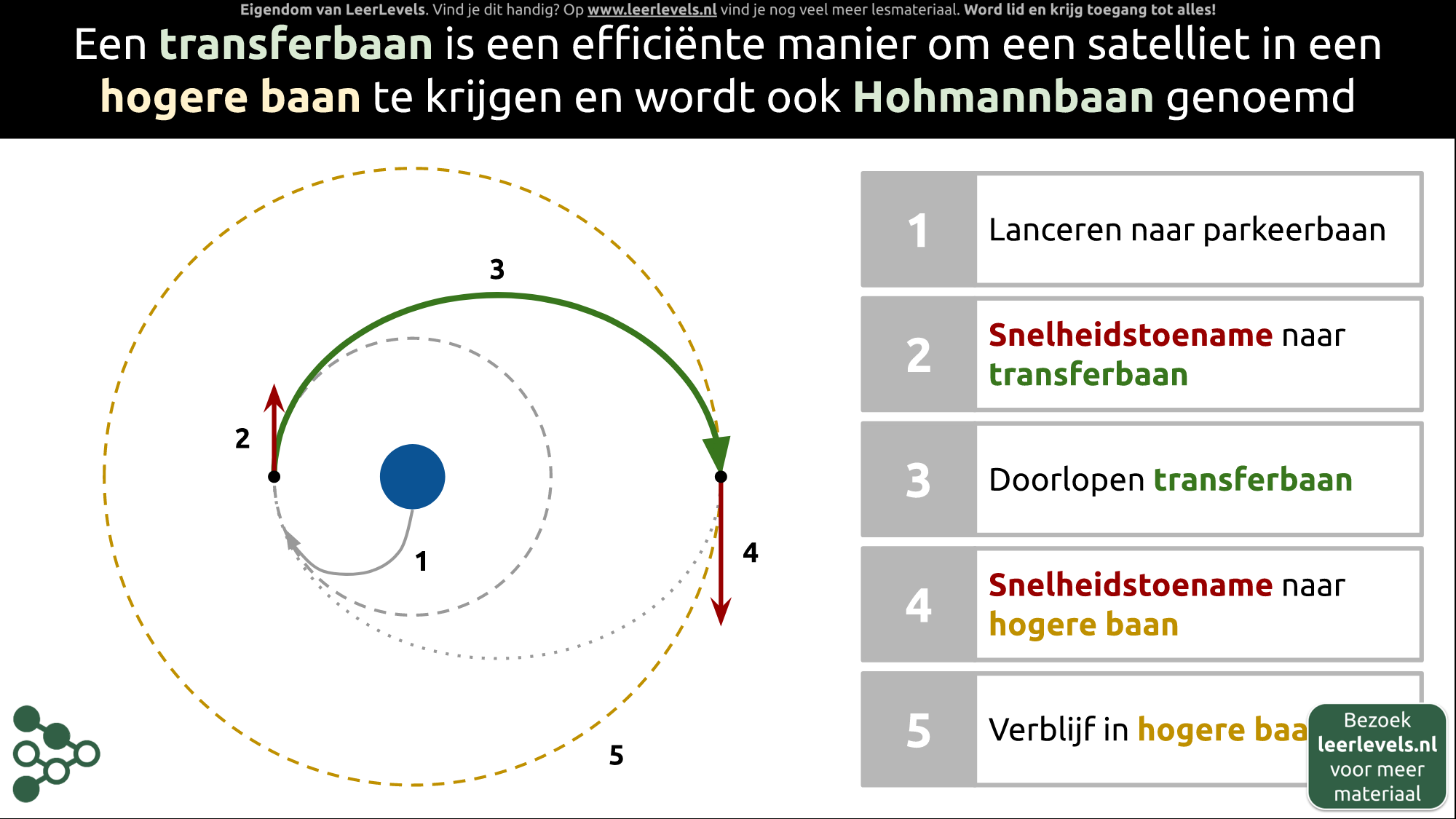
(Afbeelding: Animatie voor Transferbaan)

Terug naar overzicht Meld je aan

Transformator

Transformator werking

Een transformator maakt gebruik van het principe van elektromagnetisme en inductie. Hij bestaat uit een weekijzeren kern en twee spoelen. De primaire spoel bevindt zich aan de linkerkant en de secundaire spoel aan de rechterkant. Wanneer er een wisselspanning op de primaire spoel wordt aangesloten, ontstaat er een wisselend magnetisch veld. Dit magnetisch veld wordt door de weekijzeren kern geleid naar de secundaire spoel. Het wisselende magnetische veld induceert een spanning in de secundaire spoel. De opgewekte spanning is afhankelijk van het aantal windingen; door het aantal windingen van de primaire (Np) en secundaire (Ns) spoel te variëren, kan de spanning groter of kleiner worden gemaakt. Dus, een transformator maakt gebruik van het principe van elektromagnetisme en inductie.

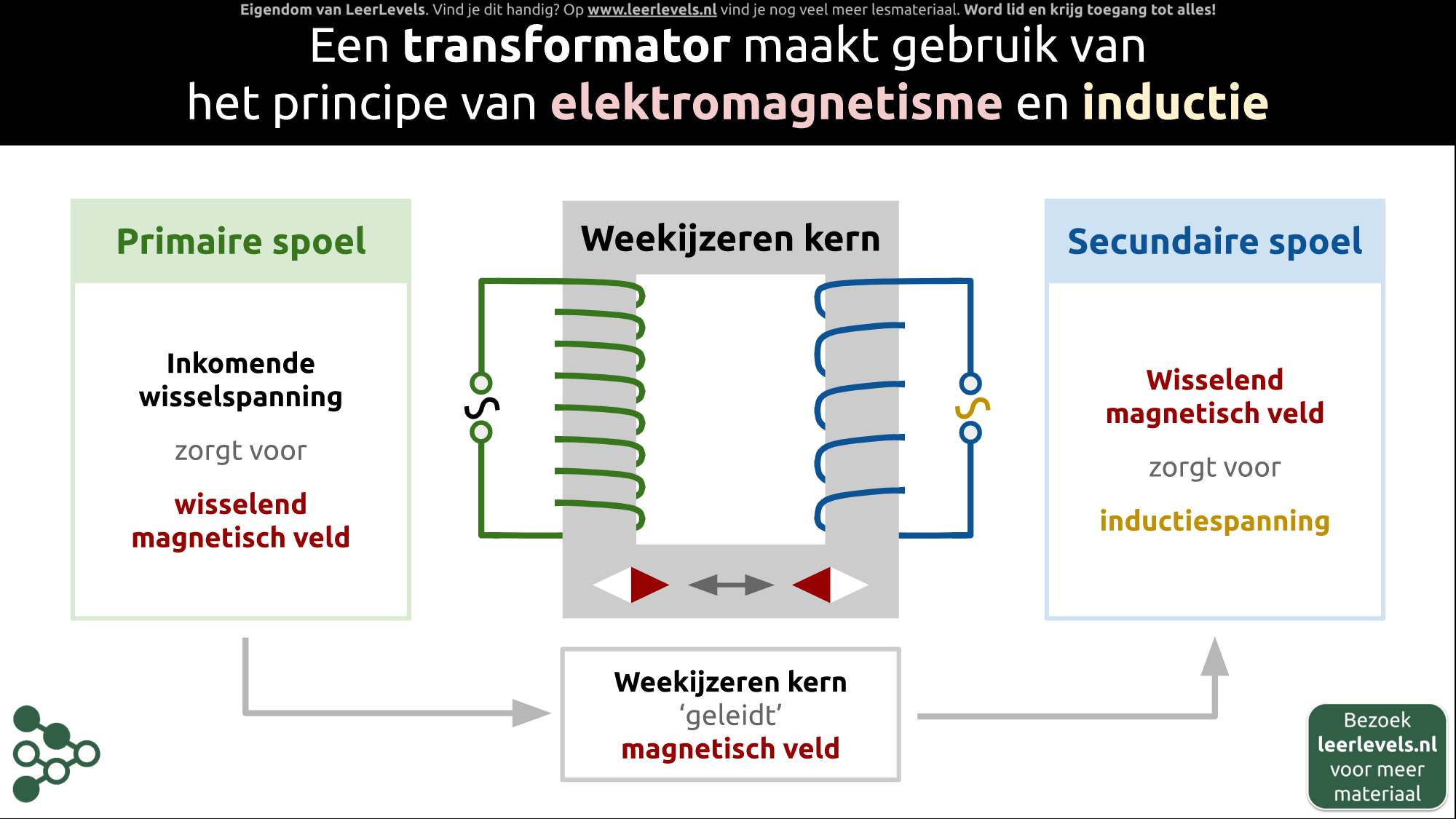
(Afbeelding: Animatie voor Transformator werking)

Terug naar overzicht Meld je aan

Trilling

Een trilling is een beweging die steeds weer herhaald wordt. Er zijn twee bekende voorbeelden van trillingen: de schommel en het massa-veersysteem. Bij de schommel beweeg je van de ene uiterste stand naar de andere en weer terug. Bij het massa-veersysteem breng je de massa omhoog, valt deze naar beneden en wordt daarna weer omhoog getrokken door de veer. Dit herhaalt zich steeds weer. Soms wordt de beweging gestopt door bijvoorbeeld wrijving. De trilling verdwijnt dan totdat de beweging stopt in de evenwichtsstand. Maar in principe blijft het steeds een herhaaldelijke beweging.

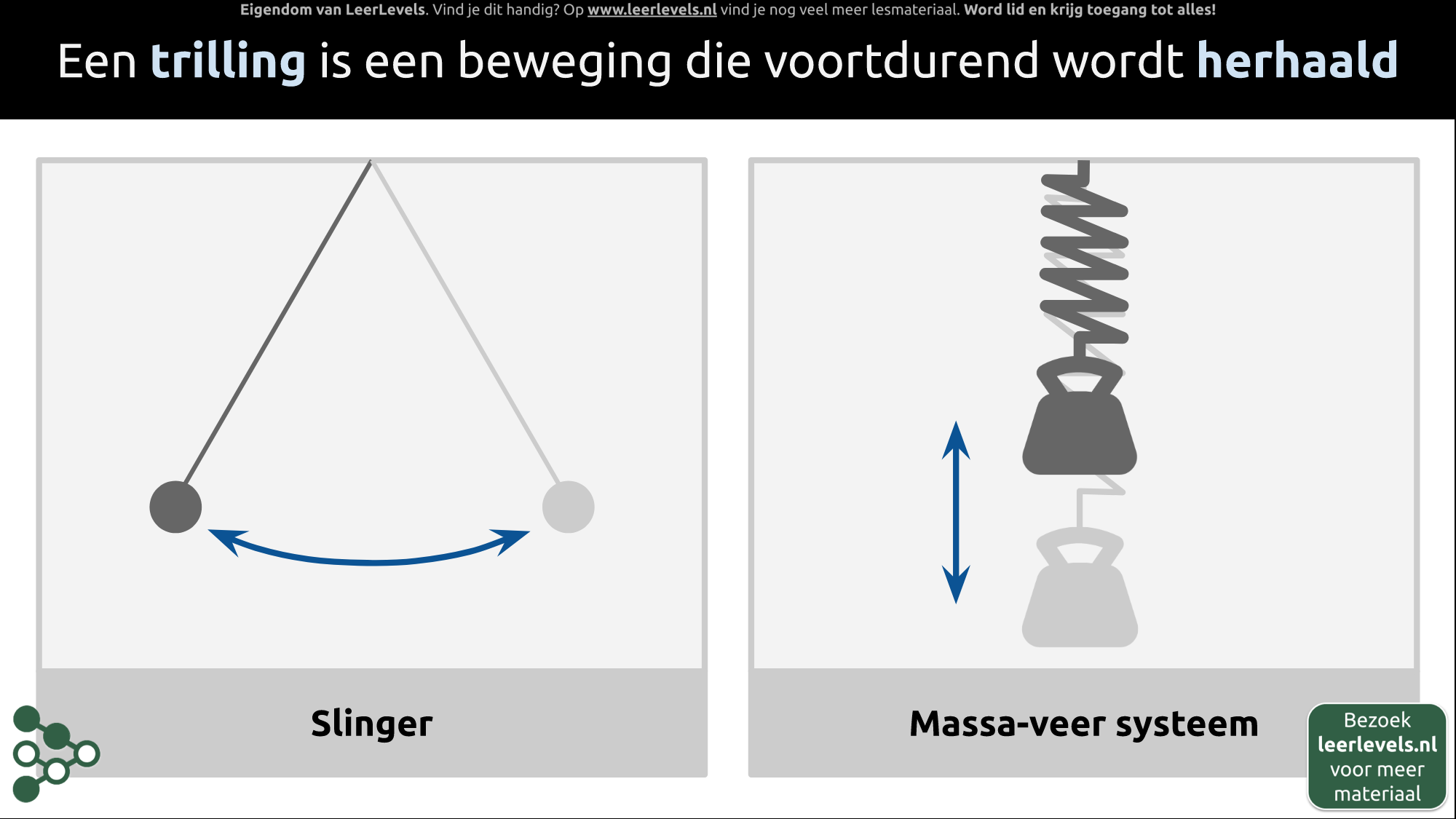
(Afbeelding: Animatie voor Trilling)

Trilling weergeven

Een ut-diagram laat de beweging van een trilling zien. Bijvoorbeeld als je kijkt naar de beweging van een massa-veer-systeem en je kiest ervoor dat de massa van -20 tot 20 centimeter gaat bewegen, dan kun je dit in een ut-diagram laten zien. Ook de tijd wordt in seconden aangegeven op de groene as. Zo krijg je een beeld van de beweging van de massa. De massa begint op het laagste punt en zal door de veerkracht omhoog gaan. Na een bepaalde tijd is de massa bijvoorbeeld op het hoogste punt aangekomen en zal de snelheid langzaam afnemen. Uiteindelijk komt de massa weer bij het laagste punt. Dit proces zal zich blijven herhalen totdat er demping optreedt. In het ut-diagram kun je ook de amplitude van de trilling en de trillingstijd zien. Amplitude is de afstand tussen de evenwichtsstand (het midden) en de uiterste stand van de massa. Trillingstijd is de tijd die nodig is om een volledige trilling uit te voeren.

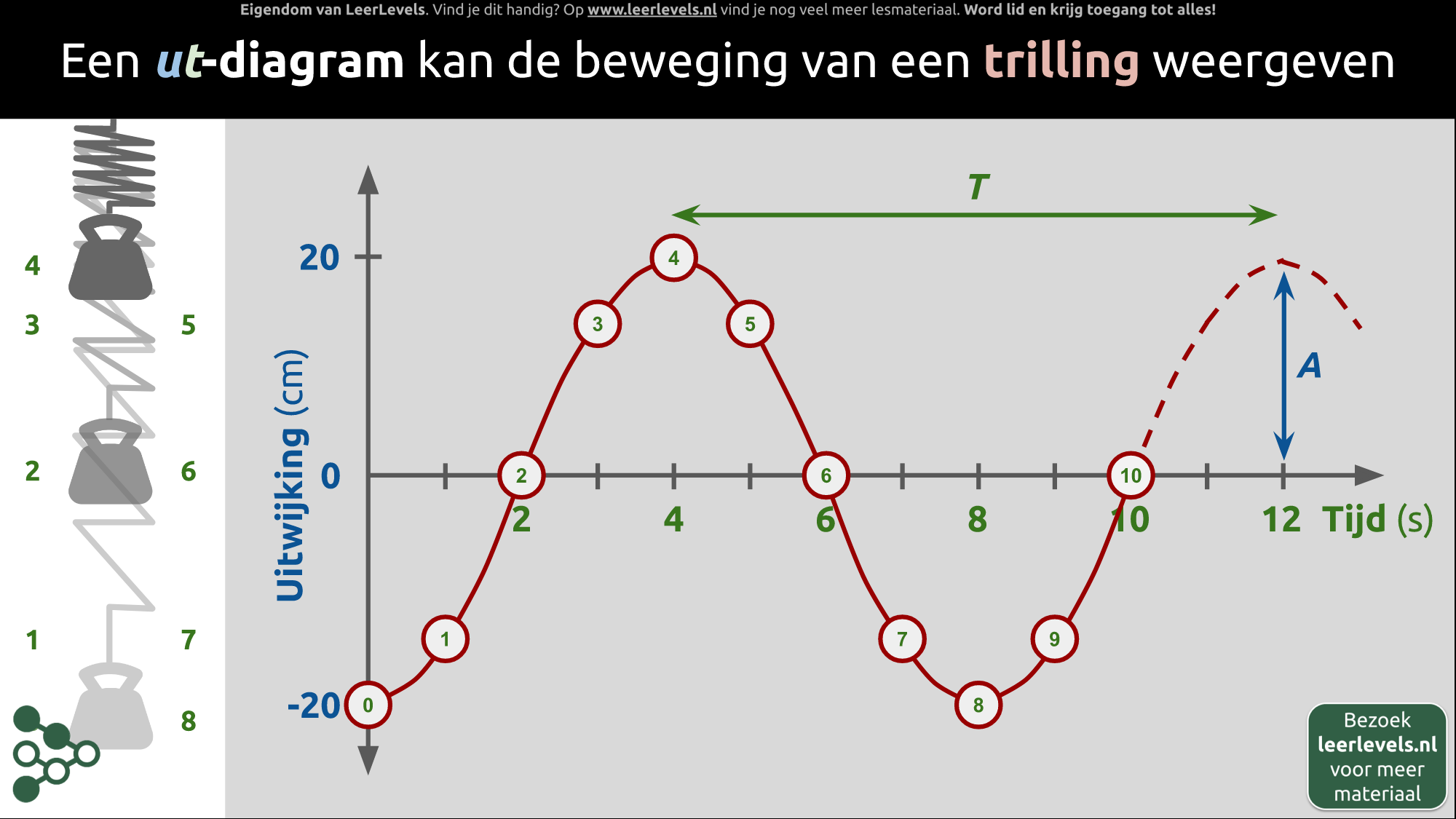
(Afbeelding: Animatie voor Trilling weergeven)

Terug naar overzicht Meld je aan

Trillingstijd

De trillingstijd T, ook wel de periode genoemd, geeft de duur aan van een volledige trilling voordat deze opnieuw begint. Neem bijvoorbeeld een slinger. Deze beweegt van de ene uiterste stand naar de andere en weer terug. Deze volledige beweging vormt één trillingstijd. Een ander voorbeeld is een massa-veersysteem. De massa beweegt omhoog en vervolgens weer naar beneden voordat de trilling opnieuw begint. De trillingstijd T is dus de tijd die nodig is om deze volledige beweging te voltooien.

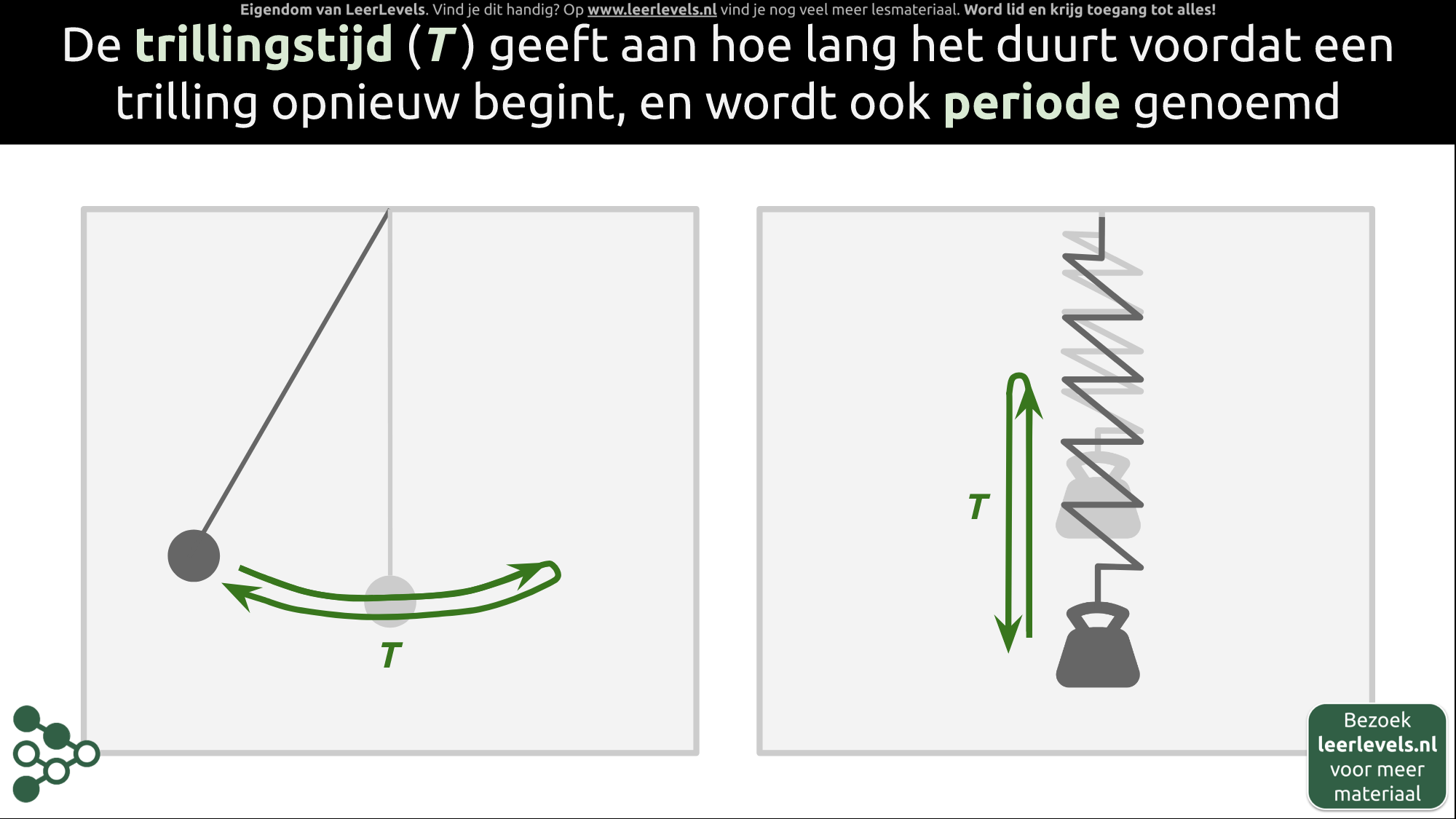
(Afbeelding: Animatie voor Trillingstijd)

Trillingstijd formules

De trillingstijd (t) van sommige schommelingen kan je berekenen als je de juiste informatie hebt over het systeem. Zo kan je bijvoorbeeld kijken naar een slinger om te weten hoe lang de trilling duurt. De trillingstijd kan je berekenen met de formule t = 2π√( l/g ), waarbij l de lengte is van de slinger in meters en g de zwaartekrachtversnelling van 9,81 m/s² op aarde is. In deze formule wordt de massa van de slinger meestal verwaarloosd en wordt ervan uitgegaan dat alle massa zich in één punt bevindt, waarbij de lengte precies de afstand is van het ophangpunt tot het massamiddelpunt. Deze aanname is meestal goed genoeg. Voor een massa-veersysteem kan je de trillingstijd berekenen met de formule t = 2π√( m/c ), waarbij m de massa is van het systeem in kilogram en c de veerconstante is in Newton per meter. In beide formules wordt ervan uitgegaan dat de trillingen harmonisch zijn, wat betekent dat de trillingen steeds op dezelfde manier verlopen. Als de formules niet werken, dan klopt er waarschijnlijk iets niet in de aannames. Over het algemeen kan je goed werken met deze formules om de trillingstijd van bepaalde trillingen in seconden te berekenen, mits je genoeg informatie hebt over het systeem.

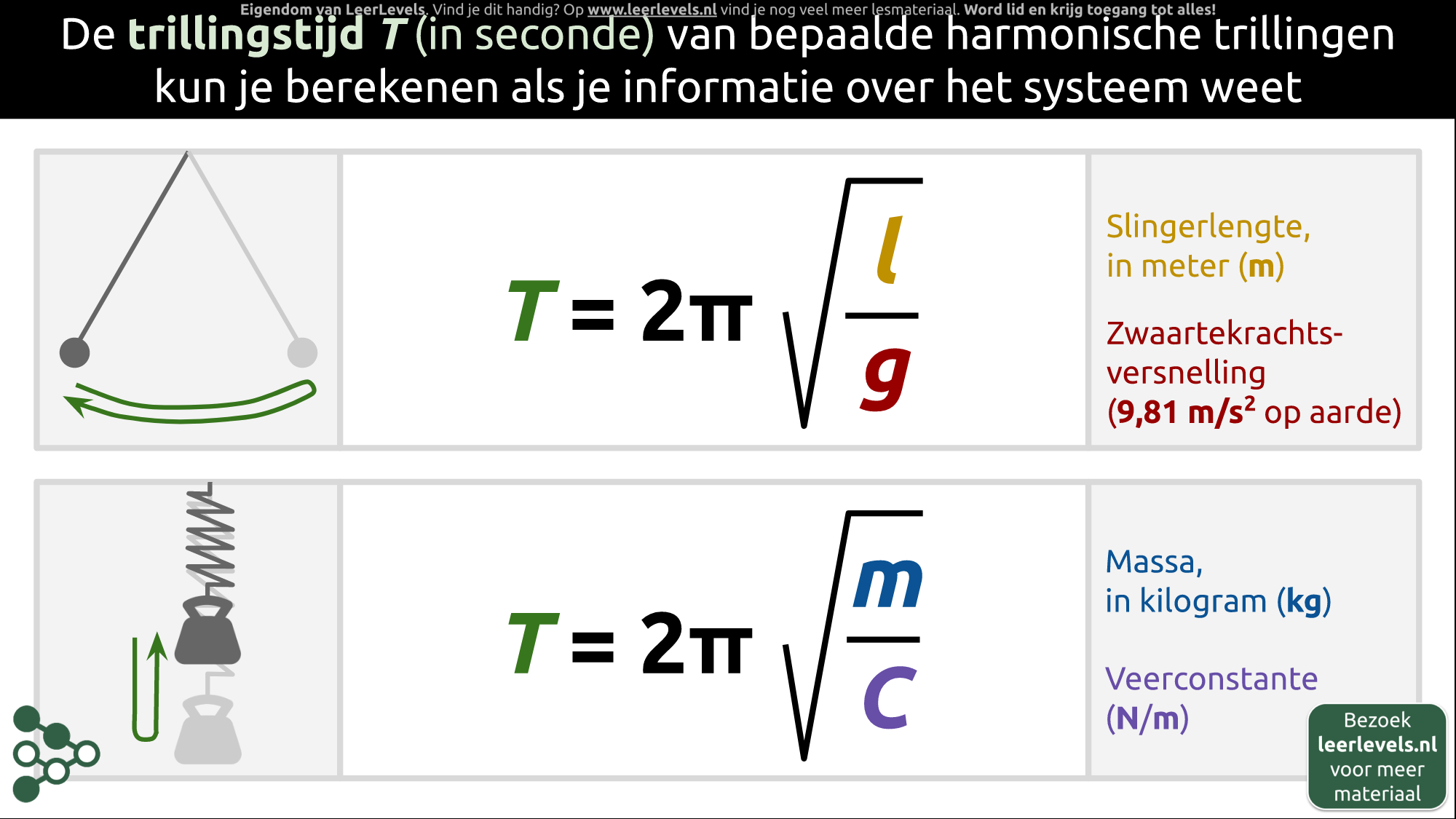
(Afbeelding: Animatie voor Trillingstijd formules)

Trillingstijd uit grafiek halen

Er zijn twee manieren om de tijd tussen trillingen te berekenen vanaf een grafiek. Als er slechts één trilling zichtbaar is, kun je de tijd tussen begin en einde van die trilling aflezen. Bij meerdere trillingen moet je meer nauwkeurigheid hebben en moet je zoveel mogelijk trillingen in je berekeningen meenemen. Bijvoorbeeld als je ziet dat er 2,5 trillingen zichtbaar zijn in een grafiek van 0,5 tot 6,0 seconden, heb je in totaal 5,5 seconden en dus een tijd van ongeveer 2,2 s/trilling. Gebruik de eerste methode wanneer er slechts één zichtbare trilling is, en gebruik de tweede methode wanneer er meerdere zichtbare trillingen zijn.

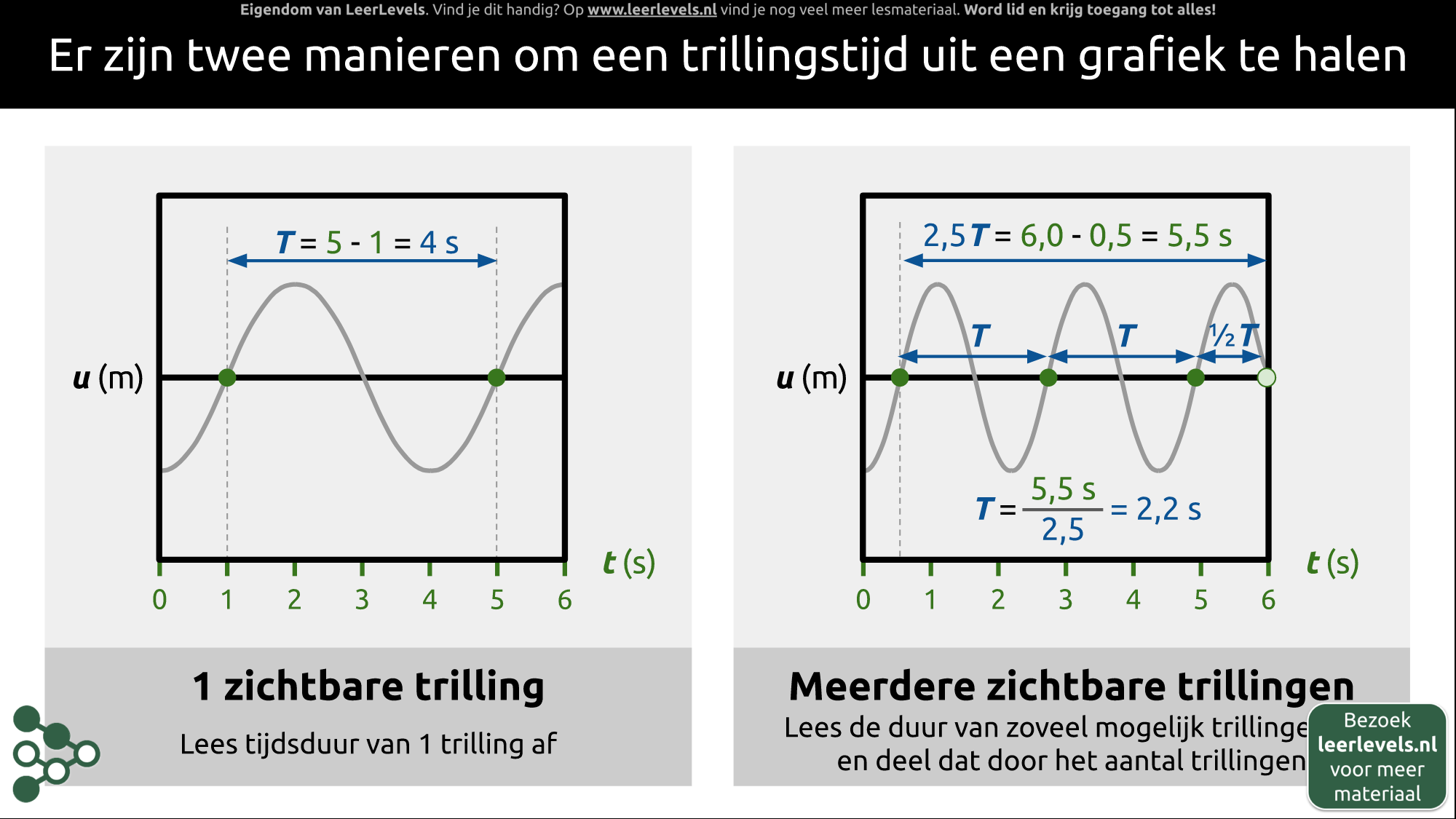
(Afbeelding: Animatie voor Trillingstijd uit grafiek halen)

Terug naar overzicht Meld je aan

Tunnelen

Tunnelen concept

Bij tunneling gaat een kwantumdeeltje door een barrière heen zonder dat het volgens de klassieke natuurkunde daar voldoende energie voor heeft. Laten we eens kijken naar een systeem met een oneindig diepe potentiaalput, die we schematisch kunnen weergeven als een draad met twee grote ladingen dicht bij elkaar. Als we binnen deze put een barrière creëren, bijvoorbeeld door een negatieve lading in de buurt te plaatsen, ontstaat er een potentiële energiebarrière in de put.

We plaatsen een kwantumdeeltje, bijvoorbeeld een elektron, aan de linkerkant van deze barrière. De golffunctie van het elektron kunnen we links van de barrière schetsen. In de barrière neemt de golffunctie exponentieel af. Als we dit tekenen, ontstaat er een vergelijkbaar plaatje. Het opvallende is dat de golffunctie niet noodzakelijkerwijs nul is aan de andere kant van de barrière. Er kan rechts van de barrière nog steeds een golffunctie bestaan. De amplitude van deze golffunctie is kleiner dan aan de linkerkant, maar het kwadraat van de amplitude is niet nul. Dit betekent dat er een zekere kans is om het deeltje rechts van de barrière aan te treffen.

Het merkwaardige is dat zodra we het kwantumdeeltje rechts meten, we weten dat het daar is. Vanaf dat moment verschuift de waarschijnlijkheidsverdeling, met een grotere kans aan de rechterkant en een kleinere kans aan de linkerkant. Het elektron kan dus door de barrière tunnelen, zelfs als het niet genoeg klassieke energie heeft om over de barrière heen te komen.

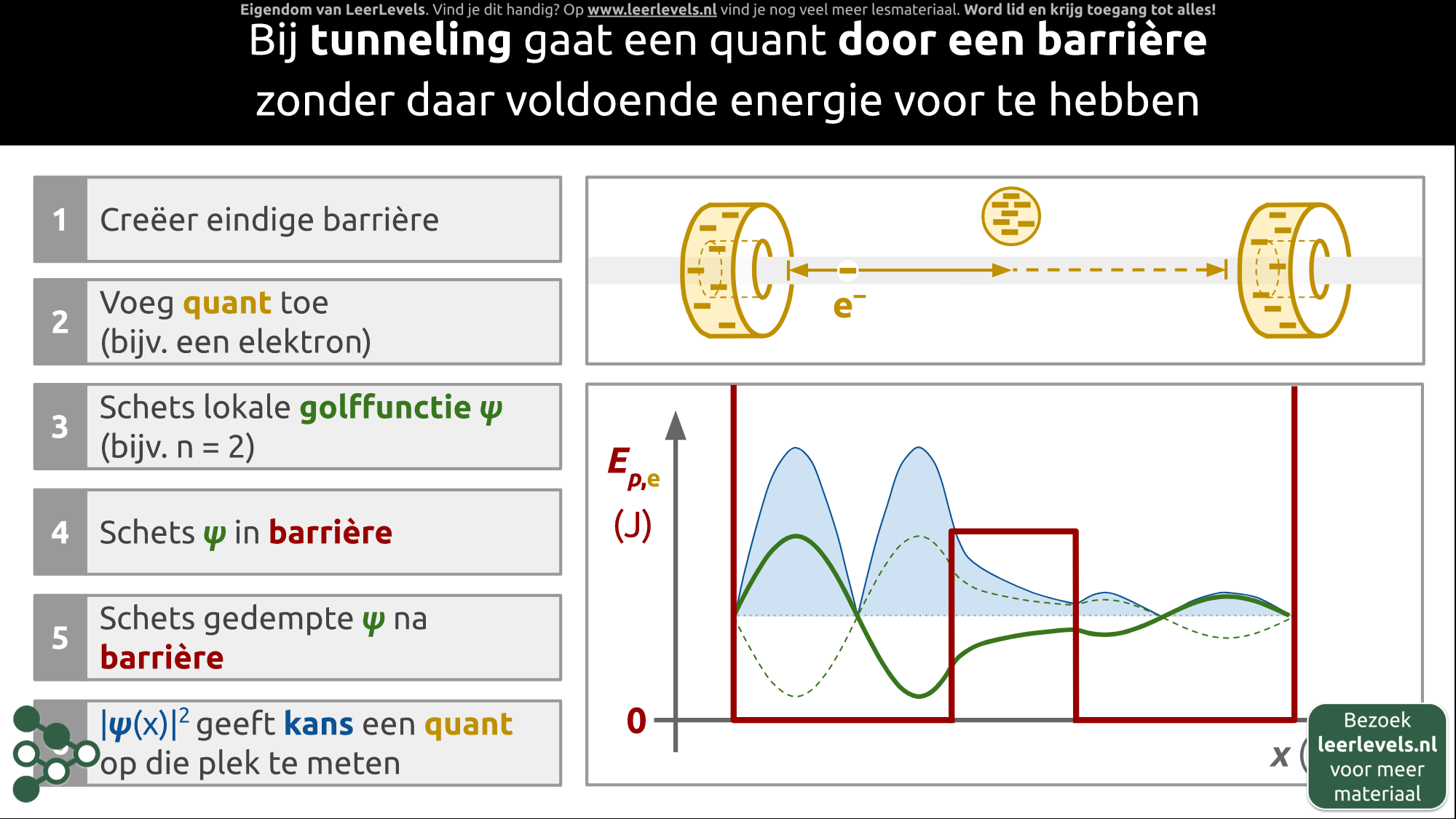
(Afbeelding: Animatie voor Tunnelen concept)

Tunnelen kans

De kans (P) dat een deeltje door een barrière tunnelt, hangt af van verschillende factoren. Stel dat je een smalle barrière hebt met een bepaalde golffunctie aan de linkerkant; dan is er nog steeds een aanzienlijke kans dat je het deeltje aan de rechterkant aantreft. Hoewel deze kans iets kleiner is, blijft deze wel bestaan, wat betekent dat de barrière niet zo'n grote invloed heeft.

Wanneer de barrière echter breder wordt, heeft dit een aanzienlijke invloed, en de kans dat een deeltje erdoorheen tunnelt, wordt kleiner. Met andere woorden, de dikte van de barrière is een belangrijk aspect dat bepaalt hoe groot de tunnelkans is: een grotere dikte betekent een kleinere kans.

Daarnaast speelt de hoogte van de barrière ten opzichte van de energie van het deeltje ook een rol. Als de energie van het deeltje vergelijkbaar is met de hoogte van de barrière, dan gaat een aanzienlijk deel van de golffunctie erdoorheen, en is er een redelijke kans dat het deeltje aan de andere kant zichtbaar is. Maar als je de energie van het deeltje verlaagt en de barrière verhoogt, dan neemt deze kans sterk af.

Het verschil tussen de kinetische energie van het deeltje en de potentiële energie van de barrière beïnvloedt ook de tunnelkans. Een groot energieverschil betekent een kleinere kans.

Ten slotte, als het deeltje bijvoorbeeld een elektron is, dat een kleine massa heeft, kan het relatief gemakkelijk door een barrière tunnelen. Maar als je het vervangt door een proton met een veel grotere massa, dan wordt de kans op tunnelen aanzienlijk kleiner. De massa van het deeltje speelt dus ook een rol in de tunnelkans.

Deze voorbeelden zijn kwalitatief bedoeld; het is niet zo dat een verdubbeling van de massa direct een kleine kans betekent. De situatie is complexer dan dat, maar de dikte van de barrière, de hoogte ten opzichte van de deeltjesenergie, en de massa van het deeltje zijn de drie belangrijkste factoren die de tunnelkans bepalen.

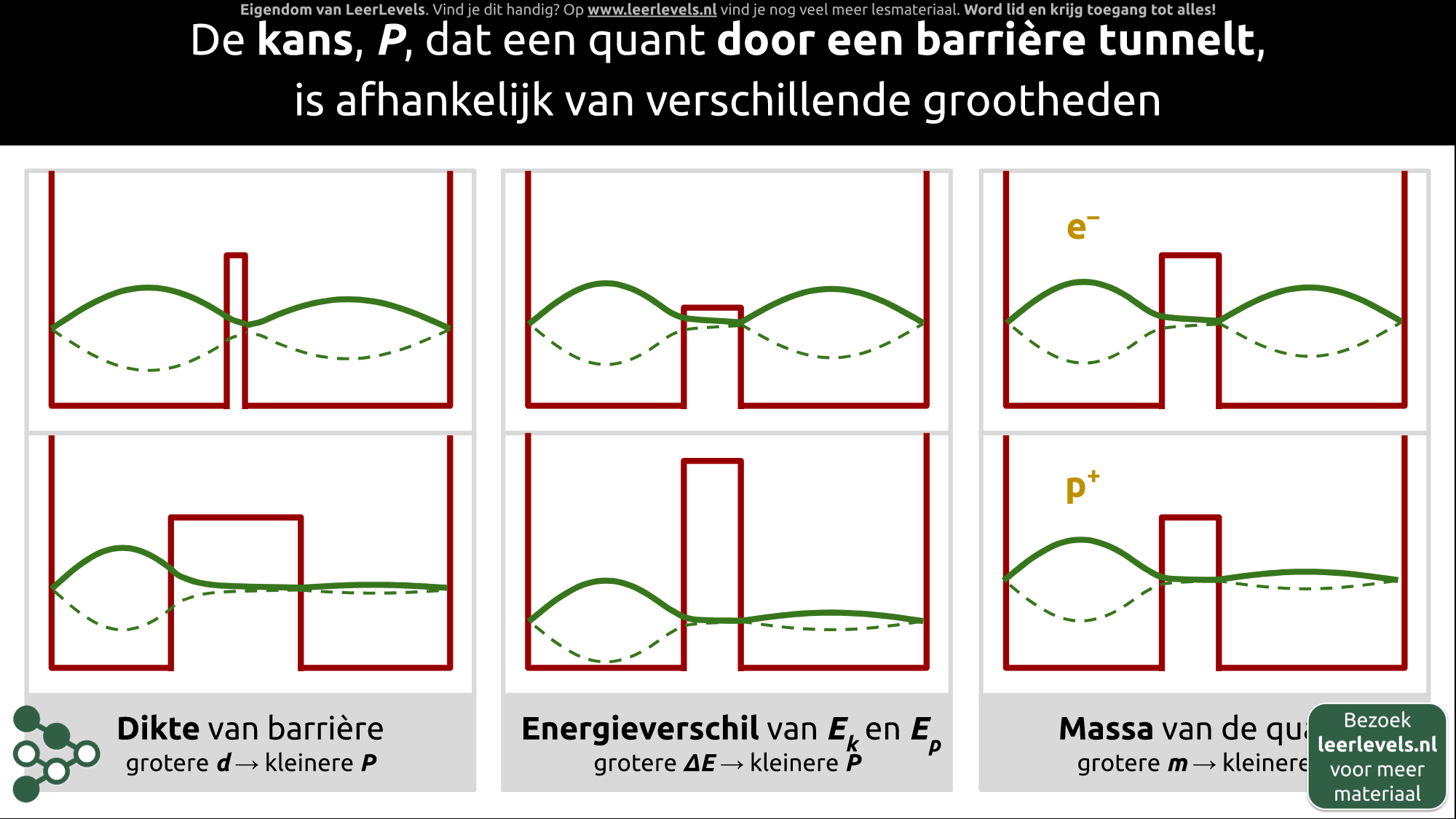
(Afbeelding: Animatie voor Tunnelen kans)

Tunnelen voorbeelden

Het tunnelen van deeltjes door een barrière verklaart alfaverval en maakt de Scanning Tunneling Microscope (STM) mogelijk.

Laten we eerst kijken naar alfaverval. Neem bijvoorbeeld Uranium-235. In die kern kunnen soms 2 protonen en 2 neutronen "besluiten" te ontsnappen. Klassiek gezien is dat niet mogelijk, want deze vier deeltjes — samen een alfa-deeltje genoemd — zouden de kern verlaten en de kern daarmee negatief geladen achterlaten. Door de aantrekkingskracht tussen de negatieve restkern en het positieve alfa-deeltje is het niet logisch dat het alfa-deeltje de kern verlaat. Hoe kan het deeltje dan toch ontsnappen? Dit gebeurt door tunneling. De elektrische aantrekkingskracht werkt als een barrière. Wanneer het alfa-deeltje deze barrière passeert, is de aantrekking niet langer sterk genoeg om het deeltje terug naar de kern te trekken. Hierdoor kan Uranium-235 vervallen naar Thorium-231 en Helium-4.

Een ander voorbeeld waar tunneling essentieel is, is de Scanning Tunneling Microscope (STM). Dit apparaat werkt als volgt: het onderzoekt een oppervlak waarvan je de structuur en hoogte nauwkeurig wilt bepalen. Door een zeer scherpe punt dicht bij het oppervlak te brengen en het geheel geleidend te maken, bijvoorbeeld met een geleidende coating, kan er een stroom beginnen te lopen.

Wanneer je een spanning aanlegt, blijkt dat elektronen bewegen tussen de punt van de scanner en het oppervlak. Klassiek gezien is dat onmogelijk, want er is geen geleider die de punt met het oppervlak verbindt. Toch gebeurt het, dankzij tunneling. Als je inzoomt, zie je een scherpe punt en een oppervlak met daartussen een barrière waar elektronen klassiek niet genoeg energie voor hebben. Dankzij het golf-gedrag kunnen we verklaren dat elektronen er toch doorheen tunnelen.

De STM beweegt de kop verticaal om een constante tunnel-stroom te behouden. Hierdoor blijft de kop op een constante afstand van het oppervlak. Door de kop horizontaal te bewegen, wordt de kop gedwongen om het oppervlak nauwkeurig te volgen en informatie over de positie van de kop te verzamelen. Op deze manier kun je precies achterhalen hoe het oppervlak eruitziet. Door op deze manier in kolommen of rijen te scannen, ontstaat er een driedimensionaal beeld van het hele oppervlak.

Zowel bij alfaverval als bij de STM is tunneling de verklarende factor.

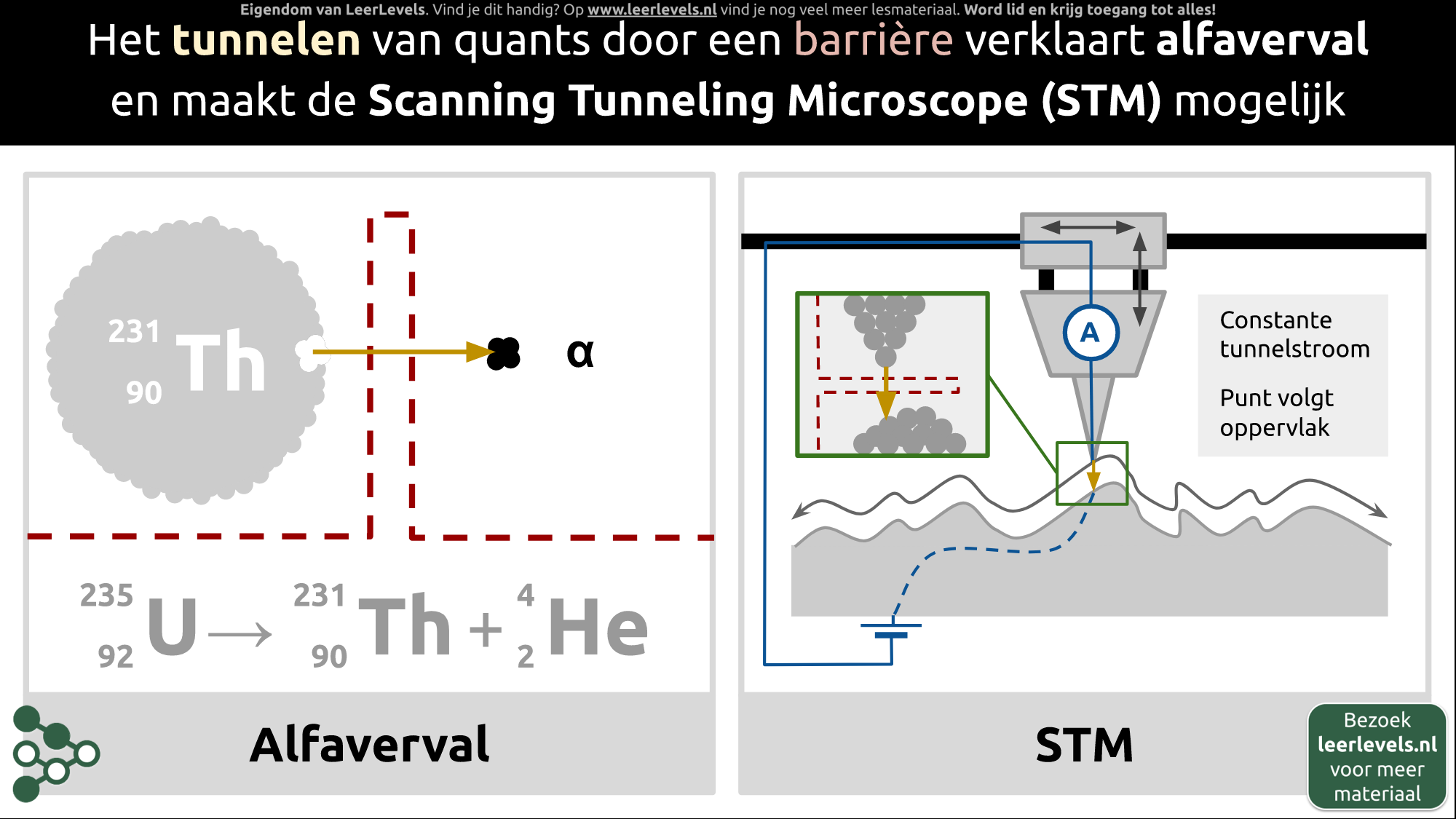
(Afbeelding: Animatie voor Tunnelen voorbeelden)

Terug naar overzicht Meld je aan

Tweede wet van Newton

Tweede wet van Newton concept

Volgens de tweede wet van Newton zorgt een resulterende kracht (Fres) altijd voor een versnelling (a). Als de resulterende kracht 0 is, is er geen versnelling. Dit gebeurt in een situatie waarin er geen krachten op een object werken of wanneer er krachten op een object werken die even groot maar tegengesteld zijn.

Als twee tegengestelde krachten op een object werken die niet even groot zijn, dan is de resulterende kracht niet 0 en is er dus sprake van een versnelling. Naarmate het verschil tussen de krachten groter wordt, neemt de resulterende kracht toe, en daarmee ook de versnelling.

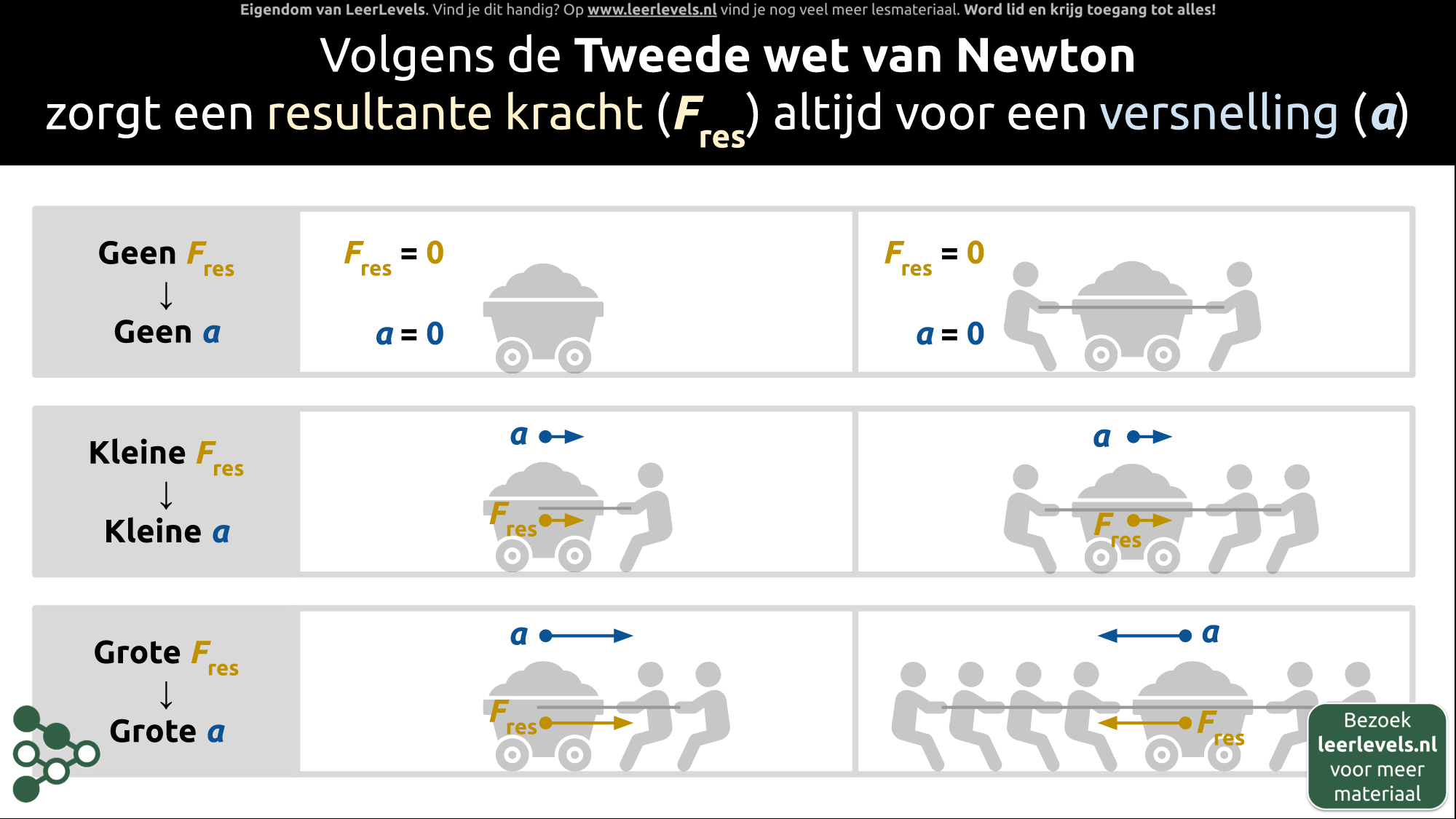
(Afbeelding: Animatie voor Tweede wet van Newton concept)

Tweede wet van Newton formule

De resulterende kracht, aangeduid als Fres, is recht evenredig met de massa en de versnelling. Dit principe staat bekend als de tweede wet van Newton. In formulevorm ziet dit er als volgt uit:

Fres = m · a

Hierbij staat Fres voor de kracht in newton, m voor de massa in kilogram en a voor de versnelling in meter per seconde kwadraat (m/s²).

(Afbeelding: Animatie voor Tweede wet van Newton formule)

Tweede wet van Newton versnelling

Volgens de tweede wet van Newton is de versnelling van een object afhankelijk van de kracht die erop wordt uitgeoefend en de massa van het object. Stel je voor dat er een grote kracht, zoals bij een explosie, op een object wordt uitgeoefend. Als het object een kleine massa heeft, zoals een veertje, zal het met een grote versnelling bewegen. Daarentegen, als het object een grote massa heeft, zal de versnelling minder zijn. Bij een kleine kracht op een kleine massa, zoals bij het veertje, zal er wel versnelling optreden, maar minder dan wanneer een grote kracht op de massa wordt uitgeoefend.

(Afbeelding: Animatie voor Tweede wet van Newton versnelling)

Tweede wet van Newton versnelling formule

De versnelling van een voorwerp is recht evenredig met de resulterende kracht en omgekeerd evenredig met de massa. De formule hiervoor is

a = (Fres)/(m)

Hierbij staat Fres voor de resulterende kracht in newton (N) en m voor de massa in kilogram (kg). De versnelling wordt gemeten in meter per seconde kwadraat (m/s²). Dit is de tweede wet van Newton en geeft aan er meer kracht nodig is om een zwaarder voorwerp te versnellen.

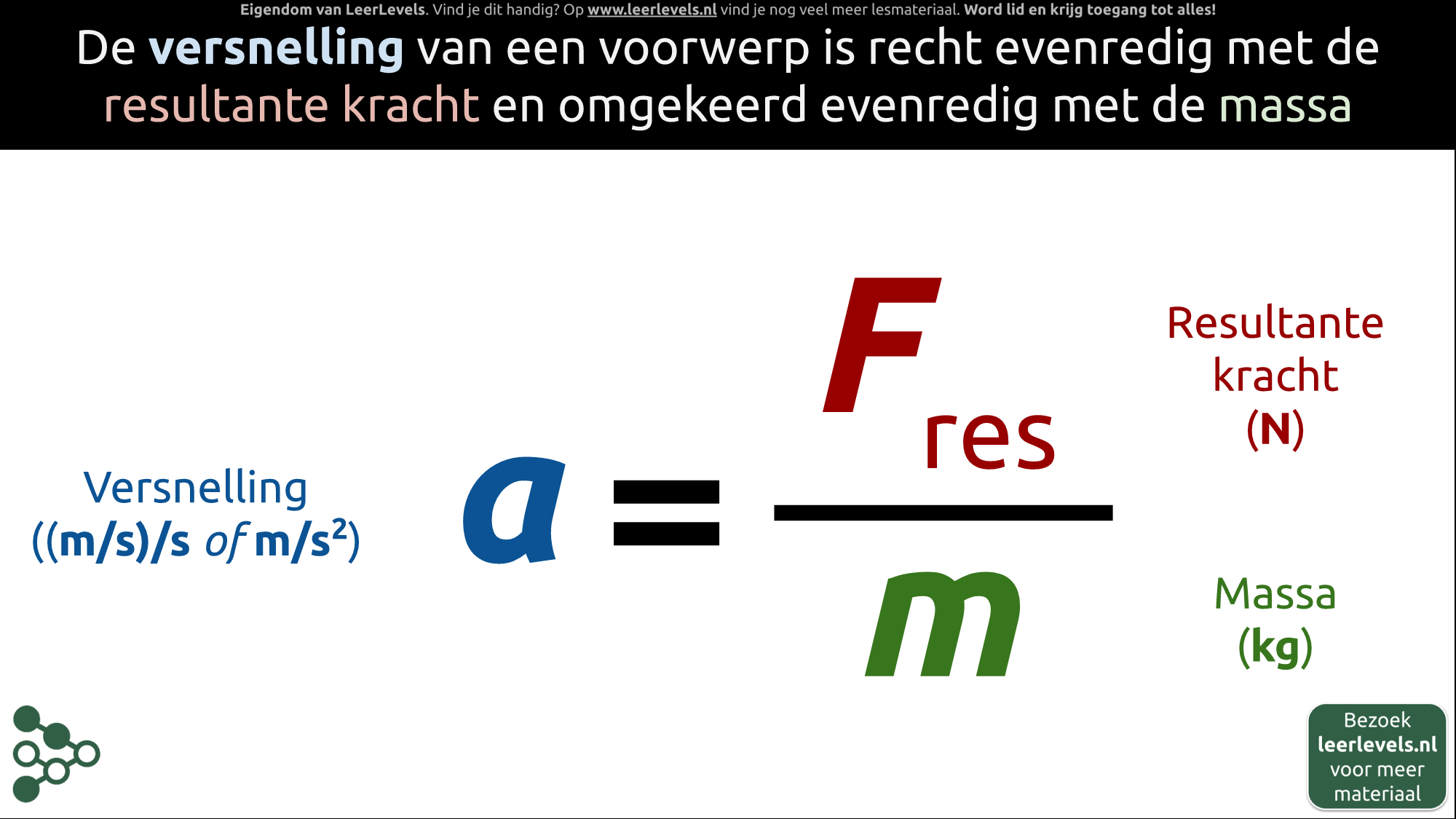
(Afbeelding: Animatie voor Tweede wet van Newton versnelling formule)

Tweede wet van Newton bij gekoppeld systeem

Voor een gekoppeld systeem geldt de tweede wet van Newton zowel voor het geheel als voor de afzonderlijke massa's. Laten we kijken naar twee blokken waarop een kracht wordt uitgeoefend. Dit zorgt voor een bepaalde versnelling. De versnelling van het systeem wordt gegeven door

asys = (Fr)/(msys) = (Fr)/(m1 + m2)

Vervolgens kun je de kracht op de afzonderlijke massa’s bepalen. Als je asys eenmaal weet, kun je de kracht op het eerste blok berekenen

Fr,1 = m1 · asys

Voor het tweede blok geldt

Fr,2 = m2 · asys

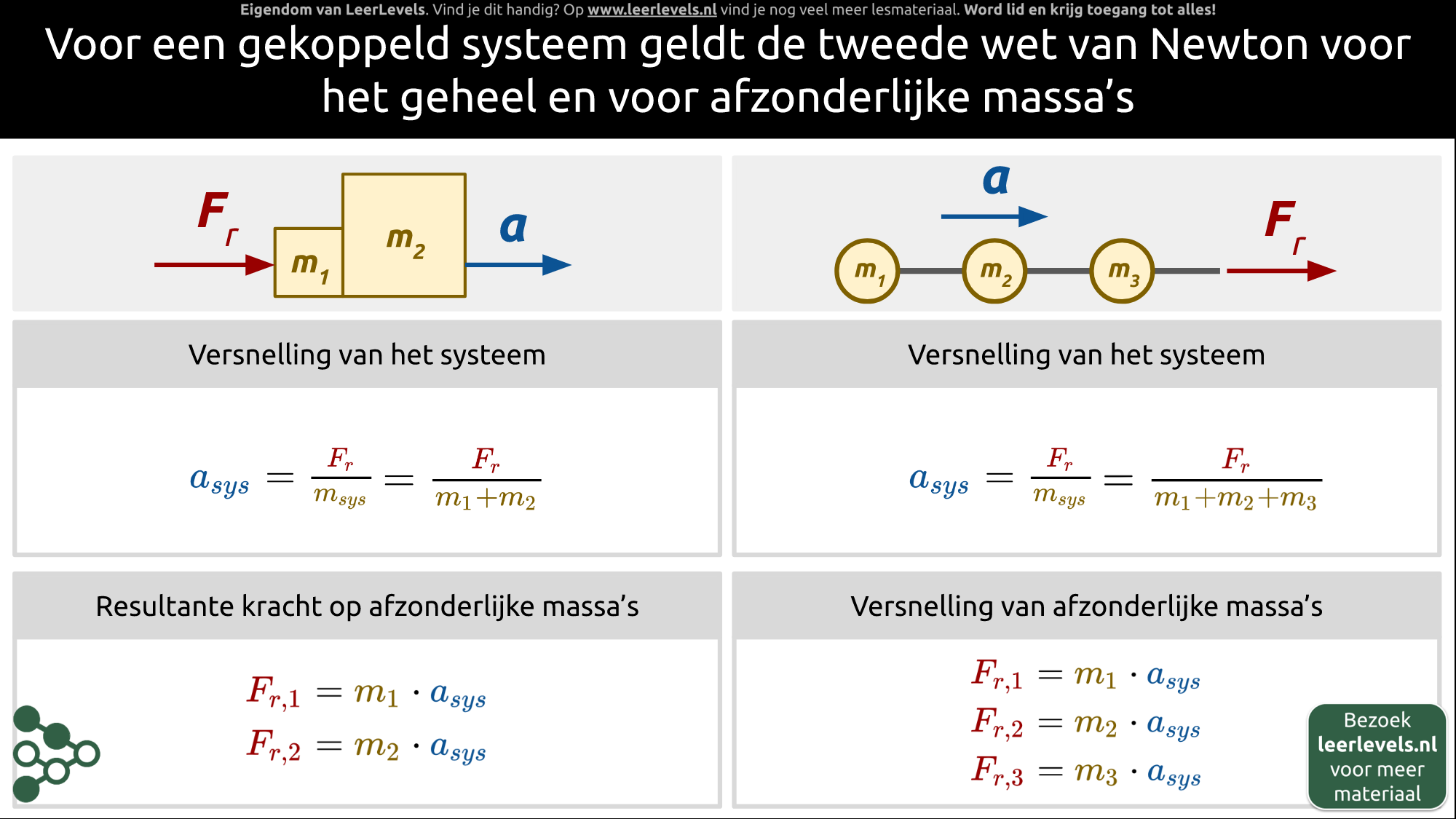
(Afbeelding: Animatie voor Tweede wet van Newton bij gekoppeld systeem)

Terug naar overzicht Meld je aan

Uitzetting

Uitzetting concept

Een materiaal zet uit wanneer mechanische spanning of een temperatuurstijging de ruimte tussen de deeltjes vergroot. Dit kunnen we illustreren met een draad. Wanneer er mechanische spanning op de draad wordt uitgeoefend, worden de deeltjes uit elkaar getrokken, wat betekent dat de ruimte tussen de deeltjes toeneemt. In het geval van temperatuurstijging krijgen de deeltjes meer bewegingsenergie, waardoor ze rondom hun positie heen en weer gaan bewegen. Als de temperatuur stijgt, neemt de gemiddelde bewegingsenergie van de deeltjes toe, wat leidt tot meer beweging en een grotere gemiddelde afstand tussen de deeltjes. In beide gevallen, mechanische spanning en temperatuurstijging, zal het materiaal dus uitzetten.

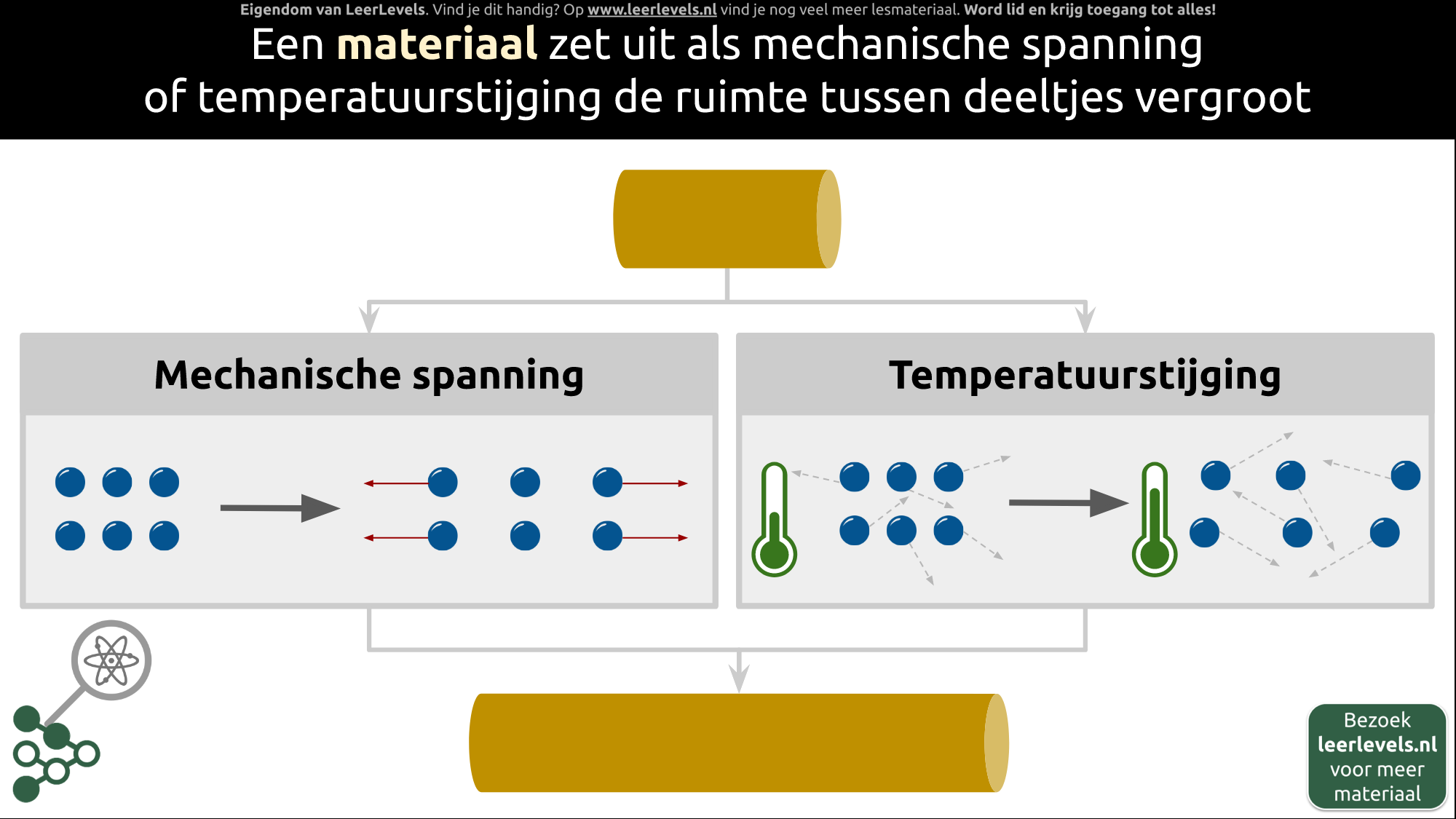
(Afbeelding: Animatie voor Uitzetting concept)

Relatieve uitzetting formule

Wanneer een materiaal warmer wordt, gaat het uitzetten. De mate waarin het uitzet is afhankelijk van hoe warm het wordt. Dit wordt de "relatieve uitzetting" genoemd. Het wordt gemeten als de hoeveelheid extra ruimte (in kubieke meters) die het materiaal krijgt per kubieke meter van het originele volume. De evenredigheidsconstante die hiervoor gebruikt wordt heet de kubieke uitzettingscoëfficiënt (γ). De temperatuurstijging (gemeten in kelvin) wordt vermenigvuldigd met de kubieke uitzettingscoëfficiënt om de relatieve uitzetting te berekenen.

Vaste stoffen hebben een kubieke uitzettingscoëfficiënt die drie keer zo groot is als de lineaire uitzettingscoëfficiënt. Dit komt omdat de uitzetting in lengte, breedte en hoogte plaatsvindt. Bij vloeistoffen en gassen zijn de waarden van de kubieke uitzettingscoëfficiënten opgenomen in tabellen, zoals de BINAS.

De formule om de relatieve uitzetting te vinden is: (Δ V)/(V) = γ Δ T, waarbij Δ V de volumetoename is, V het originele volume is, γ de kubieke uitzettingscoëfficiënt is en Δ T de temperatuurstijging in kelvin is.

(Afbeelding: Animatie voor Relatieve uitzetting formule)

Terug naar overzicht Meld je aan

Validiteit

Validiteit en betrouwbaarheid

De betrouwbaarheid gaat over hoe consistent de metingen zijn die je doet. Als je meerdere keren hetzelfde meet, krijg je waarschijnlijk niet exact hetzelfde resultaat, maar er zal wel een bepaalde spreiding zijn. Dit noemen we toevallige meetfout en het beperkt de betrouwbaarheid van het meetinstrument.

De validiteit gaat juist over of het meetinstrument meet wat het moet meten. Er kan namelijk ook een systematische meetfout zijn, waardoor de metingen systematisch afwijken van de werkelijke waarde. Dit noemen we de structurele meetfout en het beperkt de validiteit van het meetinstrument.

Een voorbeeld: stel je hebt een meetinstrument waarmee je de temperatuur wilt meten. Als je dit instrument meerdere keren gebruikt op dezelfde plek, zou je verwachten dat je steeds ongeveer dezelfde waarde krijgt. Als dit niet zo is, is er sprake van toevallige meetfout en is het instrument minder betrouwbaar. Als je het instrument op verschillende plekken gebruikt en je krijgt steeds dezelfde waarde, kan het zijn dat het instrument bijvoorbeeld alleen de temperatuur op de zon meet en niet de omgevingstemperatuur. In dat geval is er sprake van structurele meetfout en is het instrument niet valide.

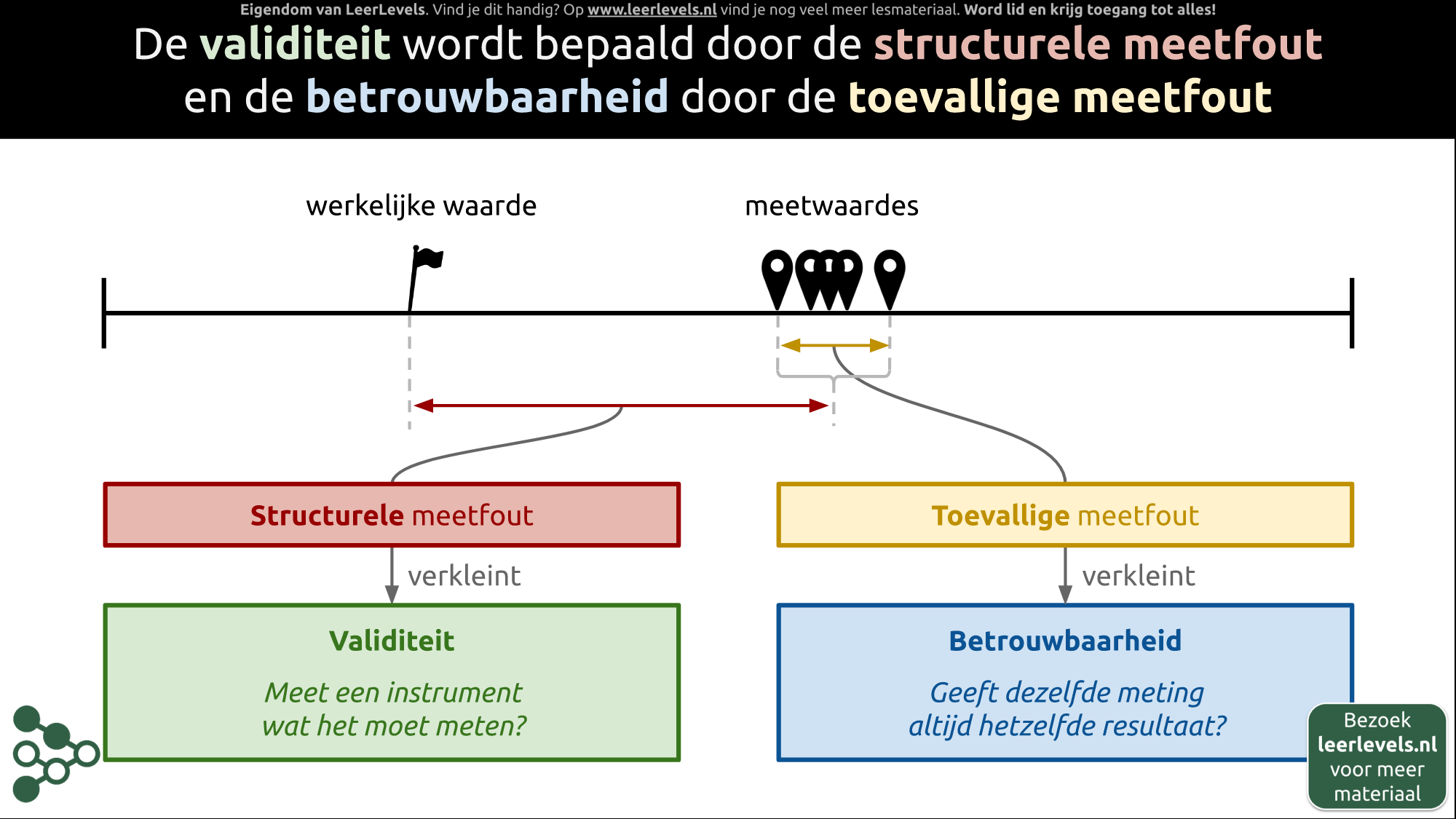
(Afbeelding: Animatie voor Validiteit en betrouwbaarheid)

Terug naar overzicht Meld je aan

Vectoren

Vectoren tekenen

In de natuurkunde worden eigenschappen zoals kracht en snelheid voorgesteld als vectoren die getekend worden met pijlen. Deze pijlen hebben drie belangrijke eigenschappen. Ten eerste is het beginpunt van de pijl de plek waar de eigenschap aangrijpt (bijvoorbeeld het punt tussen de hamer en de spijker bij kracht). Ten tweede geeft de richting van de pijl de richting van de eigenschap aan (bijvoorbeeld recht naar beneden voor kracht). Ten derde geeft de lengte van de pijl de grootte van de eigenschap aan (bijvoorbeeld een langere pijl betekent dat er harder wordt geslagen met de hamer). Als de snelheid hoger is, verandert de richting van de pijl, maar de beginplek blijft hetzelfde. Bij hogere snelheid wordt er met meer kracht geslagen. Vectoren worden dus gebruikt om eigenschappen zoals kracht en snelheid te visualiseren.

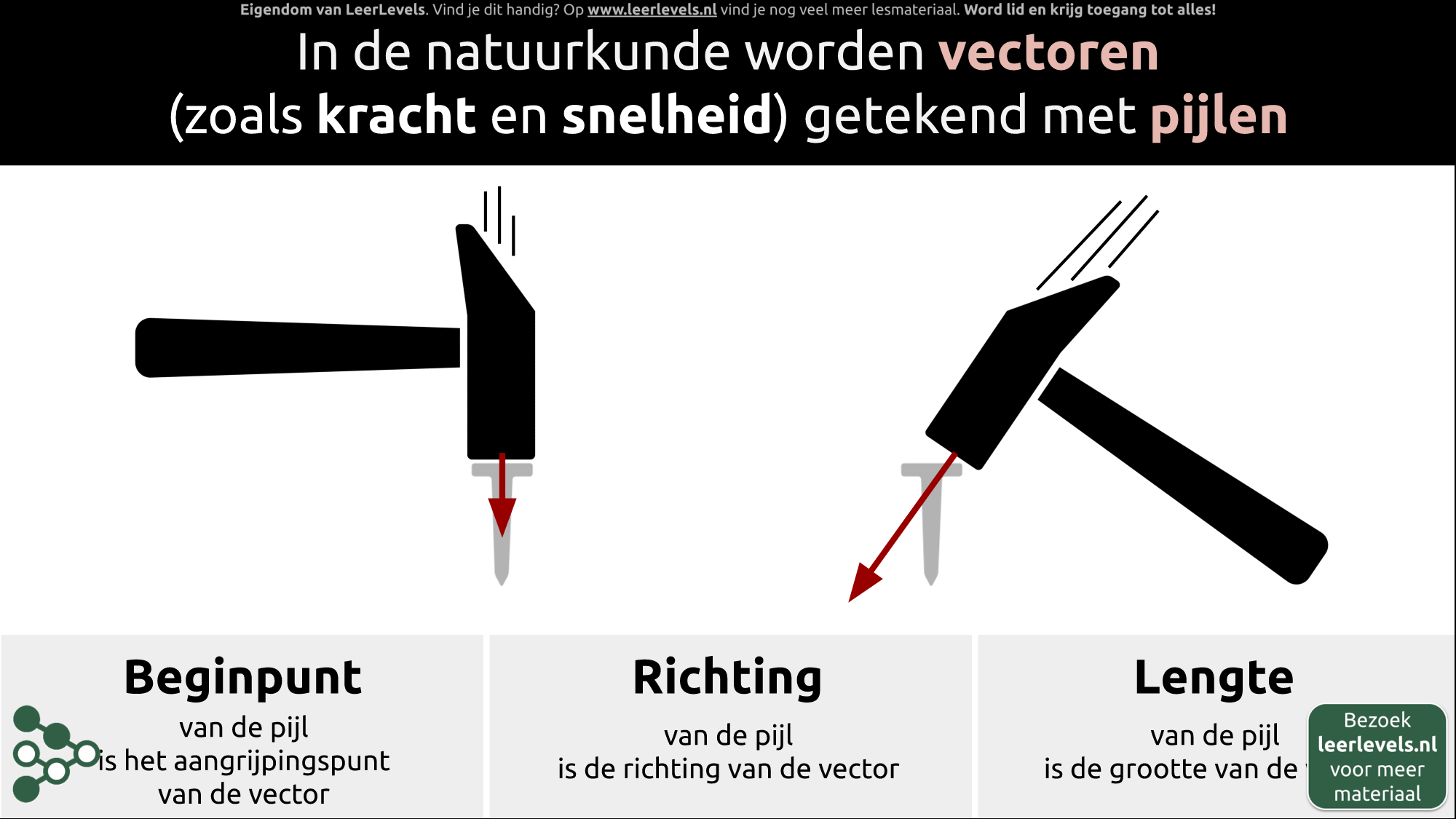
(Afbeelding: Animatie voor Vectoren tekenen)

Vectoren optellen 1D

Vectoren zijn pijlen die aangeven welke richting en hoe ver iets beweegt of werkt. In één dimensie kan je vectoren optellen en aftrekken. Stel dat je drie afstanden aflegt, één stap naar rechts, nog een stap naar rechts en drie stappen naar links. Deze afstanden hebben allemaal dezelfde dimensie omdat ze in dezelfde richting liggen, en je kan ze optellen door middel van de kop-staart-methode. Deze methode werkt ook bij kracht. Als twee poppetjes een kracht uitoefenen van 10 N naar rechts en een ander poppetje een kracht van 30 N naar links uitoefent, dan kan je deze krachten op elkaar toepassen en berekenen dat het resultaat een kracht van 10 N naar links is.

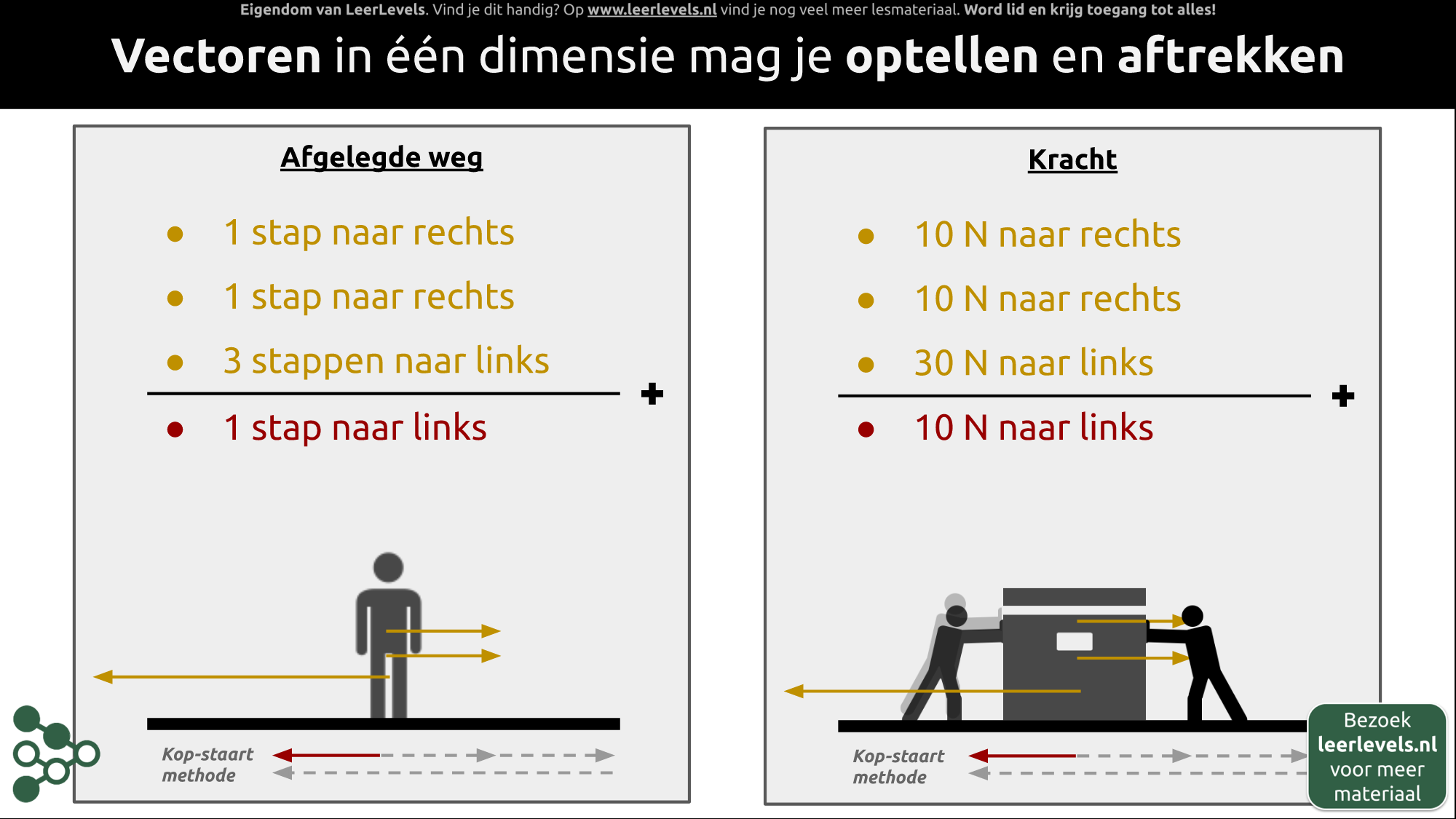
(Afbeelding: Animatie voor Vectoren optellen 1D)

Vectoren optellen 2D

Vectoren optellen betekent dat je kijkt naar de afgelegde weg in 2D of 3D. De kop-staart methode legt een vector aan het einde van een andere vector, zodat je de totale verplaatsing kunt zien. Bijvoorbeeld, als je eerst 3 stappen naar rechts zet en daarna 4 stappen naar beneden, dan heb je in totaal 7 stappen gezet. Maar om vanaf het begin meteen bij het eindpunt te zijn, moet je eigenlijk 5 stappen naar rechts-onder doen, omdat de afgelegde weg de hypotenusa van een rechthoekige driehoek is. Dit kan berekend worden met de stelling van Pythagoras: √(a²⁺b²) = c. Dit werkt ook zo bij krachten, waar de vectoren eerst langs de kop-staart methode gelegd moeten worden om de totale kracht te vinden.

(Afbeelding: Animatie voor Vectoren optellen 2D)

Vector ontbinden concept

Om vector F op te delen in FA en FB, volg je deze drie stappen:

1. Teken hulplijnen vanaf de kop van vector F parallel aan vector A naar vector B en parallel aan vector B naar vector A.
2. Teken gestippelde ontbindingsrichtingen A en B door de staart van vector F.
3. Teken de componenten FA en FB parallel aan A en B vanaf de staart van F tot aan het kruispunt met de hulplijnen.

Notatie: F, A, B, FA, FB.

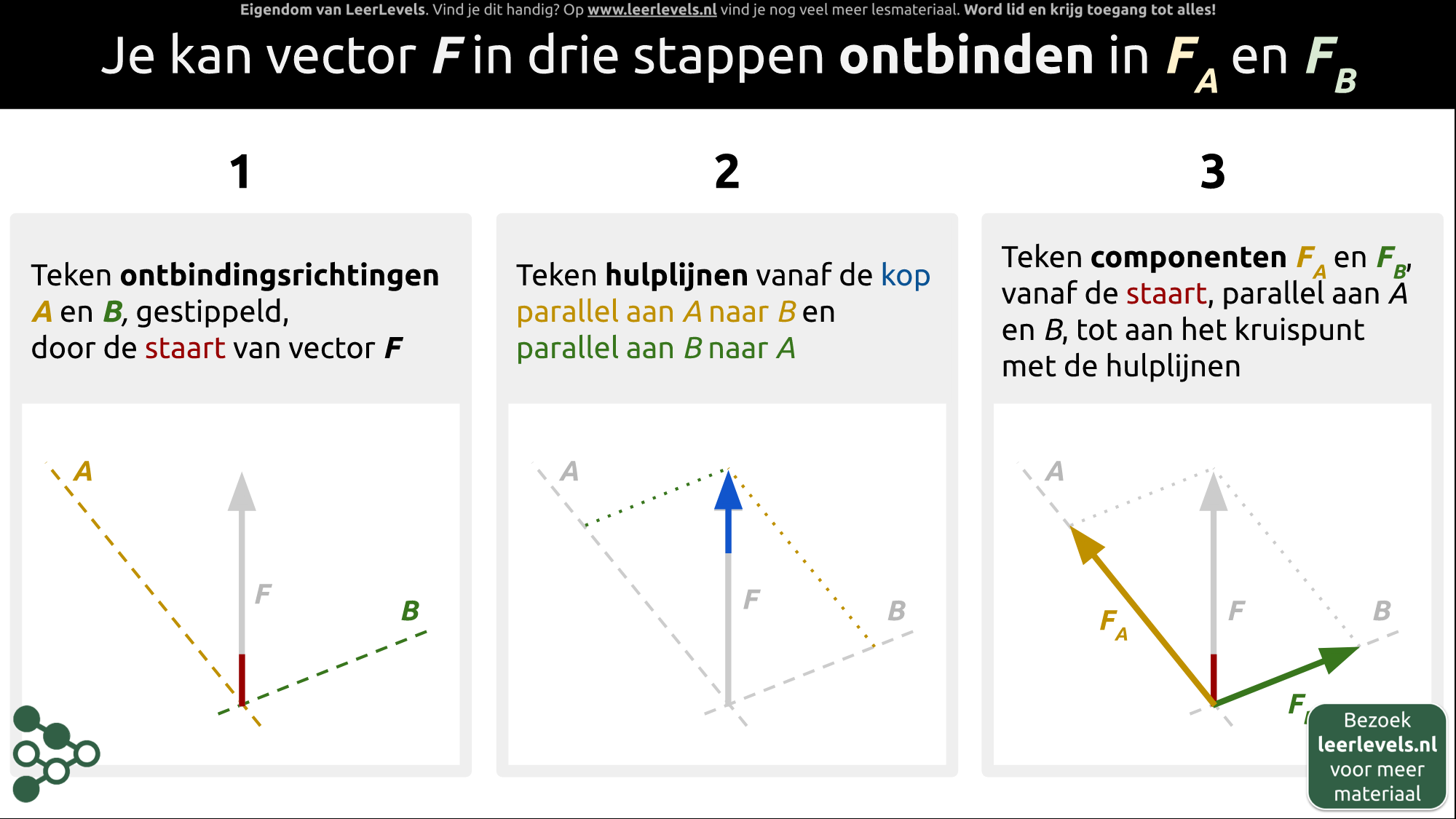
(Afbeelding: Animatie voor Vector ontbinden concept)

Notatie vectoren in 3D

We gebruiken een speciale notatie om de richting van een 3D-vector in 2D weer te geven. In een plat vlak kun je gemakkelijk zien welke kant een vector opgaat, maar als er een derde dimensie bijkomt (de z-as) wordt het lastiger. We hebben afgesproken om een kruisje te tekenen wanneer een vector van je afloopt en een puntje wanneer een vector naar je toe komt. Op die manier krijgt vector E een kruisje en vector F een puntje. Zo weten we welke kant de vectoren opgaan.

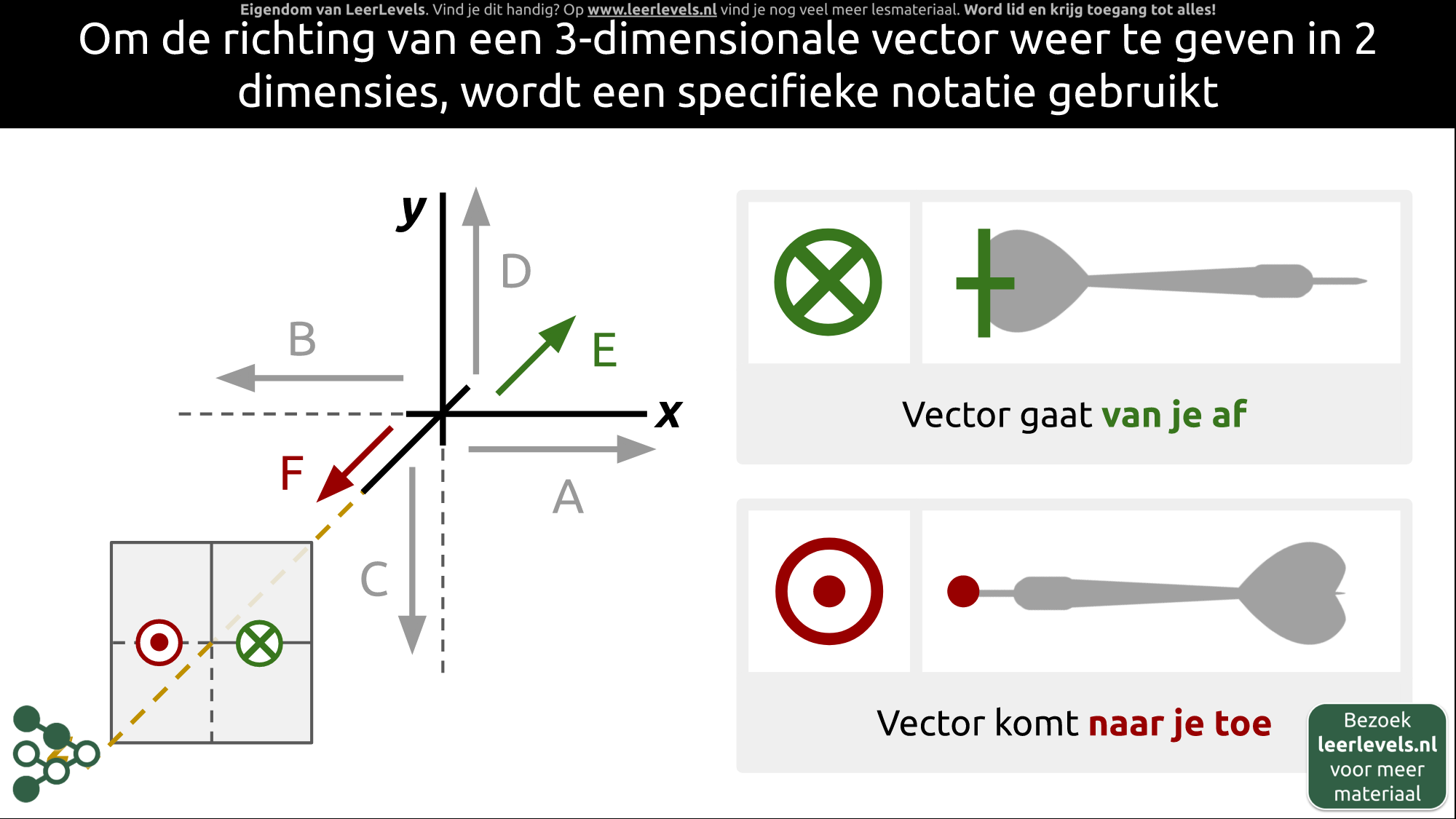
(Afbeelding: Animatie voor Notatie vectoren in 3D)

Scalars en vectoren

Een grootheid is iets wat je kunt meten, zoals temperatuur, volume en afgelegde weg. Grootheden kunnen scalar of vector zijn. Een scalar heeft geen richting, terwijl een vector wel richting heeft. Voorbeelden van scalars zijn temperatuur, volume en massa. Deze hebben geen richting, maar zijn simpelweg eigenschappen van een voorwerp. Voorbeelden van vectoren zijn afgelegde weg, snelheid en kracht. Afgelegde weg en snelheid hebben richting, terwijl kracht een effect heeft op andere voorwerpen en dus ook een vector is.

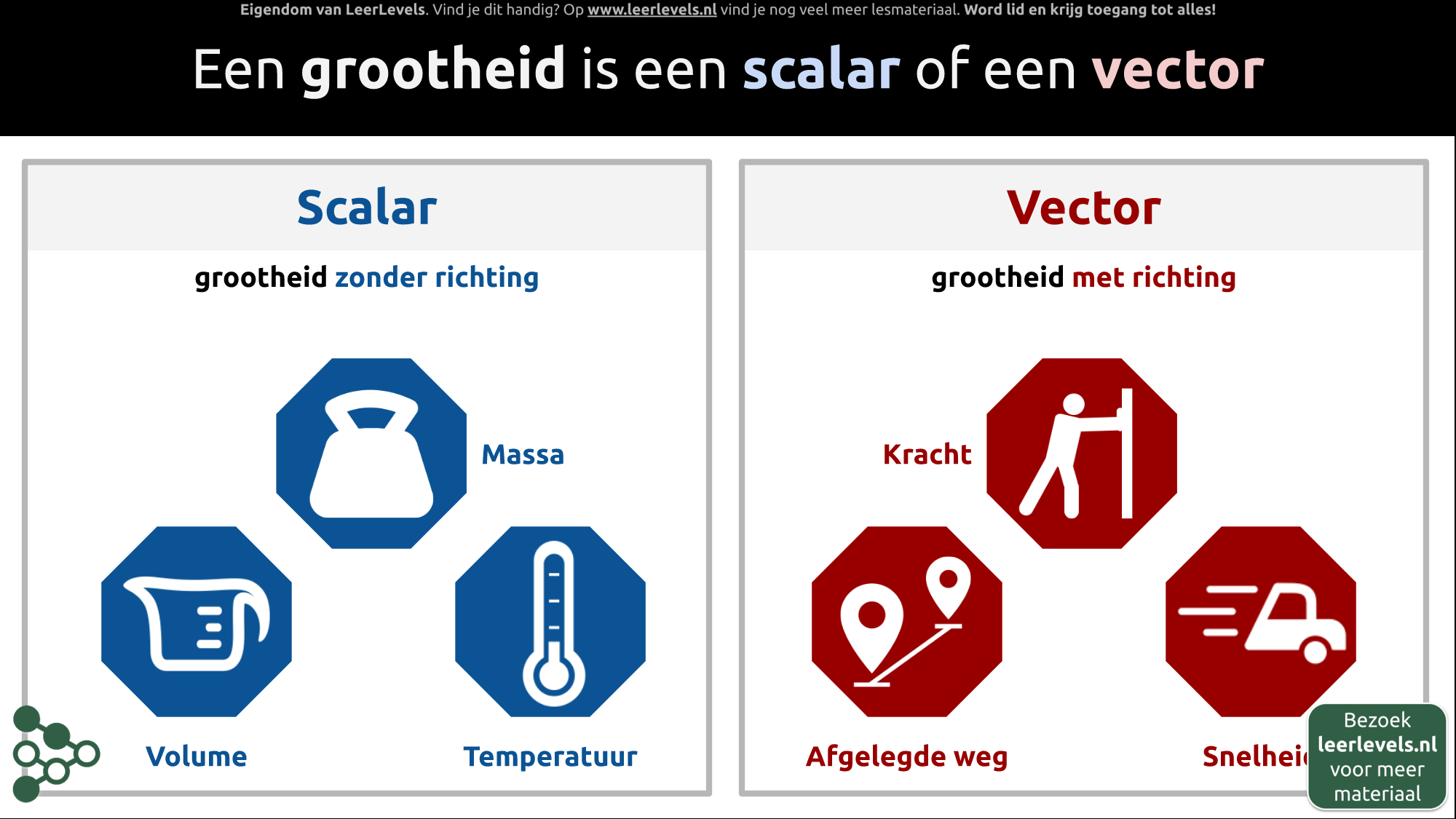
(Afbeelding: Animatie voor Scalars en vectoren)

Kop-staart methode

In de natuurkunde zijn er verschillende manieren om vectoren bij elkaar op te tellen. Een van deze manieren heet de kop-staartmethode en bestaat uit 3 stappen. Stap 1 is het herkennen van de pijlen die de vectoren voorstellen. Stap 2 is het verschuiven van de tweede vector zodat de staart van de eerste raakt aan de kop van de tweede. Stap 3 is het tekenen van een nieuwe vector vanaf de staart van de eerste tot aan de kop van de tweede. Dit werkt ook voor meerdere vectoren. Het resultaat van deze methode is een nieuwe vector die begint bij de staart van de eerste vector en eindigt bij de kop van de laatste vector. Er worden geen formules, grootheden of eenheden besproken in deze uitleg.

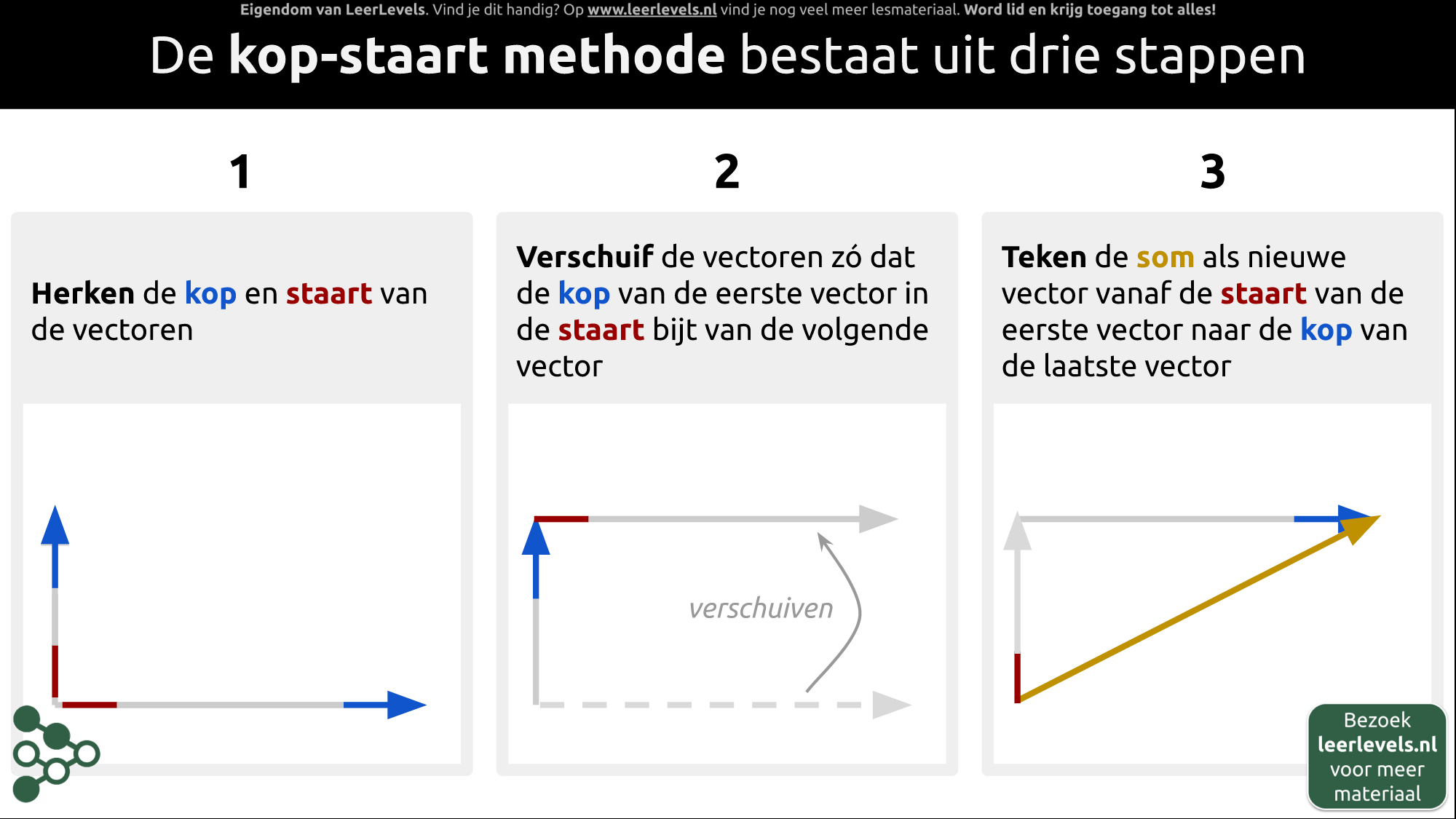
(Afbeelding: Animatie voor Kop-staart methode)

Vectoren optellen met constructie

Met de parallellogrammethode kun je twee vectoren optellen. Je begint met het tekenen van een parallele hulplijn door je geodriehoek langs één van de vectoren. Vervolgens teken je langs het eindpunt van de andere vector een lijn. Daarna teken je een tweede hulplijn langs de andere vector, waar je de geodriehoek neerlegt. Het kruispunt van de twee hulplijnen is het eindpunt van de som van de twee vectoren, die je tekent vanaf het beginpunt tot het kruispunt. De lengte van de som kun je bepalen met behulp van een verhoudingstabel.

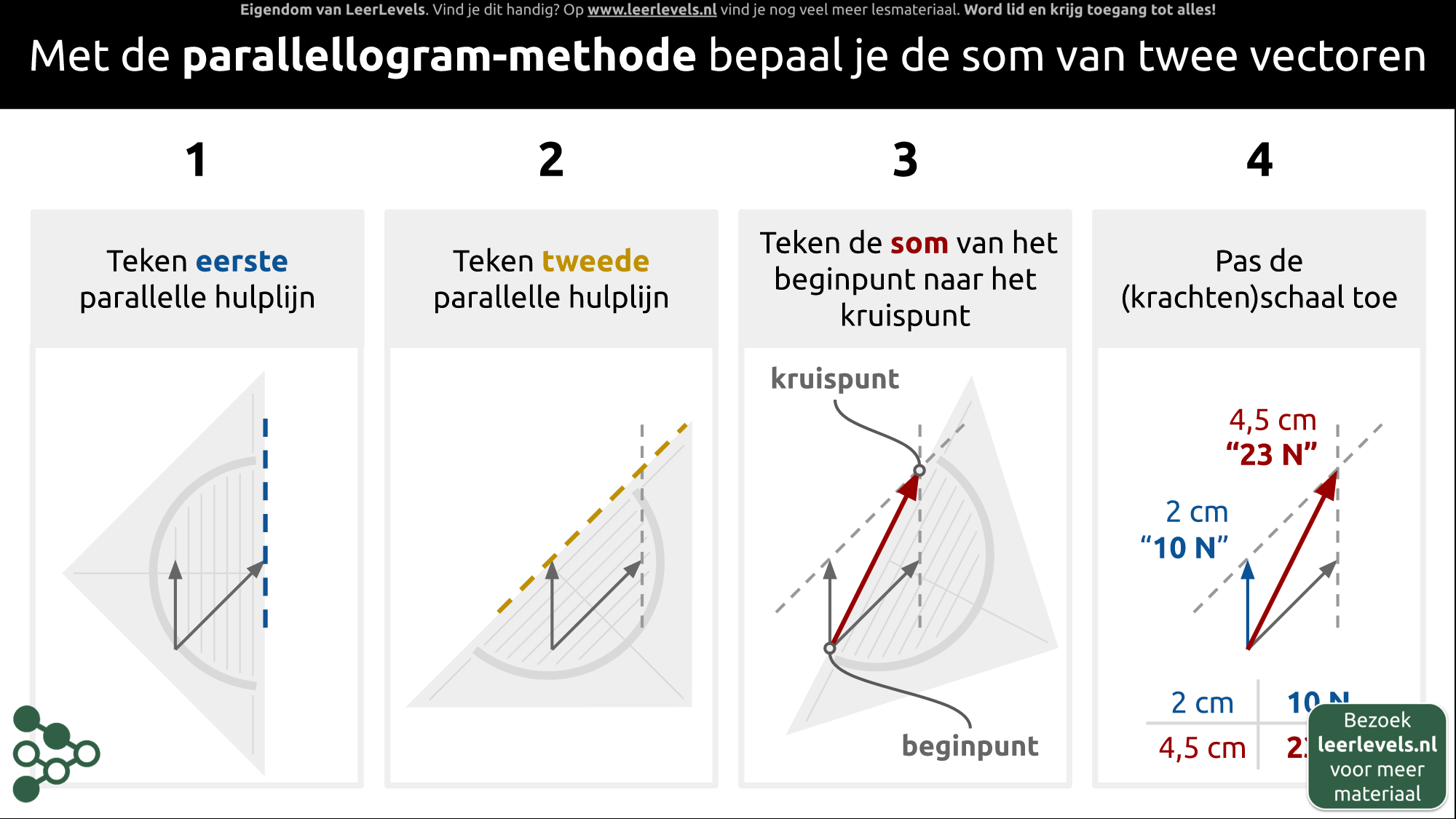
(Afbeelding: Animatie voor Vectoren optellen met constructie)

Terug naar overzicht Meld je aan

Veerenergie

Veerenergie concept

De energie die is opgeslagen in een veer wordt bepaald door de veerconstante en de uitrekking. Stel dat je een katapult hebt met een elastiek en je schiet een balletje weg. Op dat moment wordt de energie die in het elastiek is opgeslagen omgezet in de beweging van het balletje, waardoor het een bepaalde afstand kan afleggen. Als je het balletje verder of harder wilt schieten, heb je meer energie nodig in het elastiek. Dit kun je op twee manieren bereiken.

De eerste manier is door een grotere veerconstante te kiezen, oftewel stuggere veren te gebruiken. Een stuggere veer slaat meer energie op, die vrijkomt bij het schieten. Vervang je de veer door een dikkere en gebruik je dezelfde uitrekking om een balletje weg te schieten, dan zal het balletje verder vliegen. Dit komt doordat je de veerconstante vergroot en dus meer energie hebt opgeslagen.

De tweede manier om meer energie aan het balletje te geven, is door dezelfde veer te gebruiken en deze verder uit te rekken. Het effect van het vergroten van de uitrekking is aanzienlijk. Als je de veerconstante verdubbelt, wordt de veerenergie twee keer zo groot. Maar als je de uitrekking verdubbelt, wordt de veerenergie zelfs vier keer zo groot.

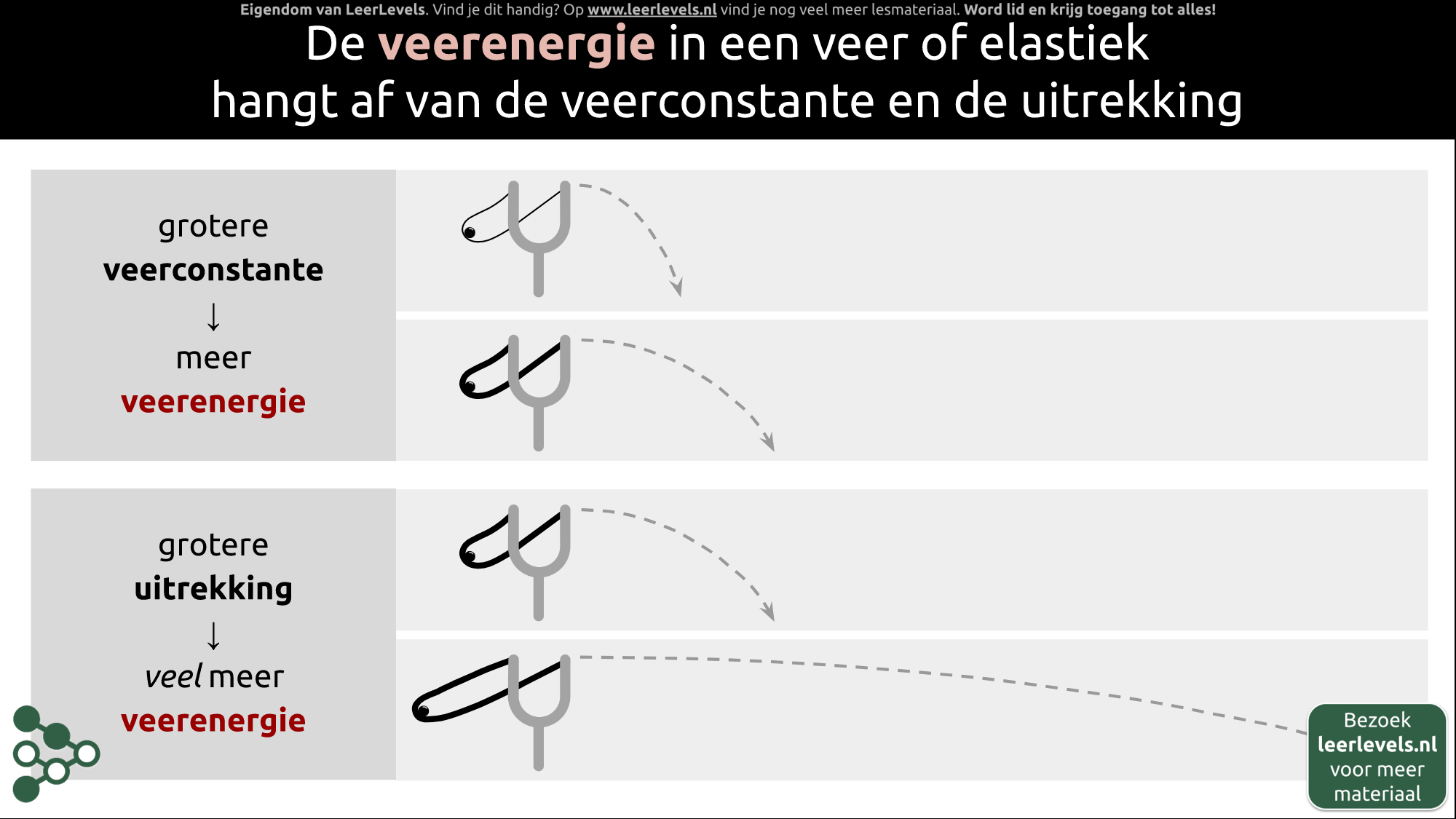
(Afbeelding: Animatie voor Veerenergie concept)

Veerenergie afleiding

Je kunt energie opslaan in een veer door arbeid te verrichten. Om de formule voor de veerenergie af te leiden, beginnen we met een veer in evenwichtstoestand: de veer is in rust en bevat geen energie. Als we de veer uitrekken, hebben we een bepaalde kracht nodig over een bepaalde afstand en verrichten we arbeid met onze spierkracht. De arbeid die we verrichten wordt opgeslagen in de veer. De veerkracht is recht evenredig met de uitrekking. De verrichte arbeid is gelijk aan de oppervlakte onder de (F, u)-grafiek.

Bij een uitrekking u is de veerkracht gelijk aan

Fv = c · u

Om de oppervlakte onder de grafiek te bepalen, moeten we de oppervlakte van een driehoek met zijden u en Fv bepalen. Dus

W = Ev = ½ · u · Fv

Dit geeft

Ev = ½ · u · c · u

Dus de veerenergie is

Ev = ½ · c · u²

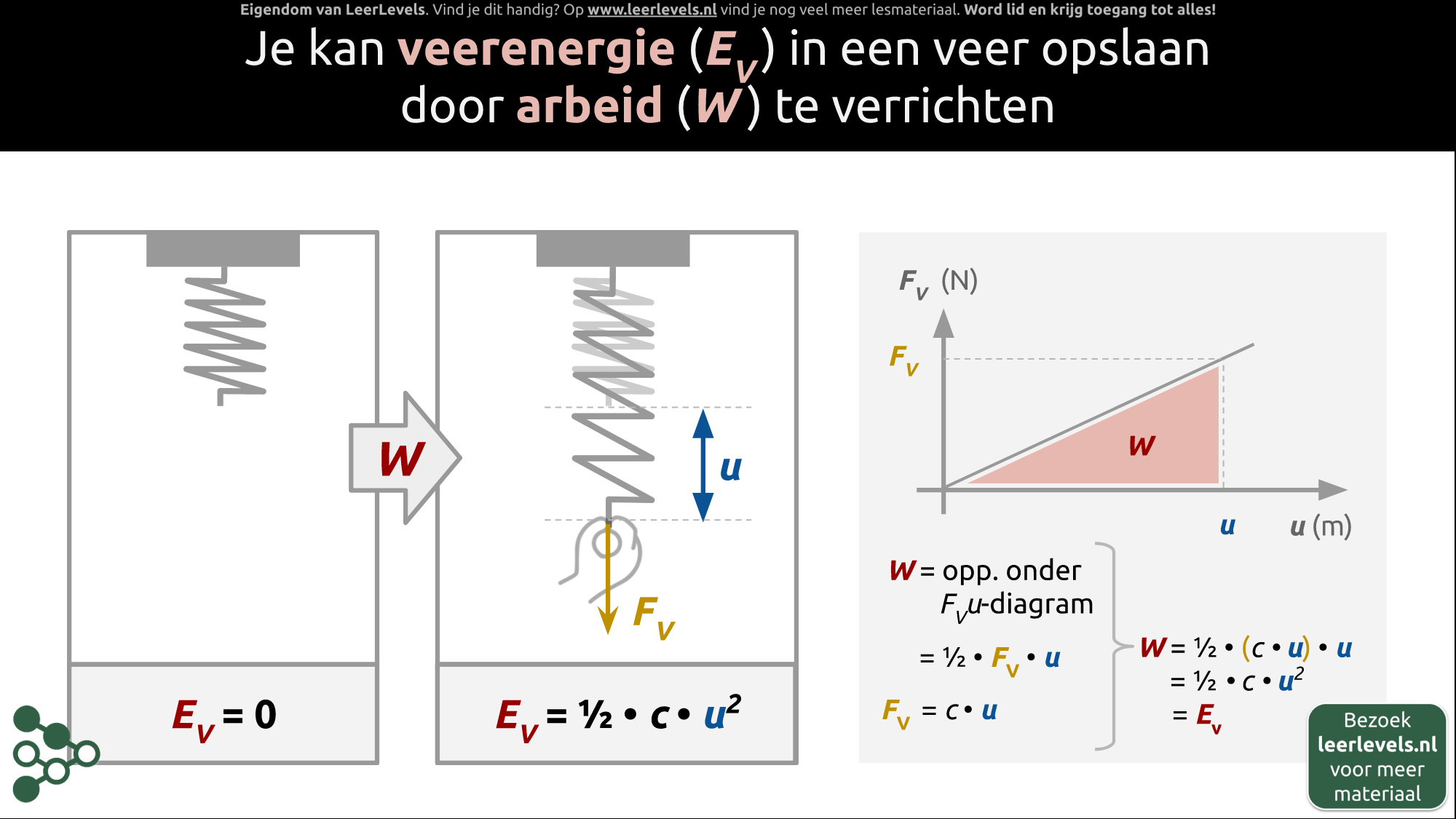
(Afbeelding: Animatie voor Veerenergie afleiding)

Veerenergie formule

De energie die is opgeslagen in een uitgerekte veer is recht evenredig met de veerconstante en kwadratisch evenredig met de uitrekking. Dit kunnen we in formulevorm schrijven als

Ev = ½ · c · u²

Waarbij Ev de veerenergie in Joule (J) is, c de veerconstante in Newton per meter (N/m), en u de uitrekking ten opzichte van de evenwichtsstand in meter (m).

(Afbeelding: Animatie voor Veerenergie formule)

Terug naar overzicht Meld je aan

Veerkracht

Veerkracht concept

Een veer heeft een rusttoestand waarin hij in evenwicht is. Als je de veer een klein beetje uitrekt of indrukt, zal de veerkracht klein zijn en zal de veer terugkeren naar de rusttoestand. Maar als je de veer verder uitrekt of indrukt, zal er meer kracht nodig zijn en zal de terugkerende kracht ook groter zijn. De uitrekking en terugkerende kracht van een veer zijn evenredig. Als de veer twee keer zo ver wordt uitgerekt, zal de terugkerende kracht ook twee keer zo groot zijn. Dit geldt ook als de veer wordt ingedrukt. Sommige uitrekkingen van de veer zijn positief en andere zijn negatief, afhankelijk van of de veer wordt uitgerekt of ingedrukt. De afstand van de uitrekking of indrukking is ongeveer hetzelfde als de bijbehorende kracht. Dit wordt weergegeven als een formule: F = kx, waarbij F de kracht is, k de veerconstante en x de uitrekking of indrukking van de veer.

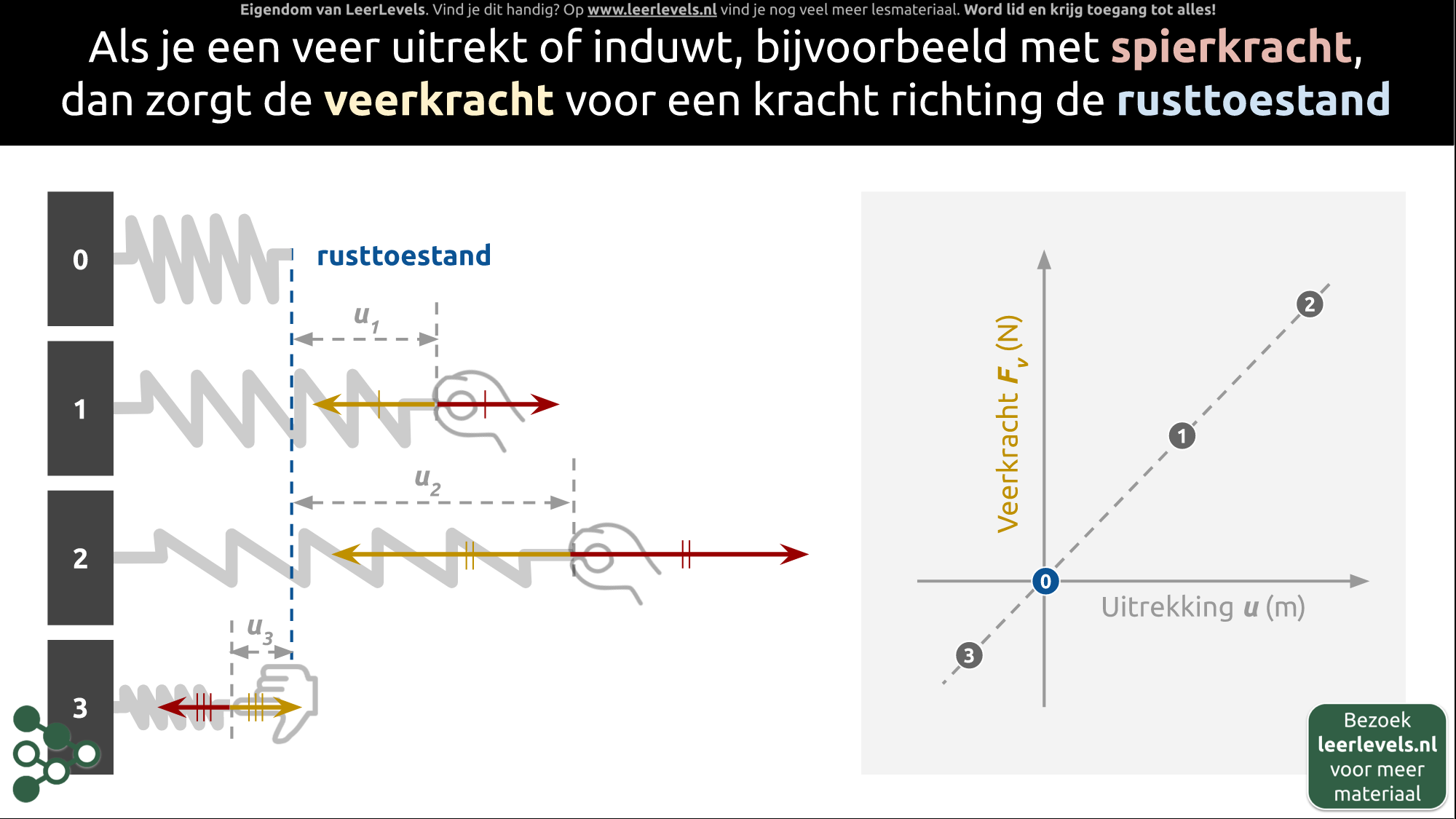
(Afbeelding: Animatie voor Veerkracht concept)

Veerconstante bepalen

Je kunt uitrekenen hoeveel een veer 'meeveren' door metingen te doen. Dat heet de veerconstante. Een formule hiervoor is Fv = c · u, waarbij Fv de kracht is waarmee de veer wordt uitgerekt, u de afstand van de uitrekking is en c de veerconstante. Als je bijvoorbeeld een veer bekijkt waar een gewichtje van 20 N aanzit en deze veer 0,9 meter uitrekt, kun je uitrekenen dat de veerconstante 22 N/m is.

Om meer nauwkeurigheid te krijgen, kun je meer metingen doen en het gemiddelde hiervan nemen. Door de meetpunten met elkaar te verbinden via een lijn kun je de veerconstante nog nauwkeuriger bepalen. Dit kun je doen door de helling van die lijn te nemen. Bijvoorbeeld: een raaklijn door meerdere meetpunten geeft een helling van 20 N/m als veerconstante. Dus, voor een nauwkeurige bepaling van de veerconstante kun je meerdere metingen doen en de helling van de beste passende lijn aflezen.

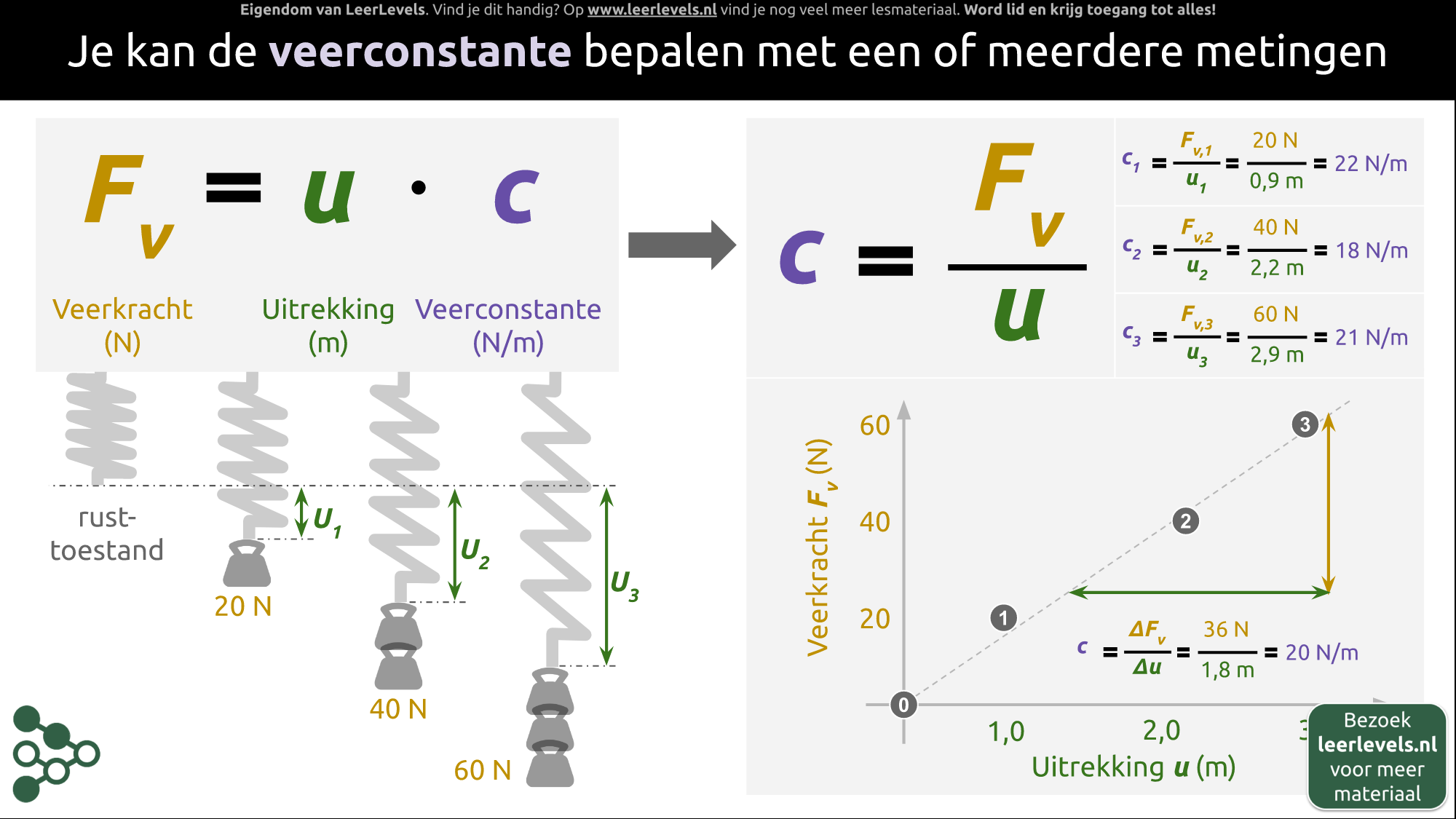
(Afbeelding: Animatie voor Veerconstante bepalen)

Veerkracht formule

Veerkracht is recht evenredig met de uitrekking en de veerconstante. De formule hiervoor is als volgt:

Fv = u · c

waarbij Fv de veerkracht is in N, u de uitrekking in m en c de veerconstante in N/m.

(Afbeelding: Animatie voor Veerkracht formule)

Terug naar overzicht Meld je aan

Veerunster

Veerunster werking

Een veerunster zet de uitrekking van een veer om in een massa of gewicht met behulp van een bekende veerconstante en de zwaartekrachtversnelling.

Als de uitrekking 1 centimeter is en de veerconstante bijvoorbeeld 50 N/m bedraagt, kunnen we de veerkracht berekenen. De veerkracht is dan 0,01 m × 50 N/m = 0,5 N.

Dankzij de veerunster kun je, zodra je de veerkracht kent, de zwaartekracht bepalen. Omdat de massa stilhangt, is de resultante kracht 0. Dus de veerkracht moet gelijk zijn aan de zwaartekracht. In dit geval is de zwaartekracht ook 0,5 N.

Zodra we Fz kennen en die 0,5 N bedraagt, kunnen we de massa bepalen. De zwaartekracht wordt gegeven door m × g, dus m = (Fz)/(g). Het is bekend dat g = 9,81 m/s² op aarde. Met Fz = 0,5 N kunnen we berekenen dat de massa ongeveer 0,05 kg is, oftewel ongeveer 50 g.

Een veerunster is zo ontworpen dat er naast de schaal in Newton ook een schaal in gram is. Het is niet bedoeld om slechts één waarde te meten, maar heeft een hele schaal waarop voor elke uitrekking de bijbehorende kracht en massa zijn aangegeven. Kortom, een veerunster zet de uitrekking van de veer om in een massa of gewicht met behulp van een bekende veerconstante en de zwaartekrachtversnelling.

(Afbeelding: Animatie voor Veerunster werking)

Veerunster concept

Een veerunster gebruikt het evenwicht tussen veerkracht en zwaartekracht om te bepalen hoe zwaar iets is. De veerunster heeft een ophangpunt, een veer, een markering die standaard op nul staat, een staafje tussen de veer en het haakje en een haakje. Hoewel er staat dat de veerunster de massa bepaalt, bepaalt hij eigenlijk het gewicht, de kracht waarmee aan het haakje wordt getrokken, en wordt die kracht omgerekend naar de bijbehorende massa. Als je iets lichts aan de haak hangt, zal de afleeswaarde ook laag zijn. Dit komt doordat er maar een kleine uirekking (u) is. Dat betekent dat er maar een kleine veerkracht (Fv) is. Dat betekent dat er dus een kleine zwaartekracht (Fz) was en dat dus de massa (m) klein moest zijn. Je kan ook in omgekeerde richting redeneren, bijvoorbeeld bij een zwaar voorwerp.

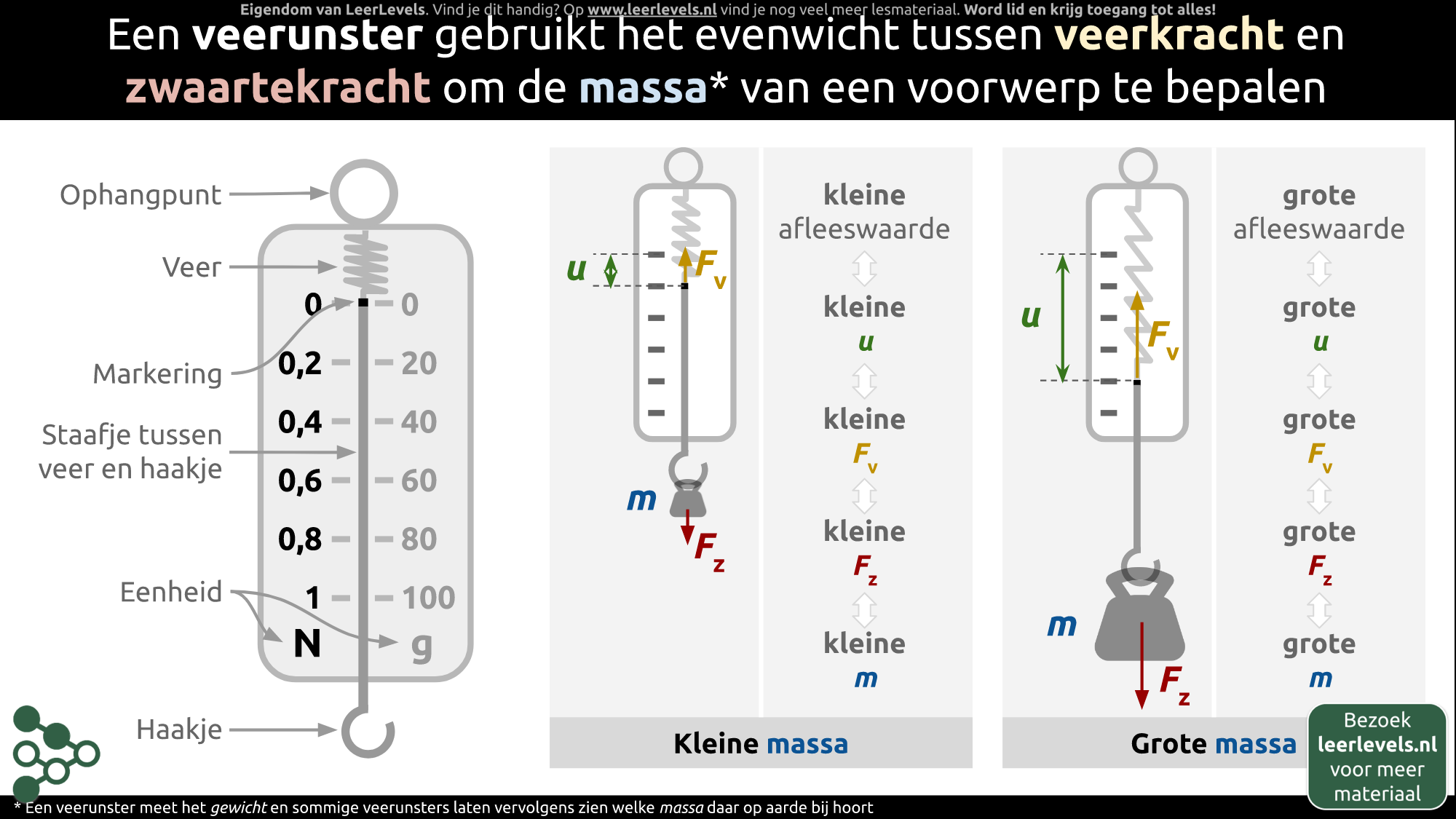
(Afbeelding: Animatie voor Veerunster concept)

Terug naar overzicht Meld je aan

Verbrandingswarmte

Verbrandingswarmte concept

De verbrandingswarmte laat zien hoeveel energie er vrijkomt als iets wordt verbrand. 1 kilo hout branden zorgt bijvoorbeeld voor ongeveer 15 megajoule aan warmte. Diesel heeft per kilogram ongeveer 45 megajoule aan warmte, ook al wordt het vaak per liter genoteerd. Voor waterstof is dit zelfs 140 megajoule per kilogram. Het kan lastig zijn om te bepalen hoeveel verbrandingswarmte waterstof heeft per liter, omdat dit afhankelijk is van of het gas- of vloeistofvormig is. Verschillende stoffen hebben verschillende verbrandingswarmtes.

(Afbeelding: Animatie voor Verbrandingswarmte concept)

Verbrandingswarmte formule

Met behulp van de verbrandingswarmte kun je berekenen hoeveel energie vrijkomt bij de verbranding van een bepaalde hoeveelheid van een stof. Voor vaste stoffen gebruik je de formule:

E = m · sM

waarbij E de energie in MJ is, m de massa in kg en sM de verbrandingswarmte in MJ/kg.

Voor vloeistoffen of gassen hanteer je meestal het volume van de stof die verbrand wordt, uitgedrukt in kubieke meters. De formule hiervoor is:

E = V · sV

waarbij V het volume in m³ is en sV de verbrandingswarmte in MJ/m³. Het is belangrijk op te merken dat de standaardeenheid voor energie de joule is, niet de megajoule. Waarom wordt er vaak gesproken in termen van megajoule? Dit komt doordat bij veel toepassingen van verbranding grote hoeveelheden energie vrijkomen. Daarom drukt men de verbrandingswarmte vaak uit in megajoule.

(Afbeelding: Animatie voor Verbrandingswarmte formule)

Terug naar overzicht Meld je aan

Vereenvoudigen

Als je een vergelijking moet oplossen, kan het helpen om deze zo snel mogelijk eenvoudiger te maken. Zorg dat de termen aan beide kanten van de vergelijking gelijk zijn. Gebruik wetenschappelijke notatie en voorvoegsels om getallen makkelijker te lezen. Bijvoorbeeld: A • B • (C + D) is hetzelfde als G • B • A keer E • F is hetzelfde als F • E keer E • 10-5. Om onbekenden te vinden, gebruik je algebra en manipuleer je de vergelijking. Je kunt vergelijkingen ook oplossen door de eenheden te veranderen. Bijvoorbeeld, als 4 km • 5 Mm hetzelfde is als 10 Gm, dan is l gelijk aan 2 m.

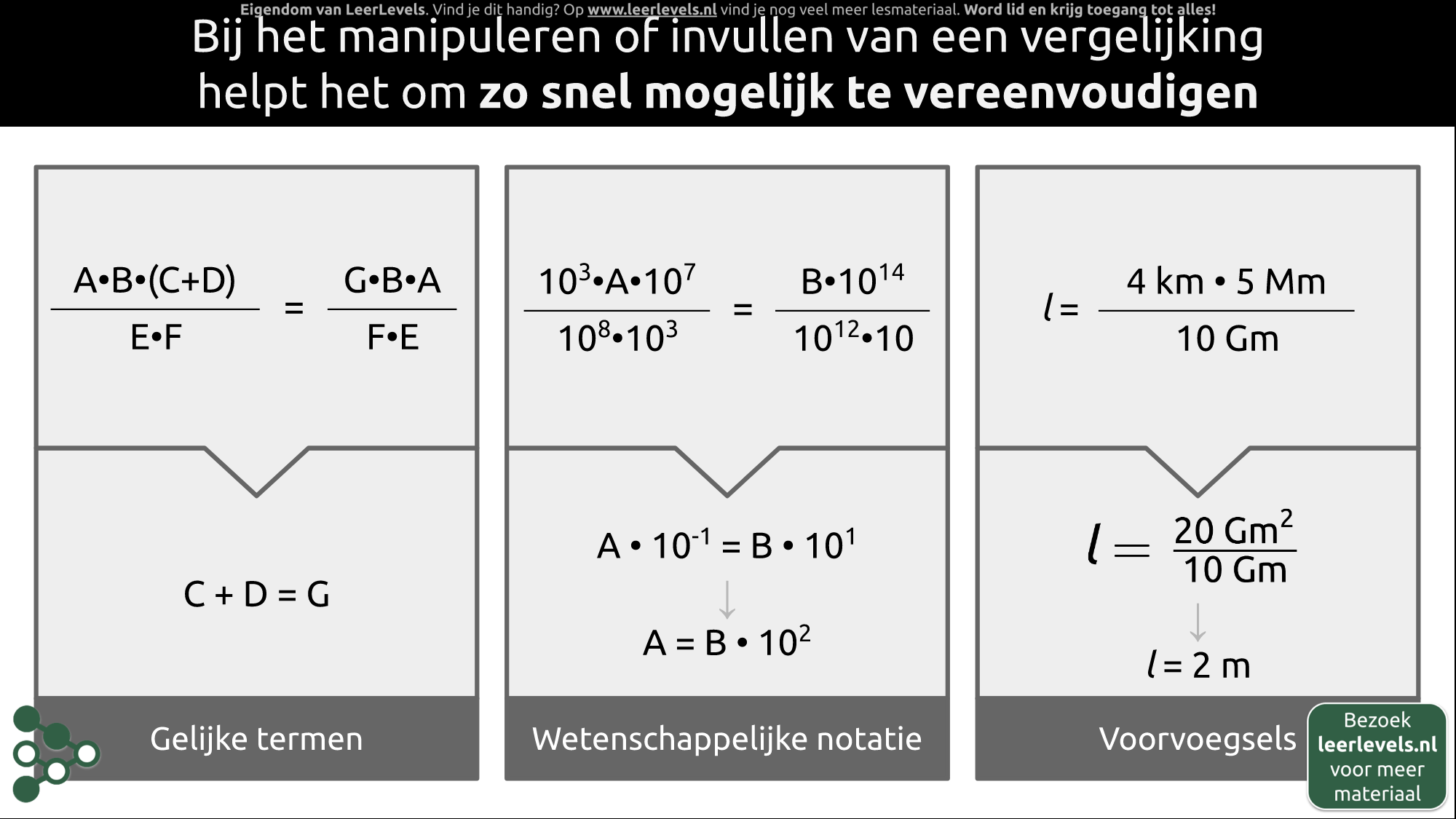
(Afbeelding: Animatie voor Vereenvoudigen)

Terug naar overzicht Meld je aan

Vergelijkingen

' = ' is ' = '

Een is-teken in een formule betekent dat links en rechts dezelfde waarde hebben. Bijvoorbeeld, als er links van het is-teken vier rondjes en rechts weer vier rondjes staan, dan is dat hetzelfde als 8 rondjes. Je mag het is-teken gebruiken omdat de twee groepen dezelfde waarde hebben. Hetzelfde geldt voor bijvoorbeeld twee briefjes van 5 en een briefje van 10. Hoewel ze niet precies hetzelfde zijn, hebben ze wel dezelfde waarde en daarom mag je het is-teken gebruiken in de vergelijking.

Wanneer je een taart in drieën deelt en een stuk neemt, is dat hetzelfde als de taart in zessen verdelen en twee stukken nemen. Maar je kunt niet zomaar twee verschillende woorden in een vergelijking plaatsen, alleen als ze dezelfde waarde hebben. Bijvoorbeeld, hoewel een gitaal een muziekinstrument is, is niet elk muziekinstrument een gitaal. Ze hebben dus niet dezelfde waarde.

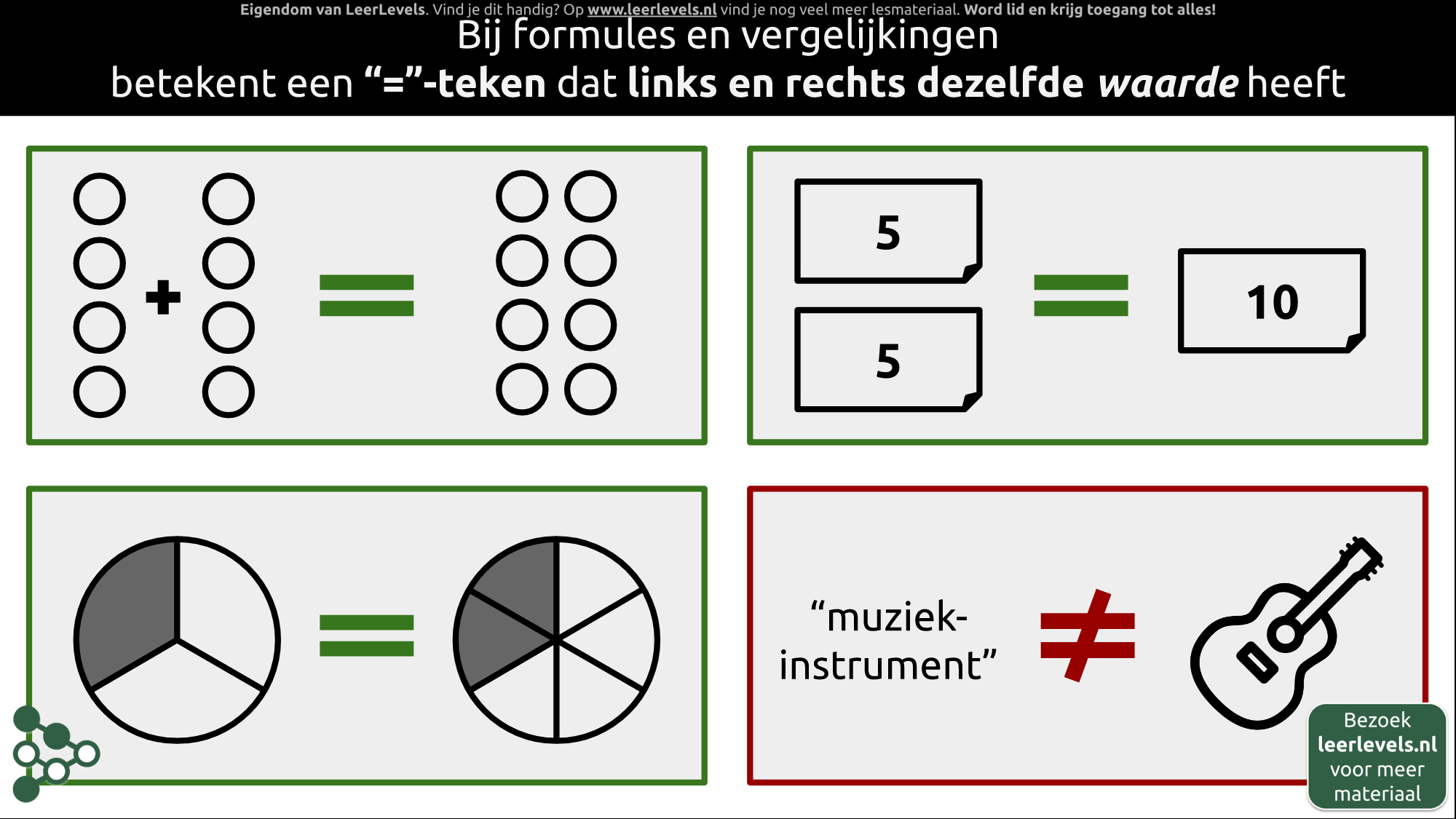
(Afbeelding: Animatie voor ' = ' is ' = ')

Toegestane operaties vergelijking

Bij het oplossen van een wiskundig probleem zijn er vijf toegestane operaties die je kunt uitvoeren op beide kanten van een vergelijking om de balans te behouden. Deze operaties zijn:

1. Verwisselen: Je kunt beide kanten van de vergelijking omdraaien. Dus als a = b, geldt ook b = a.

2. Optellen: Je mag aan beide kanten van de vergelijking dezelfde term optellen.

3. Aftrekken: Je mag aan beide kanten van de vergelijking dezelfde term aftrekken.

4. Vermenigvuldigen: Je kunt beide kanten van de vergelijking met dezelfde factor vermenigvuldigen.

5. Delen: Je mag beide kanten van de vergelijking door dezelfde factor delen (mits deze factor niet nul is).

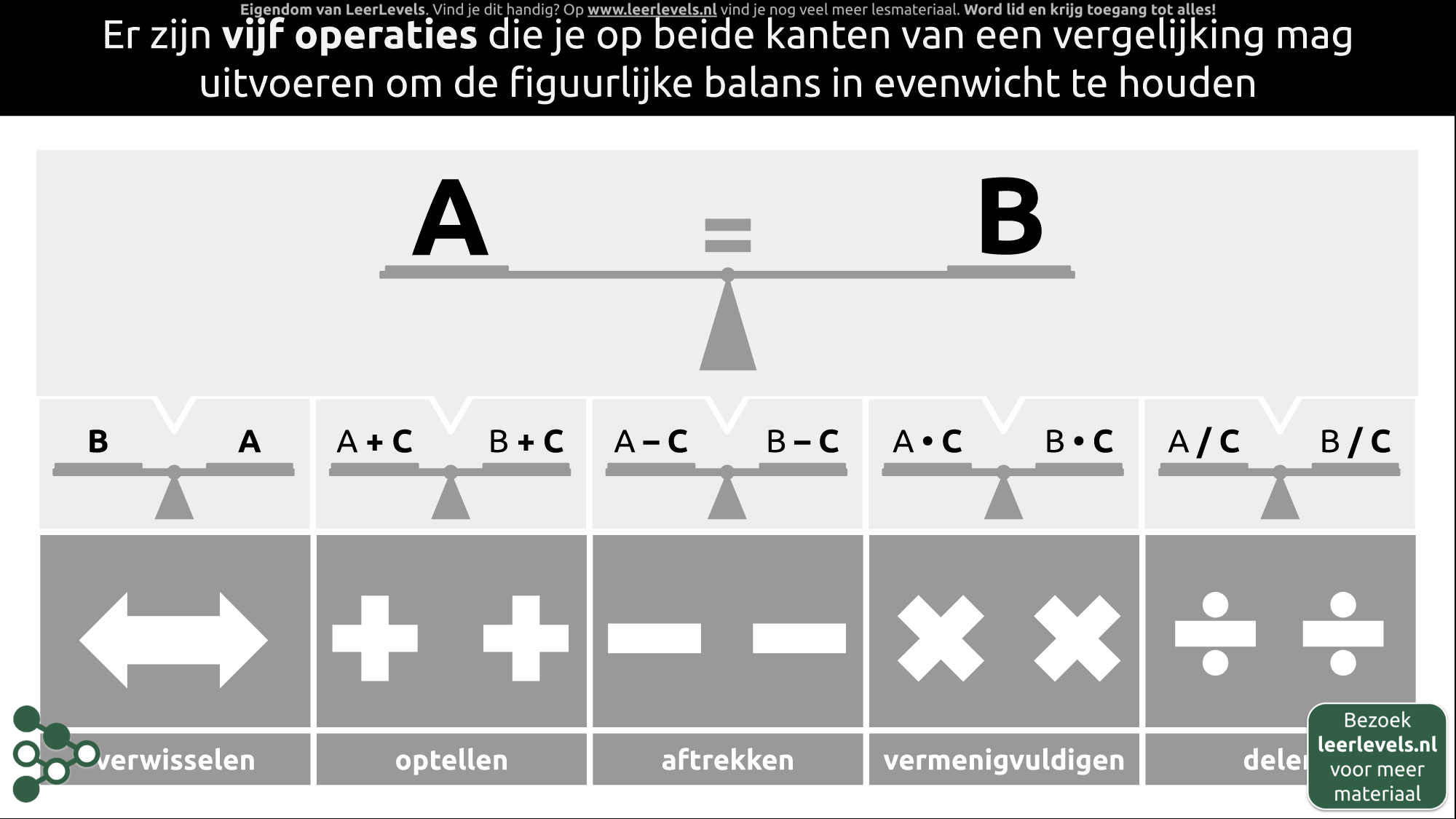
(Afbeelding: Animatie voor Toegestane operaties vergelijking)

Manipuleren van vergelijkingen

Met de vijf toegestane operaties voor vergelijkingen kun je een willekeurige variabele vrijmaken.

Stel dat je een simpele vergelijking hebt:

l · b = A

en je b wilt vrijmaken, dan kun je links en rechts van het gelijkteken delen door l. Je krijgt dan:

b = A/l

.

Iets ingewikkelder is wanneer je bij de vergelijking

v = s/t

, s wilt vrijmaken. Om de t in de noemer weg te krijgen, kun je links en rechts van het gelijkteken vermenigvuldigen met t. We krijgen dan:

v · t = s/t · t = s

Nu kun je beide kanten van de vergelijking verwisselen, dan krijgen we: s = v · t.

Een complexer voorbeeld is de volgende. Stel, we willen de formule van de trillingstijd van een slinger gebruiken:

T = 2 π √( l/g )

Uit deze vergelijking willen we g vrijmaken. Dit kunnen we doen in de volgende stappen. Eerst gaan we beide kanten delen door 2 π. We krijgen dan:

(T)/(2 π) = √( l/g )

We kunnen nu de wortel weghalen door beide kanten van de vergelijking te kwadrateren. Dit mag als beide kanten groter zijn dan nul. We krijgen nu:

(T²)/(4 π² = l/g

We kunnen links en rechts vermenigvuldigen met g om g uit de noemer te halen. We krijgen dan:

g · (T²)/(4 π² = l

Om g te isoleren, moet de factor (T²)/(4 π² weg. Dat kunnen we doen door te vermenigvuldigen met 4 π² en te delen door T². We kunnen beide vermenigvuldigingen in één keer doen. We krijgen:

g = (4 π² · l)/(T²

(Afbeelding: Animatie voor Manipuleren van vergelijkingen)

Terug naar overzicht Meld je aan

Vergroting

Vergroting formule

De vergroting (N) is de verhouding tussen de beeldafstand (b) en de voorwerpsafstand (v), of de verhouding tussen de beeldgrootte (LB) en de voorwerpgrootte (LV)

N = b/v = (LB)/(LV)

Om dit te verduidelijken, laten we een voorwerp fotograferen. Het voorwerp heeft een grootte van LV en het resulterende beeld heeft een grootte van LB. De afstand tussen het voorwerp en de lens is v, en de afstand tussen het beeld en de lens is b.

In deze opstelling hebben we twee gelijkvormige driehoeken, driehoek 1 en driehoek 2.

De vergroting, of vergrotingsfactor (N), kan worden berekend door kleine b te delen door kleine v. Hierbij is N de vergroting (een dimensieloze factor), b de beeldafstand in meters en v de voorwerpsafstand in meters. Vanwege de gelijkvormigheid van de driehoeken kan de vergroting ook worden berekend door grote LB, de beeldgrootte in meters, te delen door grote LV, de voorwerpgrootte in meters.

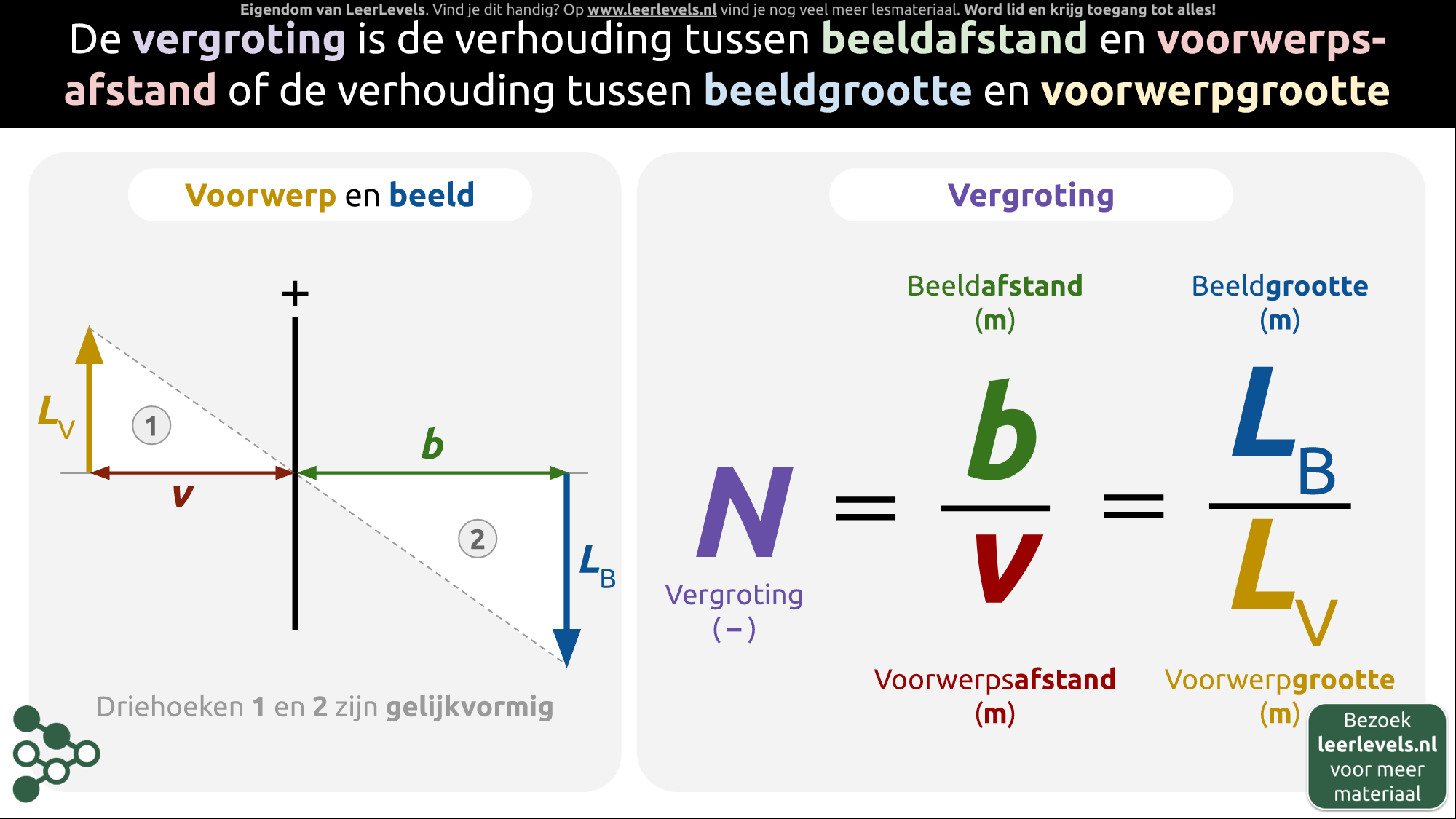
(Afbeelding: Animatie voor Vergroting formule)

Terug naar overzicht Meld je aan

Verhoudingstabel

Een verhoudingstabel kan helpen bij het berekenen van onbekende waarden. Als je bijvoorbeeld weet dat drie appels 650 gram wegen en je wilt weten hoeveel appels er nodig zijn om samen 2200 gram te wegen, gebruik je zo'n tabel. In de tabel zie je dat 3 appels gelijk zijn aan 650 gram. Nu is de vraag hoeveel appels, x, gelijk zijn aan 2200 gram. Je kunt dit berekenen door 3 appels te vermenigvuldigen met 2200 gram en te delen door 650 gram. Dit geeft ongeveer 10 appels.

Een ander voorbeeld gaat over de lading van protonen. Als je weet dat de lading van een proton gelijk is aan 1,602 × 10⁻¹⁹ Coulomb, kun je uitrekenen hoeveel protonen je nodig hebt voor een lading van 1 Coulomb. Dit kun je op dezelfde manier doen als bij de appels. Door een nieuwe kolom te maken in de verhoudingstabel, kun je berekenen dat 1 Coulomb gelijk is aan ongeveer 6,24 × 10¹⁸ protonen. Dit is het aantal protonen dat samen een lading van 1 Coulomb hebben.

(Afbeelding: Animatie voor Verhoudingstabel)

Terug naar overzicht Meld je aan

Vermogen

Eenheid pk

De eenheid 'paardenkracht' (pk) komt overeen met een vermogen van ongeveer 740 W. Eerst is het belangrijk om te begrijpen dat paardenkracht geen kracht is, maar een maat voor vermogen. Het zijn dus verschillende grootheden. Paardenkracht wordt gebruikt om vermogen uit te drukken.

Waarom is een vermogen van 740 watt gekozen? Dit komt doordat paardenkracht oorspronkelijk is gedefinieerd als het vermogen dat een paard levert wanneer het gedurende een minuut een massa van 150 kilogram over een hoogte van 30 meter optilt.

We kunnen eenvoudig aantonen dat dit leidt tot ongeveer 740 watt. Vermogen is energie gedeeld door tijd, en in dit geval is de energie gelijk aan de arbeid die het paard verricht. De arbeid is gelijk aan de zwaarte-energie die aan het blok wordt overgedragen, oftewel:

150 kg × 9,81 m/s² × 30 m

Dit komt neer op 44,145 J. De tijd is 60 seconden. Door deze gegevens in te vullen en de berekening te maken, kom je tot de conclusie dat het vermogen gelijk is aan:

(44,145 J)/(60 s)

Dit komt neer op ongeveer 736 W, oftewel 0,736 kW.

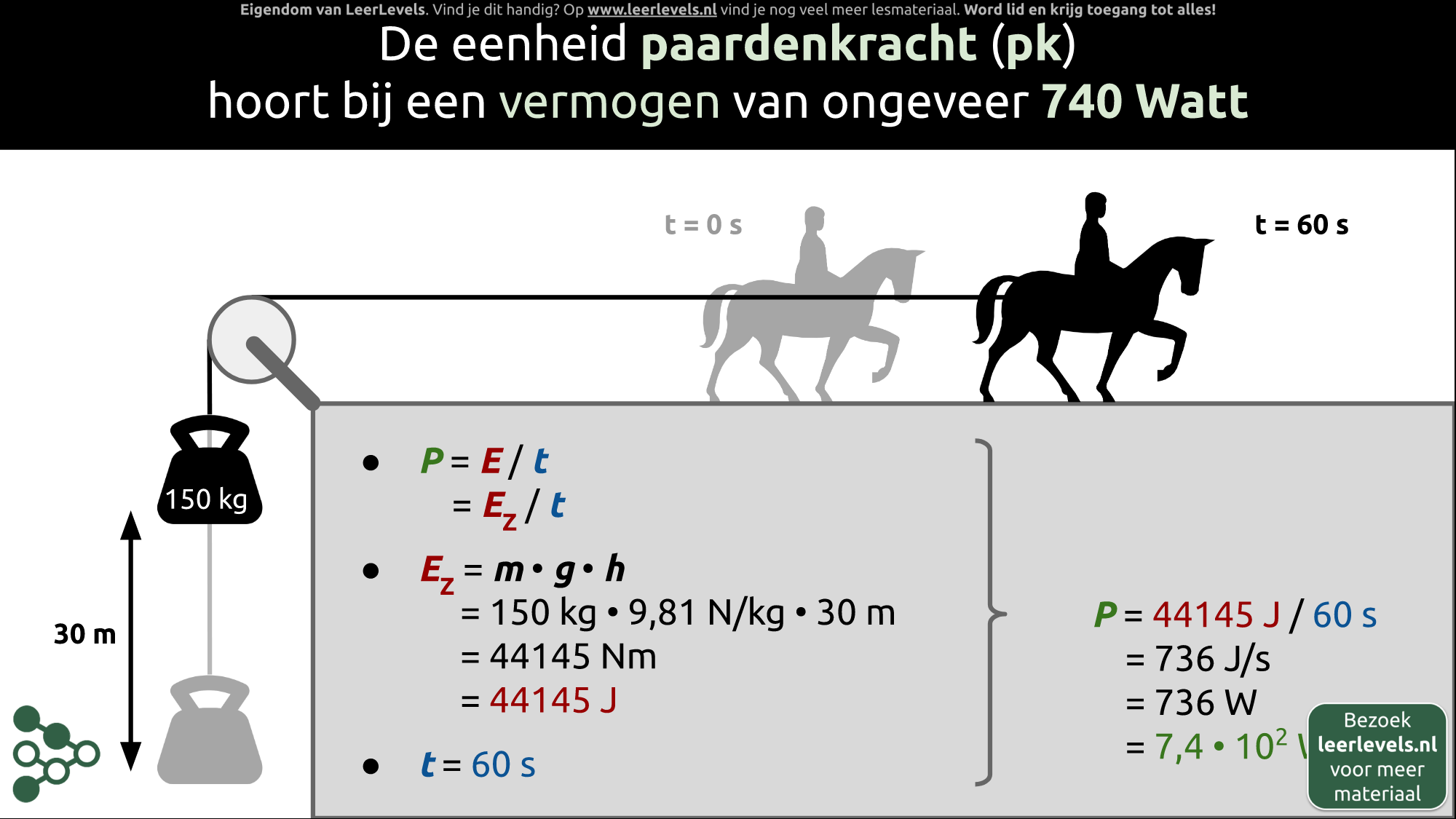
(Afbeelding: Animatie voor Eenheid pk)

Vermogen, kracht en snelheid

Als de snelheid bekend en constant is, kan het vermogen berekend worden dat door een bepaalde kracht geleverd wordt. Neem bijvoorbeeld een auto die rijdt met een constante motorkracht. Om de auto in beweging te houden, moet deze kracht de wrijvingskracht overwinnen. Dit betekent dat de motor vermogen moet leveren om deze wrijvingskracht te overwinnen.

Om het vermogen te berekenen, moeten we weten welke hoeveelheid energie de motor in een bepaalde tijd levert. De energie die de motor levert, is gelijk aan de arbeid die gedaan wordt, oftewel de kracht maal de afgelegde afstand: E = F · s. Als de afstand niet direct bekend is, kunnen we deze vervangen door de snelheid waarmee de auto rijdt, vermenigvuldigd met een willekeurige tijdsduur: s = v · t

Het vermogen dat de auto levert, is de energie gedeeld door de tijd: P = E/t . Dit kan verder worden uitgedrukt als:

P = F · v

waarbij F de kracht in newton (N) is en v de snelheid in meter per seconde (m/s). Zo kunnen we het vermogen P in watt (W) berekenen. Daarnaast kan het vermogen ook uitgedrukt worden in paardenkracht (pk). Bij een constante kracht en een constante snelheid is deze formule nuttig voor het berekenen van het geleverde vermogen.

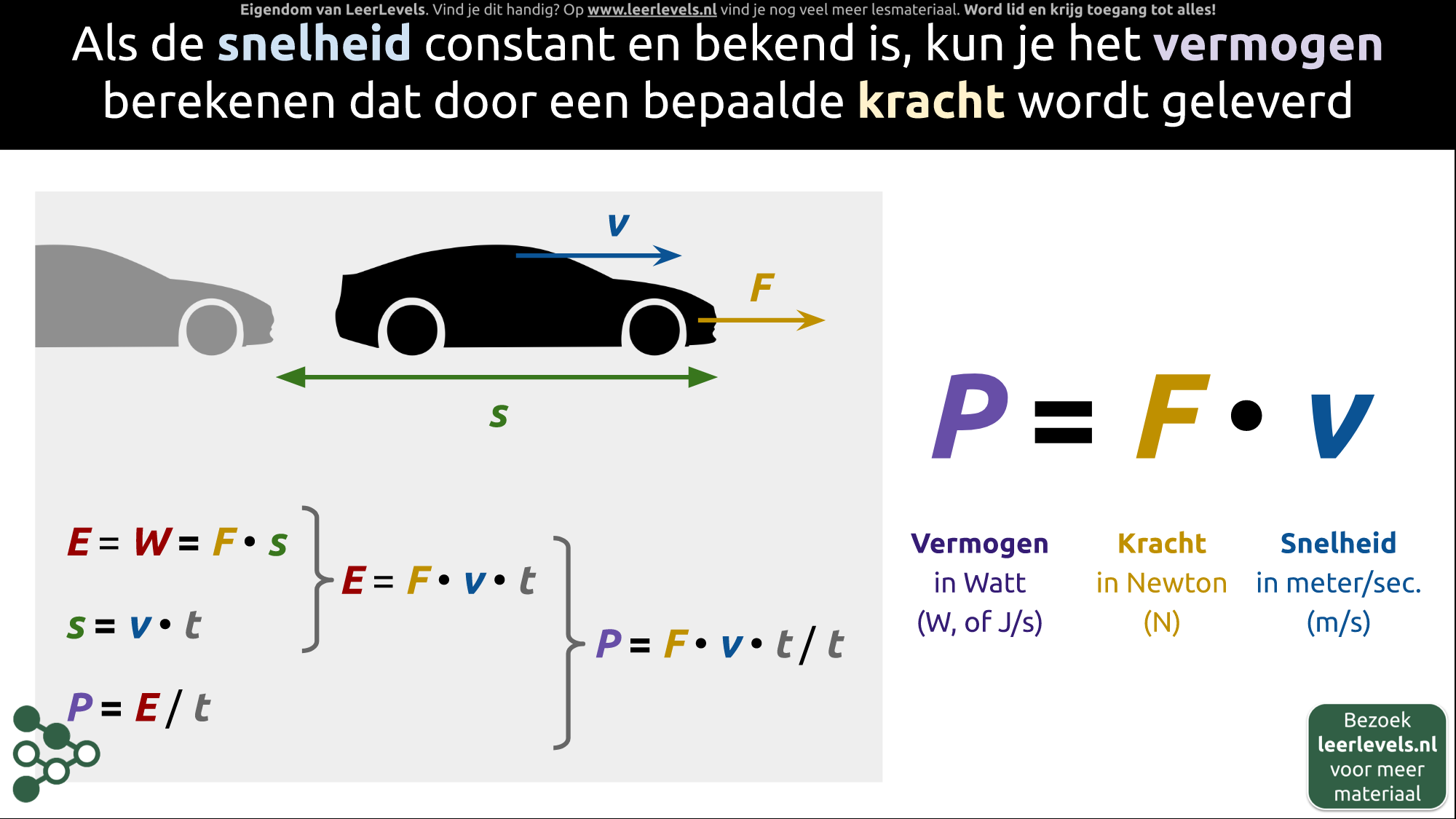
(Afbeelding: Animatie voor Vermogen, kracht en snelheid)

Vermogen concept

Vermogen (P) is de hoeveelheid energie die per seconde wordt omgezet. Stel dat je een berg beklimt; daarbij verbruik je energie om de top te bereiken. Dit kan op verschillende manieren. Je kunt bijvoorbeeld ontspannen en langzaam de berg op fietsen, wat weinig energie per seconde vraagt en dus een klein vermogen vereist. Aan de andere kant kun je als professioneel wielrenner besluiten om de berg in hoog tempo te beklimmen, wat veel energie per seconde vergt en dus een groot vermogen vereist. Hierbij wordt de energie in je lichaam omgezet in potentiële energie. In beide gevallen is de totale energie die je nodig hebt om de top te bereiken ongeveer gelijk, maar de ene persoon doet het langzaam met een klein vermogen, terwijl de andere het snel doet met een groot vermogen.

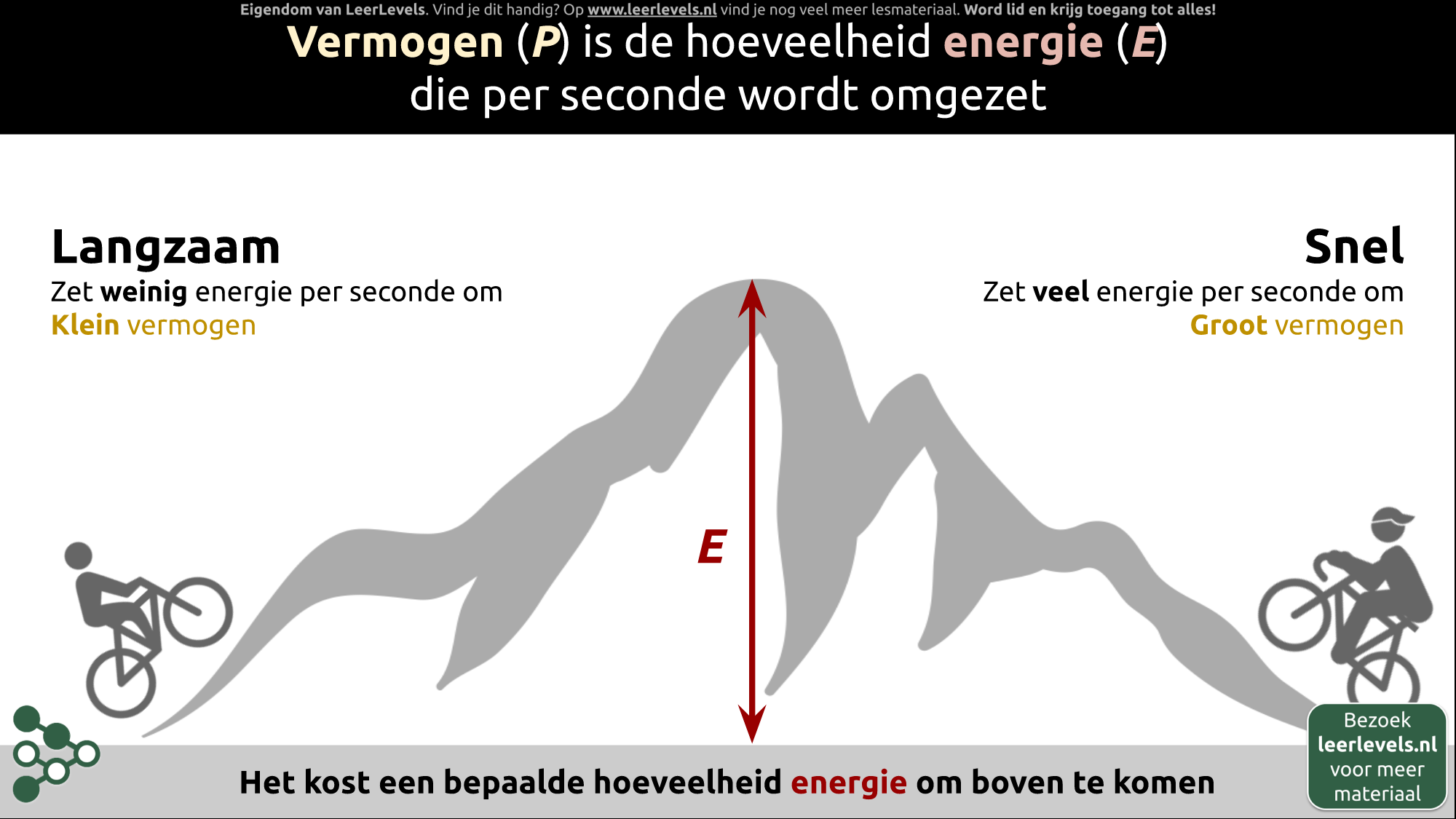
(Afbeelding: Animatie voor Vermogen concept)

Vermogen formule

Vermogen is recht evenredig met de omgezette energie en omgekeerd evenredig met de benodigde tijd. In formulevorm ziet dit er als volgt uit:

P = E/t

Hierbij wordt het vermogen uitgedrukt in joule per seconde (J/s), wat ook wel watt (W) wordt genoemd.

(Afbeelding: Animatie voor Vermogen formule)

Terug naar overzicht Meld je aan

Verplaatsing

Verplaatsing en afgelegde weg

Er is een verschil tussen afgelegde weg en verplaatsing. De afgelegde weg is de totale lengte van de route die je hebt gelopen. De verplaatsing is de kortste afstand tussen het beginpunt en het eindpunt. Laten we dit verduidelijken met drie voorbeelden.

In het eerste voorbeeld loop je in een rechte lijn van punt A naar punt B. De afgelegde weg is bijvoorbeeld 10 meter. Omdat je in een rechte lijn loopt, is de verplaatsing ook 10 meter, aangezien dit de kortste afstand tussen A en B is.

In het tweede voorbeeld loop je opnieuw van punt A naar punt B, maar je neemt een kronkelige route. Hierdoor is de afgelegde weg langer, bijvoorbeeld 15 meter. De verplaatsing blijft echter 10 meter, omdat de kortste afstand tussen het beginpunt en het eindpunt hetzelfde blijft.

In het derde voorbeeld ga je in een rechte lijn van A naar B en keer je vervolgens weer in een rechte lijn terug naar A. De afgelegde weg is dan 10 + 10 = 20 meter. De verplaatsing is echter 0 meter, omdat je beginpunt en eindpunt hetzelfde zijn.

Kortom, er is een onderscheid tussen afgelegde weg en verplaatsing.

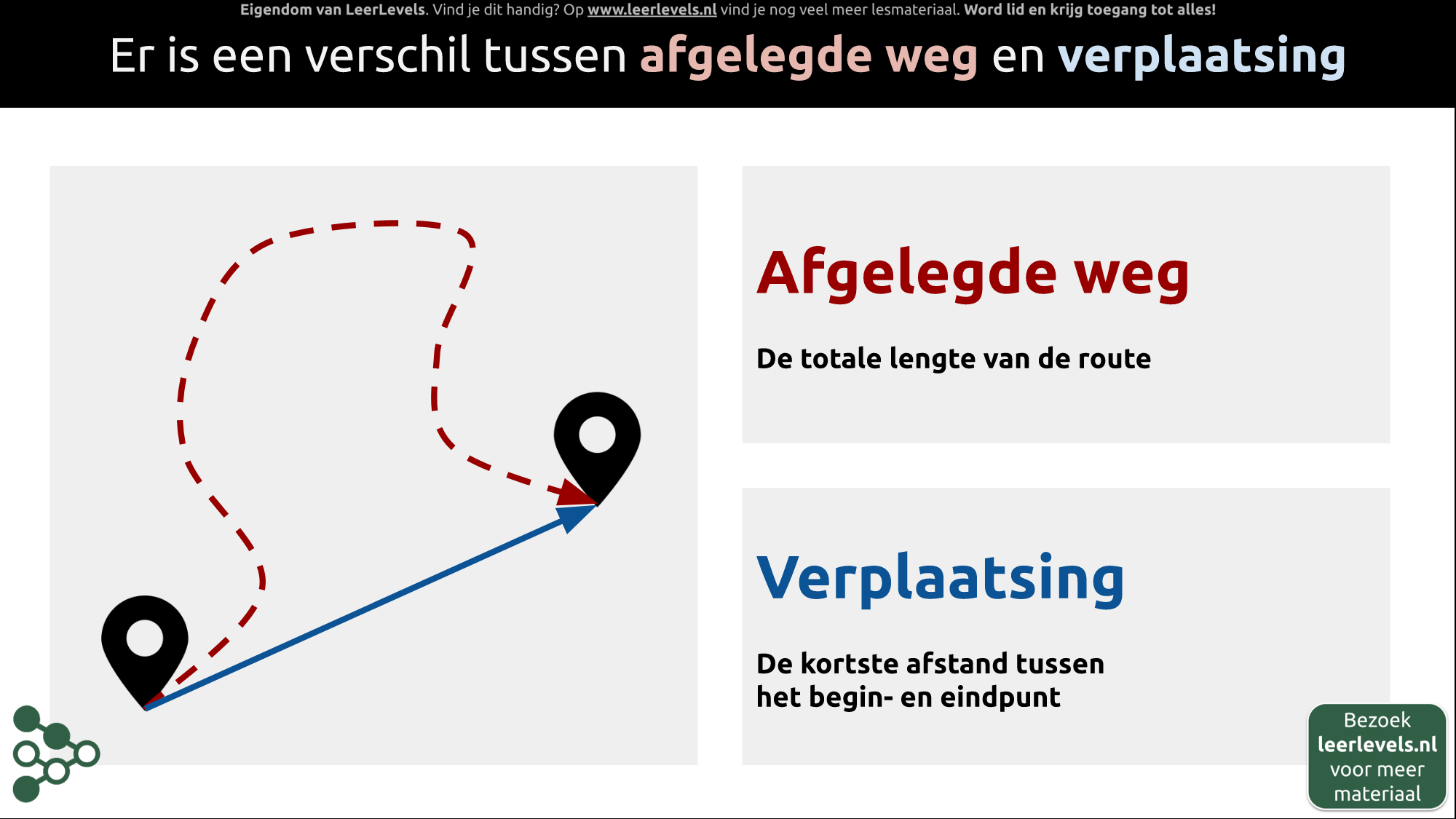
(Afbeelding: Animatie voor Verplaatsing en afgelegde weg)

Terug naar overzicht Meld je aan

Versnelling

Versnelling concept

Wanneer een voorwerp versnelt, neemt de snelheid toe. Indien het echter niet versnelt, is de versnelling nul en blijft de snelheid constant. In de afbeelding is dit weergegeven met de rode streepjes. Neem bijvoorbeeld een fietser: als deze een versnelling heeft, begint hij of zij met een bepaalde snelheid. De fietser zal vervolgens proberen steeds sneller te gaan met een bepaalde versnelling. Deze versnelling zorgt ervoor dat de fietser na verloop van tijd sneller gaat, en daarna nóg sneller. Elke seconde wordt de snelheid van de fietser verder vergroot. Versnelling is de verandering van snelheid.

(Afbeelding: Animatie voor Versnelling concept)

Gemiddelde versnelling formule

De gemiddelde versnelling is recht evenredig met het snelheidsverschil en omgekeerd evenredig met het tijdsverschil. In formulevorm wordt dit weergegeven als:

a = (Δ v)/(Δ t)

waarbij a staat voor de gemiddelde versnelling in meter per seconde kwadraat (m/s²). Δ v is het snelheidsverschil in meter per seconde (m/s) en Δ t is het tijdsverschil in seconden (s). Als je de snelheid op twee verschillende tijdstippen kent, kun je de versnelling berekenen door het snelheidsverschil te delen door het tijdsverschil.

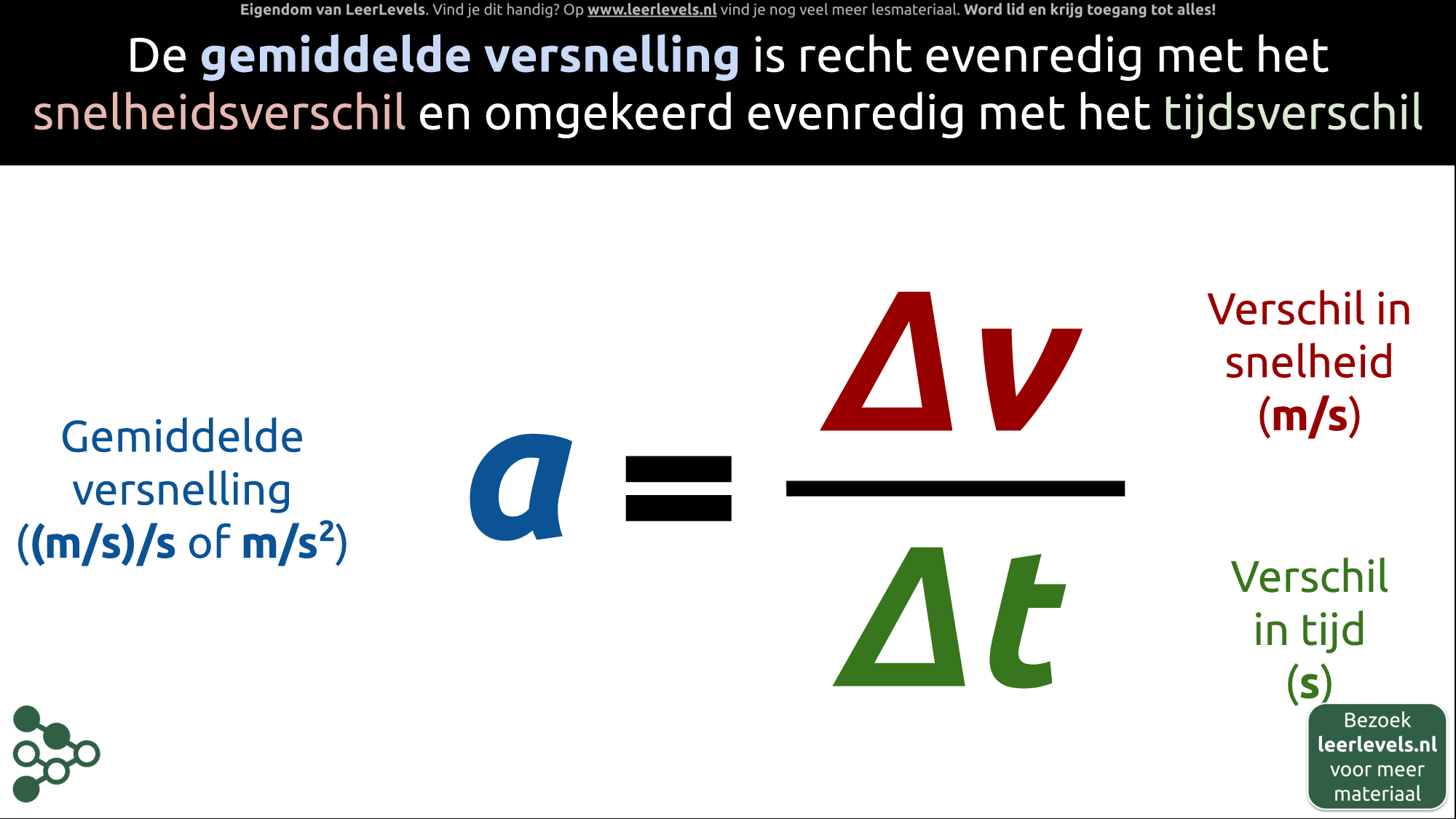
(Afbeelding: Animatie voor Gemiddelde versnelling formule)

Versnellen en vertragen

Als iets versnelt, gaat het steeds sneller. Dit kunnen we zien in een grafiek waarbij de snelheid toeneemt. Als iets een constante snelheid heeft, is de grafiek een constante blauwe lijn. Als iets vertraagt, bijvoorbeeld omdat er een parachute wordt geopend, gaat de grafiek juist omlaag. Bij versnelling wordt de snelheid groter en bij vertraging juist kleiner. Dit kun je berekenen met formules en grootheden zoals v voor snelheid en t voor tijd, weergegeven als v(t).

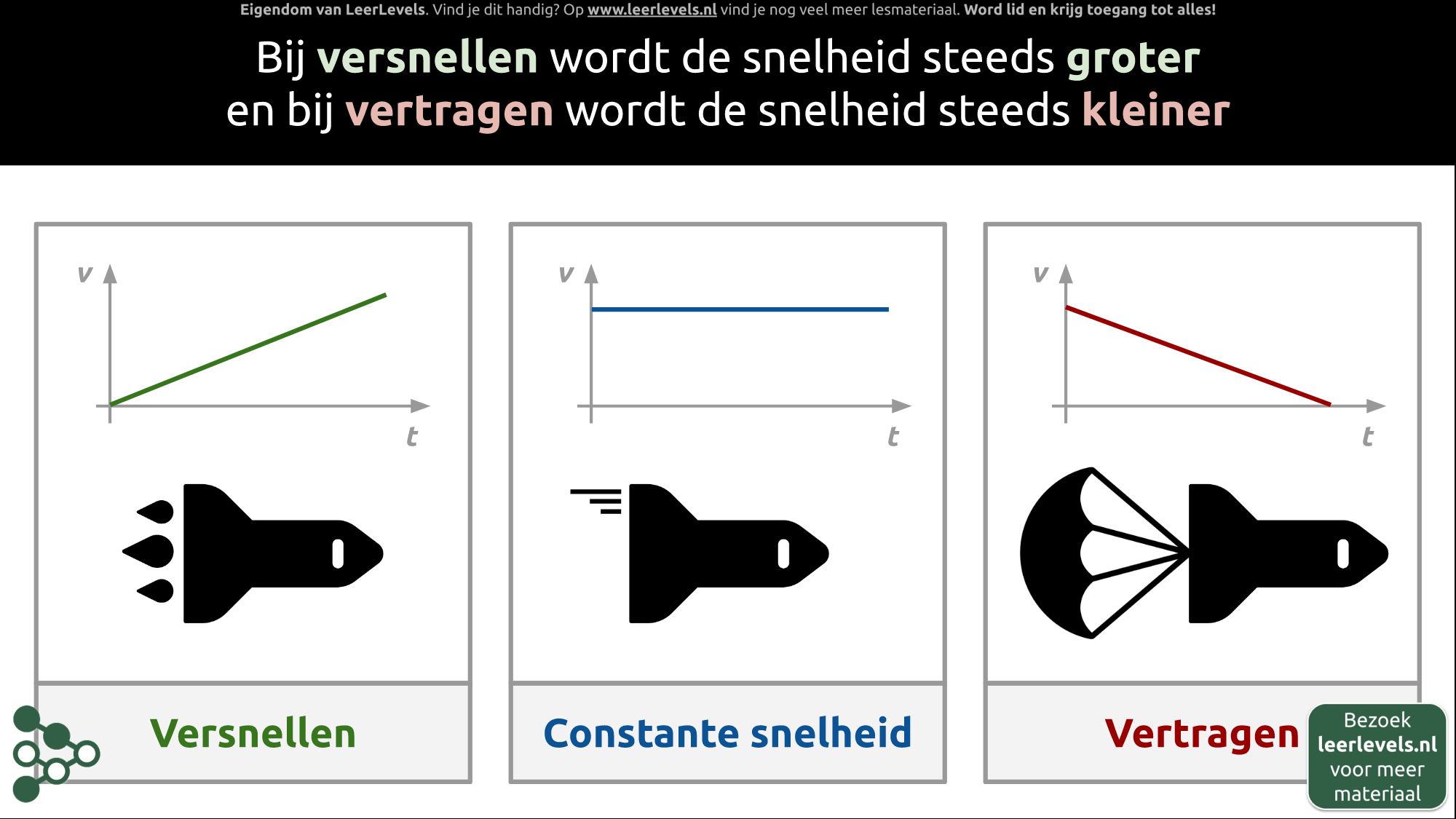
(Afbeelding: Animatie voor Versnellen en vertragen)

Terug naar overzicht Meld je aan

Verticale worp

Een verticale worp geeft een voorwerp een beginsnelheid. Als er geen wrijving is, valt het voorwerp met een constante versnelling naar beneden totdat het de grond raakt. Stel dat we een bal vanaf de grond omhoog gooien. Op t = 0 heeft de bal een bepaalde beginsnelheid naar boven. Vervolgens ondervindt de bal een vertraging door zwaartekracht. Hierdoor heeft de bal op t = 1 een kleinere opwaartse snelheid en op t = 2 bereikt de bal het hoogste punt met een snelheid van nul. Op t = 3 heeft de bal dezelfde snelheid als op t = 1, maar nu naar beneden gericht. Op t = 4 is de bal geland met dezelfde snelheid als de beginsnelheid, maar nu naar beneden gericht. Tijdens de hele beweging is de versnelling constant en gelijk aan de valversnelling, ongeveer gelijk aan -10 m/s². Dit betekent dat de snelheid elke seconde met 10 m/s verandert. De hoogte van de bal is te zien in het ht-diagram, waarbij de kromme gevormd wordt wanneer de bal het hoogste punt bereikt. Na de landing blijft de bal op dezelfde hoogte liggen, wat betekent dat er een flinke versnelling omhoog was tijdens de botsing met de grond. Bij het begin van de beweging is er een versnelling en afgelegde weg nodig om de bal een beginsnelheid te geven. De praktijk is lastiger omdat er meer ruimte nodig is om de bal te versnellen en daardoor zal de versnelling die aan de bal wordt gegeven veel groter moeten zijn.

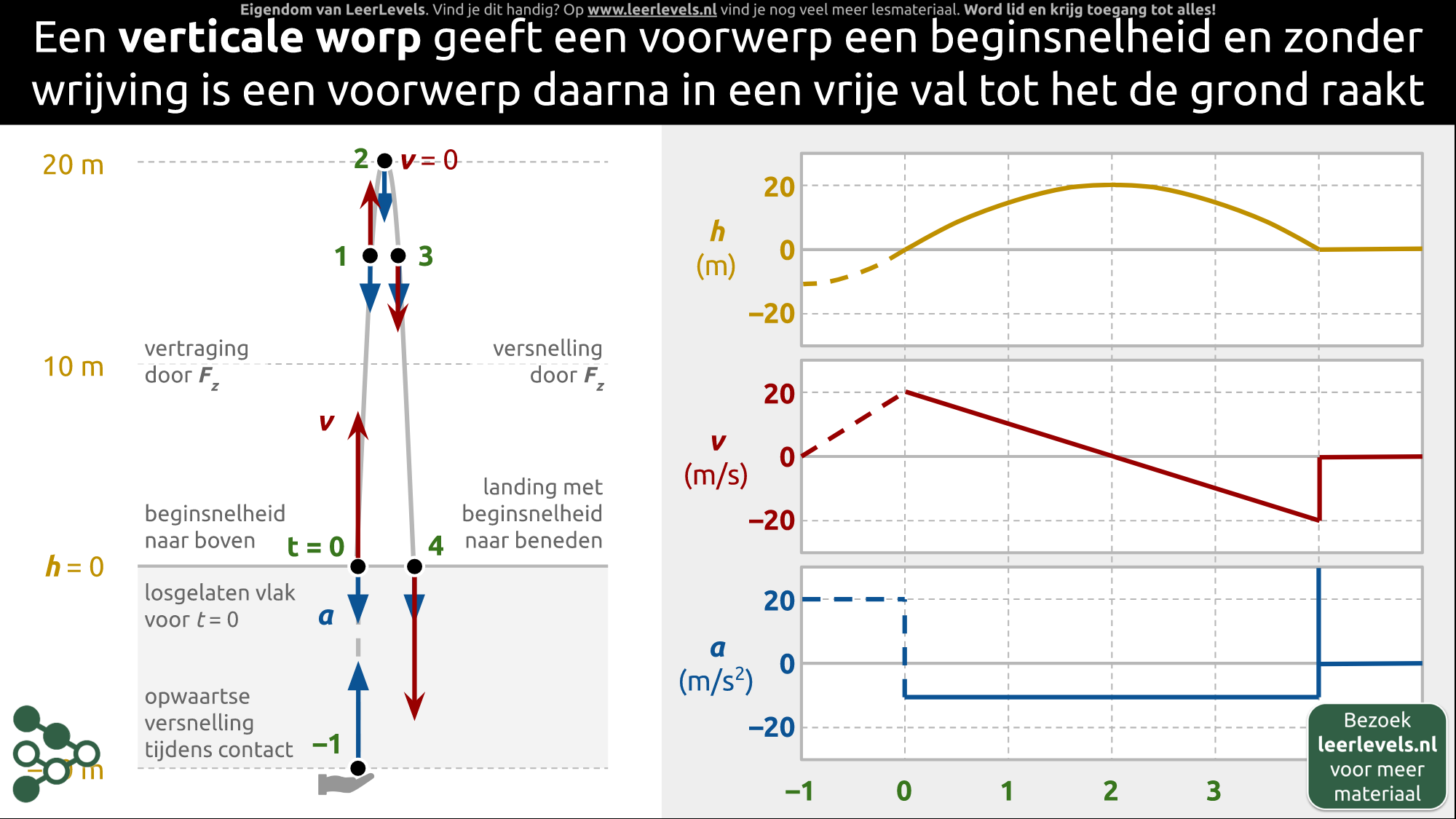
(Afbeelding: Animatie voor Verticale worp)

Terug naar overzicht Meld je aan

Verval

Vervalvergelijking

Bij vervalreacties blijven de totale lading en het aantal deeltjes behouden. Laten we een voorbeeld bekijken: het verval van uranium-235. Voor het verval heeft de kern 235 deeltjes en een lading van 92. Dit betekent dat deze waarden ook na het verval gelijk moeten zijn. Als je het verval van uranium-235 opzoekt in de BiNaS, zie je dat het een alfaverval betreft waarbij een heliumkern vrijkomt. Dit houdt in dat één van de reactiedeeltjes He⁴₂ is. Voor en na het verval moeten de aantallen deeltjes gelijk blijven. Het andere product heeft dus een aantal kerndeeltjes van 235 - 4 = 231. Voor de lading geldt hetzelfde principe, wat resulteert in een lading van 92 - 2 = 90. Dit betekent dat het overgebleven element thorium Th²³⁹₉₀ is.

Stel dat je begint met zuurstof, dan moet het aantal kerndeeltjes zowel voor als na 19 zijn en de lading 8. Een elektron komt vrij, waardoor het andere deeltje F¹⁹₉ moet zijn.

Ten slotte, dit principe werkt ook andersom. Als je weet dat een bepaalde vervalreactie resulteert in de vrijlating van een neutron en een positron, moet het totale aantal deeltjes en de totale lading hetzelfde blijven. Dit betekent dat er oorspronkelijk een proton aanwezig was.

(Afbeelding: Animatie voor Vervalvergelijking)

Terug naar overzicht Meld je aan

Vervalreeks

Vervalreeks concept

Een vervalreeks omvat alle opeenvolgende vervalreacties die plaatsvinden vanaf het moment dat een element instabiel wordt. Neem bijvoorbeeld het verval van bismut-212. We beginnen met bismut-212, dat instabiel is. Na een bepaalde tijd ondergaat het alfa-verval, waarbij een alfadeeltje vrijkomt. Door dit proces ontstaat thallium-208, dat nog steeds instabiel is. Vervolgens vindt er bèta-min-verval plaats, waarbij een elektron vrijkomt en het resulteert in lood-208 dat stabiel is. Op dit punt eindigt de vervalreeks.

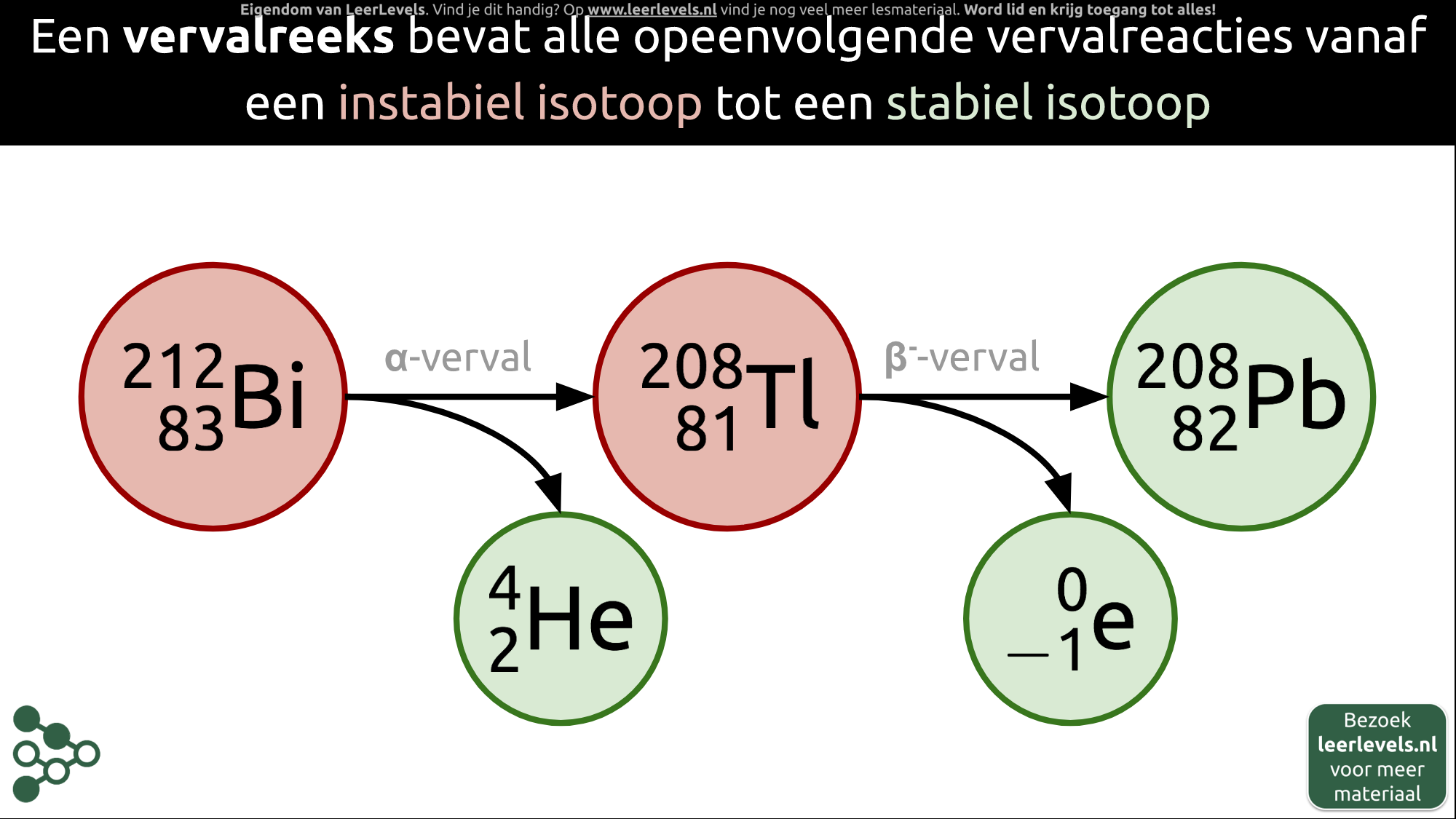
(Afbeelding: Animatie voor Vervalreeks concept)

Terug naar overzicht Meld je aan

Vervalvergelijking

Vervalvergelijking met Binas

Om een vervalvergelijking te maken met behulp van Binas, moet je drie stappen volgen. Als voorbeeld nemen we Uranium-236.

Stap 1 is het zoeken van het vervalproduct in de Isotopentabel van Binas. Voor uranium-236 zien we alfa en gamma verval. We kiezen alleen het eerstgenoemde, dus alfa-verval.

Stap 2 is het kloppend maken van de vervalvergelijking. We schrijven het vervalproduct na de pijl, het massagetal als A en het atoomnummer als Z. In dit geval is A gelijk aan 232 en Z is 90.

Stap 3 is het bepalen van de dochterkern door het atoomnummer van 90 op te zoeken in de tabel. Dit blijkt Thorium-232 te zijn (Th). We kunnen dit symbool nu toevoegen aan de vergelijking. De volledige vervalreactie is Uranium-236 → Thorium-232 + Helium-4.

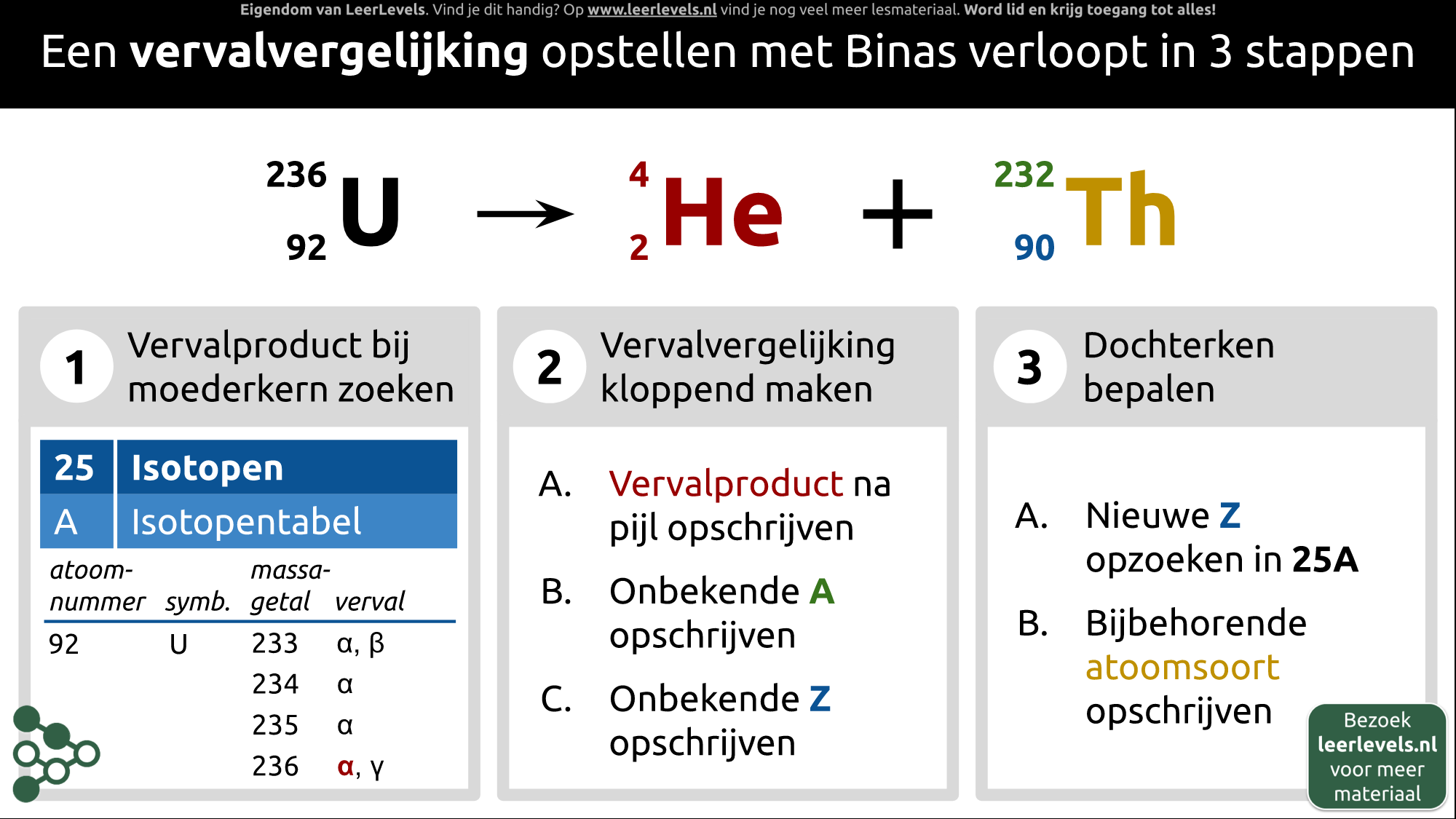
(Afbeelding: Animatie voor Vervalvergelijking met Binas)

Terug naar overzicht Meld je aan

Vervorming

Vervorming concept

Als je een materiaal uitrekt, kan het op twee manieren vervormen: tijdelijk of permanent. Tijdelijke vervorming betekent dat het materiaal terugveert naar zijn oorspronkelijke vorm als je stopt met trekken. Een elastiekje is hiervan een voorbeeld. Permanente vervorming betekent dat het materiaal in een nieuwe vorm blijft, zelfs als je stopt met trekken. Er zijn drie vormen van permanente vervorming: vloeien, insnoeren en breken. Vloeien gebeurt als een draad langer wordt wanneer de spanning wegvalt. Insnoeren gebeurt als een draad niet alleen langer wordt, maar ook dunner in het midden. Als de spanning te hoog is, kan de draad breken. Hierbij gebruiken we formules en eenheden zoals F (kracht) en L (lengte), maar deze zijn niet relevant voor deze uitleg.

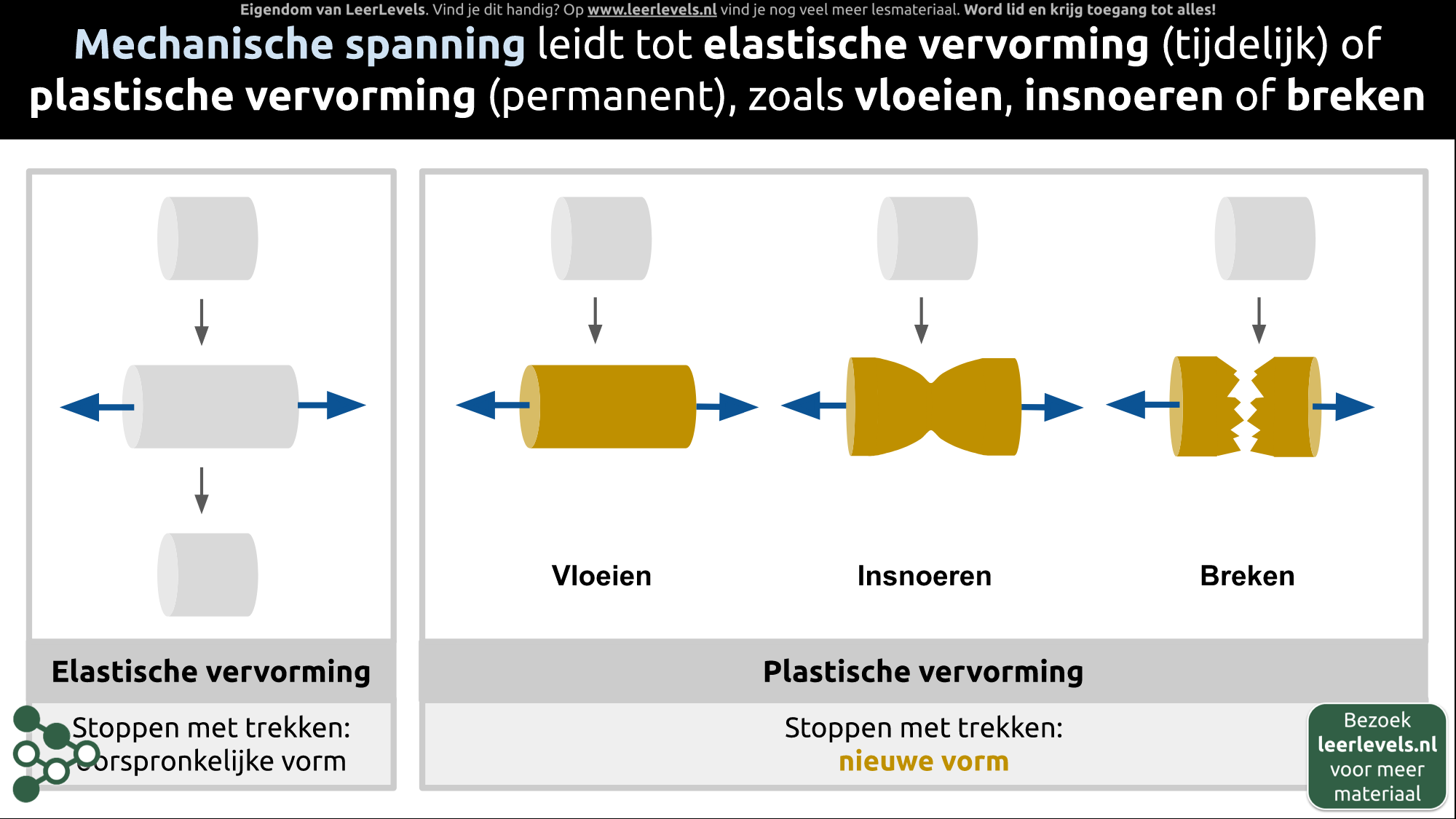
(Afbeelding: Animatie voor Vervorming concept)

Terug naar overzicht Meld je aan

Volume

Volume definitie

Het volume, aangeduid met V, geeft aan hoeveel ruimte een object in drie dimensies inneemt en wordt ook wel de inhoud genoemd. Lijnen en vlakken zijn tweedimensionaal en hebben geen volume. Een dobbelsteen heeft bijvoorbeeld een klein volume. Een voorwerp met een groot volume neemt daarentegen veel ruimte in.

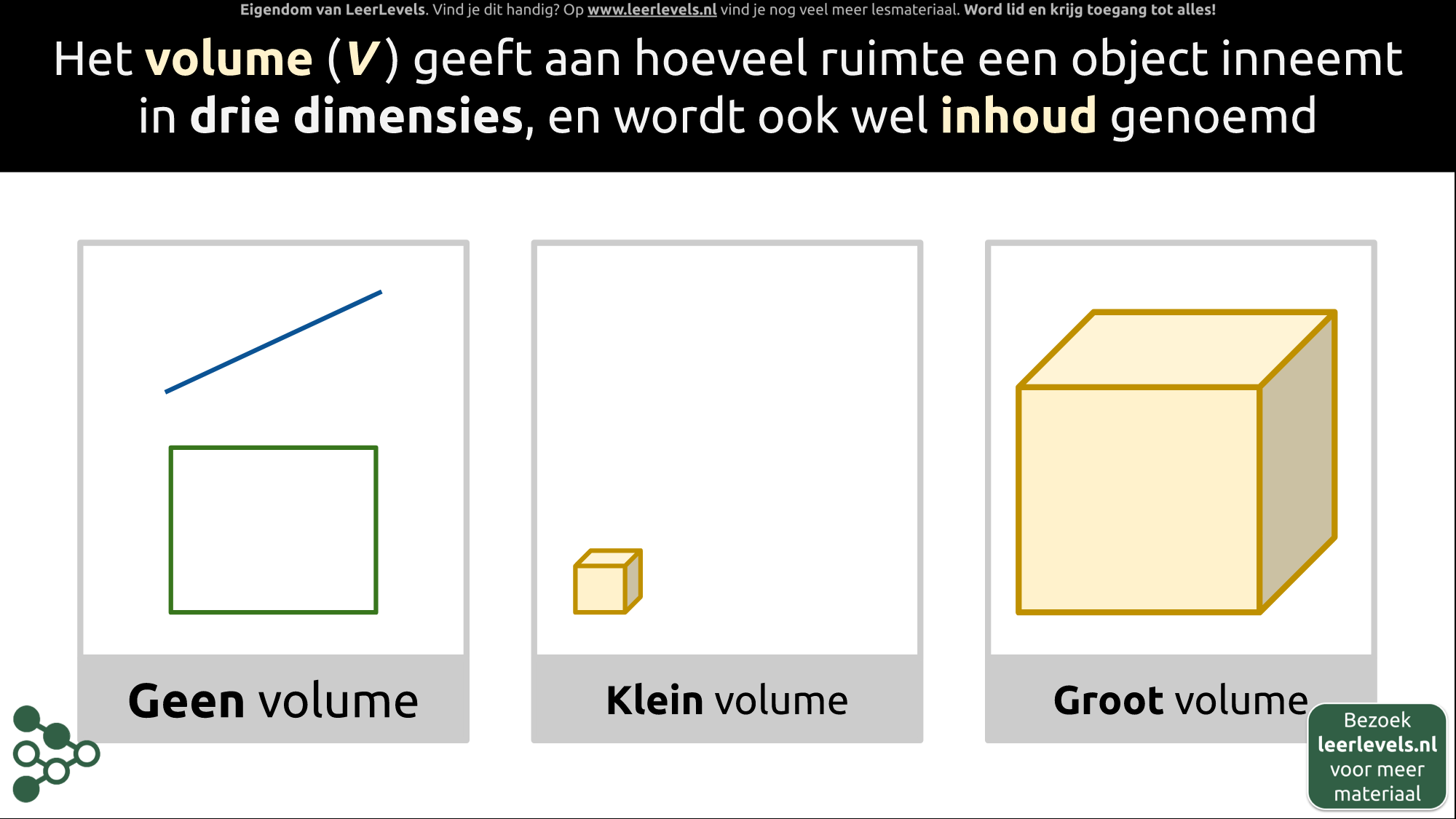
(Afbeelding: Animatie voor Volume definitie)

Volume formules

Als je het volume van een voorwerp wilt berekenen, heb je een formule nodig die afhankelijk is van de vorm van het voorwerp. Deze formules staan in tabel 35 van het boek Binas. Als je bijvoorbeeld een balk hebt met een lengte van l, breedte van b en hoogte van h in meters, kun je het volume berekenen door de formule V = l · b · h te gebruiken. Het antwoord is dan in kubieke meters. Als je een bol hebt met een straal van r in meters, kun je het volume berekenen met de formule V = 4/3 · π · r³. Bij een cilinder is het volume de oppervlakte van de bodem maal de hoogte, dus V = oppervlakte · h. Bij een piramide of kegel is het volume gelijk aan een derde van het grondvlak maal de hoogte, dus V = 1/3 · grondvlak · h.

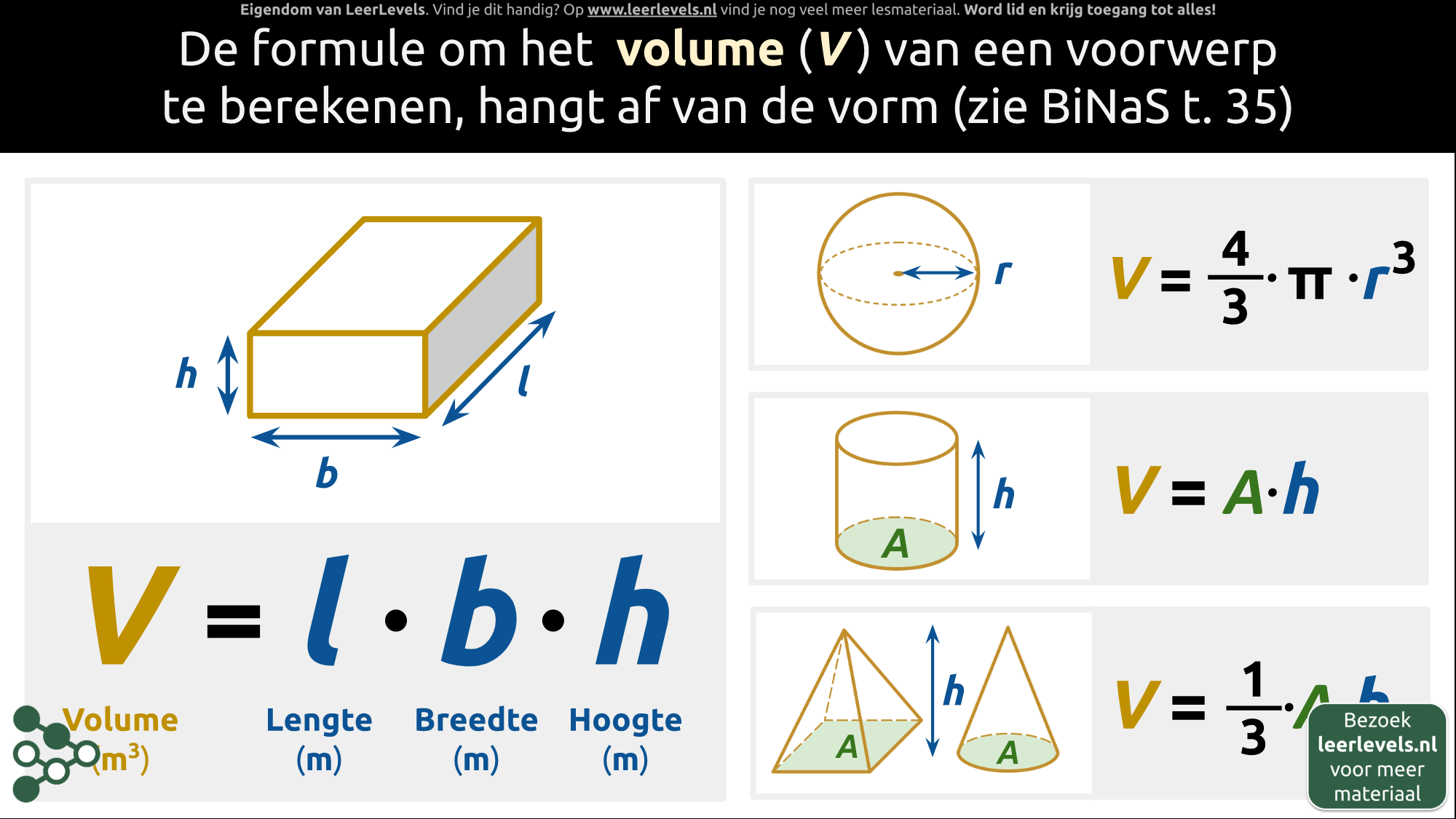
(Afbeelding: Animatie voor Volume formules)

Terug naar overzicht Meld je aan

Voorvoegsels

SI-Voorvoegsels kennen

Het gebruik van SI-voorvoegsels maakt extreme waarden beter leesbaar. Laten we beginnen met het getal 1, dat we simpelweg 'één' noemen. Dit getal heeft geen voorvoegsels nodig. Nu bekijken we een groter getal, bijvoorbeeld 1,000. Dit is lastig om steeds op te schrijven, daarom gebruiken we het voorvoegsel 'k' voor kilo. Voor een miljoen, dat nog vervelender is om op te schrijven, gebruiken we het voorvoegsel 'M' voor mega.

Naast deze voorvoegsels maken we ook gebruik van wetenschappelijke notatie, wat een wiskundige manier is om grote getallen eenvoudig op te schrijven. Voor duizend schrijven we 1 × 10³ (oftewel 10 x 10 x 10) en voor een miljoen 1 × 10⁶. Voor het getal 1 is dit 1 × 10⁰. Dat lijkt misschien vreemd, maar wiskundig is het correct, want alles tot de macht nul is 1.

We kunnen nu de rijen invullen voor andere getallen boven de 1, zoals 10, 100, een miljard en een biljoen. De rijen voor tien en honderd zijn vaak grijs gemaakt omdat we meestal werken met voorvoegsels in machten van 3, zoals 10 tot de 3e, 6e, 9e, etc. Deca en hecto worden in de wetenschap relatief weinig gebruikt.

Er zijn ook voorvoegsels voor kleine getallen, zoals voor een duizendste, miljoenste of miljardste. De bijbehorende voorvoegsels zijn milli, micro en nano. Ook voor een tiende en een honderdste hebben we aparte woorden, maar deci en centi worden beide weinig gebruikt.

Laten we ten slotte naar wat voorbeelden kijken. Beschouw een computer-byte of een meter als eenheden. Voor een millimeter denken we aan een klein speldenknopje, voor een micrometer aan bacteriën en voor een nanometer aan de diameter van een DNA-molecuul. Voor grote getallen kunnen we kijken naar de typische grootte van bestanden. Een tekstbestand is meestal enkele kilobytes, een foto enkele megabytes, een film enkele gigabytes, en op veel harde schijven past tegenwoordig enkele terabytes.

Kortom, dankzij SI-voorvoegsels en wetenschappelijke notatie kunnen we zowel hele grote als hele kleine getallen beter leesbaar maken.

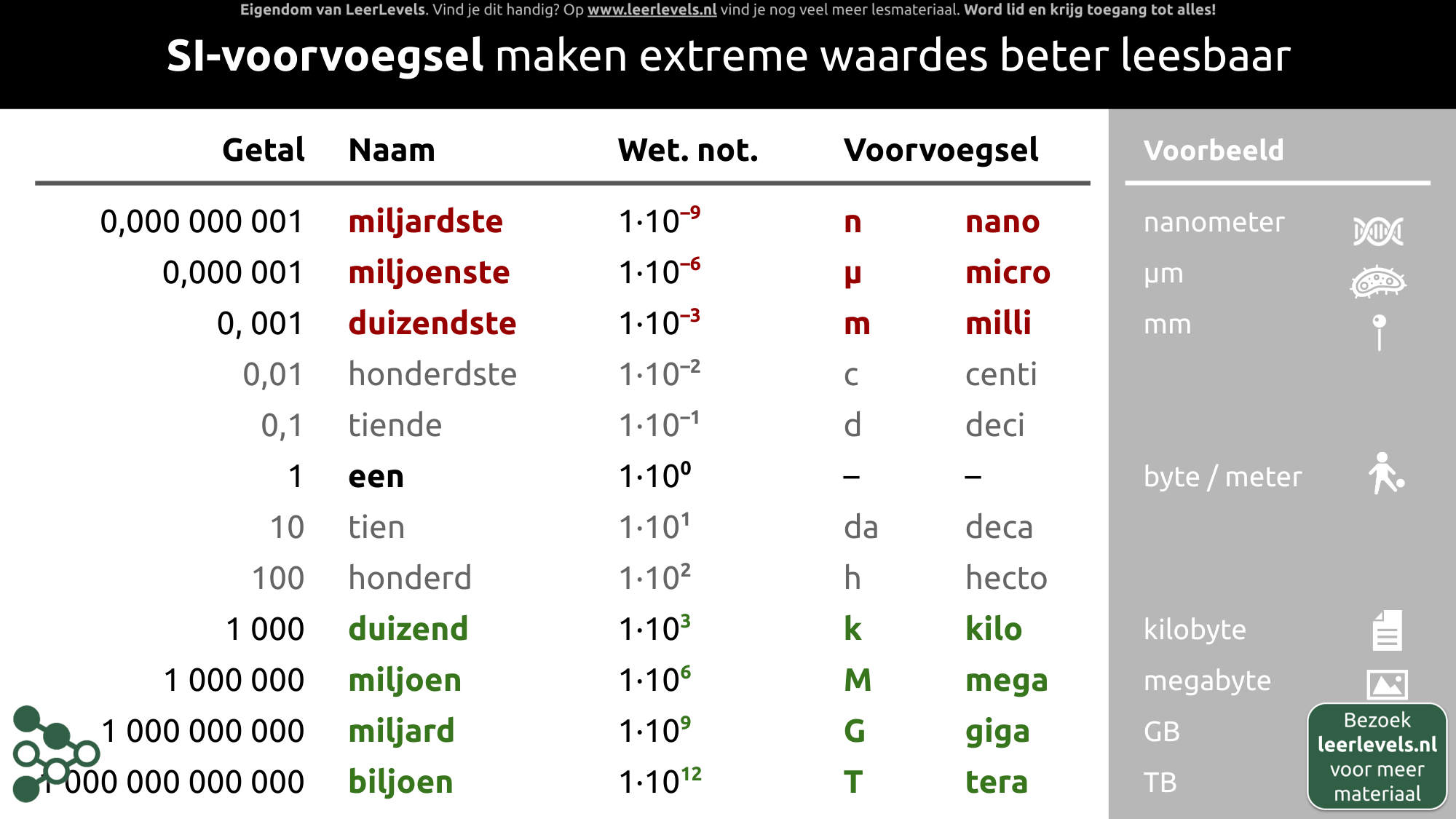
(Afbeelding: Animatie voor SI-Voorvoegsels kennen)

Terug naar overzicht Meld je aan

Vrije val

Vrije val en gewichtloosheid

Bij een vrije val werkt alleen de zwaartekracht en hebben objecten geen gewicht. Dit komt omdat er geen weerstandskrachten zijn. De versnelling van de vrije val is gelijk aan de valversnelling (ongeveer 9,81 m/s² op aarde). Als we kijken naar een veer en een massa, werkt er een kleinere kracht op de veer en een grotere kracht op de massa. De versnelling van de massa is gelijk aan de valversnelling. Dit komt doordat de versnelling wordt berekend met de formule a = Fres/m, waarbij in vacuum geldt Fres = Fz = m · g. Dit wordt gebruikt om astronauten te trainen. Tijdens een duikvlucht ervaar je gewichtloosheid doordat je dezelfde versnelling hebt als alles om je heen. Zo kun je ervaren hoe het is om in de ruimte te zijn.

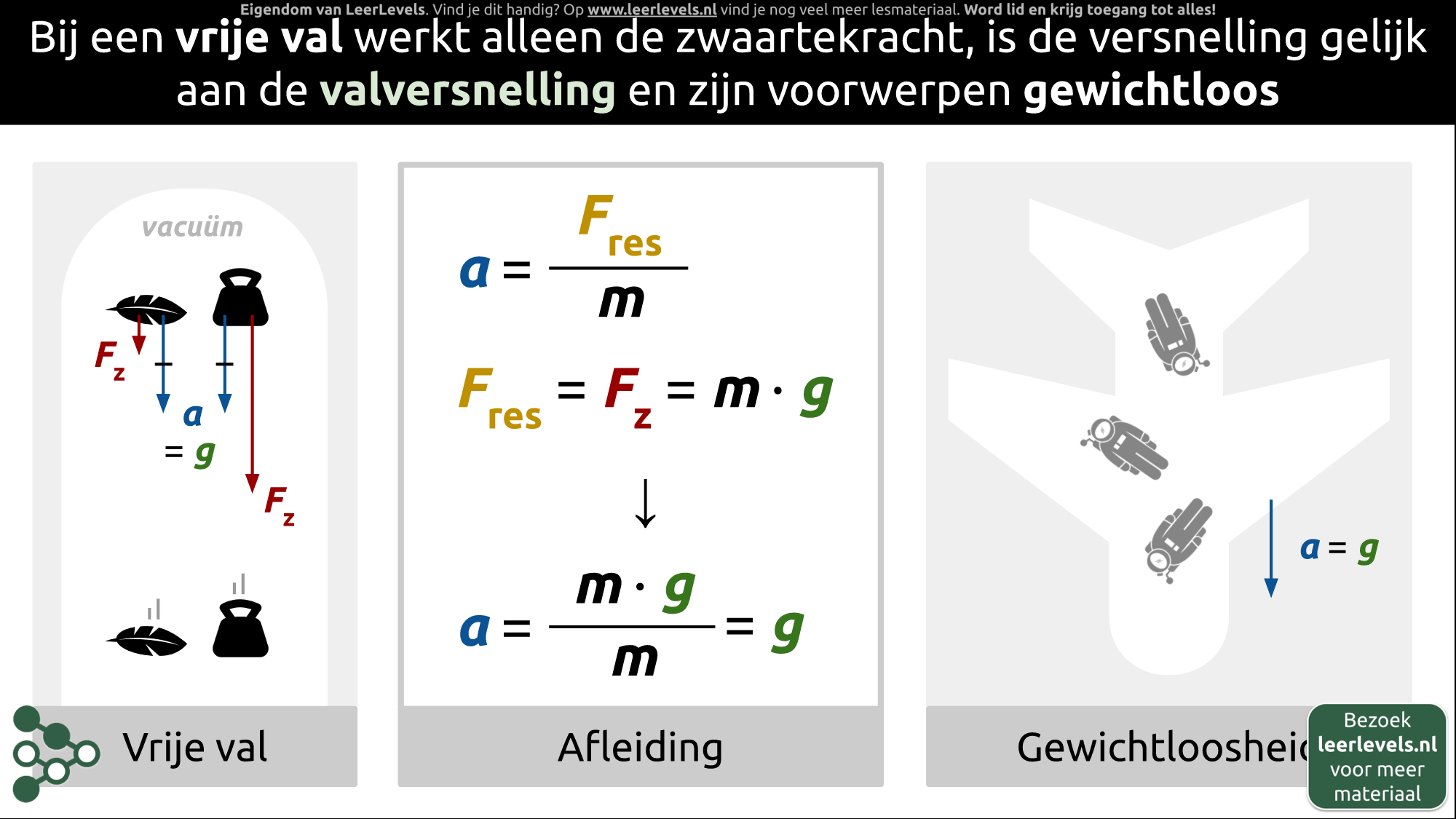
(Afbeelding: Animatie voor Vrije val en gewichtloosheid)

Terug naar overzicht Meld je aan

Warmte

Warmte-overdracht concept

Bij warmte-overdracht gebeurt het volgende: een voorwerp dat warm is, geeft warmte af aan een ander voorwerp dat koud is. Hierdoor koelt het warme voorwerp af en warmt het koude voorwerp op. Warmte-overdracht gebeurt altijd van een warm voorwerp naar een koud voorwerp, nooit andersom.

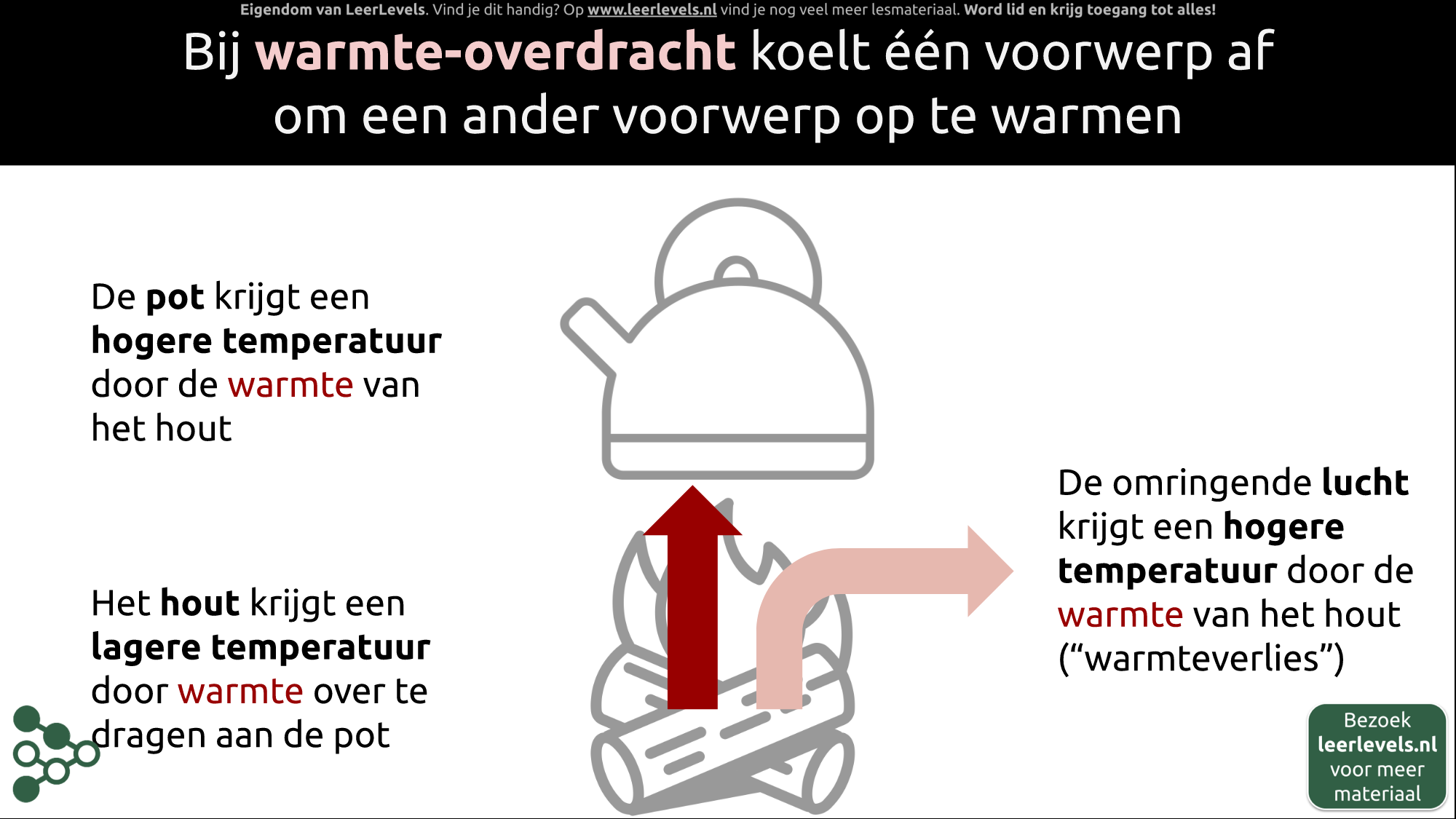
(Afbeelding: Animatie voor Warmte-overdracht concept)

Warmte-overdracht formule

De hoeveelheid warmte die wordt opgenomen, hangt af van de hoeveelheid warmte die wordt afgestaan en hoe efficiënt dit proces verloopt. Dit wordt berekend met de formule:

Qopgenomen = Qafgestaan × η

Het rendement η wordt vaak weergegeven als een percentage.

(Afbeelding: Animatie voor Warmte-overdracht formule)

Terug naar overzicht Meld je aan

Warmtegeleidingscoëfficiënt

Warmtegeleidingscoëfficiënt concept

De warmtegeleidingscoëfficiënt van een materiaal geeft aan hoe goed het materiaal warmte kan doorgeven. Materialen met een hoge warmtegeleidingscoëfficiënt kunnen warmte goed doorgeven, zoals staal dat bijvoorbeeld veel wordt gebruikt voor het maken van pannen. Materialen met een matige warmtegeleidingscoëfficiënt geleiden warmte minder goed, zoals baksteen dat wordt gebruikt voor het maken van muren om warmte binnen of buiten te houden. Materialen met een lage warmtegeleidingscoëfficiënt geleiden warmte slecht, zoals stilstaande lucht. Dubbelglas maakt gebruik van een laagje stilstaande lucht om warmte binnen te houden en is daarom goed voor het isoleren van een huis. De warmtegeleidingscoëfficiënt geeft de mate van warmtegeleidingscapaciteit van het materiaal aan.

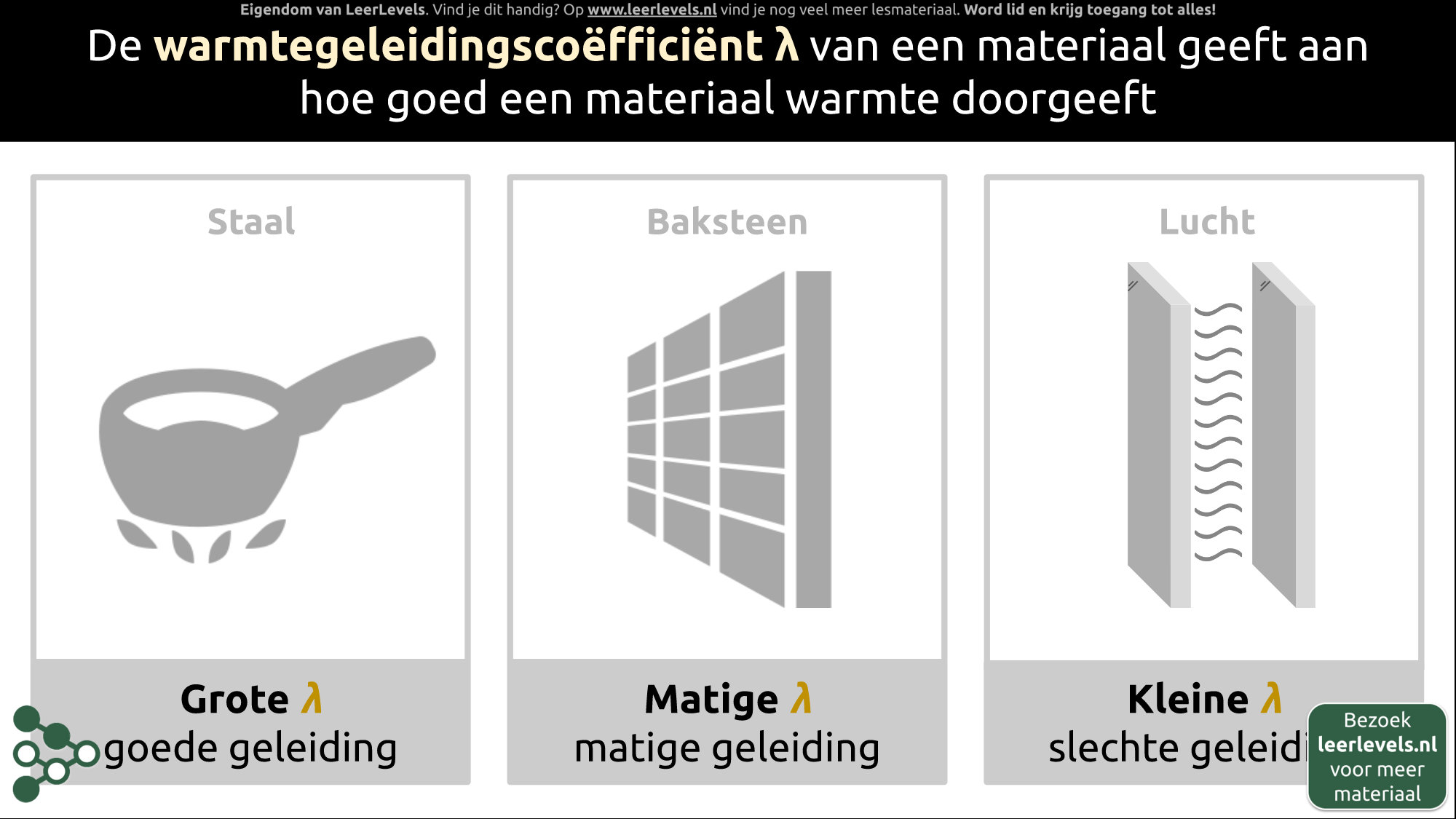
(Afbeelding: Animatie voor Warmtegeleidingscoëfficiënt concept)

Terug naar overzicht Meld je aan

Warmtestroom

Warmtestroom concept

Om warmte door een materiaal te geleiden, zijn er vier factoren die van invloed zijn op de hoeveelheid warmte die door het materiaal gaat: de warmtegeleidingscoëfficiënt, de oppervlakte van het materiaal, het temperatuurverschil aan beide zijden (delta t) en de dikte van het materiaal.

Als we een materiaal met een grotere warmtegeleidingscoëfficiënt kiezen, zal er meer warmte door het materiaal gaan omdat het beter is in het geleiden van warmte. Als het oppervlak van het materiaal groter is, zal er meer warmte beschikbaar zijn om door te worden gegeven. Als we het temperatuurverschil aan beide zijden van het materiaal verhogen, zal er meer bewegingsenergie beschikbaar zijn om de warmte door te geven en zal de warmtestroom door het materiaal ook groter zijn.

Als we de dikte van het materiaal vergroten, moet de bewegingsenergie die aanvankelijk door een kleiner aantal deeltjes werd verdeeld, nu worden verdeeld over meer tussenliggende deeltjes. Daardoor zal de warmtestroom door het materiaal kleiner zijn.

Kortom, de hoeveelheid warmte die door een materiaal gaat, is recht evenredig met de warmtegeleidingscoëfficiënt, het oppervlak van het materiaal en het temperatuurverschil aan beide zijden, maar omgekeerd evenredig met de dikte van het materiaal. De eenheid van de warmtegeleidingscoëfficiënt is W/(m · K).

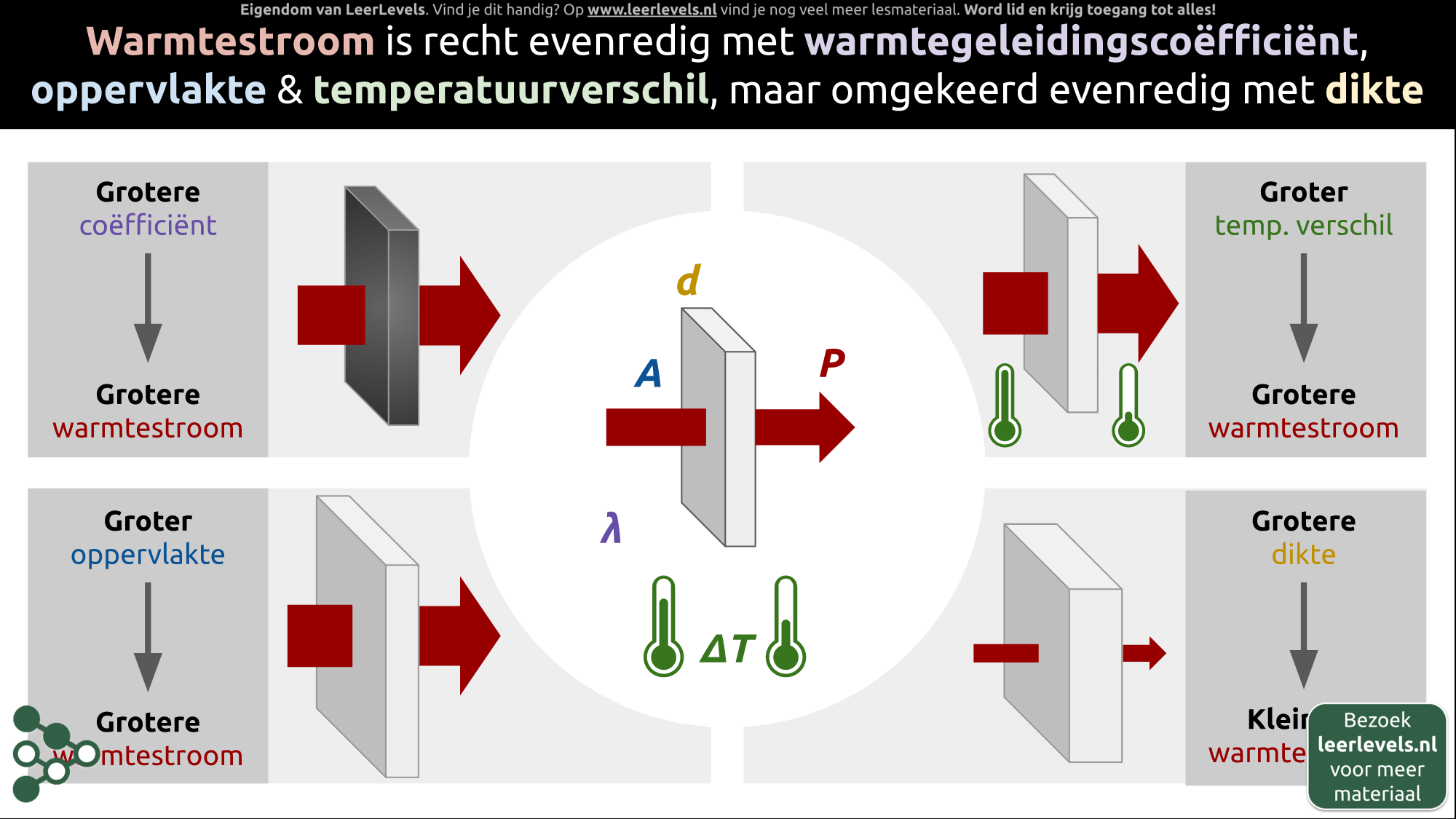
(Afbeelding: Animatie voor Warmtestroom concept)

Warmtestroom formule

Als iets warmtegeleiding heeft, dan kan de hoeveelheid warmte die erdoorheen gaat uitgerekend worden met een warmtegeleidingscoëfficiënt (λ). Deze coëfficiënt hangt af van het materiaal en van eigenschappen ervan, zoals de oppervlakte (A), het temperatuurverschil (Δ T) en de dikte (d). Als A, Δ T en λ toenemen, neemt de hoeveelheid warmte die erdoorheen gaat ook toe. De eenheid van de hoeveelheid warmte die erdoorheen gaat is watt en wordt vaak aangeduid met Q. De formule om Q te berekenen is: Q = λ · A · Δ T. De waarde van λ wordt uitgedrukt in watt per meter per kelvin (W/mK) en de waarde van A in vierkante meter (m²). De waarde van Δ T wordt in kelvin (K) uitgedrukt. De warmtestroom is omgekeerd evenredig met de dikte (d) van het materiaal. Dit betekent dat als de dikte toeneemt, de hoeveelheid warmte die erdoorheen gaat afneemt. De eenheid van de dikte is meter (m). Samengevat: de hoeveelheid warmte die erdoorheen gaat wordt bepaald door λ, A en Δ T, en is omgekeerd evenredig met de dikte (d) van het materiaal.

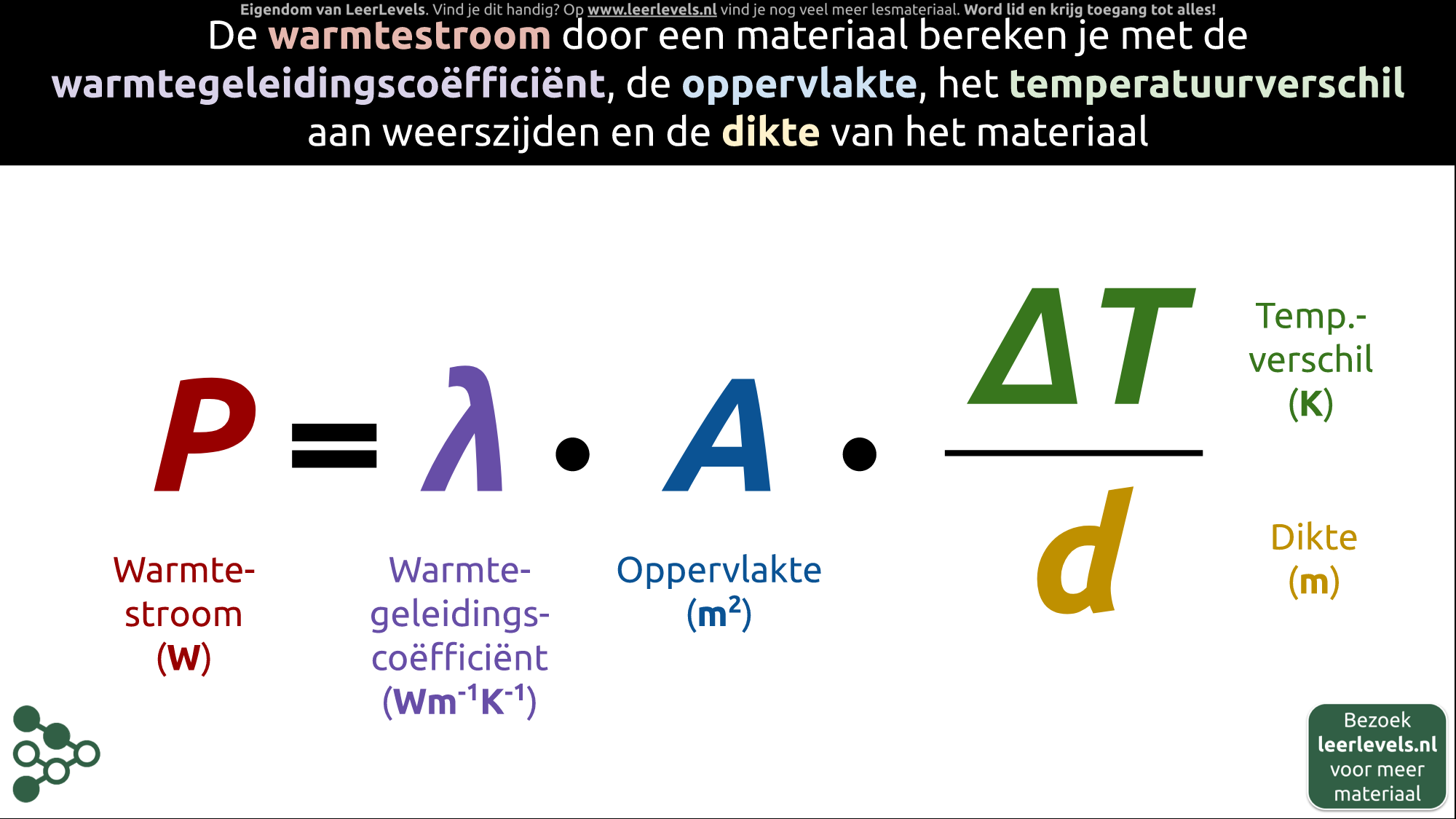
(Afbeelding: Animatie voor Warmtestroom formule)

Terug naar overzicht Meld je aan

Warmtetransport

Warmtetransport macroscopisch

Om warmte te transporteren zijn er drie manieren: stroming, geleiding en straling.

Stroming is wanneer het medium zelf beweegt, bijvoorbeeld wanneer warm water door een verwarmingsbuis stroomt en ergens anders zijn warmte afgeeft.

Geleiding vindt plaats via direct contact, bijvoorbeeld wanneer een pannetje op het vuur wordt gezet en de warmte via het materiaal naar het handvat wordt doorgegeven.

Straling is een vorm van warmtetransport zonder tussenkomst van materie. Een voorbeeld hiervan is warmte voelen op de huid door de zon.

Samenvattend zijn er drie manieren van warmtetransport: stroming, geleiding en straling.

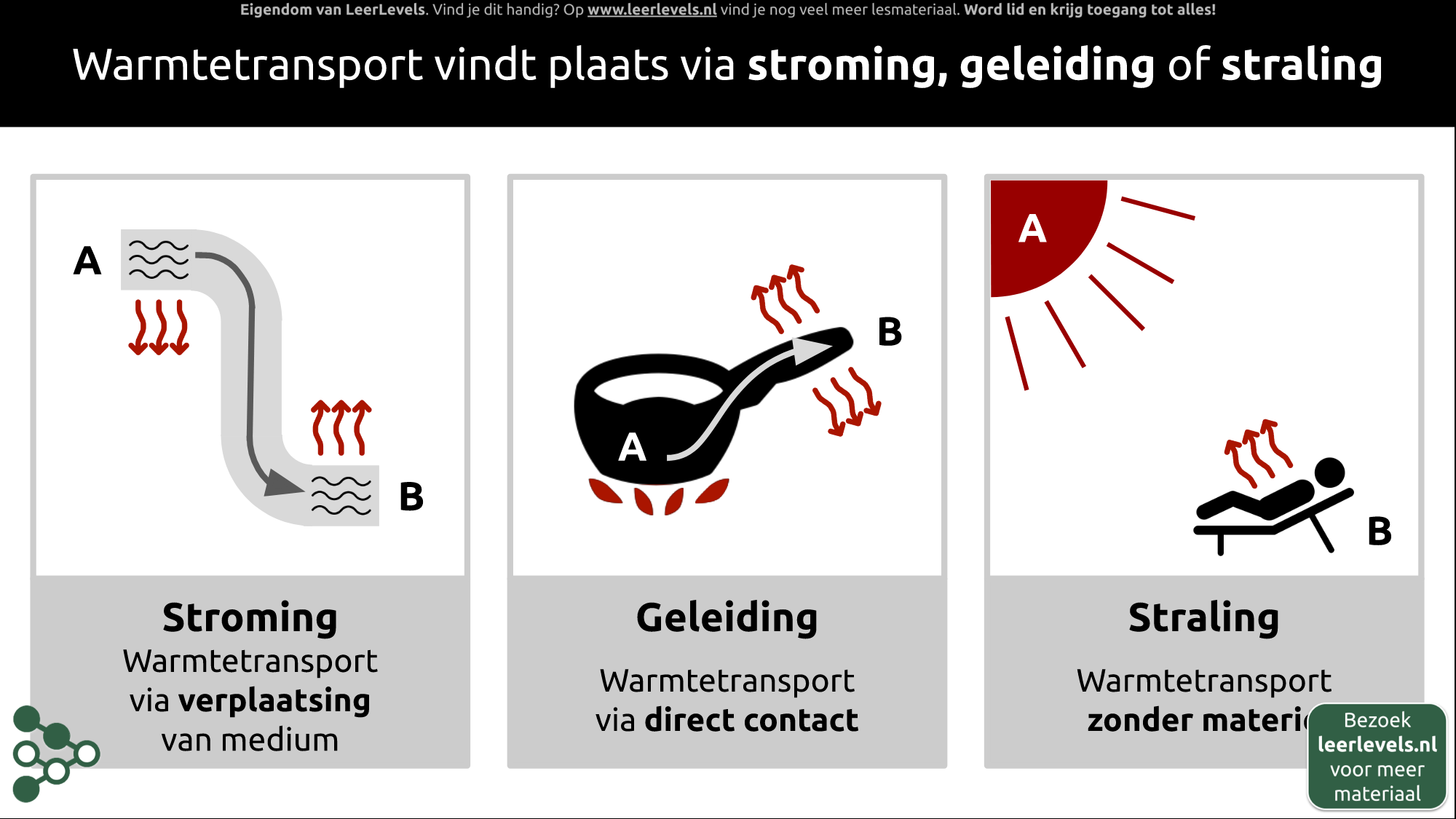
(Afbeelding: Animatie voor Warmtetransport macroscopisch)

Warmtetransport microscopisch

Warmte kan op drie manieren van een warme naar een koude plaats worden getransporteerd op deeltjesniveau: stroming, geleiding en straling. Bij stroming bewegen deeltjes van warme stof van plaats en nemen zo de warmte mee naar een koude plaats. Bij geleiding wordt de trilling van deeltjes van een warme stof doorgegeven via botsingen met tussenliggende deeltjes. Bij straling zenden warme deeltjes IR-straling uit die wordt geabsorbeerd door deeltjes van een koude stof en omgezet in warmte. Dit gebeurt door toegenomen bewegingsenergie op molecuulniveau.

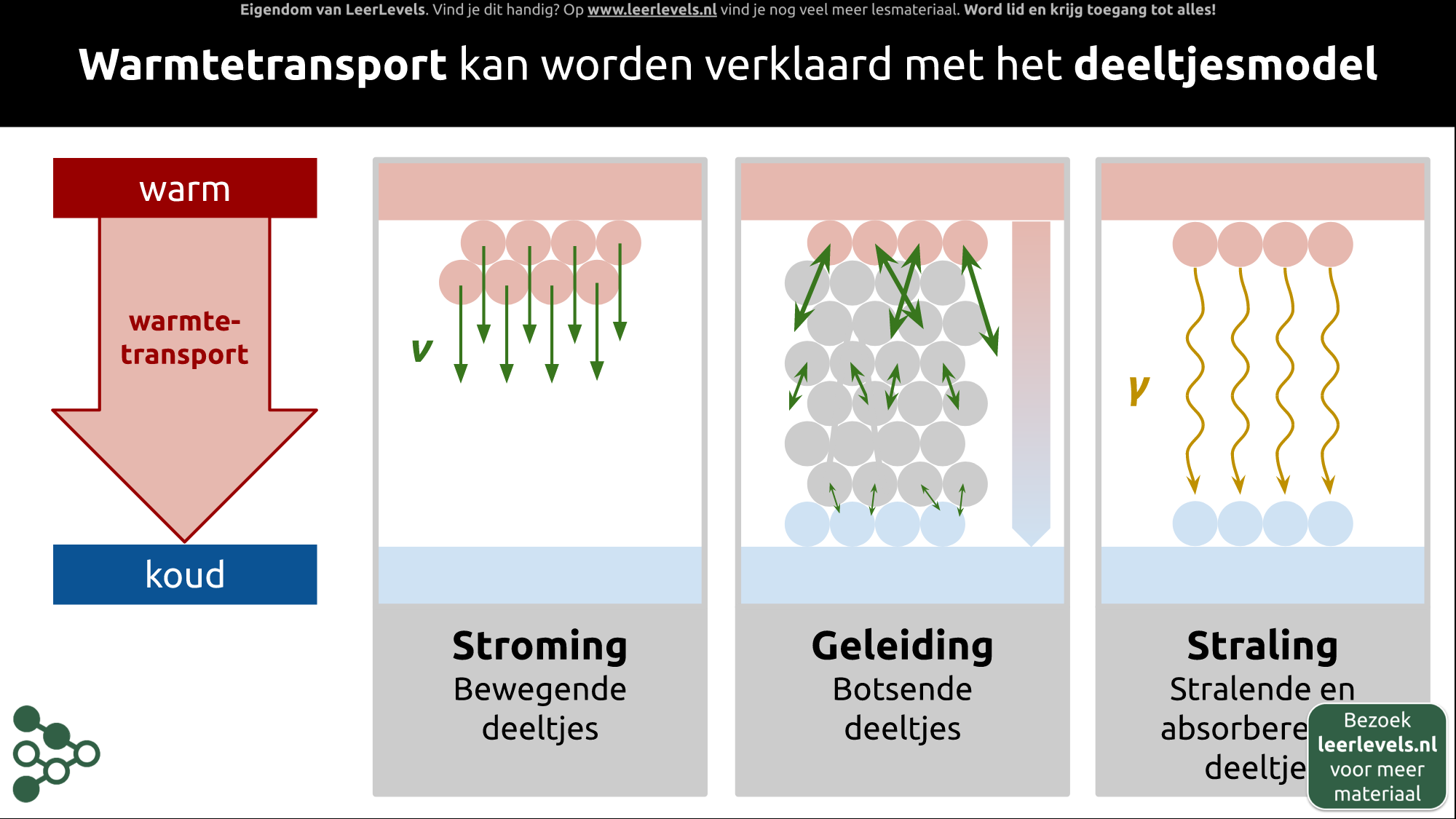
(Afbeelding: Animatie voor Warmtetransport microscopisch)

Terug naar overzicht Meld je aan

Weerstand

Weerstand concept

De elektrische weerstand van een object geeft aan hoe moeilijk stroom erdoorheen kan gaan. Als je een dikke, grote draad gebruikt, gaat stroom er makkelijk doorheen (vergelijkbaar met water in een dikke buis), dit betekent een kleine weerstand. Een normale weerstand verkrijg je met een wat dunner draadje. Als je een heel lange draad gebruikt, moeten de elektronen een lange weg afleggen en gaat stroom er moeilijk doorheen (vergelijkbaar met drinken door een heel lang dun rietje), wat resulteert in een grote weerstand. Als je niets aansluit, is de weerstand oneindig groot en kan er geen stroom doorheen. De eenheid van elektrische weerstand is de ohm (Ω).

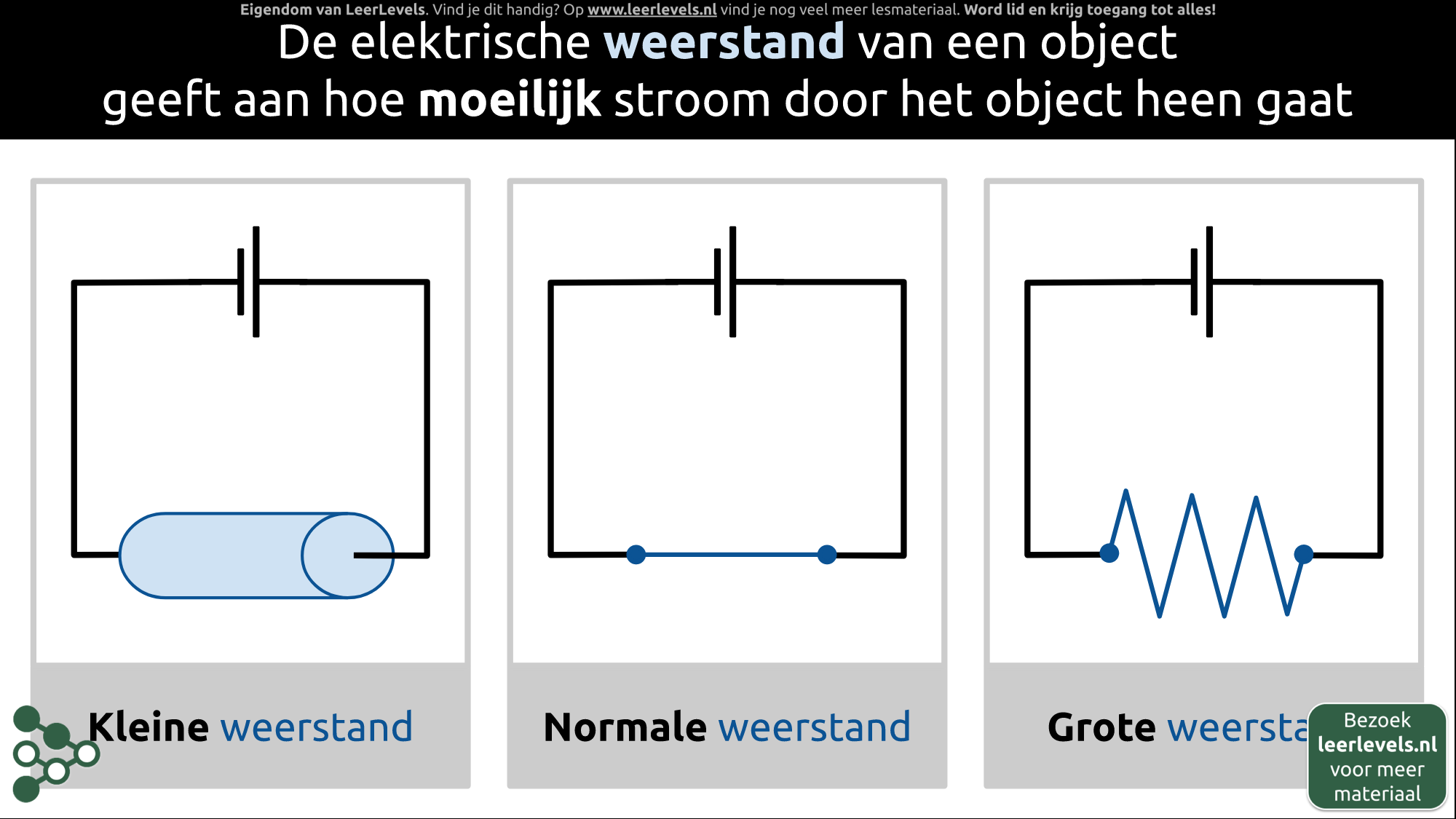
(Afbeelding: Animatie voor Weerstand concept)

Vervangingsweerstand concept

Een vervangingsweerstand (Rv) maakt een schakeling eenvoudiger door bestaande weerstanden te vervangen door een enkele nieuwe weerstand. Laten we eens kijken naar twee weerstanden die in serie zijn geschakeld. Als we deze vervangen door een vervangingsweerstand, zal de nieuwe weerstand groter zijn dan de individuele oude weerstanden. De waarde van de vervangingsweerstand is gelijk aan de som van de oude weerstandswaarden. Het kan lastig zijn om dit handmatig uit te rekenen. Dus in een serie schakeling wordt de vervangingsweerstand groter dan de individuele weerstanden.

Bij een parallelle schakeling geldt hetzelfde principe. Als we twee weerstanden parallel schakelen, zal de totale weerstand kleiner zijn dan elke individuele weerstand. Dit komt doordat in een parallelle schakeling de ruimte voor de stroom toeneemt, waardoor de vervangingsweerstand juist kleiner wordt.

Het berekenen van de vervangingsweerstand hangt af van het type schakeling, serie- of parallel. Het is belangrijk om te onthouden dat een vervangingsweerstand de schakeling vereenvoudigt en het gemakkelijker maakt om de totale weerstandswaarde te berekenen.

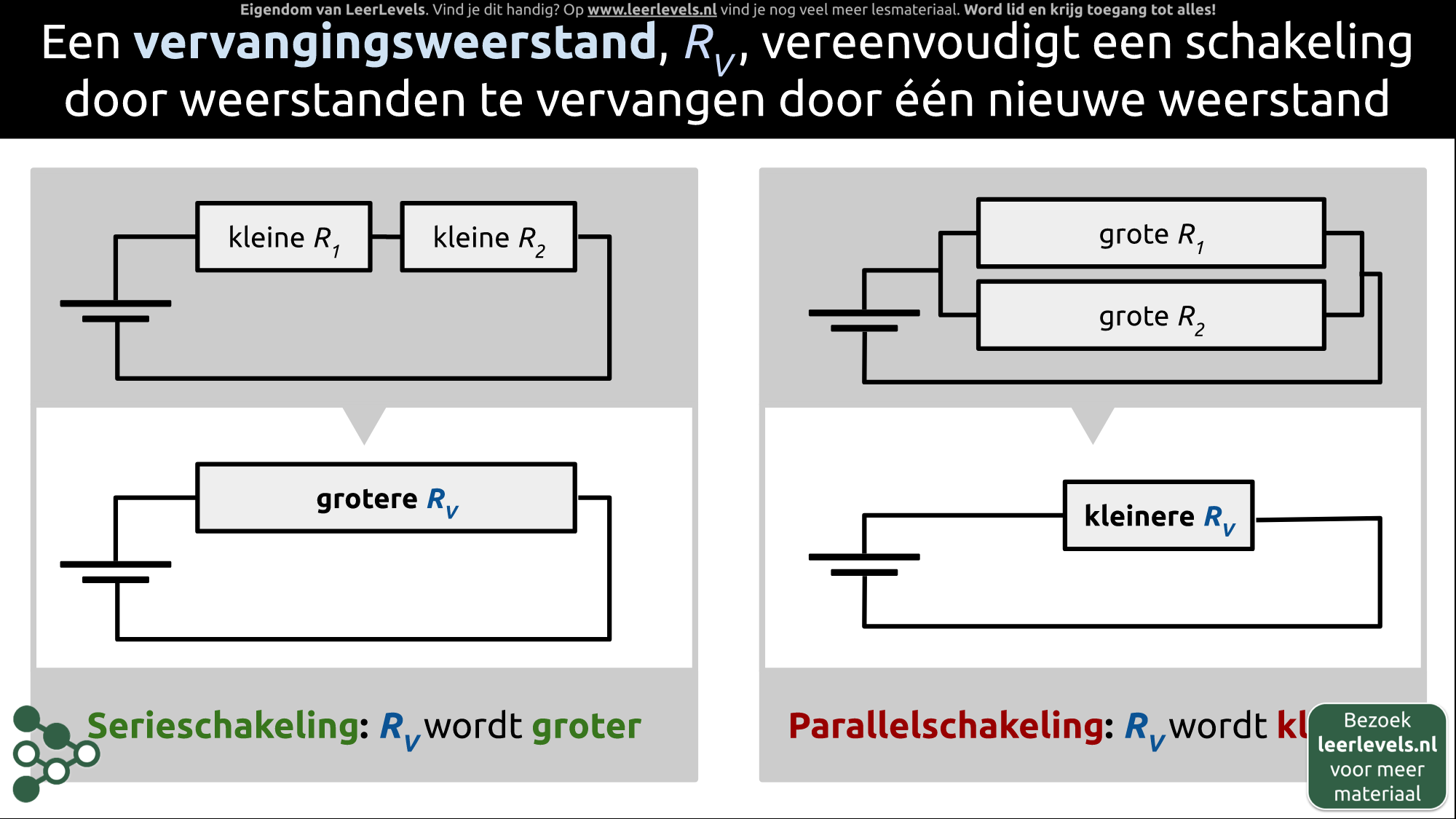
(Afbeelding: Animatie voor Vervangingsweerstand concept)

Vervangingsweerstand in serie

In een serieschakeling van drie weerstanden, kan de vervangingsweerstand berekend worden door de oorspronkelijke weerstanden op te tellen. Hierdoor hoef je niet door elke weerstand apart te gaan. Als je een nieuwe weerstand wilt toevoegen met dezelfde totale weerstand als de drie oorspronkelijke weerstanden, kun je dit doen met één weerstand van 6,5 Ω. Dit maakt het makkelijker om de totale stroom van de schakeling te berekenen, als je de spanning weet. Kortom, de vervangingsweerstand is de som van de oorspronkelijke weerstanden, waardoor je efficiënter kunt rekenen en eventueel een nieuwe weerstand kunt toevoegen zonder de schakeling te verstoren.

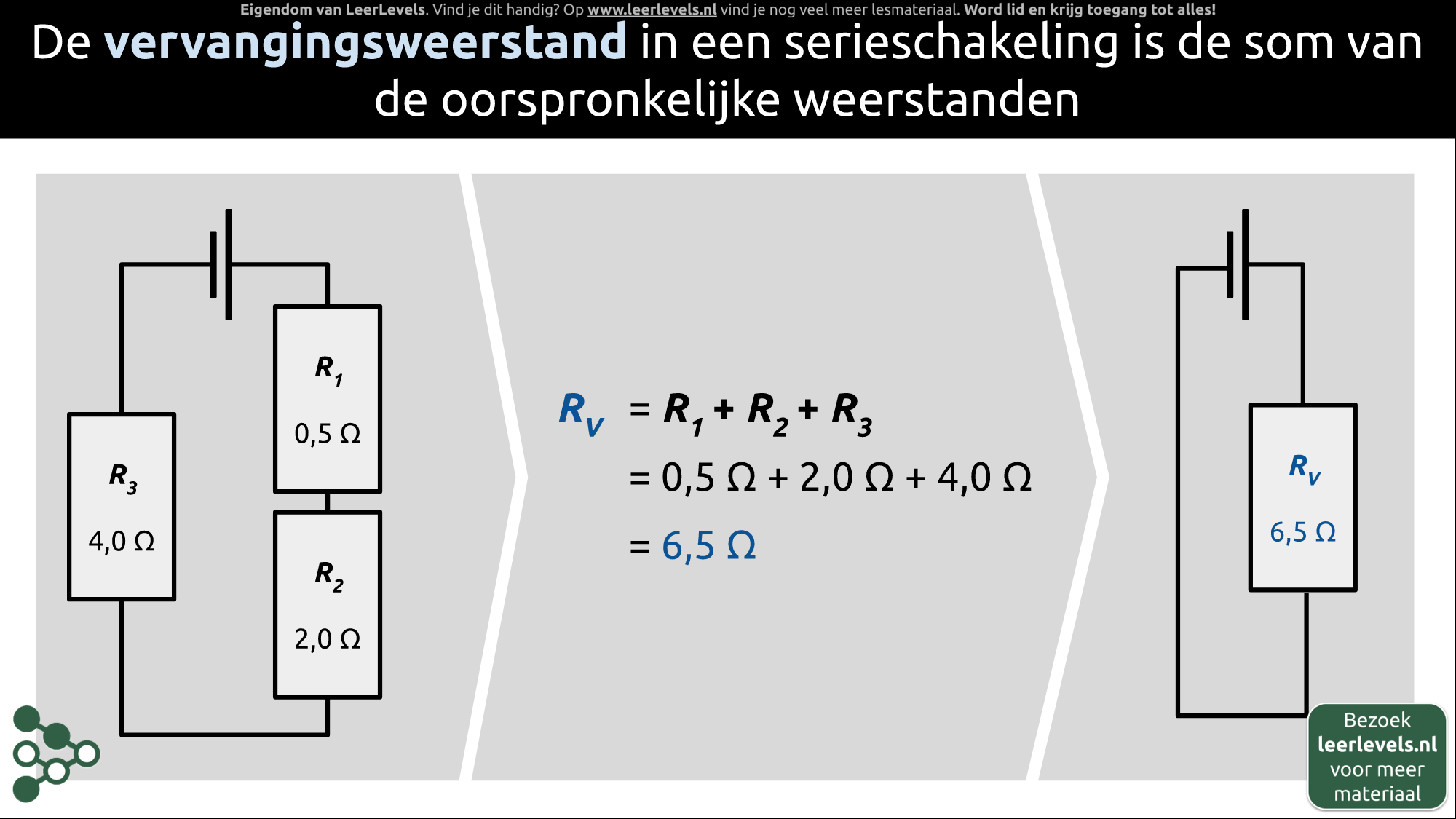
(Afbeelding: Animatie voor Vervangingsweerstand in serie)

Vervangingsweerstand parallel

Bij een parallelschakeling wil ik de vervangingsweerstand uitrekenen. Er zijn drie weerstanden, waarvan er één 3 Ohm is. Ik moet drie stappen volgen om de vervangingsweerstand te vinden:

1. De totale geleidbaarheid van de oorspronkelijke schakeling berekenen door de geleidbaarheid van elke weerstand te berekenen. De geleidbaarheid is het omgekeerde van de weerstand. Bijvoorbeeld, de geleidbaarheid van weerstand g1 is 1/0,5 = 2.

2. Tel de geleidbaarheden op om de vervangingsgeleidbaarheid te krijgen. Dit is gelijk aan g1 + g2 + g3 en is 2,75 siemens.

3. Bereken de vervangingsweerstand door 1 te delen door de vervangingsgeleidbaarheid. De vervangingsweerstand is dan 0,36 ohm.

Kortom, de vervangingsweerstand in deze parallelschakeling is 0,36 ohm.

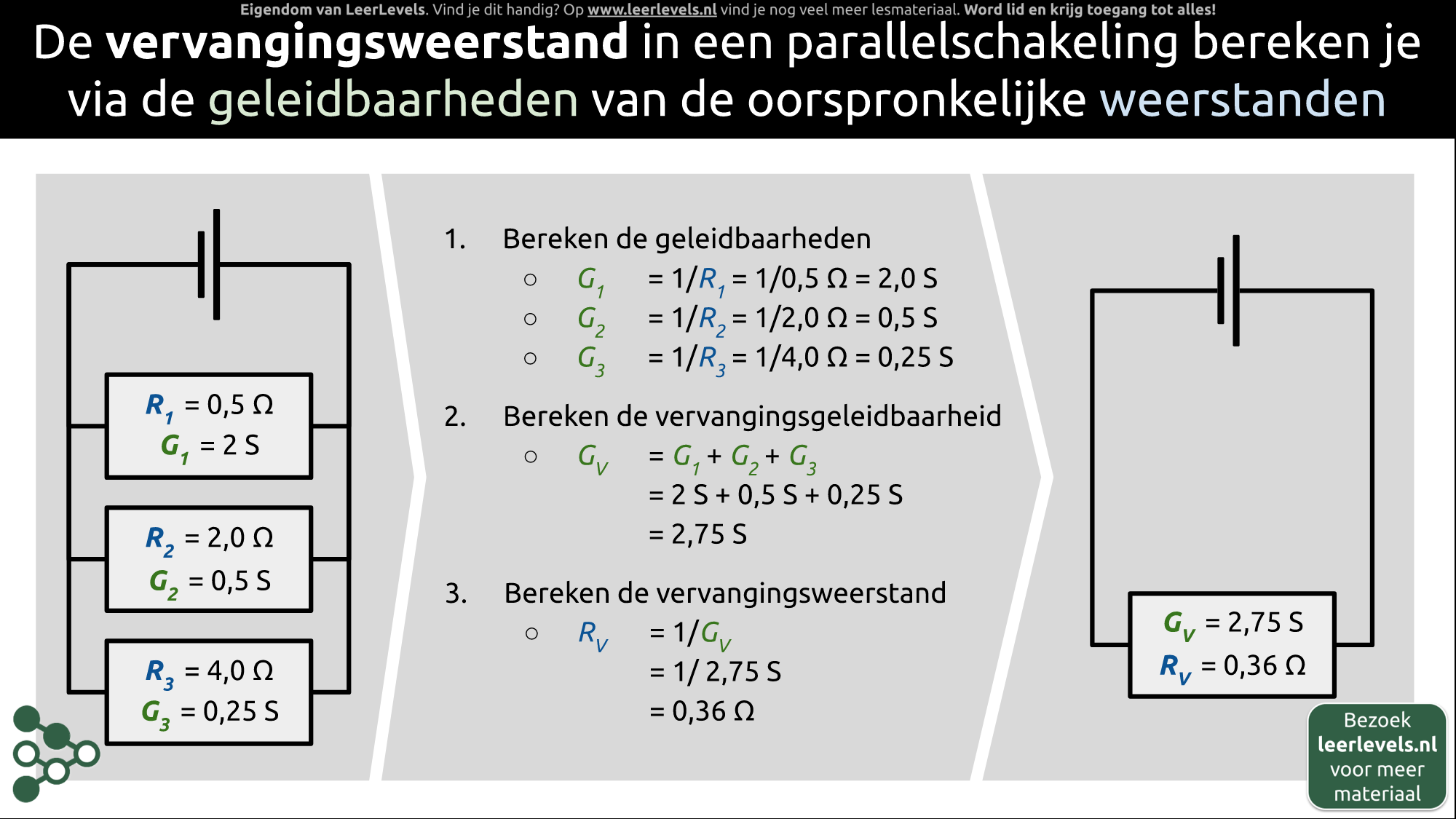
(Afbeelding: Animatie voor Vervangingsweerstand parallel)

Soorten weerstand

De PTC-, NTC-, ohmse en LDR-weerstanden hebben verschillende eigenschappen.

De PTC staat voor positieve temperatuurcoëfficiënt. Dit betekent dat in een (R,T)-diagram, waarbij R de weerstand is en T de temperatuur, de weerstand toeneemt naarmate de temperatuur stijgt. Als je zo'n weerstand naar 0 Kelvin brengt, kan dit voor sommige weerstanden leiden tot supergeleiding: een weerstand van nul. Het belangrijkste kenmerk van een PTC is dus dat de weerstand toeneemt met de temperatuur. Veel gloeilampen zijn PTC's: naarmate de gloeidraad opwarmt, wordt de weerstand van de lamp groter.

De NTC heeft een negatieve temperatuurcoëfficiënt. Dit betekent dat de weerstand juist kleiner wordt naarmate de temperatuur toeneemt. De weerstand zal echter nooit helemaal nul worden.

Een ohmse weerstand, ook wel constantaandraad genoemd, heeft een constante weerstand, vooral binnen het temperatuurgebied dat relevant is in het dagelijks leven.

De LDR, of lichtgevoelige weerstand, heeft een lagere weerstand naarmate er meer licht op valt. Dit komt doordat licht bepaalde ladingen vrijmaakt die anders vastzitten, waardoor er meer geleiding plaatsvindt en de weerstand afneemt.

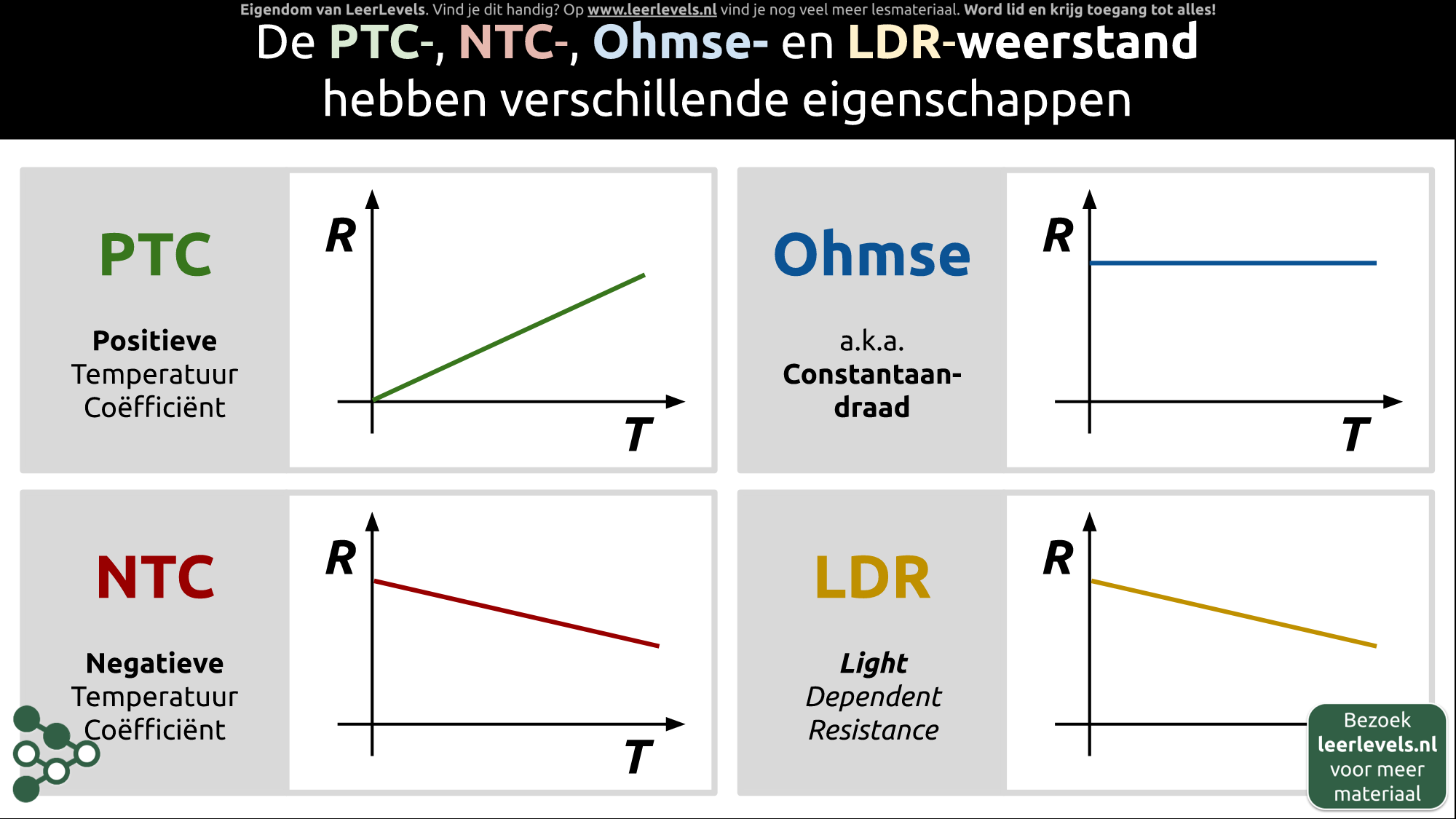
(Afbeelding: Animatie voor Soorten weerstand)

Vervangingsweerstand complexe schakeling

Om de vervangingsweerstand (rv) van een complexe schakeling te berekenen, moet je deze eerst opsplitsen in kleinere parallel- en serieschakelingen. De totale vervangingsweerstand van de schakeling hangt af van de vervangingsweerstand van deze kleinere delen.

Bijvoorbeeld, als R1 en R2 parallel staan en deze parallelle combinatie wordt gevolgd door R3 in serie, dan moet je eerst de vervangingsweerstand van R1 en R2 berekenen (genaamd R12). Daarna kun je de vervangingsweerstand van de gehele schakeling berekenen met behulp van de formule 1/(R12 + R3).

Door deze methode toe te passen op de hele schakeling, kun je de totale vervangingsweerstand van een complexe schakeling bepalen door deze op te splitsen in parallel- en serieschakelingen.

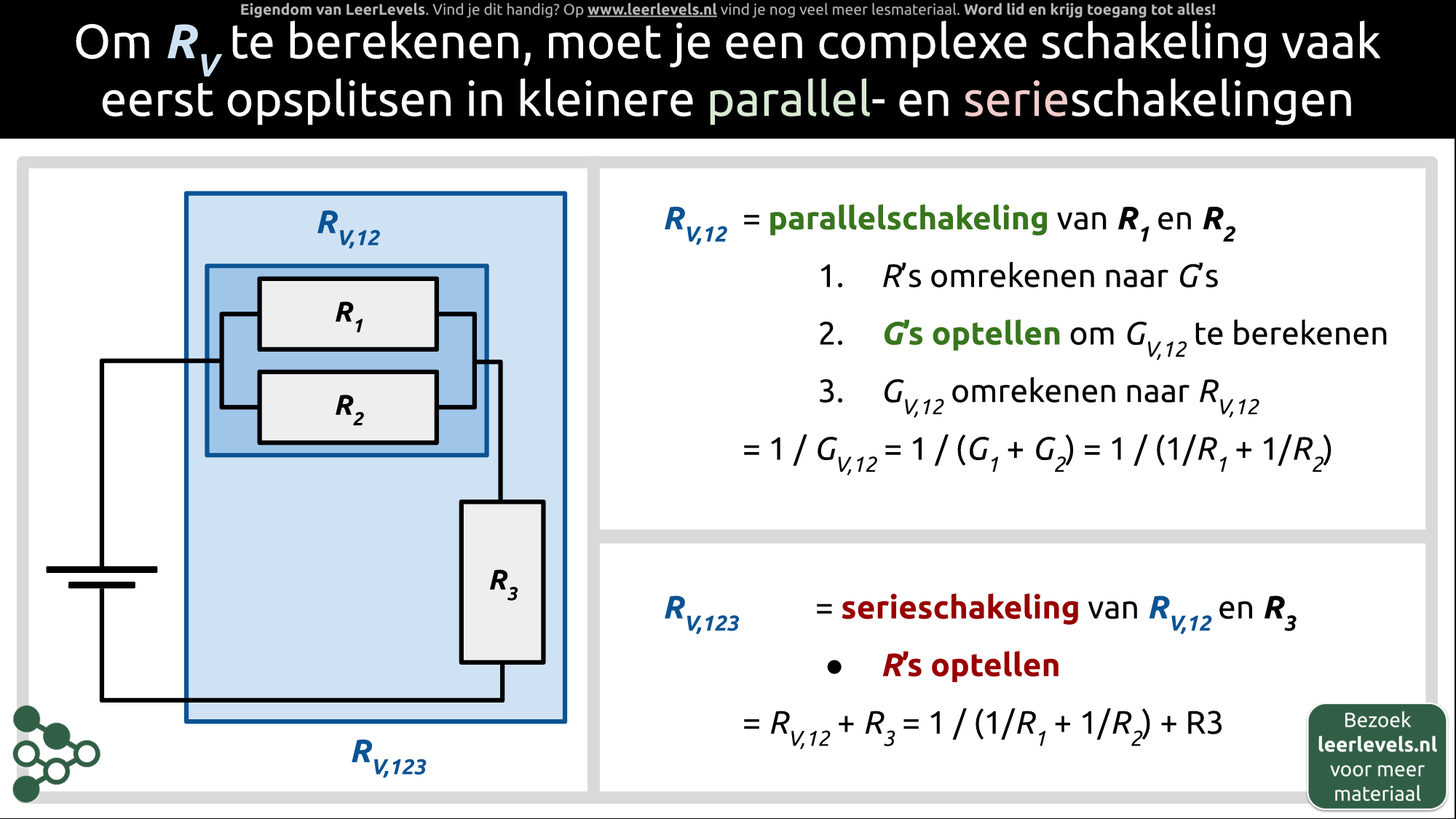
(Afbeelding: Animatie voor Vervangingsweerstand complexe schakeling)

Terug naar overzicht Meld je aan

Welke-spleetdetectie

Welke-spleetdetectie fotonen

Wanneer je meet door welke spleet een foton gaat, verdwijnt het interferentiepatroon. Dit patroon ontstaat wanneer je met een laser fotonen afvuurt op een dubbelspleet, en vervolgens naar het scherm kijkt om de verdeling te analyseren. In wezen weet je alleen waar de fotonen beginnen en eindigen: ze komen uit de laser en belanden ergens op het scherm. Maar wat gebeurt er tijdens de reis?

Om deze vraag te onderzoeken, werd het experiment enigszins aangepast. Men keek specifiek of het foton door de bovenste of onderste spleet ging. Op deze manier kun je bepalen hoe bijvoorbeeld de fotonen die door de bovenste spleet gingen, bijdragen aan het patroon. Met slechts een paar fotonen is het lastig om conclusies te trekken. Met iets meer fotonen lijkt het erop dat de fotonen door de bovenste spleet vaker in de bovenste helft van het scherm belanden.

Zodra er meer metingen zijn gedaan, wordt duidelijk dat het patroon sterk veranderd is. In plaats van een interferentiepatroon ontstaat er nu een verzameling stippen achter de gele spleet, en een soortgelijke verzameling achter de blauwe spleet. We zien dus het resultaat van een enkelspleetpatroon plus een enkelspleetpatroon. Blijkbaar kunnen we het experiment nu niet langer beschouwen als een foton dat met zichzelf interfereert!

De tussentijdse meting, die informatie geeft over de route van het foton, zorgt ervoor dat het interferentiepatroon verdwijnt.

(Afbeelding: Animatie voor Welke-spleetdetectie fotonen)

Terug naar overzicht Meld je aan

Wereldbeelden

Ons wereldbeeld is voortdurend in ontwikkeling dankzij astronomische waarnemingen. Eeuwen voor Christus werd ons wereldbeeld nog bepaald door de kerk. Destijds geloofde men in een geocentrisch model, waarbij de aarde centraal stond en de zon daaromheen draaide. Zelfs in die tijd werden er al waarnemingen gedaan, bijvoorbeeld van Mars. In het geocentrische model leek Mars zich op een vreemde manier rond de aarde te bewegen.

In 1543 publiceerde Copernicus echter zijn heliocentrische wereldbeeld. Hij had vele waarnemingen verzameld en maakte ook gebruik van de observaties van anderen. Copernicus dacht: "Het is vreemd dat Mars zulke ingewikkelde bewegingen maakt. Ik ben ervan overtuigd dat er een heliocentrisch model bestaat, waarbij de zon centraal staat en de aarde daaromheen draait." In dit heliocentrische model beweegt Mars op een ordelijke, cirkelvormige manier, wat veel logischer is.

In de 20e eeuw zijn onze waarnemingsmethoden aanzienlijk gemoderniseerd en hebben we nieuwe modellen van het heelal ontwikkeld. Het idee dat de zon in het midden van het heelal staat, is verlaten; we bevinden ons nu in een uitgestrekte arm van het universum. We ontdekken nog voortdurend meer en proberen ook te begrijpen wat donkere materie precies is. Ons wereldbeeld blijft veranderen en is al veel verder ontwikkeld dan het geocentrische model van eeuwen geleden.

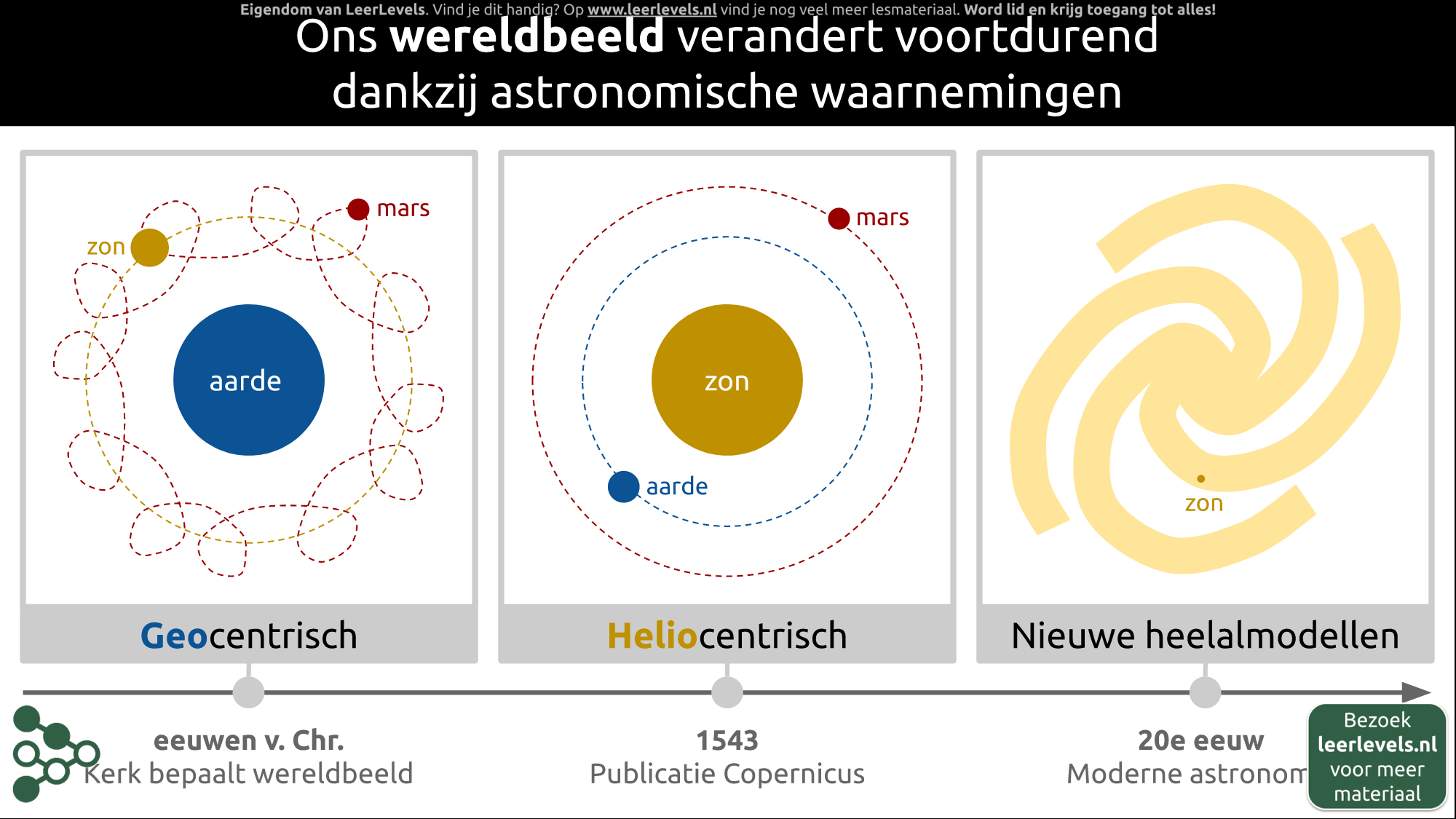
(Afbeelding: Animatie voor Wereldbeelden)

Terug naar overzicht Meld je aan

Wet van Boyle

Wet van Boyle concept

De wet van Boyle zegt dat als je een afgesloten ruimte kleiner maakt, de druk in die ruimte groter wordt. Als je het volume verkleint, komen de moleculen namelijk dichter bij elkaar en botsen ze vaker. Hierdoor wordt de druk hoger. Als je de ruimte juist groter maakt, wordt de druk lager omdat de moleculen dan minder vaak tegen elkaar botsen. Dit verband tussen volume en druk wordt uitgedrukt met de formule P · V = constant.

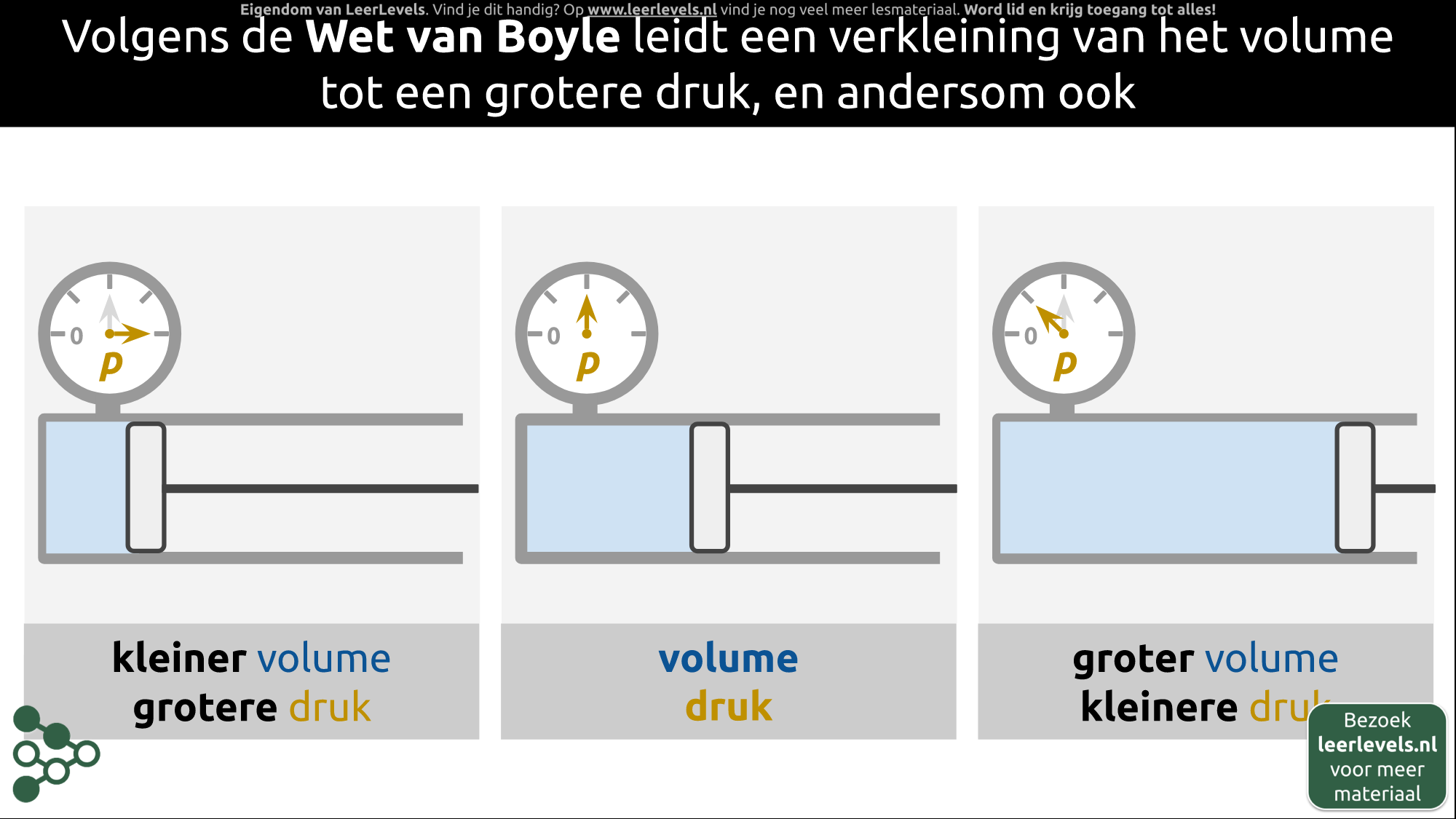
(Afbeelding: Animatie voor Wet van Boyle concept)

Wet van Boyle formule

Als je een ruimte hebt die helemaal is afgesloten en waarin de temperatuur altijd hetzelfde is, dan geldt de wet van Boyle. Dit betekent dat als het volume groter wordt, de druk kleiner wordt en andersom. De druk wordt gemeten in Pascal (Pa) en het volume in kubieke meters (m³). Deze wet wordt vaak gebruikt in opdrachten en kun je ook opschrijven als p1 x V1 = p2 x V2. Hierbij zijn p1 en V1 de druk en het volume in de eerste situatie en p2 en V2 in de tweede.

(Afbeelding: Animatie voor Wet van Boyle formule)

Terug naar overzicht Meld je aan

Wet van Hubble

Wet van Hubble concept

De Wet van Hubble beschrijft het verband tussen de snelheid waarmee sterren zich van de aarde verwijderen en hun afstand tot de aarde. Wanneer we vanaf de aarde naar een ster kijken, ontdekken we vaak dat deze zich van ons af beweegt. Sterren die relatief dichtbij staan, bewegen zich relatief langzaam van ons af. Daarentegen bewegen sterren die verder weg staan steeds sneller van ons af. Dit verband is lineair en werd door Hubble vastgesteld.

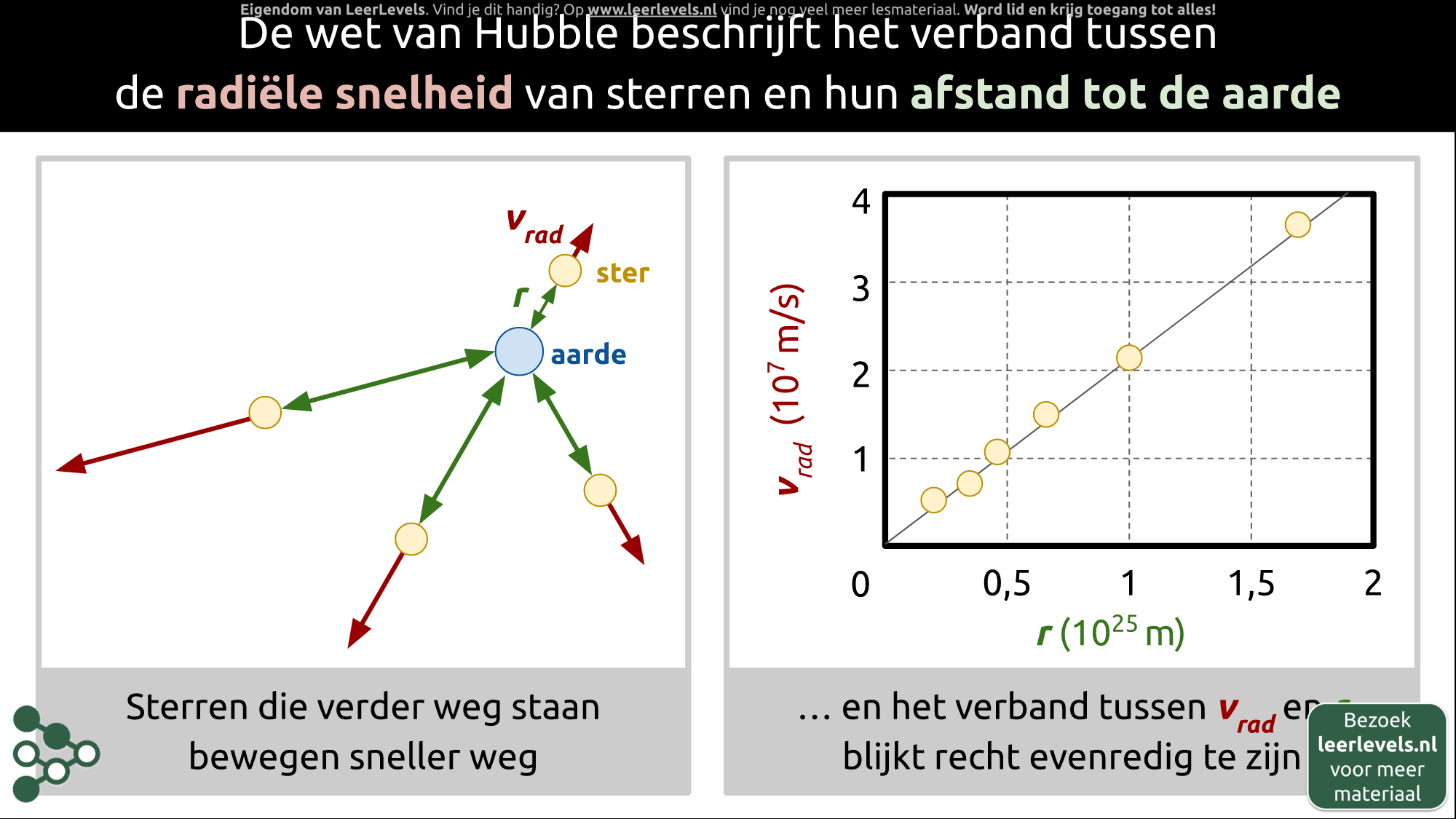
(Afbeelding: Animatie voor Wet van Hubble concept)

Wet van Hubble formule

Volgens de Wet van Hubble is de radiële snelheid van een ster recht evenredig met de afstand tot die ster. De bijbehorende formule is:

vr = H0 · r

Hierbij is vr de radiële snelheid van de ster in m/s, H0 de Hubbleconstante, en r de afstand van de aarde tot de ster in m. De Hubbleconstante heeft een waarde van ongeveer 2,28 × 10⁻¹⁸ Hz.

(Afbeelding: Animatie voor Wet van Hubble formule)

Terug naar overzicht Meld je aan

Wet van Kirchhoff

Stroomwet van Kirchhoff

Volgens de wet van Kirchhoff moet bij elk knooppunt de inkomende stroom gelijk zijn aan de uitgaande stroom. Dit kan worden vergeleken met waterstromen. Als er bijvoorbeeld 6 liter water per seconde in een buis wordt gestopt, en er aan de bovenkant 4 liter per seconde uitgaat, dan moet er aan de onderkant 2 liter per seconde uitgaan. Dit principe geldt ook voor stroom: als er 6 ampère binnenkomt, moet er aan de andere kant ook 6 ampère uitgaan. De formele notatie van Kirchhoff is

∑j = Ij

Bij het toepassen van deze formule is de definitie van positief en negatief cruciaal. Alle inkomende stromen worden als positief beschouwd en uitgaande stromen als negatief. Door deze bij elkaar op te tellen moet de som nul zijn.

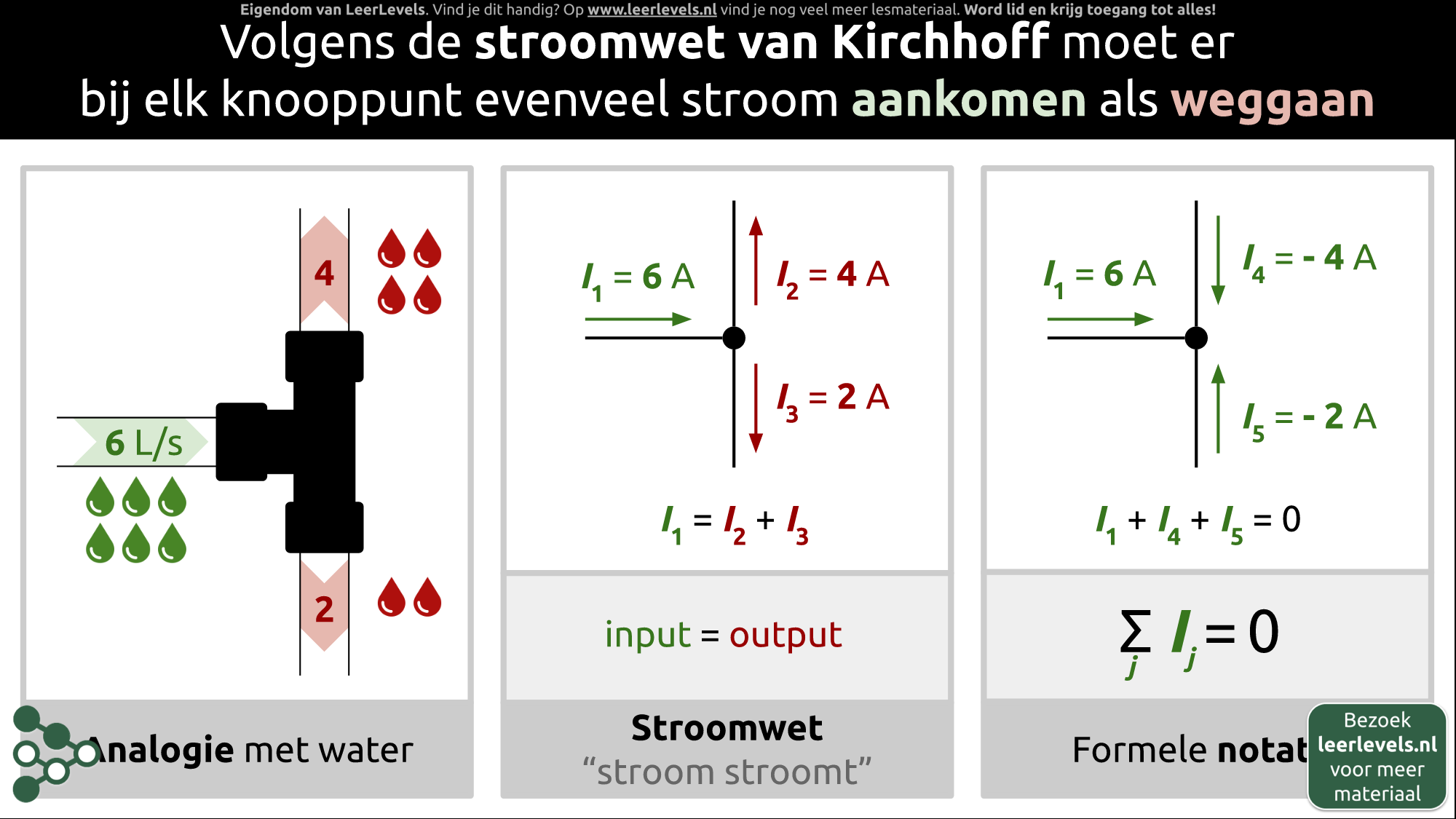
(Afbeelding: Animatie voor Stroomwet van Kirchhoff)

Spanningswet van Kirchhoff concept

In een elektrische schakeling moet de energie die erin gaat ook weer uitgaan, anders zou er steeds meer energie accumuleren. We kijken naar een schakeling met een batterij en een lampje als verbruiker. De stroom die door de schakeling loopt moet evenveel energie winnen als verliezen. Een voorbeeld: een schakeling met een spanning van 9 volt met een onbekende weerstand en een lampje. Als we een ronde doen met 1 coulomb stroom, krijgt deze 9 J energie van de batterij. Die ene coulomb moet ook weer 9 J kwijt, anders zou er energie accumuleren. Als de weerstanden 2 en 4 ohm zijn, verdeelt de spanning zich volgens de wet van Ohm. Het lampje heeft dan 6 V en de bovenste weerstand 3 V. Onze rondreizende coulomb geeft dan 3 J af bij de bovenste weerstand en de resterende 6 J bij het lampje. De energie neemt toe bij de batterij en af bij de weerstanden, omdat er niets anders dan energie-omzetting is in een gesloten stroomkring.

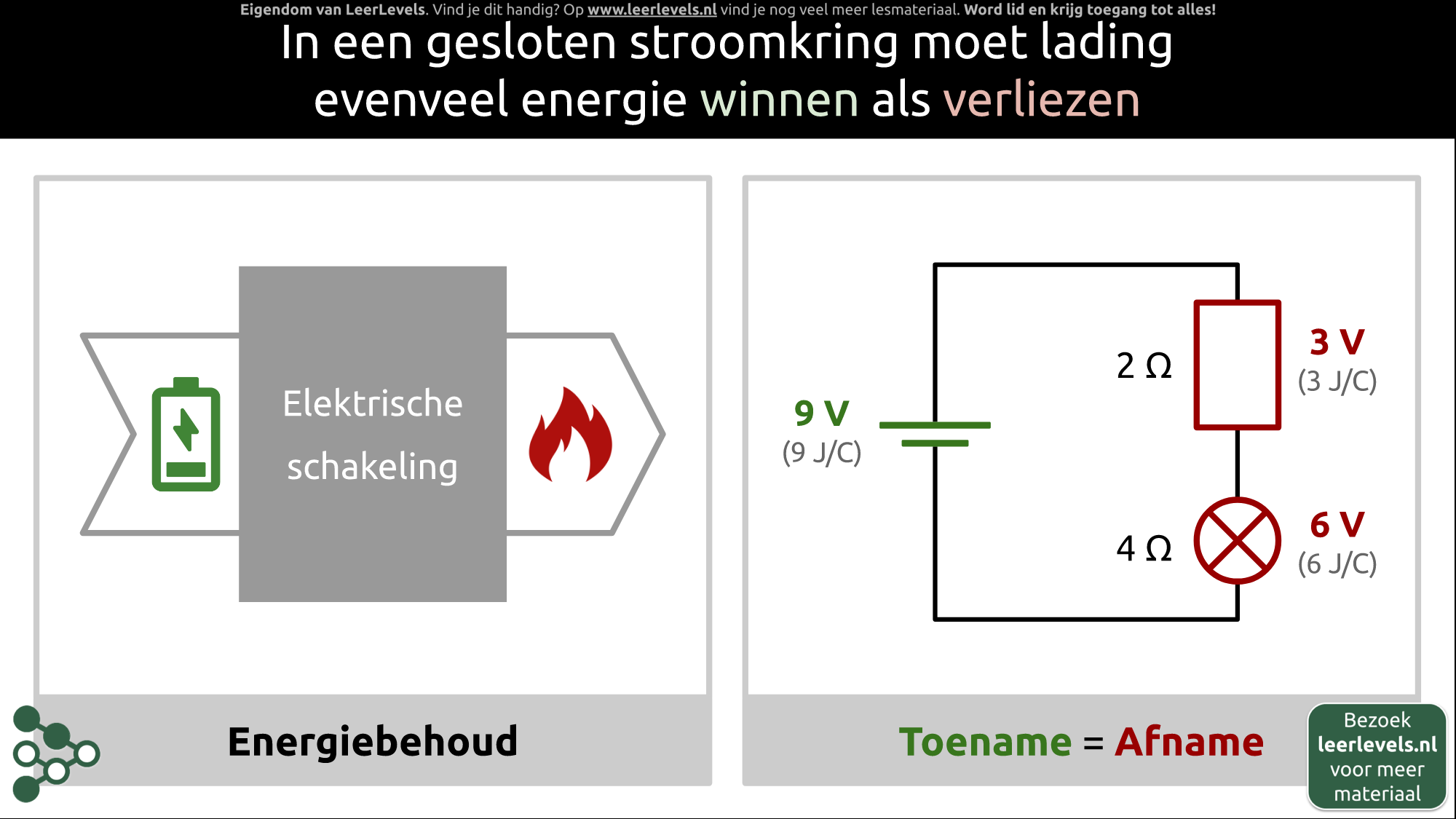
(Afbeelding: Animatie voor Spanningswet van Kirchhoff concept)

Spanningswet van Kirchhoff formule

De spanningswet van Kirchhoff zegt dat de totale spanningstoename in een gesloten stroomkring altijd nul is. Dit betekent dat als we de spanning van alle onderdelen in de stroomkring bij elkaar optellen, de uitkomst altijd nul moet zijn (∑ Ui = 0).

Om de spanning van een onderdeel te bepalen, moeten we weten of het een batterij of een weerstand is. Als we door een batterij heen gaan van min naar plus, krijgt de lading energie. De spanning van een batterij is daarom gelijk aan U0. Als de stroom de andere kant op gaat, verliest de lading energie en is de spanning dus -U0. Als we met de stroom mee door een weerstand gaan, neemt de energie per lading af. De spanning van een weerstand is dus -I× R, waarbij I staat voor de stroom en R voor de weerstandswaarde. Als we tegen de stroom in gaan, neemt de energie per lading juist toe en is de spanning + I× R.

Een handige manier om de spanningswet te onthouden is de uitspraak "Spanning fietst". Dit betekent dat na een rondje door de stroomkring de totale spanningstoename weer op nul uitkomt.

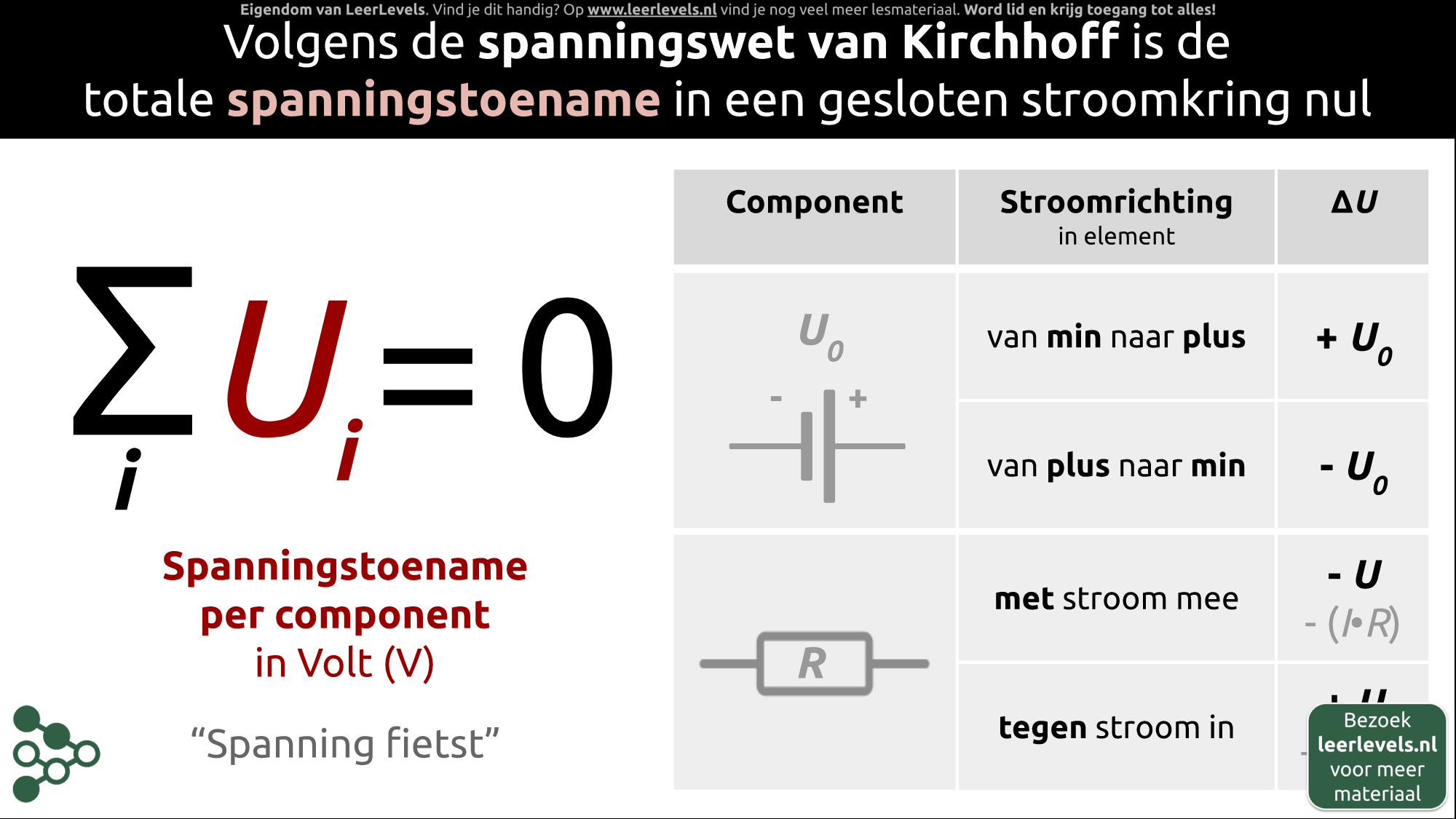
(Afbeelding: Animatie voor Spanningswet van Kirchhoff formule)

Spanningswet van Kirchhoff toepassen

Het toepassen van Kirchhoffs spanningswet verloopt in 6 stappen.

Stappenplan
1. Schets de schakeling
2. Teken of kies de stroomrichting
3. Vul gegevens in
4. Kies geschikte kring
5. Pas toe:

∑ Ui = 0

6. Los op voor de gevraagde variabele

Voorbeeld - Bereken R1

Gegeven:
- R3 = 12 Ω
- U0 = 6,0 V
- I3 = 0,80 A
- I2 = 1,1 A

Toepassen van Kirchhoffs spanningswet:

∑ Ui = 0

U1 - I1 · R1 + I2 · R2 = 0

I1 · R1 = I2 · R2 + U1

R1 = (I2 · R2 + U1)/(I1)

Invullen van de waarden:

R1 = (0,8 · 12 + 6)/(1,1)

R1 = 14,2 Ω

Afronden:

R1 = 14 Ω

Als R3 = 4 Ω, dan moet U0 = 17 V

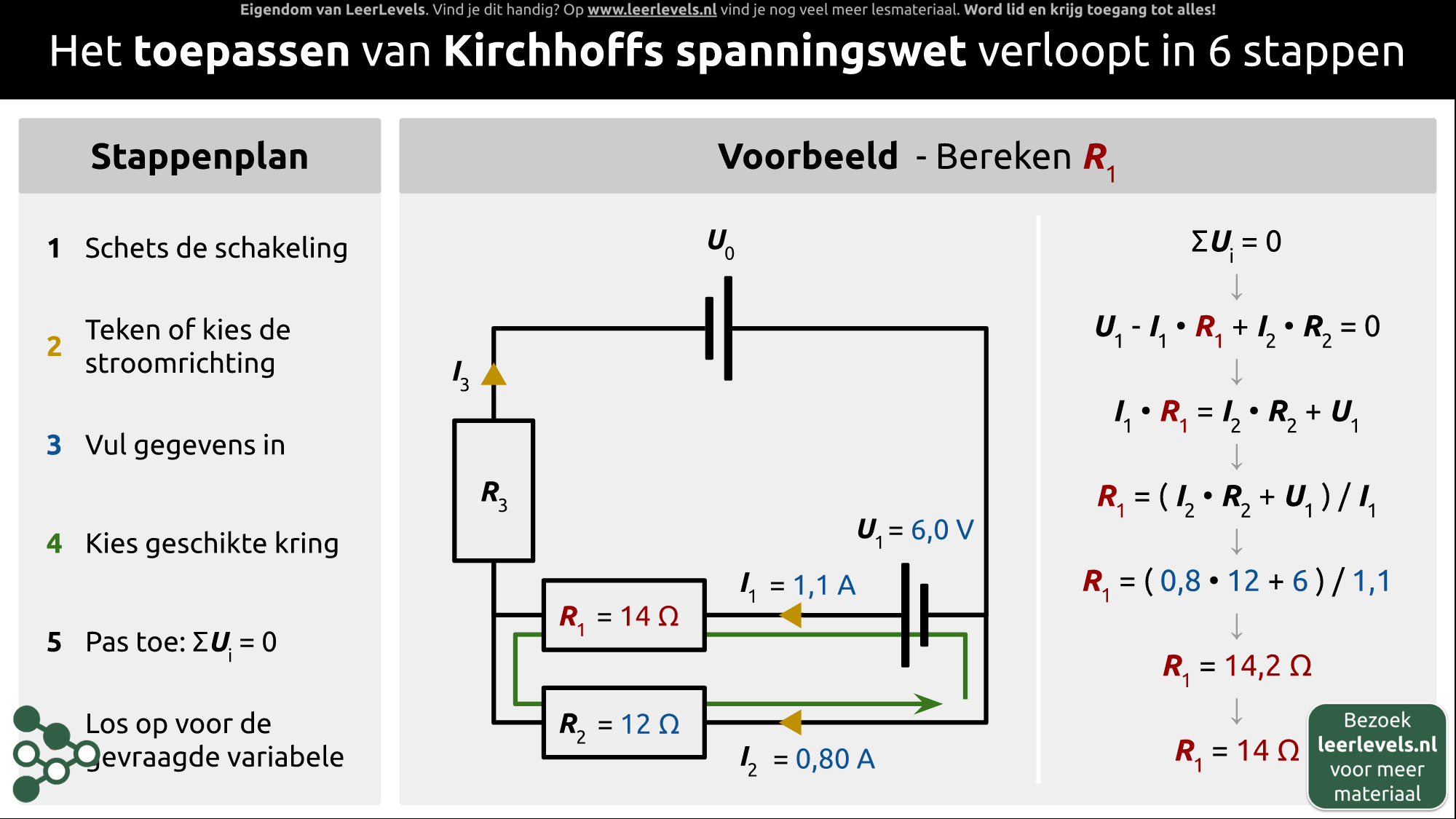
(Afbeelding: Animatie voor Spanningswet van Kirchhoff toepassen)

Terug naar overzicht Meld je aan

Wet van Ohm

Wet van Ohm concept

De Wet van Ohm beschrijft de relatie tussen de spanning, stroom en weerstand in een elektrisch circuit. Wanneer we een weerstand op een spanningsbron aansluiten met behulp van draden, zal er een elektrische stroom gaan vloeien. Hoe deze stroom afhangt van de gekozen spanning en weerstand, wordt als volgt verklaard:

Stel dat we een lage spanning toepassen, bijvoorbeeld met een enkele batterij, en een kleine weerstand gebruiken. In dit geval krijgen we een matige stroom. Als we de spanning verhogen, bijvoorbeeld door drie batterijen in serie te schakelen, wat gebeurt er dan met de stroom? Deze wordt groter. Meer specifiek, wanneer je de spanning drie keer zo groot maakt, zal de stroomsterkte ook drie keer zo groot worden.

In plaats van de spanning te wijzigen, kunnen we ook de weerstand verhogen. Weerstanden bestaan vaak uit een lange opgerolde draad. Een grotere weerstand kan dus gerealiseerd worden door de draad drie keer zo lang te maken. Wat gebeurt er dan met de stroom? Deze wordt kleiner. Bij een drie keer zo grote weerstand, wordt de stroom drie keer zo klein.

Wanneer we zowel de spanning als de weerstand vergroten, krijgen we opnieuw dezelfde matige stroom als waarmee we begonnen. Dit betekent dat een toename in spanning de stroom vergroot, terwijl een verhoging van de weerstand de stroom juist vermindert.

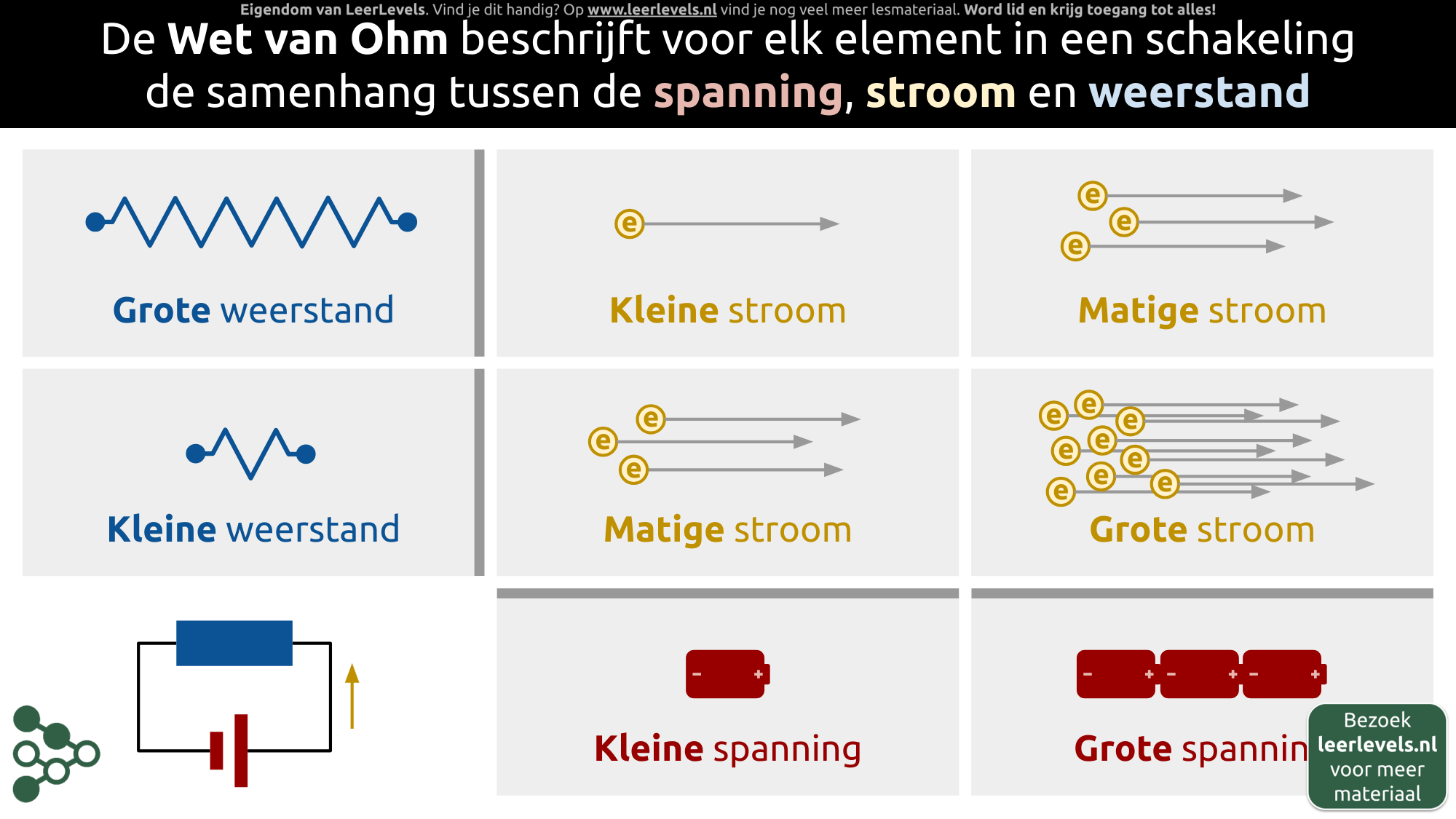
(Afbeelding: Animatie voor Wet van Ohm concept)

Wet van Ohm formule

Met de Wet van Ohm kun je de spanning, stroom of weerstand van een deel van een schakeling berekenen, mits je de andere twee waarden kent. Volgens de Wet van Ohm geldt: de stroomsterkte I is de spanning U gedeeld door de weerstand R. De formule is

U = I/R

Een grotere spanning resulteert in een grotere stroom. Daarom staat spanning U in de teller en weerstand R in de noemer. In deze formule staat I voor de stroomsterkte in ampère (A), U voor spanning in volt (V) en R voor weerstand in ohm (Ω).

De formule kan op twee andere manieren worden geschreven, die vaak voorkomen. Door beide kanten van de formule te vermenigvuldigen met R, krijg je

U = I · R

Dit kun je gemakkelijk onthouden met het ezelsbruggetje “uier”.

De tweede veelvoorkomende versie is

R = U/I

Dit is de officiële vorm van de Wet van Ohm. Afhankelijk van de beschikbare gegevens en de opdracht kun je zelf kiezen welke van de drie vormen je gebruikt.

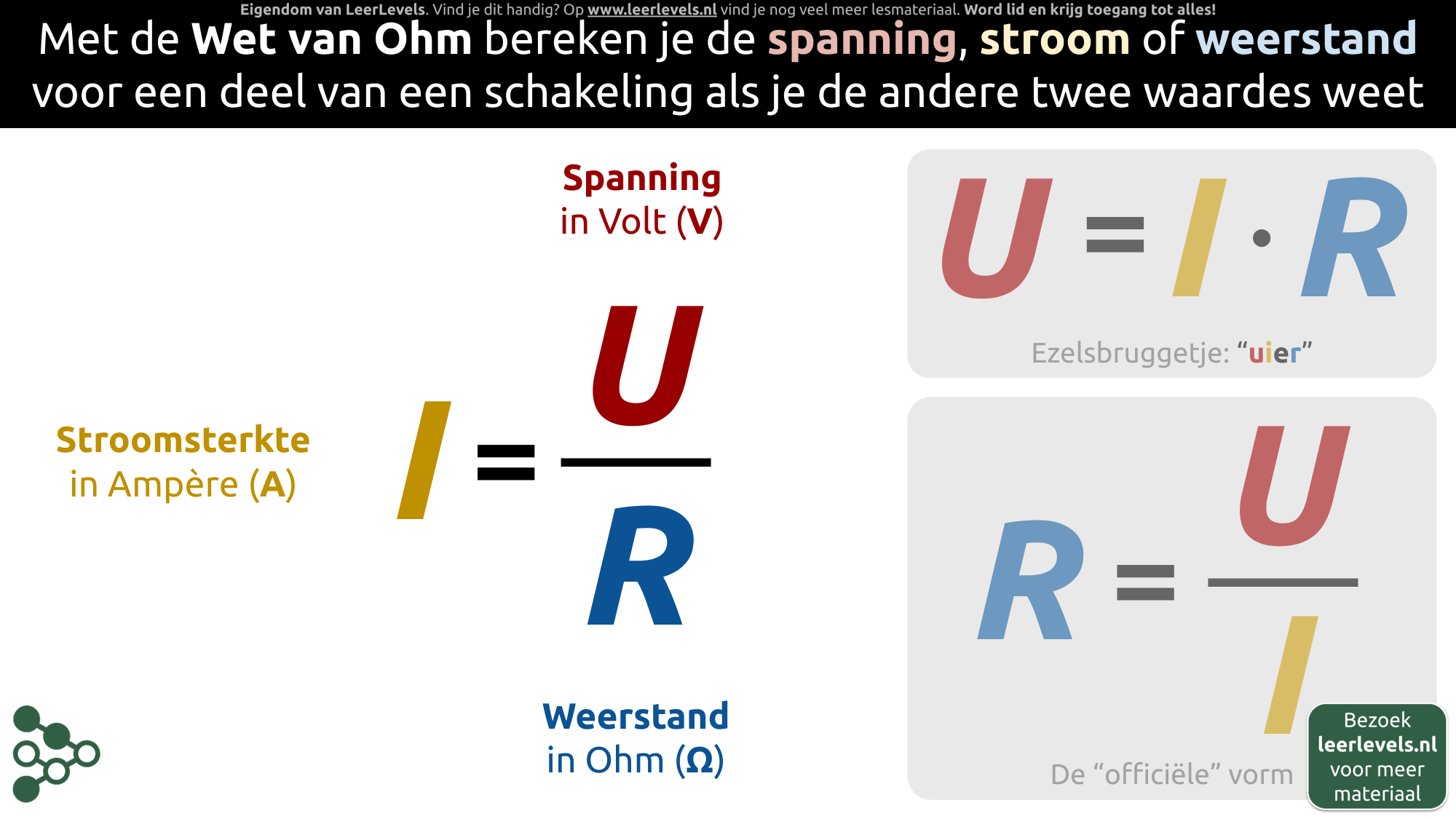
(Afbeelding: Animatie voor Wet van Ohm formule)

Terug naar overzicht Meld je aan

Wet van Stefan-Boltzmann

Wet van Stefan-Boltzmann concept

Volgens de wet van Stefan-Boltzmann is het stralingsvermogen van een voorwerp sterk afhankelijk van de temperatuur. Neem bijvoorbeeld een gloeilamp: bij normale temperatuur straalt de lamp een bepaald vermogen uit. Wanneer we de lamp uitzetten en laten afkoelen tot kamertemperatuur, zendt deze nog steeds een klein beetje vermogen uit, maar dit is minimaal. Wordt de temperatuur verhoogd, bijvoorbeeld door de lamp weer aan te zetten, dan neemt het uitgestraalde vermogen sterk toe. Bij hogere temperaturen kan dit vermogen zelfs enorm worden. Als je het stralingsvermogen plaatst tegenover de temperatuur, zie je dat het vermogen exponentieel toeneemt met de temperatuur, tot zelfs de vierde macht. Dit illustreert dat volgens de wet van Stefan-Boltzmann het stralingsvermogen van een voorwerp sterk afhankelijk is van de temperatuur.

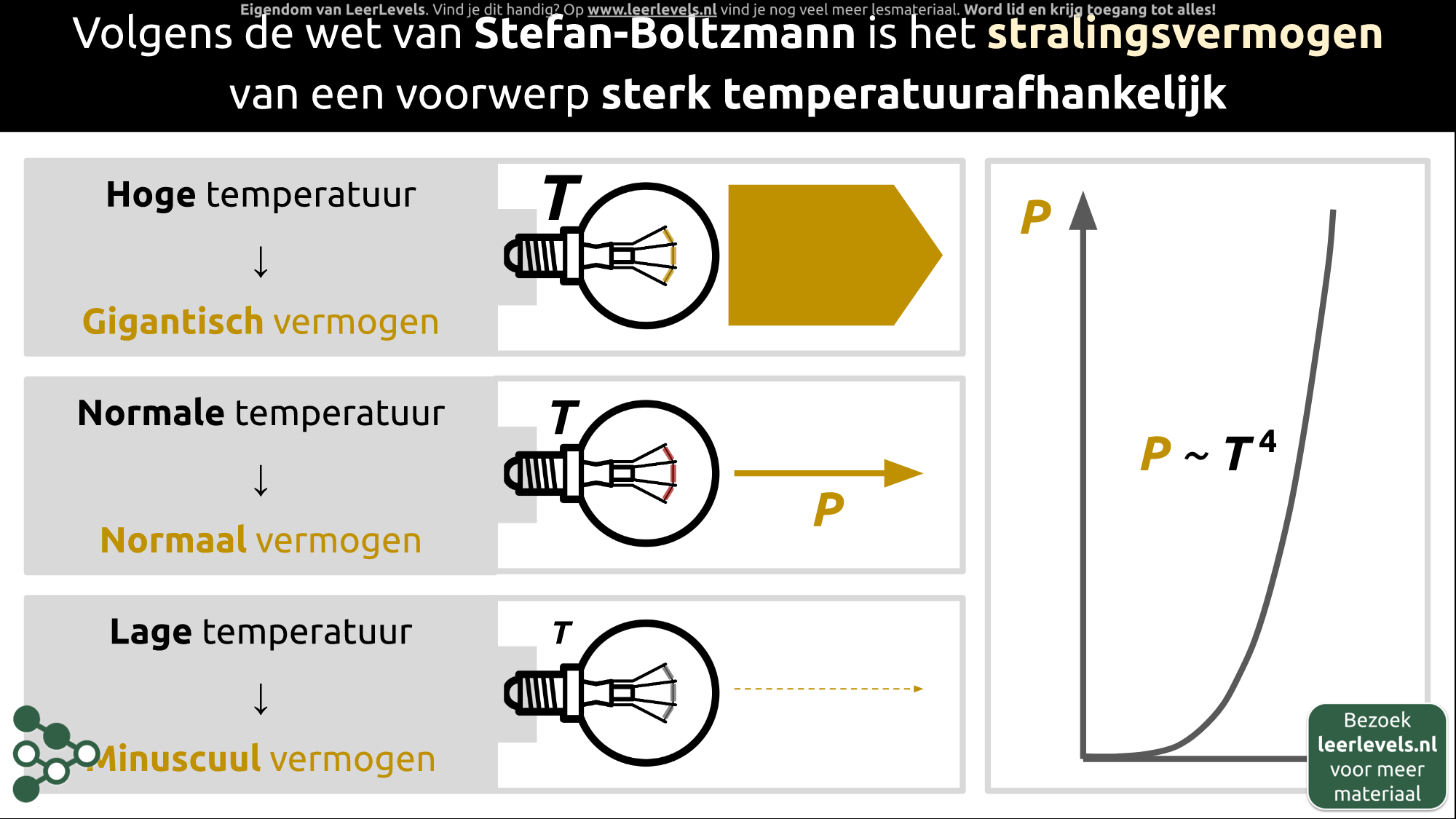
(Afbeelding: Animatie voor Wet van Stefan-Boltzmann concept)

Wet van Stefan-Boltzmann formule

De wet van Stefan-Boltzmann zegt dat hoe hoger de temperatuur is, hoe meer warmte een object uitstraalt. Dit wordt berekend met de formule P = σ A T⁴, waarbij P het uitgestraalde vermogen in watt is, A het oppervlak in vierkante meter is, T de temperatuur in Kelvin is en σ de constante van Stefan-Boltzmann is met een waarde van 5,670 x 10⁻⁸ W/(m² · K⁴). Het belangrijkste om te onthouden is dat als de temperatuur van een object verdubbelt, het uitgestraalde vermogen 16 keer zo groot wordt, omdat de temperatuur tot de vierde macht in de formule staat.

(Afbeelding: Animatie voor Wet van Stefan-Boltzmann formule)

Terug naar overzicht Meld je aan

Wet van Wien

Wet van Wien concept

De wet van Wien zegt dat de kleur van licht afhankelijk is van de temperatuur van de lichtbron. Dit komt doordat de golflengte waarop het meeste licht uitgezonden wordt, verschilt per temperatuur. Het menselijk oog kan alleen licht zien met golflengtes tussen 400 en 700 nanometer (nm).

Als we kijken naar voorwerpen met verschillende temperaturen, zoals 4000 K, 5000 K en 6000 K, dan zien we dat de golflengte waarop de meeste licht uitgezonden wordt, verschilt. Bij een lage temperatuur is de kleur van het licht meer rood, terwijl het licht bij een hoge temperatuur meer blauw is. De wet van Wien beschrijft de precieze relatie tussen de temperatuur van de lichtbron en de golflengte waarop het licht het meeste wordt uitgezonden. Deze relatie is weergegeven in een grafiek die gestippeld is.

Belangrijkste begrippen: wet van Wien, golflengte, temperatuur, Planckcurve, spectrum.

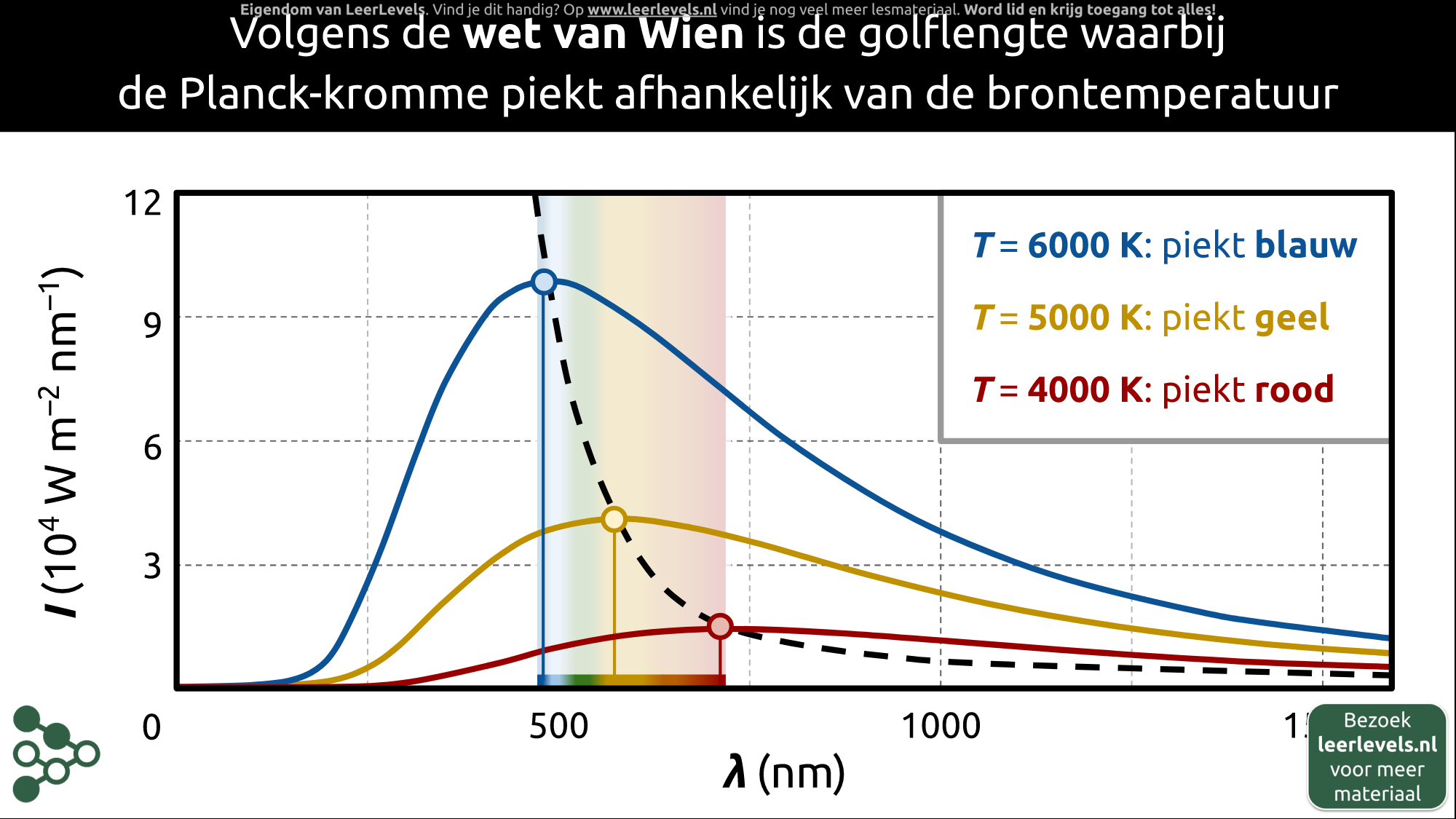
(Afbeelding: Animatie voor Wet van Wien concept)

Wet van Wien formule

Volgens de wet van Wien is de golflengte waarbij de Planck-kromme een piek bereikt, omgekeerd evenredig met de temperatuur van de bron. In formulevorm ziet dit er zo uit:

λmax = (kw)/(T)

Hierin is λmax de golflengte waarbij het object de maximale intensiteit uitstraalt, kw de constante van Wien, en T de temperatuur van de bron in kelvin. De constante van Wien is 2,89777 × 10⁻³ Km.

(Afbeelding: Animatie voor Wet van Wien formule)

Terug naar overzicht Meld je aan

Wetenschappelijke notatie

Rekenen met voorvoegsels en wetenschappelijke notatie

Voor voorvoegsels en de wetenschappelijke notatie gelden dezelfde rekenregels als voor normale getallen.

Bijvoorbeeld: 1 km is gelijk aan 1 × 10³ m, wat gelijk is aan 1 × 1000 m.

Je mag voorvoegsels bij elkaar optellen. Bijvoorbeeld:

7 × 10⁴ + 2 × 10⁴ = (7 + 2) × 10⁴ = 9 × 10⁴.

Je mag voorvoegsels ook van elkaar aftrekken. Bijvoorbeeld:

2 × 10² - 5 × 10¹.

De voorvoegsels zijn niet hetzelfde, maar we kunnen een gemeenschappelijke factor buiten haakjes halen. We krijgen:

(2 × 10¹ - 5) × 10¹ = 25 × 10¹.

Je kunt voorvoegsels met elkaar vermenigvuldigen. Bijvoorbeeld, het voorvoegsel kilo (k) met zichzelf vermenigvuldigen geeft:

k × k = M.

Omdat k = 10³ en M = 10⁶. Tot slot kun je voorvoegsels door elkaar delen, bijvoorbeeld:

G/M = k,

omdat G = 10⁹ en M = 10⁶.

(Afbeelding: Animatie voor Rekenen met voorvoegsels en wetenschappelijke notatie)

Wetenschappelijke notatie concept

De wetenschappelijke notatie wordt gebruikt om grote of kleine getallen makkelijker weer te geven. Bijvoorbeeld, het getal 365,000 kan geschreven worden als 3,65 keer 100,000 of als 3,65 maal 10 tot de 5e macht. Het lijkt misschien moeilijk, maar het is vaak makkelijker. Een ander voorbeeld is 0,000 000 19, wat geschreven kan worden als 1,9 keer 10 tot de -7e macht. De wetenschappelijke notatie bestaat uit een klein getal, het grondtal 10 en een exponent (dat zowel positief als negatief kan zijn). Het grondtal 10 kan worden geschreven als E of EXP op een rekenmachine.

(Afbeelding: Animatie voor Wetenschappelijke notatie concept)

Terug naar overzicht Meld je aan

Wortelverband

Een wortelverband is een verband waarbij als één grootheid verviervoudigt, de andere grootheid verdubbelt. Dit wordt weergegeven in de formule y = a√(n). Een voorbeeld hiervan is de eindsnelheid van een valbeweging, die gelijk is aan een constante keer de wortel van de hoogte. Het wortelteken heeft een aparte vorm en gaat niet asymptotisch naar een eindsnelheid toe. Het blijft altijd groter dan wat het zou moeten zijn, wat kenmerkend is voor een wortelverband. Het kan soms lastig zijn om een wortelverband te onderscheiden van een recht evenredig verband, tenzij je veel metingen hebt voor kleine waardes van x (of in dit geval, kleine waardes van de hoogte). Zorg dat je uiteenlopende waardes hebt om te zien wat er gebeurt.

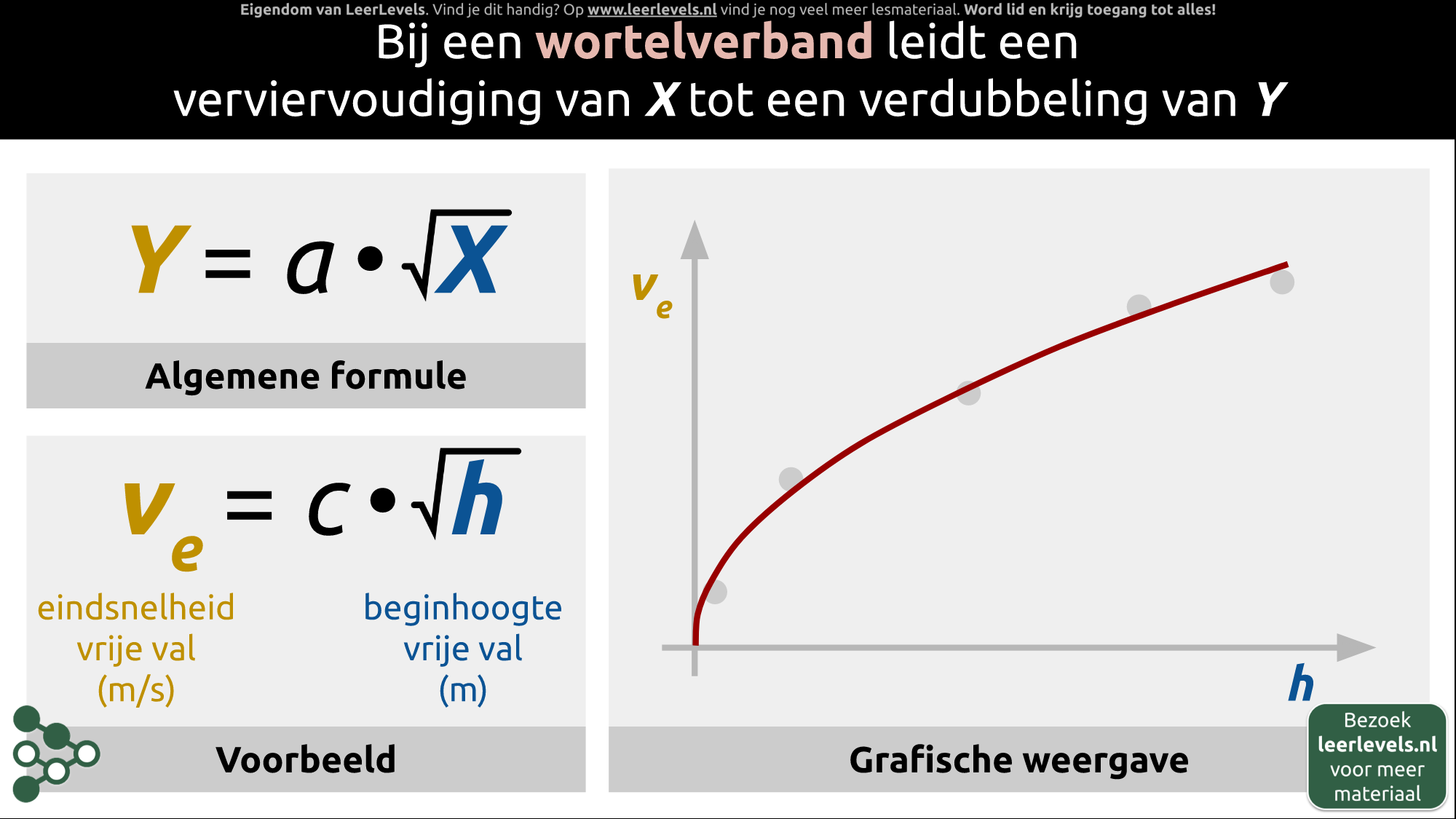
(Afbeelding: Animatie voor Wortelverband)

Terug naar overzicht Meld je aan

Wrijving

Schuifwrijving concept

Schuifwrijving is een kracht die ontstaat als voorwerpen langs elkaar schuiven. Bijvoorbeeld als je op schaatsen op het ijs staat. Als de schaatsen stil staan is er geen schuifwrijving, maar zodra je gaat bewegen ontstaat er schuifwrijving. Schaatsen hebben een lage schuifwrijving, wat zorgt dat het schaatsen heel makkelijk gaat. Normale schoenen hebben meer schuifwrijving op het ijs, en schoenen met punten hebben nog meer schuifwrijving. Als twee voorwerpen makkelijk langs elkaar kunnen schuiven, is de schuifwrijving laag. Maar als de schuifwrijving groter is, dan is ook de kracht die ze op elkaar uitoefenen groter.

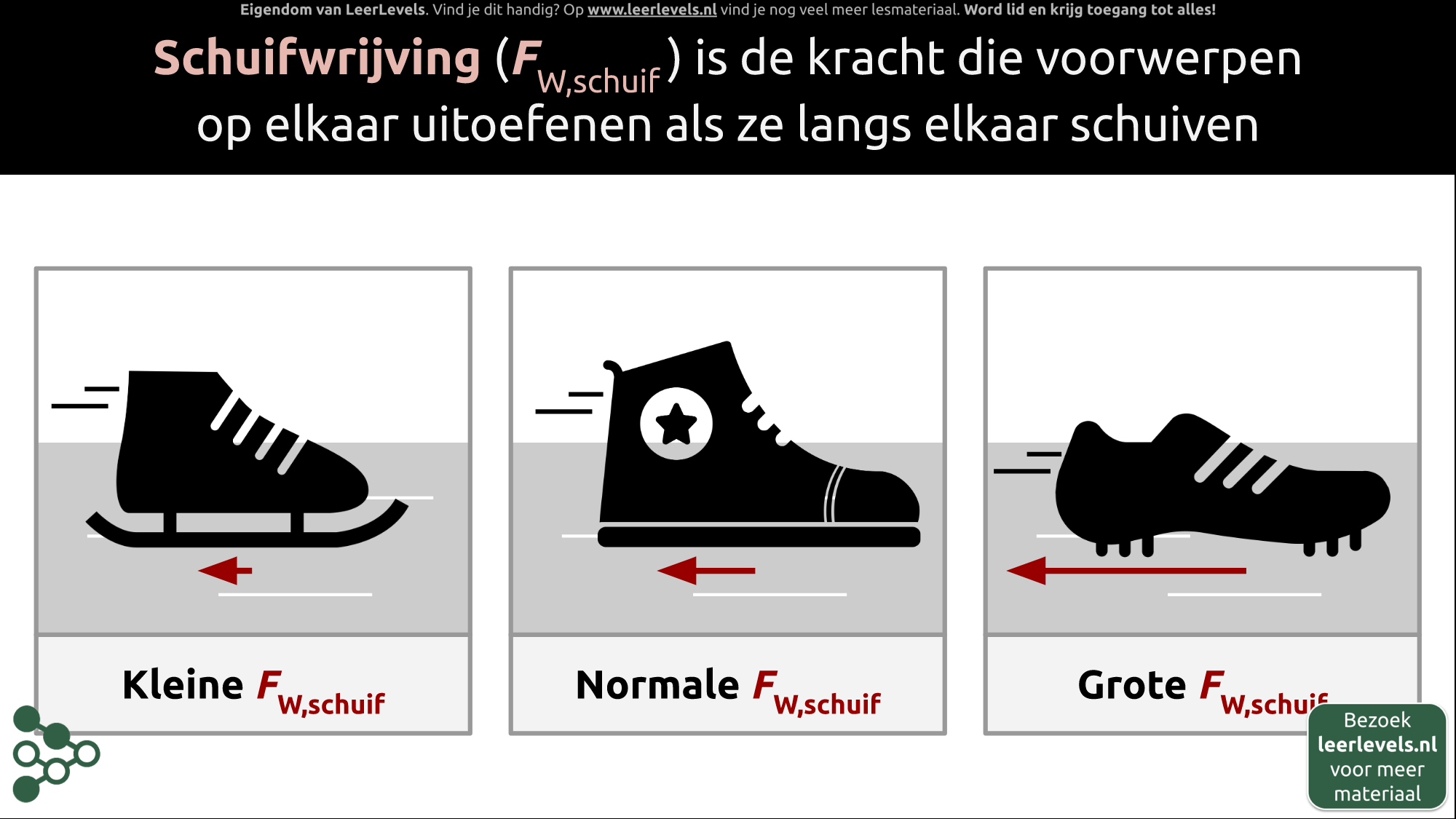
(Afbeelding: Animatie voor Schuifwrijving concept)

Terug naar overzicht Meld je aan

Wrijvingskracht

Statische en dynamische wrijvingskracht

Als je iets duwt of trekt, kan er wrijving ontstaan tussen de oppervlakken die tegen elkaar wrijven. Als de voorwerpen stilstaan, heet dit statische wrijving en is er geen kracht. Maar als je iets gaat duwen, komt er op een gegeven moment een maximale kracht die je kunt uitoefenen voordat het voorwerp begint te bewegen. Dit heet de maximale statische wrijvingskracht (Fw,s,max). Als je harder duwt dan deze maximale kracht, begint het voorwerp te bewegen en verandert de wrijvingskracht in dynamische wrijving (Fw,d). Deze dynamische wrijvingskracht heeft een constante waarde en is niet afhankelijk van hoe hard je duwt. Als je het voorwerp stopt met duwen, zal het langzaam tot stilstand komen door deze dynamische wrijvingskracht.

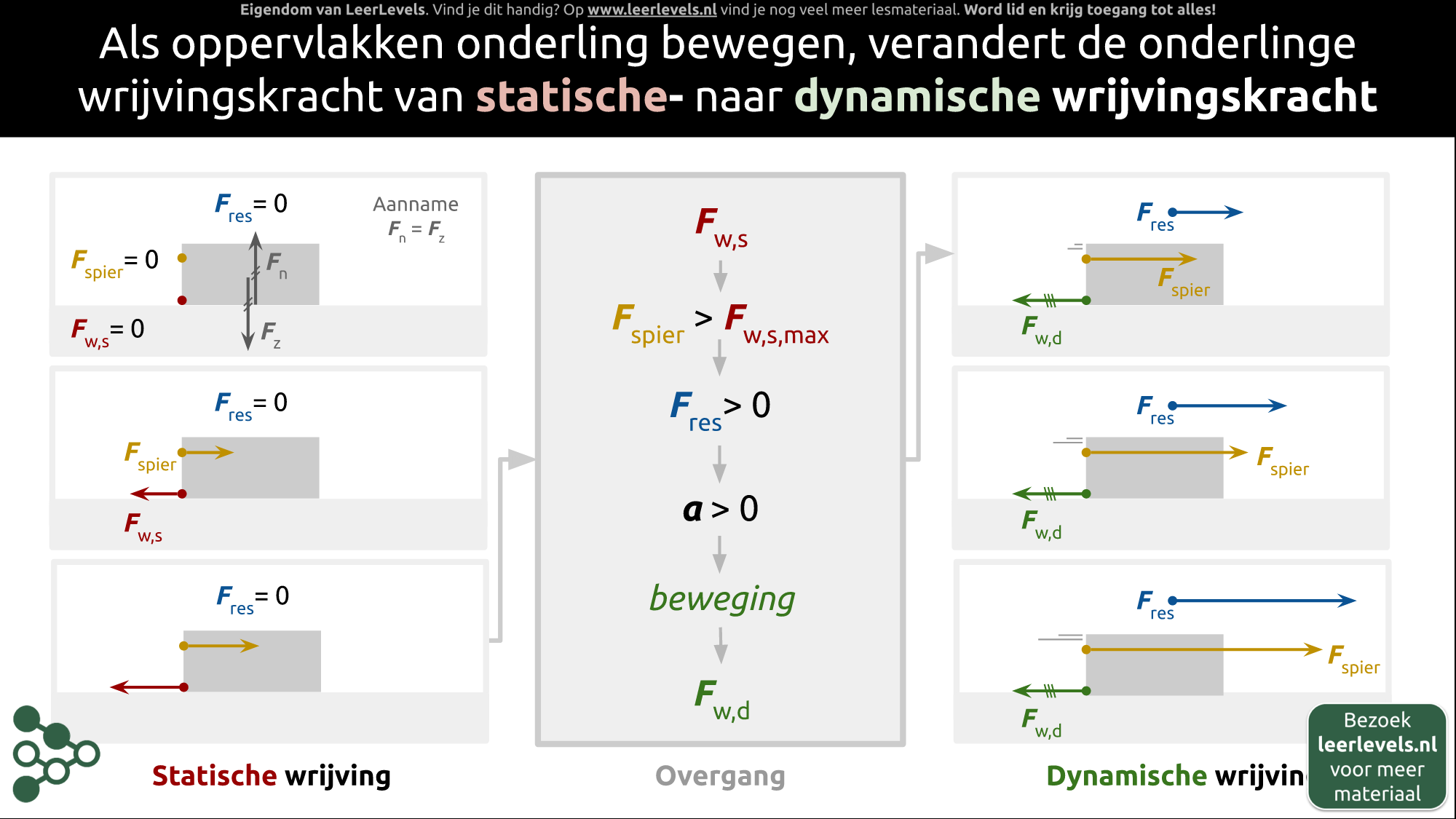
(Afbeelding: Animatie voor Statische en dynamische wrijvingskracht)

Wrijvingskracht formules

Wanneer twee oppervlakken langs elkaar wrijven, hangt de wrijvingskracht af van drie dingen: de wrijvingscoëfficiënt (een getal dat aangeeft hoe glad of ruw de oppervlakken zijn), de snelheid waarmee de oppervlakken langs elkaar bewegen en de kracht waarmee ze elkaar raken. Als de oppervlakken stil liggen, heet dit statische wrijving en is de maximale wrijvingskracht altijd kleiner of gelijk aan het product van de kracht waarmee de oppervlakken elkaar raken en de statische wrijvingscoëfficiënt. Als de oppervlakken wel bewegen, heet dit dynamische wrijving en is de wrijvingskracht gelijk aan het product van de kracht waarmee de oppervlakken elkaar raken en de dynamische wrijvingscoëfficiënt, die anders kan zijn dan de statische wrijvingscoëfficiënt. Het kan moeilijker zijn om iets in beweging te krijgen dan om het in beweging te houden, afhankelijk van welke wrijvingscoëfficiënt van toepassing is.

(Afbeelding: Animatie voor Wrijvingskracht formules)

Terug naar overzicht Meld je aan

Zicht

Dieren kunnen zien doordat voorwerpen licht uitzenden of weerkaatsen en ogen dat licht vervolgens opvangen. Het licht wordt weerkaatst door een voorwerp en het oog absorbeert dat licht. Achterin het oog bevinden zich kleine zenuwen, kegeltjes en staafjes genoemd, die het licht detecteren. De kegeltjes werken goed in daglicht en kunnen kleuren onderscheiden. De staafjes werken beter in het donker en leveren grijstinten op. Het oog stuurt het signaal van het opgevangen licht via zenuwen naar de hersenen. In de hersenen wordt het signaal omgezet in een beeld. Dit is wat we zien.

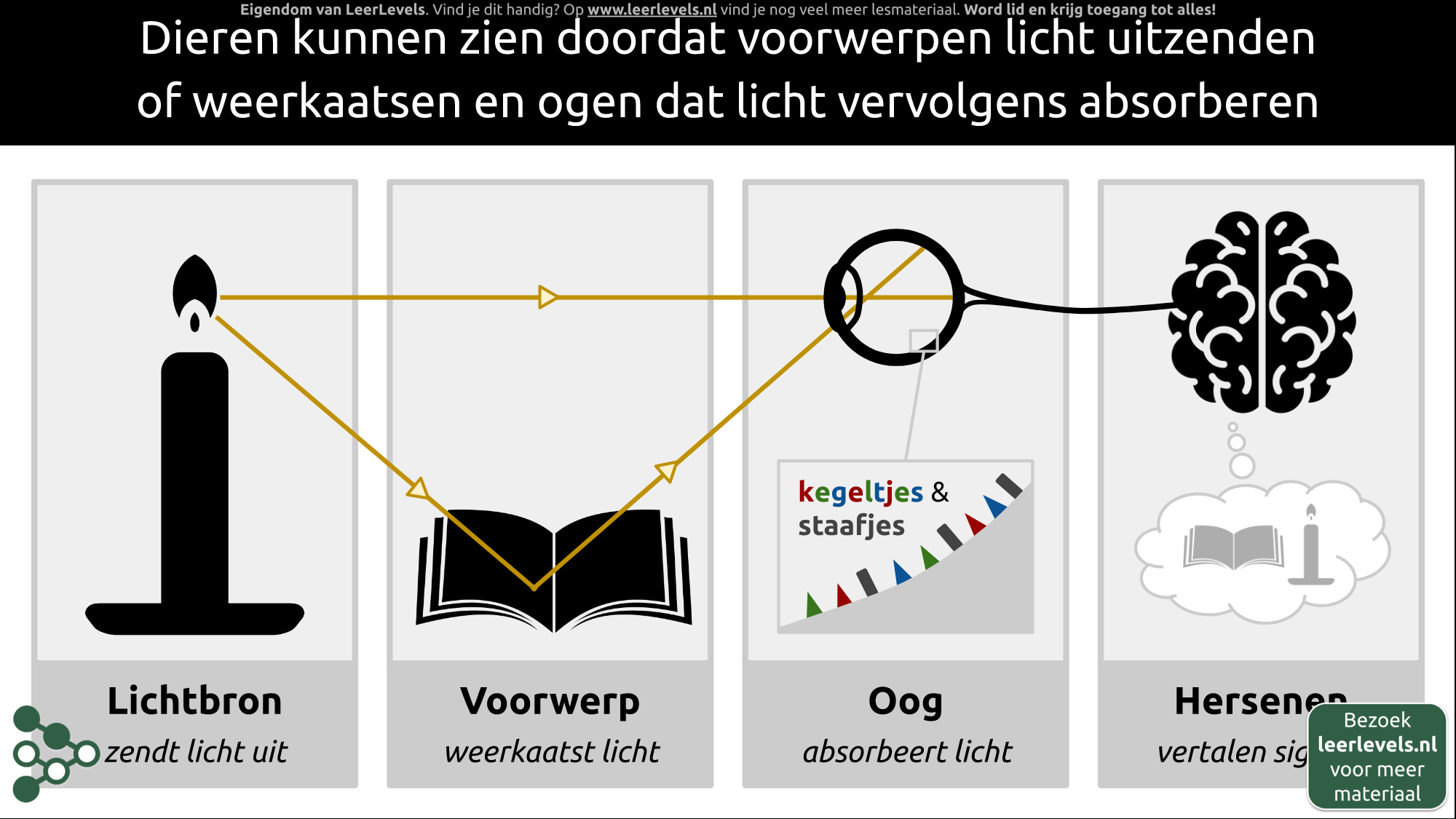
(Afbeelding: Animatie voor Zicht)

Terug naar overzicht Meld je aan

Zon

Levensloop zon

Wanneer het waterstof in de zon opraakt, volgt de zon een voorspelbaar pad in het Hertzsprung-Russell-diagram. De zon begint in het midden rechts. Zodra het waterstof in de kern volledig is omgezet in onder andere helium, blijft er minder massa in de kern over, wat leidt tot het uitzetten van de buitenste laag. Dit komt omdat er minder massa in het centrum is. Door deze uitbreiding daalt de effectieve temperatuur, aangezien de buitenste laag verder van de kern af staat. Omdat de ster groter wordt, kan zij over een veel groter oppervlak energie uitstralen. Hierdoor neemt de lichtkracht netto toe. Wegens de exacte evenwichten vertoont deze rode lijn een slingerbeweging. Naarmate de stralingsdruk door afnemende fusie afneemt, overwint de zwaartekracht de stralingsdruk, waardoor de ster krimpt. De straal verkleint, en omdat de buitenkant nu warmer wordt, stijgt de effectieve temperatuur van de ster. Wanneer de fusie uiteindelijk volledig stopt, vermindert de lichtkracht en daalt de effectieve temperatuur, waardoor de ster naar rechtsonder verschuift. Hoewel de exacte levensloop van sterren complexer is dan hier beschreven, is dit in hoofdzaak wat er met de zon zal gebeuren.

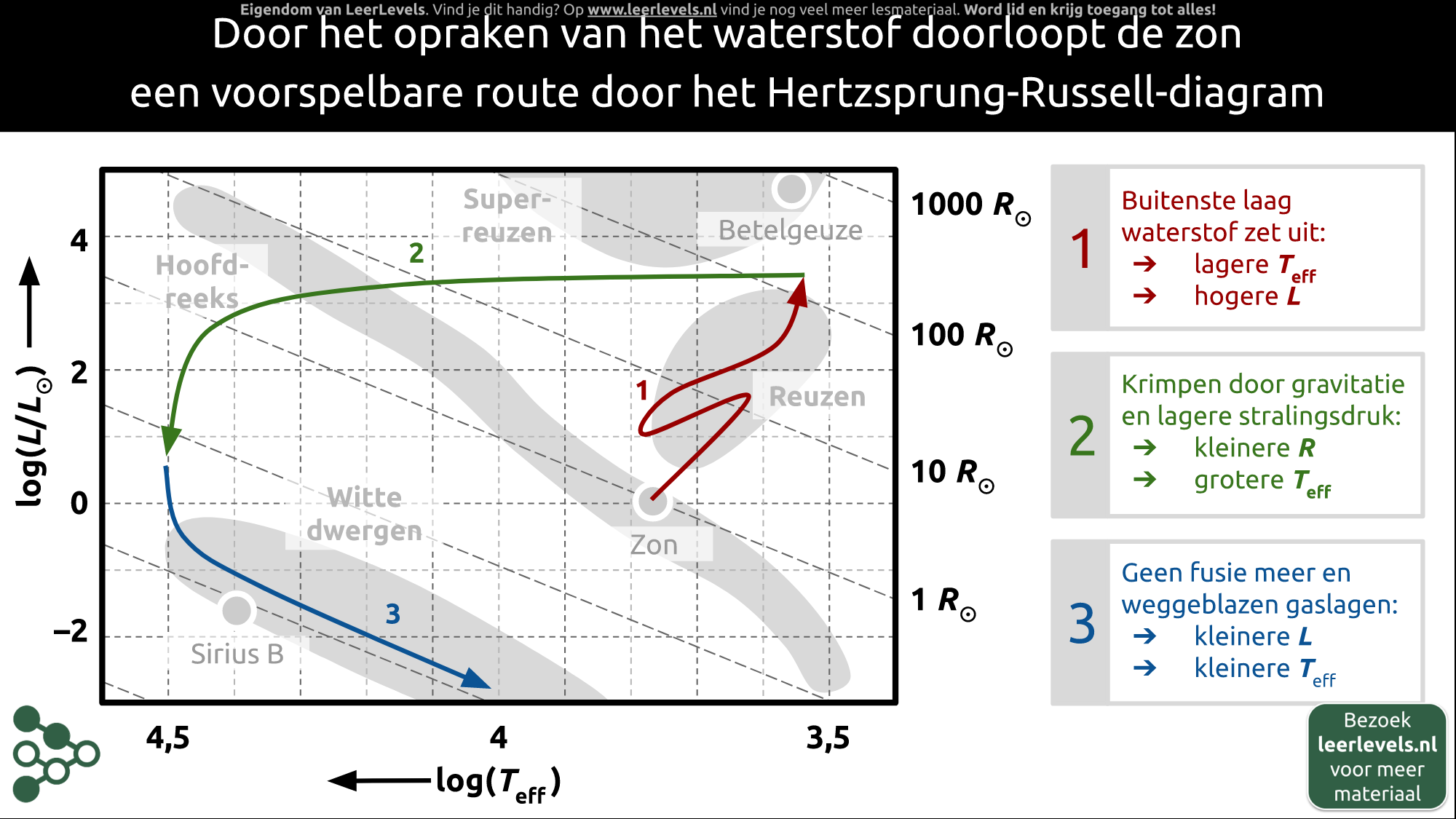
(Afbeelding: Animatie voor Levensloop zon)

Terug naar overzicht Meld je aan

Zonneconstante

De zonneconstante is de gemiddelde intensiteit van het zonlicht net buiten onze atmosfeer. Ongeveer de helft daarvan bereikt Nederland.

Laten we de zon en de aarde nader bekijken. De zon straalt een totaal vermogen uit van 3,85 × 10²⁶ W. Je kunt je afvragen hoeveel daarvan de aarde bereikt en met welke intensiteit. Om dit te berekenen, moet je weten over welk oppervlak het vermogen van de zon zich verspreidt tegen de tijd dat het licht de aarde bereikt. De bijbehorende bol heeft een straal van 1 astronomische eenheid. Het oppervlak van een bol is 4 π r², wat resulteert in 2,81 × 10²³ m². De intensiteit bij de aarde wordt dan berekend met:

I = (Pzon)/(Abol) = 1,4 × 10³ W/m²

Deze 1,4 × 10³ W/m² wordt ook wel de zonneconstante genoemd. Dit is de intensiteit van het zonlicht buiten onze atmosfeer. Wil je weten hoeveel daarvan het oppervlak in Nederland bereikt, dan moet je rekening houden met wat er in de atmosfeer gebeurt. Het gaat niet alleen om wolken, maar ook om de atmosfeer zelf. In de atmosfeer bevinden zich moleculen die ons beschermen tegen bijvoorbeeld een overschot aan UV-straling. Daarnaast vindt er ook reflectie plaats. Het resultaat is dat ongeveer de helft van deze intensiteit door de atmosfeer gaat, wat neerkomt op ongeveer 7,0 × 10² W/m². Dit is de intensiteit overdag als het niet bewolkt is. Als je het effect van nachten en bewolking meeneemt, blijkt dat we gemiddeld slechts ongeveer 1,0 × 10² W/m² overhouden. Dit getal is relevant als je wilt inschatten wat de opbrengst van zonnepanelen op jaarbasis is.

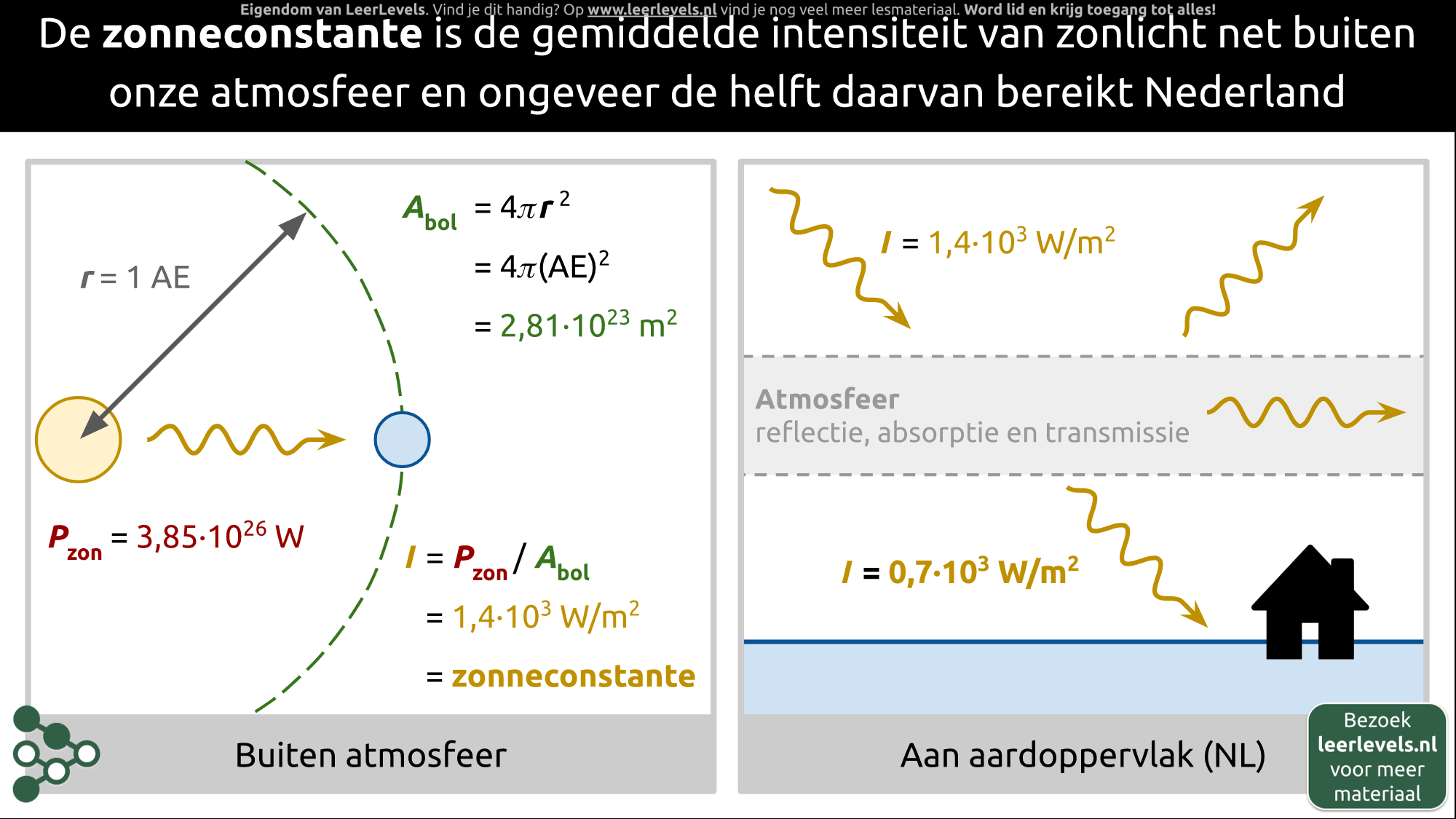
(Afbeelding: Animatie voor Zonneconstante)

Terug naar overzicht Meld je aan

Zonnestelsel

In ons zonnestelsel draait naast de zon nog acht planeten, manen en een planetoïdengordel. Deze informatie is te vinden in tabel 31 van het boek Binas. De eerste vier planeten gezien vanaf de zon zijn Mercurius, Venus, Aarde en Mars en worden rotsplaneten genoemd. De grootte van de planeten in de tabel is op schaal, maar de afstanden tussen de planeten en de zon zijn dat niet. De volgende twee planeten - Jupiter en Saturnus - zijn gasreuzen, en Uranus en Neptunus worden ijsreuzen genoemd. Sommige planeten hebben manen, zoals onze eigen maan en Jupiters maan Europa waar mogelijk leven is geweest. Er is ook een planetoïdengordel tussen Mars en Jupiter die bestaat uit rotsblokken van verschillende grootte.

(Afbeelding: Animatie voor Zonnestelsel)

Terug naar overzicht Meld je aan

Zuivere stoffen

Zuivere stoffen en mengsels

Alle materie kan worden ingedeeld in twee categorieën: zuivere stoffen en mengsels. Bij een zuivere stof bestaat de materie uit één soort atomen of moleculen, zoals goud of suiker. Goud bestaat bijvoorbeeld alleen uit goudatomen en suiker bestaat uit glucosemoleculen. Mengsels zijn combinaties van verschillende stoffen, zoals lucht met allerlei verschillende soorten moleculen en water met opgeloste stoffen. In een mengsel zijn verschillende soorten atomen of moleculen aanwezig. Formules, grootheden en eenheden worden niet gebruikt in deze uitleg.

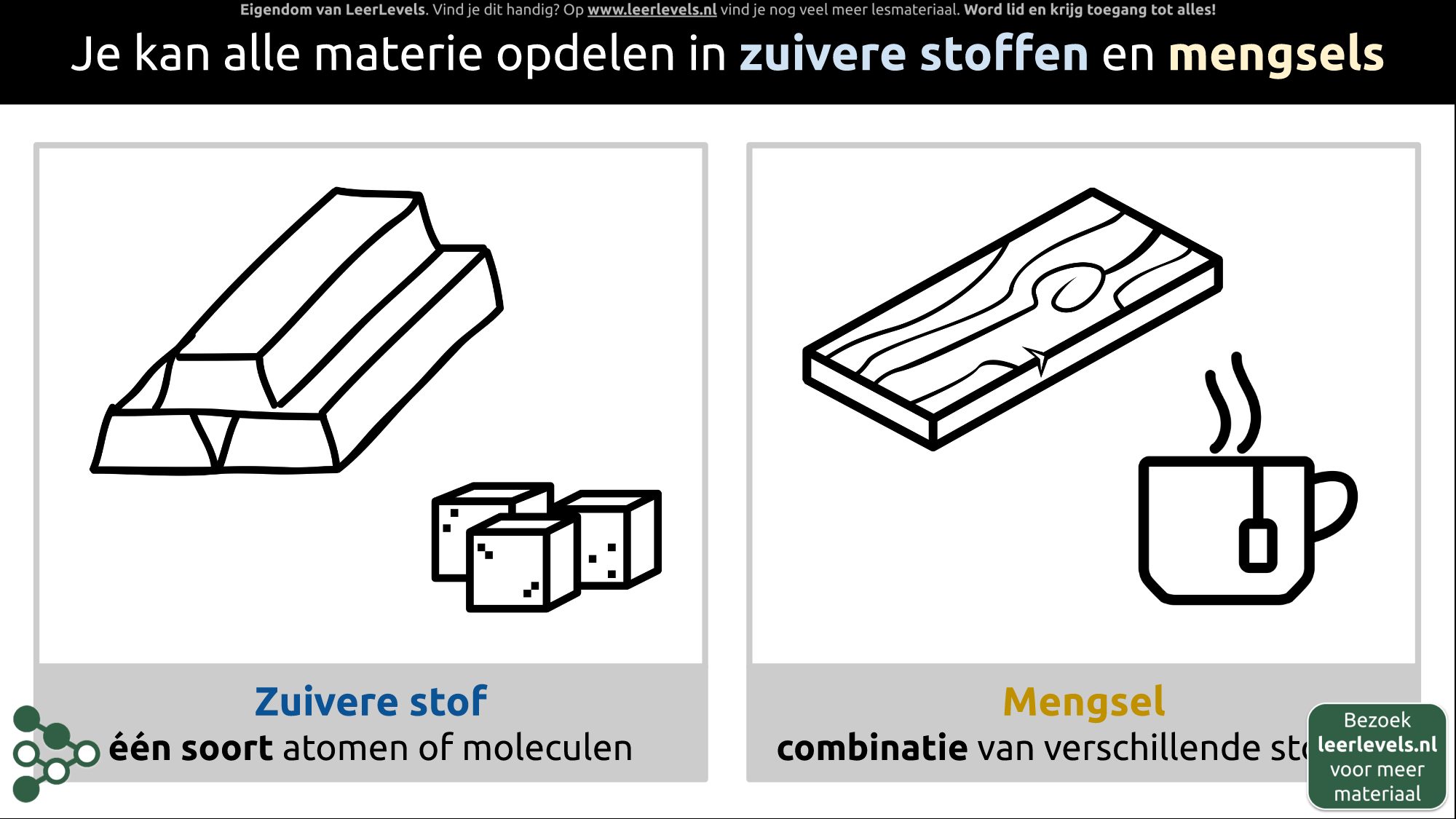
(Afbeelding: Animatie voor Zuivere stoffen en mengsels)

Terug naar overzicht Meld je aan

Zwaarte-energie

Zwaarte-energie concept

Een voorwerp heeft zwaarte-energie wanneer het de potentie heeft om naar beneden te vallen.Een voorwerp dat op de grond ligt, heeft geen hoogte en kan daardoor niet naar beneden vallen. Het bezit daarom geen zwaarte-energie. Als je een voorwerp in je hand houdt, heeft het wel een hoogte en kan het naar beneden vallen, waardoor het zwaarte-energie heeft. Omdat de hoogte van een voorwerp in je hand relatief klein is, is de zwaarte-energie van dit voorwerp ook klein. Een voorwerp op grotere hoogte heeft een grotere zwaarte-energie, omdat het een grotere potentie heeft om naar beneden te vallen.

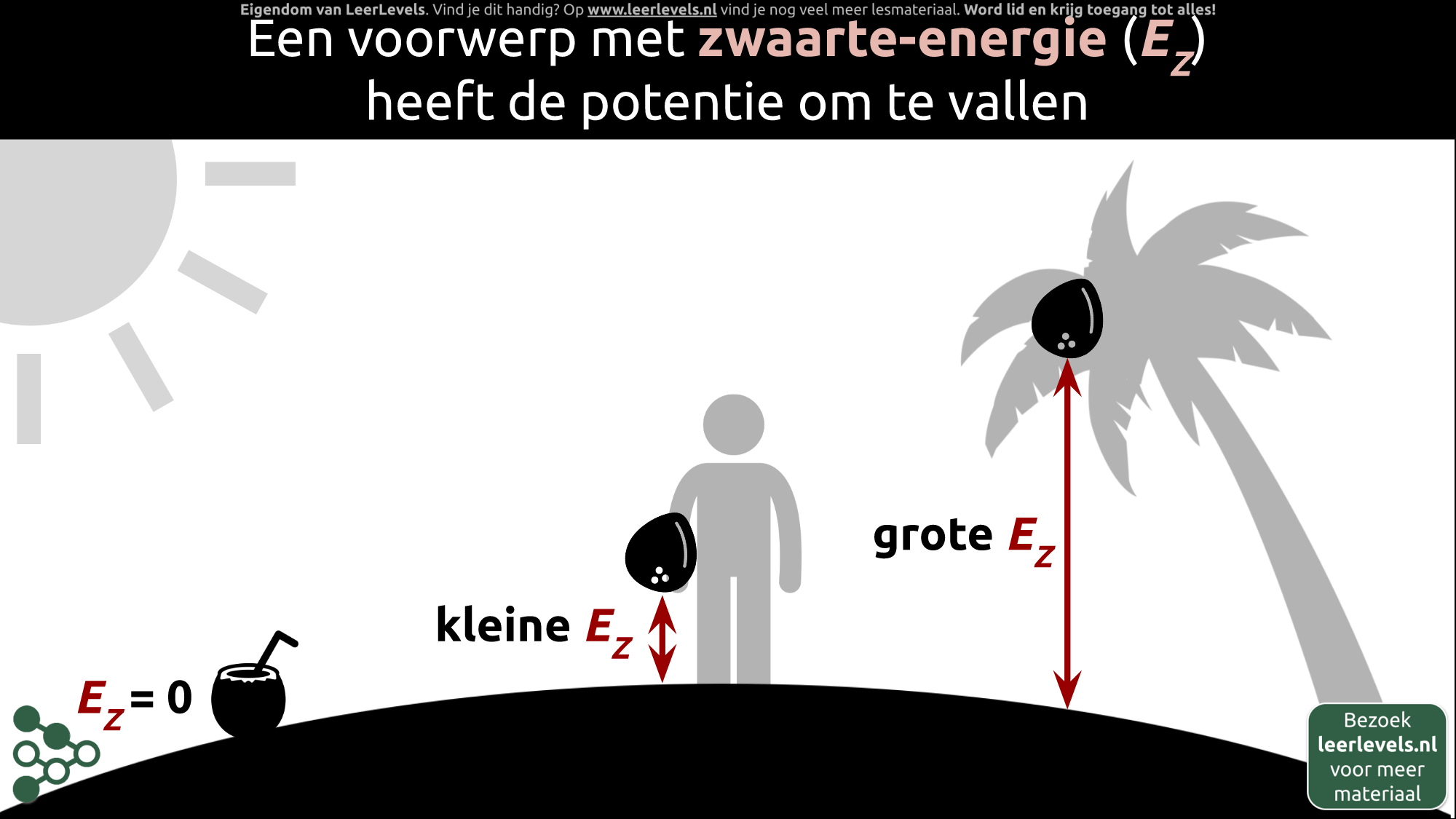
(Afbeelding: Animatie voor Zwaarte-energie concept)

Zwaarte-energie formule

De zwaarte-energie van een voorwerp hangt af van de massa, de valversnelling en de hoogte. Dit kan worden weergegeven met de formule:

Ez = m · g · h

Hierbij is Ez de zwaarte-energie in joule, m de massa in kilogram, g de valversnelling en h de hoogte in meters. Vaak werken we met verandering van de zwaarte-energie. In dat geval gebruiken we het verschil in hoogte.

(Afbeelding: Animatie voor Zwaarte-energie formule)

Terug naar overzicht Meld je aan

Zwaartekracht

Zwaartekracht formule

De zwaartekracht op een voorwerp hangt af van twee dingen: hoe zwaar het voorwerp is en hoe sterk de zwaartekracht trekt. Dit kan worden uitgedrukt met een formule: Fz = m x g. In deze formule is Fz de kracht in newton (N), m de massa in kilogram (kg) en g de zwaartekrachtsversnelling in meter per seconde kwadraat (m/s²). Op aarde is de zwaartekrachtsversnelling g gelijk aan 9,81 m/s². Met deze formule kun je berekenen hoeveel zwaartekracht er op een voorwerp werkt.

(Afbeelding: Animatie voor Zwaartekracht formule)

Terug naar overzicht Meld je aan

Zwaartepunt

Zwaartepunt uitleggen

Als je een voorwerp ophangt zodat het kan draaien, zal het zwaartepunt altijd onder het ophangpunt liggen. Als je het ophangt via het zwaartepunt, dan zal het niet draaien. Als je het ophangt aan een spijker, zal het draaien zodat het zwaartepunt onder de spijker komt. Bij symmetrische voorwerpen zit het zwaartepunt in het midden en zal het stabiel hangen. Onregelmatig gevormde voorwerpen kunnen lastiger zijn omdat het gewicht niet gelijk verdeeld is. Om het zwaartepunt te vinden kan je het voorwerp op verschillende punten ophangen en kijken waar het stabiel hangt.

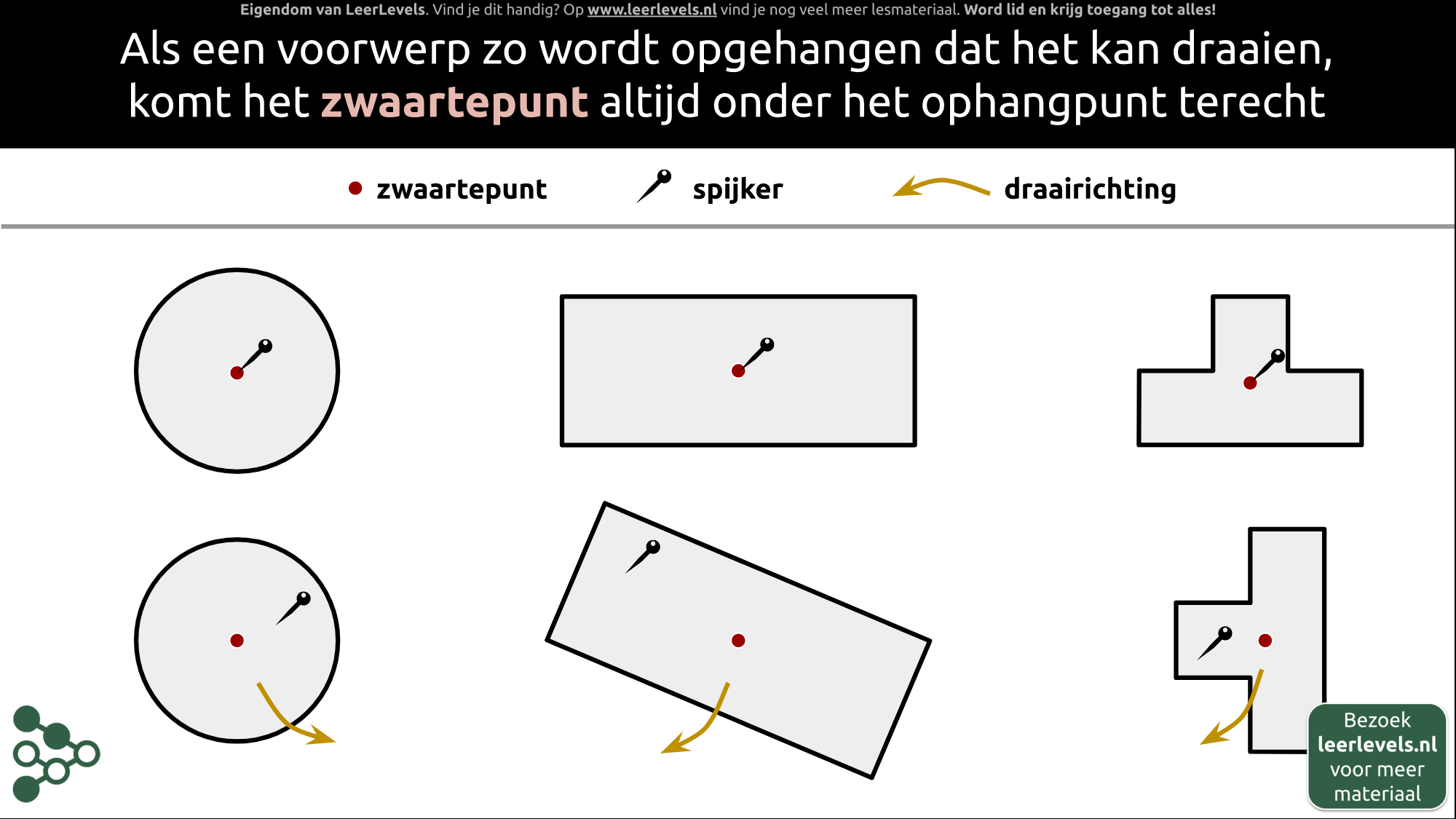
(Afbeelding: Animatie voor Zwaartepunt uitleggen)

Terug naar overzicht Meld je aan

Zwarte straler

Zwarte straler concept

Een zwarte straler kan alle kleuren licht absorberen en uitzenden. Een wit object reflecteert alle kleuren en heeft bij een bepaalde temperatuur geen emissie. Een geel object heeft selectieve absorptie en absorbeert alleen rood en blauw, waardoor we het als geel waarnemen. Een zwarte straler kan alle mogelijke overgangen absorberen en alle kleuren licht uitzenden als het wordt opgewarmd. Bijvoorbeeld, een gloeilamp is eerst zwart als het uit staat, maar geeft alle kleuren licht als het wordt opgewarmd.

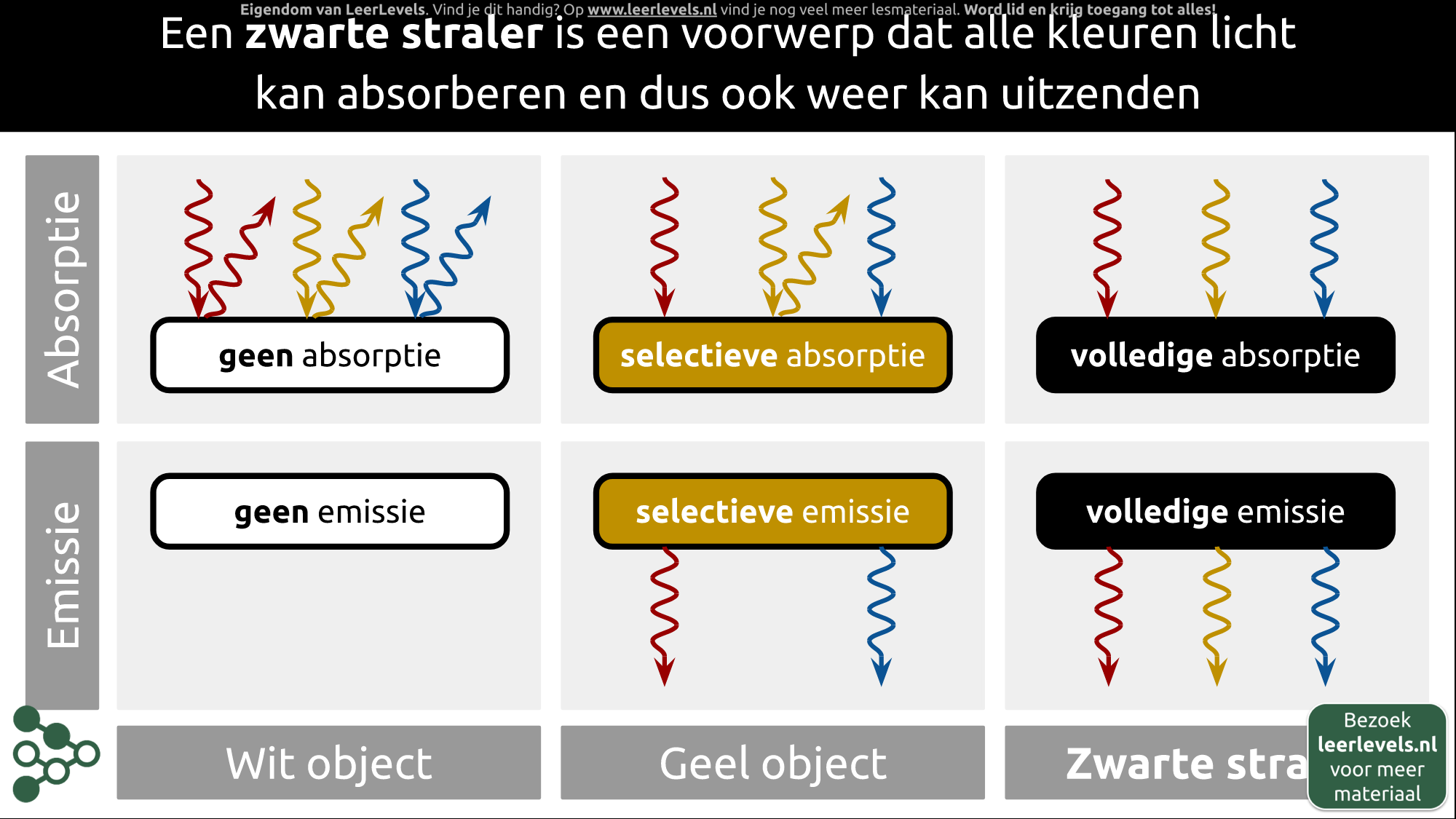
(Afbeelding: Animatie voor Zwarte straler concept)

Terug naar overzicht Meld je aan